Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: gordonm888Quote: avianrandyNot really a math problem but involves numbers. How many times does the word one appear on the current one dollar bill?
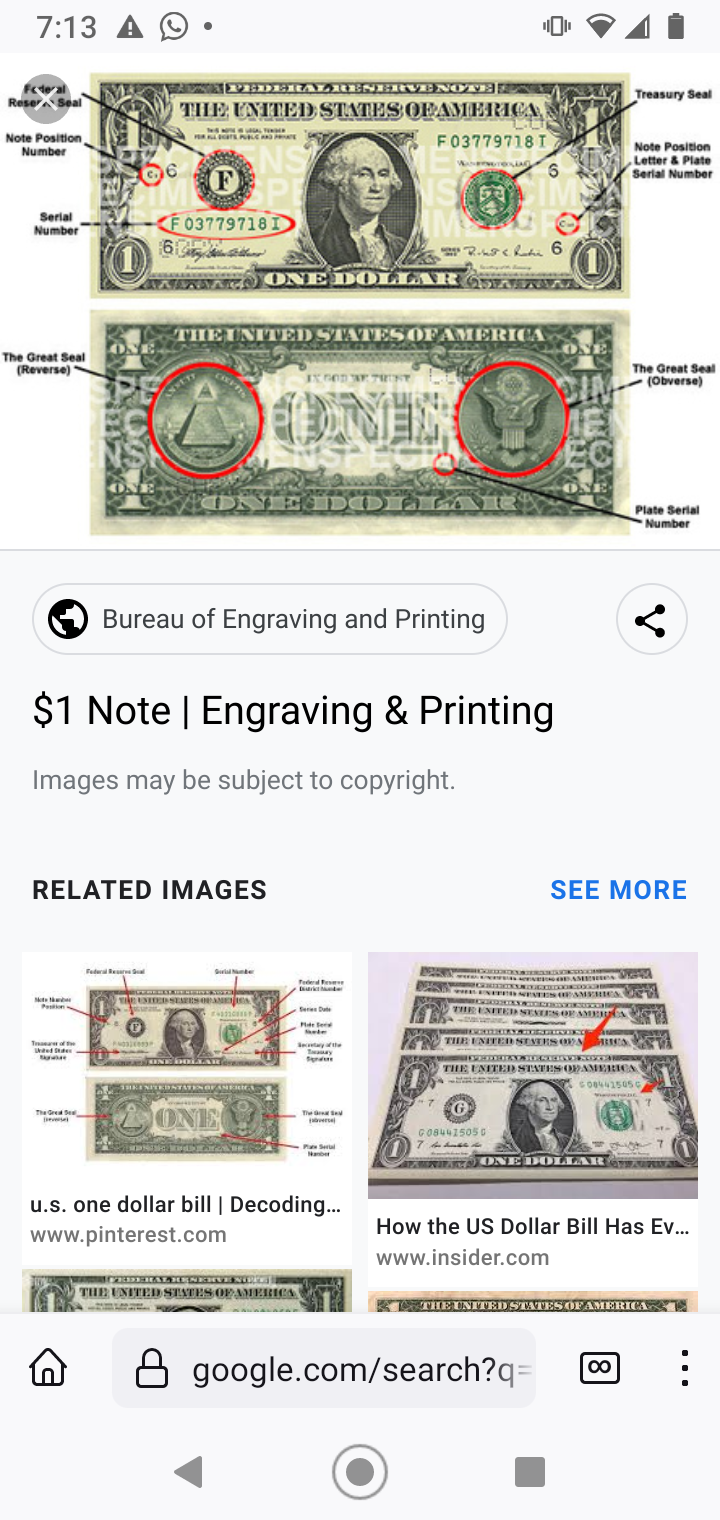
link to original post
It appears to be six times on the back of the one dollar bill and another, 7th, time on the front of the bill.
One might claim the word 'ONE' actually appears a 2nd time on the front of the bill. On the top of the front of the bill are the words:FEDERAL RESERVE NOTE
which does contain the word ONE displayed backwards.
link to original post[/qtwice on the front once under Washington picture and also a one covered up by the green seal
that was the answer I came up withQuote: charliepatrickMy $1 are quite old (Series 1999 etc) and I notice they have different cities. Personally I can see six on the back and two on the front. Also there would be the possibility of the characters in the three names (City, Treasurer, Secretary).
link to original post
The words "e pluribus unum" appear on the seal on the back of the bill. Unum translates to one.


On its March 1961 cover, MAD Magazine pointed out that 1961 was the first “upside-up” year — the first year that reads the same upside down — since 1881. Assume it is 1961 and your new copy of Mad gets you thinking.
When will the next upside-up year occur?

A kazoo costs $1 plus half its price.
How much does it cost?
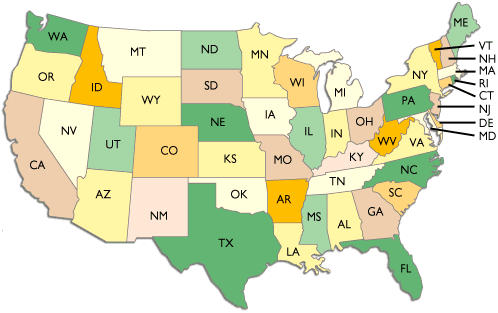
John lives in an East Coast state and Mary in a West Coast state. During a phone conversation one night, they realize that it is the same time in both locations.
How can this be?

You’re new to hell, and you’re given a choice: You can go directly to the fourth circle and suffer minor agony for 1000 years, or you can play simultaneous chess games against Alexander Alekhine and Aron Nimzowitsch. Alekhine always plays black and smokes a pipe of brimstone. Nimzowitsch plays white and wears cufflinks made of human teeth. Neither has ever lost.
If you can manage even a draw against either player, you’ll be set free. But if they both beat you, you’ll go to the eighth circle and suffer intense agony for eternity.
What should you do?
btw typical Bank Hoiday weather here, short birst of hail with some thunder mid afternoon!
My final idea for the minute is it's such a long phone call that they've both seen the same time (e.g. 12noon-3pm, and 9am-12noon).
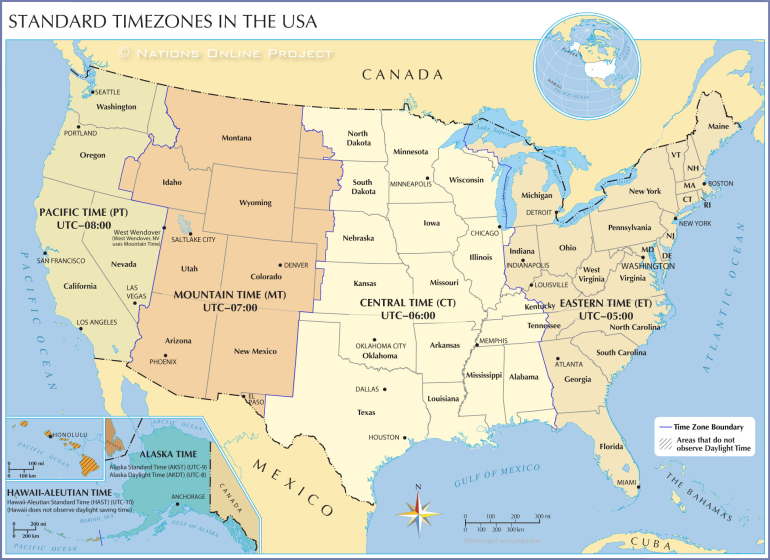 Perhaps I should have remembered my round trip from Reno to Jackpot and Ely!
Perhaps I should have remembered my round trip from Reno to Jackpot and Ely!After Nimzowitsch makes his move as White, I will make the same move against Alekhine. When Alekhine, playing Black, responds to my move as White, I make the identical response against Nimzowitsch. I continue in this same manner, never making my own moves at all, but repeating the moves of my opponents. In effect, they are playing each other.
If Nimzowitsch beats me as White, I will do so against Alekhine. If Alekhine beats me as Black, I will win against Nimzowitsch. And of course, both games could end up a draw.
Quote: Gialmere
On its March 1961 cover, MAD Magazine pointed out that 1961 was the first “upside-up” year — the first year that reads the same upside down — since 1881. Assume it is 1961 and your new copy of Mad gets you thinking.
When will the next upside-up year occur?
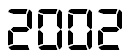
It really depends on the font, doesn't it? :)
Quote:
John lives in an East Coast state and Mary in a West Coast state. During a phone conversation one night, they realize that it is the same time in both locations.
How can this be?
Now, it just so happens that it is the end of Daylight Savings Time, and John has just turned his clock back from 2:00 to 1:00. So for that hour, Mountain and Central Time Zones have the same time.
It can't start with a 2, 3, 4, or 5, so it has to be at least 6000; the next one is 6009
Let p be the price: p = 1 + 1/2 p, so the price is $2
One is in Pensacola, FL, which is in the Central time zone, and the other is in Ontario, OR, which, mainly because of its proximity to Boise, is in the Mountain time zone.
At 2 AM CST on the third Sunday in March, the clocks are turned back in the Central time zone one hour, so one minute later, it is 1:01 CDT in Pensacola and 1:01 MST in Ontario.
Let Nimzowich move first, then just copy Nimzowich's moves against Alekhine and copy Alekhine's moves against Nimzowich. The two games are the same, except that you are white in one and black in the other. Either you will win one and lose one, or draw both.
Simple. They are next door neighbors in Fairbanks, Alaska
One lives in a “west coast” state and the other lives in an “east coast” state. This is possible since AK is the northernmost, westernmost and easternmost state
Quote: charliepatrick(i) As only the digits 0 1 6/9 work, the next year is 6009 (ii) x=1+x/2, implies x=2 (iii) Depending on how pedantic you want to be the answer could be obviously both are at the same time, alebit their clocks read differently; or, more likely, one of them is visiting the other so in the same time zone (it only says they live in place X not that they are there at the moment) (iv) Wait for the player who's playing White to move (where you're Black), then make the same opening move on the other board. Wait for the reply there, and then using Black's response, go back to the other board and make the same (Black's) move there. Repeat and rinse. Since both games are the same you either win one/lose one or draw both.
btw typical Bank Hoiday weather here, short birst of hail with some thunder mid afternoon!
link to original post
Quote: charliepatrickI've now found the answer, but won't put it here as I would never have got it. But I did found this map helped to understand the answer.Perhaps I should have remembered my round trip from Reno to Jackpot and Ely!
link to original post
Quote: EdCollins.Ah, this old classic. I'd choose to play the simul.
After Nimzowitsch makes his move as White, I will make the same move against Alekhine. When Alekhine, playing Black, responds to my move as White, I make the identical response against Nimzowitsch. I continue in this same manner, never making my own moves at all, but repeating the moves of my opponents. In effect, they are playing each other.
If Nimzowitsch beats me as White, I will do so against Alekhine. If Alekhine beats me as Black, I will win against Nimzowitsch. And of course, both games could end up a draw.
link to original post
Quote: Joeman
It really depends on the font, doesn't it? :)John is in the western part of Florida, perhaps Pensacola, which is in the Central Time Zone. Mary is in eastern Oregon, maybe Sheaville, which is in the Mountain Time Zone.
Now, it just so happens that it is the end of Daylight Savings Time, and John has just turned his clock back from 2:00 to 1:00. So for that hour, Mountain and Central Time Zones have the same time.
link to original post
Quote: ThatDonGuy
It can't start with a 2, 3, 4, or 5, so it has to be at least 6000; the next one is 6009
Let p be the price: p = 1 + 1/2 p, so the price is $2
One is in Pensacola, FL, which is in the Central time zone, and the other is in Ontario, OR, which, mainly because of its proximity to Boise, is in the Mountain time zone.
At 2 AM CST on the third Sunday in March, the clocks are turned back in the Central time zone one hour, so one minute later, it is 1:01 CDT in Pensacola and 1:01 MST in Ontario.
Let Nimzowich move first, then just copy Nimzowich's moves against Alekhine and copy Alekhine's moves against Nimzowich. The two games are the same, except that you are white in one and black in the other. Either you will win one and lose one, or draw both.
link to original post
Correct!!
Comments...
---------------------------------------
Quote: Ace2
Simple. They are next door neighbors in Fairbanks, Alaska
One lives in a “west coast” state and the other lives in an “east coast” state. This is possible since AK is the northernmost, westernmost and easternmost state
link to original post
Heh. I actually had to find a US map that did not include Alaska so I wouldn't have to open this can of worms. Good point though.
Quote: Gialmere
John lives in an East Coast state and Mary in a West Coast state. During a phone conversation one night, they realize that it is the same time in both locations.
How can this be?
link to original post
Part of Florida is in the central time zone. Part of Oregon is in the Mountain time zone. In the fall, when Florida "falls back" that western piece of Florida will have the same time as the mountain time zone, for one hour.

Brett plays poker with a large group of friends. With so many friends playing at the same time, Brett needs more than the 52 cards in a standard deck. This got Brett and his friends wondering about a deck with more than four suits.
Suppose you have a deck with more than four suits, but still 13 cards per suit. And further suppose that you’re playing a game of five-card stud — that is, each participant is dealt five cards that they can’t trade.
As the number of suits increases, the probability of each hand changes. With four suits, a straight is more likely than a full house (a three-of-a-kind and a different two-of-a-kind in the same hand).
How many suits would the deck need so that a straight (not including straight flushes which are a different hand ranking) is less likely than a full house?
I find that if the number of suits is 17, straights are less likely than full houses.
Here is the inequality I solved, where N is the number of suits:
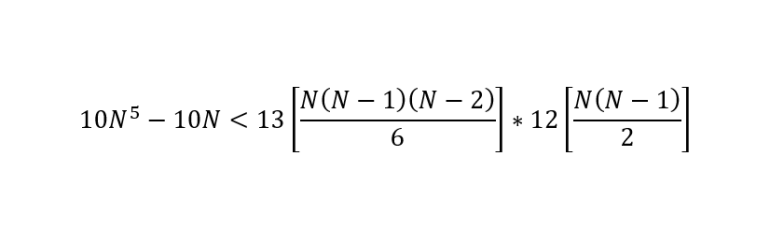
btw the multiple suits idea isn't bad (I feel a side-bet is there based on the fifth suit) and someone did try four suits of 16 cards (AKQJ..2 11 12 13) for a BJ variant - they kindly gave me a deck!
Sods' law!
Here is a really easy puzzle based on my experience this afternoon waiting for a bus. There are two buses (U1C and 1) that regularly go into town from where I live. For mathematical purposes they depart from their depots (University or Winchester) every 10 minutes or every 15 minutes during the daytime. However as you don't know how bad the traffic is that day you can't tell for sure when they will arrive, just that they are always 10 and 15 minutes apart. What is the chances you have to wait 9 minutes or more for the next bus into town!!
I'll be repeating this experiment later this evening to go to the pub!
Quote: acesideThis is cool! It’s so related to the real casino game of poker; however, it’s unrealistic to have a deck of cards with more than four suits in real casinos. What is more realistic is a deck of 53 cards that include a standard deck of 52 cards and an extra joker as the wild card. The joker may substitute for any of the remaining 52 cards. In this 53-card poker game, what is the probability of a straight? And that of a full house?
link to original post
There was a video poker game years ago that had a fifth suit. I believe the fifth suit was a "star" but I am not positive.
Quote: GialmereBrett plays poker with a large group of friends. With so many friends playing at the same time, Brett needs more than the 52 cards in a standard deck. This got Brett and his friends wondering about a deck with more than four suits.
Suppose you have a deck with more than four suits, but still 13 cards per suit. And further suppose that you’re playing a game of five-card stud — that is, each participant is dealt five cards that they can’t trade.
As the number of suits increases, the probability of each hand changes. With four suits, a straight is more likely than a full house (a three-of-a-kind and a different two-of-a-kind in the same hand).
How many suits would the deck need so that a straight (not including straight flushes which are a different hand ranking) is less likely than a full house?
link to original post
Toughie Tuesday is the word for it - I don't think there's a "direct" way to solve it, as I end up with a polynomial of degree 5, which has no general solution.
Let N be the number of suits
For the full house, there are 13 choices for the rank of the three of a kind, and for each one, C(N,3) sets of three cards, and there are 12 choices for the rank of the pair, and for each one, C(N,2) sets of two cards, for a total of 156 (N (N-1) (N-2) / 6) (N (N-1) / 2) = 13 N^2 (N-1)^2 (N-2) possible full houses.
For the straight, there are 10 choices for the lowest rank (Ace, for A-5, through 10, for 10-A); for each one, there are N choices for the first card, N for the second, ..., N for the fifth, but N of those are straight flushes, so the number of straights is 10 (N^5 - N).
The question is, what is the smallest integer N >= 3 (otherwise you can't make any full houses) such that 13 N^2 (N-1)^2 (N-2) > 10 (N^5 - N)?
13 N^5 - 52 N^4 + 65 N^3 - 26 N^2 > 10 N^5 - 10 N
3 N^5 - 52 N^4 + 65 N^3 - 26 N^2 + 10 N > 0
For 16 suits, there are 2400 more straights than full houses;
for 17 suits, there are 228,480 more full houses than straights
Quote: ChesterDog
I find that if the number of suits is 17, straights are less likely than full houses.
Here is the inequality I solved, where N is the number of suits:
link to original post
Quote: ThatDonGuyToughie Tuesday is the word for it - I don't think there's a "direct" way to solve it, as I end up with a polynomial of degree 5, which has no general solution.
Let N be the number of suits
For the full house, there are 13 choices for the rank of the three of a kind, and for each one, C(N,3) sets of three cards, and there are 12 choices for the rank of the pair, and for each one, C(N,2) sets of two cards, for a total of 156 (N (N-1) (N-2) / 6) (N (N-1) / 2) = 13 N^2 (N-1)^2 (N-2) possible full houses.
For the straight, there are 10 choices for the lowest rank (Ace, for A-5, through 10, for 10-A); for each one, there are N choices for the first card, N for the second, ..., N for the fifth, but N of those are straight flushes, so the number of straights is 10 (N^5 - N).
The question is, what is the smallest integer N >= 3 (otherwise you can't make any full houses) such that 13 N^2 (N-1)^2 (N-2) > 10 (N^5 - N)?
13 N^5 - 52 N^4 + 65 N^3 - 26 N^2 > 10 N^5 - 10 N
3 N^5 - 52 N^4 + 65 N^3 - 26 N^2 + 10 N > 0
For 16 suits, there are 2400 more straights than full houses;
for 17 suits, there are 228,480 more full houses than straights
link to original post
Correct!!!
Excellent.
This one was a recent Riddler puzzle so there was also a bonus question. The scenario was the same except they're now playing 7 Card Stud. They recommend you don't try to solve it unless you have quite a bit of time on your hands.
---------------------------------------
Poker Player: I owe some people some money so I will be paying my debt to these guys.
Interviewer: And what about the rest?
Poker player: Well... I guess they'll have to wait.
Quote: Gialmere
Yes, 17 suits are needed. (That's a lot of pink hearts, orange stars, yellow moons and green clovers!)
Reminds me of Fat Tony's poker games on the Simpsons!

Quote: DRichThere was a video poker game years ago that had a fifth suit. I believe the fifth suit was a "star" but I am not positive.
link to original post
That was Lucky Suit Poker
Doc Oct
:strip_icc()/pic7453788.png)
The pink shaded area has the same value as the perimeter of the regular octagon.
What is this value?
We have, x^2=8x.
Solving this, we get x = 8
Therefore, the area is 64
Quote: acesideLet the octagon side length = x, we have the pink shades area = x^2 and the perimeter = 8x.
We have, x^2=8x.
Solving this, we get x = 8
Therefore, the area is 64
link to original post
Quote: Wizard64
link to original post
Correct!!
Very good.
Usually, Shearer problems are for Toughie Tuesday. For this batch, however, I felt the card suits puzzle was more difficult. But what's really difficult is finding puzzles that are easy, but not too easy, for a forum populated by professional mathematicians.
---------------------------------------
Quote: Gialmere
---------------------------------------
Sorry, I'm getting off on a tangent right now.
link to original post
That one is simultaneously hilarious and groan-evoking.

Today's puzzle is simply a math trivia pop quiz. Questions range from easy to somewhat difficult. Good luck...
1) The mathematical symbol for division that has a horizontal line with a dot above and a dot below it is called a what?
2) In algebra, what word means a number or constant placed in front of a variable to multiply that variable, such as the 4 in 4x + y?
3) What 2016 film starred Taraji P. Henson, Octavia Spencer, and Janelle Monae as real-life NASA mathematicians from the 1960s?
4) In the insurance business, what is the name for a person whose job it is to analyze statistics to calculate risks and price premiums accordingly?
5) A dodecahedron is a perfect solid that has how many sides? And what shape are the sides?
6) What is the acronym for the correct sequence of steps to follow when using the order of operations for a math expression?
7) Although the word is often used in popular culture to reference a specific film franchise, technically the definition of a certain math term is "a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns." What is this term?
8) A tesseract is a 4-dimensional shape consisting of how many 3-dimensional cubes?
9) The Mobius strip was the inspiration for a universal symbol first created in 1970 and composed of 3 arrows in a roughly triangular shape. This symbol stands for what action?
10) What 2001 film told the story of John Nash, the American mathematician who made fundamental contributions to game theory and partial differential equations, all while overcoming his personal issues with schizophrenia?
1) The mathematical symbol for division that has a horizontal line with a dot above and a dot below it is called a what?
2) In algebra, coefficient means a number or constant placed in front of a variable to multiply that variable, such as the 4 in 4x + y.
3) Hidden Figures starred Taraji P. Henson, Octavia Spencer, and Janelle Monae as real-life NASA mathematicians from the 1960s.
4) In the insurance business, an actuary is a person whose job it is to analyze statistics to calculate risks and price premiums accordingly.
5) A dodecahedron is a perfect solid that has twelve sides. Pentagons are the sides.
6) PEMDAS is the acronym for the correct sequence of steps to follow when using the order of operations for a math expression.
7) Although the word is often used in popular culture to reference a specific film franchise, technically the definition of a certain math term is "a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns." Matrix is this term.
8) A tesseract is a 4-dimensional shape consisting of eight 3-dimensional cubes.
9) The Mobius strip was the inspiration for a universal symbol first created in 1970 and composed of 3 arrows in a roughly triangular shape. This symbol stands for recycling.
10) A Beautiful Mind told the story of John Nash, the American mathematician who made fundamental contributions to game theory and partial differential equations, all while overcoming his personal issues with schizophrenia.
Quote: ChesterDog
1) The mathematical symbol for division that has a horizontal line with a dot above and a dot below it is called a what?
2) In algebra, coefficient means a number or constant placed in front of a variable to multiply that variable, such as the 4 in 4x + y.
3) Hidden Figures starred Taraji P. Henson, Octavia Spencer, and Janelle Monae as real-life NASA mathematicians from the 1960s.
4) In the insurance business, an actuary is a person whose job it is to analyze statistics to calculate risks and price premiums accordingly.
5) A dodecahedron is a perfect solid that has twelve sides. Pentagons are the sides.
6) PEMDAS is the acronym for the correct sequence of steps to follow when using the order of operations for a math expression.
7) Although the word is often used in popular culture to reference a specific film franchise, technically the definition of a certain math term is "a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns." Matrix is this term.
8) A tesseract is a 4-dimensional shape consisting of eight 3-dimensional cubes.
9) The Mobius strip was the inspiration for a universal symbol first created in 1970 and composed of 3 arrows in a roughly triangular shape. This symbol stands for recycling.
10) A Beautiful Mind told the story of John Nash, the American mathematician who made fundamental contributions to game theory and partial differential equations, all while overcoming his personal issues with schizophrenia.
link to original post
Correct!!
ChesterDog passes the pop quiz with an A.
1) Obelus
2) Coefficient
3) Hidden Figures
4) Actuary
5) 12 sides, Pentagons
6) PEMDAS
7) Matrix
8) 8 cubes
9) Recycling
10) A Beautiful Mind
-------------------------------------------------------------
Petals Around the Rose is a dice puzzle from the 1970s. It received some fame when a tech magazine wrote about Bill Gates trying to solve it one day while waiting at an airport. The object is to figure out how the throws of 5 dice are being scored. What's weird is that newcomers may only be told 3 things: the name of the game (which has significance), the fact that the answer is always even (which includes 0), and the answer for any particular throw.
At the other end, if you solve the puzzle you may neither announce the solution nor explain how you arrived at it. You may only prove you understand it by correctly declaring the value of several rolls in a row. When you can do this consistently, you become a Potentate of the Rose, pledged “to be a cruel and heartless wretch who will never divulge the secret of the game to anyone else.”
If you are already a Potentate (perhaps you program computers), say nothing here. Let the initiates earn their entry.
Let us begin.
-----------------------------
Roll #1 at the top of this post has a value of 2.
⚄ ⚅ ⚄ ⚃ ⚃
Next roll soon.
1. ?
2. ?
3. Hidden figures
4. Actuary (yay!)
5. 12, pentagons
6. PEMDAS
7. Matrix
8. Infinite
9. Recycle
10. A Beautiful Mind
Quote: Wizard
link to original post
Quote: Gialmere
⚄ ⚅ ⚄ ⚃ ⚃
Next roll soon.
link to original post
--------------------------
Roll #3 ⚂ ⚄ ⚄ ⚄ ⚅
What is the value?
Next roll soon.
--------------------------
Roll #4 ⚁ ⚅ ⚁ ⚀ ⚃
What is the value?
Next roll soon.
--------------------------
Roll #5 ⚃ ⚂ ⚁ ⚀ ⚂
What is the value?
Next roll soon.
--------------------------
Roll #6 ⚅ ⚄ ⚅ ⚁ ⚁
What is the value?
Next roll soon.
No explanations, as I expect I'm under a secrecy order.
--------------------------
Roll #7 ⚃ ⚂ ⚃ ⚀ ⚁
What is the value?
Dieter has risen from the ranks of the initiates and become a Potentate of the Rose. Congratulations!
Next roll soon.
--------------------------
Roll #8 ⚄ ⚄ ⚀ ⚂ ⚃
What is the value?
Next roll soon.
--------------------------
Roll #9 ⚃ ⚃ ⚄ ⚂ ⚁
What is the value?
Next roll soon.
If you're having trouble, take heart. Bill gates spent hours at it and that was with a new roll every minute or so.
6
--------------------------
Roll #10 ⚄ ⚂ ⚃ ⚂ ⚄
What is the value?
Next roll soon.
Apologies for my tardiness. Things got busy at work.
12



