Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: MichaelBluejaySave any time versus what, versus both of you walking? Seems like it:
walk 3mph = 20m/mile
bike 12mph = 5m/mile
A starts on bike
B starts on foot
00:00 A departs on bike, B departs on foot
00:05 A finishes Mile 1 on bike and starts walking
20:00 B picks up bike at Mile 1
25:00 A finishes Mile 2 on foot at same time B finishes on bike
So after 2 miles, each person took 25 minutes (a 5-minute bike mile and a 20-minute walk mile). That's 12.5 minutes per mile, and beats walking.
This helped me wrap my mind around why it works that way: Imagine just a single person taking the trip, alternating walking and biking each mile. After every mile s/he walks, there happens to be a bicycle there. So, s/he's walking and biking half the time, which is gonna be faster than just walking. The presence of the other person is just a distraction, it doesn't change the time taken.
link to original post
Quote: charliepatrickAs has been said regardless of the two relative speeds, assuming the cycling is quicker than walking, one person cycles the first mile and then walks. The other person has to walk a mile before they reach the bicycle. By the time the two meet again the first person has cycled a mile and walked for some time, while the second person walked a mile and cycled for some distance. When they meet the time elapsed and distance covered is the same. If you were to plot the distance against time on a graph, the slopes of the walking would be the same, and the slopes of the cycling would be the same. Hence the shape of the two lines form a rhombus (is that the correct name for a rectangle where all the sides are equal). Hence each person, in whichever order, walked one mile and cycled one mile; and they meet every two miles.
Thus the combination of cycling and walking is clearly quicker than just walking.
link to original post
Quote: ThatDonGuy
He is. Your claim that "every inch of the distance is traversed by someone on foot" does not take into account that there are times when both of you are walking simultaneously, so it is faster than a single person walking the entire distance.
link to original post
Correct!!
Well done.
--------------------------------------------------
I tried.

Only one of these statements is true. Which is it?
A. All of the below
B. None of the below
C. One of the above
D. All of the above
E. None of the above
F. None of the above
Quote: Gialmere
Only one of these statements is true. Which is it?
A. All of the below
B. None of the below
C. One of the above
D. All of the above
E. None of the above
F. None of the above
link to original post
I will go with E
if A is true, then B - F are true, but that contradicts problem construction of only one true
if B is true, then C is false, which means neither A nor B are true, contradiction.....note Can't be A&B both true either by problem construction of only one true
if C is true, then A or B are true, which is again ruled out by problem construction of only one true
if D is true....again, A - C are true, again violates problem construction of only one true.
if F is true, Then E would be false, meaning one of A-D is also true, again violating only one true.
E is true....so A-D are false (which agrees with above), F is not affected by E, but F is seen to not be true
It cannot be A, as that would mean 5 are true
If B is true, then C is false, but that is contradicted by the fact that B is true; therefore, B is false
It cannot be C, because A and B are both false
It cannot be D, as that would mean 3 are true
This makes E true; as a result, F is false
The only correct statement is E
Quote: chevy
I will go with E
if A is true, then B - F are true, but that contradicts problem construction of only one true
if B is true, then C is false, which means neither A nor B are true, contradiction.....note Can't be A&B both true either by problem construction of only one true
if C is true, then A or B are true, which is again ruled out by problem construction of only one true
if D is true....again, A - C are true, again violates problem construction of only one true.
if F is true, Then E would be false, meaning one of A-D is also true, again violating only one true.
E is true....so A-D are false (which agrees with above), F is not affected by E, but F is seen to not be true
link to original post
Quote: JoemanE.
link to original post
Quote: ThatDonGuy
It cannot be A, as that would mean 5 are true
If B is true, then C is false, but that is contradicted by the fact that B is true; therefore, B is false
It cannot be C, because A and B are both false
It cannot be D, as that would mean 3 are true
This makes E true; as a result, F is false
The only correct statement is E
link to original post
Correct!!
Well done.
--------------------------------------

You're playing a carnival game where the object is to throw a quarter onto a flat surface with circles on it; you win if the quarter is entirely within any of the circles.
In the picture, part of the quarter is just outside of the circle, so this is a loss.
For purposes of the problem, assume the surface is infinite, and you are equally likely to land the quarter on any point on the surface.
The circles are placed in a square grid pattern.
The diameter of each circle = 2 times the diameter of the quarter, and the distance between the closest edges of any two "adjacent" circles is also 2 times the diameter of the quarter.
What is the probability of landing a quarter entirely within a circle?
pi / 64
Pi/64
So let the width of the coin be C = 2R.
Therefore the area the centre of the coin needs to land in is Pi R2.
The pattern repeats itself every 4 coin widths, so the height/width can be considered as 4C = 8R. So the pattern's area is 64 R2.
Hence the probability of winning is Pi/64.
Quote: Ace2
pi / 64
link to original post
Quote: aceside
Pi/64
link to original post
Quote: charliepatrickThe trick is to realise where the centre of the coin must land, that's within a circle the same size as the coin.
So let the width of the coin be C = 2R.
Therefore the area the centre of the coin needs to land in is Pi R2.
The pattern repeats itself every 4 coin widths, so the height/width can be considered as 4C = 8R. So the pattern's area is 64 R2.
Hence the probability of winning is Pi/64.
link to original post
All correct.
I would post the solution here, but charliepatrick's is the one I used.
Quote: Ace2If it was a carnival game, the player would get five tries to get the quarter in the dot. Win pays even money
link to original post
Actually, this is a carnival game, but usually, the circles aren't quite as big, they're surrounded by a different-color ring which, in turn, is inside of a square/rectangle.
Something like this:

Quote: Ace2I was only trying to make an example of carnival house edges, which tend to be outrageous
link to original post
If a carnival game's house edge isn't 100%, the carny isn't doing their job properly.

Each player in a game of cribbage has a hand of four cards. A single further card is turned up and serves as the fifth card in every player’s hand. Part of the game involves scoring your hand. You get points for any combination of cards that adds to 15, like 9 4 2; for two or more of any rank, like 3 3; or for any run of three or more, like Ace 2 3. As in blackjack, the Jack, Queen, and King each have a point value of 10.
If a 5 is turned up as the community card, is it possible to have a hand that doesn't score any points?
(i) You can't have any cards with a value of 10 (as with the 5 they add up to 15), so this immediately rules out K Q J T
(ii) You can't have any pairs, so this rules out 5, and means the remaining cards have to be four different from A 2 3 4 6 7 8 9.
(iii) You can't have two cards that add up to 10 (as with the 5 they add up to 15), so you have to have one for each of these four pairs
(a) 1 or 9 (i.e. if you have 1 you can't have 9, if you have 9 you can't have 1, but you have to have one from each of a b c d)
(b) 2 or 8
(c) 3 or 7
(d) 4 or 6.
(iv) You can't have a straight, so can't have 7 and 6, and also can't have 4 and 3. Hence you have 74 or 63.
(v) You can't have two cards adding up to 15, hence 74 can't have 8 (7+8=15), and 63 can't have 9 (6+9=15); so this means 742 or 369. But you can't have 369 and 6+9-15. Thus leaving 742.
(vi) You can't have three/four cards adding up to 10. With 742 you can't have 1 (7+2+1+5=15), and you can't have 9 (4+2+9=15).
Thus there are no four cards that prevent you from scoring.
You must have a 15, straight or pair somewhere.
No.
I did an exhaustive (hopefully) search to avoid pairs, straights, and fifteens and couldn't find any zero-point hands with a cut card of 5.
The hand has no 10-point cards, as otherwise they would go with the 5 for a 15
Since pairs score, the four cards are different, and none are 5s
A 2 cannot have 3 (A-2-3 run), 7 (A-2-7-5 15), 8 (2-8-5 15), or 9 (A-9-5 15), leaving 4 and 6, so the only possible hand is A 2 4 6, which has 4-6-5 15
A 3 cannot have 7 (3-7-5 15) or 9 (A-9-5 15), leaving 4, 6, 8
A 3 4 6 has 4-6-5 15; A 3 4 8 has 3-4-8 15; A 4 6 8 has 4-6-5 15
A 4 cannot have 6 (4-6-(5) 15) or 9 (A-9-5 15), leaving 7 and 8, so the only possible hand is A-4-7-8, which is 7-8 15
A 6 7 8 has 7-8 15; A 6 7 9 and A 6 8 9 both have 6-9 15; A 7 8 9 has 7-8 15
Therefore, the hand cannot have an Ace
2 3 cannot have 4 (2-3-4 run), 7 (3-7-5 15), or 8 (2-8-5 15), leaving 6 and 9, so the only possible hand is 2 3 6 9, which has 6-9 15
2 4 cannot have 6 (4-6-5 15) or 8 (2-8-5 15), leaving 7 and 9, so the only possible hand is 2 4 7 9, which has 2-4-9 15
2 6 cannot have 8 (2-8-5 15), leaving 7 and 9, so the only possible hand is 2 6 7 9, which has 6-9 15
2 7 8 9 has 7-8 15
Therefore, the hand cannot have a 2
3 4 is a 3-4-5 run
3 6 cannot have a 7 (3-7-5 15), leaving 8 and 9, so the only possible hand is 3 7 8 9, which is 7-8 15
3 7 8 9 is also 7-8 15
Therefore, the hand cannot have a 3
4 cannot have a 6, so the only possible hand is 4 7 8 9, which is another 7-8 15
The only remaining hand is 6 7 8 9, which is yet still even another 7-8 15 (not to mention a 6-9 15 and, when you include the 5, a run of 5)
Therefore, a 5-card hand with a 5 cannot be scoreless
Quote: charliepatrickI don't think it's possible to have an non-scoring hand.
(i) You can't have any cards with a value of 10 (as with the 5 they add up to 15), so this immediately rules out K Q J T
(ii) You can't have any pairs, so this rules out 5, and means the remaining cards have to be four different from A 2 3 4 6 7 8 9.
(iii) You can't have two cards that add up to 10 (as with the 5 they add up to 15), so you have to have one for each of these four pairs
(a) 1 or 9 (i.e. if you have 1 you can't have 9, if you have 9 you can't have 1, but you have to have one from each of a b c d)
(b) 2 or 8
(c) 3 or 7
(d) 4 or 6.
(iv) You can't have a straight, so can't have 7 and 6, and also can't have 4 and 3. Hence you have 74 or 63.
(v) You can't have two cards adding up to 15, hence 74 can't have 8 (7+8=15), and 63 can't have 9 (6+9=15); so this means 742 or 369. But you can't have 369 and 6+9-15. Thus leaving 742.
(vi) You can't have three/four cards adding up to 10. With 742 you can't have 1 (7+2+1+5=15), and you can't have 9 (4+2+9=15).
Thus there are no four cards that prevent you from scoring.
You must have a 15, straight or pair somewhere.
link to original post
Quote: ChesterDog
No.
I did an exhaustive (hopefully) search to avoid pairs, straights, and fifteens and couldn't find any zero-point hands with a cut card of 5.
link to original post
Quote: ThatDonGuy
The hand has no 10-point cards, as otherwise they would go with the 5 for a 15
Since pairs score, the four cards are different, and none are 5s
A 2 cannot have 3 (A-2-3 run), 7 (A-2-7-5 15), 8 (2-8-5 15), or 9 (A-9-5 15), leaving 4 and 6, so the only possible hand is A 2 4 6, which has 4-6-5 15
A 3 cannot have 7 (3-7-5 15) or 9 (A-9-5 15), leaving 4, 6, 8
A 3 4 6 has 4-6-5 15; A 3 4 8 has 3-4-8 15; A 4 6 8 has 4-6-5 15
A 4 cannot have 6 (4-6-(5) 15) or 9 (A-9-5 15), leaving 7 and 8, so the only possible hand is A-4-7-8, which is 7-8 15
A 6 7 8 has 7-8 15; A 6 7 9 and A 6 8 9 both have 6-9 15; A 7 8 9 has 7-8 15
Therefore, the hand cannot have an Ace
2 3 cannot have 4 (2-3-4 run), 7 (3-7-5 15), or 8 (2-8-5 15), leaving 6 and 9, so the only possible hand is 2 3 6 9, which has 6-9 15
2 4 cannot have 6 (4-6-5 15) or 8 (2-8-5 15), leaving 7 and 9, so the only possible hand is 2 4 7 9, which has 2-4-9 15
2 6 cannot have 8 (2-8-5 15), leaving 7 and 9, so the only possible hand is 2 6 7 9, which has 6-9 15
2 7 8 9 has 7-8 15
Therefore, the hand cannot have a 2
3 4 is a 3-4-5 run
3 6 cannot have a 7 (3-7-5 15), leaving 8 and 9, so the only possible hand is 3 7 8 9, which is 7-8 15
3 7 8 9 is also 7-8 15
Therefore, the hand cannot have a 3
4 cannot have a 6, so the only possible hand is 4 7 8 9, which is another 7-8 15
The only remaining hand is 6 7 8 9, which is yet still even another 7-8 15 (not to mention a 6-9 15 and, when you include the 5, a run of 5)
Therefore, a 5-card hand with a 5 cannot be scoreless
link to original post
Correct!!
Good show.
--------------------------------------------
Twenty-five ants are placed randomly on a meter stick. Each faces east or west. At a signal they all start to march at 1 centimeter per second. Whenever two ants collide they reverse directions.
How long must we wait to be sure that all the ants have left the stick?
Two U.S. state capitals have the same last 8 letters in their names.
Which capitals are they?
Only two U.S. state names can be typed with a single hand on a normal keyboard.
What are they?

You’re playing darts and trying to maximize the number of points you earn with each throw. You are deciding which sector to aim for. Your dart has a 50 percent chance of landing in that sector and a 25 percent chance of landing in one of the two neighboring sectors. Reading clockwise, the sectors are worth 20, 1, 18, 4, 13, 6, 10, 15, 2, 17, 3, 19, 7, 16, 8, 11, 14, 9, 12 and 5 points, as shown above. (For the purposes of this puzzle, don’t worry about the bullseye, the outer ring that’s worth double or the inner ring that’s worth triple.)
Which sector should you aim for to maximize your expected score?
Extra credit: How would you “fairly” (by some definition of fair for you to define) assign the point values around a dartboard? Explain your thinking.
Carson City and Jefferson City
My guess is 100 seconds.
If only one ant was placed facing right on the left end of the meter stick, it would have to walk 100 centimeters.
And if there were two ants placed facing each other on the meter stick with at least one on an end, then at least one of them would have to walk 100 centimeters.
I'm hoping that if 25 ants are put randomly on the meter stick, then 100 centimeters is the most any of them would have to walk.
Quote: ChesterDog
Carson City and Jefferson City
link to original post
Quote: JoemanOhio (right hand) & Texas (left hand)You should aim for the 7, which would earn you 12.25 points per throw.
link to original post
Quote: ChesterDog
My guess is 100 seconds.
If only one ant was placed facing right on the left end of the meter stick, it would have to walk 100 centimeters.
And if there were two ants placed facing each other on the meter stick with at least one on an end, then at least one of them would have to walk 100 centimeters.
I'm hoping that if 25 ants are put randomly on the meter stick, then 100 centimeters is the most any of them would have to walk.
link to original post
Correct!!
Very good.
Ants: The key is to realize that two ants colliding and switching directions is equivalent to two ants passing through one another. So the answer is 100 seconds — the time it takes one ant to travel the full length of the stick.
Riddler Darts: Now the average value of all the sectors was the sum of the numbers from 1 to 20 divided by 20, or 1/20*20(21)/2, or 10.5. Surely it was possible to do better than that.
Aiming for the 16-point sector did fairly well. Half of 16 plus a quarter of 7 plus a quarter of 8 resulted in an expected score of 11.75 points. Meanwhile, both the 19-point and 14-point sectors were better targets. Half of 19 plus a quarter of 3 plus a quarter of 7 resulted in an expected score of 12 points. And half of 14 plus a quarter of 9 plus a quarter of 11 similarly resulted in 12 points.
But the best sector to aim for was the 7-point sector. Half of 7 plus a quarter of 16 plus a quarter of 19 resulted in an expected score of 12.25 points. While the individual sectors ranged from 1 to 20 points, the expected scores formed a much tighter distribution around the mean of 10.5, ranging only from 8.75 to 12.25 points.
For extra credit, you had to “fairly” (by some definition of fair for you to define) assign the point values around a dartboard in some other way. Solver Michael Greenberg worked under the assumption that you still had a 50 percent chance of hitting your target sector and a 25 percent chance of hitting either neighbor. Michael then sought to have all 20 expected values be as close as possible to the average of 10.5.
He immediately realized they couldn’t all equal 10.5, since targeting the 20-point sector (with minimal neighbors worth 1 and 2 points) resulted in an expected score of 10.75 points. But Michael still came up with the following ordering of sectors: 20, 1, 19, 3, 17, 5, 15, 7, 13, 9, 11, 10, 12, 8, 14, 6, 16, 4, 18 and 2. The 20-point and 10-point sectors both had an expected score of 10.75 points, while the 11-point and 1-point sectors both had an expected score of 10.25 points. The remaining 16 sectors were right on target, with an expected score of 10.5 points. As noted by solver Emily Kelly, this arrangement decreased the standard deviation of the expected scores by an order of magnitude. Not bad!
----------------------------------------------
What’s the house edge or player advantage for this scenario?
Estimates are acceptable.
Quote: Ace2A casino offers you a 50% loss rebate if you make at least 500 bets. You accept the offer and decide to make exactly 500 passline bets (no more, no less) with 3-4-5 odds. All losses are valid for the rebate including odds.
What’s the house edge or player advantage for this scenario?
Estimates are acceptable.
link to original post
Assume your bet is 2, with 6/8/10 odds
4/36 x 155/155 of the time, you roll craps; result is -1
8/36 x 155/155 of the time, you roll 7 or 11; result is +2
6/36 of the time, you roll a 4 or 10; that means 6/36 x 55/165 of the time, you make a point for +14, and 6/36 x 110/165 of the time, you seven out for -4
8/36 of the time, you roll a 5 or 9; that means 8/36 x 66/165 of the time, you make a point for +14, and 8/36 x 99/165 of the time, you seven out for -6
10/36 of the time, you roll a 6 or 8; that means 10/36 x 75/165 of the time, you make a point for +14, and 10/36 x 90/165 of the time, you seven out for -8
Wins = ((8 x 155 x 2) + (6 x 55 x 14) + (8 x 66 x 14) + (10 x 75 x 14)) / (36 x 165) = 24,920 / 5940
Losses: ((4 x 155 x 1) + (6 x 110 x 4) + (8 x 99 x 5) + (10 x 90 x 6)) / (36 x 165) = 12,620 / 5940
Expected Win = 12,300 / 5940 = 205 / 99
"House Edge / Player Advantage" depends on what you use as the basis for the bet. If you use the expected average bet:
The average bet = 12/36 x 2 + 6/36 x 8 + 8/36 x 10 + 10/36 x 12 = 68/9
PA = (205 / 99) / (68 / 9) = 205 / 748, or about 27.4%
Of course, this assumes that I understand how the loss rebate works in this case. I am assuming that every lost bet is refunded 50%. Is this correct, or is it only that if the result after 500 bets is a loss, then that amount is cut in half?
I’ll restate the problem as:
A casino offers you a 50% loss rebate (all loses including odds) if you make at least 500 bets. You decide to make exactly 500 passline bets for $100 each, adding 3-4-5 odds whenever possible. The loss rebate only comes into effect after 500 bets are resolved and, obviously, only if you had a loss. What is your expected result, expressed in dollars, net of any rebate, after 500 bets?
Estimates acceptable
Quote: Ace2I don’t think you need to choose a basis for the bet.
link to original post
You don't, if you want the answer in terms of dollars, as opposed to a house edge percentage of some sort.
You may express the answer in:
1) dollars
2) edge/advantage as a percentage of passline bets: divide #1 by (500 * $100)
3) edge/advantage as a percentage of total money wagered: multiply #2 by 9/34
4) British pounds. Divide #1 by 1.2
If you play with or without odds, on average you lose 1.4c per bet. Thus for 500 of these, you would lose $7.07.
I get the SD without odds for a wager to be 1, so 500 bets would be 22.36 (SQRT(500)). This means that you come out ahead if you can get (roughtly) 7/22 SDs above average, which is about 37.6% (using https://www.mathsisfun.com/data/standard-normal-distribution-table.html ).
I get the SD when you play with odds as being 4.91, so 500 bets would be 109.92. This means the average loss would be $7.07 but the chances of coming out ahead are about 47.44%.
Without integrating what I've done is put it into a spreadsheet and look at losses for each $1 (e..g "-1000" means somewhere between -1000.99 and -1000) and looking at the chances of being in that range (excel can work out the normal curve figures).
For the 500 bets...
No odds - average loss $7.07, with rebate loss $0.62.
With odds - average loss $7.07, with rebate profit $16.67.
What makes the difference is being able to make an odds bet which is odds against but gets you half back if you lose. If you were able to do this for several days, your best tactic would be to make one large bet of $500 each day; even better would be to find someone else who does Don't Pass at the same time and share the spoils!
There may be a way of comparing the areas of profit (i.e. 0 and more) with losses (-14.14 and less) as they will have the same area under the curve; without rebate they would offset each other to give the expected loss (e.g. {0 and -14.14}, {10,-24.14}, {20,-34.14}/etc to get an average loss of -7.07), with rebate these would be {0,-7.07} {10,-12.07} {20,-17.14} so you see that eventually they become a profit. Similarly look the the bits between which happen about 5% of the time.
Quote: Ace2Estimates acceptable
link to original post
Estimates? The very idea!
The profit after 500 bets is:
73,757,475,375,627,846,307,350,078
436,536,886,123,015,558,692,237,218,084
692,158,059,537,793,457,579,981,781,280
182,993,521,187,538,472,164,180,680,104
217,264,621,453,665,842,270,932,365,204
942,756,160,837,394,641,602,376,922,656
629,794,518,893,012,361,700,069,097,416
708,674,157,480,315,734,489,616,273,805
841,861,659,192,166,453,194,723,121,455
402,733,639,736,117,928,058,574,923,471
985,905,474,167,372,420,726,357,160,161
714,830,811,049,311,991,163,790,306,775
217,342,204,513,295,346,053,543,267,155
091,722,965,213,587,322,592,091,184,261
888,503,257,423,955,271,125,909,335,321
085,870,653,981,415,068,197,230,888,165
194,549,612,640,658,289,777,497,642,374
530,061,655,801,041,398,886,370,606,794
078,624,886,187,002,018,927,625,285,361
252,209,596,541,827,484,009,843,207,339
376,072,806,708,086,053,131,731,384,222
419,601,413,874,419,308,397,355,071,283
711,920,733,625,187,423,386,013,113,845
397,688,991,700,058,688,933,903,173,922
957,188,360,650,204,798,031,091,450,228
517,324,439,397,176,579,838,520,595,787
348,987,299,858,068,169,644,388,697,047
798,520,683,822,967,546,322,989,483,881
578,884,410,987,254,394,717,299,161,910
568,910,618,715,338,590,480,118,154,645
973,621,103,368,869,246,254,710,034,831
349,743,888,352,326,236,336,073,655,374
472,227,348,791,547,146,536,842,860,495
433,652,597,587,169,315,756,780,910,907
731,574,923,761,737,606,578,220,402,431
121,446,885,304,781,886,395,603,759,804
433,288,175,819,835,762,580,462,804,643
982,068,455,329,633,522,755,627,202,911
420,301,976,650,964,536,429,078,444,685
337,566,843,945,290,394,622,153,941,570
979,710,497,050,636,449,149,466,379,610
505,427,600,358,589,952,417,606,956,897
505,093,547,354,024,938,297,228,697,200
377,334,691,775,391,981,743,970,269,332
382,613,429,384,835,428,021,547,149,800
/ 44,236,710,902,545,405,050,796
404,815,190,850,027,930,221,278,714,599
195,789,778,277,649,763,799,461,902,327
371,231,286,828,943,268,385,811,111,488
120,198,541,892,140,231,717,967,876,724
046,239,601,920,203,992,964,896,389,039
344,997,195,963,829,255,017,438,251,051
754,687,994,692,111,708,115,758,815,593
374,976,010,576,333,330,473,099,097,386
454,801,684,422,038,823,391,543,541,041
974,980,155,343,119,980,886,850,504,008
708,396,711,569,534,389,188,261,872,140
309,272,246,723,195,686,848,883,432,521
876,598,048,902,585,547,405,783,719,488
237,187,245,460,774,470,553,661,980,941
080,554,457,783,304,438,494,999,144,847
322,711,341,848,960,050,536,218,365,730
907,349,167,327,826,236,961,756,150,046
484,582,719,322,552,647,275,077,585,443
173,085,181,490,593,579,344,698,250,759
360,244,575,561,141,916,614,363,644,631
261,006,968,541,000,662,429,458,926,774
155,659,104,576,141,463,795,527,596,798
877,045,312,333,133,695,491,022,986,069
805,704,995,012,490,575,045,371,655,154
524,286,569,340,473,172,471,151,346,992
741,189,267,831,995,511,097,951,317,464
254,747,255,117,610,040,877,913,431,478
528,615,907,773,963,290,997,106,502,615
258,949,547,301,399,014,303,393,153,089
052,314,018,843,818,959,342,660,924,164
585,256,646,606,155,013,500,856,276,966
677,928,371,220,664,440,358,750,978,933
266,728,430,731,930,155,416,690,876,804
265,188,146,586,505,318,494,814,346,253
667,638,709,388,362,157,471,936,553,875
607,111,494,063,131,520,726,726,320,942
341,418,907,899,052,315,127,527,695,927
499,313,792,634,507,998,219,095,975,038
767,886,526,317,550,161,438,802,951,888
106,932,499,250,644,356,243,419,380,219
377,367,834,340,577,780,226,639,835,644
698,559,792,815,488,239,473,434,482,025
398,819,256,435,458,692,998,385,910,044
589,763,856,492,936,611,175,537,109,375
or about 1667.3363338
The rebate needed for the house edge to be zero is about 14.8894165%
I’ll accept that answer. 16.7 unit gain. I assume you “Markoved” it for 500 iterations and backed out half the value of all the lossesQuote: ThatDonGuyQuote: Ace2Estimates acceptable
link to original post
Estimates? The very idea!
The profit after 500 bets is:
73,757,475,375,627,846,307,350,078
436,536,886,123,015,558,692,237,218,084
692,158,059,537,793,457,579,981,781,280
182,993,521,187,538,472,164,180,680,104
217,264,621,453,665,842,270,932,365,204
942,756,160,837,394,641,602,376,922,656
629,794,518,893,012,361,700,069,097,416
708,674,157,480,315,734,489,616,273,805
841,861,659,192,166,453,194,723,121,455
402,733,639,736,117,928,058,574,923,471
985,905,474,167,372,420,726,357,160,161
714,830,811,049,311,991,163,790,306,775
217,342,204,513,295,346,053,543,267,155
091,722,965,213,587,322,592,091,184,261
888,503,257,423,955,271,125,909,335,321
085,870,653,981,415,068,197,230,888,165
194,549,612,640,658,289,777,497,642,374
530,061,655,801,041,398,886,370,606,794
078,624,886,187,002,018,927,625,285,361
252,209,596,541,827,484,009,843,207,339
376,072,806,708,086,053,131,731,384,222
419,601,413,874,419,308,397,355,071,283
711,920,733,625,187,423,386,013,113,845
397,688,991,700,058,688,933,903,173,922
957,188,360,650,204,798,031,091,450,228
517,324,439,397,176,579,838,520,595,787
348,987,299,858,068,169,644,388,697,047
798,520,683,822,967,546,322,989,483,881
578,884,410,987,254,394,717,299,161,910
568,910,618,715,338,590,480,118,154,645
973,621,103,368,869,246,254,710,034,831
349,743,888,352,326,236,336,073,655,374
472,227,348,791,547,146,536,842,860,495
433,652,597,587,169,315,756,780,910,907
731,574,923,761,737,606,578,220,402,431
121,446,885,304,781,886,395,603,759,804
433,288,175,819,835,762,580,462,804,643
982,068,455,329,633,522,755,627,202,911
420,301,976,650,964,536,429,078,444,685
337,566,843,945,290,394,622,153,941,570
979,710,497,050,636,449,149,466,379,610
505,427,600,358,589,952,417,606,956,897
505,093,547,354,024,938,297,228,697,200
377,334,691,775,391,981,743,970,269,332
382,613,429,384,835,428,021,547,149,800
/ 44,236,710,902,545,405,050,796
404,815,190,850,027,930,221,278,714,599
195,789,778,277,649,763,799,461,902,327
371,231,286,828,943,268,385,811,111,488
120,198,541,892,140,231,717,967,876,724
046,239,601,920,203,992,964,896,389,039
344,997,195,963,829,255,017,438,251,051
754,687,994,692,111,708,115,758,815,593
374,976,010,576,333,330,473,099,097,386
454,801,684,422,038,823,391,543,541,041
974,980,155,343,119,980,886,850,504,008
708,396,711,569,534,389,188,261,872,140
309,272,246,723,195,686,848,883,432,521
876,598,048,902,585,547,405,783,719,488
237,187,245,460,774,470,553,661,980,941
080,554,457,783,304,438,494,999,144,847
322,711,341,848,960,050,536,218,365,730
907,349,167,327,826,236,961,756,150,046
484,582,719,322,552,647,275,077,585,443
173,085,181,490,593,579,344,698,250,759
360,244,575,561,141,916,614,363,644,631
261,006,968,541,000,662,429,458,926,774
155,659,104,576,141,463,795,527,596,798
877,045,312,333,133,695,491,022,986,069
805,704,995,012,490,575,045,371,655,154
524,286,569,340,473,172,471,151,346,992
741,189,267,831,995,511,097,951,317,464
254,747,255,117,610,040,877,913,431,478
528,615,907,773,963,290,997,106,502,615
258,949,547,301,399,014,303,393,153,089
052,314,018,843,818,959,342,660,924,164
585,256,646,606,155,013,500,856,276,966
677,928,371,220,664,440,358,750,978,933
266,728,430,731,930,155,416,690,876,804
265,188,146,586,505,318,494,814,346,253
667,638,709,388,362,157,471,936,553,875
607,111,494,063,131,520,726,726,320,942
341,418,907,899,052,315,127,527,695,927
499,313,792,634,507,998,219,095,975,038
767,886,526,317,550,161,438,802,951,888
106,932,499,250,644,356,243,419,380,219
377,367,834,340,577,780,226,639,835,644
698,559,792,815,488,239,473,434,482,025
398,819,256,435,458,692,998,385,910,044
589,763,856,492,936,611,175,537,109,375
or about 1667.3363338
link to original post
I used ((500^.5) * 4.92 * (2pi)^-.5 + 7.07) / 2 - 7.07 = 18.39 unit gain where 4.92 is the standard deviation and 7.07 the expected loss.
This number would be more accurate with more iterations
Quote: Ace2I assume you “Markoved” it for 500 iterations and backed out half the value of all the losses
link to original post
You assume correctly.
I accept your answer as well.Quote: charliepatrickTo the first four significant digts I agree with both ThatDonGuy's figures
based on a simple spreadsheet using its builtin function NORM.DIST .1666.76, 0.14893
link to original post
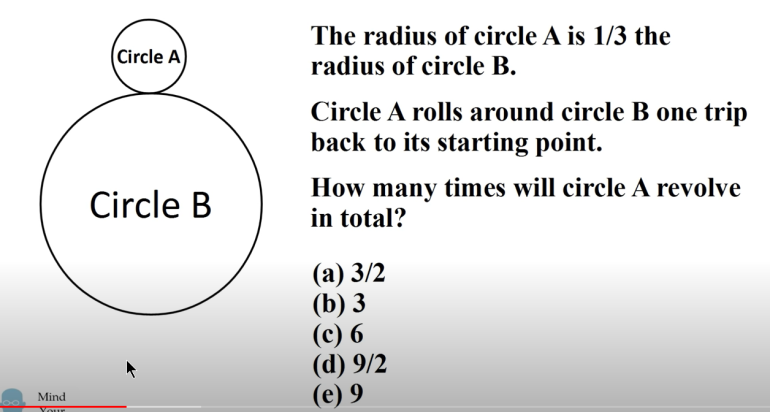
This question was on the SAT exam many years ago. I am sure those of you that have studied math will get this easily but I chose what I thought was the obvious answer and was wrong.
In school, I learned that that the earth revolves around the sun whereas the earth rotates about the earth's axis.
Probably this SAT question should have worded the question as, "How many times will Circle A rotate in total?"
My answer is 4 rotations, but that is not one of the choices. Maybe, the questions should have included: (f) none of the above.
The small circle's circumference is 1/3 pf the large circle so as it reaches 120 degrees (4 o'clock on the big circle) the chalk mark will be at the surface of the large circle. Thus the chalk mark will be at 10 o'clock. So at this stage the chalk mark/small circle has rotated 1 1/3 revolutions.
As this process continues, the other revolutions will also be 1 1/3, giving a total of 4 revolutions.
Another way of looking at this is when the small circle is a 3 o'clock, the chalk mark will be back at 6 o'clock, so rotated once.
seed
+iced
------
spice
1663
+9263
---------
10926
I get four as well.
The formula I use is (radius of A)/(radius of A) + 1.
If circle A were inside circle B, then you would subtract one, instead of add.
To be honest, I can't explain why, in plain simple English, why you add one.
Quote: Wizard
I get four as well.
The formula I use is (radius of A)/(radius of A) + 1.
If circle A were inside circle B, then you would subtract one, instead of add.
To be honest, I can't explain why, in plain simple English, why you add one.
link to original post
Mark the point on circle A where it is initially tangent to circle B.
Now, stretch circle B into a line whose length is the circle's circumference.
Each time you rotate circle A one circumference, the mark will once again be tangent to the line. The number of rotations = B's circumference / A's circumference = B's radius / A's radius.
However, when this is done while B is a circle, each time the mark is tangent to the line, you have to add the amount of rotation to A added by B's curvature. When you are done, the rotation is 1 complete revolution, which is why it is B / A + 1.
If the circle is on the inside, then the marked point's rotation is in the opposite direction, so you are subtracting B's curvature, which is why it is B / A - 1.
Quote: ThatDonGuy
Mark the point on circle A where it is initially tangent to circle B.
Now, stretch circle B into a line whose length is the circle's circumference.
Each time you rotate circle A one circumference, the mark will once again be tangent to the line. The number of rotations = B's circumference / A's circumference = B's radius / A's radius.
However, when this is done while B is a circle, each time the mark is tangent to the line, you have to add the amount of rotation to A added by B's curvature. When you are done, the rotation is 1 complete revolution, which is why it is B / A + 1.
If the circle is on the inside, then the marked point's rotation is in the opposite direction, so you are subtracting B's curvature, which is why it is B / A - 1.
link to original post
That's good, thanks. I'm ready for a fresh problem to wake up this thread.
Quote: MichaelBluejayWhen I did tech support at Apple in the 90s, a small percentage of customers were so literally unbelievably dumb that we all wondered how they were able to even conduct the transaction in the store to buy the computer and then get the computer home, much less have any kind of job where they could earn money to buy a computer. I suggested we put an intelligence test on the phone tree that customers would have to pass before they would could speak to a tech. The question I suggested was: "John, Mary, and Bob are in a room. Bob leaves. Who left?"
link to original post
Please tell me I am not the only person who sees the problem with the question as stated.
Quote: ThatDonGuyPlease tell me I am not the only person who sees the problem with the question as stated.
link to original post
I don't see the problem with it, other than the question itself offending people.
Quote: WizardQuote: ThatDonGuyPlease tell me I am not the only person who sees the problem with the question as stated.
link to original post
I don't see the problem with it, other than the question itself offending people.
link to original post
"Who left?" can be interpreted as "Who's left in the room?" Change the end of the question to, "Who left the room?"
It's funnier as just "Who left?", and that's the point: it's a joke. No way would this be actually implemented, so there are no actual problems with a customer misinterpreting it.Quote: ThatDonGuy"Who left?" can be interpreted as "Who's left in the room?" Change the end of the question to, "Who left the room?"
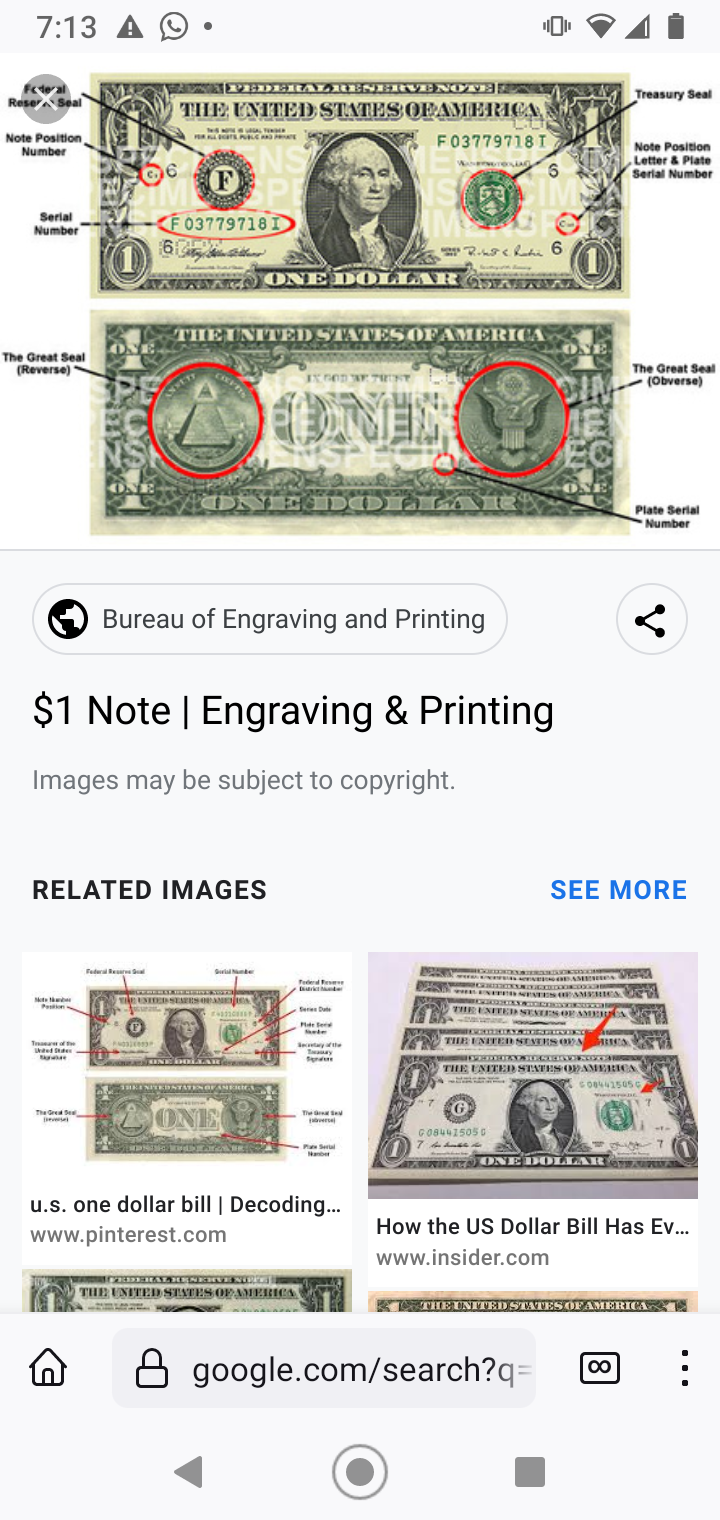
Quote: avianrandyNot really a math problem but involves numbers. How many times does the word one appear on the current one dollar bill?

link to original post
It appears to be six times on the back of the one dollar bill and another, 7th, time on the front of the bill.
One might claim the word 'ONE' actually appears a 2nd time on the front of the bill. On the top of the front of the bill are the words:
which does contain the word ONE displayed backwards.


