Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
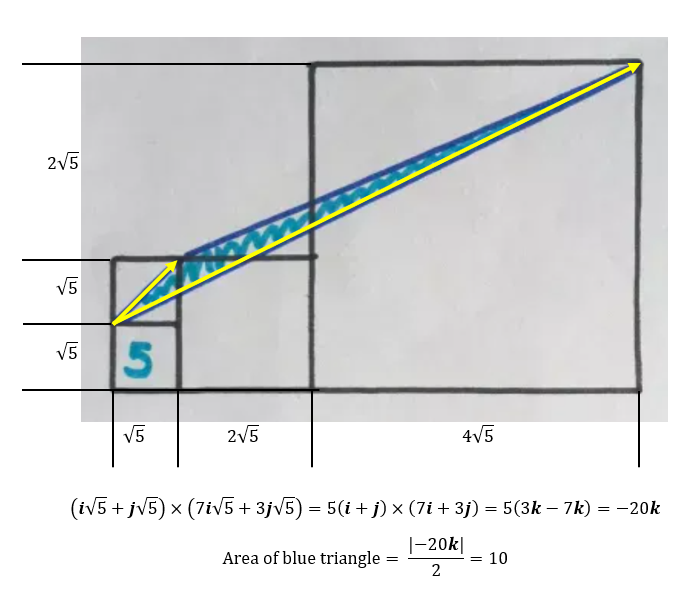
Aceside, I think you're right that the area of the blue triangle doesn't depend on the area of the square on the right!
Quote: acesideThe base line of the shaded area crosses the side midpoints of the three upper squares. We divide the shaded area into two triangle areas and then calculate each area.
The area of the triangle in the small square is
(Sqrt(5) /2) x Sqrt(5) /2
The area of the triangle spanning the two larger squares is
(Sqrt(5) /2) x [2 x sqrt(5) + 2.5x2x sqrt(5)] /2
Adding them together, we get the total area
Area=( 5 +7 x 5) /4= 10
link to original post
Quote: ChesterDog
Since the problem stated that it uses bad drawing geometry, I assumed that the largest square has four times the area of the next smaller square.
link to original post
Quote: ThatDonGuy
Use the Bounding Box method - to make it easier to describe, let x be the square root of 5
The box has (0,0) at its lower left corner and (7x, 3x) at its upper right corner; its area = 21 x^2
The vertices of the triangle are (0, 0), (x, x), and (7x, 3x)
The bounding box outside of the triangle can be broken up into four pieces: a triangle at (0, 0), (7x, 0), and (7x, 3x), which has area 21/2 x^2; a triangle at (0, 0), (0, x), and (x, x), which has area 1/2 x^2; a triangle at (x, x), (x, 3x), and (7x, 3x), which has area 6x^2; and a rectangle with lower left (x, x) and upper right (2x, 3x), which has area 2 x^2.
The area of the triangle = x^2 (21 - 21/2 - 1/2 - 6 - 2) = 2 x^2 = 2 (sqrt(5))^2 = 10.
link to original post
Correct!!!
Excellent.
:strip_icc()/pic7291623.png)
1/ Note that both small squares have area = 5. The medium square is the size of four small squares so it has area=20. Amazingly, it doesn't matter how big the biggest square is!
2/ The green lines are parallel. Therefore, as the blue and pink triangles have the same base and same height, their areas are equal.
3/ Again, the green lines are parallel, so the blue triangle has the same area as the pink triangle.
4/ The grey triangle is half the 20 square, so the area = 10. This is the same as the original blue triangle!
------------------------------------


Three men play a game, agreeing that in each round the loser will double the money of each of the other two. After three rounds, each man has lost one time, and each man has $24.
How much did each have at the start of the game?
I found it best to work backwards. If game #3 ended with everyone having $24 apiece, then the loser would have had double that amount and the winners would have had half that amount at the start of the game. So, game #2 must have ended at $12, $12, $48, which means it had to have begun $6, $42, $24. Thus game #1 began $39, $21, $12.
Now what would have happened if the guy with only $12 at the start loses game #1?
Quote: JoemanIn order of who lost each game: $39, $21, $12.
I found it best to work backwards. If game #3 ended with everyone having $24 apiece, then the loser would have had double that amount and the winners would have had half that amount at the start of the game. So, game #2 must have ended at $12, $12, $48, which means it had to have begun $6, $42, $24. Thus game #1 began $39, $21, $12.
Now what would have happened if the guy with only $12 at the start loses game #1?
link to original post
Correct!!
Very good.
---------------------------------------
:strip_icc()/pic7293707.png)
Wizard Knievel is attempting to jump his unicycle over the fountains at Caesars Palace. Traveling at 5 meters per second, he will launch himself from the dizzying heights of the platform on the left, over a 3 meter section of the fountains, and (hopefully) land on the lower platform to the right.
Does he have any chance of making the jump?
a) He fails, but only just.
b) No hope.
c) Yes, but only just, and neglecting air resistance.
d) Yes! He's easily successful.
Assume gravity = 10m/s^2 and that he succeeds in sticking the landing if he reaches the other platform.
Quote: Gialmere
Wizard Knievel is attempting to jump his unicycle over the fountains at Caesars Palace. Traveling at 5 meters per second, he will launch himself from the dizzying heights of the platform on the left, over a 3 meter section of the fountains, and (hopefully) land on the lower platform to the right.
Does he have any chance of making the jump?
a) He fails, but only just.
b) No hope.
c) Yes, but only just, and neglecting air resistance.
d) Yes! He's easily successful.
Assume gravity = 10m/s^2 and that he succeeds in sticking the landing if he reaches the other platform.
link to original post
At vx = 5 m/s, the Wiz will travel the 3 m gap in (5 m/s)/(3 m) = 0.6 s.
Once he hits the gap, his acceleration in the minus y-direction is constant at g = 10 m/s², so his change in elevation can be calculated as ∆y = -½*g*t², so after 0.6 s we get
∆y = -0.5*(10 m/s²)*(0.6 s)² = -1.8 m
Thus, he will be 0.8 m below the receiving platform... Ouch!
Dog Hand
A more interesting question is whether Knievel can make the jump by using a ramp, assuming he will still be launched at an upward angle at 5 m/sec but with a horizontal velocity of less than 5 m/sec. I'm too lazy to do the math, but I am guessing the answer is NO. He's just not traveling fast enough.
Quote: Gialmere
Wizard Knievel is attempting to jump his unicycle over the fountains at Caesars Palace. Traveling at 5 meters per second, he will launch himself from the dizzying heights of the platform on the left, over a 3 meter section of the fountains, and (hopefully) land on the lower platform to the right.
Does he have any chance of making the jump?
a) He fails, but only just.
b) No hope.
c) Yes, but only just, and neglecting air resistance.
d) Yes! He's easily successful.
Assume gravity = 10m/s^2 and that he succeeds in sticking the landing if he reaches the other platform.
link to original post
His speed in the forward direction would remain constant at 5 meters per second. The time to go horizontally 3 meters at that speed would be (3 m) / (5 m/s) = 0.6 seconds.
But in 0.6 seconds, he would fall (10 m/s2)(0.6 s)2 / 2 = 1.8 meters. And 1 meter - 1.8 meters = -0.8 meters. So, the bottom of his wheel would be 0.8 meters below its destination. The unicycle wouldn't make it, but Wizard Knievel could safely end on his destination level, but on his hands and knees.
Thus the speed of 5 m/s could correspond to 4 m/s vertical and 3 m/s horizontal. After .8 sec the speed would have got to -4 m/s, hence WK would be level with the takeoff, but 2.4 meters covered horizontally. I get that in the next .2 sec the speed increases to -6 m/s, so the average is -5 m/s, so WK falls 1m. However during the same time, the horizontal distance is 3*.2 = 0.6. Also, because it's a second, the total horizontal distance covered is 3m. So WK just makes it.
The other way round (3v 4h) WK would also be level after .6 sec, and also would have also travelled 2.4m. The difference is the vertical speed at this time is only -3m/s. So since WK is going horizontally faster and not descending so fast, I'm guessing he makes it.
Quote: gordonm888At 5 m/sec Knievel will travel across the 3 meter distance in 0.6 seconds, in which time he will descend more than 1 meter. He will wipe out against the wall of his target building - a landing he most certainly will stick! The answer is B) No hope!
A more interesting question is whether Knievel can make the jump by using a ramp, assuming he will still be launched at an upward angle at 5 m/sec but with a horizontal velocity of less than 5 m/sec. I'm too lazy to do the math, but I am guessing the answer is NO. He's just not traveling fast enough.
link to original post
Vertical speed at launch is also 3.53553 m/s (cos and sin have same value at 45 degrees).
Y = vt - 1/2gt^2
Plugging in:
Y = 3.53533 * 0.848529 - 1/2*10*(0.848529)^2
Y = -0.600001 m
So above the target and sticks the landing!
Edited to fix math error that changes answer.
Quote: DogHand
(b)
At vx = 5 m/s, the Wiz will travel the 3 m gap in (5 m/s)/(3 m) = 0.6 s.
Once he hits the gap, his acceleration in the minus y-direction is constant at g = 10 m/s², so his change in elevation can be calculated as ∆y = -½*g*t², so after 0.6 s we get
∆y = -0.5*(10 m/s²)*(0.6 s)² = -1.8 m
Thus, he will be 0.8 m below the receiving platform... Ouch!
Dog Hand
link to original post
Quote: gordonm888At 5 m/sec Knievel will travel across the 3 meter distance in 0.6 seconds, in which time he will descend more than 1 meter. He will wipe out against the wall of his target building - a landing he most certainly will stick! The answer is B) No hope!
A more interesting question is whether Knievel can make the jump by using a ramp, assuming he will still be launched at an upward angle at 5 m/sec but with a horizontal velocity of less than 5 m/sec. I'm too lazy to do the math, but I am guessing the answer is NO. He's just not traveling fast enough.
link to original post
Quote: ChesterDog
His speed in the forward direction would remain constant at 5 meters per second. The time to go horizontally 3 meters at that speed would be (3 m) / (5 m/s) = 0.6 seconds.
But in 0.6 seconds, he would fall (10 m/s2)(0.6 s)2 / 2 = 1.8 meters. And 1 meter - 1.8 meters = -0.8 meters. So, the bottom of his wheel would be 0.8 meters below its destination. The unicycle wouldn't make it, but Wizard Knievel could safely end on his destination level, but on his hands and knees.
link to original post
Correct!!
Well done.
For now though, tragically, Wizard Knievel did not make the unicycle jump. He broke 40 bones in his body and spent several weeks in a medically induced coma. But he's also become part of the legend of the fountains. Will this daredevil heal his wounds and jump in another puzzle? Stay tuned.
--------------------------------------------


Mr. Meek has a new four digit extension number at work and he loves it because the middle two digits are the same, just like his name.
The repeated digit also happens to be the same as the first digit of Mr. Humble's new extension.
And the first digit of Mr. Meek's extension is the same as the first digit of Mr. Lowly's new extension.
If you exchange the first and last digits of Mr. Lowly's number, you get Mr. Humble's number.
If you subtract Mr. Lowly's number from Mr. Humble's, you get Mr. Meek's.
What is Meek's new number?
No need for exact math, just a ballpark figure will do.
Quote: Gialmere
Mr. Meek has a new four digit extension number at work and he loves it because the middle two digits are the same, just like his name.
The repeated digit also happens to be the same as the first digit of Mr. Humble's new extension.
And the first digit of Mr. Meek's extension is the same as the first digit of Mr. Lowly's new extension.
If you exchange the first and last digits of Mr. Lowly's number, you get Mr. Humble's number.
If you subtract Mr. Lowly's number from Mr. Humble's, you get Mr. Meek's.
What is Meek's new number?
link to original post
Meek's repeated digit is Humble's first digit, which is also Lowly's fourth digit
Meek's first digit is Lowly's first digit, as well as Humble's last digit
Humble's and Lowly's second digits are the same, as are their third digits
Using letters for the digits, we have:
Meek - ABBC
Humble - BDEA
Lowly - ADEB
Since Humble - Lowly = Meek, we have Meek + Lowly = Humble, or ABBC + ADEB = BDEA
Third digits: B + E = E, so B is either 0 or 9 (with a carry from the fourth digit); B cannot be 0 as it is A + A (plus a possible carry), so B = 9
First Digits: A + A = 9, so A = 4 with a carry
499C + 4DE9 = 9DE4; C = 5, so Meek's number is 4995
Quote: ThatDonGuy
Meek's repeated digit is Humble's first digit, which is also Lowly's fourth digit
Meek's first digit is Lowly's first digit, as well as Humble's last digit
Humble's and Lowly's second digits are the same, as are their third digits
Using letters for the digits, we have:
Meek - ABBC
Humble - BDEA
Lowly - ADEB
Since Humble - Lowly = Meek, we have Meek + Lowly = Humble, or ABBC + ADEB = BDEA
Third digits: B + E = E, so B is either 0 or 9 (with a carry from the fourth digit); B cannot be 0 as it is A + A (plus a possible carry), so B = 9
First Digits: A + A = 9, so A = 4 with a carry
499C + 4DE9 = 9DE4; C = 5, so Meek's number is 4995
link to original post
Correct!!
Well done sir.
---------------------------------------
You are playing a game of Fox and Geese - well, in this case, Fox and Goose. The game is played on a 9 x 7 grid of squares, with you, as the goose, starting in one corner, and the fox starting in the opposite corner.
Each turn, both you and the fox select a move, then simultaneously move your pieces. Each move must be to a horizontally or vertically adjacent space that is closer (in terms of moves) to the opponent's starting square. In other words, if the fox starts in the upper right corner and the goose in the lower left, the goose can only move up or right, and the fox can only move down or left.
The fox wins if either the fox and geese are ever in the same square, or they start a move in adjacent squares and exchange squares in that move.
The goose wins if it reaches the fox's starting square before then.
What's your strategy, and how likely is it that you will win?
Quote: acesideA picture is worth 1000 words. Post a relevant picture. Basically this is related to asymmetry between horizontal and vertical grids, I guess.
link to original post
Here you go:
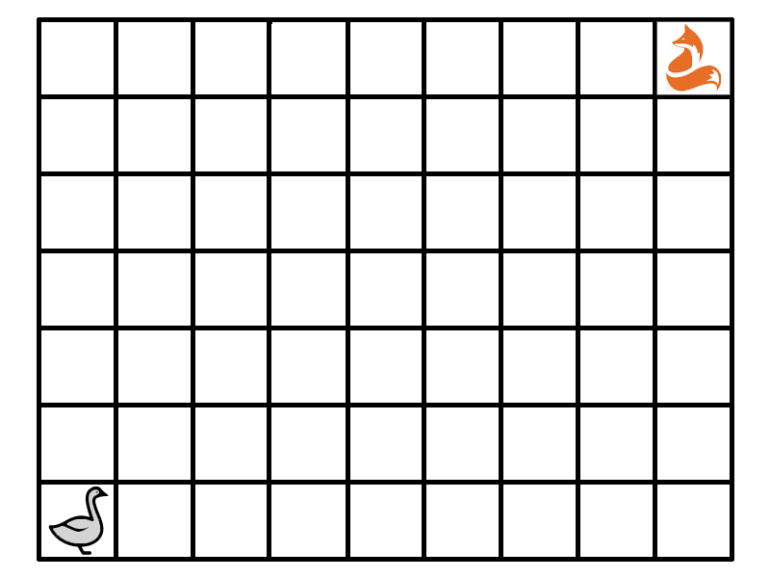
The fox in the upper right corner can move only left or down; the goose in the lower left corner can move only right or up.
The fox is trying to end up in the same square as the goose, or exchanging squares with the goose in the same move.
The goose is trying to end up in the upper right corner without this happening.
Quote: ThatDonGuy
What's your strategy, and how likely is it that you will win?
link to original post
This is my third answer, and probably won't be the last.
I think the fox will always want to minimize the direct distance between the two locations and the goose will want to maximize it.
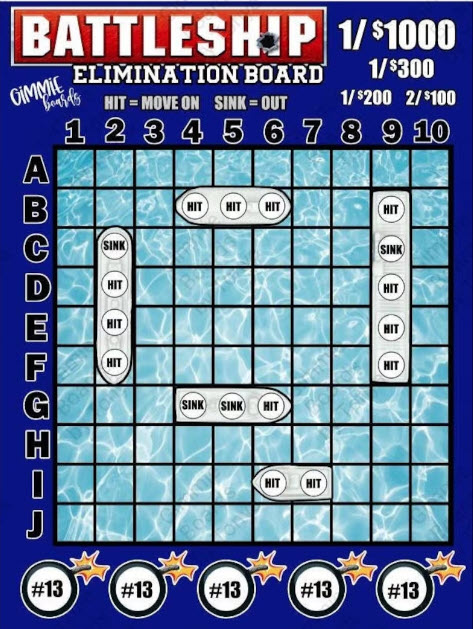
Using Battleship notation, the Goose starts on K1 and the Fox on A11. Using my strategy above, this would leave both to these locations:
G = B1
F = A4
At this turn, the Goose should go to B2, not wanting to be limited at the fence. The fox would still go to A3.
The next turn, they both randomize.
Then it turns into a 50/50 game.
So, my answer is 50%.
You as the goose want to cross the fox's vertical or horizontal position as soon as possible. So start moving up. Then on each turn move the same way (horizontal/vert) that the fox did the previous turn.
I think if the fox plays optimally (maybe always trying to keep goose on the diagonal) this seems to end with them separated on adjacent diagonals, which becomes a 50% chance of meeting on next turn.
But you also win all the times the fox doesn't play optimally. (e.g. fox just keeps moving horizontally)
So success is >=50%???
I get 1/2 as the probability for the fox's winning.
The goose's strategy is to move upward five consecutive times. During these moves, the fox would know to move to the left five times. (The fox would know that he would lose if he wasted a move going downward.)
For the goose's sixth move, he would have to move to the right to avoid an eventual loss. And the fox's sixth move would be another left move.
The goose and fox would then find themselves diagonally adjacent to each other. For their seventh move, each should make a random choice (P = 1/2) from their two legal moves. Then the fox would have a probability of 1/2 of landing in the goose's square.
Quote: ChesterDog
I get 1/2 as the probability for the fox's winning.
The goose's strategy is to move upward five consecutive times. During these moves, the fox would know to move to the left five times. (The fox would know that he would lose if he wasted a move going downward.)
For the goose's sixth move, he would have to move to the right to avoid an eventual loss. And the fox's sixth move would be another left move.
The goose and fox would then find themselves diagonally adjacent to each other. For their seventh move, each should make a random choice (P = 1/2) from their two legal moves. Then the fox would have a probability of 1/2 of landing in the goose's square.
link to original post
Following the strategy in my post above, this is exactly what would happen. So, I agree 100%.
I await the official answer.
Quote: WizardQuote: ChesterDog
I get 1/2 as the probability for the fox's winning.
The goose's strategy is to move upward five consecutive times. During these moves, the fox would know to move to the left five times. (The fox would know that he would lose if he wasted a move going downward.)
For the goose's sixth move, he would have to move to the right to avoid an eventual loss. And the fox's sixth move would be another left move.
The goose and fox would then find themselves diagonally adjacent to each other. For their seventh move, each should make a random choice (P = 1/2) from their two legal moves. Then the fox would have a probability of 1/2 of landing in the goose's square.
link to original post
Following the strategy in my post above, this is exactly what would happen. So, I agree 100%.
I await the official answer.
link to original post
I think I found a flaw in my strategy.
The goose can do better than a 50% chance of winning.
If the goose makes four moves up, instead of five, and then makes one move right while the fox is moving left five moves, the fox would have to decide to move left or down on his sixth move.
If the goose would move right for the sixth move, the fox would eventually lose if he moves left and have a 50% chance of winning if he moves down. Likewise if the goose would move up for his sixth move, the fox would eventually lose if he moves down and have a 50% chance of winning if he moves left.
If the goose and fox each choose their sixth move at random (P = 1/2), then the goose's probability of winning would jump to 75%.
But that 75% is just for this one scenario. I don't know what the overall answer would be.
Quote: ChesterDog
I think I found a flaw in my strategy.
The goose can do better than a 50% chance of winning.
If the goose makes four moves up, instead of five, and then makes one move right while the fox is moving left five moves, the fox would have to decide to move left or down on his sixth move.
If the goose would move right for the sixth move, the fox would eventually lose if he moves left and have a 50% chance of winning if he moves down. Likewise if the goose would move up for his sixth move, the fox would eventually lose if he moves down and have a 50% chance of winning if he moves left.
If the goose and fox each choose their sixth move at random (P = 1/2), then the goose's probability of winning would jump to 75%.
But that 75% is just for this one scenario. I don't know what the overall answer would be.
link to original post
That got me to thinking.
The goose should go right first, to I2. Assuming the fox goes left, to B10, they now form a square. By the same logic as CD, the Goose would have a 63/64 chance of survival.
Quote: WizardQuote: ChesterDog
I think I found a flaw in my strategy.
The goose can do better than a 50% chance of winning.
If the goose makes four moves up, instead of five, and then makes one move right while the fox is moving left five moves, the fox would have to decide to move left or down on his sixth move.
If the goose would move right for the sixth move, the fox would eventually lose if he moves left and have a 50% chance of winning if he moves down. Likewise if the goose would move up for his sixth move, the fox would eventually lose if he moves down and have a 50% chance of winning if he moves left.
If the goose and fox each choose their sixth move at random (P = 1/2), then the goose's probability of winning would jump to 75%.
But that 75% is just for this one scenario. I don't know what the overall answer would be.
link to original post
That got me to thinking.
The goose should go right first, to I2. Assuming the fox goes left, to B10, they now form a square. By the same logic as CD, the Goose would have a 63/64 chance of survival.
link to original post
We have a winner!
The secret is that once the goose is on a higher row than the fox, or in a column to the right of the fox, then the goose cannot be caught.
Label the rows 1-7 from top to bottom, and the columns A-I from left to right; the goose starts at A1, and the fox at I7.
The goose's first move is to the right, to B1.
If the fox moves down, to I6, then the goose's next six moves are all up; the fox cannot catch the goose before the goose reaches B7, and since the fox cannot move up, it cannot catch the goose as it then moves to the right until it reaches I7.
If the fox moves to the left, to H7, they are on opposite corners of a 7x7 grid.
In this case, if both of their next moves are vertical, the fox is 6 columns from the goose, but the goose is 6 rows from getting into a row the fox cannot reach, so the goose keeps moving up until reaching the top row, then to the right.
Similarly, if both move horizontal, the fox is 6 rows from the goose, but the goose is 6 columns from getting into a column the fox cannot reach, so the goose keeps moving right until reaching the rightmost column, then up.
Any other pair of moves has them on opposite corners of a 6 x 6 grid, where the same applies.
From the 7 x 7 situation, the fox has to guess the goose's move correctly 6 times to end up in the same square as the goose; any mistake, and the goose escapes.
The probability of doing this is (1/2)^6 = 1/64, so the probability that the goose wins is 1 - 1/64 = 63 / 64.
Quote: acesideBut my strategy is correct too.
link to original post
Maybe I read it wrong, but how are they different?
Quote: ThatDonGuyQuote: acesideBut my strategy is correct too.
link to original post
Maybe I read it wrong, but how are they different?
link to original post
My strategy should be correct, but my number is 1/2+1/64. It seems like you are saying the number should be 1-1/64. Anyway, this is very interesting!

Youíre on a drug regimen that requires you to take one pill a day from each of two bottles, A and B. One day you tap one pill into your palm from the A bottle and, inadvertently, two pills from the B bottle. Unfortunately the A and B pills are indistinguishable, and taking more than one B pill per day is fatal. And the pills are very expensive, so you canít afford to throw out the handful and start over.
How can you arrange to take the correct dose without wasting any pills?

Meteors are more commonly seen between midnight and dawn than between dusk and midnight.
Why?
:strip_icc()/pic7300943.png)
White must place four white rooks on the board, one at a time, giving check with each one. After each placement the black king can respond with any normal legal move.
How can White plan his moves so that the fourth rook reliably gives checkmate?
Quote: GialmereIt's easy Monday. Time for some more brief befuddlements...
Youíre on a drug regimen that requires you to take one pill a day from each of two bottles, A and B. One day you tap one pill into your palm from the A bottle and, inadvertently, two pills from the B bottle. Unfortunately the A and B pills are indistinguishable, and taking more than one B pill per day is fatal. And the pills are very expensive, so you canít afford to throw out the handful and start over.
How can you arrange to take the correct dose without wasting any pills?
Meteors are more commonly seen between midnight and dawn than between dusk and midnight.
Why?To kill some time before a meeting of chess grandmasters, Burt Hochberg offered this anonymous puzzle from the 15th century...
White must place four white rooks on the board, one at a time, giving check with each one. After each placement the black king can respond with any normal legal move.
How can White plan his moves so that the fourth rook reliably gives checkmate?
link to original post
Carefully tap one more A pill into your palm. Now, you have two A pills and two B pills in your hand. Drop the four pills into a grinder and powder them.
Divide the powder into two equal piles. Consume one pile today and one pile tomorrow.
Quote: GialmereIt's easy Monday. Time for some more brief befuddlements...
Youíre on a drug regimen that requires you to take one pill a day from each of two bottles, A and B. One day you tap one pill into your palm from the A bottle and, inadvertently, two pills from the B bottle. Unfortunately the A and B pills are indistinguishable, and taking more than one B pill per day is fatal. And the pills are very expensive, so you canít afford to throw out the handful and start over.
How can you arrange to take the correct dose without wasting any pills?
Meteors are more commonly seen between midnight and dawn than between dusk and midnight.
Why?
PillsI know how to do this.
First, break all three pills into two halves and take a half of each today.
Second, take out a new pill from bottle A and break it into two halves, and then take one half of it today.
Third, take all the remaining halves tomorrow.
MeteorsWe can think all these meteors as dusts in a wind. If you move against the wind, you will hit more dusts. If you move along with the wind, you will hit less dusts. Between midnight and dawn, you move toward the metetors, so you will see more.
Quote: ChesterDog
Carefully tap one more A pill into your palm. Now, you have two A pills and two B pills in your hand. Drop the four pills into a grinder and powder them.
Divide the powder into two equal piles. Consume one pile today and one pile tomorrow.
link to original post
I agree, except I was planning to cut them in half. Then again, whenever I do that in real life, I seldom make a clean 50/50 cut.
I smell a lawsuit.Quote: GialmereUnfortunately the A and B pills are indistinguishable, and taking more than one B pill per day is fatal.
A very lucrative lawsuit.Quote:And the pills are very expensive, so you canít afford to throw out the handful and start over.
Quote: JoemanI smell a lawsuit.Quote: GialmereUnfortunately the A and B pills are indistinguishable, and taking more than one B pill per day is fatal.
A very lucrative lawsuit.Quote:And the pills are very expensive, so you canít afford to throw out the handful and start over.
link to original post
Quote: unJonI think you can add another A pill so you know you have 2 A and 2 B pills. Then cut them each in half and take half of each of the 4 pills today and the same tomorrow.Iíve never thought of this before. My guess is that itís because Earth rotates in the same direction it revolves around the sun. So between dusk and midnight, that part of Earth is facing away from the direction of travel along the path of the sun. Almost like looking out the rear windshield. And after midnight, you face the direction of travel as Earth is going through the field of meteors.
link to original post
Quote: ChesterDog
Carefully tap one more A pill into your palm. Now, you have two A pills and two B pills in your hand. Drop the four pills into a grinder and powder them.
Divide the powder into two equal piles. Consume one pile today and one pile tomorrow.
link to original post
Quote: acesidePills
I know how to do this.
First, break all three pills into two halves and take a half of each today.
Second, take out a new pill from bottle A and break it into two halves, and then take one half of it today.
Third, take all the remaining halves tomorrow.
MeteorsWe can think all these meteors as dusts in a wind. If you move against the wind, you will hit more dusts. If you move along with the wind, you will hit less dusts. Between midnight and dawn, you move toward the metetors, so you will see more.
link to original post
Quote: WizardI agree, except I was planning to cut them in half. Then again, whenever I do that in real life, I seldom make a clean 50/50 cut.
link to original post
Correct!!
Well done.
Prediction: Joeman wins his lawsuit and his next of kin collect the money.
Quote: unJon...Iíve never thought of this before....
Yeah. The closest I've come is an inarticulate thought wondering why these damn meteor showers always seem to be on so late and never at a reasonable hour.
I'll let the chess puzzle ride another day.
---------------------------------------------

Rook#1: place it at H5 so that King must move down;
Rook #2: place it two squares directly underneath King;
Rook 3: place it in the same column above Rook #2 to check.
Rook #4: place it in the same column with Rook #3 to checkmate.
:strip_icc()/pic7302462.png)
How many ways are there to arrange four dots on a plane (or piece of paper) such that whichever two dots you choose, the distance between these two points is one of two values? In a square, any two vertices are separated by either the length of a side or the length of a diagonal ó no matter which two points are chosen, the distance between them will be one of two values.
Besides the square, how many other shape configurations have this property?
Quote: acesideI guess only two ways. One is this square, and the other one is a triangle with a 4th dot on its weight center.
link to original post
Too lazy to solve but I would have thought there would also be a
Quote: unJonQuote: acesideI guess only two ways. One is this square, and the other one is a triangle with a 4th dot on its weight center.
link to original post
Too lazy to solve but I would have thought there would also be atrapezoid solution where the diagonal distance equals the length of the longer side. And the three short sides are the same distance.
link to original post
In that case

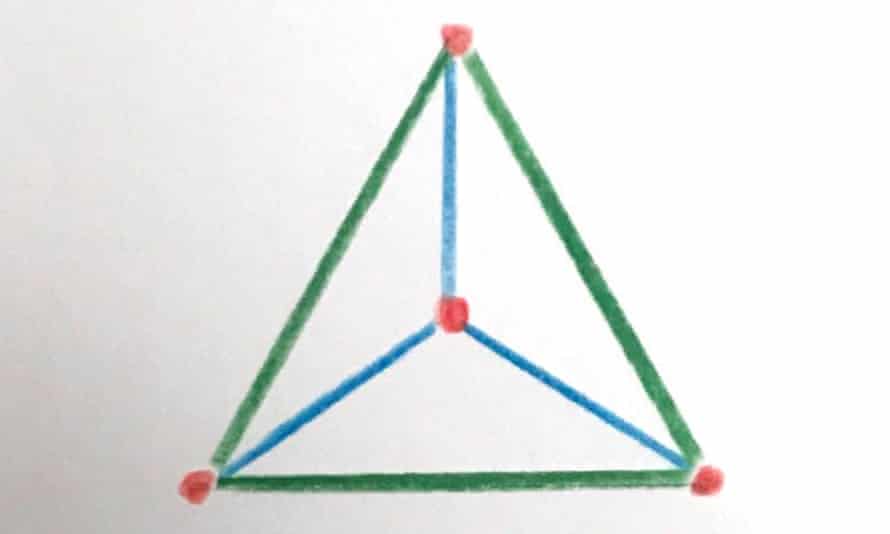
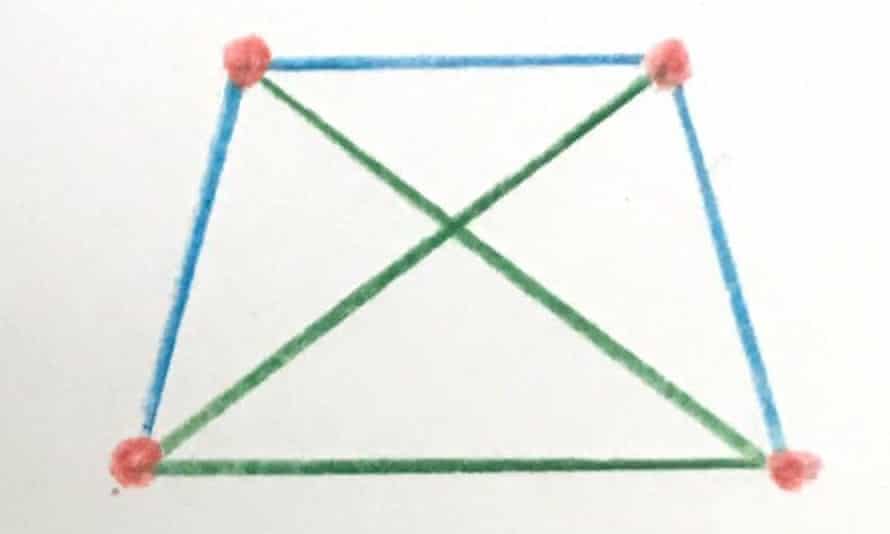

You guys are getting close to all of them.
Quote: GialmereSo far we correctly have...
You guys are getting close to all of them.
link to original post
Looking at the triangle, I see how you could make a
Quote: unJonQuote: GialmereSo far we correctly have...
You guys are getting close to all of them.
link to original post
Looking at the triangle, I see how you could make aan upside down kite shape where you move the center dot straight down until the distance between it and the top dot is the same as the sides of the equilateral triangle (the green lines).
link to original post
Two more shapes
#6: Another 4-sided shape from outside contacting an isosceles triangle and an equilateral triangle on their bases.




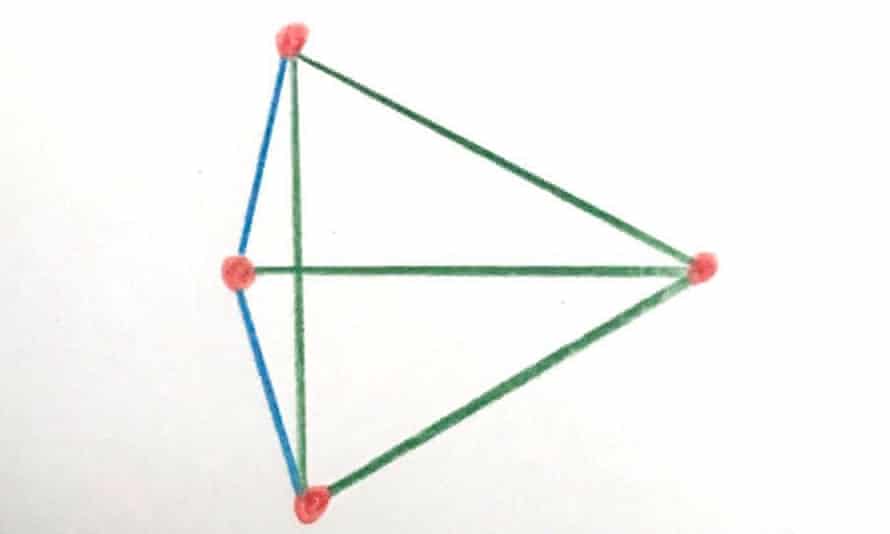
You're on the bell lap with one shape to go.
Dart
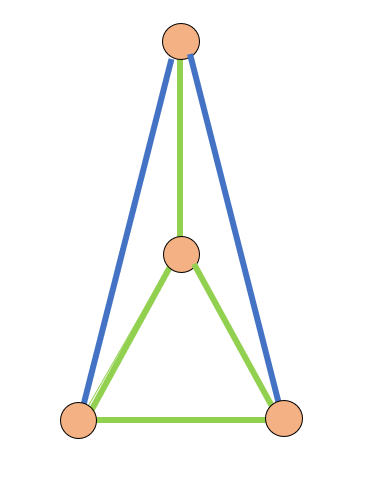
Quote: ChesterDog
Dart
link to original post
Oh thatís a really clever one.