Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
January 31st, 2023 at 3:17:44 PM
permalink
Quote: WizardQuote: unJonDoes the surface area include a lid on top?
link to original post
No, but does include the bottom.
Also, my IP had an incorrect number for the area of the actual McDonalds cup. I forgot to include the bottom. My revised figure is 61.653416 square inches. Do you agree CD?
link to original post
Yes, I get the sum of areas of the bottom and side as 61.653416 square inches, too. But I get a volume of 42.804200 cubic inches.
January 31st, 2023 at 3:32:00 PM
permalink
Quote: ChesterDogYes, I get the sum of areas of the bottom and side as 61.653416 square inches, too. But I get a volume of 42.804200 cubic inches.
link to original post
Hmmm. The way I did it was to extend the cup into a cone and subtract off the part under the bottom. Here are some steps along the way:
Top radius = 1.75
Bottom radius = 1.25
Height of cup = 6
Height of large cone = 21
Height of small code = 15
Volume of large cone = 67.3478925113312
Volume of small cone = 34.3611696486384
Volume of cup = 32.9867228626928
Where do we part company?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 31st, 2023 at 3:48:29 PM
permalink
Quote: WizardQuote: ChesterDogYes, I get the sum of areas of the bottom and side as 61.653416 square inches, too. But I get a volume of 42.804200 cubic inches.
link to original post
Hmmm. The way I did it was to extend the cup into a cone and subtract off the part under the bottom. Here are some steps along the way:
Top radius = 1.75
Bottom radius = 1.25
Height of cup = 6
Height of large cone = 21
Height of small code = 15
Volume of large cone = 67.3478925113312
Volume of small cone = 34.3611696486384
Volume of cup = 32.9867228626928
Where do we part company?
link to original post
I see that you used a height of 21 for the small cone, but you know that 15 is its height.
Volume of small cone = (1/3)(pi)(15)(1.25)2 = 24.5436926061703.
January 31st, 2023 at 5:09:59 PM
permalink
Quote: ChesterDog
I see that you used a height of 21 for the small cone, but you know that 15 is its height.
Volume of small cone = (1/3)(pi)(15)(1.25)2 = 24.5436926061703.
link to original post
You're absolutely right. Formula error. I fixed it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 1st, 2023 at 8:08:02 AM
permalink
Are you ignoring the surface area of the bottom rim that extends below the bottom of the cup?
:max_bytes(150000):strip_icc():format(webp)/Buffalo-McDonalds-Coffee-Cup-Litterer-FT-BLOG0622-5e5281391a2c466d9a8ca5b25fb197bb.jpg)
Dog Hand
Dog Hand
February 1st, 2023 at 8:23:53 AM
permalink
Quote: DogHandAre you ignoring the surface area of the bottom rim that extends below the bottom of the cup?
Dog Hand
link to original post
Nice catch. Of course, it is common for recreational mathematicians to simplify such things as the shape of objects when swapping math problems with each other.
But this is a good illustration of why engineers occupy a higher stratum than mathematicians on the hierarchy of biological life forms.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
February 1st, 2023 at 9:25:48 AM
permalink
Quote: DogHandAre you ignoring the surface area of the bottom rim that extends below the bottom of the cup?
link to original post
Yes
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 1st, 2023 at 9:26:56 AM
permalink
Quote: gordonm888But this is a good illustration of why engineers occupy a higher stratum than mathematicians on the hierarchy of biological life forms.
link to original post
Hey! I think you should serve a 5-minute off-the-record suspension for that.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 1st, 2023 at 9:42:13 AM
permalink
Quote: WizardQuote: gordonm888But this is a good illustration of why engineers occupy a higher stratum than mathematicians on the hierarchy of biological life forms.
link to original post
Hey! I think you should serve a 5-minute off-the-record suspension for that.
link to original post
Separating myself from the forum for 5 long minutes? Oh, the humanity! the humanity!
*meekly complies*
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
February 1st, 2023 at 10:39:58 AM
permalink
Quote: gordonm888Quote: DogHandAre you ignoring the surface area of the bottom rim that extends below the bottom of the cup?
Dog Hand
link to original post
Nice catch. Of course, it is common for recreational mathematicians to simplify such things as the shape of objects when swapping math problems with each other.
But this is a good illustration of why engineers occupy a higher stratum than mathematicians on the hierarchy of biological life forms.
link to original post
At least it's not one of those extra-pointy shapes that takes more paint to cover the outside than it can hold inside.
Checking that five minutes is up...
May the cards fall in your favor.
February 1st, 2023 at 10:57:29 AM
permalink
Speaking as an engineer, I think you let Gordon off too easily, Wiz! ;)Quote: WizardQuote: gordonm888But this is a good illustration of why engineers occupy a higher stratum than mathematicians on the hierarchy of biological life forms.
link to original post
Hey! I think you should serve a 5-minute off-the-record suspension for that.
link to original post
A pessimist says the glass is half-empty.
An optimist says the glass is half-full.
An engineer says the glass is twice as big as it needs to be!
"Dealer has 'rock'... Pay 'paper!'"
February 4th, 2023 at 10:31:07 AM
permalink
Quote: ThatDonGuyTime for a toughie...hopefully I didn't post this already years ago:
You download a free calculator, but you notice a small problem: while the keys [0] through [9], [ + ], [ - ], [ = ], [ ( ], [ ) ], and [ 1/x ] work, whenever you press the multiplication and division keys, a message pops up asking if you want to upgrade to the premium version that includes those keys for a small fee.
There's one other feature; you can't use any particular key more than 50 times without the app shutting down.
You're better than that - using the keys you are given, multiply 256 by 4096 in a single equation. None of this "4096 + 4096 + ... + 4096 =, then write down the answer, then reload the app, then do it again until you have added 4096 256 times" nonsense, either.
link to original post
I never did answer this...
I will answer this in general, multiplying P by Q.
Let A = 1 / (1 / P - 1 / (P + 1)) = P^2 + P
Let B = 1 / (1 / Q - 1 / (Q + 1)) = Q^2 + Q
Let C = 1 / (1 / (P + Q) - 1 / ((P + Q) + 1)) = (P + Q)^2 + (P + Q)
Then C - A - B = 2PQ
PQ = 1 / (1 / (C - A - B) + 1 / (C - A - B))
= 1 / (1 / (1 / (1 / (P + Q) - 1 / ((P + Q) + 1))) - 1 / (1 / P - 1 / (P + 1)) - 1 / (1 / Q - 1 / (Q + 1)) + 1 / (1 / (P + Q) - 1 / ((P + Q) + 1))) - 1 / (1 / P - 1 / (P + 1)) - 1 / (1 / Q - 1 / (Q + 1)) ) )
Replace P with 256 and Q with 4096
February 4th, 2023 at 10:44:16 AM
permalink
Here's another one:
Remove the 13 hearts from a deck of cards, shuffle them, and lay them out on a table, left to right. Starting with the 2, remove the cards in order, 2, 3, 4, and so on through Ace.
What is the probability that only one of the 12 cards that you removed after the deuce was to the left of the card you previously removed?
For example, in the above picture, the only time you go from right to left is when going from the 5 to the 6.
Remove the 13 hearts from a deck of cards, shuffle them, and lay them out on a table, left to right. Starting with the 2, remove the cards in order, 2, 3, 4, and so on through Ace.
What is the probability that only one of the 12 cards that you removed after the deuce was to the left of the card you previously removed?
For example, in the above picture, the only time you go from right to left is when going from the 5 to the 6.
February 4th, 2023 at 2:34:04 PM
permalink
I don't understand your instruction here "Starting with the 2, remove the cards in order, 2, 3, 4, and so on through Ace." Also, there are 13 cards here, why do you say 12 cards?
February 4th, 2023 at 2:58:11 PM
permalink
Quote: ThatDonGuyHere's another one...What is the probability that only one of the 12 cards that you removed after the deuce was to the left of the card you previously removed?...
Rather than thinking about removing cards consider placing the cards down starting with Ace, King etc. If this is random then it's 50-50 whether the King goes right or left of the Ace. If your example every card except the 5 would have been placed left of the previous one. It doesn't really matter the position of the card being placed with respect of the ones already down there, just whether it's right or left of the previous one.
Thus the question is equivalent to asking if you toss 12 coins (the first card is just placed so can't be "left or right" of the previous one, thus leaving 12 decision points) whether there is only one Heads. The chances of that = 12 / 212 = 3/1024.
Thus the question is equivalent to asking if you toss 12 coins (the first card is just placed so can't be "left or right" of the previous one, thus leaving 12 decision points) whether there is only one Heads. The chances of that = 12 / 212 = 3/1024.
February 4th, 2023 at 3:21:31 PM
permalink
Quote: acesideI don't understand your instruction here "Starting with the 2, remove the cards in order, 2, 3, 4, and so on through Ace." Also, there are 13 cards here, why do you say 12 cards?
link to original post
Remove the 2 first, then the 3, then the 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, and Ace, in that order.
The "12 cards" are the 12 cards you removed after the 2. Since you remove the 2 first, it can't possibly be "to the left of the card you previously removed."
February 6th, 2023 at 11:23:14 AM
permalink
Our local alternative weekly runs a math puzzle every week. Here's one they ran back in September:
Study the relationship between the numbers to find the pattern.
1, 2, 3 > 3
1, 6, 3 > -1
4, 2, 3 > ?
My question is, is there a way to solve this besides brute force?
Study the relationship between the numbers to find the pattern.
1, 2, 3 > 3
1, 6, 3 > -1
4, 2, 3 > ?
My question is, is there a way to solve this besides brute force?
Let A, B, C = the digits. Formula is 2A + C - B. So the answer is 9.
I run Easy Vegas ( https://easy.vegas )
February 6th, 2023 at 5:00:37 PM
permalink
Quote: MichaelBluejayOur local alternative weekly runs a math puzzle every week. Here's one they ran back in September:
Study the relationship between the numbers to find the pattern.
1, 2, 3 > 3
1, 6, 3 > -1
4, 2, 3 > ?
My question is, is there a way to solve this besides brute force?Let A, B, C = the digits. Formula is 2A + C - B. So the answer is 9.
link to original post
If this is of the form pA + qB + rC = s, then the solution to the third one can be anything.
The first one is A + 2B + 3C = 3, and the second is A + 6B + 3C = -1, so B = -1 and A + 3C = 5
The third one is 4A + 2B + 3C = x; this is 3A + A + 2B + 3C = x, or 3A + 3 = x
If A = 2, then x = 12, but if A = 5 (and C = 0), then x = 18.
February 6th, 2023 at 5:55:49 PM
permalink
Why not sum the three terms and say the third line is greater than all integers less than 9?
Or take the products and it will work for all integers under 24
Just about anything will satisfy those conditions
Or take the products and it will work for all integers under 24
Just about anything will satisfy those conditions
It’s all about making that GTA
February 7th, 2023 at 4:01:28 PM
permalink
Quote: charliepatrickQuote: ThatDonGuyHere's another one...What is the probability that only one of the 12 cards that you removed after the deuce was to the left of the card you previously removed?...
Rather than thinking about removing cards consider placing the cards down starting with Ace, King etc. If this is random then it's 50-50 whether the King goes right or left of the Ace. If your example every card except the 5 would have been placed left of the previous one. It doesn't really matter the position of the card being placed with respect of the ones already down there, just whether it's right or left of the previous one.
Thus the question is equivalent to asking if you toss 12 coins (the first card is just placed so can't be "left or right" of the previous one, thus leaving 12 decision points) whether there is only one Heads. The chances of that = 12 / 212 = 3/1024.
link to original post
Not quite.
Since you only go from right to left once, all 13 cards are in one of two left-to-right "runs".
For example, with 8, 9, 2, 3, 10, 4, 5, J, Q, K, 6, A, 7, the first run is 2-7, then left for the 8, and the second run is 8-Ace.
If you select the positions for the first run, the cards starting with 2 must appear in those positions in left-to-right order, and the remaining cards have to be in the remaining positions, also in left-to-right order.
There are 2^13 = 8192 ways to select which cards would be in the first run.
However, one of those is "all 13 cards" and another is "no cards," both of which mean that you can go from left to right in a single run.
Also, for each N from 1 to 12, if you choose the N cards starting from the left, then all of the cards in the second one are to the right of the last card of the first run, so again, it is a single run.
(i.e. if N = 3, then if the first 3 cards are 2, 3, 4 in that order, then the remaining cards are 5, 6, 7, 8, 9, 10, J, Q, K, A in that order, but there is no "right to left" move.)
There are a total of 8192 - 2 - 12 = 8178 permutations out of the 13! that work.
The solution is 8178 / 13!, which, in lowest terms, is 1363 / 1,037,836,800.
February 7th, 2023 at 4:59:08 PM
permalink
Yes I see. It took me a while to understand but using the same concept here's an alternative way I managed to come to the same solution...Quote: ThatDonGuy...Not quite...Here's the answer
Place 13 cards, count how many times you have to go left to reach the next one.
If there's only one such time then there is a set of numbers which are in order, followed by a second set.
The first set cannot occupy the first N spaces, otherwise they're all in order.
We might also define that "2" has to be in the first set.
Similarly we can define that "A" has to be in the second set.
Each "first set" will consist of a sequence of numbers/cards (e.g. 2 3 4)…
… so the only decision is which slots the first set occupies.
The second set, also has to be in order, is then defined to occupy the other (empty) slots.
So let's look at how many combinations there are for the "first set" of various sizes.
If there's only one such time then there is a set of numbers which are in order, followed by a second set.
The first set cannot occupy the first N spaces, otherwise they're all in order.
We might also define that "2" has to be in the first set.
Similarly we can define that "A" has to be in the second set.
Each "first set" will consist of a sequence of numbers/cards (e.g. 2 3 4)…
… so the only decision is which slots the first set occupies.
The second set, also has to be in order, is then defined to occupy the other (empty) slots.
So let's look at how many combinations there are for the "first set" of various sizes.
| Size = 1 | 12 | The "2" can be placed in the 2nd thru 13th position (COMBIN(12,1)) |
| Size = 2 | 77 | The "2" can be placed in the 1st thru 12th position, then the "3" can be placed after that, except not 1st and 2nd (COMBIN(13,2)-1). |
| Size =3 | 285 | The "2","3","4" can be placed any where (in order) in positions 1 thru 13, but not 1st/2nd/3rd. |
| Size = 4 | 714 | similarly for 2 3 4 5 |
| Size = 5 | 1 286 | …and 2 3 4 5 6 |
| Size = 6 | 1 715 | …and 2 3 4 5 6 7 |
| 7-12 similar to 6-1 | 4 089 | |
8 178 | 1 363 | |
6 227 020 800 | 1 037 836 800 |
February 17th, 2023 at 11:18:19 AM
permalink
There’s a new casino game using a single 20-sided die numbered 1-20. Very simple rules: you roll the die until the cumulative total of your rolls is 20 or higher. If you hit 20, you get paid 6 to 1. You lose if you go over 20 without hitting it.
What’s the house edge?
Markov chains and simulations are not acceptable. Sorry ThatDonGuy
What’s the house edge?
Markov chains and simulations are not acceptable. Sorry ThatDonGuy
It’s all about making that GTA
February 17th, 2023 at 1:53:20 PM
permalink
When you roll a 20 first, you have 1 way to win but 0 way to lose.
When you roll a 19 first, you have 1 way to win but 19 ways to lose.
When you roll a 18 first, you have 2 ways to win but 37 ways to lose.
When you roll a 17 first, you have 4 ways to win but 73 ways to lose.
When you roll a 16 first, you have 8 ways to win but 145 ways to lose.
When you roll a 15 first, you have 16 ways to win but 289 ways to lose.
... ...
Adding all these numbers together, we get 0.052631574 chance of winning but 0.947368426 chance of losing.
This gives a house edge of 63.158%.
February 17th, 2023 at 2:23:18 PM
permalink
DisagreeQuote: aceside
When you roll a 20 first, you have 1 way to win but 0 way to lose.
When you roll a 19 first, you have 1 way to win but 19 ways to lose.
When you roll a 18 first, you have 2 ways to win but 37 ways to lose.
When you roll a 17 first, you have 4 ways to win but 73 ways to lose.
When you roll a 16 first, you have 8 ways to win but 145 ways to lose.
When you roll a 15 first, you have 16 ways to win but 289 ways to lose.
... ...
Adding all these numbers together, we get 0.052631574 chance of winning but 0.947368426 chance of losing.
This gives a house edge of 63.158%.
link to original post
It’s all about making that GTA
February 17th, 2023 at 2:58:13 PM
permalink
Quote: Ace2There’s a new casino game using a single 20-sided die numbered 1-20. Very simple rules: you roll the die until the cumulative total of your rolls is 20 or higher. If you hit 20, you get paid 6 to 1. You lose if you go over 20 without hitting it.
What’s the house edge?
Markov chains and simulations are not acceptable. Sorry ThatDonGuy
link to original post
Do I need an exact, as in rational number, answer?
Well, not so much an approximation, but this is about as close to a closed form as I can get at the moment:
There is 1 way to roll 20 with 1 roll; the probability is 1/20.
There are 19 ways to do it with 2 rolls; the probability of each is (1/20)^2.
There are C(19,2) ways to do it with 3 rolls; the probability of each is (1/20)^3.
...
There are C(19,N-1) ways to do it with N rolls, where N is in {1, 2, ..., 20}; the probability of each N-roll result is (1/20)^N.
The sum is C(19,0) / 20 + C(19,1) / 20^2 + C(19,2) / 20^3 + ... + C(19,19) / 20^20 = about 0.12634751
The house edge = ((1 - p) - 6p) x 100% = about 11.5567%
February 17th, 2023 at 3:11:27 PM
permalink
Final numbers look good, but looking for an exact answerQuote: ThatDonGuyQuote: Ace2There’s a new casino game using a single 20-sided die numbered 1-20. Very simple rules: you roll the die until the cumulative total of your rolls is 20 or higher. If you hit 20, you get paid 6 to 1. You lose if you go over 20 without hitting it.
What’s the house edge?
Markov chains and simulations are not acceptable. Sorry ThatDonGuy
link to original post
Do I need an exact, as in rational number, answer?
Well, not so much an approximation, but this is about as close to a closed form as I can get at the moment:
There is 1 way to roll 20 with 1 roll; the probability is 1/20.
There are 19 ways to do it with 2 rolls; the probability of each is (1/20)^2.
There are C(19,2) ways to do it with 3 rolls; the probability of each is (1/20)^3.
...
There are C(19,N-1) ways to do it with N rolls, where N is in {1, 2, ..., 20}; the probability of each N-roll result is (1/20)^N.
The sum is C(19,0) / 20 + C(19,1) / 20^2 + C(19,2) / 20^3 + ... + C(19,19) / 20^20 = about 0.12634751
The house edge = ((1 - p) - 6p) x 100% = about 11.5567%
link to original post
Last edited by: Ace2 on Feb 17, 2023
It’s all about making that GTA
February 17th, 2023 at 4:25:00 PM
permalink
Quote: Ace2...but looking for an exact answer...
1-POWER(21,19)/POWER(20,20)*7
February 17th, 2023 at 4:34:42 PM
permalink
I agree!Quote: charliepatrickQuote: Ace2...but looking for an exact answer...
1-POWER(21,19)/POWER(20,20)*7
link to original post
This morning I was studying number compositions and realized that there are (n+1)^(n-1) ways in n^n permutations to get total of n. So, for instance, rolling a six-sided die labeled 1-6 you have a 7^5 / 6^6 =~ 36% chance of having a cumulative total of 6 before going over 6.
But I haven’t figured out why this works. Have you?
It’s all about making that GTA
February 17th, 2023 at 4:36:25 PM
permalink
Quote: Ace2Final numbers look good, but looking for an exact answerQuote: ThatDonGuyQuote: Ace2There’s a new casino game using a single 20-sided die numbered 1-20. Very simple rules: you roll the die until the cumulative total of your rolls is 20 or higher. If you hit 20, you get paid 6 to 1. You lose if you go over 20 without hitting it.
What’s the house edge?
Markov chains and simulations are not acceptable. Sorry ThatDonGuy
link to original post
Do I need an exact, as in rational number, answer?
Well, not so much an approximation, but this is about as close to a closed form as I can get at the moment:
There is 1 way to roll 20 with 1 roll; the probability is 1/20.
There are 19 ways to do it with 2 rolls; the probability of each is (1/20)^2.
There are C(19,2) ways to do it with 3 rolls; the probability of each is (1/20)^3.
...
There are C(19,N-1) ways to do it with N rolls, where N is in {1, 2, ..., 20}; the probability of each N-roll result is (1/20)^N.
The sum is C(19,0) / 20 + C(19,1) / 20^2 + C(19,2) / 20^3 + ... + C(19,19) / 20^20 = about 0.12634751
The house edge = ((1 - p) - 6p) x 100% = about 11.5567%
link to original post
link to original post
The sum is C(19,0) / 20 + C(19,1) / 20^2 + C(19,2) / 20^3 + ... + C(19,19) / 20^20
= 1 / 20^20 * (20^19 1^0 C(19,0) + 20^18 1^1 C(19,1) + 20^17 1^2 C(19,2) + ... + 20^1 1^18 C(19,18) + 20^0 1^19 C(19,19))
= (20 + 1)^19 / 20^20 = 21^19 / 20^20
The house edge 1 - 7 x 21^19 / 20^20 = 12,118,123,517,682,817,120,934,533 / 104,857,600,000,000,000,000,000,000, or about 11.556743%.
February 17th, 2023 at 4:50:04 PM
permalink
Quote: Ace2This morning I was studying number compositions and realized that there are (n+1)^(n-1) ways in n^n permutations to get total of n. So, for instance, rolling a six-sided die labeled 1-6 you have a 7^5 / 6^6 =~ 36% chance of having a cumulative total of 6 before going over 6.
But I haven’t figured out why this works. Have you?
link to original post
I think I have.
If the target is n:
Start with a set of n 1s (i.e. {1, 1, 1, ..., 1, 1}).
By placing k-1 dividers between consecutive elements in the set, such that no two consecutive elements have more than one divider, you partition n into k positive integers whose sum is n. There are n-1 places to place the dividers, so there are C(n-1, k-1) partitions of n into k positive integers.
In other words:
There are C(n-1, 0) ways to roll n with a single roll; the probability is 1 / n, or n^(n-1) / n^n.
There are C(n-1, 1) ways to roll n with two rolls; the probability is 1 / n^2, or n^(n-2) / n^n.
...
There are C(n-1, k) ways to roll n with k rolls; the probability is 1 / n^k, or n^(n-k) / n^n.
The sum of the probabilities is
(C(n-1, 0) n^(n-1) + C(n-1, 1) n^(n-2) + C(n-1, 2) n^(n-3) + ... + C(n-1, n-2) n^1 + C(n-1, n-1) n^0) / n^n
= (C(n-1, 0) n^(n-1) 1^0 + C(n-1, 1) n^(n-2) 1^1 + C(n-1, 2) n^(n-3) 1^2 + ... + C(n-1, n-2) n^1 1^(n-2) + C(n-1, n-1) n^0 1^(n-1)) / n^n
= (n + 1)^(n - 1) / n ^ n
QED
February 17th, 2023 at 4:54:18 PM
permalink
Good work!Quote: ThatDonGuyQuote: Ace2This morning I was studying number compositions and realized that there are (n+1)^(n-1) ways in n^n permutations to get total of n. So, for instance, rolling a six-sided die labeled 1-6 you have a 7^5 / 6^6 =~ 36% chance of having a cumulative total of 6 before going over 6.
But I haven’t figured out why this works. Have you?
link to original post
I think I have.
If the target is n:
Start with a set of n 1s (i.e. {1, 1, 1, ..., 1, 1}).
By placing k-1 dividers between consecutive elements in the set, such that no two consecutive elements have more than one divider, you partition n into k positive integers whose sum is n. There are n-1 places to place the dividers, so there are C(n-1, k-1) partitions of n into k positive integers.
In other words:
There are C(n-1, 0) ways to roll n with a single roll; the probability is 1 / n, or n^(n-1) / n^n.
There are C(n-1, 1) ways to roll n with two rolls; the probability is 1 / n^2, or n^(n-2) / n^n.
...
There are C(n-1, k) ways to roll n with k rolls; the probability is 1 / n^k, or n^(n-k) / n^n.
The sum of the probabilities is
(C(n-1, 0) n^(n-1) + C(n-1, 1) n^(n-2) + C(n-1, 2) n^(n-3) + ... + C(n-1, n-2) n^1 + C(n-1, n-1) n^0) / n^n
= (C(n-1, 0) n^(n-1) 1^0 + C(n-1, 1) n^(n-2) 1^1 + C(n-1, 2) n^(n-3) 1^2 + ... + C(n-1, n-2) n^1 1^(n-2) + C(n-1, n-1) n^0 1^(n-1)) / n^n
= (n + 1)^(n - 1) / n ^ n
QED
link to original post
It’s all about making that GTA
February 17th, 2023 at 5:04:30 PM
permalink
Can you guys help look into my solution to see where I made a mistake in this probability calculation? I am a beginner. I just cannot find any problems with my numbers, but my result is incorrect.
February 17th, 2023 at 8:21:21 PM
permalink
Quote: acesideCan you guys help look into my solution to see where I made a mistake in this probability calculation? I am a beginner. I just cannot find any problems with my numbers, but my result is incorrect.
link to original post
"When you roll a 18 first, you have 2 ways to win but 37 ways to lose" - but you make it sound like each is equally possible, which is not true.
Of the two ways to win, one (rolling a 2) has a probability of 1/20, while the other (rolling two 1s) has a probability of 1/400.
Meanwhile, of the 37 ways to lose, 19 (rolling a 1, then a 2-20) each have a probability of 1/400, while the other 18 (rolling a 3-20) each have a probability of 1/20.
February 18th, 2023 at 6:28:44 AM
permalink
Very nice of you! I’ll plugin these 1/20 coefficients to do another calculation. Thank you.
February 19th, 2023 at 12:42:48 PM
permalink
Quote: ThatDonGuyQuote: Ace2There’s a new casino game using a single 20-sided die numbered 1-20. Very simple rules: you roll the die until the cumulative total of your rolls is 20 or higher. If you hit 20, you get paid 6 to 1. You lose if you go over 20 without hitting it.
What’s the house edge?
Markov chains and simulations are not acceptable. Sorry ThatDonGuy
link to original post
Do I need an exact, as in rational number, answer?
Well, not so much an approximation, but this is about as close to a closed form as I can get at the moment:
There is 1 way to roll 20 with 1 roll; the probability is 1/20.
There are 19 ways to do it with 2 rolls; the probability of each is (1/20)^2.
There are C(19,2) ways to do it with 3 rolls; the probability of each is (1/20)^3.
...
There are C(19,N-1) ways to do it with N rolls, where N is in {1, 2, ..., 20}; the probability of each N-roll result is (1/20)^N.
The sum is C(19,0) / 20 + C(19,1) / 20^2 + C(19,2) / 20^3 + ... + C(19,19) / 20^20 = about 0.12634751
The house edge = ((1 - p) - 6p) x 100% = about 11.5567%
link to original post
I got the correct answer by plugging in these 1/20 coefficients, but I noticed that you used a simpler method. I still don't understand this part, there are C(19,2) ways to roll a sum 20 with 3 rolls. How do you get this C(19,2) ?
February 19th, 2023 at 1:02:09 PM
permalink
Consider a road twenty miles long where there's a pub (and milemarker) every mile. You're going to cover all twenty miles finishing at the Mile20 pub, but decide to break the journey into three segments. The question is how many ways are there to do this?Quote: aceside...I still don't understand this part, there are C(19,2) ways to roll a sum 20 with 3 rolls. How do you get this C(19,2) ?
The answer is you have to select two other pubs to stop at. These will be somewhere between or including MP1 and MP19. Thus there are 19 possible pubs selections and you have to choose two of them.
February 19th, 2023 at 1:47:05 PM
permalink
This illustration is very effective!
February 20th, 2023 at 11:38:05 AM
permalink
Our local alternative weekly runs a math puzzle every week. Here's the one from 11/4/22:
Without using a ruler or scissors, can you measure exactly 6 inches by folding a standard (8.5" x 11") piece of paper?
Without using a ruler or scissors, can you measure exactly 6 inches by folding a standard (8.5" x 11") piece of paper?
I run Easy Vegas ( https://easy.vegas )
February 20th, 2023 at 12:00:21 PM
permalink
Quote: MichaelBluejayOur local alternative weekly runs a math puzzle every week. Here's the one from 11/4/22:
Without using a ruler or scissors, can you measure exactly 6 inches by folding a standard (8.5" x 11") piece of paper?
link to original post
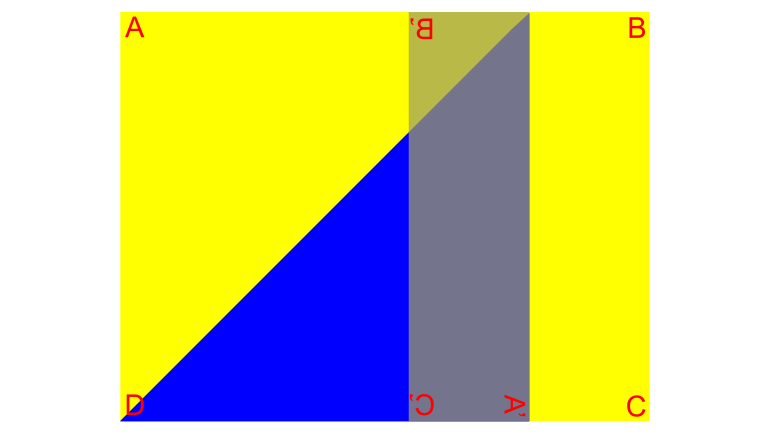
Let ABCD be the four corners, with AB and CD being the two 8 1/2" sides.
Fold AB such that B now touches side AD.
Fold CD such that C now touches side AD.
The distance between the new locations of B and C is 6 inches.
February 20th, 2023 at 12:01:13 PM
permalink
The first fold is to create the blue triangle, i.e. so AD becomes DA'; so DA' = 8.5". The second is to fold over the right hand part thus, note that this (A'C) was 11-8.5" = 2.5" wide. Thus this creates a length of A'C' of 2.5", hence DC' =8.5-2.5=6".
February 20th, 2023 at 1:52:20 PM
permalink
Quote: ThatDonGuyQuote: MichaelBluejayOur local alternative weekly runs a math puzzle every week. Here's the one from 11/4/22:
Without using a ruler or scissors, can you measure exactly 6 inches by folding a standard (8.5" x 11") piece of paper?
link to original post
Let ABCD be the four corners, with AB and CD being the two 8 1/2" sides.
Fold AB such that B now touches side AD.
Fold CD such that C now touches side AD.
The distance between the new locations of B and C is 6 inches.
link to original post
That seems quite clever.
May the cards fall in your favor.
February 20th, 2023 at 1:56:50 PM
permalink
You guys are doing it in fewer steps than
The given solution is a diagram, I'll write it out as text: Orient the paper tall (portrait), not wide (landscape). Fold the top-left corner to align with the right side. Draw a horizontal line at the overlap, or fold the unoverlapped part up and then back down to make a crease. Repeat with the bottom-left corner. The area between the two marks or creases is 6".
I run Easy Vegas ( https://easy.vegas )
February 20th, 2023 at 2:09:29 PM
permalink
What’s more likely:
Flipping a fair coin four times and getting no heads
Flipping a fair coin fourteen times and getting no consecutive heads
Flipping a fair coin four times and getting no heads
Flipping a fair coin fourteen times and getting no consecutive heads
It’s all about making that GTA
February 20th, 2023 at 4:24:34 PM
permalink
Quote: Ace2What’s more likely:
Flipping a fair coin four times and getting no heads
Flipping a fair coin fourteen times and getting no consecutive heads
link to original post
There is 1 way to toss 14 coins without any heads.
If there is 1 head, it can be in any of the 14 positions, so there are 14 sets of tosses with 1 head.
For more than 1 head, each head must come either at the beginning, at the end, or between two tails.
Let N be the number of heads; there are 14-N tails, which have 14-N-1, or 13-N, places between them, plus one at the beginning and one at the end, for a total of 15-N; therefore, there are C(15-N, N) sets of tosses with N heads where no two are consecutive.
The total number is 1 + 14 + C(13,2) + C(12,3) + C(11,4) + C(10,5) + C(9,6) + C(8,7) = 987.
The probability is 987 / 2^14, or about 1 / 16.6.
The probability of 4 tosses without any heads is 1 / 16, or 1024 / 2^14.
Therefore, flipping a coin four times and getting no heads is more likely.
February 20th, 2023 at 5:46:47 PM
permalink
Agree. The slicker way to get 987 ways in 2^14 is to use the 16th Fibonacci number, which can be directly calculated as: round(Φ^16 / 5^.5)Quote: ThatDonGuyQuote: Ace2What’s more likely:
Flipping a fair coin four times and getting no heads
Flipping a fair coin fourteen times and getting no consecutive heads
link to original post
There is 1 way to toss 14 coins without any heads.
If there is 1 head, it can be in any of the 14 positions, so there are 14 sets of tosses with 1 head.
For more than 1 head, each head must come either at the beginning, at the end, or between two tails.
Let N be the number of heads; there are 14-N tails, which have 14-N-1, or 13-N, places between them, plus one at the beginning and one at the end, for a total of 15-N; therefore, there are C(15-N, N) sets of tosses with N heads where no two are consecutive.
The total number is 1 + 14 + C(13,2) + C(12,3) + C(11,4) + C(10,5) + C(9,6) + C(8,7) = 987.
The probability is 987 / 2^14, or about 1 / 16.6.
The probability of 4 tosses without any heads is 1 / 16, or 1024 / 2^14.
Therefore, flipping a coin four times and getting no heads is more likely.
link to original post
It’s all about making that GTA
February 22nd, 2023 at 12:59:27 PM
permalink
You and I have to travel from Startville to Endville, but we have only one bicycle between us. So we decide to leapfrog: We’ll leave Startville at the same time, you walking and I riding. I’ll ride for 1 mile, and then I’ll leave the bicycle at the side of the road and continue on foot. When you reach the bike you’ll ride it for 1 mile, passing me at some point, then leave the bike and continue walking. And so on — we’ll continue in this way until we’ve both reached the destination.
Will this save any time? You say yes: Each of us is riding for part of the distance, and riding is faster than walking, so using the bike must increase our average speed.
I say no: One or the other of us is always walking; ultimately every inch of the distance between Startville and Endville is traversed by someone on foot. So the total time is unchanged — leapfrogging with the bike is no better than walking the whole distance on foot.
Who’s right?
Have you tried 22 tonight? I said 22.
February 22nd, 2023 at 2:02:17 PM
permalink
Save any time versus what, versus both of you walking? Seems like it:
walk 3mph = 20m/mile
bike 12mph = 5m/mile
A starts on bike
B starts on foot
00:00 A departs on bike, B departs on foot
00:05 A finishes Mile 1 on bike and starts walking
20:00 B picks up bike at Mile 1
25:00 A finishes Mile 2 on foot at same time B finishes on bike
So after 2 miles, each person took 25 minutes (a 5-minute bike mile and a 20-minute walk mile). That's 12.5 minutes per mile, and beats walking.
This helped me wrap my mind around why it works that way: Imagine just a single person taking the trip, alternating walking and biking each mile. After every mile s/he walks, there happens to be a bicycle there. So, s/he's walking and biking half the time, which is gonna be faster than just walking. The presence of the other person is just a distraction, it doesn't change the time taken.
walk 3mph = 20m/mile
bike 12mph = 5m/mile
A starts on bike
B starts on foot
00:00 A departs on bike, B departs on foot
00:05 A finishes Mile 1 on bike and starts walking
20:00 B picks up bike at Mile 1
25:00 A finishes Mile 2 on foot at same time B finishes on bike
So after 2 miles, each person took 25 minutes (a 5-minute bike mile and a 20-minute walk mile). That's 12.5 minutes per mile, and beats walking.
This helped me wrap my mind around why it works that way: Imagine just a single person taking the trip, alternating walking and biking each mile. After every mile s/he walks, there happens to be a bicycle there. So, s/he's walking and biking half the time, which is gonna be faster than just walking. The presence of the other person is just a distraction, it doesn't change the time taken.
Last edited by: MichaelBluejay on Feb 22, 2023
I run Easy Vegas ( https://easy.vegas )
February 22nd, 2023 at 5:22:08 PM
permalink
As has been said regardless of the two relative speeds, assuming the cycling is quicker than walking, one person cycles the first mile and then walks. The other person has to walk a mile before they reach the bicycle. By the time the two meet again the first person has cycled a mile and walked for some time, while the second person walked a mile and cycled for some distance. When they meet the time elapsed and distance covered is the same. If you were to plot the distance against time on a graph, the slopes of the walking would be the same, and the slopes of the cycling would be the same. Hence the shape of the two lines form a rhombus (is that the correct name for a rectangle where all the sides are equal). Hence each person, in whichever order, walked one mile and cycled one mile; and they meet every two miles.
Thus the combination of cycling and walking is clearly quicker than just walking.
Thus the combination of cycling and walking is clearly quicker than just walking.
February 22nd, 2023 at 5:48:07 PM
permalink
Quote: Gialmere
You and I have to travel from Startville to Endville, but we have only one bicycle between us. So we decide to leapfrog: We’ll leave Startville at the same time, you walking and I riding. I’ll ride for 1 mile, and then I’ll leave the bicycle at the side of the road and continue on foot. When you reach the bike you’ll ride it for 1 mile, passing me at some point, then leave the bike and continue walking. And so on — we’ll continue in this way until we’ve both reached the destination.
Will this save any time? You say yes: Each of us is riding for part of the distance, and riding is faster than walking, so using the bike must increase our average speed.
I say no: One or the other of us is always walking; ultimately every inch of the distance between Startville and Endville is traversed by someone on foot. So the total time is unchanged — leapfrogging with the bike is no better than walking the whole distance on foot.
Who’s right?
link to original post
He is. Your claim that "every inch of the distance is traversed by someone on foot" does not take into account that there are times when both of you are walking simultaneously, so it is faster than a single person walking the entire distance.
February 22nd, 2023 at 10:09:41 PM
permalink
Quote: charliepatrickAs has been said regardless of the two relative speeds, assuming the cycling is quicker than walking, one person cycles the first mile and then walks. The other person has to walk a mile before they reach the bicycle. By the time the two meet again the first person has cycled a mile and walked for some time, while the second person walked a mile and cycled for some distance. When they meet the time elapsed and distance covered is the same. If you were to plot the distance against time on a graph, the slopes of the walking would be the same, and the slopes of the cycling would be the same. Hence the shape of the two lines form a rhombus (is that the correct name for a rectangle where all the sides are equal). Hence each person, in whichever order, walked one mile and cycled one mile; and they meet every two miles.
Thus the combination of cycling and walking is clearly quicker than just walking.
link to original post
So far as I know, a rectangle with sides of equal length is usually called a square.
A rhombus is a 4 sided figure with equal length sides, opposite sides parallel, but does not imply right angles.
Parallelograms do not imply 4 equal length sides.
Trapezoids only imply that two (opposite) sides are parallel.
Kites are 4 sided, with adjacent sides of equal length.
It's been a while since geometry for me too, so I'm keen to know any 4-gon names I missed or screwed up.
May the cards fall in your favor.
