Easy math puzzles

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 27th, 2020 at 8:24:42 PM permalink

I agree, the answer is as quoted above.

I'll post a new problem shortly, but anybody else is welcome to do so before me.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 27th, 2020 at 8:49:07 PM permalink

Anaswer = 5^0.5 * 5^0.25 * 5^0.125 * 5^0.0625 *........
= 5^(0.5+0.25+0.125+0.0625+ .....)
= 5^1
= 5

0.5+0.25+0.125+0.0625+ .... is a geometric series, r=0.5, Sn = 0.5( 1- 0.5^infinity)/(1-0.5) = 2 * 0.5 = 1

ChesterDog

ChesterDog

Threads: 9
Posts: 1730

Joined: Jul 26, 2010

March 27th, 2020 at 9:46:00 PM permalink

Quote: djtehch34t

Let x = sqrt(5*sqrt...
x^2 = 5*sqrt....
x^2/5 = x
...

Instead of next dividing both sides by x, try subtracting x from both sides and factoring.

djtehch34t

djtehch34t

Threads: 2
Posts: 57

Joined: May 7, 2016

March 28th, 2020 at 4:56:46 AM permalink

Quote: ChesterDog

Instead of next dividing both sides by x, try subtracting x from both sides and factoring.

Dividing by x should be legit because we can clearly tell that x > 0?

ChesterDog

ChesterDog

Threads: 9
Posts: 1730

Joined: Jul 26, 2010

March 28th, 2020 at 5:41:40 AM permalink

Quote: djtehch34t
Dividing by x should be legit because we can clearly tell that x > 0?

It took me a while, but now it's clear to me that x must be greater than zero.

Thanks.

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

March 28th, 2020 at 4:07:01 PM permalink

If x = SQRT(5*SQRT(5*....)) = SQRT(5*x). It then seems obvious x=5, but mathematically squaring each side to get x^2 = x*5, so x=5.

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 29th, 2020 at 8:09:01 PM permalink

Here is your next puzzle that is too simple to be beer-worthy, but is nevertheless pretty challenging.

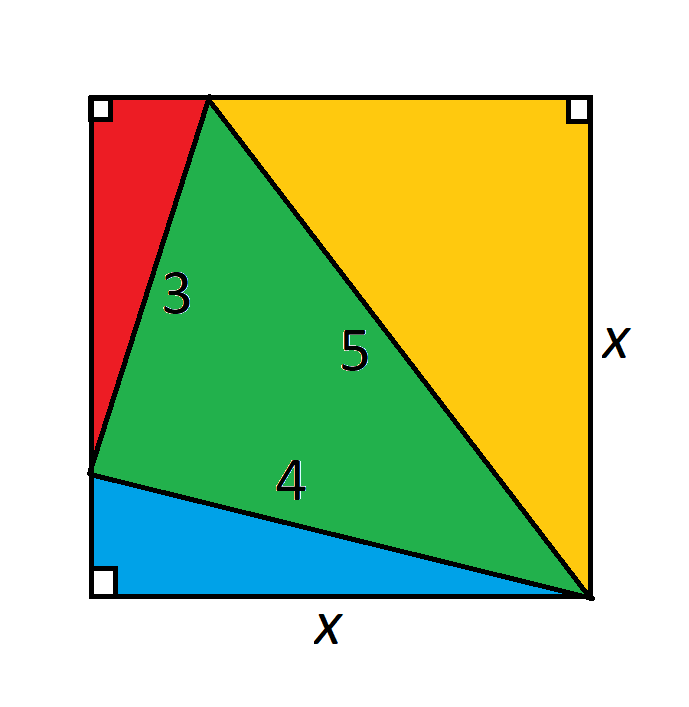
A 3-4-5 triangle is inscribed in a square of length x.

Find x.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ksdjdj

ksdjdj

Threads: 94
Posts: 1707

Joined: Oct 20, 2013

March 29th, 2020 at 9:02:15 PM permalink

Quote: Wizard

(snip)
A 3-4-5 triangle is inscribed in a square of length x.

Find x.

Could I possibly find an answer or approximate answer if I had:

Pen or pencil, grid paper (cm*** markings/spacing), ruler (cm*** markings/spacing) and a math compass

but there is probably an "easier/better" way^^^
***:

As long as the grid paper markings and ruler markings are the same, then you can use any unit of measurement, eg inches, mm, etc...

^^^:

Surely the Wiz doesn't expect us to have all this equipment lying around, to solve an "easier than normal" problem, so there must be a better way (I just can't think of it).

was I at least correct that this is the equipment needed for one way of getting the answer/ approximate answer (or am I wrong?)

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

Thanked by

March 29th, 2020 at 9:13:18 PM permalink

Graph paper would certainly be useful to get an estimate, but for full credit, I want to see an algebraic solution.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 29th, 2020 at 10:07:21 PM permalink

See image : https://imge.to/i/yV3aUG

From blue triangle, cos(θ) = x/4,

and

From red triangle, cos(θ) = a/3

Therefore, a/3= x/4, a=3x/4, and b = x/4

b^2+x^2 = 4^2

(x/4)^2 + x^2 = 16

x= 16/(17)^0.5 = 3.8806

ksdjdj

ksdjdj

Threads: 94
Posts: 1707

Joined: Oct 20, 2013

March 29th, 2020 at 10:09:21 PM permalink

Note: I know that this formula works for at least one type of "area of a triangle inside a square " problem, but I don't know if it works for the type you posted.

Length of side "X" = Square root of the "area of the square" =
Square root of ("Area of the Triangle" x 2)

Using the above, for a triangle where: 3 = base and 4 = height , then X would be = 3.46... (or square root of 12 to be exact).

X = √ 12 (where X must be a positive number )

I hope this is correct, as I will not be attempting any more answers to this problem if it is wrong (in other words, "too hard for me")

Edit:
Going by the answer above by ssho88, I am going to say my answer is almost certainly wrong.

Last edited by: ksdjdj on Mar 29, 2020

gordonm888
Administrator

gordonm888

Threads: 61
Posts: 5373

Joined: Feb 18, 2015

Thanked by

March 29th, 2020 at 11:58:04 PM permalink

Let's hope there is not a pandemic lockdown during the next total eclipse in 2024.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

March 30th, 2020 at 2:19:15 AM permalink

Quote: Wizard
Here is your next puzzle that is too simple to be beer-worthy, but is nevertheless pretty challenging.

A 3-4-5 triangle is inscribed in a square of length x.

Find x.

Nice puzzle - thanks.

The angle of the 3-4-5 triangle is a right angle, so the angle of the blue triangle at 34 and the red triangle add up to 90. So the blue triangle and red triangle are similar.
Thus if the base of blue is x, the base of red is 3/4 x. So the side of blue is 1/4x.
(Academically you can now work your way round to show the all parts clockwise are x 1/4x 3/4x 3/16x 13/16x x.)

Looking at blue triangle x^2 + (1/4 x)^2 = 16 = 17/16 x^2. So x^2 = 256/17.

If you do the same maths with the others you get the same result (e.g. 25 = (169+256)/256 x^2 = 425/256 x^2).

X = SQRT (256/17).

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 6:46:47 AM permalink

Congratulation to ssho88 and Charlie for a correct answer!

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 6:47:08 AM permalink

Quote: gordonm888
Let's hope there is not a pandemic lockdown during the next total eclipse in 2024.

Amen to that.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 6:57:12 AM permalink

Here is your next problem.

The state of Denial has a population of 20 million. They are in the early states of an epidemic. They estimate one person in 500 will need to be on a ventilator when the epidemic is at its peak. How many ventilators should they have on hand to have a 95% chance of having enough?

Last edited by: Wizard on Mar 30, 2020

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 30th, 2020 at 7:22:11 AM permalink

39671 ?

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 7:25:50 AM permalink

Quote: ssho88
39671 ?

Shouldn't the mean needed be 20,000,000 / 500 = 40,000? Wouldn't they have a greater than 50% chance of running out with less? We're looking to have a 5% chance only of running out.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 30th, 2020 at 7:31:30 AM permalink

mean = 1/500 = 0.002, Var = 0.002(assumed), SD =0.04472

For > 95% of chance, Z > -1.645
(X -40000)/0.04472/(20,000,000)^0.5 > -1.645
X > 39671

I am not sure about the Variance value . . .

Last edited by: ssho88 on Mar 30, 2020

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

March 30th, 2020 at 8:43:37 AM permalink

I think ssho88 has the figure the wrong way up (so to speak) but agree with his idea.

N=20m, p=1/500, q=499/500.
Average = Np = 40k.
SD = SQRT(N p q) = SQRT(20m / 500 * 499/500 ) = 199.7999. (Since q is nearly 1, this happens to be SQRT (Average) )
Number of SDs for 90% (i.e. 5% at either end) = 1.644854 ( https://en.wikipedia.org/wiki/Standard_deviation ).
So number (over average) needed is 328.642.

Hence number to ensure 95% = 40k + 328.642 = 40329.

If the government is going to buy the normal amount it might as well buy a few extra. The main problem is guessing whether 1 in 500 is correct in the first place. For instance if it was 1 in 496 then you'd now only have a 50% chance of having enough.

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 30th, 2020 at 8:57:43 AM permalink

Quote: charliepatrick
I think ssho88 has the figure the wrong way up (so to speak) but agree with his idea.
N=20m, p=1/500, q=499/500.
Average = Np = 40k.
SD = SQRT(N p q) = SQRT(20m / 500 * 499/500 ) = 199.7999. (Since q is nearly 1, this happens to be SQRT (Average) )
Number of SDs for 90% (i.e. 5% at either end) = 1.644854 ( https://en.wikipedia.org/wiki/Standard_deviation ).
So number (over average) needed is 328.642.

Hence number to ensure 95% = 40k + 328.642 = 40329.
If the government is going to buy the normal amount it might as well buy a few extra. The main problem is guessing whether 1 in 500 is correct in the first place. For instance if it was 1 in 496 then you'd now only have a 50% chance of having enough.

I think we have the same mean and variance, mean and variance calculated by me is 40000 and 200 [0.04472 * (20,000,000)^0.5]

(X - 40000)/200 >-1.645

X > 39671

The difference is I used Z > -1.645 instead of +1.645 ??? Which one is correct ? I am not sure.

ThatDonGuy

Threads: 122
Posts: 6735

Joined: Jun 22, 2011

March 30th, 2020 at 9:05:34 AM permalink

Quote: ssho88
Quote: charliepatrick
I think ssho88 has the figure the wrong way up (so to speak) but agree with his idea.
N=20m, p=1/500, q=499/500.
Average = Np = 40k.
SD = SQRT(N p q) = SQRT(20m / 500 * 499/500 ) = 199.7999. (Since q is nearly 1, this happens to be SQRT (Average) )
Number of SDs for 90% (i.e. 5% at either end) = 1.644854 ( https://en.wikipedia.org/wiki/Standard_deviation ).
So number (over average) needed is 328.642.

Hence number to ensure 95% = 40k + 328.642 = 40329.
If the government is going to buy the normal amount it might as well buy a few extra. The main problem is guessing whether 1 in 500 is correct in the first place. For instance if it was 1 in 496 then you'd now only have a 50% chance of having enough.

I think we have the same mean and variance, mean and variance calculated by me is 40000 and 200 [0.04472 * (20,000,000)^0.5]

(X - 40000)/200 >-1.645

X > 39671

The difference is I used Z > -1.645 instead of +1.645 ??? Which one is correct ? I am not sure.

Presumably, to be 95% confident, you find the value such that 90% of the values are within that many SDs on either side of the mean; 5% will be greater than the mean + that many SDs, so 95% are less than that value.

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 30th, 2020 at 9:40:47 AM permalink

Quote: ThatDonGuy
Quote: ssho88
Quote: charliepatrick
I think ssho88 has the figure the wrong way up (so to speak) but agree with his idea.
N=20m, p=1/500, q=499/500.
Average = Np = 40k.
SD = SQRT(N p q) = SQRT(20m / 500 * 499/500 ) = 199.7999. (Since q is nearly 1, this happens to be SQRT (Average) )
Number of SDs for 90% (i.e. 5% at either end) = 1.644854 ( https://en.wikipedia.org/wiki/Standard_deviation ).
So number (over average) needed is 328.642.

Hence number to ensure 95% = 40k + 328.642 = 40329.
If the government is going to buy the normal amount it might as well buy a few extra. The main problem is guessing whether 1 in 500 is correct in the first place. For instance if it was 1 in 496 then you'd now only have a 50% chance of having enough.

I think we have the same mean and variance, mean and variance calculated by me is 40000 and 200 [0.04472 * (20,000,000)^0.5]

(X - 40000)/200 >-1.645

X > 39671

The difference is I used Z > -1.645 instead of +1.645 ??? Which one is correct ? I am not sure.

Presumably, to be 95% confident, you find the value such that 90% of the values are within that many SDs on either side of the mean; 5% will be greater than the mean + that many SDs, so 95% are less than that value.

I agree. "to have a 95% chance of having enough" means LESS THAN that Z value. I interpreted it as MORE THAN in previous calculations.

Last edited by: ssho88 on Mar 30, 2020

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 11:05:56 AM permalink

I agree with Charlie's answer.

The problem meant to ask how many ventilators should they have so that the probability of running out would be 5%, which is equivalent to a 95% chance of not running out.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 7:59:16 PM permalink

Here is the next one.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ChumpChange

ChumpChange

Threads: 131
Posts: 5112

Joined: Jun 15, 2018

March 30th, 2020 at 8:29:03 PM permalink

Hey 19

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 30th, 2020 at 8:31:27 PM permalink

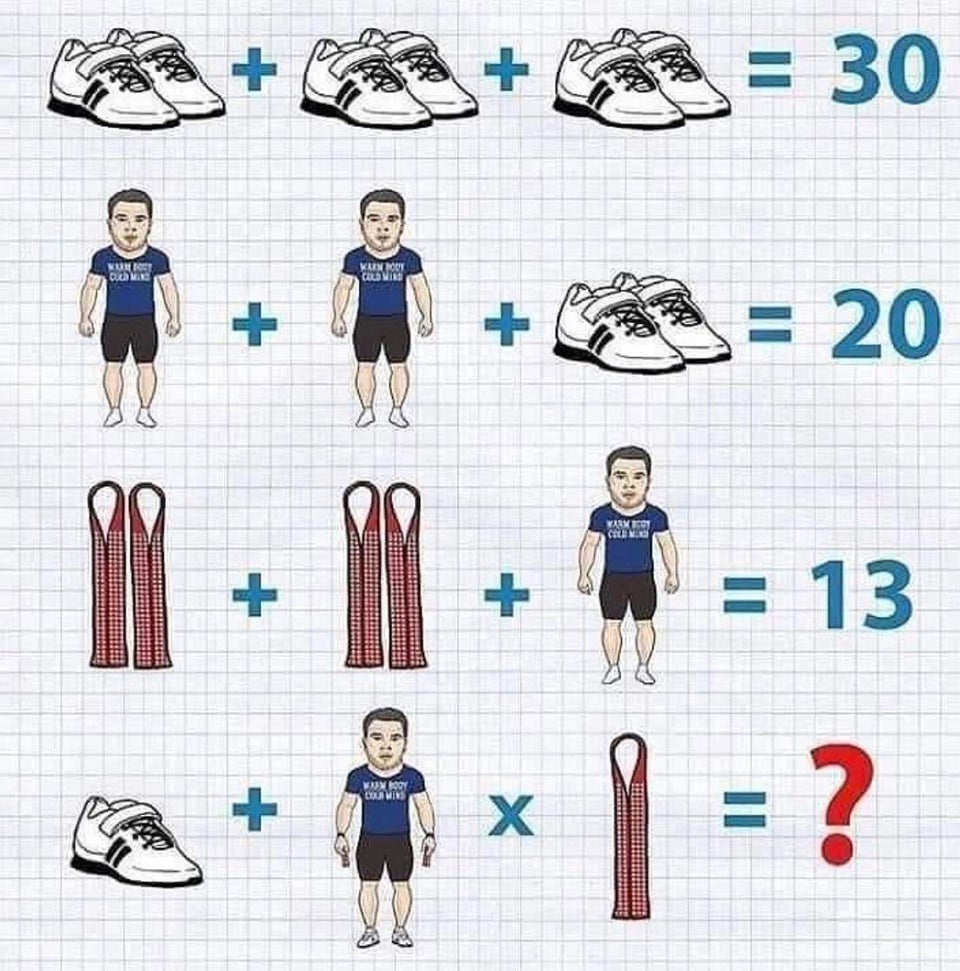
Quote: ChumpChange
Hey 19

I disagree

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 30th, 2020 at 8:33:34 PM permalink

I get 20

Have you tried 22 tonight? I said 22.

TomG

TomG

Threads: 16
Posts: 2465

Joined: Sep 26, 2010

March 30th, 2020 at 9:02:52 PM permalink

Quote: Wizard
Here is the next one.

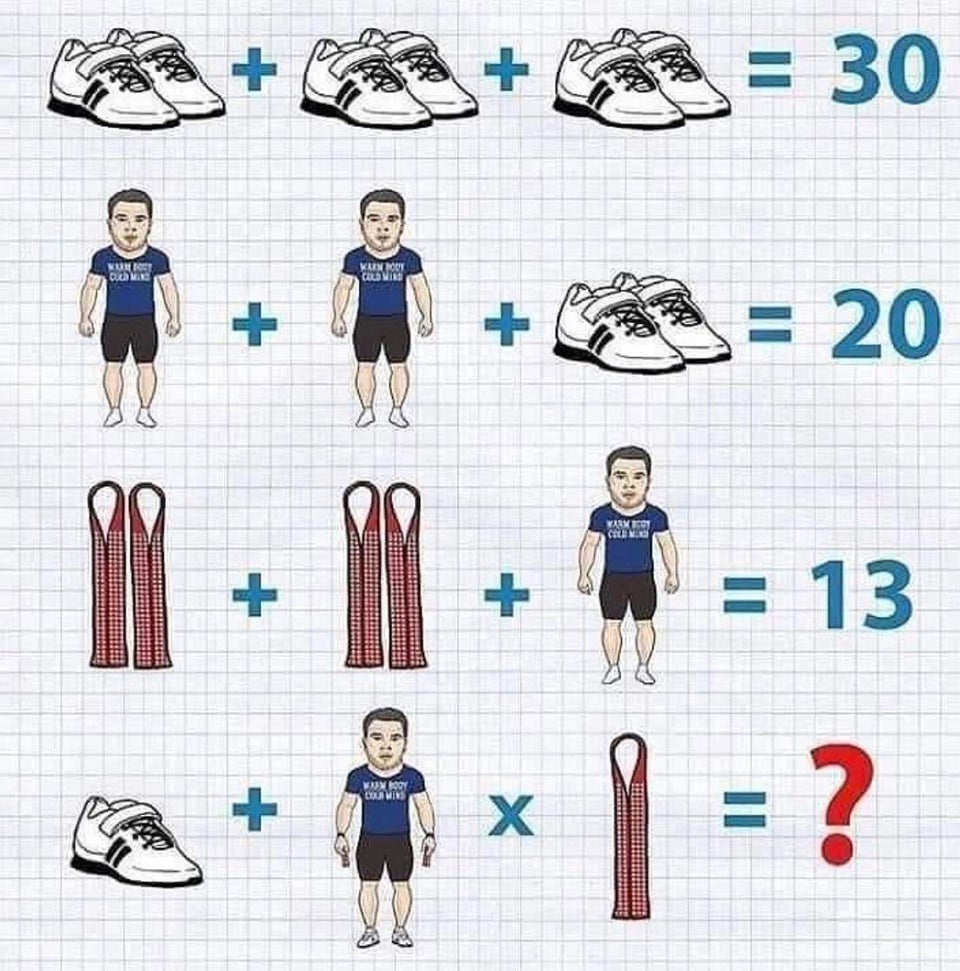
edit

an irrational number rounded to 403.16227766

For anyone who wants to win a beer or sugar free rockstar from this question, what shoe is featured in the picture?

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 30th, 2020 at 9:37:56 PM permalink

5 +5 x 2 = 15

TomG

TomG

Threads: 16
Posts: 2465

Joined: Sep 26, 2010

Thanked by

March 30th, 2020 at 9:52:39 PM permalink

Quote: ssho88
5 +5 x 2 = 15

Hint:

there is a place they try to trick you

Show your work:

Let shoe = s, man = m, lifting strap = l

ss + ss + ss = 30, ss = 10, s = 3.16227766...

m + m + ss = 20, m =5

ll + ll + m = 13, ll = 4, l = 2

now look very closely at the picture, preferably on something other than your phone

s + mllss x l

3.16227766 + (5 x 4 x 10) x 2 = 403.16227766

EdCollins

EdCollins

Threads: 20
Posts: 1739

Joined: Oct 21, 2011

March 30th, 2020 at 10:13:11 PM permalink

Ah, nevermind. Just now noticed the man is different.

Gialmere

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 30th, 2020 at 10:19:52 PM permalink

Quote: EdCollins
Ah, nevermind. Just now noticed the man is different.

Oh yeah. Heh. TomG is right about cell phones.

Have you tried 22 tonight? I said 22.

ssho88

Threads: 58
Posts: 682

Joined: Oct 16, 2011

March 30th, 2020 at 11:38:05 PM permalink

Quote: TomG
Hint:

there is a place they try to trick you

Show your work:

Let shoe = s, man = m, lifting strap = l

ss + ss + ss = 30, ss = 10, s = 3.16227766...

m + m + ss = 20, m =5

ll + ll + m = 13, ll = 4, l = 2

now look very closely at the picture, preferably on something other than your phone

s + mllss x l

3.16227766 + (5 x 4 x 10) x 2 = 403.16227766

yeah, LOL

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 31st, 2020 at 2:23:52 AM permalink

Quote: TomG
Hint:

there is a place they try to trick you

Show your work:

Let shoe = s, man = m, lifting strap = l

ss + ss + ss = 30, ss = 10, s = 3.16227766...

m + m + ss = 20, m =5

ll + ll + m = 13, ll = 4, l = 2

now look very closely at the picture, preferably on something other than your phone

s + mllss x l

3.16227766 + (5 x 4 x 10) x 2 = 403.16227766

I have a different interpretation.

I interpret the two shoes to mean s + s. We do agree that two ties are 2t, so why would two shoes not be 2s?

Using my logic, the answer is 43.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

unJon

unJon

Threads: 16
Posts: 4806

Joined: Jul 1, 2018

March 31st, 2020 at 7:51:00 AM permalink

This one will be truly easy for those on this forum, but it�s an old classic and I used to use it as an interview question (updated for the current crisis):

With 10% of the population having COVID-19, the world is in extreme crisis. Thankfully, a new Pharma company has just created an instant COVID-19 test that is 90% accurate. World leaders have mandated that everyone take the test in the hopes this will enable the virus to finally be contained. You dutifully show up at Walmart (wearing your N95 mask and staying six feet away from everyone else) to get tested in the pharmacy. Bad news: the test is positive for COVID-19.

What is the probability you actually have COVID-19?

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

unJon

unJon

Threads: 16
Posts: 4806

Joined: Jul 1, 2018

March 31st, 2020 at 7:55:56 AM permalink

Quote: Wizard
Quote: TomG
Hint:

there is a place they try to trick you

Show your work:

Let shoe = s, man = m, lifting strap = l

ss + ss + ss = 30, ss = 10, s = 3.16227766...

m + m + ss = 20, m =5

ll + ll + m = 13, ll = 4, l = 2

now look very closely at the picture, preferably on something other than your phone

s + mllss x l

3.16227766 + (5 x 4 x 10) x 2 = 403.16227766

I have a different interpretation.

I interpret the two shoes to mean s + s. We do agree that two ties are 2t, so why would two shoes not be 2s?

Using my logic, the answer is 43.

What makes you think Tom is saying two ties is 2t and not t^2? It�s the same answer since t=2

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 31st, 2020 at 8:03:54 AM permalink

Quote: unJon
What makes you think Tom is saying two ties is 2t and not t^2? It�s the same answer since t=2

Good point. However, I'm sticking with my answer, but admit it is subject to interpretation.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27115

Joined: Oct 14, 2009

March 31st, 2020 at 8:05:56 AM permalink

Quote: unJon
This one will be truly easy for those on this forum, but it�s an old classic and I used to use it as an interview question (updated for the current crisis):

With 10% of the population having COVID-19, the world is in extreme crisis. Thankfully, a new Pharma company has just created an instant COVID-19 test that is 90% accurate. World leaders have mandated that everyone take the test in the hopes this will enable the virus to finally be contained. You dutifully show up at Walmart (wearing your N95 mask and staying six feet away from everyone else) to get tested in the pharmacy. Bad news: the test is positive for COVID-19.

What is the probability you actually have COVID-19?

This is a classic problem in conditional probability.

Prob(CV given positive test) = Prob(CV and positive test) / Prob(positive test) = 0.1 * 0.9 / (0.1 * 0.9 + 0.9*0.1) = 0.5

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ThatDonGuy

Threads: 122
Posts: 6735

Joined: Jun 22, 2011

March 31st, 2020 at 8:39:03 AM permalink

I never liked the "picture equations", because...

...I keep forgetting to count the number of items - for example, where there are two shoes in the first equation and just one in the last one

ThatDonGuy

Threads: 122
Posts: 6735

Joined: Jun 22, 2011

March 31st, 2020 at 8:44:15 AM permalink

Quote: Wizard
This is a classic problem in conditional probability.

I never liked these either, because you have to assume that the condition for which you are testing is uniform - in this case, the probability that you have COVID-19 is 10%.

Doc

Doc

Threads: 46
Posts: 7287

Joined: Feb 27, 2010

March 31st, 2020 at 9:45:39 AM permalink

I punted on the symbols problem from the very beginning, because I thought there were just too many ways to interpret the combinations of symbols.

Suppose that you could determine that a shoe represents the number 5. Do two shoes right beside each other represent 2*5 = 10, or 5*5 = 25, or a double-digit-symbol = 55? With that much ambiguity in the symbols -- even without the hidden shoes and straps added to the man (which I didn't see) -- I just thought the numerous ways to reverse-interpret a set of equations was not something I wanted to try.

ThatDonGuy

Threads: 122
Posts: 6735

Joined: Jun 22, 2011

March 31st, 2020 at 11:03:30 AM permalink

Quote: Doc
I punted on the symbols problem from the very beginning, because I thought there were just too many ways to interpret the combinations of symbols.

Suppose that you could determine that a shoe represents the number 5. Do two shoes right beside each other represent 2*5 = 10, or 5*5 = 25, or a double-digit-symbol = 55? With that much ambiguity in the symbols -- even without the hidden shoes and straps added to the man (which I didn't see) -- I just thought the numerous ways to reverse-interpret a set of equations was not something I wanted to try.

Almost always, two symbols = 2 x one symbol in these.

rdw4potus

rdw4potus

Threads: 80
Posts: 7237

Joined: Mar 11, 2010

March 31st, 2020 at 12:53:12 PM permalink

Except for this most recent one and the joke in the bottom line, aren't these picture puzzles just designed to start fights about order of operations? They lay out 3 items of various values, then combine them on a line with both + and * operations. Apparently there's a big age-based divide there, with PEMDAS being replaced by a left-to-right approach.

Last edited by: rdw4potus on Mar 31, 2020

"So as the clock ticked and the day passed, opportunity met preparation, and luck happened." - Maurice Clarett

GMan

GMan

Threads: 2
Posts: 81

Joined: Jan 5, 2013

March 31st, 2020 at 1:17:33 PM permalink

Answer: 30

LOL, I went from the first puzzle straight to the last post.

G Man

Wizard
Administrator