Easy math puzzles

Joined: Jun 22, 2011

Threads: 116
Posts: 5859

Thanks for this post from:

April 2nd, 2020 at 3:14:09 PM permalink

Quote: Joeman
Max volume = π

Call h the height of the rectangle and d its width, which is also the cylinder's diameter. The volume of the cylinder is:

V = π(d/2)² x h

Given the perimeter of the rectangle as 6, the perimeter equation looks like:

2d + 2h = 6

or, solving for h, would be

h = 3 - d

Substitute h into the volume equation:

V = π(d/2)² x (3 - d)

multiply and you get:

V = 3π/4 x d² - π/3 x d³

To get a maximum, take the first derivative, dV/dd, and set it equal to 0:

3π/2d - 3π/4d² = 0

Now, solve for d and you get:

d = 2, which means h = 1.

Plug d and h into the volume equation, and you get:

V = π(2/2)² x 1

which yields:

V = π

"V = 3π/4 x d² - π/3 x d³

To get a maximum, take the first derivative, dV/dd, and set it equal to 0:

3π/2d - 3π/4d² = 0"

Isn't dV/dd = 3π/2 x d - π x d²?

Also, pardon me for being pedantic, but you didn't show that this makes V a maximum as opposed to a minimum or an inflection point.

charliepatrick

charliepatrick

Joined: Jun 17, 2011

Threads: 39
Posts: 2896

Thanks for this post from:

April 2nd, 2020 at 4:06:27 PM permalink

I agree with above...

Using r saves a lot of 1/4 appearing as follows.

Area of top of cyclinder = Pi r^2.

Vol = h * Pi r^2.
Vol = (3 - 2r) * Pi r^2.
Vol = 3 Pi r^2 - 2 Pi r^3.

dV/dr = 6 Pi r - 6 Pi r^2 = 6 Pi r *(1 - r)
This is 0 when r=0 or r=1.

Clearly when r=0, v=0; and r = 1.5 v=0. Hence at r=1 this is a maximum.

r=1 gets d=2, h=1, Vol = Pi.

Joeman

Joeman

Joined: Feb 21, 2014

Threads: 35
Posts: 2328

April 2nd, 2020 at 5:03:52 PM permalink

Quote: ThatDonGuy
Quote: Joeman
Max volume = π

Call h the height of the rectangle and d its width, which is also the cylinder's diameter. The volume of the cylinder is:

V = π(d/2)² x h

Given the perimeter of the rectangle as 6, the perimeter equation looks like:

2d + 2h = 6

or, solving for h, would be

h = 3 - d

Substitute h into the volume equation:

V = π(d/2)² x (3 - d)

multiply and you get:

V = 3π/4 x d² - π/3 x d³

To get a maximum, take the first derivative, dV/dd, and set it equal to 0:

3π/2d - 3π/4d² = 0

Now, solve for d and you get:

d = 2, which means h = 1.

Plug d and h into the volume equation, and you get:

V = π(2/2)² x 1

which yields:

V = π

"V = 3π/4 x d² - π/3 x d³

To get a maximum, take the first derivative, dV/dd, and set it equal to 0:

3π/2d - 3π/4d² = 0"

Isn't dV/dd = 3π/2 x d - π x d²?

Also, pardon me for being pedantic, but you didn't show that this makes V a maximum as opposed to a minimum or an inflection point.

You are correct! Not sure how that happened. I did this by hand and then copied it over. Must have lost (or gained!) something in translation!

And yes, I did not demonstrate that it was a maximum. I did check my answer before posting, and the volume decreased using both d = 2.01 and 1.99. I figured that was good enough for an internet message board! :)

d = 0 is also a solution, but obviously not a meaningful one for a maximum volume.

"Dealer has 'rock'... Pay 'paper!'"

Wizard
Administrator

Wizard

Joined: Oct 14, 2009

Threads: 1470
Posts: 25734

April 2nd, 2020 at 6:33:47 PM permalink

I agree that pi is the correct answer. Congratulations to all those who solved it.

�Extraordinary claims require extraordinary evidence.� -- Carl Sagan

ssho88

ssho88

Joined: Oct 16, 2011

Threads: 53
Posts: 655

April 2nd, 2020 at 11:07:10 PM permalink

Quote: Wizard
I agree that pi is the correct answer. Congratulations to all those who solved it.

Just use 2 formulas and differentiation( dy/dx) will get it.

r = radius of cylinder
h= cylinder height

dV/dr = PI(6r - 6r^2) = 0

r=1

V = PI *(1)^1 *1= PI

Mosca

Mosca

Joined: Dec 14, 2009

Threads: 189
Posts: 3956

April 3rd, 2020 at 6:30:51 AM permalink

Shouldn�t the volume be expressed as cubic units? Am I missing something here? If so, sorry for being not math literate.

NO KILL I

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5859

Thanks for this post from:

April 3rd, 2020 at 6:53:09 AM permalink

Quote: Mosca
Shouldn�t the volume be expressed as cubic units? Am I missing something here? If so, sorry for being not math literate.

The units in the volume are cubic units - not the number. If the perimeter is, say, 6 cm, then the maximum volume is π cm³.

Mosca

Mosca

Joined: Dec 14, 2009

Threads: 189
Posts: 3956

April 3rd, 2020 at 7:03:12 AM permalink

Quote: ThatDonGuy
The units in the volume are cubic units - not the number. If the perimeter is, say, 6 cm, then the maximum volume is π cm³.

Thanks, that�s what I thought.

NO KILL I

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2540

April 3rd, 2020 at 12:59:39 PM permalink

New puzzle:

Imagine the following game, which costs $1.00 to play. At the beginning of each round, a random number between 0 and 1 is generated and then multiplied by $1.00. You get paid a portion of that as follows. If, for instance, you�re on round 3 and the random number is 0.8169 then you get paid 0.8169 / (3 * 3.8169) = $0.07.

You can play as many rounds as you want and you keep winnings from all rounds. Total winnings are paid when you decide to stop playing, and that is the only time they are rounded to the nearest cent.

For calculation purposes, you can assume players will play forever. What is the house edge of this game?

Last edited by: Ace2 on Apr 3, 2020

It�s all about making that GTA

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1306

April 3rd, 2020 at 1:21:04 PM permalink

Quote: Ace2
New puzzle:

Imagine the following game, which costs $1.00 to play. At the beginning of each round, a random number between 0 and 1 is generated and then multiplied by $1.00. You get paid a portion of that as follows. If, for instance, you�re on round 3 and the random number is 0.8169 then you get paid 0.8169 / (3 * 3.8169) = $0.07.

You can play as many rounds as you want and you keep winnings from all rounds. Total winnings are paid when you decide to stop playing, and that is the only time they are rounded to the nearest cent.

What is the house edge on this game?

House edge = negative infinity

Edit: Never mind. I see that on each round, the player get paid RAND / [ round * ( RAND + round)]. So, the series of wins would converge, and my guess is definitely wrong. (RAND = the random number, round = the round number.)

gordonm888
Administrator

gordonm888

Joined: Feb 18, 2015

Threads: 59
Posts: 4643

April 3rd, 2020 at 2:00:10 PM permalink

Quote: unJon
This one will be truly easy for those on this forum, but it�s an old classic and I used to use it as an interview question (updated for the current crisis):

With 10% of the population having COVID-19, the world is in extreme crisis. Thankfully, a new Pharma company has just created an instant COVID-19 test that is 90% accurate. World leaders have mandated that everyone take the test in the hopes this will enable the virus to finally be contained. You dutifully show up at Walmart (wearing your N95 mask and staying six feet away from everyone else) to get tested in the pharmacy. Bad news: the test is positive for COVID-19.

What is the probability you actually have COVID-19?

10%. Because the statement says that 10% of the population have Covid-19. And the question is not about the probability of testing positive, its about whether you actually have the disease.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

charliepatrick

charliepatrick

Joined: Jun 17, 2011

Threads: 39
Posts: 2896

April 3rd, 2020 at 2:28:52 PM permalink

Quote: Ace2
New puzzle:

Imagine the following game, which costs $1.00 to play. At the beginning of each round, a random number between 0 and 1 is generated and then multiplied by $1.00. You get paid a portion of that as follows. If, for instance, you�re on round 3 and the random number is 0.8169 then you get paid 0.8169 / (3 * 3.8169) = $0.07.

You can play as many rounds as you want and you keep winnings from all rounds. Total winnings are paid when you decide to stop playing, and that is the only time they are rounded to the nearest cent.

For calculation purposes, you can assume players will play forever. What is the house edge of this game?

This puzzle shows the problem with coming up with a quick test that isn't accurate enough and why it's taking so long to develop a test that is reliable enough to use. It's all down to Bayes Theorem...

We know the test shows the patient has the disease. We also know that (i) 90% of the people are clear and (ii) the test is 90% accurate. Essentially there are two possibilities, the patient is clear but has been given a false negative or the patient has the disease and has been correctly diagnosed as having it.

Keeping things simple take a step back and look at a typical population of 100.
90 of them are clear, but if tested 81 would show up clear and 9 would get a false positive.
The other 10 have the disease, and if tested 9 would show up as having the disease and 1 would get a false negative.

Thus
(a) 9 are clear but get a false positive.
(b) 9 have the disease and get the correct result.

So if someone comes back with a positive test result it could be any of the 9 (a) or any of the 9 (b). Thus it is 50-50 whether they have the disease.

This is why it's so important to get a better test.

Using a test which is 99% correct, then in 1000 people; 900 clear, 9 get false positives; 100 have it, and 99 get correct result; so we're 91% (99/108) certain they have the disease. Similarly 95% test gets 68%, so you need a better test to be useful. Still better than 50% with the 90% test.

This explains why the test has to be so accurate before it can become useful.

TomG

TomG

Joined: Sep 26, 2010

Threads: 16
Posts: 2395

April 3rd, 2020 at 3:18:42 PM permalink

Quote: Ace2
New puzzle:

Imagine the following game, which costs $1.00 to play. At the beginning of each round, a random number between 0 and 1 is generated and then multiplied by $1.00. You get paid a portion of that as follows. If, for instance, you�re on round 3 and the random number is 0.8169 then you get paid 0.8169 / (3 * 3.8169) = $0.07.

You can play as many rounds as you want and you keep winnings from all rounds. Total winnings are paid when you decide to stop playing, and that is the only time they are rounded to the nearest cent.

For calculation purposes, you can assume players will play forever. What is the house edge of this game?

I guess an EV of 60-cents, for a house edge of 40%

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1306

April 3rd, 2020 at 3:18:53 PM permalink

Quote: Ace2
New puzzle:

Imagine the following game, which costs $1.00 to play. At the beginning of each round, a random number between 0 and 1 is generated and then multiplied by $1.00. You get paid a portion of that as follows. If, for instance, you�re on round 3 and the random number is 0.8169 then you get paid 0.8169 / (3 * 3.8169) = $0.07.

You can play as many rounds as you want and you keep winnings from all rounds. Total winnings are paid when you decide to stop playing, and that is the only time they are rounded to the nearest cent.

For calculation purposes, you can assume players will play forever. What is the house edge of this game?

a house edge of about 42.295%.

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2540

April 3rd, 2020 at 3:41:44 PM permalink

Quote: ChesterDog
a house edge of about 42.295%.

That�s in the ballpark. But, as usual, I�m looking for a closed-form solution

It�s all about making that GTA

Wizard
Administrator

Wizard

Joined: Oct 14, 2009

Threads: 1470
Posts: 25734

April 3rd, 2020 at 3:51:27 PM permalink

Quote: gordonm888
10%. Because the statement says that 10% of the population have Covid-19. And the question is not about the probability of testing positive, its about whether you actually have the disease.

Certain the positive test result increases your probability of actually being positive.

�Extraordinary claims require extraordinary evidence.� -- Carl Sagan

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1306

April 3rd, 2020 at 5:18:59 PM permalink

Quote: Ace2
Quote: ChesterDog
a house edge of about 42.295%.

That�s in the ballpark. But, as usual, I�m looking for a closed-form solution

if the player decides to play n rounds, then the house edge would be:

1 + LN(n+1) - H_n.

H_n is the "n-th Harmonic Number," which = 1/1 + 1/2 + 1/3 +... + 1/n.
And LN(n+1) is the natural log of n+1.

Looking up the limit as n approaches infinity of H_n - LN(n), I see it has a name, which is the "Euler-Mascheroni constant (gamma)." Gamma is about 0.5772156649.

The limit of H_n - LN(n) would equal the limit of H_n - LN(n+1), so the house edge, for infinite play, would equal 1 - gamma = 0.4227843351...

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5859

April 3rd, 2020 at 6:23:00 PM permalink

Quote: Ace2
Quote: ChesterDog
a house edge of about 42.295%.

That�s in the ballpark. But, as usual, I�m looking for a closed-form solution

In round n, the expecting winnings is INTEGRAL(0,1) {x / (n (n + x)) dx}
= 1/n INTEGRAL(0,1) {x / (n + x) dx}
= 1/n INTEGRAL(0,1) {(1 - n / (n + x)) dx}
= 1/n INTEGRAL(0,1) {1 dx} - 1/n * n INTEGRAL(0,1) {1 / (n + x) dx}
= 1/n (1 - 0) - (ln (n + 1) - ln n)
= 1/n - ln ((n + 1) / n)

The expected winnings over the entire game is the sum of this over all positive integers n, so the house edge = (1 - the expected winnings) x 100%.
The sum over n rounds is 1 + 1/2 + 1/3 + ... + 1/n - (ln 2 - ln 1 + ln 3 - ln 2 + ln 4 - ln 3 + ... + ln (n+1) - ln n)
= 1 + 1/2 + 1/3 + ... + 1/n - ln (n + 1)
The expected winnings is the limit of this as n approaches positive infinity.
However, I do not know how to calculate this, especially as both the sum and the logarithm diverge.
Using Excel, the house edge through 5000 rounds is 42.2884%.

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2540

April 3rd, 2020 at 8:36:05 PM permalink

Good job, ChesterDog, on getting the correct formulaic answer.

The integral from 1 to n of 1/x dx is Ln(n). You can think of that as the harmonic series in continuous form, which is why, as n gets larger, Ln(n) gets closer to H(n)...the difference converges to the Euler�Mascheroni constant (γ) of ~0.5772

That constant is equal to the integral from 1 to infinity of (1/[x] - 1/x) dx where [x] is the floor function (same as rounddown). Makes sense, it�s just summing all the differences between 1/x (all numbers) and 1/[x] (all parts of harmonic numbers).

The formula for this game, (rand / (round * (round + rand)), is just another way of expressing (1/[x] -1/x). So summed from 1 to infinity it will equal γ. Or I should say, the average of many games will equal γ. Therefore the house edge is 1 - γ =~ 0.4228

Harmonic numbers come up a lot in probability...many �Coupon collector� problems use them. Incidentally, I recently learned that the estimate for the Nth harmonic number can be further refined by adding the term 1/2n - 1/12n^2 + 1/120n^4, which makes approximations very accurate, even for small N. For instance, H(3) is 1/1 + 1/2 + 1/3 = 11/6 = 1.8333333. Using the approximation of Ln(3) + γ + 1/(2*3) - 1/(12*3^2) + 1/(120*3^4) we get 1.833338, so already good to 5 decimal places

Last edited by: Ace2 on Apr 3, 2020

It�s all about making that GTA

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

April 14th, 2020 at 7:11:02 PM permalink

Four points are chosen at random on the surface of a sphere. What is the probability that the center of the sphere lies inside the tetrahedron whose vertices are at the four points? (It is understood that each point is independently chosen relative to a uniform distribution on the sphere.)

I posted this problem on the song thread as a joke. It's a level 6 question on the Putnam test meaning it's really hard. The reason I'm placing it here is that it contains a shortcut. Using logic and visual intuition, it's possible solve the problem in your head without picking up a pencil. So, if you decide to have a go, there's no need to show your work. Just post the answer.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

April 30th, 2020 at 7:38:25 PM permalink

In the unlikely event someone is still contemplating this, try reducing the problem down by one dimension and consider a triangle inside of a circle.

Have you tried 22 tonight? I said 22.

gordonm888
Administrator

gordonm888

Joined: Feb 18, 2015

Threads: 59
Posts: 4643

Thanks for this post from:

April 30th, 2020 at 8:56:48 PM permalink

Its a beautiful graphic.

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

unJon

Joined: Jul 1, 2018

Threads: 14
Posts: 4222

Thanks for this post from:

April 30th, 2020 at 9:01:34 PM permalink

Quote: Gialmere
In the unlikely event someone is still contemplating this, try reducing the problem down by one dimension and consider a triangle inside of a circle.

My guess for a triangle in a square is 1/3.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 1st, 2020 at 6:56:21 PM permalink

Quote: unJon
Quote: Gialmere
In the unlikely event someone is still contemplating this, try reducing the problem down by one dimension and consider a triangle inside of a circle.

My guess for a triangle in a square is 1/3.

I'm not sure where the "square" comes from but, your answer (although incorrect) is in the ballpark.

Have you tried 22 tonight? I said 22.

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1306

Thanks for this post from:

May 1st, 2020 at 7:21:26 PM permalink

Quote: Gialmere
Quote: unJon
Quote: Gialmere
In the unlikely event someone is still contemplating this, try reducing the problem down by one dimension and consider a triangle inside of a circle.

My guess for a triangle in a square is 1/3.

I'm not sure where the "square" comes from but, your answer (although incorrect) is in the ballpark.

For the 2-dimensional problem, calculus gives 1/4 as the probability of three random points on a circle enclosing the circle's center.

Now, I have to figure how to use this result to answer the 3-dimensional problem.

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1306

Thanks for this post from:

May 2nd, 2020 at 5:02:04 AM permalink

Quote: Gialmere
In the unlikely event someone is still contemplating this, try reducing the problem down by one dimension and consider a triangle inside of a circle.

3-dimensional problem: The probability that the tetrahedron made by 4 random points on a sphere enclose the center of the center is 1/8?

2-dimensional problem: The probability that the triangle made by 3 random points on a circle enclose the center of the circle is 1/4.

1-dimensional problem: The probability that the segment made by 2 random points on a line segment enclose the center of the line segment is 1/2.

0-dimensional problem: The probability that the point made by 1 random point on a point encloses the center of the point is 1.

unJon

Joined: Jul 1, 2018

Threads: 14
Posts: 4222

Thanks for this post from:

May 2nd, 2020 at 5:58:17 AM permalink

Quote: Gialmere
Quote: unJon
Quote: Gialmere
In the unlikely event someone is still contemplating this, try reducing the problem down by one dimension and consider a triangle inside of a circle.

My guess for a triangle in a square is 1/3.

I'm not sure where the "square" comes from but, your answer (although incorrect) is in the ballpark.

Oops circle.

I think the trick is that the problem is equal to the average % surface area encompassed by X-1 points.

So for a two dimensional circle, what is the average % circumference enclosed by two random points on the circle (use the smaller circumference segment)?

Three dimensional: what is the average % surface area covered by the shape enclosed by three random points (use the smaller surface area)?

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

Thanks for this post from:

May 2nd, 2020 at 11:38:27 AM permalink

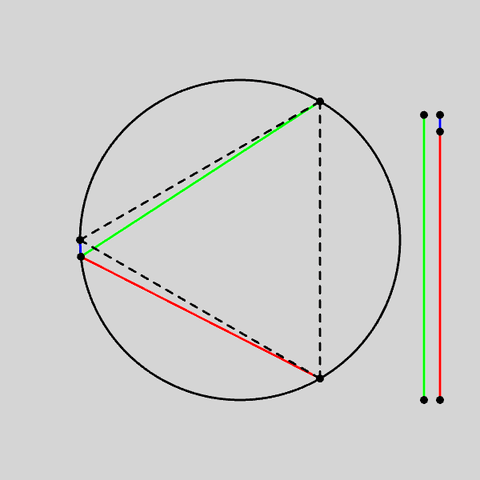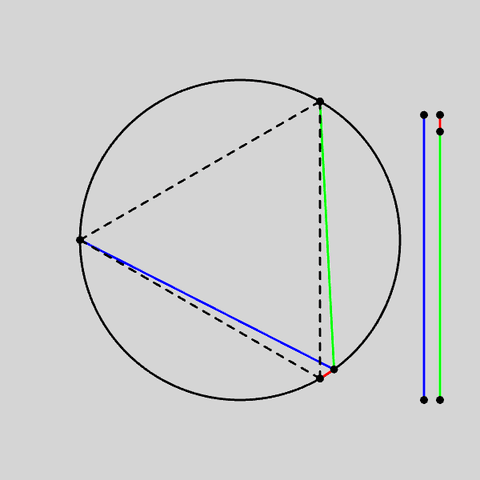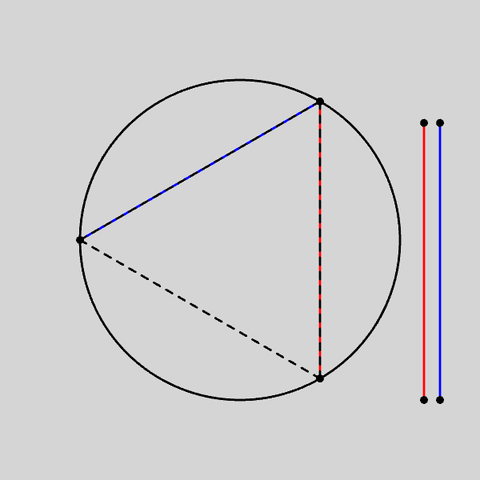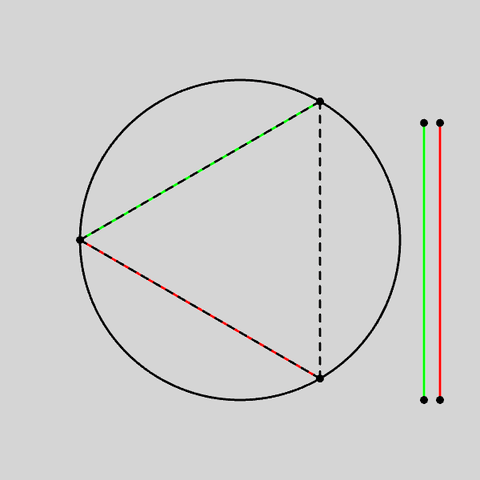
Quote: ChesterDog
3-dimensional problem: The probability that the tetrahedron made by 4 random points on a sphere enclose the center of the center is 1/8?

Ding! Ding! Ding!

You are absolutely correct.

I'm not a big math wiz but I do enjoy logic problems. Since math and logic problems often overlap, YouTube suggested I watch this video and I thought it was pretty cool...

Have you tried 22 tonight? I said 22.

charliepatrick

charliepatrick

Joined: Jun 17, 2011

Threads: 39
Posts: 2896

May 2nd, 2020 at 11:52:37 AM permalink

Quote: unJon
...for a two dimensional circle, what is the average % circumference enclosed by two random points on the circle (use the smaller circumference segment)?...

Thanks for the thought - here's a simple proof. (Now to worry about the sphere issue!)

If the first point picked is assumed to be at the South (Pole), then the secondwill be somewhere (for simplicity assume the RHS) between North and South - in the diagram Point A.

For the triangle to contain the centre the point would have to be between B (where AB crosses the centre) and N (where NS crosses the centre). Thus the probability is length of arc NB / length of circumference. Length(NB)=Length(AS)=length of arc.

Length of arc is uniformly between 1/2 (A=N) and 0 (A=S), so the average is 1/4.

Note it took some time for me to create this diagram so I landed up posting this after the above video. btw thanks for the video it's very instructive.

Last edited by: charliepatrick on May 2, 2020

Wizard
Administrator

Wizard

Joined: Oct 14, 2009

Threads: 1470
Posts: 25734

May 2nd, 2020 at 4:18:00 PM permalink

Good problem. I had seen it before, so stayed out of it. I wouldn't have filed it as an "easy math problem" (the title of the thread).

�Extraordinary claims require extraordinary evidence.� -- Carl Sagan

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5859

May 2nd, 2020 at 4:54:32 PM permalink

Quote: Wizard
Good problem. I had seen it before, so stayed out of it. I wouldn't have filed it as an "easy math problem" (the title of the thread).

Well, here's an easy one:

For what positive value p does 1 + 2 p + 3 p² + 4 p³ + 5 p⁴ + ... = 25?
Show your work - none of this "I approximated it on Excel" stuff.

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2277

May 2nd, 2020 at 5:19:20 PM permalink

Quote: ThatDonGuy
Well, here's an easy one:

For what positive value p does 1 + 2 p + 3 p² + 4 p³ + 5 p⁴ + ... = 25?
Show your work - none of this "I approximated it on Excel" stuff.

Let equation A be 25=1 +2p +3p^2 etc... (the equation as stated)
Let equation B be 25p = p + 2p^2 + 3p^3 etc.

Let C equal A minus B to get 25(1-p) = 1 + p + p^2 + p^3 + p^4 etc

Let D be p*C = p + p^2 + p^3 etc

Then C minus D is 25(1-p)^2 = 1

solve to get p=4/5

Last edited by: rsactuary on May 2, 2020

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5859

May 2nd, 2020 at 5:53:43 PM permalink

Quote: rsactuary
Let equation A be 25=1 +2p +3p^2 etc... (the equation as stated)
Let equation B be 25p = p + 2p^2 + 3p^3 etc.

Let C equal A minus B to get 25(1-p) = 1 + p + p^2 + p^3 + p^4 etc

Let D be p*C = p + p^2 + p^3 etc

Then C minus D = 25(1-p)^2 = 1

solve to get p=4/5

Correct.

Another way to do this is to note that:
1 + 2 p + 3 p² + 4 p³ + ... = (1 + p + p² + p³ + ...)².

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2277

May 2nd, 2020 at 6:00:05 PM permalink

Quote: ThatDonGuy
Correct.

Another way to do this is to note that:
1 + 2 p + 3 p² + 4 p³ + ... = (1 + p + p² + p³ + ...)².

Yeah, it's been too long since I did stuff like this on a regular basis or I would have recognized that. I kind of got there by first principles.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 2nd, 2020 at 7:11:00 PM permalink

This one made a splash in India a few years back.

Have you tried 22 tonight? I said 22.

unJon

Joined: Jul 1, 2018

Threads: 14
Posts: 4222

Thanks for this post from:

May 3rd, 2020 at 5:20:49 AM permalink

Quote: Gialmere
This one made a splash in India a few years back.

I count

18

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 3rd, 2020 at 11:30:10 AM permalink

Quote: unJon
I count
18

Correct!

Your geometry teacher would be proud.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 3rd, 2020 at 12:24:52 PM permalink

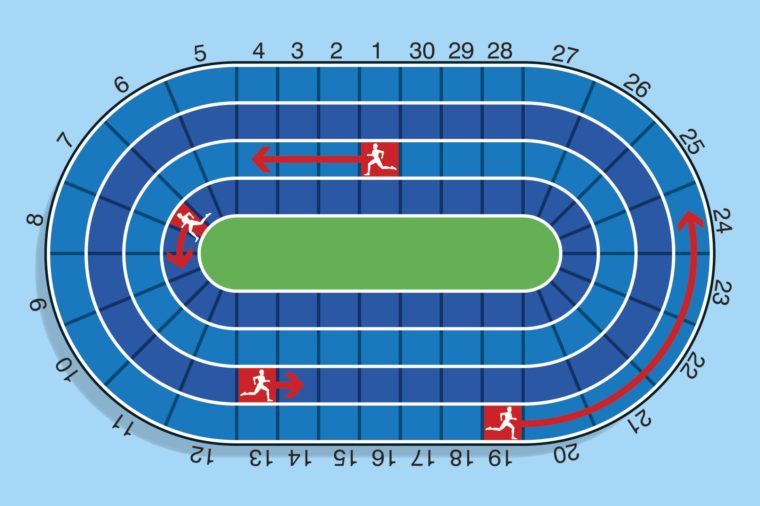
You're playing a track and field board game with your family during the lockdown. If each of the runner pawns travels the indicated number of spaces every turn, at which numbered spot will all of the runners end up next to one another?

Have you tried 22 tonight? I said 22.

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2277

Thanks for this post from:

May 3rd, 2020 at 2:42:26 PM permalink

At t=6, they will all be at 19. Again at t=36 etc

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 3rd, 2020 at 8:41:54 PM permalink

Quote: rsactuary
At t=6, they will all be at 19. Again at t=36 etc

Correct!

You should consider a career as a game designer.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 3rd, 2020 at 8:43:59 PM permalink

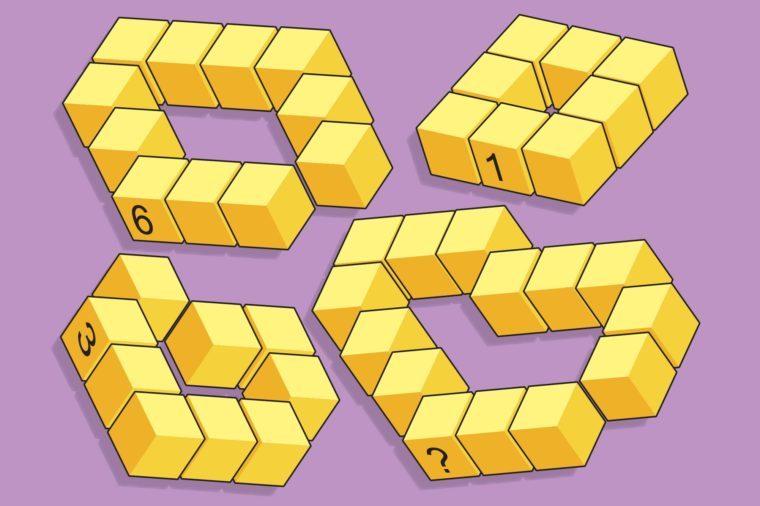
What number should replace the question mark on the bottom right loop?

Have you tried 22 tonight? I said 22.

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2540

Thanks for this post from:

May 3rd, 2020 at 8:55:41 PM permalink

I�d say 9

It�s all about making that GTA

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 3rd, 2020 at 11:40:37 PM permalink

Quote: Ace2
I�d say 9

Correct!

I'd tell the cubes to dance but they're a bunch of squares.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2753

May 3rd, 2020 at 11:59:45 PM permalink

The playing card suits in the cells above are placed according to a pattern. What�s the missing symbol?

Have you tried 22 tonight? I said 22.

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2277

May 4th, 2020 at 6:35:02 AM permalink

Quote: Ace2
I�d say 9

logic please? I'm not seeing anything here.

unJon

Joined: Jul 1, 2018

Threads: 14
Posts: 4222

May 4th, 2020 at 7:32:18 AM permalink

Quote: rsactuary
logic please? I'm not seeing anything here.

Number of missing squares in the middle of the shape. Or how many cubes it takes to fill the holes.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2277

May 4th, 2020 at 7:37:54 AM permalink

jeez. lol. thanks!

Joeman

Joeman

Joined: Feb 21, 2014

Threads: 35
Posts: 2328

Thanks for this post from:

May 4th, 2020 at 7:52:11 AM permalink

Quote: Gialmere

The playing card suits in the cells above are placed according to a pattern. What�s the missing symbol?

The missing suit is a ♠.

If we assign numeric values to each suit, we can get the same total adding up each known row/column/long diagonal in the grid. The easiest I found is ♢ = 1, ♡ = 2, ♠ = 3, and ♣ = 4. This makes the sum of each known row/column/diagonal = 10. The remaining box must be 3 to make the sums of the unknown row, column, & diagonal = 10.

Since ♠ = 3, the missing suit is a ♠.

"Dealer has 'rock'... Pay 'paper!'"

Gialmere