Easy math puzzles

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 8th, 2020 at 8:15:54 PM permalink

Speaking of adding things up to 100...

You have three prime numbers, and they equal 100 when you add them together. You know nothing about your numbers except that one is less than a half but more than a third of one of the others. What are your numbers?

Have you tried 22 tonight? I said 22.

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2664

May 8th, 2020 at 8:33:39 PM permalink

deleted

Last edited by: Ace2 on May 8, 2020

It�s all about making that GTA

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2297

May 8th, 2020 at 8:44:41 PM permalink

delete

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2297

Thanks for this post from:

May 8th, 2020 at 8:46:12 PM permalink

wait.. how about 2, 31, 67. 2 has to be one of the numbers. There are three ways to sum the other two up to 98, but only one that satisfies the constraints.

EdCollins

EdCollins

Joined: Oct 21, 2011

Threads: 20
Posts: 1739

May 8th, 2020 at 8:49:25 PM permalink

Quote: rsactuary
wait.. how about 1, 2 and 97

Or 2, 19, 79.

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2297

May 8th, 2020 at 8:53:18 PM permalink

Quote: EdCollins
Or 2, 19, 79.

doesn't satisfy the constraints.

EdCollins

EdCollins

Joined: Oct 21, 2011

Threads: 20
Posts: 1739

May 8th, 2020 at 8:59:45 PM permalink

Quote: rsactuary
doesn't satisfy the constraints.

It satisfies the post that was now deleted... mentioning that three prime numbers can't possibly add up to 100. One example of three prime numbers that DO add up to 100 was given... and the example I provided is another. I wasn't attempting to answer the puzzle.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 8th, 2020 at 8:59:53 PM permalink

Quote: rsactuary
wait.. how about 2, 31, 67. 2 has to be one of the numbers. There are three ways to sum the other two up to 98, but only one that satisfies the constraints.

Correct!

Let's hear it for number 2! It became a prime number against all odds.

Have you tried 22 tonight? I said 22.

rsactuary

Joined: Sep 6, 2014

Threads: 29
Posts: 2297

May 8th, 2020 at 9:04:05 PM permalink

Quote: EdCollins
I wasn't attempting to answer the puzzle.

I was, and got it wrong on my first attempt. Thought that was the purpose of the thread?

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 8th, 2020 at 11:42:46 PM permalink

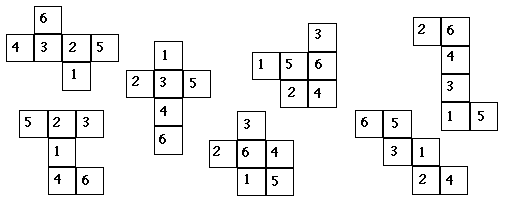
You visit your friend who's an eccentric inventor. He's working on a way to help casinos recover post Covid-19. His idea is disposable paper craps dice. When players finish their shoots they simply crumple up the dice and throw them away. He shows you a sheet with various die patterns on it and asks your opinion. Which of the nets (if any) will make a genuine craps die?

Have you tried 22 tonight? I said 22.

CrystalMath

CrystalMath

Joined: May 10, 2011

Threads: 8
Posts: 1909

Thanks for this post from:

May 9th, 2020 at 4:29:56 AM permalink

Quote: Gialmere

You visit your friend who's an eccentric inventor. He's working on a way to help casinos recover post Covid-19. His idea is disposable paper craps dice. When players finish their shoots they simply crumple up the dice and throw them away. He shows you a sheet with various die patterns on it and asks your opinion. Which of the nets (if any) will make a genuine craps die?

The lower right is the only one that comes close, with opposite sides adding to 7, but the orientation is wrong, and my friend needs to swap the 1 and 6. Even then, there are lots of ways to mess up the pip layout.

I heart Crystal Math.

ThatDonGuy

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5947

Thanks for this post from:

May 9th, 2020 at 8:17:42 AM permalink

Quote: Gialmere
The lower right is the only one that comes close, with opposite sides adding to 7, but the orientation is wrong, and my friend needs to swap the 1 and 6. Even then, there are lots of ways to mess up the pip layout.

The one in the lower right is the only one that does not have two already adjacent sides that add up to 7

The "upper four" have 4-3 (and 2-5), 3-4, 5-2, and 4-3; the two to the left of the lower three have 5-2 and 6-1

ThatDonGuy

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5947

Thanks for this post from:

May 9th, 2020 at 8:58:15 AM permalink

Quote: ChesterDog
I can't prove it, yet, but I can see that the house edge = 1 - ln(2).

Edit: I forgot, it costs only $250 to play, so the house edge should be 1 - (6/5)ln2.

This was a little beyond my math pay grade, so I looked it up on Math StackExchange.

The return is 300 x (1 x 1/2 + 1/2 x 1/4 + 1/3 x 1/8 + 1/4 x 1/16 + ...)

Doing a Taylor series expansion on f(x) = ln (x + 1) with respect to x = 0:
ln (x + 1) = x - x² / 2 + x³ / 3 - x⁴ / 4 + ...
Let x = -1/2:
ln 1/2 = -1/2 - (1/4 x 1/2) + (-1/8 x 1/3) - (1/16 x 1/4) + ...
= - (1/2 + 1/4 x 1/2 + 1/8 x 1/3 + 1/16 x 1/4 + ...)
-ln 1/2 = 1/2 + 1/4 x 1/2 + 1/8 x 1/3 + 1/16 x 1/4 + ...
Since -ln 1/2 = ln 2, this is:
ln 2 = (1 x 1/2) + (1/2 x 1/4) + (1/3 x 1/8) + (1/4 x 1/16) + ...

Thus, the return on a bet of 250 is 300 ln 2, and the HE = (250 - 300 ln 2) / 250 = 0.168223 = 16.8223%

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 9th, 2020 at 4:41:52 PM permalink

Quote: CrystalMath
The lower right is the only one that comes close, with opposite sides adding to 7, but the orientation is wrong, and my friend needs to swap the 1 and 6. Even then, there are lots of ways to mess up the pip layout.

Quote: ThatDonGuy

The one in the lower right is the only one that does not have two already adjacent sides that add up to 7

The "upper four" have 4-3 (and 2-5), 3-4, 5-2, and 4-3; the two to the left of the lower three have 5-2 and 6-1

Correct!!

Looking at his work you start to wonder if your friend has upgraded from "eccentric" to full blown "crazy". Then you remember how you laughed at him when he urged you last January to buy a six month supply of toilet paper.
-------------------------------------

Did you hear about the guy who was murdered by being brutally stoned with those large size novelty dice?

According to police reports he died to death.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 9th, 2020 at 4:55:52 PM permalink

At Cutting Edge you see a new game called "Midnight Double Lucky". Two standard 6-sided fair dice are rolled repeatedly. When a 6-6 is rolled, the game ends with players betting on Midnight winning. If, however, a 7 is rolled back-to-back before midnight, then the game ends with players betting on Double Lucky winning.

What's the better bet?

Have you tried 22 tonight? I said 22.

gordonm888
Administrator

gordonm888

Joined: Feb 18, 2015

Threads: 60
Posts: 4805

Thanks for this post from:

May 9th, 2020 at 5:34:00 PM permalink

Quote: Gialmere

At Cutting Edge you see a new game called "Midnight Double Lucky". Two standard 6-sided fair dice are rolled repeatedly. When a 6-6 is rolled, the game ends with players betting on Midnight winning. If, however, a 7 is rolled back-to-back before midnight, then the game ends with players betting on Double Lucky winning.

What's the better bet?

The Midnight is the better bet.

On the first roll, there is a 1/36 chance of winning the Midnight wager but no chance of winning the Double Lucky wager (Back to back 7's).

On subsequent rolls, there is an equal chance of winning the Midnight and the Lucky.

Edit: Hmmm, after more thought I am unsure that my answer is correct.

Nah, my answer above is correct. Consider an infinite set of rolls of two die that are not stopped for any reason. For n>1, the nth roll will have the following outcomes: a 6,6=12 with a probability of 1/36, a 7 with a probability of 6/36, and other outcomes with a probability of 29/36. Considering that the (n-1)th roll also had a probability of 6/36 of being a 7, we can say that the nth roll has a probability of 1/36 of being a 12 and a probability of 1/36 of being the second of back to back 7's.

However the first roll only has a chance of being a 12, so the Midnight wager must have a higher probability of winning.

The Midnight wager has a win probability of 0.50+1/72.
The Double Lucky wager has a win probability of 0.50-1/72.

Last edited by: gordonm888 on May 9, 2020

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2664

Thanks for this post from:

May 9th, 2020 at 6:31:23 PM permalink

Doubles has a 6/13 chance of winning. Midnight has a 1 - 6/13 = 7/13 chance, so midnight is the better play

Chance of doubles winning is calculated as

x = 29/36x + 1/6y
y = 1/6 + 29/36x
Solve for x

Incidentally, the chance of winning is inversely proportional to the average waiting time for the events to happen, which is 42 rolls for doubles and 36 for midnight. However, this relationship does not hold true for all situations, and I�m not sure why or why not. For instance, if you roll a pair of dice and calculate the probability of 1 four coming before 2 sevens, the four has a 5/9 chance of winning even though the average waiting time is 12 rolls for both. Can anyone explain?

Last edited by: Ace2 on May 9, 2020

It�s all about making that GTA

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1368

Thanks for this post from:

May 9th, 2020 at 7:33:25 PM permalink

Quote: Gialmere
...At Cutting Edge you see a new game called "Midnight Double Lucky". Two standard 6-sided fair dice are rolled repeatedly. When a 6-6 is rolled, the game ends with players betting on Midnight winning. If, however, a 7 is rolled back-to-back before midnight, then the game ends with players betting on Double Lucky winning.

What's the better bet?

Midnight.

Probability of win is 7/13?

Edit: Now, I see that my guess agrees with Ace2's answer.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 9th, 2020 at 9:51:59 PM permalink

Quote: gordonm888

The Midnight is the better bet.

On the first roll, there is a 1/36 chance of winning the Midnight wager but no chance of winning the Double Lucky wager (Back to back 7's).

On subsequent rolls, there is an equal chance of winning the Midnight and the Lucky.

Edit: Hmmm, after more thought I am unsure that my answer is correct.

Nah, my answer above is correct. Consider an infinite set of rolls of two die that are not stopped for any reason. For n>1, the nth roll will have the following outcomes: a 6,6=12 with a probability of 1/36, a 7 with a probability of 6/36, and other outcomes with a probability of 29/36. Considering that the (n-1)th roll also had a probability of 6/36 of being a 7, we can say that the nth roll has a probability of 1/36 of being a 12 and a probability of 1/36 of being the second of back to back 7's.

However the first roll only has a chance of being a 12, so the Midnight wager must have a higher probability of winning.

The Midnight wager has a win probability of 0.50+1/72.
The Double Lucky wager has a win probability of 0.50-1/72.

Quote: Ace2
Doubles has a 6/13 chance of winning. Midnight has a 1 - 6/13 = 7/13 chance, so midnight is the better play

Chance of doubles winning is calculated as

x = 29/36x + 1/6y
y = 1/6 + 29/36x
Solve for x

Incidentally, the chance of winning is inversely proportional to the average waiting time for the events to happen, which is 42 rolls for doubles and 36 for midnight. However, this relationship does not hold true for all situations, and I�m not sure why or why not. For instance, if you roll a pair of dice and calculate the probability of 1 four coming before 2 sevens, the four has a 5/9 chance of winning even though the average waiting time is 12 rolls for both. Can anyone explain?

Hmm... That is interesting.

Quote: ChesterDog
Midnight.

Probability of win is 7/13?

Edit: Now, I see that my guess agrees with Ace2's answer.

Correct!

It's one of those overlapping probability things.
------------------------

My dog ate my lucky dice.

Now I'm hoping she'll shoot some craps.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 9th, 2020 at 10:01:35 PM permalink

A casino dealer is working on a new Three Card Poker variant. She takes all the face cards from a standard deck and thoroughly shuffles them. She then deals 3 cards to Player #1, three cards to Player #2, three cards to Player #3, and the final three cards to Player #4. What is the probability that all four hands will contain a straight (J-Q-K of any suit)?

Have you tried 22 tonight? I said 22.

Ace2

Joined: Oct 2, 2017

Threads: 31
Posts: 2664

May 9th, 2020 at 10:18:02 PM permalink

(4!)^3 * (3!)^4 / 12!

It�s all about making that GTA

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1368

May 9th, 2020 at 11:34:48 PM permalink

I get 12*8*4*9*6*3*6*4*2*1*1*1 / 12! = (4!)^3 * (3!)^3 / 12! = (3!4!)^3 / 12! = 12/1925.

charliepatrick

charliepatrick

Joined: Jun 17, 2011

Threads: 39
Posts: 2933

May 10th, 2020 at 4:03:20 AM permalink

I'm just looking at the chances at each stage of dealing he nexr card correctly.
First player, first card - must be correct.
First player, second card - must be one of the 8 from 11 cards that don't match the first card.
First player, third card - must be one of the 4 from 10 cards that don't match the first or second cards.
So P(player 1) = 1 * 8/11 * 4/10.
Similarly P(player 2) = 1 * 6/8 * 3/7
Similarly P(Player 3) = 1 * 4/5 * 2/4
And then Player 4 must get a straight.

These are the same numbers as ChesterDog starts with but I then get 72/1925.

(I think this is because he needs 3*2*1 as the numerators for the 4th player.)

ssho88

Joined: Oct 16, 2011

Threads: 53
Posts: 655

May 10th, 2020 at 5:03:38 AM permalink

Quote: charliepatrick
I'm just looking at the chances at each stage of dealing he nexr card correctly.
First player, first card - must be correct.
First player, second card - must be one of the 8 from 11 cards that don't match the first card.
First player, third card - must be one of the 4 from 10 cards that don't match the first or second cards.
So P(player 1) = 1 * 8/11 * 4/10.
Similarly P(player 2) = 1 * 6/8 * 3/7
Similarly P(Player 3) = 1 * 4/5 * 2/4
And then Player 4 must get a straight.

These are the same numbers as ChesterDog starts with but I then get 72/1925.

(I think this is because he needs 3*2*1 as the numerators for the 4th player.)

I guess your answer include the STRAIGHT FLUSH. I also get (4^3)/12C3 * (3^3)/9C3 * (2^3)/6C3 * (1^3)/3C3 = 72/1925 (include STRAIGHT FLUSH)

What if only consider STRAIGHT(WITHOUT any STRAIGHT FLUSH) ?

Last edited by: ssho88 on May 10, 2020

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1368

May 10th, 2020 at 8:22:40 AM permalink

Quote: charliepatrick
...These are the same numbers as ChesterDog starts with but I then get 72/1925.

(I think this is because he needs 3*2*1 as the numerators for the 4th player.)

Thanks! Now, I see that I missed the 3*3*1.

So, I agree it should be 12*8*4 * 9*6*3 * 6*4*2 * 3*2*1 / 12! = 72/1925.

Quote: ssho88
...What if only STRAIGHT but WITHOUT any STRAIGHT FLUSH?

I guess that's the real trick of the puzzle. I get:
72/1925 - 12*2*1*9*2*1*6*2*1*3*2*1 = 72/1925 - 1/15400 = 23/616

ssho88

Joined: Oct 16, 2011

Threads: 53
Posts: 655

May 10th, 2020 at 8:48:11 AM permalink

Quote: ChesterDog
Quote: charliepatrick
...These are the same numbers as ChesterDog starts with but I then get 72/1925.

(I think this is because he needs 3*2*1 as the numerators for the 4th player.)

Thanks! Now, I see that I missed the 3*3*1.

So, I agree it should be 12*8*4 * 9*6*3 * 6*4*2 * 3*2*1 / 12! = 72/1925.

I guess that's the real trick of the puzzle. I get:
72/1925 - 12*2*1*9*2*1*6*2*1*3*2*1 = 72/1925 - 1/15400 = 23/616

If EXCLUDED any straight flush, I get 453/15400 = 0.0294

ChesterDog

Joined: Jul 26, 2010

Threads: 8
Posts: 1368

Thanks for this post from:

May 10th, 2020 at 9:17:13 AM permalink

Quote: ssho88
...If EXCLUDED any straight flush, I get 453/15400 = 0.0294

Thanks; I see that I made a mistake on excluding the straight flushes.

How do you calculate the correct answer?

ssho88

Joined: Oct 16, 2011

Threads: 53
Posts: 655

May 10th, 2020 at 9:34:04 AM permalink

Quote: ChesterDog
Thanks; I see that I made a mistake on excluding the straight flushes.

How do you calculate the correct answer?

Prob(all straight including straight flush) - Prob(1 SF + 3 ST) - Prob(2 SF + 2 ST) - Prob(4 SF) = 72/1925 - 2496/369600 - 432/369600 - 24/369600 = 453/15400 = 0.0294

EDITED : Here are the detail calculations

A) Case - All straight or straight flush for all player

Prob(ALL) = (4^3)/12C3 * (3^3)/9C3 * (2^3)/6C3 * (1^3)/3C3 = 72/1925

B) Case - 1 SF + 3 ST, there are four permutations, [SF][ST][ST][ST], [ST][SF][ST][ST], [ST][ST][SF][ST] and [ST][ST][ST][SF].

Let just consider [SF][ST][ST][ST],

i) Probability for player 1 get SF = 4/12C3

ii) When player 1 get SF(removed JsQsKs), cards left in the deck :-

JhQhKh
JcQcKc
JdQdKd

There are total 24 straight combinations(18 straight combinations with two type of suit and 6 straight combinations with three type of suit) for player 2.

a) when player 2 get straight with two type of suit(removed JhQhKc), then left 6 straight combinations for player 3
Prob case a) = 18/9C3 * 6/6C3 * 1/3C3

b) when player 2 get straight with three type of suit(removed JhQcKd), then left 8 straight combinations for player 3
Prob case b) = 6/9C3 * 8/6C3 * 1/3C3

So Prob for case [SF][ST][ST][ST] = 4/12C3 * (18/9C3 * 6/6C3 * 1/3C3 + 6/9C3 * 8/6C3 * 1/3C3)

There are four permutations, so Total Prob = 4 * 4/12C3 * (18/9C3 * 6/6C3 * 1/3C3 + 6/9C3 * 8/6C3 * 1/3C3) = 2496/369600

C) Case - 2 SF + 2 ST, there are six permutations, [SF][SF][ST][ST], [SF][ST][SF][ST], [SF][ST][ST][SF], [ST][SF][SF][ST], [ST][SF][ST][SF] and [ST][ST][SF][SF].

Let just consider [SF][SF][ST][ST],

Probability for player 1 get SF and player 2 get SF = 4/12C3 *3/9C3

Cards left in the deck :-

JcQcKc
JdQdKd

So there are 6 straight combinations for player 3,

Prob for case [SF][SF][ST][ST] = 4/12C3 *3/9C3 *6/6C3* (1^3)/3C3

There are six permutations, so Total Prob = 6 * 4/12C3 *3/9C3 *6/6C3* (1^3)/3C3 = 432/369600

D) Case - 3 SF + 1 ST, DOES NOT EXIST

Prob = 0

E) Case - 4 SF, only one permutations

Prob = 4/12C3 * 3/9C3 * 2/6C3 * 1/3C3 = 24/369600

So Prob(only straight) = Prob A) - Prob B) - Prob C) - Prob D) - Prob E) = = 72/1925 - 2496/369600 - 432/369600 - 0 - 24/369600 = 453/15400 = 0.0294

Last edited by: ssho88 on May 10, 2020

charliepatrick

charliepatrick

Joined: Jun 17, 2011

Threads: 39
Posts: 2933

May 10th, 2020 at 10:13:13 AM permalink

Accepting that the chances of the ranks being correct is 72/1925, it is also 576/15400.

Assume that player #1 gets Ks, #2 Kh, #3 Kd, #4 Kc. Then look at how the Queens and Jacks might be distributed.
There are 24 ways to organise the Queens and also 24 ways to organise the Jacks.
4 players have SF : 1 way.
3 players have SF : no way (as the 4th would also have one!)
2 players have SF : 6 ways to pick the players, the other two have four ways to place their Q and J but one of these gives them a SF, so 3 ways left. Hence total ways = 6*3 = 18.
1 player has straight flush.
(i) This can be any one of the four players so first factor is 4.
(ii) Let's assume it's the first player so the remaining cards can be HDC HCD DHC DCH CHD CDH.
With HDC, all three Queens are correct so now all three Jacks have to be wrong, two ways DCH CHD. 2 ways
With HCD, DHC or CDH, one of the Queens is correct, so now only the specific Jack has to be wrong. 4 ways x 3 combinations.
With DCH or CHD all the Queens are wrong, so any combination of Jacks is fine. 6 ways x 2 combinations.

4 players = 1 way
2 players = 18 ways (6 x 3)
1 player = 104 (4 x (2+4x3+6x2), 4x26)
Total 123 ways

Leaving 576-123 ways where no players have a SF.

So Pr = 453/15400.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 10th, 2020 at 10:13:05 PM permalink

Apologies for my tardiness. It's Mothers Day and my daughter's birthday so if I'm inattentive I get a lot of women mad at me. Also apologies for the question. I wanted to jazz it up a little. It should simply be "What is the probability of each hand having 1 K, 1 Q, 1 J (of any suit)?

I'm showing the probability is 16/55 × 9/28 × 2/5 × 1 = 0.0374025974.

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Wizard

Joined: Oct 14, 2009

Threads: 1474
Posts: 25954

May 10th, 2020 at 10:24:27 PM permalink

Quote: Gialmere
A casino dealer is working on a new Three Card Poker variant. She takes all the face cards from a standard deck and thoroughly shuffles them. She then deals 3 cards to Player #1, three cards to Player #2, three cards to Player #3, and the final three cards to Player #4. What is the probability that all four hands will contain a straight (J-Q-K of any suit)?

I get 216/5775 = apx. 0.037402597.

�Extraordinary claims require extraordinary evidence.� -- Carl Sagan

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 11th, 2020 at 4:12:21 PM permalink

Your lodge member friend has invited you to his lodge for some beers. While hanging out at the bar you notice people playing a game with voting balls. Your friend explains that 6 black and 3 white balls are mixed in a cloth bag. Two people then alternate blindly drawing balls out of the bag without replacement. The winner is the player who draws the second white ball. (It doesn't matter who drew the first.) The loser buys the next round of drinks.

You finish your beers and your friend asks if you'd like to play the game for your next round. He places 6 black and 3 white balls in a bag, mixes them and then asks if you'd like to draw first or second.

How do you reply?

Have you tried 22 tonight? I said 22.

ssho88

Joined: Oct 16, 2011

Threads: 53
Posts: 655

Thanks for this post from:

May 11th, 2020 at 5:38:38 PM permalink

Quote: Gialmere

Your lodge member friend has invited you to his lodge for some beers. While hanging out at the bar you notice people playing a game with voting balls. Your friend explains that 6 black and 3 white balls are mixed in a cloth bag. Two people then alternate blindly drawing balls out of the bag without replacement. The winner is the player who draws the second white ball. (It doesn't matter who drew the first.) The loser buys the next round of drinks.

You finish your beers and your friend asks if you'd like to play the game for your next round. He places 6 black and 3 white balls in a bag, mixes them and then asks if you'd like to draw first or second.

How do you reply?

What is your intention? To get a free beer for yourself or to buy your friend a beer ? LOL

If you want to get a free beer for yourself, then you let your friend to draw a ball first, your winning probability is 11/21 = 0.5238 ?

Last edited by: ssho88 on May 11, 2020

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 11th, 2020 at 7:07:10 PM permalink

Quote: ssho88
What is your intention? To get a free beer for yourself or to buy your friend a beer ? LOL

If you want to get a free beer for yourself, then you let your friend to draw a ball first, your probability is 11/21 = 0.5238 ?

Correct!

Interestingly, the odds are about the same with replacement.
---------------------------

"Trust me, you can dance." -Beer

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 11th, 2020 at 7:11:59 PM permalink

And now, for a change of pace...

How many numbers do you see?

Have you tried 22 tonight? I said 22.

ThatDonGuy

ThatDonGuy

Joined: Jun 22, 2011

Threads: 116
Posts: 5947

May 11th, 2020 at 9:31:30 PM permalink

Quote: Gialmere
How many numbers do you see?

Ten, if you use a little imagination

More or less from top to bottom:
6, 8, 3 (the "right side" of the 8), two 0s (the two circles of the 8), 9, 2, 4, 1, and 7 (to see the 7, start about halfway across the bottom part of the 2, go to where it crosses the 1, then go down)

gordonm888
Administrator

gordonm888

Joined: Feb 18, 2015

Threads: 60
Posts: 4805

May 11th, 2020 at 10:17:52 PM permalink

I see 44 numbers, or 43 distinct numbers ( if we can't count both zeros as being different numbers).

6, 9, 8, 0, 0, 3, 9, 4, 1, 7, 69, 691, 96, 196, 84, 48, 697, 796, 79, 97, 19, 91, 81, 18, 34, 31, 13, 43. 60, 604, 406, 40, 601, 106, 10, 37, 73, 100, 400, 706, 607, 78, 87, 700

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

charliepatrick

charliepatrick

Joined: Jun 17, 2011

Threads: 39
Posts: 2933

May 12th, 2020 at 2:50:07 AM permalink

Quote: gordonm888

I see 44 numbers, or 43 distinct numbers ( if we can't count both zeros as being different numbers).

6, 9, 8, 0, 0, 3, 9, 4, 1, 7, 69, 691, 96, 196, 84, 48, 697, 796, 79, 97, 19, 91, 81, 18, 34, 31, 13, 43. 60, 604, 406, 40, 601, 106, 10, 37, 73, 100, 400, 706, 607, 78, 87, 700

I see "007" has been busy again!

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 12th, 2020 at 8:24:10 AM permalink

Quote: gordonm888

I see 44 numbers, or 43 distinct numbers ( if we can't count both zeros as being different numbers).

6, 9, 8, 0, 0, 3, 9, 4, 1, 7, 69, 691, 96, 196, 84, 48, 697, 796, 79, 97, 19, 91, 81, 18, 34, 31, 13, 43. 60, 604, 406, 40, 601, 106, 10, 37, 73, 100, 400, 706, 607, 78, 87, 700

Yes. It is a sort of an Escheresque drawing from the Night Gallery.

ThatDonGuy comes closest. The ten digits "0, 1, 2, 3, 4, 5, 6, 7, 8 and 9" are all represented in the image. (This requires looking at it from different angles including upside down.)

---------------------------------

Q: Why did the Star Wars movies come out in the sequence 4, 5, 6, 1, 2, 3?

A: Because in charge of sequence, Yoda was.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 12th, 2020 at 10:14:04 AM permalink

Speaking of Escheresque oddities...

How is this possible?

Have you tried 22 tonight? I said 22.

RideTheEdge

RideTheEdge

Joined: Apr 30, 2020

Threads: 2
Posts: 158

Thanks for this post from:

May 12th, 2020 at 10:50:29 AM permalink

In spite of appearances, the larger figures are not triangles. The "hypotenuse" of the top triangle is slightly concave, while the bottom is slightly convex. Look at the point (8,3) treating the left corner of the triangles as the origin.

Joeman

Joeman

Joined: Feb 21, 2014

Threads: 35
Posts: 2371

Thanks for this post from:

May 12th, 2020 at 10:55:29 AM permalink

The entire figures in each case appear to be right triangles, but they are not. The "hypotenuses" of the apparent right triangles are not straight lines: despite what your lyin' eyes may tell you, the red and green triangles are not similar. The angle formed by the red and green triangles' hypotenuses is slightly more than 180° in the top figure, and slightly less than 180° in the bottom figure, thus accounting for the 'missing' square unit in the bottom figure.

"Dealer has 'rock'... Pay 'paper!'"

gordonm888
Administrator

gordonm888

Joined: Feb 18, 2015

Threads: 60
Posts: 4805

Thanks for this post from:

May 12th, 2020 at 1:55:01 PM permalink

Quote: Gialmere
Quote: gordonm888

I see 44 numbers, or 43 distinct numbers ( if we can't count both zeros as being different numbers).

6, 9, 8, 0, 0, 3, 9, 4, 1, 7, 69, 691, 96, 196, 84, 48, 697, 796, 79, 97, 19, 91, 81, 18, 34, 31, 13, 43. 60, 604, 406, 40, 601, 106, 10, 37, 73, 100, 400, 706, 607, 78, 87, 700

Yes. It is a sort of an Escheresque drawing from the Night Gallery.

ThatDonGuy comes closest. The ten digits "0, 1, 2, 3, 4, 5, 6, 7, 8 and 9" are all represented in the image. (This requires looking at it from different angles including upside down.)

I cry FOUL! You did not ask for digits or numerals, you asked us for numbers. Do you not see 691 in the drawing? or all the other numbers I listed?

So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 12th, 2020 at 4:18:41 PM permalink

Heh. You have a point although that's how the question for this type of picture is usually worded. I never considered multi digit numbers. To be honest, I stare at it with furrowed brow still wondering exactly where in the hell the 5 is supposed to be.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 12th, 2020 at 4:27:31 PM permalink

Quote: RideTheEdge
In spite of appearances, the larger figures are not triangles. The "hypotenuse" of the top triangle is slightly concave, while the bottom is slightly convex. Look at the point (8,3) treating the left corner of the triangles as the origin.

Quote: Joeman
The entire figures in each case appear to be right triangles, but they are not. The "hypotenuses" of the apparent right triangles are not straight lines: despite what your lyin' eyes may tell you, the red and green triangles are not similar. The angle formed by the red and green triangles' hypotenuses is slightly more than 180° in the top figure, and slightly less than 180° in the bottom figure, thus accounting for the 'missing' square unit in the bottom figure.

Correct!

The green triangle has dimensions 2 x 5 and gradient 2 / 5 = 0.4

The red triangle has dimensions 3 x 8 and gradient 3 / 8 = 0.375
----------------------------------------------

Q: Why was the hypotenuse so bad in bed?

A: He could never find the right angle.

Have you tried 22 tonight? I said 22.

CrystalMath

CrystalMath

Joined: May 10, 2011

Threads: 8
Posts: 1909

May 12th, 2020 at 5:57:49 PM permalink

Quote: Gialmere
Heh. You have a point although that's how the question for this type of picture is usually worded. I never considered multi digit numbers. To be honest, I stare at it with furrowed brow still wondering exactly where in the hell the 5 is supposed to be.

I don�t see a 5.

I heart Crystal Math.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 12th, 2020 at 6:18:08 PM permalink

One video I saw superimposes a 5 over the 8. I didn't care for that one. The best I can do is look at the 6 and tilt my head 45 degrees to the left (or my cell phone 45 degrees to the right). The 6 then (kind of) becomes a fancifully fonted 5.

Another video (although a minority view) skips the 5 as part of the answer so there is a definite "no 5" argument to be made.

Have you tried 22 tonight? I said 22.

Gialmere

Joined: Nov 26, 2018

Threads: 44
Posts: 2799

May 13th, 2020 at 10:05:07 AM permalink

You have a friend who hustles three card monte on the Las Vegas Strip. You offer him $100 to teach you some of his tricks. Instead, he proposes a wager for his fee.

You'll put down two C-notes on the table and he'll put down one. Then, without cheating, he'll start dealing three card monte for you at $100 dollars a round. The first person to win all three of the C-notes keeps them.

Intrigued by the idea, you agree. As your friend starts the first round, however, you can see that, between his lighting fast shuffle and quick misdirection moves, you'll have no idea which card hides the lucky lady.

Expressed as a fraction, what are your chances of winning his $100 vs his chance of winning your $200?

Last edited by: Gialmere on May 13, 2020

Have you tried 22 tonight? I said 22.

Ace2