Easy math puzzles

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

May 31st, 2020 at 12:41:52 PM permalink

A hunter met two shepherds, one of whom had three loaves of bread and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal.

How should the two shepherds divide this money?

Have you tried 22 tonight? I said 22.

Gandler

Gandler

Threads: 35
Posts: 1801

Joined: Jan 27, 2014

May 31st, 2020 at 4:24:36 PM permalink

Quote: Gialmere

The break room at your work has a vintage hot beverage machine with only three selections: "coffee", "tea" and "random" (50/50 coffee or tea). Unfortunately the machine was labeled incorrectly when it was built so that each button does not give what it claims.

If a drink costs 75 cents, what is the minimum amount of money you must put in the machine in order to correctly relabel the buttons?

Edit- misread

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

Thanked by

May 31st, 2020 at 5:05:34 PM permalink

Quote: Gialmere

A hunter met two shepherds, one of whom had three loaves of bread and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal.

How should the two shepherds divide this money?

1 coin for the man with 3 loaves, and 7 coins for the man with 5 loaves

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

May 31st, 2020 at 5:23:00 PM permalink

Quote: rsactuary
1 coin for the man with 3 loaves, and 7 coins for the man with 5 loaves

Correct!

It's nonintuitive, but that's the math of it.
------------------------------------

I saw on the news that rioters set fire to a bread factory.

Now the company is toast.

Have you tried 22 tonight? I said 22.

Joeman

Joeman

Threads: 36
Posts: 2452

Joined: Feb 21, 2014

Thanked by

June 1st, 2020 at 5:24:28 AM permalink

Quote: Gialmere

A hunter met two shepherds, one of whom had three loaves of bread and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal.

How should the two shepherds divide this money?

The shepherds should split the coins equally among themselves, 4 for each.

The basis of splitting up the coins equally is not mathematical, but philosophical.

The shepherds shared their bread with the hunter out of their generosity. After their meal, the hunter, likewise, shares his money with the shepherds out of his generosity. He was not obligated to pay them. Since it was a gift, and not payment, it should be received as such, and split evenly between the shepherds.

Also, who is to say that the hunter was moved to give this gift not because of the food shared, but because of the hospitality and company of the two shepherds?

"Dealer has 'rock'... Pay 'paper!'"

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

Thanked by

June 1st, 2020 at 8:23:00 AM permalink

Quote: Joeman
The shepherds should split the coins equally among themselves, 4 for each.

The basis of splitting up the coins equally is not mathematical, but philosophical.

The shepherds shared their bread with the hunter out of their generosity. After their meal, the hunter, likewise, shares his money with the shepherds out of his generosity. He was not obligated to pay them. Since it was a gift, and not payment, it should be received as such, and split evenly between the shepherds.

Also, who is to say that the hunter was moved to give this gift not because of the food shared, but because of the hospitality and company of the two shepherds?

Heh. Maybe we should start a companion thread at DT on math puzzle ethics.

Meanwhile...

You're still experimenting with various mechanics for a new casino dice game...

You roll two standard dice.

What is the expected value of the die with the higher number?

You roll two standard dice. You can see all the numbers on the cubes except for the two facing down on the table.

If you added up all ten visible numbers, what would be the most likely sum?

Have you tried 22 tonight? I said 22.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

June 1st, 2020 at 8:30:28 AM permalink

The sum on each die is 21 (1+2+3+4+5+6)=(1+6)+(2+5)+(3+4)=7x3. Since the total of the faces on each die is 21, take twice that and subtract what's on the bottom. If you were playing Craps where the face down number counted, then the most common number would be 7. Thus the answer is 21+21-7=35.

There are 11 ways to get 6-?, 9 to get 5-?, 11x6+9x5+7x4+5x3+3x2+1x1 = 161. So avg = 161/36 ~= 4.472.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

June 1st, 2020 at 8:30:30 AM permalink

system made a duplicate post

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 1st, 2020 at 10:25:17 AM permalink

Quote: charliepatrick
The sum on each die is 21 (1+2+3+4+5+6)=(1+6)+(2+5)+(3+4)=7x3. Since the total of the faces on each die is 21, take twice that and subtract what's on the bottom. If you were playing Craps where the face down number counted, then the most common number would be 7. Thus the answer is 21+21-7=35.

There are 11 ways to get 6-?, 9 to get 5-?, 11x6+9x5+7x4+5x3+3x2+1x1 = 161. So avg = 161/36 ~= 4.472.

Correct!

And a new speed record!
---------------------------------

It seems German authorities are raiding establishments where citizens have been playing dice games.

They're doing all they can to stop the reformation of the Yahtzee party.

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Wizard

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

Thanked by

June 1st, 2020 at 4:49:05 PM permalink

Quote: Gialmere

A hunter met two shepherds, one of whom had three loaves of bread and the other, five loaves. All the loaves were the same size. The three men agreed to share the eight loaves equally between them. After they had eaten, the hunter gave the shepherds eight bronze coins as payment for his meal.

How should the two shepherds divide this money?

Sorry to go back to an old problem, but this is one of my favourites for long car rides, hikes, of generally when I want to torture someone with a logic puzzle and there is a lot of time to kill.

The usual answer is 3 and 5 and it often difficult to convince the 3-5 camp that 1-7 is the fair compensation according to what they gave the hunter.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 2nd, 2020 at 8:03:20 AM permalink

Today's easy math puzzle is brought to you by...

Q*bert

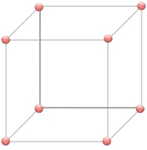
Eight bugs are at the eight corners of an equilateral cube. Each bug randomly picks a direction and moves along the edge of the cube until the next corner.

What is the probability that none of the bugs will meet each other?

You want to place N cubes so that each cube touches every other cube.

What is the largest possible N?

The two red lines in the diagram are drawn diagonally on the faces of a cube.

What is the angle between them at the point where they join?

Have you tried 22 tonight? I said 22.

DogHand

DogHand

Threads: 2
Posts: 1798

Joined: Sep 24, 2011

June 2nd, 2020 at 9:20:04 AM permalink

Quote: Gialmere
Today's easy math puzzle is brought to you by...

The two red lines in the diagram are drawn diagonally on the faces of a cube.

What is the angle between them at the point where they join?

Number 3 answer:

Let the length of each red line be "s", and let the unknown angle be alpha. The length of the third side of the triangle will be s*Sqrt(2), so one-half of its length is s/Sqrt(2). Thus, sin(alpha/2) = (s/Sqrt(2))/s = 1/Sqrt(2), so alpha/2 = 45 degrees. Therefore, alpha = 90 degrees.

Dog Hand

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 2nd, 2020 at 11:07:13 AM permalink

Quote: DogHand
Quote: Gialmere
Today's easy math puzzle is brought to you by...

The two red lines in the diagram are drawn diagonally on the faces of a cube.

What is the angle between them at the point where they join?

Number 3 answer:

Let the length of each red line be "s", and let the unknown angle be alpha. The length of the third side of the triangle will be s*Sqrt(2), so one-half of its length is s/Sqrt(2). Thus, sin(alpha/2) = (s/Sqrt(2))/s = 1/Sqrt(2), so alpha/2 = 45 degrees. Therefore, alpha = 90 degrees.

Dog Hand

Sorry, incorrect.

Have you tried 22 tonight? I said 22.

unJon

Threads: 16
Posts: 4756

Joined: Jul 1, 2018

Thanked by

June 2nd, 2020 at 11:11:08 AM permalink

Quote: Gialmere
Quote: DogHand
Quote: Gialmere
Today's easy math puzzle is brought to you by...

The two red lines in the diagram are drawn diagonally on the faces of a cube.

What is the angle between them at the point where they join?

Number 3 answer:

Let the length of each red line be "s", and let the unknown angle be alpha. The length of the third side of the triangle will be s*Sqrt(2), so one-half of its length is s/Sqrt(2). Thus, sin(alpha/2) = (s/Sqrt(2))/s = 1/Sqrt(2), so alpha/2 = 45 degrees. Therefore, alpha = 90 degrees.

Dog Hand

Sorry, incorrect.

For 3 I get

60 degrees. You can draw another diagnol on a third face that forms a triangle of red lines that are all the same length so it�s the corner of an equilateral triangle.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 2nd, 2020 at 11:19:30 AM permalink

Quote: unJon
For 3 I get
60 degrees. You can draw another diagnol on a third face that forms a triangle of red lines that are all the same length so it�s the corner of an equilateral triangle.

Correct!

Imagine sawing along the red lines.

Have you tried 22 tonight? I said 22.

unJon

Threads: 16
Posts: 4756

Joined: Jul 1, 2018

Thanked by

June 2nd, 2020 at 12:07:37 PM permalink

Quote: Gialmere
Today's easy math puzzle is brought to you by...

Q*bert

Eight bugs are at the eight corners of an equilateral cube. Each bug randomly picks a direction and moves along the edge of the cube until the next corner.

What is the probability that none of the bugs will meet each other?

You want to place N cubes so that each cube touches every other cube.

What is the largest possible N?

The two red lines in the diagram are drawn diagonally on the faces of a cube.

What is the angle between them at the point where they join?

For 2, assuming the cubes are all solid I think

8 is the max. Make a cube of 8 cubes and they all touch each other at least at the middle point. I could also fit a ninth, larger, hollow cube around that 2x2x2 cube where all 9 touch. And if the cubes are made out of bosons instead of fermions I suppose we could have infinite cubes since the Pauli exclusion principle wouldn�t apply. :-)

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 2nd, 2020 at 6:14:33 PM permalink

Quote: unJon
For 2, assuming the cubes are all solid I think
8 is the max. Make a cube of 8 cubes and they all touch each other at least at the middle point. I could also fit a ninth, larger, hollow cube around that 2x2x2 cube where all 9 touch. And if the cubes are made out of bosons instead of fermions I suppose we could have infinite cubes since the Pauli exclusion principle wouldn�t apply. :-)

Hmm... I gotta give this one to you.

I believe the puzzle is considering real world cubes such as building blocks and therefore what you describe is impossible. The best you can achieve is six cubes place thusly...

However, you make an excellent point. In the mathematical world, eight cubes that share a common point would all "touch" (for want of a better word) and so your solve is valid with bonus points for the wraparound cube idea.

[Perhaps a geometry expert would like to chip in.]

Have you tried 22 tonight? I said 22.

ksdjdj

ksdjdj

Threads: 94
Posts: 1707

Joined: Oct 20, 2013

June 2nd, 2020 at 6:22:03 PM permalink

Quote: Gialmere
Today's easy math puzzle is brought to you by...

Q*bert

Eight bugs are at the eight corners of an equilateral cube. Each bug randomly picks a direction and moves along the edge of the cube until the next corner.

What is the probability that none of the bugs will meet each other?

(snip)

I will show the method I used for getting this answer, if the answer is correct...

I would guess 16/6,561
Edit (625 pm): 12/6,561

Last edited by: ksdjdj on Jun 2, 2020

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

Thanked by

June 2nd, 2020 at 6:44:04 PM permalink

Quote: ksdjdj
Quote: Gialmere
Today's easy math puzzle is brought to you by...

Q*bert

Eight bugs are at the eight corners of an equilateral cube. Each bug randomly picks a direction and moves along the edge of the cube until the next corner.

What is the probability that none of the bugs will meet each other?

(snip)

I will show the method I used for getting this answer, if the answer is correct...
I would guess 16/6,561
Edit (625 pm): 12/6,561

Incorrect, but you're hot on the trail.

Have you tried 22 tonight? I said 22.

ksdjdj

ksdjdj

Threads: 94
Posts: 1707

Joined: Oct 20, 2013

June 2nd, 2020 at 6:53:20 PM permalink

Quote: Gialmere
Quote: ksdjdj
Quote: Gialmere
Today's easy math puzzle is brought to you by...

Q*bert

Eight bugs are at the eight corners of an equilateral cube. Each bug randomly picks a direction and moves along the edge of the cube until the next corner.

What is the probability that none of the bugs will meet each other?

(snip)

I will show the method I used for getting this answer, if the answer is correct...
I would guess 16/6,561
Edit (625 pm): 12/6,561

Incorrect, but you're hot on the trail.

Which part was incorrect, the "12", "/6,561" (or maybe both)?

Also, because of the way the lines (edges?) are shown, it "tricks" my brain into thinking the cube is either doing this:
1) From the "face that appears to be the closest", it seems to travel "up and to the right"
or
2) From the "face that appears to be the closest", it seems to travel "down and to the left".
(At first, I only noticed "1)", but now it seems to flip between both of them quite "evenly").

unJon

Threads: 16
Posts: 4756

Joined: Jul 1, 2018

Thanked by

June 2nd, 2020 at 6:56:03 PM permalink

Quote: ksdjdj
Quote: Gialmere
Quote: ksdjdj
Quote: Gialmere
Today's easy math puzzle is brought to you by...

Q*bert

Eight bugs are at the eight corners of an equilateral cube. Each bug randomly picks a direction and moves along the edge of the cube until the next corner.

What is the probability that none of the bugs will meet each other?

(snip)

I will show the method I used for getting this answer, if the answer is correct...
I would guess 16/6,561
Edit (625 pm): 12/6,561

Incorrect, but you're hot on the trail.

Which part was incorrect, the "12", "/6,561" (or maybe both)?

Also, because of the way the lines (edges?) are shown, it "tricks" my brain into thinking the cube is either doing this:
1) From the "face that appears to be the closest", it seems to travel "up and to the right"
or
2) From the "face that appears to be the closest", it seems to travel "down and to the left".
(At first, I only noticed "1)", but now it seems to flip between both of them quite "evenly").

There are 3^8 possible outcomes for sure. I�ve been to lazy to work out how many end up meeting the conditions of (I) no two travel to same endpoint so meet at the end and (ii) no two travel to the endpoint the other one started at and hence meet in the middle.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

June 2nd, 2020 at 7:05:22 PM permalink

Qbert was sooo much fun!

ssho88

ssho88

Threads: 58
Posts: 681

Joined: Oct 16, 2011

June 3rd, 2020 at 7:19:30 AM permalink

To ensure no bugs meet each other, any 4 bugs on same plane only allow to move on same plane, either move clockwise or anticlockwise.

Prob = (1/3)^4 * (1/3)^4 * 4 * 3 = 12/6561

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 3rd, 2020 at 9:19:22 AM permalink

Quote: ssho88

To ensure no bugs meet each other, any 4 bugs on same plane only allow to move on same plane, either move clockwise or anticlockwise.

Prob = (1/3)^4 * (1/3)^4 * 4 * 3 = 12/6561

Incorrect, but you also are hot on the trail.

Have you tried 22 tonight? I said 22.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

June 3rd, 2020 at 10:34:06 AM permalink

Consider the bugs on the front face are ABCD and the ones on the back are EFGH.

There seem to be two ways the bugs can move, remember they can't just swap positions as they would then meet.

Two square faces, all four sides used.
The first method is similar to ABCD just moving one position round, and the other four EFGH do the same. Considering how A might move, there are three ways of selecting its face (ABCD, ABFE, ADHE). (Faces ADCB, AEFB and AEHD are the same idea where the rotation is reversed.) Thus there are three sets of face pairs, and each face may go two directions (clockwise or counter-clockwise). Hence this accounts for 12 ways.

The second method looks like a chair.
In the first scenario three sides of the face ABCD are used: A goes to B, B goes to C, C goes to D, but then D goes to H. From there the moves are forced. For any given chair the direction can be A to B or B to A. One of the links of the face ABCD isn't used, so there are four ways of that to happen and two directions of travel. Hence this accounts for 8 ways.

In the second scenario two sides of the face ABCD are used. A could be connected to either B or D and this defines the chair. Again either direction,. Hence this accounts for 4 ways.

The total number of ways is 24. Hence, as others have done, divide this was 3^8 to get the probability.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 3rd, 2020 at 5:24:58 PM permalink

Quote: charliepatrick
Consider the bugs on the front face are ABCD and the ones on the back are EFGH.

There seem to be two ways the bugs can move, remember they can't just swap positions as they would then meet.

Two square faces, all four sides used.
The first method is similar to ABCD just moving one position round, and the other four EFGH do the same. Considering how A might move, there are three ways of selecting its face (ABCD, ABFE, ADHE). (Faces ADCB, AEFB and AEHD are the same idea where the rotation is reversed.) Thus there are three sets of face pairs, and each face may go two directions (clockwise or counter-clockwise). Hence this accounts for 12 ways.

The second method looks like a chair.
In the first scenario three sides of the face ABCD are used: A goes to B, B goes to C, C goes to D, but then D goes to H. From there the moves are forced. For any given chair the direction can be A to B or B to A. One of the links of the face ABCD isn't used, so there are four ways of that to happen and two directions of travel. Hence this accounts for 8 ways.

In the second scenario two sides of the face ABCD are used. A could be connected to either B or D and this defines the chair. Again either direction,. Hence this accounts for 4 ways.

The total number of ways is 24. Hence, as others have done, divide this was 3^8 to get the probability.

Correct!

Very good. There are indeed two paths that fit the criteria so the chance of no bugs meeting is around 0.4%.

Will Q*bert return?

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 4th, 2020 at 8:05:00 AM permalink

Sst! Avast there. Today's easy math tale be brought to you by pirates. Arrrrrrrrrr...

On a boat in the middle of a lake, five pirates stop to divvy up a chest of gold coins they had "liberated" from a passing vessel. They divide the coins and find that there are two left over.

They throw one pirate overboard and split the coins again: there are three coins left over. They throw another pirate overboard. This time, two coins are left over. They throw another pirate over. This time, one coin is left.

The last two pirates stare at each other. They both reach for their weapons...

So speak up ya bilge rats. What be the fewest number of coins to be found in the treasure chest?
------------------------

BONUS: As each scalawag was tossed overboard, did the water level of the lake rise, lower or stay the same?

Last edited by: Gialmere on Jun 4, 2020

Have you tried 22 tonight? I said 22.

rsactuary

rsactuary

Threads: 29
Posts: 2315

Joined: Sep 6, 2014

Thanked by

June 4th, 2020 at 8:15:34 AM permalink

47. Lake level will stay the same.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 4th, 2020 at 8:37:06 AM permalink

Quote: rsactuary
47. Lake level will stay the same.

Well shiver me timbers! Your answer to the main puzzle is both quick and Correct!

But yarrrr. For your bonus response, well....

Have you tried 22 tonight? I said 22.

Joeman

Joeman

Threads: 36
Posts: 2452

Joined: Feb 21, 2014

June 4th, 2020 at 8:37:29 AM permalink

Quote: Gialmere
BONUS: As each scallywag was tossed overboard, did the water level of the lake rise, lower or stay the same?

Wouldn't that depend on the specific gravity of said scalawags? And possibly the depth of the lake?

"Dealer has 'rock'... Pay 'paper!'"

CrystalMath

CrystalMath

Threads: 8
Posts: 1911

Joined: May 10, 2011

Thanked by

June 4th, 2020 at 8:55:08 AM permalink

The level will drop, assuming the pirate is more dense than the water.

Inside the boat, the pirate displaces his weight. Under water, the pirate displaces his volume.

I heart Crystal Math.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 4th, 2020 at 9:13:20 AM permalink

Quote: CrystalMath
The level will drop, assuming the pirate is more dense than the water.

Inside the boat, the pirate displaces his weight. Under water, the pirate displaces his volume.

Well hoist the Jolly Roger matey! You be Correct!

Have you tried 22 tonight? I said 22.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

June 17th, 2020 at 4:04:06 PM permalink

Imagine a game called Quick Craps, or something even more vulgar, which is played with a single die as follows.

On the come-out roll, 1-3 are points, 4-5 are �craps� and lose, 6 wins even money.

When a point is established, you must roll that point before 4&5 to win the point. A win on 1 is paid even money, a win on 2 is paid 2:1 and a win on 3 is paid 3:1. The bet loses if 4 or 5 come before the point. While rolling for a point, all 6�s are paid even money as soon as they are rolled, irrespective of whether the point wins or loses

What�s the house edge and variance of the game?

And would you play it?

Last edited by: Ace2 on Jun 17, 2020

It�s all about making that GTA

ChesterDog

ChesterDog

Threads: 9
Posts: 1703

Joined: Jul 26, 2010

June 17th, 2020 at 7:38:22 PM permalink

Quote: Ace2
Imagine a game called Quick Craps, or something even more vulgar, which is played with a single die as follows.

On the come-out roll, 1-3 are points, 4-5 are �craps� and lose, 6 wins even money.

When a point is established, you must roll that point before 4&5 to win the point. A win on 1 is paid even money, a win on 2 is paid 2:1 and a win on 3 is paid 3:1. The bet loses if 4 or 5 come before the point. While rolling for a point, all 6�s are paid even money as soon as they are rolled, irrespective of whether the point wins or loses

What�s the house edge and variance of the game?

And would you play it?

On a per decision basis, I get a house edge of 1/6, and a variance of 19/12.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

June 17th, 2020 at 7:48:12 PM permalink

1/6 edge sounds high but maybe you�re right

It�s all about making that GTA

ChesterDog

ChesterDog

Threads: 9
Posts: 1703

Joined: Jul 26, 2010

June 17th, 2020 at 8:14:59 PM permalink

Quote: Ace2
1/6 edge sounds high but maybe you�re right

upon reading your comment.

Now, I get a house edge of zero, and a variance of 5/3.

I neglected every six's winning 1:1.

unJon

Threads: 16
Posts: 4756

Joined: Jul 1, 2018

Thanked by

June 17th, 2020 at 8:33:03 PM permalink

Quote: ChesterDog

upon reading your comment.

Now, I get a house edge of zero, and a variance of 5/3.

I neglected every six's winning 1:1.

Was just coming to post that I get a 1/6 edge if you ignore multiple 6s that could roll while a point is established.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Ace2

Ace2

Threads: 32
Posts: 2706

Joined: Oct 2, 2017

June 18th, 2020 at 11:44:42 AM permalink

Quote: ChesterDog

upon reading your comment.

Now, I get a house edge of zero, and a variance of 5/3.

I neglected every six's winning 1:1.

Correct !

This could be a fun game between two people that had a single die. Zero edge

It�s all about making that GTA

Wizard
Administrator

Wizard

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

June 22nd, 2020 at 4:04:26 PM permalink

What is a strategy that will win on the Price is Right game Now or Then every time, without knowing anything about the prices of the items?

Here are the rules.

There is a circular board with six slices, like a Trivia Pursuit token. For purposes of discussion, let's number the slices like this:

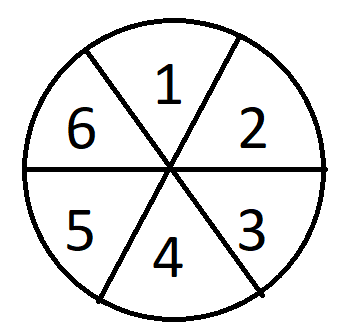
Each slice will contain an item and a price. For example a jar of peanut butter and $2.99
Each price will be either the accurate price now or at some time about ten years in the past.
The player may pick any slice
The player must guess whether the item in that slice displays the price "now" or "then."
The player must get three consecutive slices correct to win the game.
It is not stated on the show, but there have traditionally been four Now items and two Then.

It is important to emphasize the player may jump around locations on the wheel, he doesn't need to go consecutively, as many players foolishly do.

Examples

Direct: https://www.youtube.com/watch?v=J_3ys7UIi64

Listen very closely starting at 3:52. Drew correctly states the player must get the pretzels to win. However, notice how he hints "However, you can go anywhere you want."

Direct: https://www.youtube.com/watch?v=BheLUPGbfvw

At the 2:35 point, Drew says "Which way do you want to go?" This would seem to imply the player must pick slices consecutively, but he doesn't.

The question asks what is a strategy that will guarantee a win every time, not nothing anything about prices?

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

June 22nd, 2020 at 4:33:49 PM permalink

Quote: Wizard
What is a strategy that will win on the Price is Right game Now or Then every time, without knowing anything about the prices of the items?

Guess Now for #1
If you are correct, guess Then for #2 and #6
If both #2 and #6 are Now, you have 6-1-2 for a win
If both #2 and #6 are Then, then all of the others are Now, so guess Now for #3, #4, and #5, and you have a 3-4-5 win
If #2 is Now and #6 is Then, you have #1 and #2 correct; guess anything for #4 and #5 to reveal all but #3, which you can then guess correctly for a 1-2-3 win
If #2 is Then and #6 is Now, guess anything for #3 and #4 to reveal what #5 has to be; you have a 5-6-1 win

If #1 is Then, guess Now for #2 and #6
Since there are only two Thens, at least one of them is a Now
If either one is a Then, then #3, #4, and #5 all have to be Now, and you will have a 3-4-5 win
If both of them are Now, then guess Now for #3 and #5; at least one of them has to be correct, and you will know what #4 is, so you will have either a 2-3-4 or a 4-5-6 win.

Here's some Now...or Then trivia:

Notice that the word "or" is a different color. This is because the game was originally called "Now and Then," but Bob Barker pointed out that a price can't be both now and then; it's one or the other.

In Bob's day, he would always say, "Now is today," without mentioning a date. This is because the show has been airing repeats during the summer months for over 40 years. Similarly, on Check Game, the checks were originally dated "Today, 19-Now" for the same reason.

Ever see the game "Hit Me?" It was blackjack, but the player's cards were determined by selecting items, each of which had their prices multiplied by a different integer from 1 to 10. There was always a 1, which was an ace, and always a 10; the player won ties, even if the player had a 3-card 21 to the dealer's 2-card 21.
Usually, the following strategy worked; there was only one item that ended in zero, so that had to be the 10, and there was one that was not a multiple of 2, 3, 5, or 7, so it had to be the ace.

The strangest thing about the game was, it wasn't quite played correctly; in one playing, I think a player had 20, and the house had A-8. Despite the fact that there was a sign that said "House hits to 16 and stands on 17," the host said, "The house counts that ace as 1, and hits"; the house ended up drawing to 21, and the player lost. In another playing, the player stopped at 15 for some reason; the house got a hard 16, and the host announced, "Sorry, but you lose," only for the producer to tell him, "The house has to hit 16," and the host replied, "Why? The house is ahead!", but eventually the house did hit, and busted, so the player won.

Wizard
Administrator

Wizard

Threads: 1517
Posts: 27009

Joined: Oct 14, 2009

June 22nd, 2020 at 9:14:19 PM permalink

Quote: ThatDonGuy

Guess Now for #1
If you are correct, guess Then for #2 and #6
If both #2 and #6 are Now, you have 6-1-2 for a win
If both #2 and #6 are Then, then all of the others are Now, so guess Now for #3, #4, and #5, and you have a 3-4-5 win
If #2 is Now and #6 is Then, you have #1 and #2 correct; guess anything for #4 and #5 to reveal all but #3, which you can then guess correctly for a 1-2-3 win
If #2 is Then and #6 is Now, guess anything for #3 and #4 to reveal what #5 has to be; you have a 5-6-1 win

If #1 is Then, guess Now for #2 and #6
Since there are only two Thens, at least one of them is a Now
If either one is a Then, then #3, #4, and #5 all have to be Now, and you will have a 3-4-5 win
If both of them are Now, then guess Now for #3 and #5; at least one of them has to be correct, and you will know what #4 is, so you will have either a 2-3-4 or a 4-5-6 win.

I will take it on faith your strategy works. Not quite the same as mine, which I'll link to below.

Regarding Hit Me, I didn't know that. I barely remember that show.

First, pick any three slices in a row and guess �Now� for all of them. For example, the top three, which are 6, 1, and 2.

Here is how to proceed, according to what happened with the first three slices.
1. If all three were NOW, then you win!
2. If any two were THEN, then the rest must be NOW. Lock in a win by picking NOW for the other three slices.
3. If you get one THEN on either end (slice 2 or 6), guess anything for the two slices closest to the THEN slice. If you find the other THEN, the remaining slice must be NOW. If you don�t find the other THEN, then the last THEN must be the last slice. Note that this was the situation in the example video I mentioned above, but the player didn�t follow Drew�s hint by fishing for information on slices other than the needed one.
4. If you get one THEN in the middle (slice 1), then pick NOW for slices 3 and 5. If they are both NOW, then you will win by picking THEN for slice 4. If one is THEN, then pick NOW for slice 4 for the win.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

June 23rd, 2020 at 10:10:44 AM permalink

Quote: Wizard
I will take it on faith your strategy works. Not quite the same as mine, which I'll link to below.

If #1 is Now, guess Now (instead of Then - note the rest of the solution assumes you did guess Now) for #2 and #6.
I have a feeling that my solution matches yours, since my solution always guesses Now for 1, 2, and 6.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

June 23rd, 2020 at 10:41:26 AM permalink

Once I realised "consecutive" didn't mean three guesses in a row, I had thought, without going through all the details, an approach that matches the wizard's method...

Take the top three pieces picking "Now", you could find three "Now" (win), one "Then" in the middle, one "Then" to the side, or two "Then". Each option has a method to ensure success. One important fact is if you have two correct in a row, then leave the one you need to find out about, pick all the others and you then know the contents of the unpicked piece.

Always pick Now unless you know the last one is a Then.
NNN - win
NTN - pick one adjacent - if (NTN)T, then the rest are N's - if (NTN)N, then go the other way ?(NTNN) to ensure you know where the other T is.
NNT/TNN - similarly, work your way round from the T-side (NNT)??/??(TNN) so you know where the other T is.
TTN/TNT/NNT - then the other three are all N's.

Gialmere

Threads: 45
Posts: 3044

Joined: Nov 26, 2018

June 24th, 2020 at 11:12:56 AM permalink

It's been several years since the Apocalypse, but the zombies are still everywhere. I've been caught out in the open on my own and am being attacked by three hungry zombies intent on eating my brains.

Fortunately I have six bullets in my gun. Unfortunately the ammo is old and degraded so that it only works 80% of the time.

Also, although my aim it's excellent, my shots get inaccurate when I'm nervous, such as when I'm surrounded by creatures trying to feast on my flesh. It turns out that the closer they get, the more nervous I get, so my chance of firing a kill shot to the head (the only way they'll die) is a mere 63%.

I worked it out. There is roughly a 50% chance that any particular round will end up killing a zombie.

I have just enough time to fire all six bullets. What are my chances of surviving this hellish encounter?

Have you tried 22 tonight? I said 22.

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

June 24th, 2020 at 11:33:41 AM permalink

It depends on whether you have time to see if a particular shot is a killing shot before aiming your next shot.

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

Thanked by

June 24th, 2020 at 12:41:44 PM permalink

Is this the same as tossing six coins and seeing whether you get three or more heads?

The solution is to consider combinations and the 32 possibilities. Ranging from 0 thru 6 they are 1 6 15 20 15 6 1. So the chances of 3-3 is 20/64 and a strict majority 22/64. So the total chances are 42/64 = 65.625%.

ThatDonGuy

Threads: 122
Posts: 6659

Joined: Jun 22, 2011

June 24th, 2020 at 1:15:15 PM permalink

Quote: charliepatrick
Is this the same as tossing six coins and seeing whether you get three or more heads?
The solution is to consider combinations and the 32 possibilities. Ranging from 0 thru 6 they are 1 6 15 20 15 6 1. So the chances of 3-3 is 20/64 and a strict majority 22/64. So the total chances are 42/64 = 65.625%.

it may be the same as tossing two red coins, two white coins, and two blue coins, and seeing if at least one coin of each color comes up heads

charliepatrick

Threads: 39
Posts: 3011

Joined: Jun 17, 2011

June 24th, 2020 at 1:32:18 PM permalink

Quote: ThatDonGuy

it may be the same as tossing two red coins, two white coins, and two blue coins, and seeing if at least one coin of each color comes up heads

Then I'm confused. If you fire the first bullet and it kills a zombie then you now have 5 bullets to kill the other two zombies. Now if you're saying you fire both shots of a double-barreled shotgun at the first zombie, then the chances of killing it is 3/4. So the chances of all three is 3/4 ^ 3. But this isn't how I interpreted the question.

unJon