Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
May 13th, 2020 at 10:16:37 PM
permalink
Quote: Gialmere
You have a friend who hustles three card monte on the Las Vegas Strip. You offer him $100 to teach you some of his tricks. Instead, he proposes a wager for his fee.
You'll put down two C-notes on the table and he'll put down one. Then, without cheating, he'll start dealing three card monte for you at $100 dollars a round. The first person to win all three of the C-notes keeps them.
Intrigued by the idea, you agree. As your friend starts the first round, however, you can see that, between his lighting fast shuffle and quick misdirection moves, you'll have no idea which card hides the lucky lady.
Expressed as a fraction, what are your chances of winning his $100 vs his chance of winning your $200?
Zero.
And if you disagree, then you have never played three card monte.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
May 14th, 2020 at 6:37:05 AM
permalink
Quote: gordonm888
Zero.
And if you disagree, then you have never played three card monte.
Have you tried 22 tonight? I said 22.
May 14th, 2020 at 6:39:25 AM
permalink
Quote: Ace2This can be easily solved with linear equations for the different states or using the gamblers ruin formula :
(1 - (p/q)^b) / (1 - (p/q)^(a+b))
Where p = 2/3
q = 1 - p
a = dealer bankroll = 1
b = player bankroll = 2
B has 3/7 chance of winning
Correct!
You really want to win that first round.
------------------------------------------
Studies show that 9 out of 8 Americans are bad at fractions.
Have you tried 22 tonight? I said 22.
May 14th, 2020 at 6:45:00 AM
permalink
What the...?
Have you tried 22 tonight? I said 22.
May 14th, 2020 at 7:08:48 AM
permalink
Quote: GialmereWhat the...?
Zero - the triangle in and of itself violates the triangle inequality, where the length of any side of a triangle is less than the sum of the lengths of the other two sides
Let's make it a little harder: what is x if the length 3 side is 7/2?
For that matter, how about a more general solution: replace 5 with a, 3 with b, the left 4 with c, and the right 4 with d?
Last edited by: ThatDonGuy on May 14, 2020
May 14th, 2020 at 7:41:44 AM
permalink
Quote: GialmereWhat the...?
1
May 14th, 2020 at 8:08:46 AM
permalink
Quote: ChesterDogQuote: GialmereWhat the...?
1
You got me on that one - the original question doesn't actually say that it's a triangle, now does it?
May 14th, 2020 at 8:43:52 AM
permalink
Quote: ChesterDog
1
Correct!
Heh. This thread is really starting to degenerate.
Have you tried 22 tonight? I said 22.
May 14th, 2020 at 9:29:47 AM
permalink
For a single-zero roulette wheel, what is the expected number of spins, expressed as an integer, to hit all 37 numbers?
It’s all about making that GTA
May 14th, 2020 at 5:51:30 PM
permalink
Quote: Ace2For a single-zero roulette wheel, what is the expected number of spins, expressed as an integer, to hit all 37 numbers?
I had to use the quotient of two integers:
2040798836801833 / 13127595717600
2040798836801833 / 13127595717600
May 14th, 2020 at 6:40:58 PM
permalink
Correct. How did you get the answer?Quote: ChesterDogI had to use the quotient of two integers:
2040798836801833 / 13127595717600
It’s all about making that GTA
May 14th, 2020 at 7:09:14 PM
permalink
Quote: Ace2Correct. How did you get the answer?Quote: ChesterDogI had to use the quotient of two integers:
2040798836801833 / 13127595717600
The probability of getting the first number in one spin is 37/37, and we know that the average number spins to get it is the reciprocal of the probability, which 1/(37/37) = 37/37.
The probability of getting the second number in one spin is 36/37, so the average number of spins to get it is 1/(36/37) = 37/36.
On so on. The average number of spins to get all the numbers is 37/37 + 37/36 + 37/35 + … +37/1.
The hard part, of course, is to express this as a rational number. I typed 37(1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+1/10+1/11+1/12+1/13+1/14+1/15+1/16 +1/17+1/18+1/19+1/20+1/21+1/22+1/23+1/24+1/25+1/26+1/27+1/28+1/29+1/30 +1/31+1/32+1/33+1/34+1/35+1/36+1/37) into WolframAlpha, and it kept working without timing out, but it didn't give an answer.
Next, I started working in Excel by allotting about 9 cells (5 digits per cell) to the common denominator and to each of the 37 terms in the numerator. I took a break and tried WolframAlpha again, and it gave the answer right away.
May 14th, 2020 at 7:15:42 PM
permalink
Quote: Ace2Correct. How did you get the answer?Quote: ChesterDogI had to use the quotient of two integers:
2040798836801833 / 13127595717600
Use markov chain formula(with "dynamic" probability)
E0 = 37/37*( 1 + E1) + 0/37 * (1 + E0) - - -- Eq 1
E1 = 36/37*( 1 + E2) + 1/37 * (1 + E1) - - -- Eq 2
E2 = 35/37*( 1 + E3) + 2/37 * (1 + E2) - - -- Eq 3
E3 = 34/37*( 1 + E4) + 3/37 * (1 + E3) - - -- Eq 4
.
.
.
.
E35 = 2/37*( 1 + E36) + 35/37 * (1 + E35) - - -- Eq 36
E36 = 1/37*( 1 + E37) + 36/37 * (1 + E36) - - -- Eq 37
E37 = 0( after you hit all 37 numbers, you don't have to spin further, E37 =0)
So E36 = 37
E35 = 37/2 + E36 = 111/2
E34 = 37/3 + E35 = 407/6
.
.
.
.
E0 = 37/37 + 37/36 + 37/35 + . . . + 37/3 + 37/2 + 37/1
E0 = 2040798836801833 / 13127595717600 = 155.458690281402
Last edited by: ssho88 on May 14, 2020
May 14th, 2020 at 7:34:43 PM
permalink
Interesting. I didn’t realize there was a calculator that would do that large of a summation in fractional format.
The answer can also be found by taking the integral from zero to infinity of:
1-(1-1/e^(x/37))^37 dx
To get 2040798836801833 / 13127595717600
=~ 155 spins
Correction: I should have asked for the answer expressed as a rational number (instead of as an integer). Though I think you guys realized what I meant
The answer can also be found by taking the integral from zero to infinity of:
1-(1-1/e^(x/37))^37 dx
To get 2040798836801833 / 13127595717600
=~ 155 spins
Correction: I should have asked for the answer expressed as a rational number (instead of as an integer). Though I think you guys realized what I meant
It’s all about making that GTA
May 14th, 2020 at 8:21:33 PM
permalink
Deleted
Last edited by: ssho88 on May 14, 2020
May 15th, 2020 at 3:11:24 AM
permalink
On day 1 an immature Covid-21 microbe enters your lungs. In two days, an immature microbe will become mature. Mature microbes will spawn one immature microbe per day.
How many total microbes will be in your lungs at the end of 21 days?
How many total microbes will be in your lungs at the end of 21 days?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 15th, 2020 at 5:14:29 AM
permalink
On Day 3 you have 1 mature microbe and a mature microbe will add a mature microbre every three days.
3*dN/dt = N
ln(N) = t/3 +c
ln(1) = 3/3 + c
c = -1
so after 21 days, N = e^(t/3-1) = e^6 = 403.43 ?
Last edited by: ssho88 on May 15, 2020
May 15th, 2020 at 7:44:20 AM
permalink
Quote: ssho88
On Day 3 you have 1 mature microbe and a mature microbe will add a mature microbre every three days.
3*dN/dt = N
ln(N) = t/3 +c
ln(1) = 3/3 + c
c = -1
so after 21 days, N = e^(t/3-1) = e^6 = 403.43 ?
I think you're solving a much harder problem. Unlike my covid-20 problem, covid-21 mature microbes spawn at EXACTLY one per day, not an average of one per day.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 15th, 2020 at 7:59:23 AM
permalink
After 3 days, there is 1 mature microbe and 0 immature ones
Each mature microbe will result in another mature microbe appearing 3 days later
This is a recursive sequence: Mn = Mn-1 + Mn-3, where the first three terms (starting with M1) are 0, 0, 1.
The sequence is 0, 0, 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595
After 21 days, there are 595 mature microbes, 277 day-old immature ones, and 406 new immature microbes, for a total of 1278.
I'll see if I can generate a non-recursive formula, but the method I learned to do it (using matrices) looks like it needs the root of a cubic equation.
May 15th, 2020 at 10:30:43 AM
permalink
The break room at your work has a vintage hot beverage machine with only three selections: "coffee", "tea" and "random" (50/50 coffee or tea). Unfortunately the machine was labeled incorrectly when it was built so that each button does not give what it claims.
If a drink costs 75 cents, what is the minimum amount of money you must put in the machine in order to correctly relabel the buttons?
Have you tried 22 tonight? I said 22.
May 15th, 2020 at 11:38:11 AM
permalink
If we know that none of the buttons are correct, then the maximum is 75 cents.
Select Random; since we know this is wrong, then whatever comes out should be labelled that way, whatever is currently labelled that way should be labelled Random (otherwise Random would already be correctly labelled), and whatever is currently Random should be labelled with the remaining choice
If one of them can be correctly labelled, I don't think it's possible to be 100% certain.
Suppose Tea is correctly labelled; if Random just happens to always give Coffee, there is no way to tell the other two buttons apart.
Last edited by: ThatDonGuy on May 15, 2020
May 15th, 2020 at 1:18:43 PM
permalink
Quote: ThatDonGuy
After 3 days, there is 1 mature microbe and 0 immature ones
Each mature microbe will result in another mature microbe appearing 3 days later
This is a recursive sequence: Mn = Mn-1 + Mn-3, where the first three terms (starting with M1) are 0, 0, 1.
The sequence is 0, 0, 1, 1, 1, 2, 3, 4, 6, 9, 13, 19, 28, 41, 60, 88, 129, 189, 277, 406, 595
After 21 days, there are 595 mature microbes, 277 day-old immature ones, and 406 new immature microbes, for a total of 1278.
I'll see if I can generate a non-recursive formula, but the method I learned to do it (using matrices) looks like it needs the root of a cubic equation.
Perhaps I didn't word the problem well. A microbe becomes mature in one day. After becoming mature, it will spawn a new microbe once a day, starting a day after maturity. To get this going:
Day 1: 1 immature, 0 mature
Day 2: 0 immature, 1 mature
Day 3: 1 immature, 1 mature
Day 4: 1 immature, 2 mature
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
May 15th, 2020 at 2:27:34 PM
permalink
Quote: WizardPerhaps I didn't word the problem well. A microbe becomes mature in one day. After becoming mature, it will spawn a new microbe once a day, starting a day after maturity. To get this going:
Day 1: 1 immature, 0 mature
Day 2: 0 immature, 1 mature
Day 3: 1 immature, 1 mature
Day 4: 1 immature, 2 mature
It's a straightforward Fibonacci sequence that starts with 0
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765
There are 6765 mature and 4181 immature microbes = 10,946 total
May 15th, 2020 at 2:30:23 PM
permalink
I agree with TDG.
(r^21 - (1 - r)^21) / 5^.5 = 10,946
where r = golden ratio = (1 + 5^.5) / 2
(r^21 - (1 - r)^21) / 5^.5 = 10,946
where r = golden ratio = (1 + 5^.5) / 2
It’s all about making that GTA
May 15th, 2020 at 2:35:04 PM
permalink
Quote: Gialmere...If a drink costs 75 cents, what is the minimum amount of money you must put in the machine in order to correctly relabel the buttons?
You only have to make one purchase, but it has to be the one marked Random.
If you place your 75 cents into the slot marked Random, then it will either land up as Tea or Coffee.
Suppose you get a cup of Tea. The one marked Coffee can't be Coffee so must be Random, and the one marked Tea must be Coffee.
Similarly if you get a cup of Coffee you can work out the other two.
If you place your 75 cents into the slot marked Random, then it will either land up as Tea or Coffee.
Suppose you get a cup of Tea. The one marked Coffee can't be Coffee so must be Random, and the one marked Tea must be Coffee.
Similarly if you get a cup of Coffee you can work out the other two.
May 15th, 2020 at 3:10:46 PM
permalink
Quote: Wizard...How many total microbes will be in your lungs at the end of 21 days?
Born | 1-day old | Old | ||
Day 1 | 1 | Microbe enters body | ||
Day 2 | 1 | Everything born yesterday is now 1-day old | ||
Day 3 | 1 | 1 | All the old ones (currently 1) create a born one | |
Day 4 | 1 | 1 | 1 | |
Day 5 | 2 | 1 | 2 | Old ones include those who were 1-day old yesterday…. |
Day 6 | 3 | 2 | 3 | …and so more are born |
Day 7 | 5 | 3 | 5 |
Assume the microbe enters your body at 00h01 and everything is born at 00h01; the first birth occurs on Day 3 at 00h01.
The numbers of Old microbes increases by how many were born 2 days ago, which is the same as how many Old ones there were two days ago. So the number of Old microbes, being the sum of the last two entries, is a Fibonacci series.
So I agree with the earlier answers, that one Day 21 there are
4181 Old microbes
2584 1-day old Microbes
4181 newly born
Total = 10946.
May 15th, 2020 at 3:58:03 PM
permalink
Quote: Gialmere
The break room at your work has a vintage hot beverage machine with only three selections: "coffee", "tea" and "random" (50/50 coffee or tea). Unfortunately the machine was labeled incorrectly when it was built so that each button does not give what it claims.
If a drink costs 75 cents, what is the minimum amount of money you must put in the machine in order to correctly relabel the buttons?
Assuming ALL three selections was labeled incorrectly, then just put 75 cents and press button "RANDOM" .
If you get coffee, then the original "RANDOM" button can be re-labeled as "COFFEE", the original "TEA" button can be re-labeled as "RANDOM", and finally the original "COFFEE"can be re-labeled as "TEA".
Just costs you 75 cents ?
May 15th, 2020 at 4:21:36 PM
permalink
If it is anything like the drink machines I remember, it will cost you at least $1.50 because upon depositing the first $0.75 and pushing a button, the cup will get stuck half way and the beverage will pour straight down the drain! ;P
"Dealer has 'rock'... Pay 'paper!'"
May 15th, 2020 at 5:17:36 PM
permalink
Quote: ThatDonGuy
If we know that none of the buttons are correct, then the maximum is 75 cents.
Select Random; since we know this is wrong, then whatever comes out should be labelled that way, whatever is currently labelled that way should be labelled Random (otherwise Random would already be correctly labelled), and whatever is currently Random should be labelled with the remaining choice
If one of them can be correctly labelled, I don't think it's possible to be 100% certain.
Suppose Tea is correctly labelled; if Random just happens to always give Coffee, there is no way to tell the other two buttons apart.
Quote: charliepatrick
You only have to make one purchase, but it has to be the one marked Random.
If you place your 75 cents into the slot marked Random, then it will either land up as Tea or Coffee.
Suppose you get a cup of Tea. The one marked Coffee can't be Coffee so must be Random, and the one marked Tea must be Coffee.
Similarly if you get a cup of Coffee you can work out the other two.
Quote: ssho88Assuming ALL three selections was labeled incorrectly, then just put 75 cents and press button "RANDOM" .
If you get coffee, then the original "RANDOM" button can be re-labeled as "COFFEE", the original "TEA" button can be re-labeled as "RANDOM", and finally the original "COFFEE"can be re-labeled as "TEA".
Just costs you 75 cents ?
All Correct!
It's sort of a mini logic problem masquerading as a mini math problem.
-------------------------------
I read about a guy last week who was so exhausted he fell asleep at the kitchen table and drowned in his oversize coffee mug. Fortunately he didn't suffer. It was instant.
Have you tried 22 tonight? I said 22.
May 17th, 2020 at 2:25:13 PM
permalink
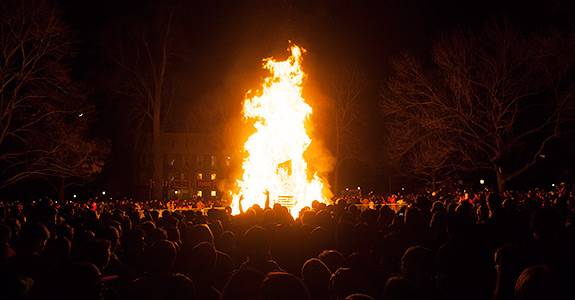
UNLV is purchasing new beds for its dorm rooms. It agrees to let the students use the old wooden beds to make a bonfire. The students take the wooden beds, weighing 200 pounds each, and arrange them into a pyramid. The base layer is 5 beds × 5 beds, the layer above is 4 beds × 4 beds, and so on until the top layer of one bed. They arrange them in such a way that each bed is resting on four beds below it, one leg on each bed.
To make the burn more exciting, the students want to put a funny display and some pyrotechnics on the top bed. If the weight on each bed is always equally distributed to all four legs, and each bed leg can only support 200 pounds, how many additional pounds can they place on top of the topmost bed without risking structural collapse?
/pic5420534.png)
Have you tried 22 tonight? I said 22.
May 17th, 2020 at 2:50:05 PM
permalink
This seems too easy so I must be missing something.
100 legs on the bottom x 200 pounds each is 20,000 pounds that can be supported.
55 beds in the structure at 200 pounds each is 11,000 pounds.
So, 9,000 additional pounds.
I doubt the assumption of the weight being distributed across all 4 legs below is realistic, but perhaps the beds can be designed in a way to accomplish that.
100 legs on the bottom x 200 pounds each is 20,000 pounds that can be supported.
55 beds in the structure at 200 pounds each is 11,000 pounds.
So, 9,000 additional pounds.
I doubt the assumption of the weight being distributed across all 4 legs below is realistic, but perhaps the beds can be designed in a way to accomplish that.
May 17th, 2020 at 2:57:37 PM
permalink
Quote: RideTheEdgeThis seems too easy so I must be missing something.
100 legs on the bottom x 200 pounds each is 20,000 pounds that can be supported.
55 beds in the structure at 200 pounds each is 11,000 pounds.
So, 9,000 additional pounds.
I doubt the assumption of the weight being distributed across all 4 legs below is realistic, but perhaps the beds can be designed in a way to accomplish that.
Sorry, no.
Note that beds carry different loads depending on their location within the structure.
Have you tried 22 tonight? I said 22.
May 17th, 2020 at 3:23:07 PM
permalink
It's a matter of working your way from the top down to the bottom.
Top Row
The top bed has 200 + 256W on it (it's easier to use 256W than getting into fractions later).
So each leg will have 50 + 64W
Second Row
Each bed has one leg on it weighing 50 + 64W.
So the total weight ofthe bed plus what it's holding = 200 + 50 + 64W.
So each leg takes 250/4 + 64W/4 = 62.5 + 16W.
Third Row
There are three types of beds.
(i) The ones at the corners only have one leg to support. So their total weight = (262.5+16W). Each leg will have 65.625+4W.
(ii) The ones on the outside have two legs to support. So their total weight = (325+32W). Each leg will have 81.25+8W.
(iii) The bed in the middle has four legs to support. So its total weight = (450+64W). Each leg will have 112.5+16W.
Fourth Row
The inside four will have one (iii), two (ii) and one (i)leg from the previous row.
Total weight to support = 200 + 112.5+16W + 162.5+16W + 65.625+4W = 540.625 + 36W.
lowest row
The middle bed will get four of the above central legs to support and 200.
Total weight = 200 + 540.625 + 36W = 740.625 + 36W.
Thus each leg of that central bed will have to support 185.15625 + 9W.
This can be a maximum of 200, so 9W = 200-185.15625 = 14.84375.
W = 1.6493055555
Original weight = 256W = 422 2/9.
Top Row
The top bed has 200 + 256W on it (it's easier to use 256W than getting into fractions later).
So each leg will have 50 + 64W
Second Row
Each bed has one leg on it weighing 50 + 64W.
So the total weight ofthe bed plus what it's holding = 200 + 50 + 64W.
So each leg takes 250/4 + 64W/4 = 62.5 + 16W.
Third Row
There are three types of beds.
(i) The ones at the corners only have one leg to support. So their total weight = (262.5+16W). Each leg will have 65.625+4W.
(ii) The ones on the outside have two legs to support. So their total weight = (325+32W). Each leg will have 81.25+8W.
(iii) The bed in the middle has four legs to support. So its total weight = (450+64W). Each leg will have 112.5+16W.
Fourth Row
The inside four will have one (iii), two (ii) and one (i)leg from the previous row.
Total weight to support = 200 + 112.5+16W + 162.5+16W + 65.625+4W = 540.625 + 36W.
lowest row
The middle bed will get four of the above central legs to support and 200.
Total weight = 200 + 540.625 + 36W = 740.625 + 36W.
Thus each leg of that central bed will have to support 185.15625 + 9W.
This can be a maximum of 200, so 9W = 200-185.15625 = 14.84375.
W = 1.6493055555
Original weight = 256W = 422 2/9.
May 17th, 2020 at 3:44:41 PM
permalink
Quote: charliepatrickIt's a matter of working your way from the top down to the bottom.
Top Row
The top bed has 200 + 256W on it (it's easier to use 256W than getting into fractions later).
So each leg will have 50 + 64W
Second Row
Each bed has one leg on it weighing 50 + 64W.
So the total weight ofthe bed plus what it's holding = 200 + 50 + 64W.
So each leg takes 250/4 + 64W/4 = 62.5 + 16W.
Third Row
There are three types of beds.
(i) The ones at the corners only have one leg to support. So their total weight = (262.5+16W). Each leg will have 65.625+4W.
(ii) The ones on the outside have two legs to support. So their total weight = (325+32W). Each leg will have 81.25+8W.
(iii) The bed in the middle has four legs to support. So its total weight = (450+64W). Each leg will have 112.5+16W.
Fourth Row
The inside four will have one (iii), two (ii) and one (i)leg from the previous row.
Total weight to support = 200 + 112.5+16W + 162.5+16W + 65.625+4W = 540.625 + 36W.
lowest row
The middle bed will get four of the above central legs to support and 200.
Total weight = 200 + 540.625 + 36W = 740.625 + 36W.
Thus each leg of that central bed will have to support 185.15625 + 9W.
This can be a maximum of 200, so 9W = 200-185.15625 = 14.84375.
W = 1.6493055555
Original weight = 256W = 422 2/9.
Correct!
It's all about that middle bed on the bottom.
------------------------------
Did you hear the joke about pyramid schemes?
Share this joke 10 times to find out how!
Have you tried 22 tonight? I said 22.
May 18th, 2020 at 9:03:15 AM
permalink
I present this easy math question two ways...
SPECTRE is threatening to launch a nuclear missile at London unless a ransom is paid. Secret agent 007 has penetrated the evil villain lair and reached the missile guidance system.
The launch sequence is activated by a simple 5-digit code number from 00000 to 99999. If he enters the correct number he can reprogram the missile to explode on launch and destroy the SPECTRE secret base. If he enters the wrong number, however, the missile will launch on London immediately.
Q-branch has given him a gadget that can access the guidance computer. It can't tell Bond what the number is directly, but it does allow him to query the computer with "yes or no" questions about the number. What is the minimum number of questions 007 will need to ask in order to be certain what the code number is?
I'm thinking of a 5-digit number from 00000 to 99999. I won't tell tell what it is, but I will truthfully answer any "yes or no" questions about it.
Not counting lucky guesses, what is the minimum number of questions you'll need to ask me to correctly ascertain the number?
SPECTRE is threatening to launch a nuclear missile at London unless a ransom is paid. Secret agent 007 has penetrated the evil villain lair and reached the missile guidance system.
The launch sequence is activated by a simple 5-digit code number from 00000 to 99999. If he enters the correct number he can reprogram the missile to explode on launch and destroy the SPECTRE secret base. If he enters the wrong number, however, the missile will launch on London immediately.
Q-branch has given him a gadget that can access the guidance computer. It can't tell Bond what the number is directly, but it does allow him to query the computer with "yes or no" questions about the number. What is the minimum number of questions 007 will need to ask in order to be certain what the code number is?
I'm thinking of a 5-digit number from 00000 to 99999. I won't tell tell what it is, but I will truthfully answer any "yes or no" questions about it.
Not counting lucky guesses, what is the minimum number of questions you'll need to ask me to correctly ascertain the number?
Last edited by: Gialmere on May 18, 2020
Have you tried 22 tonight? I said 22.
May 18th, 2020 at 9:53:12 AM
permalink
so thinking out loud...
Obviously you could starting asking questions like.. 1. is the number greater than or equal to 50000? (let's say the answer is NO)
2. is the number greater than or equal to 25000? etc etc etc..
Using that methodology, I calculated you would need 17 questions to figure out the number.
But I'm wondering if there is some easier way using a combination of the above and knowing whether numbers are multiples of primes or not, that might cut a few questions out?
Obviously you could starting asking questions like.. 1. is the number greater than or equal to 50000? (let's say the answer is NO)
2. is the number greater than or equal to 25000? etc etc etc..
Using that methodology, I calculated you would need 17 questions to figure out the number.
But I'm wondering if there is some easier way using a combination of the above and knowing whether numbers are multiples of primes or not, that might cut a few questions out?
May 18th, 2020 at 10:19:10 AM
permalink
Quote: rsactuaryso thinking out loud...
Obviously you could starting asking questions like.. 1. is the number greater than or equal to 50000? (let's say the answer is NO)
2. is the number greater than or equal to 25000? etc etc etc..
Using that methodology, I calculated you would need 17 questions to figure out the number.
But I'm wondering if there is some easier way using a combination of the above and knowing whether numbers are multiples of primes or not, that might cut a few questions out?
Correct!
As far as I know, you have to use the ol' "Price is Right" Clock Game method. Higher! Lower! Lower! Higher!
---------------------------------------
I asked my physician if he was a James Bond fan...
Dr.: No
Have you tried 22 tonight? I said 22.
May 18th, 2020 at 10:21:31 AM
permalink
A more interesting question is what technique of guessing leads to the fewest expected number of questions.Quote: rsactuaryso thinking out loud...
Obviously you could starting asking questions like.. 1. is the number greater than or equal to 50000? (let's say the answer is NO)
2. is the number greater than or equal to 25000? etc etc etc..
Using that methodology, I calculated you would need 17 questions to figure out the number.
But I'm wondering if there is some easier way using a combination of the above and knowing whether numbers are multiples of primes or not, that might cut a few questions out?
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 19th, 2020 at 6:57:24 AM
permalink
/pic5423236.png)
You're on a diet and your spouse presents you with a single pancake for breakfast. Pouting, you revert to your childhood self and decide to play with your food. Maybe you can make it appear like there's more than there is. You wonder...
What is the maximum number of sections into which a pancake may be divided by four straight cuts through it? You pick up your "scalpel", consider your circular "patient", and make your first incision...
(Note: The pieces cannot be rearranged between cuts.)
Have you tried 22 tonight? I said 22.
May 19th, 2020 at 7:02:25 AM
permalink
If you had just said 4 cuts, I would have said 12. I guess it depends how you define "straight cut". If "straight cut" means edge to edge, then 9?
May 19th, 2020 at 7:11:43 AM
permalink
Quote: rsactuaryIf you had just said 4 cuts, I would have said 12. I guess it depends how you define "straight cut". If "straight cut" means edge to edge, then 9?
A good guess but incorrect.
And yes, edge to edge.
Have you tried 22 tonight? I said 22.
May 19th, 2020 at 8:04:28 AM
permalink
Quote: Gialmere
You're on a diet and your spouse presents you with a single pancake for breakfast. Pouting, you revert to your childhood self and decide to play with your food. Maybe you can make it appear like there's more than there is. You wonder...
What is the maximum number of sections into which a pancake may be divided by four straight cuts through it? You pick up your "scalpel", consider your circular "patient", and make your first incision...
(Note: The pieces cannot be rearranged between cuts.)
14, but you'd have to be one heck of a pancake surgeon the way I see it:
#1: Looking at the pancake on it's edge (rectangular profile, assuming a cylindrical pancake), diagonally cut from the top right edge to the bottom left edge -- 2 pieces
#2: Do the same cut as #1 from the opposite edges -- 4 (wedge-shaped) pieces
#3 & #4: Back in the top-view, where the projection of the pancake is a circle, make cuts through the center that will divide the projection of the "side" wedges into 1/3's. This will also cut the "top/bottom" wedges into 4 pieces each -- 14 pieces
Now where's the syrup? :)
#1: Looking at the pancake on it's edge (rectangular profile, assuming a cylindrical pancake), diagonally cut from the top right edge to the bottom left edge -- 2 pieces
#2: Do the same cut as #1 from the opposite edges -- 4 (wedge-shaped) pieces
#3 & #4: Back in the top-view, where the projection of the pancake is a circle, make cuts through the center that will divide the projection of the "side" wedges into 1/3's. This will also cut the "top/bottom" wedges into 4 pieces each -- 14 pieces
Now where's the syrup? :)
"Dealer has 'rock'... Pay 'paper!'"
May 19th, 2020 at 8:15:18 AM
permalink
Quote: Joeman14, but you'd have to be one heck of a pancake surgeon the way I see it:
#1: Looking at the pancake on it's edge (rectangular profile, assuming a cylindrical pancake), diagonally cut from the top right edge to the bottom left edge -- 2 pieces
#2: Do the same cut as #1 from the opposite edges -- 4 (wedge-shaped) pieces
#3 & #4: Back in the top-view, where the projection of the pancake is a circle, make cuts through the center that will divide the projection of the "side" wedges into 1/3's. This will also cut the "top/bottom" wedges into 4 pieces each -- 14 pieces
Now where's the syrup? :)
Bonus points for creativity! However, we're just looking for simple top cuts. So consider a two dimensional circle and four lines.
14 is incorrect.
Have you tried 22 tonight? I said 22.
May 19th, 2020 at 8:29:40 AM
permalink
Quote: GialmereQuote: Joeman14, but you'd have to be one heck of a pancake surgeon the way I see it:
#1: Looking at the pancake on it's edge (rectangular profile, assuming a cylindrical pancake), diagonally cut from the top right edge to the bottom left edge -- 2 pieces
#2: Do the same cut as #1 from the opposite edges -- 4 (wedge-shaped) pieces
#3 & #4: Back in the top-view, where the projection of the pancake is a circle, make cuts through the center that will divide the projection of the "side" wedges into 1/3's. This will also cut the "top/bottom" wedges into 4 pieces each -- 14 pieces
Now where's the syrup? :)
Bonus points for creativity! However, we're just looking for simple top cuts. So consider a two dimensional circle and four lines.
14 is incorrect.
I think:
I get 11 pieces. First cut gives you 2. Second cut crosses the first cut and gives four. Third cut crosses the previous two (not at intersection point) and gives seven. Fourth cut crosses precious three (not at any previous intersection points) and gives 11.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
May 19th, 2020 at 8:40:51 AM
permalink
Quote: unJon
I think:
I get 11 pieces. First cut gives you 2. Second cut crosses the first cut and gives four. Third cut crosses the previous two (not at intersection point) and gives seven. Fourth cut crosses precious three (not at any previous intersection points) and gives 11.
Correct!
/pic5423237.png)
Bon Appétit!
-------------------------------
I'd like to have some pancakes for breakfast...
...or maybe not. I keep waffling.
Have you tried 22 tonight? I said 22.
May 19th, 2020 at 9:45:31 AM
permalink
16 - I got 16 by cutting it in half, then putting one half on top of the other, but then said you couldn't move the pieces.
14 - But using three of the lines, so they form a traingle in the middle, you get 7 pieces. Then cut horzontally through the pancake to double it; but then presumably the pancake is flat!
14 - But using three of the lines, so they form a traingle in the middle, you get 7 pieces. Then cut horzontally through the pancake to double it; but then presumably the pancake is flat!
May 19th, 2020 at 10:00:24 AM
permalink
Hey, no fair changing the rules after I post my answer! ;)Quote: GialmereQuote: Joeman14, but you'd have to be one heck of a pancake surgeon the way I see it:
#1: Looking at the pancake on it's edge (rectangular profile, assuming a cylindrical pancake), diagonally cut from the top right edge to the bottom left edge -- 2 pieces
#2: Do the same cut as #1 from the opposite edges -- 4 (wedge-shaped) pieces
#3 & #4: Back in the top-view, where the projection of the pancake is a circle, make cuts through the center that will divide the projection of the "side" wedges into 1/3's. This will also cut the "top/bottom" wedges into 4 pieces each -- 14 pieces
Now where's the syrup? :)
Bonus points for creativity! However, we're just looking for simple top cuts. So consider a two dimensional circle and four lines.
14 is incorrect.
"Dealer has 'rock'... Pay 'paper!'"
May 19th, 2020 at 10:02:17 AM
permalink
I have seen the horizontal cut trick used in a few puzzles. Usually they involve cutting up a cake (i.e Joeman's cylinder).
Have you tried 22 tonight? I said 22.
May 19th, 2020 at 10:03:51 AM
permalink
Quote: JoemanHey, no fair changing the rules after I post my answer! ;)Quote: GialmereQuote: Joeman14, but you'd have to be one heck of a pancake surgeon the way I see it:
#1: Looking at the pancake on it's edge (rectangular profile, assuming a cylindrical pancake), diagonally cut from the top right edge to the bottom left edge -- 2 pieces
#2: Do the same cut as #1 from the opposite edges -- 4 (wedge-shaped) pieces
#3 & #4: Back in the top-view, where the projection of the pancake is a circle, make cuts through the center that will divide the projection of the "side" wedges into 1/3's. This will also cut the "top/bottom" wedges into 4 pieces each -- 14 pieces
Now where's the syrup? :)
Bonus points for creativity! However, we're just looking for simple top cuts. So consider a two dimensional circle and four lines.
14 is incorrect.
Heh, well, flat as a pancake and all that.
Have you tried 22 tonight? I said 22.
May 19th, 2020 at 10:23:10 AM
permalink
Quote: GialmereQuote: unJon
I think:
I get 11 pieces. First cut gives you 2. Second cut crosses the first cut and gives four. Third cut crosses the previous two (not at intersection point) and gives seven. Fourth cut crosses precious three (not at any previous intersection points) and gives 11.
Correct!
Bon Appétit!
There is a general solution: N cuts will result in (N2 + N + 2) / 2 pieces.
The first cut results in 2 pieces. The Kth cut will go through each of the previous (K-1) cuts, so the Kth cut is divided into K pieces, and each of these pieces divides an existing piece of the pancake into 2, so there are K more pieces than before.
So, the first cut results in 2 pieces, the second in 2 + 2, the third in 2 + 2 + 3, the fourth in 2 + 2 + 3 + 4, and so on.
The Nth cut results in (1 + 1) + 2 + 3 + 4 + ... + N = 1 + N (N + 1) / 2.
Actually, I was going to answer, 14, using one cut to go through the thickness of the pancake.
And I haven't had pancakes in who knows how long - do you know how many carbs they (yes, the mysterious "They") can cram into just one of those things, not to mention the syrup?
