Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: acesideChess solution:
Rook#1: place it at H5 so that King must move down;
Rook #2: place it two squares directly underneath King;
Rook 3: place it in the same column above Rook #2 to check.
Rook #4: place it in the same column with Rook #3 to checkmate.
link to original post
If I am reading your instructions right:
1 - Rook in h5; King to e4
2 - Rook in e2; King to f3
3 - Rook in e3; King to g4
4 - Rook in e4; King captures Rook on h5
I think your solution is correct if you change Rook #4 to always go on h4.
Of course, if the King goes up on the first turn, then the second Rook is two squares above the King, and the fourth Rook is on h6.
Quote: ThatDonGuyQuote: acesideChess solution:
Rook#1: place it at H5 so that King must move down;
Rook #2: place it two squares directly underneath King;
Rook 3: place it in the same column above Rook #2 to check.
Rook #4: place it in the same column with Rook #3 to checkmate.
link to original post
If I am reading your instructions right:
1 - Rook in h5; King to e4
2 - Rook in e2; King to f3
3 - Rook in e3; King to g4
4 - Rook in e4; King captures Rook on h5
I think your solution is correct if you change Rook #4 to always go on h4.
Of course, if the King goes up on the first turn, then the second Rook is two squares above the King, and the fourth Rook is on h6.
link to original post
ThatDonGuy is correct! Let me revise my solution:
Rook #2: place it two squares directly underneath King;
Rook #3: place it in the same column of Rook #2 to check;
Rook #4: place it in the same column of H5 to checkmate.
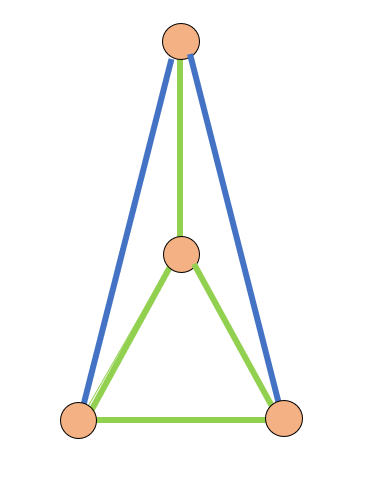
Quote: acesideI guess only two ways. One is this square, and the other one is a triangle with a 4th dot on its weight center.
link to original post
Quote: unJonToo lazy to solve but I would have thought there would also be a
trapezoid solution where the diagonal distance equals the length of the longer side. And the three short sides are the same distance.
link to original post
Quote: ChesterDog
Dart
link to original post
Correct!!!
Impressive. (As a joint solve I didn't quote every post.)

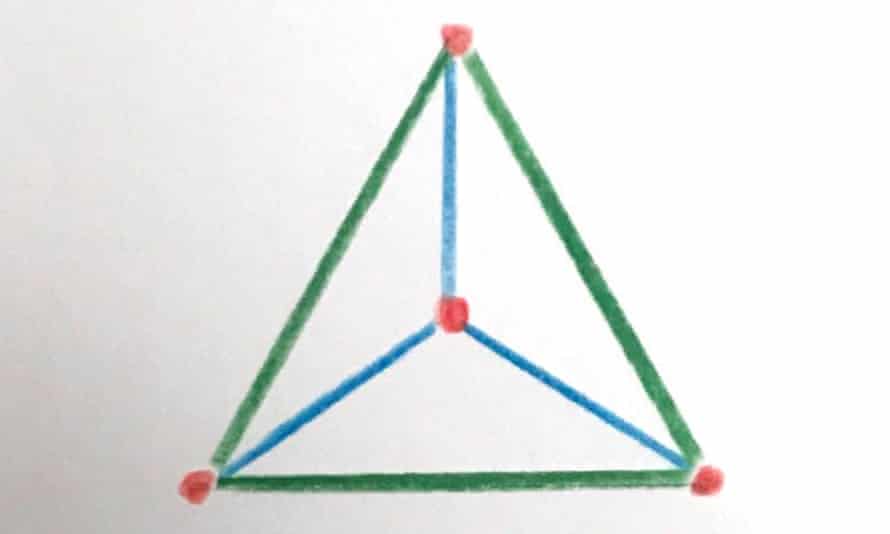
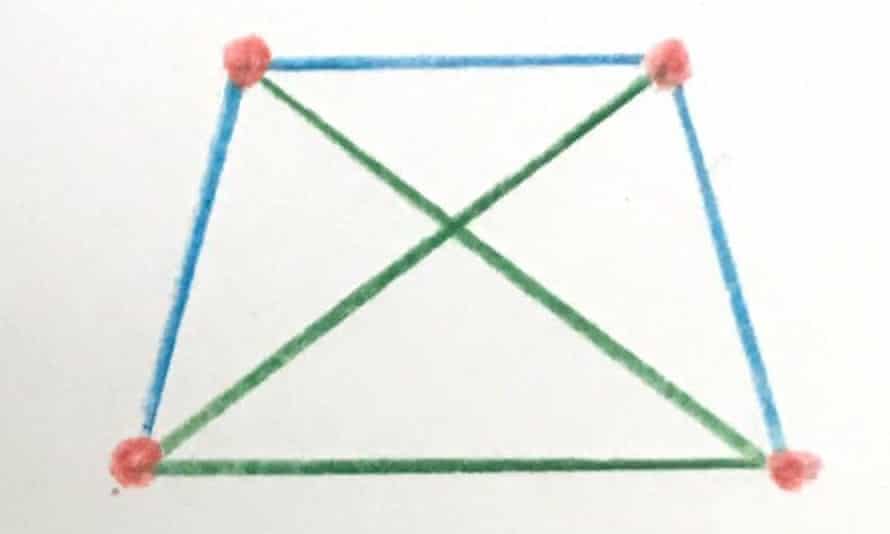

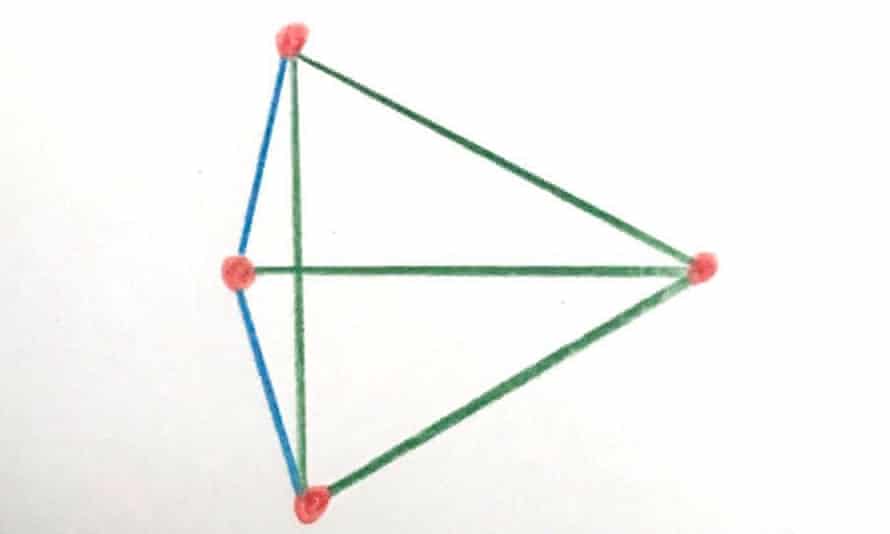
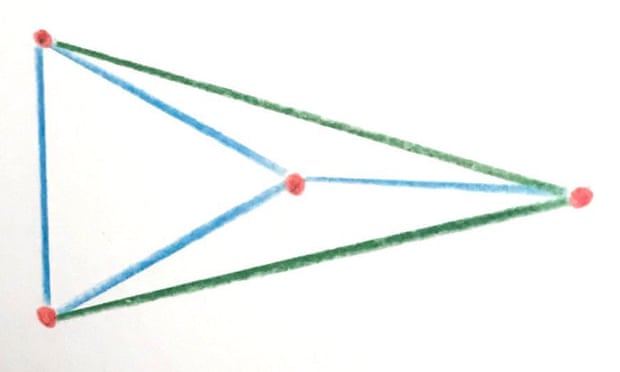
There are only 2 distances: short and long. Note that each shape has in it a triangle consisting of 2 shorts and a long. (Note also that point B can’t be higher than the dotted line since then the blue lines would no longer be the short distances.) By placing dot D somewhere around this triangle you can then try to connect it.
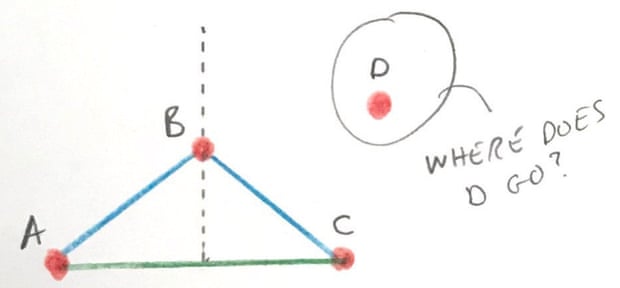
There are 8 possible ways it could do that. The distances from D to A, B and C could be
short, short, short
short, short, long
short, long, short
short, long, long
long, short, short
long, short, long
long, long, short
long, long, long
For each combo you simply check (admittedly time consuming) to see if the shape is valid.
-----------------------------------------------
Quote: GialmereTo kill some time before a meeting of chess grandmasters, Burt Hochberg offered this anonymous puzzle from the 15th century...
White must place four white rooks on the board, one at a time, giving check with each one. After each placement the black king can respond with any normal legal move.
How can White plan his moves so that the fourth rook reliably gives checkmate?
Quote: acesideChess solution:
Rook#1: place it at H5 so that King must move down;
Rook #2: place it two squares directly underneath King;
Rook 3: place it in the same column above Rook #2 to check.
Rook #4: place it in the same column with Rook #3 to checkmate.
link to original post
Quote: ThatDonGuy
If I am reading your instructions right:
1 - Rook in h5; King to e4
2 - Rook in e2; King to f3
3 - Rook in e3; King to g4
4 - Rook in e4; King captures Rook on h5
I think your solution is correct if you change Rook #4 to always go on h4.
Of course, if the King goes up on the first turn, then the second Rook is two squares above the King, and the fourth Rook is on h6.
link to original post
Quote: acesideThatDonGuy is correct! Let me revise my solution:
Rook #1: place it at H5 so that King must move down;
Rook #2: place it two squares directly underneath King;
Rook #3: place it in the same column above Rook #2 to check.
Rook #4: place it either at H4 or in the same column above Rook #2 (depending on where King is) to checkmate.
link to original post
Correct!!
Very good.
Hochberg says the grandmasters studied the position for several minutes before Paul Keres came up with an answer.
---------------------------------------------


Able, Baker, and Charlie are playing tag. Able is faster than Baker, who’s faster than Charlie. All three of them start at point P, and Able is “it.” At time -T, Baker runs north and Charlie runs south. After a count that takes time T, Able starts chasing one of the two quarries. The game ends when Able has tagged both Baker and Charlie.
If Baker and Charlie maintain their speeds and directions, who should Able chase first to minimize the time required to make the second tag?
-Whomever Able chases first, "1", will be at a location of v1*T when Able starts to run
-To catch "1", given the differences in speed takes distance/(rel. vel.) = v1*T/(vA-v1)
-So total time elapsed so far is t1 = T + T* v1/(vA-v1) = T*(1+v1/(vA-v1)) = T * vA/(vA-v1)
-In time t1, since Baker and Charlie run in opposite directions, they are a distance vB*t1 + vC*t1 = (vB+vC)*t1 apart
-To catch "2" given differences in speed takes distance/(rel. vel.) = (vB+vC)*t1 / (vA-v2)
= (vB+vC) * T * vA / (vA-v1) / (vA-v2)
=(vB+vC) * T * vA / ( (vA-v1) * (vA-v2) )
***EDIT : This is the time from catching 1 to 2 and is symmetric thus seems to not matter which is chased first.
Total time is then
t1 +t2
t2 is indecent of order, but t1=T * vA/(vA-v1) is smallest when the difference (vA-v1) is largest....
so 1 should be Charlie??
Quote: GialmereIf Baker and Charlie maintain their speeds and directions, who should Able chase first to minimize the time required to make the second tag?
link to original post
I show A should go after C first.
I tried this under the following conditions:
A, B, and C run at rates 3, 2, and 1 respectively.
The countdown is one unit of time.
I show chasing B first will take 7.5 units of time, while chasing C first takes 6 units of time.
To be honest, my initial instinct was to go after the faster person first.
Quote: WizardQuote: GialmereIf Baker and Charlie maintain their speeds and directions, who should Able chase first to minimize the time required to make the second tag?
I show A should go after C first.
I tried this under the following conditions:
A, B, and C run at rates 3, 2, and 1 respectively.
The countdown is one unit of time.
I show chasing B first will take 7.5 units of time, while chasing C first takes 6 units of time.
To be honest, my initial instinct was to go after the faster person first.
link to original post
I was editing my answer as Wiz posted his. My edit agree with Wiz's result....I originally listed just the time from first catch to second catch...edit shows full time
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
Quote: chevy
-Whomever Able chases first, "1", will be at a location of v1*T when Able starts to run
-To catch "1", given the differences in speed takes distance/(rel. vel.) = v1*T/(vA-v1)
-So total time elapsed so far is t1 = T + T* v1/(vA-v1) = T*(1+v1/(vA-v1)) = T * vA/(vA-v1)
-In time t1, since Baker and Charlie run in opposite directions, they are a distance vB*t1 + vC*t1 = (vB+vC)*t1 apart
-To catch "2" given differences in speed takes distance/(rel. vel.) = (vB+vC)*t1 / (vA-v2)
= (vB+vC) * T * vA / (vA-v1) / (vA-v2)
=(vB+vC) * T * vA / ( (vA-v1) * (vA-v2) )
***EDIT : This is the time from catching 1 to 2 and is symmetric thus seems to not matter which is chased first.
Total time is then
t1 +t2
t2 is indecent of order, but t1=T * vA/(vA-v1) is smallest when the difference (vA-v1) is largest....
so 1 should be Charlie??
link to original post
Quote: Wizard
I show A should go after C first.
I tried this under the following conditions:
A, B, and C run at rates 3, 2, and 1 respectively.
The countdown is one unit of time.
I show chasing B first will take 7.5 units of time, while chasing C first takes 6 units of time.
To be honest, my initial instinct was to go after the faster person first.
link to original post
Correct!!
Very good.
If Able chases Charlie first, then
Since both y’s are equal, the x’s show that the least time will elapse when Able chases Charlie first.
-------------------------------------------

--------------------------------------------
Quote: rackuunThe 4-points-2-distances puzzle is a good one Gialmere. I'm going to file that one away for the mathletes. The trapezoid solution is constructed by removing one vertex from a regular pentagon. And it turns out that the 5-points-2-distances problem has only one solution: the regular pentagon.
link to original post
Yeah, that's a fun one. I think young mathletes would enjoy it.
--------------------------------------------
Currently in play...
Quote: WizardSorry if this has been asked before.
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
link to original post
Quote: WizardSorry if this has been asked before.
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
link to original post
Let P(n) be the probability of two consecutive 7s being rolled first given that n 7s have been rolled
P(0) = 1/6 P(1) + 29/36 P(0)
7/36 P(0) = 1/6 P(1)
P(1) = 7/6 P(0)
P(1) = 1/6 + 29/36 P(0)
1/6 + 29/36 P(0) = 7/6 P(0)
1/6 = 13/36 P(0)
P(0) = 1/6 * 36/13 = 6/13
Thus, a 12 is more likely to happen first (7/13 of the time)
Quote: ThatDonGuy
Let P(n) be the probability of two consecutive 7s being rolled first given that n 7s have been rolled
P(0) = 1/6 P(1) + 29/36 P(0)
7/36 P(0) = 1/6 P(1)
P(1) = 7/6 P(0)
P(1) = 1/6 + 29/36 P(0)
1/6 + 29/36 P(0) = 7/6 P(0)
1/6 = 13/36 P(0)
P(0) = 1/6 * 36/13 = 6/13
Thus, a 12 is more likely to happen first (7/13 of the time)
link to original post
I agree!

A boy and a girl played rock paper scissors 10 times. Altogether the boy played rock three times, scissors six times, and paper once, and the girl played rock twice, scissors four times, and paper four times (though, in each case, the order of these plays is unknown). There were no ties.
Who won?
The boy won 7, the girl 3.
Since there were no ties, the boy's 6 scissors must have gone against the girls rock (2x) and paper (4x). Those six games would have gone four for the boy, two for the girl.
Likewise, the girl's four scissors must have gone against the boy's rock 3x and paper 1x. Those four games would have gone 3 for the boy, 1 for the girl.
Final score:
Boy 4+3 = 7
Girl 2+1=3
Quote: ThatDonGuyQuote: WizardSorry if this has been asked before.
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
link to original post
Let P(n) be the probability of two consecutive 7s being rolled first given that n 7s have been rolled
P(0) = 1/6 P(1) + 29/36 P(0)
7/36 P(0) = 1/6 P(1)
P(1) = 7/6 P(0)
P(1) = 1/6 + 29/36 P(0)
1/6 + 29/36 P(0) = 7/6 P(0)
1/6 = 13/36 P(0)
P(0) = 1/6 * 36/13 = 6/13
Thus, a 12 is more likely to happen first (7/13 of the time)
link to original post
Have a question about the math problem itself. The problem states “Which event is more likely to happen first?”, but your solution solved this “Which event is more likely to happen?”
They are different, right? Please help explain!
Quote: aceside
Have a question about the math problem itself. The problem states “Which event is more likely to happen first?”, but your solution solved this “Which event is more likely to happen?”
They are different, right? Please help explain!
link to original post
The question asks if you rolled the dice until either event happened, which event would it more likely be, and what is that exact probability.
I didn't see any flaw in Don's solution.
Quote: WizardQuote: aceside
Have a question about the math problem itself. The problem states “Which event is more likely to happen first?”, but your solution solved this “Which event is more likely to happen?”
They are different, right? Please help explain!
link to original post
The question asks if you rolled the dice until either event happened, which event would it more likely be, and what is that exact probability.
I didn't see any flaw in Don's solution.
link to original post
Thank you! But if you ask “Which event is more likely to happen first?” you mean which event takes fewer rolling turns to happen. Is this understanding correct? Or, they are the same thing?
Quote: JoemanThe boy, whom I'll call Brian, with a score of 7-3.Because boys rule!If Brian played 6 scissors and Gigi played 4 scissors, and there were no ties, then all four of Gigi's papers would have lost to Brian's scissors. Conversely, all three of Brian's rocks were pitted against Gigi's scissors, giving him 3 more victories, for a total of 7.
link to original post
Quote: Wizard
The boy won 7, the girl 3.
Since there were no ties, the boy's 6 scissors must have gone against the girls rock (2x) and paper (4x). Those six games would have gone four for the boy, two for the girl.
Likewise, the girl's four scissors must have gone against the boy's rock 3x and paper 1x. Those four games would have gone 3 for the boy, 1 for the girl.
Final score:
Boy 4+3 = 7
Girl 2+1=3
link to original post
Correct!!
Well done.
---------------------------------
Quote: acesideQuote: ThatDonGuyQuote: WizardSorry if this has been asked before.
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
link to original post
Let P(n) be the probability of two consecutive 7s being rolled first given that n 7s have been rolled
P(0) = 1/6 P(1) + 29/36 P(0)
7/36 P(0) = 1/6 P(1)
P(1) = 7/6 P(0)
P(1) = 1/6 + 29/36 P(0)
1/6 + 29/36 P(0) = 7/6 P(0)
1/6 = 13/36 P(0)
P(0) = 1/6 * 36/13 = 6/13
Thus, a 12 is more likely to happen first (7/13 of the time)
link to original post
Have a question about the math problem itself. The problem states “Which event is more likely to happen first?”, but your solution solved this “Which event is more likely to happen?”
They are different, right? Please help explain!
link to original post
No, my solution solved the probability of two consecutive 7s being rolled before a 12.
Since that probability < 1/2, the only other result - a 12 being rolled first - is more likely to happen.
Quote: ThatDonGuyQuote: acesideQuote: ThatDonGuyQuote: WizardSorry if this has been asked before.
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
link to original post
Let P(n) be the probability of two consecutive 7s being rolled first given that n 7s have been rolled
P(0) = 1/6 P(1) + 29/36 P(0)
7/36 P(0) = 1/6 P(1)
P(1) = 7/6 P(0)
P(1) = 1/6 + 29/36 P(0)
1/6 + 29/36 P(0) = 7/6 P(0)
1/6 = 13/36 P(0)
P(0) = 1/6 * 36/13 = 6/13
Thus, a 12 is more likely to happen first (7/13 of the time)
link to original post
Have a question about the math problem itself. The problem states “Which event is more likely to happen first?”, but your solution solved this “Which event is more likely to happen?”
They are different, right? Please help explain!
link to original post
No, my solution solved the probability of two consecutive 7s being rolled before a 12.
Since that probability < 1/2, the only other result - a 12 being rolled first - is more likely to happen.
link to original post
If we do an experiment to make either of the two endings happen 130 times, 70 of these will be a #12 ending and 60 of these will be a #7-#7 ending. The result says the first case is more likely to happen, but it does not say that a fewer rolling number is required to roll a #12. Is this right?
Quote: acesideQuote: ThatDonGuyQuote: acesideQuote: ThatDonGuyQuote: WizardSorry if this has been asked before.
Two six-sided dice are rolled until one of the following events occurs:
1. Two consecutive totals of seven.
2. One total of 12.
Which event is more likely to happen first?
link to original post
Let P(n) be the probability of two consecutive 7s being rolled first given that n 7s have been rolled
P(0) = 1/6 P(1) + 29/36 P(0)
7/36 P(0) = 1/6 P(1)
P(1) = 7/6 P(0)
P(1) = 1/6 + 29/36 P(0)
1/6 + 29/36 P(0) = 7/6 P(0)
1/6 = 13/36 P(0)
P(0) = 1/6 * 36/13 = 6/13
Thus, a 12 is more likely to happen first (7/13 of the time)
link to original post
Have a question about the math problem itself. The problem states “Which event is more likely to happen first?”, but your solution solved this “Which event is more likely to happen?”
They are different, right? Please help explain!
link to original post
No, my solution solved the probability of two consecutive 7s being rolled before a 12.
Since that probability < 1/2, the only other result - a 12 being rolled first - is more likely to happen.
link to original post
If we do an experiment to make either of the two endings happen 130 times, 70 of these will be a #12 ending and 60 of these will be a #7-#7 ending. The result says the first case is more likely to happen, but it does not say that a fewer rolling number is required to roll a #12. Is this right?
link to original post
It does say that. They are equivalent statements, mathematically.
Quote: acesideIn that case, we don’t need any calculation for this conclusion . Let’s just say we roll the dice once; there is a chance to get a #12 ending but absolutely no chance to get a #7-#7 ending.
link to original post
That doesn’t follow. Three 7s are more likely than 12 twelves.
Quote: WizardI'm getting confused about the point of departure, but if the original question was badly worded, I'm open to correction. I plan to make this an "ask the wizard" question in the next column and would like to word the question as well as possible.
link to original post
I think aceside just wanted to see the answers in terms of average number of rolls to roll a 12 and average number of rolls to roll consecutive 7s.
Quote: unJonQuote: WizardI'm getting confused about the point of departure, but if the original question was badly worded, I'm open to correction. I plan to make this an "ask the wizard" question in the next column and would like to word the question as well as possible.
link to original post
I think aceside just wanted to see the answers in terms of average number of rolls to roll a 12 and average number of rolls to roll consecutive 7s.
link to original post
Very nice of you! I am learning. Let me refine my question a little.
What is the average number of rolls to roll a 12 before rolling two consecutives 7s?
What is the average number of rolls to roll two consecutive 7s before rolling a 12?
Parms: sh:1000000 Time:5:44:51:271
77 2 27706
77 3 22538
77 4 21946
77 5 20792
...
77 222 1
77 241 1
77 256 1
77 304 1
12 1 27778
12 2 26843
12 3 25310
12 4 23817
...
12 220 1
12 227 1
12 230 1
12 235 1
Total: 77s : 462100 (19.85129409218784) 12s : 537900 (18.972372188139058)
Parms: sh:1000000 Time:5:44:54:62
Quote: Ace2Avg number of rolls to get 77 and twelve is 42 and 36 respectively. Coincides with the 7:6 ratio of which one is more likely to be rolled first.
link to original post
This is convincing, just like what unJon said.
Bar Bets at the Poker Table


During a break at a home poker game a player thoroughly shuffles a standard deck of cards, has you cut them, and then deals the top three cards face down onto the table. He says he'll bet you $20 that at least one of the three cards is a jack, queen or king.
Is this a fair bet?

During the next break, the player places a quarter, a half dollar, and a silver dollar on the table. He tells you to pick one of them and he'll get the other two. You'll then both place money into a pot equal to 100 times the cash amount of the coin(s). (For example, if you pick the silver dollar you'd place $100 into the pot. The other player would add his quarter and half dollar together and place $75 into the pot.)
The three fair coins are then simultaneously flipped and allowed to land on the table. A coin that comes up heads is worth its monetary value. A coin that comes up tails is worth zero. Whichever player has the highest value wins the money in the pot.
(Using the example above, if all three coins come up heads you would have a value of $1 to the player's 75¢ and would win the pot. If only, say, the quarter comes up heads, the player would have a value of 25¢ to your goose egg and he would win the pot. If all three coins are tails, they are flipped again.)
Is this a fair game?

As the poker game ends for the evening the player offers you one last chance to make money. He again thoroughly shuffles the deck and has you cut them.
He says he'll turn up the cards in pairs. If both cards are red, you'll keep them. If both cards are black, he'll keep them. If one is red and one black, they'll be set aside belonging to no one.
You'll pay him a dollar for the privilege of playing the game, and then you'll go through the whole deck. If you end up with more red cards than he has black cards he'll pay you $3 for each one you have that exceeds his total. However, if he has more black cards, you must pay him $2 for each that he has over.
Is this a fair game?
If you pick the 100c then you win with the four times A comes up, lose the three times A doesn't and one other coin does, no coins reflips. Hence your chances of winning are 4 to 3, which corresponds to the wagers you made.
If you pick the 50c then you win two times, if B comes up with C or without C. You lose on the other five outcomes. Thus 2 to 5 corresponds to the wagers you made.
Similarly for 25c you only win once --C, and lose the other six.
The deck starts with 26 Red and 26 Black, they have been arranged into 26 Pairs. Firstly get rid of all the Pairs with one of each. While it's possible this leaves no other cards, normally it will leave some cards over. Since we have removed the same number of Red and Black cards, it follows that there are the same number of Red and Black cards left. By construction these are now all in coloured Pairs. Therefore there are the same number of Red Pairs as Black Pairs. So no-one can ever obtain a "win".
You win if none of the first three cards are a Jack, Queen, or King.
The probability that none of the first three cards is a Jack, Queen, or King is 40/52 x 39/51 x 38/50 = 114/255 < 1/2, so this is a bad bet
Generalize the problem: let the three coin values be A, B, C, with A < B < C and, to make things easier, A + B < C
There are eight equally likely possible results of the coin flips.
One result is all tails; this is always a push.
If you have coin A, you win (B + C) if only A is heads, and lose A if any of the other six besides all tails occurs; the EV = (B + C - 6A) / 8.
If you have coin B, you win (A + C) if either just B or just A and B are heads, and lose B if any of the other five besides all tails occurs; the EV = (2A + 2C - 5B) / 8.
If you have coin C, you win (A + B) if C is heads (four of the results have this happen), and lose C if C is tails (and A and/or B are heads) the EV = (4A + 4B - 3C) / 8.
In this case, B = 2A and C = 4A, so the EV of choosing A is (2A + 4A - 6A) / 8 = 0, the EV of choosing B is (2A + 8A - 10A) / 8 = 0, and the EV of choosing C is (4A + 8A - 12A) / 8 = 0. No matter what coin you choose, the game is fair.
Since the number of red cards in the deck = the number of black cards, and the number of red cards in the discarded red/black pairs = the number of black cards in those pairs, then the number of red cards you have = the number of black cards he has. Since you paid $1 to play the game, this is a bad bet.
How about I pay you $90 a $100 bill?
The probability of no face card is combin(40,3)/combin(52,3) = 9880/22100 = 44.71%.
So, the probability of at least one face card is 55.29%.
Thus, I would bet on at least one face card.
Quote: acesideJack, Queen, King; Bet #1
This is not a fair game. Player has a better chance of winning, about 0.553, which is greater than 0.5. This result is very useful for gambling!
link to original post
Quote: charliepatrickFor you to win he has to miss the twelve picture cards, the chances of this are 40/52 then 39/51 then 38/50. This is about 44.706%. Hence it is not a fair betI like this as it looks as if it's a fair game regardless of which coin you pick. Let's call the 100c=A, 50c=B, 25c=C.
If you pick the 100c then you win with the four times A comes up, lose the three times A doesn't and one other coin does, no coins reflips. Hence your chances of winning are 4 to 3, which corresponds to the wagers you made.
If you pick the 50c then you win two times, if B comes up with C or without C. You lose on the other five outcomes. Thus 2 to 5 corresponds to the wagers you made.
Similarly for 25c you only win once --C, and lose the other six.
link to original post
Quote: charliepatrickMy feeling is no-one ever gets more cards than the other player, so he just takes $1 off you every hand.
The deck starts with 26 Red and 26 Black, they have been arranged into 26 Pairs. Firstly get rid of all the Pairs with one of each. While it's possible this leaves no other cards, normally it will leave some cards over. Since we have removed the same number of Red and Black cards, it follows that there are the same number of Red and Black cards left. By construction these are now all in coloured Pairs. Therefore there are the same number of Red Pairs as Black Pairs. So no-one can ever obtain a "win".
link to original post
Quote: ThatDonGuy
You win if none of the first three cards are a Jack, Queen, or King.
The probability that none of the first three cards is a Jack, Queen, or King is 40/52 x 39/51 x 38/50 = 114/255 < 1/2, so this is a bad bet
Generalize the problem: let the three coin values be A, B, C, with A < B < C and, to make things easier, A + B < C
There are eight equally likely possible results of the coin flips.
One result is all tails; this is always a push.
If you have coin A, you win (B + C) if only A is heads, and lose A if any of the other six besides all tails occurs; the EV = (B + C - 6A) / 8.
If you have coin B, you win (A + C) if either just B or just A and B are heads, and lose B if any of the other five besides all tails occurs; the EV = (2A + 2C - 5B) / 8.
If you have coin C, you win (A + B) if C is heads (four of the results have this happen), and lose C if C is tails (and A and/or B are heads) the EV = (4A + 4B - 3C) / 8.
In this case, B = 2A and C = 4A, so the EV of choosing A is (2A + 4A - 6A) / 8 = 0, the EV of choosing B is (2A + 8A - 10A) / 8 = 0, and the EV of choosing C is (4A + 8A - 12A) / 8 = 0. No matter what coin you choose, the game is fair.
Since the number of red cards in the deck = the number of black cards, and the number of red cards in the discarded red/black pairs = the number of black cards in those pairs, then the number of red cards you have = the number of black cards he has. Since you paid $1 to play the game, this is a bad bet.
link to original post
Quote: Ace2I’d counter bet #1 with:
How about I pay you $90 a $100 bill?
link to original post
Quote: Wizard
The probability of no face card is combin(40,3)/combin(52,3) = 9880/22100 = 44.71%.
So, the probability of at least one face card is 55.29%.
Thus, I would bet on at least one face card.
link to original post
Correct!!
Good show.
:strip_icc()/pic7311874.png)
Yes. It's a completely fair game regardless of which coin you select. In fact, this game is fair with any set of coins, no matter how they’re divided, provided that their values show a successive doubling (e.g., 25, 50, 100). If you added a 5% commission on wins, it might make for a fun online casino game.
There was a small controversy at the site I found this one at over the wording of the puzzle. In that version, you and the other player find the three coins and play the game to see who gets to keep all three. Needless to say, that does indeed change things.
(Heh, heh. Fortunately we never have issues over the wording of a puzzle on this thread.)
---------------------------------------
You download a free calculator, but you notice a small problem: while the keys [0] through [9], [ + ], [ - ], [ = ], [ ( ], [ ) ], and [ 1/x ] work, whenever you press the multiplication and division keys, a message pops up asking if you want to upgrade to the premium version that includes those keys for a small fee.
There's one other feature; you can't use any particular key more than 50 times without the app shutting down.
You're better than that - using the keys you are given, multiply 256 by 4096 in a single equation. None of this "4096 + 4096 + ... + 4096 =, then write down the answer, then reload the app, then do it again until you have added 4096 256 times" nonsense, either.
... to restate the terms as 2^8 * 2^12 = 2^20?
Quote: ThatDonGuyTime for a toughie..multiply 256 by 4096 in a single equation.
Since you have access to the "1/x" key it's useful to notice that 1/x-1/(x+1) = 1/(x*(x+1)) Then using the "1/x" key this gives you x*(x+1). For example 1/3-1/4 = 4/12-3/12 = 1/12. 1/(1/12)=12.
Thus if you use this method to calculate 1024*1025 and then subtract 1024.
If you're not allowed to do this then calculate 255*256 and 256*257, do this eight times and add them all up.
Quote: charliepatrickA longer run - Total: 77s : 46157503 (19.850333801635674) 12s : 53842497 (18.98714786574627) , so perhaps 18.99 or 18.98
link to original post
I thought about this again and believe your simulation result is reasonable.
Radius of top of cup = 1.75"
Radius of bottom of cup = 1.25"
Height of cup = 6"
After doing the math (hopefully correctly), here are the key figures:
volume = 42.804200 cubic inches (this equals 19.0 ounces)
surface area = 61.653416 square inches
This got me to wondering that if the goal were to hold 33 cubic inches of beverage, what would be the ideal dimensions of the cup to minimize it's surface area? The cup must be in cup shape, including the extreme cases of a cone and cylinder, as well as everything in between.
I'm looking for the top radius, bottom radius, and height to two decimal places each.
1 cm^3 = 1 ml = 1 gr (of water. close enough especially for McD coffee)
Quote: Ace2I’d suggest using metric…makes conversions so easy.
1 cm^3 = 1 ml = 1 gr (of water. close enough especially for McD coffee)
link to original post
I only mentioned the ounces to illustrate the actual size of the cup. Nobody thinks of them in cubic inches. However, I'll consider that if I make an Ask the Wizard question out of this.
Quote: WizardI was studying a McDonald's cup this morning. Here are the dimensions:
Radius of top of cup = 1.75"
Radius of bottom of cup = 1.25"
Height of cup = 6"
After doing the math (hopefully correctly), here are the key figures:
volume = 32.986723 cubic inches (this equals 19.0 ounces)
surface area = 57.383775 square inches
This got me to wondering that if the goal were to hold 33 cubic inches of beverage, what would be the ideal dimensions of the cup to minimize it's surface area? The cup must be in cup shape, including the extreme cases of a cone and cylinder, as well as everything in between.
I'm looking for the top radius, bottom radius, and height to two decimal places each.
link to original post
I get a top radius of 2.67 inches, a bottom radius of 1.47 inches, and a height of 2.38 inches.
However, I don't the same answers you did for the real McDonald's cup.
Quote: unJonDoes the surface area include a lid on top?
link to original post
No, but does include the bottom.
Also, my IP had an incorrect number for the surface area of the actual McDonalds cup. I forgot to include the bottom. My revised figure is 61.653416 square inches. Do you agree CD?



:strip_icc()/pic7300943.png)