Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
In the diagrams below are given the only types of moves if Black had made the last move.
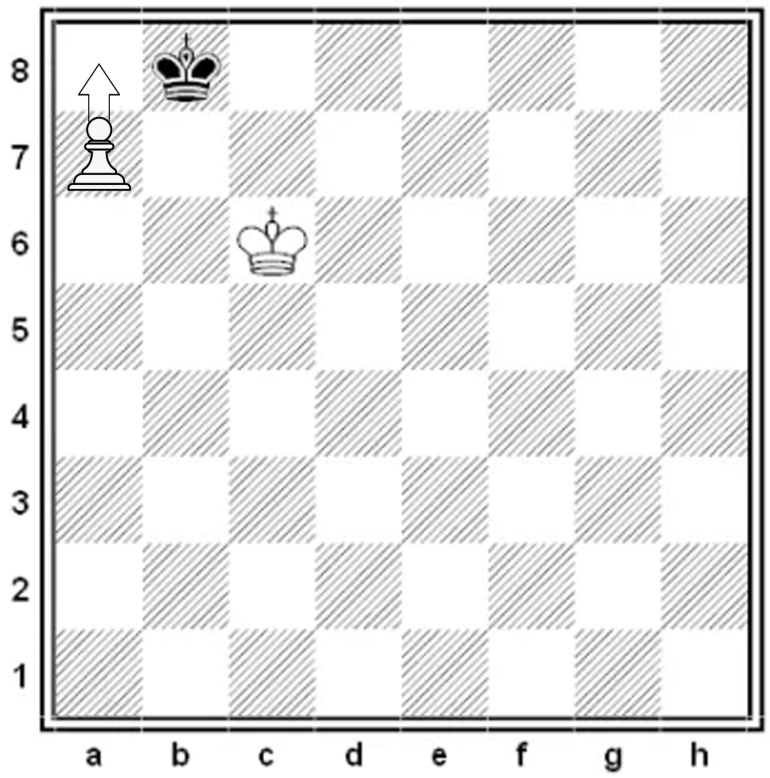 In this case the Black King could not have finished the previous move at b8 since it would have been in check. Hence it cannot have been a pawn that moved.
In this case the Black King could not have finished the previous move at b8 since it would have been in check. Hence it cannot have been a pawn that moved.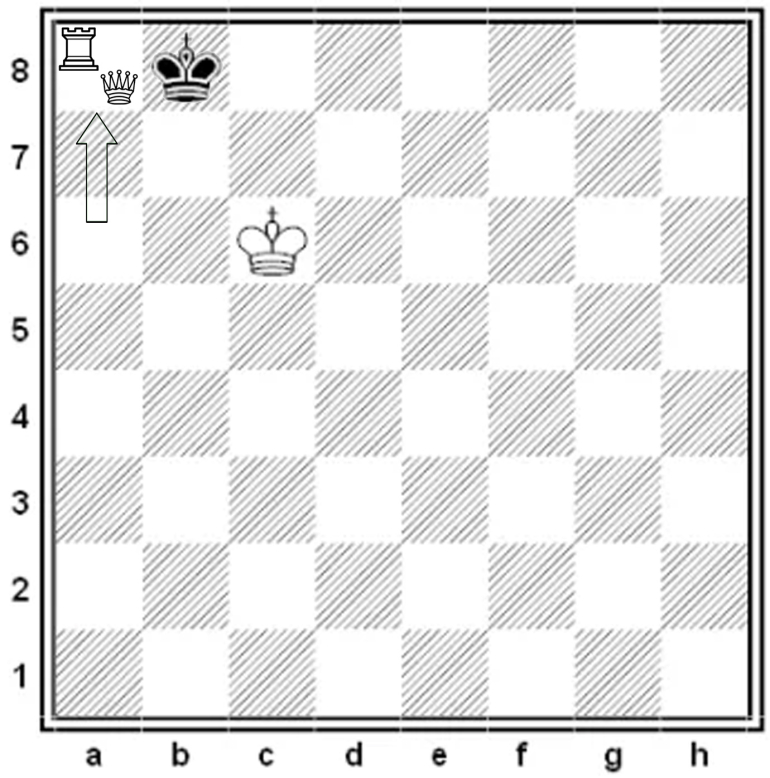 In this case, either Rook or Queen, puts Black in check. Black has no option except taking the piece - hence this position would have been declared a draw, i.e. the game would not have reached the two Kings.
In this case, either Rook or Queen, puts Black in check. Black has no option except taking the piece - hence this position would have been declared a draw, i.e. the game would not have reached the two Kings. This represents a possible play that could lead to the end position.
This represents a possible play that could lead to the end position. Others while possible, such as this, are quixotic since White should be able to be patent wins and can eventually take the pawn (in this case a4) and win.
Others while possible, such as this, are quixotic since White should be able to be patent wins and can eventually take the pawn (in this case a4) and win.Hence the white King moves last.
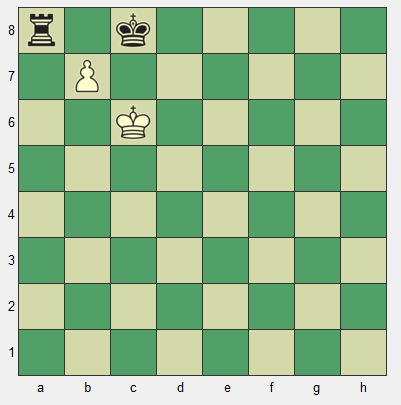
In this position, White just played b6-b7, giving check and forking the Black king and rook. Black's best move, of course, is Kb8, since Kd8 loses. White's next move is, of course, bxa8, capturing the Black rook and promoting to a rook or queen. Black, of course takes the promoted piece, giving us the final position.
In this example, Black moved last.
Quote: EdCollinsCharlie just made a case that White moved last. Well, here's an example where Black moved last.
In this position, White just played b6-b7, giving check and forking the Black king and rook. Black's best move, of course, is Kb8, since Kd8 loses. White's next move is, of course, bxa8, capturing the Black rook and promoting to a rook or queen. Black, of course takes the promoted piece, giving us the final position.
In this example, Black moved last.
link to original post
The player who wishes to claim a draw, seeing that the move he is about to make will repeat the same position, with the same player to move each time, announces that if he did make that move, it would result in a repetition of the position.
He makes this claim to the opponent and if the opponent challenges it or disagrees, the tournament director is notified, who verifies the claim. And yes, if correct, that move is never actually made on the board... and the game is indeed declared a draw.
However, this NOT the case with my simple example. There's no three-fold repetition.
Of course, I've only been playing chess since 1972. I do own 600+ chess books and I've never once read of the rule you speak of, in any of them. I've played about 500 over-the-board tournament chess games and tens of thousands of games online. I've never once heard of any rule that says if a player has no choice but to "create a draw" the game is then "declared a draw." That would certainly be a new one on me.
This is why I'd love to see a link confirming it. I'd be happy to be proven wrong. (It's been a long time (50 years?) since anyone taught me a chess rule that I wasn't aware of.) Until then, I must believe you're thinking about the three-fold repetition rule, and yea, in the case that move is not actually made on the board.
Sorry, I'm stuck at work and can't elaborate but the link above should help.
I learned something today.
Quote: GialmereIt's rule 5.2.b
Sorry, I'm stuck at work and can't elaborate but the link above should help.
link to original post

Quote: JoemanQuote: Gialmere
The Red Sox beat the Orioles 9 to 4 in 17 innings.
Where was the game played?Camden YardsIowa -- if it was the Filed of Dreams game and the Orioles were the home team.Only the visiting team can win an extra innings game by 5 or more runs. If the score is tied in the bottom half of the inning, the first run the home team scores will end the game. If a home run is hit, all the runs would count, limiting the maximum margin of an extra innings home team victory to 4 runs.
Oddly enough, if the home team batter hits a bases-loaded ground-rule double, only the first run counts.
link to original post
Quote: charliepatrickOne needs to know that when either opponent cannot create a Checkmate then the game is immediately declared a draw. This can happen if there is ever King vs King, King vs King+Knight, King vs King+Bishop, the game is somehow locked so there is no way for either side to mate, or forced moves lead to one of these.
In the diagrams below are given the only types of moves if Black had made the last move.In this case the Black King could not have finished the previous move at b8 since it would have been in check. Hence it cannot have been a pawn that moved.
In this case, either Rook or Queen, puts Black in check. Black has no option except taking the piece - hence this position would have been declared a draw, i.e. the game would not have reached the two Kings.
This represents a possible play that could lead to the end position.
Others while possible, such as this, are quixotic since White should be able to be patent wins and can eventually take the pawn (in this case a4) and win.
Hence the white King moves last.
link to original post
Correct!!
Well done.
The solves by Joeman and charliepatrick are actually better at explaining things than the official solves so I'll stick with them.
-----------------------------------------------
Here (as far as I know) are puzzles still in play...
Waiting to hear from ThatDonGuy over the response by aceside.
Quote: ThatDonGuyHere's a new one:
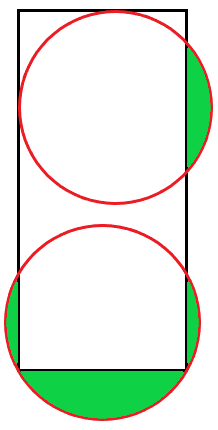
The rectangle is 8 x 20, and the circles each have diameter 10.
To make it clear, the top circle is tangent to the top and left sides of the rectangle, and the bottom circle goes through both of the rectangle's bottom corners.
What is the combined area of the green sections?
link to original post
I guess I'll let this one ride another day. It's actually really easy if you know the rule involved.
Quote: Gialmere
You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
link to original post
--------------------------------------
A physicist, a biologist, and a mathematician are sitting on a bench across from a house. Two people go into the house, and then three people come out. The physicist says, "The initial measurement was incorrect." The biologist says, "They must have reproduced." The mathematician says, "If exactly one person enters that house, it will be empty."
In this case I see two factors.
The first is only 8 people bought one of the choices, whereas the other choices were much more popular and most the people were happy. In this basis one mght not pick the 8/8 one. Also it sometimes looks suspicious with 100% score.
On the other hand with the most popular one, just over 10% were not satisfied, whereas only 3 of 48 were unhappy with one choice, giving a 94% chance that I'll be happy. It's not a really significant difference in happiness.
Thus I would tend to plump for the one that was most popular, since it's not that much worse and shows there wasn't anything obviously wrong with it.
Quote: Gialmere
Here (as far as I know) are puzzles still in play...
Waiting to hear from ThatDonGuy over the response by aceside.
link to original post
ThatDonGuy is waiting to see if anyone else is going to try and answer it.
Quote: ThatDonGuyHere's a new one:
The rectangle is 8 x 20, and the circles each have diameter 10.
To make it clear, the top circle is tangent to the top and left sides of the rectangle, and the bottom circle goes through both of the rectangle's bottom corners.
What is the combined area of the green sections?
link to original post
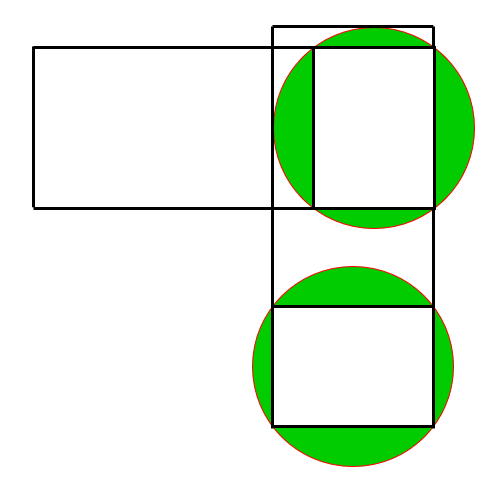
This diagram shows that the requested area is the area of one of the circles minus the area of its inscribed rectangle.
The size of its inscribed rectangle is 8 by sqrt(102 - 82), which is 8 by 6.
So, the answer is pi * 52 - 8*6 = 25 pi - 48.

You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
I guess B, because this is related to standard deviation, σ.
Here σ is proportional to Sqrt(98), while the error is 98-90=8; therefore,
8/Sqrt(98)=0.808
is the largest among all four options.
:strip_icc()/pic7276480.png)
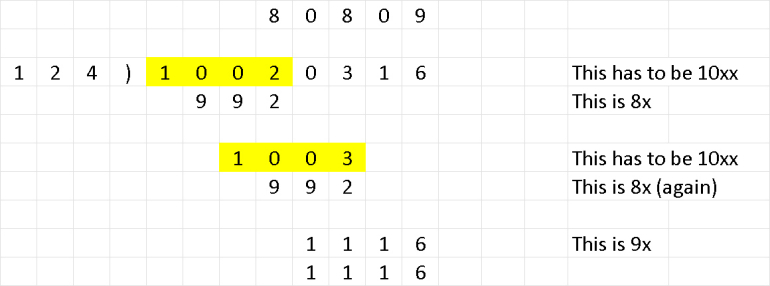
Each of the digits in this division problem has been replaced with an x — except for a single 8 in the quotient.
Can you reconstruct the problem?

You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
My answer is B.
The way I did it is to assume all results were one standard deviation lucky. The standard deviation was calculated with a probability of a positive rating of 320/352, the sum of all results.
Then the following are the expected true positive ratio:
A: 87.35%
B: 88.93%
C: 89.60%
D: 89.84%
You can see the highest percentage is for doohickey B.
Of course, that all rests on the one standard deviation assumption.
I could see reasonable arguments being made for any answer.
Quote: Wizard
You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
My answer is B.
The way I did it is to assume all results were one standard deviation lucky. The standard deviation was calculated with a probability of a positive rating of 320/352, the sum of all results.
Then the following are the expected true positive ratio:
A: 87.35%
B: 88.93%
C: 89.60%
D: 89.84%
You can see the highest percentage is for doohickey B.
Of course, that all rests on the one standard deviation assumption.
I could see reasonable arguments being made for any answer.
link to original post
I was thinking similarly but seems too complicated for easy Monday:
Think about good reviews as a white ball and negative reviews as a black ball.
A: Urn with 177 white and 21 black balls.
B: Urn with 90 white and 8 black balls.
Compare A to B: what is the probability if you draw (with replacement) 98 balls from urn A, that you would have at least 90 white balls. If more than 50% then A better otherwise B better.
Rinse and repeat with the winner vs C then D to order them.
Quote: unJon
Think about good reviews as a white ball and negative reviews as a black ball.
A: Urn with 177 white and 21 black balls.
B: Urn with 90 white and 8 black balls.
Compare A to B: what is the probability if you draw (with replacement) 98 balls from urn A, that you would have at least 90 white balls. If more than 50% then A better otherwise B better.
Rinse and repeat with the winner vs C then D to order them.
link to original post
I had a similar binomial method at first, but it just didn't hit me right. I respect your answer and still feel like mine is an itchy sweater. I'm ready to see what the correct answer supposedly is.
Quote: acesideGialmere, What’s the remainder of this division? It looks like the remainder part is cut off from this picture.
link to original post
No remainder.
Quote: GialmereIt's toughie Tuesday. In memoriam of Adam Rich, here is a puzzle called "8 is Enough". I hope your long division skills aren't rusty...
Each of the digits in this division problem has been replaced with an x — except for a single 8 in the quotient.
Can you reconstruct the problem?
link to original post

You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
Buzzzzzzzzzzzzzzz!
Add two more ratings to the sets: one negative and one positive. Count the part of negative ratings. The smaller the number the better.
A. Total: 198 + 2 = 200
(21 +1) negative of 100: P = 22 / 200 = 0.11
B. Total: 98 + 2 = 100
(8 + 1) negative of 100: P = 9 / 100 = 0.09
C. Total 48 + 2 = 50
(3 + 1) negative of 50: P = 4 / 50 = 0.08
D. Total: 8 + 2 = 10
1 negative of 10: P = 1 / 10 = 0.10
C is the best option.
-------------------------------------------------------------
However, as the Wizard mentions, you could argue for other answers. It depends on what you want to optimize. The math is interesting since you're trying to figure out the probability of probabilities. How do big and small samples compare to high and low percentages?
The 12 minute video below gives an overview (including Laplace's rule of succession near the beginning) and I highly recommend you watch the first 5 minutes or so if you want a good math fix.
P.S. Apologies. With all the math gurus here I just assumed Laplace was known and the puzzle solved in mere minutes. I, of course, have never heard of him but intend to use this rule in the future.
Quote: GialmereLaplace's rule of succession suggests a simple technique to define the most attractive option:
Add two more ratings to the sets: one negative and one positive. Count the part of negative ratings. The smaller the number the better.
A. Total: 198 + 2 = 200
(21 +1) negative of 100: P = 22 / 200 = 0.11
B. Total: 98 + 2 = 100
(8 + 1) negative of 100: P = 9 / 100 = 0.09
C. Total 48 + 2 = 50
(3 + 1) negative of 50: P = 4 / 50 = 0.08
D. Total: 8 + 2 = 10
1 negative of 10: P = 1 / 10 = 0.10
C is the best option.
-------------------------------------------------------------
However, as the Wizard mentions, you could argue for other answers. It depends on what you want to optimize. The math is interesting since you're trying to figure out the probability of probabilities. How do big and small samples compare to high and low percentages?
The 12 minute video below gives an overview (including Laplace's rule of succession near the beginning) and I highly recommend you watch the first 5 minutes or so if you want a good math fix.
P.S. Apologies. With all the math gurus here I just assumed Laplace was known and the puzzle solved in mere minutes. I, of course, have never heard of him but intend to use this rule in the future.
link to original post
That is the hardest "easy problem" I have ever seen. I've taken a lot of statistics classes in college and passed all the associate actuary exams and never heard of Laplace's rule of succession. I had a look at the Wikipedia page and it is, shall we say, a way of making a conservative estimate about something of unknown probability.
It suggests, for example, if you have witnessed the sun rise 10 out of 10 days, the probability it will rise tomorrow is 11/12. Personally, for that situation, I would use a Maximum Likelihood Estimate, which suggests the 10 out of 10 results are most likely to be observed with a 100% probability.
I don't want to get into the pros and cons of the Laplace's rule of succession, but suffice it to say it is just one of many ways to answer the problem at hand.
However, your video does bring up some good ideas of how to look at the problem and I may take another stab at it.
Quote: GialmereI hope I'm not stepping on the last puzzle (which is beyond my modest skills) but...
It's easy Monday. Here's another trilogy of tiny teasers...
You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
link to original post
I remarked before this is the hardest "Easy Monday" problem I've ever seen. It ultimately comes down how much the person making the decision values the high positive rating rate vs. large sample size. Ultimately, it goes to show that sometimes assumptions need to be made in math to solve a problem.
To that end, I'd like to suggest the following:
75% of doohickey shops provide a positive product/service 95% of the time.
25% of doohickey shops provide a positive product/service 80% of the time.
That said, with the data G provided, with the goal of buying from a shop that provides a good product/service 95% of the time, which one offers the best odds of achieving that goal?
Quote: acesideI got this one.
Total area = 25 Pi -48 ~ 30.54.
If you draw straight lines from each circle center to its intersection points, and then draw lines toward the arc midpoint, all of the angles are formed by right triangles of sides (3, 4, 5). Each shaded area is just the area of the big fan formed by 2x the angle subtracted by 2x the triangle area. I just add all of them up.
link to original post
Quote: ChesterDog
This diagram shows that the requested area is the area of one of the circles minus the area of its inscribed rectangle.
The size of its inscribed rectangle is 8 by sqrt(102 - 82), which is 8 by 6.
So, the answer is pi * 52 - 8*6 = 25 pi - 48.
link to original post
Both correct
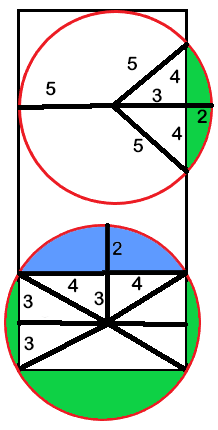
It's not quite to scale, but the blue section in the bottom circle is the same size as the green section in the top circle, so the sum of the green sections = the area of the bottom circle minus the rectangle inside of it = PI x 5^2 - 6 x 8 = 25 PI - 48
Quote: charliepatrickQuote: GialmereIt's toughie Tuesday. In memoriam of Adam Rich, here is a puzzle called "8 is Enough". I hope your long division skills aren't rusty...
Each of the digits in this division problem has been replaced with an x — except for a single 8 in the quotient.
Can you reconstruct the problem?
link to original postThe trick seems to be noticing that in the first and second divisions one starts with xxxx less xxx giving xx (thereupon xx is carried down, suggesting the 2nd and 4th digits of the top line are 0). This also suggests the xxx is 8 times the left hand xxx. This means the bottom one (xxxx being greater than xxx) is 9 times. Thus the top line seems to be 80809. 10000.../80809=123.748.... 125x8 is 1000, therefore the answer is 124. (124*8=992, 124*9=1116, 124*80809=10020316.)
link to original post
Correct!!
Excellent.
In long division, whenever two digits are brought down instead of one — as happens twice in this problem — a zero must appear in the quotient. That tells us that the quotient is x080x.
The visible 8 multiplied by the divisor produces a three-digit number. But when the last number in the quotient is multiplied by the divisor, it produces a four-digit number. So the last digit in the quotient must be 9.
The divisor has three digits and produces a three-digit number when multiplied by the visible 8. So the divisor must be less than 125, because 8 × 125 = 1000.
That tells us something further. When the divisor is multiplied by the first digit of the quotient, it produces a three-digit number, and when this is subtracted from the first four digits of the dividend it yields a two-digit difference. That means that the first digit of the quotient must be greater than 7, because 7 × 124 = 868, and that would yield a three-digit difference when subtracted from even the smallest possible four-digit number, 1000 (1000 – 868 = 132). An 8 or a 9 could produce a two-digit difference, but a 9 would produce a four-digit number when multiplied by the divisor. So the first digit of the quotient is 8, and the full quotient is 80809.
Now, 80809 × 123 = 9939507, which has only seven digits, and the dividend has eight. So the divisor is less than 125 and greater than 123, which means it’s 124. That gives us everything we need:
:strip_icc()/pic7276518.png)

Pageboy haircut says, "Good job!"
-----------------------------------------
:strip_icc()/pic7277974.png)
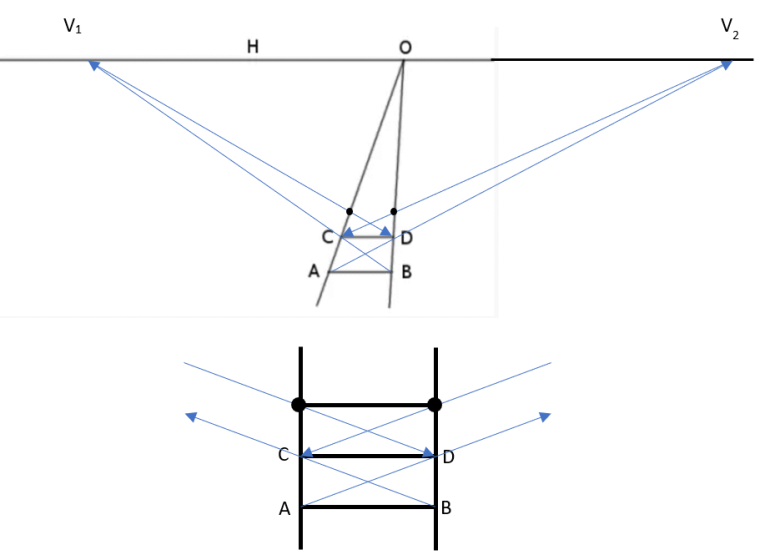
AB and CD are consecutive ties across a pair of railroad tracks that appear to meet at O on the horizon, H.
If the ties are parallel to the horizon and are equally spaced along the tracks, how can we draw the next tie in this perspective figure?
Quote: WizardQuote: GialmereI hope I'm not stepping on the last puzzle (which is beyond my modest skills) but...
It's easy Monday. Here's another trilogy of tiny teasers...
You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)
link to original post
I remarked before this is the hardest "Easy Monday" problem I've ever seen. It ultimately comes down how much the person making the decision values the high positive rating rate vs. large sample size. Ultimately, it goes to show that sometimes assumptions need to be made in math to solve a problem.
To that end, I'd like to suggest the following:
75% of doohickey shops provide a positive product/service 95% of the time.
25% of doohickey shops provide a positive product/service 80% of the time.
That said, with the data G provided, with the goal of buying from a shop that provides a good product/service 95% of the time, which one offers the best odds of achieving that goal?
link to original post
Quote: Gialmere
AB and CD are consecutive ties across a pair of railroad tracks that appear to meet at O on the horizon, H.
If the ties are parallel to the horizon and are equally spaced along the tracks, how can we draw the next tie in this perspective figure?
link to original post
|EF|/|CD| = |CD|/|AB|.
Solve this, then
|EF| = |CD|^2 /|AB|.
To draw this particular length of EF, we follow this procedure to draw a rectangle, given the length of one side (in this case, it is |AB|), equal in area to a given square (in this case, it is |CD|^2.). Just search the YouTube video for details.
Quote: Gialmere
AB and CD are consecutive ties across a pair of railroad tracks that appear to meet at O on the horizon, H.
If the ties are parallel to the horizon and are equally spaced along the tracks, how can we draw the next tie in this perspective figure?
link to original post
In the perspective drawing of the ground, any set of parallel lines that is not parallel with AB will appear to meet somewhere on the horizon H.
The diagonals between the ends of adjacent ties are two sets of parallel lines. One set is parallel to AD and the other is parallel to BC.
In the diagram, we can extend AD to find its intersection with H, V2. And from V2, we can draw a line to C. The point where this line meets the right rail is the right end of the next tie.
Likewise, we can extend BC to H and draw the line from that intersection, V1 toward D to find the left end of the next tie.
,
Quote: acesideSet the line segment EF to be the next tie, then the trapeziums EFDC and CDBA are similar shapes; therefore
|EF|/|CD| = |CD|/|AB|.
Solve this, then
|EF| = |CD|^2 /|AB|.
To draw this particular length of EF, we follow this procedure to draw a rectangle, given the length of one side (in this case, it is |AB|), equal in area to a given square (in this case, it is |CD|^2.). Just search the YouTube video for details.
link to original post
Quote: ChesterDog
In the perspective drawing of the ground, any set of parallel lines that is not parallel with AB will appear to meet somewhere on the horizon H.
The diagonals between the ends of adjacent ties are two sets of parallel lines. One set is parallel to AD and the other is parallel to BC.
In the diagram, we can extend AD to find its intersection with H, V2. And from V2, we can draw a line to C. The point where this line meets the right rail is the right end of the next tie.
Likewise, we can extend BC to H and draw the line from that intersection, V1 toward D to find the left end of the next tie.
,
link to original post
Correct!
Very good.
The official solve from the problem where I saw this uses the ChesterDog method...
:strip_icc()/pic7277975.png)
Another way, if the picture has only one vanishing point is this...

---------------------------------

You're a contestant on "The Price is Right" and have made it to the Big Wheel of the Showcase Showdown.
Click here if you don't know the rules.
Scenario 1) You're the first of the three players to spin the wheel. After your first spin, what's your best "stay or spin again" strategy?
Scenario 2) You're the second player to spin and the first player went over $1 and is out. After your first spin, what's your best "stay or spin again" strategy?
Scenario 3) You're the second player to spin and the first player stayed at 50¢. For your first spin, the wheel stops on 50¢. What's your best "stay or spin again" strategy?
Oh no! You're over a dollar and are out.
Scenario 1) Stay with 65¢ or higher, otherwise spin again.
Scenario 2) Stay with 55¢ or higher, otherwise spin again. (Here, it's a two player game and the math changes.)
Scenario 3) Stay (and hope for the best).
One of several places that analyze the game.
However, this strategy only considers the game at hand. But suppose you really were on "The Price is Right." Are there not other considerations? Obviously if you win you'll go to the Showcase and play for prizes worth tens of thousands. That's something to consider. And what about the wheel bonuses? If you get a dollar total on one or two spins you win $1000. You also get a bonus spin where the two green stops pay $10k and the red stop pays $25k.
On special shows these usually increase. You might win $3k or $10k for getting $1 on your first or second spin. On the bonus spin, green and red stop dollar amounts are sometimes doubled or even tripled. During "Dream Car Week" the bonus spin red stop gives a--well--dream car. For "Big Money Week" they once made the 45¢ space an extra green stop that paid $45k. And hitting the red stop occasionally pays $100k and very rarely a cool one million domars. That's certainly worth considering.
Actually being on the show is a once in a lifetime opportunity. You could search every casino in the world and you'll never find a slot machine that pays like this. Should you just stand there with 50 or 55 cents hoping Player 3 goes bust? Or consider scenario 1. The first player has around a 30% chance of winning, and 65¢ is the weakest amount to stand on. If you spin again you'll lose 65% of the time, but you have a (not great but not terrible) 35% chance of improving your score with another opportunity to win $1000 plus a bonus spin and with the Showcase beckoning.
Just something to think about.
------------------------------
:strip_icc()/pic7281762.png)
I have picked one color (black or white) and one shape (square or circle). A symbol that possesses exactly one of the properties I have picked is called a THOG. The black circle is a THOG. For each of the other symbols, is it (a) definitely a THOG, (b) undecidable, or (c) definitely not a THOG?
Quote: GialmereTry to do this one in your head...
I have picked one color (black or white) and one shape (square or circle). A symbol that possesses exactly one of the properties I have picked is called a THOG. The black circle is a THOG. For each of the other symbols, is it (a) definitely a THOG, (b) undecidable, or (c) definitely not a THOG?
link to original post
Quote: GialmereTry to do this one in your head...
I have picked one color (black or white) and one shape (square or circle). A symbol that possesses exactly one of the properties I have picked is called a THOG. The black circle is a THOG. For each of the other symbols, is it (a) definitely a THOG, (b) undecidable, or (c) definitely not a THOG?
link to original post
Since the black circle is a THOG, the selected (color, shape) pair is either (black, square) or (white, circle)
The white square has one of the attributes in each pair, so it is definitely a THOG
For each of the pairs, one of the white circle and black square has both of the attributes, and the other has neither, so both are definitely not THOGs
Quote: unJon
In my head, the White Square is a THOG, the black square and white square are not THOGs as they either have both or neither property.
link to original post
Quote: ThatDonGuySince the black circle is a THOG, the selected (color, shape) pair is either (black, square) or (white, circle)
The white square has one of the attributes in each pair, so it is definitely a THOG
For each of the pairs, one of the white circle and black square has both of the attributes, and the other has neither, so both are definitely not THOGs
link to original post
Quote: charliepatrickThe easiest way I thought of it was to consider a two-digit binary number. The numbers are 00 01 10 11 and say that each "1" represents the properties if the chosen symbol. You are told that a THOG is any number with exactly one "1". Thus you can conculde "01" and "10" are Thogs and "00" and "11" aren't. The statement that a black circle is a THOG just confirms which one corresponds to "11", and hence the other mappings.
link to original post
Correct!!
Very good.
“In one sense the THOG problem is utterly trivial,” writes Wason. “And yet it is non-trivial in the sense that it is astonishingly easy for some individuals and astonishingly difficult for others. At the very least it does seem a cogent test of formal operational thought in an abstract sphere.”
----------------------------------------

A man who likes trains walks occasionally to a nearby railroad track and waits for one to go by. Afterward he notes whether he saw a passenger train or a freight. After several years his notes show that 90 percent of the trains he’s seen have been passenger trains. One day he meets an official of the railroad and is surprised to learn that the passenger and freight trains on this line are precisely equal in number.
If the man timed his trips to the track at random, why did he see such a disproportionate number of passenger trains?

A group of wealthy, globetrotting tourists land their private jet at an airport in the continental United States. They rent a luxury RV and take grand tour of the country crossing the Ohio River twice, the Mississippi River three times and the Continental Divide four times. They then return to their plane at the airport and jet set away.
What is the only state they for sure visited?

:strip_icc()/pic7287751.png)
White mates in four.
2) Kf2 Kd1
3) Ke3 Ke1
4) Rc1++
Black has only one possible move after each of White's moves.
Quote: Gialmere
A man who likes trains walks occasionally to a nearby railroad track and waits for one to go by. Afterward he notes whether he saw a passenger train or a freight. After several years his notes show that 90 percent of the trains he’s seen have been passenger trains. One day he meets an official of the railroad and is surprised to learn that the passenger and freight trains on this line are precisely equal in number.
If the man timed his trips to the track at random, why did he see such a disproportionate number of passenger trains?
btw if anyone plays 18xx, we're playing 1862 next month https://boardgamegeek.com/boardgame/66837/1862-railway-mania-eastern-counties It has three different types of trains!
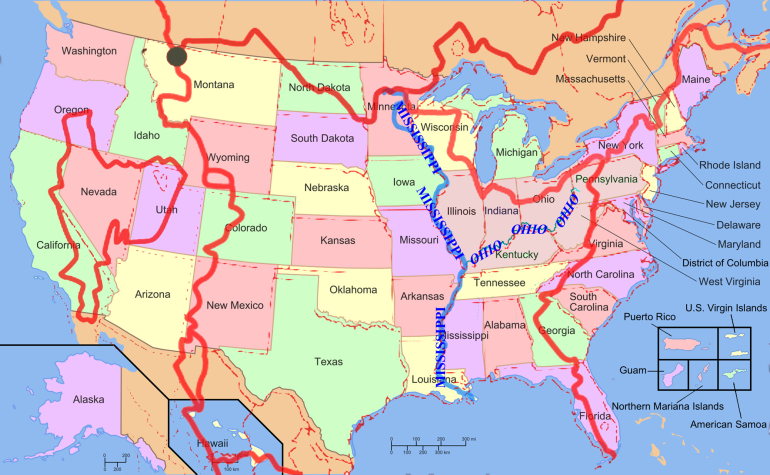
Indeed! Also of note is that most of Nevada is in a basin. When I first read the question, I was going to ask for clarification of which continental divides were crossed, until I realized it didn't matter!Quote: charliepatrickThe red line is the continental divide (which has its interesting properties - such as the stream which can flow either into the Pacific or Atlantic)
Quote: JoemanMinnesota. If you cross the Mississippi an odd number of times and return to the same spot, you would need to pass north of its headwaters. The only place to do this and stay within US borders is in Minnesota.1)Kf1 Kd2
2) Kf2 Kd1
3) Ke3 Ke1
4) Rc1++
Black has only one possible move after each of White's moves.
link to original post
Quote: charliepatrickI've seen a similar puzzle based on the Circle Line in London when you used to be able to go round the whole Circle. Co-incidentally I was thinking about this puzzle this afternoon as I tend to catch the #1 bus home rather than the #2. The solution is that freight trains pass at (say) on the hour but passenger trains at 54 minutes (or 6 minutes to) each hour. Thus if the observer arrives between the hour and 54 minutes past the hour, they will wait until 54 minutes past the hour to see a passenger train. Only if the observer arrives between 6 minutes before the hour and the hour, will they see the freight train first.
btw if anyone plays 18xx, we're playing 1862 next month https://boardgamegeek.com/boardgame/66837/1862-railway-mania-eastern-counties It has three different types of trains!As has been said crossing something an even number of times doesn't help identify the state, but because you only cross the Mississippi three times and get back to your original place, then you have to go round the (top of the) source of the river. Thus you have to pass the line North of Lake Itasca, which means you must be in Minnesota.
link to original post
Correct!!
Well done.
------------------------------------

Shear Beauty
:strip_icc()/pic7289714.png)
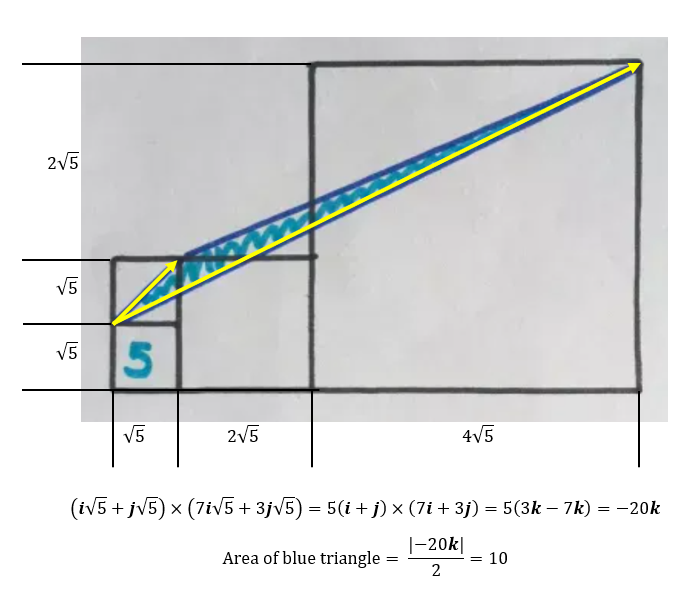
The area of the bottom left square is 5. What’s the area of the blue triangle?
The area of the triangle in the small square is
(Sqrt(5) /2) x Sqrt(5) /2
The area of the triangle spanning the two larger squares is
(Sqrt(5) /2) x [2 x sqrt(5) + 2.5x2x sqrt(5)] /2
Adding them together, we get the total area
Area=( 5 +7 x 5) /4= 10
Since the problem stated that it uses bad drawing geometry, I assumed that the largest square has four times the area of the next smaller square.
Quote: GialmereIt's toughie Tuesday. Time for more bad drawing geometry. This one's called...
Shear Beauty
The area of the bottom left square is 5. What’s the area of the blue triangle?
link to original post
I don't think it can be calculated without knowing at least one of (a) the area of the large square, or (b) the ratio of the lengths of the two line segments of the top side of area 20 square where one side of the triangle intersects it. I noticed that the existing answers assume the large square has area 80.
Use the Bounding Box method - to make it easier to describe, let x be the square root of 5
The box has (0,0) at its lower left corner and (7x, 3x) at its upper right corner; its area = 21 x^2
The vertices of the triangle are (0, 0), (x, x), and (7x, 3x)
The bounding box outside of the triangle can be broken up into four pieces: a triangle at (0, 0), (7x, 0), and (7x, 3x), which has area 21/2 x^2; a triangle at (0, 0), (0, x), and (x, x), which has area 1/2 x^2; a triangle at (x, x), (x, 3x), and (7x, 3x), which has area 6x^2; and a rectangle with lower left (x, x) and upper right (2x, 3x), which has area 2 x^2.
The area of the triangle = x^2 (21 - 21/2 - 1/2 - 6 - 2) = 2 x^2 = 2 (sqrt(5))^2 = 10.