Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
136
Since the sum of two randomly selected numbers in a range would be a probability distribution centered on the highest number (the maximum) of the range. 22 + 114 = 136
Edit: the same principle should apply to the highest and lowest numbers in a sample of randomly selected values: in the absence of any other information the sum of the highest and lowest values should be the center of the 'expectation distribution' for the max of the range that you are sampling from.
Quote: gordonm888without much thinking:
136
Since the sum of two randomly selected numbers in a range would be a probability distribution centered on the highest number (the maximum) of the range. 22 + 114 = 136
link to original post
...but my line of reasoning was, since there are 21 possible numbers below the range, there are probably 21 possible numbers above it, so the total = 114 + 21 = 135.
I'll guess about 135 tanks. Also, serial numbers from about five tanks were taken.
If we have N sequential integers, 1 through N, and choose n of them at random, the minimum and maximum will have expected values.
If we set the formula for the expected value of the minimum to 22 and the formula for the expected value of the maximum to 114, we can solve for N and n.
Instead, I did a short simulation and found that n is about 5 and N is about 135.
Quote: ThatDonGuyQuote: gordonm888without much thinking:
136
Since the sum of two randomly selected numbers in a range would be a probability distribution centered on the highest number (the maximum) of the range. 22 + 114 = 136
link to original post
...but my line of reasoning was, since there are 21 possible numbers below the range, there are probably 21 possible numbers above it, so the total = 114 + 21 = 135.
link to original post
Quote: ChesterDog
I'll guess about 135 tanks. Also, serial numbers from about five tanks were taken.
If we have N sequential integers, 1 through N, and choose n of them at random, the minimum and maximum will have expected values.
If we set the formula for the expected value of the minimum to 22 and the formula for the expected value of the maximum to 114, we can solve for N and n.
Instead, I did a short simulation and found that n is about 5 and N is about 135.
link to original post
Correct!!
Very good.
Unfortunately, their estimates differed greatly from the standard intelligence predictions. When the war ended, however, the Allies had access to the German records. In a typical month, say August 1942, the statisticians had estimated 327 panzers were built while standard intelligence had estimated 1,550. The records showed the Jerries built 342.
Math wins.
Because of this revelation, many modern militaries now randomize their weapon and component serial numbers. (More work for mathematicians I suppose.)
-------------------------------------------------------
Here's a bad tank joke...
On another topic, there was a Final Jeopardy question a while back that came down to something like this:
Quote: Jeopardy
This is the name of an animal common to Texas, which German immigrants gave the name panzerschwein.
Quote: Jeopardy
This is the name of an animal common to Texas, which German immigrants game the name panzerschwein.
link to original postThat's been the unofficial mascot of my city Austin, since artist Jim Franklin popularized it in a series of posters starting in the 70s. I had lunch with him some years ago.
Quote: WizardHere is a tangential question. Suppose the only bit of information that survived was the largest Uberpanzers serial number recorded was 114. What is the best estimate of the total number of Uberpanzers?
Quote: Jeopardy
This is the name of an animal common to Texas, which German immigrants gave the name panzerschwein.
link to original post
If the serial numbers are in the range of [22, Max] and 114 is the largest sample among two random samples, the calculation for Max is
114=(2xMax+22)/3.
Solving this equation, we have
Max=160.
This result is based on the theory that the largest number is at 2/3 of the [22, Max] interval.
Quote: acesideQuote: WizardHere is a tangential question. Suppose the only bit of information that survived was the largest Uberpanzers serial number recorded was 114. What is the best estimate of the total number of Uberpanzers?
Quote: Jeopardy
This is the name of an animal common to Texas, which German immigrants gave the name panzerschwein.
link to original post
If the serial numbers are in the range of [22, Max] and 114 is the largest sample among two random samples, the calculation for Max is
114=(2xMax+22)/3.
Solving this equation, we have
Max=160.
This result is based on the theory that the largest number is at 2/3 of the [22, Max] interval.
link to original post
I donít think you can use the 22. All you know is 114. So I would have thought itís 114 * 2 = 228.
Edit: oh, Wiz said we know 2 things. 114 and that lower numbers were found but we donít know what they are.
Quote: WizardHere is a tangential question. Suppose the only bit of information that survived was the largest Uberpanzers serial number recorded was 114. What is the best estimate of the total number of Uberpanzers?
On another topic, there was a Final Jeopardy question a while back that came down to something like this:Quote: Jeopardy
This is the name of an animal common to Texas, which German immigrants gave the name panzerschwein.
link to original post
If n integers are selected without replacement from the integers 1 through N, the expected value of the maximum of the n integers is: n ( N + 1 ) / ( n + 1 ). (By the way, I would like to see the proof of this.)
The number 114 might be from just one observation, so n = 1. Then (N+1)/2 = 114 solves to N = 217.
If the maximum of 114 was found from two observation, then n = 2. Then 2(N+1)/3 = 114 solves to N = 170.
When n = N, then N = 114.
With 114 as the only piece of information, I think 217 would be the best estimate for the number of Uberpanzers.
We know that the max observed serial number was 114, but the number of observed serial numbers, n, could be any value from 1 to 114. Lacking any other information, we should assume that n could be 1 to 114 with equal probability.
Making this assumption, I calculate that the mean value of the estimated total number of Uberpanzers is 118.3. However, the mode of the estimated total number of Uberpanzers (the most frequently occurring value) is 114! The median value of estimated total number of Uberpanzers is 115.
The meaning of "best value of total number of Uberpanzers" is a bit unclear. The most likely number is 114. I guess I would say that the total number of Uberpanzers is 115 +/- 1 with about 70% confidence.
Quote: unJonEdit: oh, Wiz said we know 2 things. 114 and that lower numbers were found but we donít know what they are.
link to original post
We only know ONE thing -- that 114 was the maximum serial number served.
During the war, Germany numbered their uber-tanks sequentially, starting at 1. It is not known how many they made in total. A scout was sent out to record tank serial numbers. However, he died in action and his report was significantly damaged. The only bit of information that survived was the highest serial number observed was 114.
What is the most likely total number of uber-tanks made?
Quote: Wizard...Based on Gordon's reply...What is the most likely total number of uber-tanks made?...
I think the proof runs as follows:-
Let's assume the scout actually saw N tanks. Clearly he can't have seen more than 114 (assuming he didn't record dupicates), so let's look at that case first.
Scout looks at 114 in all
If there were 114 tanks there was no chance than the scout could have seen a tank greater than 114, hence the chances of the first 114 tanks seen would be 100%. If there were 115 tanks, then the scout has to avoid seeing the 115th tank before seeing the other 114. The chances of this happenning are 1 in 115 (since if he had waited until seeing 115 the last one seen could have been any of the other 115).
Similar logic applies for larger numbers.
Thus if you knew the scout found 114 tanks, then it's exceedingly likely there were 114 tanks.
Scout looks at 113 in all
We know there are at least 114 tanks. Let's assume he sees #114 first, there is now a 100% chance all the rest would be smaller.
If there had been 115 tanks, if he sees #114 first, the chance of not seeing 115 is 2 in 115 (i.e. that tank has to be one of the last two).
Therefore the most likely number of tanks is 114.
Scout looks at fewer and fewer
Similar logic applies until you get to the scout having just looked at one.
If there were 114 tanks then the chances of seeing #114 is 1 in 114. If there are a larger number, then the chances are 1/N.
Therefore again the most likely number is 114.
Note because the question is looking at the most likely it is the same as asking how long does it take before someone throws a 7. The most likely roll is the first (P=1/6), and other rolls have reducing chances being P=5/6N*1/6. However the average is 6.
So remember the most likely day, since it's getting late here, that something good will happen is tomorrow!!!

After the war, your country decides to build 720 of the ubertanks to augment its army. Now aware of how enemies can utilize serial numbers, it's decided to randomly assign each tank a number from a larger pool (without replacement).
What is the minimum number of digits the serial number should contain to (essentially) prevent collisions?
So 720 tanks require a 7 digit serial number.
Of course the enemy has mathematicians too. They might see a seven digit number and deduce 100 to 999 tanks built and fine tune from there. The shooting war may have ended but the war between military mathematicians is eternal.
Note that this type of math overlaps with the classic "same birthday" type of math puzzles.
-------------------------------------------


Take two standard decks of cards, shuffle them together and deal them face down into two piles of 52 cards.
What is the probability that the number of red cards in the Pile A equals the number of black cards in Pile B?
How many cards would you have to turn over to be certain of your answer?
or a
:strip_icc()/pic7216058.png)
White mates in two.
with your morning coffee?
:strip_icc()/pic7216058.png)
1. Nd2
which leaves Black three legal replies:
1. ... c4
2. Ne4#
1. ... e4
2. Nc4#
1. ... Kxd5
2. Qd7#
I'd try the other, but I still haven't had my morning coffee.
Dog Hand
Quote: DogHand
1. Nd2
which leaves Black three legal replies:
1. ... c4
2. Ne4#
1. ... e4
2. Nc4#
1. ... Kxd5
2. Qd7#
I'd try the other, but I still haven't had my morning coffee.
Dog Hand
link to original post
Quote: charliepatrickYes it's a variation of the mixing wine with water question. Since there are 52 cards in eash pile, then the total number of Reds in Pile 1 (R1) and the total number of Blacks in Pile 1 (B1) = (R1+B1)=52. Also the total number of Reds in both piles (R1+R2)=52. Hence R2=B1. Similarly R1=B2. This will always be the case so you don't need to turn any cards over.
link to original post
Both Correct!!
----------------------------------------------


Going, Going, 'gon
:strip_icc()/pic7217505.png)
Six identical squares and a smaller rectangle are fitted into this regular hexagon.
What fraction of the hexagon do they cover?
Quote: acesideDo you mean 6 squares and the one rectangular adding together coverage?
link to original post
Yes.
The area of each square is 0.518^2=0.269.
We divide the rectangle into four pieces from its center to corners, and the area of the triangle on the short edge is
[1-0.518xsqrt(2)]^2xcos(30 deg)x0.5=0.0311
The area of triangle on the long edge is
[1-0.518xsqrt(2)]^2xsin(60 deg)x0.5=0.0311
So the total area of the 6 squares and one rectangle is
0.269x6+0.0311x4
So, the area coverage is
66.9%
Quote: GialmereQuote: acesideDo you mean 6 squares and the one rectangular adding together coverage?
link to original post
Yes.
link to original post
I get two-thirds.
The answer is so simple that it's probably right.
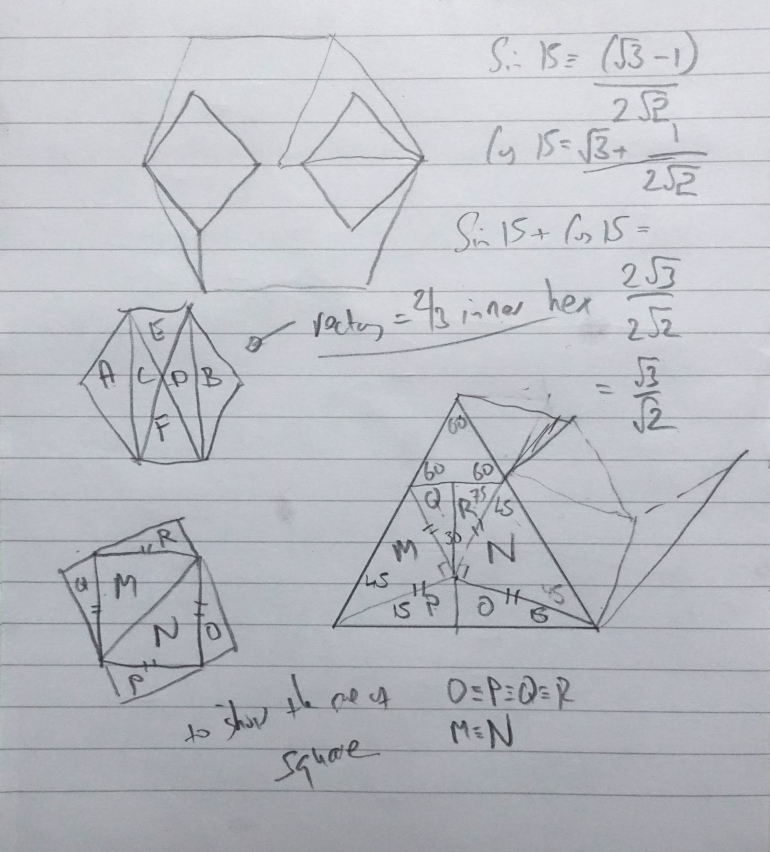
Ignoring the centre rectangle for the moment, the squares and the large hexagon have six way symmetry. Thus let's look at one of the sides and what lies within the equilateral triangle.
Half one of the squares and half of the other (M and N) lie within it, and as the angle of the square has been split, the angle is 45. Thus this leaves two traingles (15 90 75) O and P. At the inside of the squares there are two identical triangles (Q and R) and this leaves a small equilateral triangle.
All six of these equilateral triangles form a small hexagon, which can be seen in the parts A thru F. The rectangle is CDEF, and as all triangles shown have the same area this is 2/3rds of the smaller hexagon.
Now look at MN (which can form a square) and adding the four triangles, which forms a larger square. What we need to find out is the ratio of the square (MNOPQR) to square MN. Thus we need to add Sin 15 and Cos 15, as this will give the length of the larger square.
Sin 15 = (SQRT(3)-1)/(2*SQRT(2)) and Cos 15 = (SQRT(3)+1)/(2*SQRT(2)); so Sin 15 + Cos 15 = SQRT(3)/SQRT(2). So the large square is 3/2 of the small square, or that can be rewritten as the small square is 2/3 of the large one.
The large square has an area equal corresponding to MNOPQR (six of these make up the large hexagon minus the inner hexagon). The small square corresponds to the area of one "square" (six of these make up all the squares on the original puzzle).
Therefore the six squares are 2/3 of the inner hexagonal part, and the rectangle is 2/3 of the small hexagon.
Hence the six squares and the rectangle are 2/3 of the area of the large hexagon.
Quote: ChesterDog
I get two-thirds.
The answer is so simple that it's probably right.
link to original post
Quote: charliepatrick
Ignoring the centre rectangle for the moment, the squares and the large hexagon have six way symmetry. Thus let's look at one of the sides and what lies within the equilateral triangle.
Half one of the squares and half of the other (M and N) lie within it, and as the angle of the square has been split, the angle is 45. Thus this leaves two traingles (15 90 75) O and P. At the inside of the squares there are two identical triangles (Q and R) and this leaves a small equilateral triangle.
All six of these equilateral triangles form a small hexagon, which can be seen in the parts A thru F. The rectangle is CDEF, and as all triangles shown have the same area this is 2/3rds of the smaller hexagon.
Now look at MN (which can form a square) and adding the four triangles, which forms a larger square. What we need to find out is the ratio of the square (MNOPQR) to square MN. Thus we need to add Sin 15 and Cos 15, as this will give the length of the larger square.
Sin 15 = (SQRT(3)-1)/(2*SQRT(2)) and Cos 15 = (SQRT(3)+1)/(2*SQRT(2)); so Sin 15 + Cos 15 = SQRT(3)/SQRT(2). So the large square is 3/2 of the small square, or that can be rewritten as the small square is 2/3 of the large one.
The large square has an area equal corresponding to MNOPQR (six of these make up the large hexagon minus the inner hexagon). The small square corresponds to the area of one "square" (six of these make up all the squares on the original puzzle).
Therefore the six squares are 2/3 of the inner hexagonal part, and the rectangle is 2/3 of the small hexagon.
Hence the six squares and the rectangle are 2/3 of the area of the large hexagon.
link to original post
Correct!!!
Excellent. (And a half point to aceside for being so close.)
----------------------------------------------
Dirty joke...


The following set of number pairs refers to some coincidences in American history, spanning the period from the founding of the nation in 1776 to the present.
2, 6
?, ?
9, 23
17, 36
26, 32
What number pair should be in the second position?
Quote: acesideMy guess is 7, 18 because they are very related to American history
link to original post
Sorry no.
Quote: Gialmere
What number pair should be in the second position?
link to original post
I can't find one that keeps the first numbers in order, but I will say 22, 24
Each pair represents a pair of numbers of Presidents that have the same last name. Since you count Theodore Roosevelt as 26, you are counting Grover Cleveland as both 22 and 24.
A good guess by aceside, but it's ThatDonGuy who gets a half point for being on top of it.
2, 6 = John Adams, John Quincy Adams
?, ?
9, 23 = William Henry Harrison, Benjamin Harrison
The missing numbers are 41, 43 for George H. W. Bush and George W Bush. Why are they second on the list? In a final twist, the pairs are presented alphabetically. So you have: Adams, Bush, Harrison, Johnson, Roosevelt.
----------------------------------------
:strip_icc()/pic7208141.png)
The above is called a calculation maze. The object is to begin in the upper left red space with the start value shown and end at the lower right yellow space with the specified target value. Your value changes according to the calculation on the space you enter.
For this example maze your starting value is 2 and the target value is 6. If you went down two spaces then right two spaces your running calculation value would be: start=2, 1, 2, 6, 7. Oops. That's 1 too many.
You must follow the lines between spaces, traveling either up/down or left/right. This means you may move backwards to the space you just came from, however, you may never move diagonally. You may enter and re-enter a space as many times as you wish.
If you re-enter the start space your value will immediately revert to the starting value, essentially making you start over. (You're trying to get through the maze in as few moves as possible.) If you enter the end space with the wrong total, treat it as any other space by adjusting your value and continue on.
Target Value = 6
:strip_icc()/pic7208142.png)
start=2, 1, 3, 5, 4, 5, 6=end
--------------
Target Value = 21
:strip_icc()/pic7208143.png)
Start Value = 0
Target Value = 10
:strip_icc()/pic7208144.png)
The red candle is 5" tall and takes 6 hours to burn out.
The blue candle is 3" tall and takes 10 hours to burn out.
You light them both at the same time.
In how many hours will they be the same height?

Quote: Gialmere
The above is called a calculation maze. The object is to begin in the upper left red space with the start value shown and end at the lower right yellow space with the specified target value. Your value changes according to the calculation on the space you enter.
For this example maze your starting value is 2 and the target value is 6. If you went down two spaces then right two spaces your running calculation value would be: start=2, 1, 2, 6, 7. Oops. That's 1 too many.
You must follow the lines between spaces, traveling either up/down or left/right. This means you may move backwards to the space you just came from, however, you may never move diagonally. You may enter and re-enter a space as many times as you wish.
If you re-enter the start space your value will immediately revert to the starting value, essentially making you start over. (You're trying to get through the maze in as few moves as possible.) If you enter the end space with the wrong total, treat it as any other space by adjusting your value and continue on.Start Value = 2
Target Value = 6
start=2, 1, 3, 5, 4, 5, 6=end
--------------Starting Value = 0
Target Value = 21This maze has the added restriction that you must leave a space along a different path from the one you used to enter it.
Start Value = 0
Target Value = 10
link to original post
Second thought on Puzzle #1
=0, down+1, right x4, right x2, down -2, down x2, left -2, left +2, down +0, right +2, up -2, up +2, right -2, right +2, up -2, right -2, down x2, down +1, down +0 = 21
Quote: WizardYou have two candles.
The red candle is 5" tall and takes 6 hours to burn out.
The blue candle is 3" tall and takes 10 hours to burn out.
You light them both at the same time.
In how many hours will they be the same height?
link to original post
This one should be easy.
5-5x/6=3-3x/10.
Solving this, we get x=3.75 hours.
Quote: WizardYou have two candles.
The red candle is 5" tall and takes 6 hours to burn out.
The blue candle is 3" tall and takes 10 hours to burn out.
You light them both at the same time.
In how many hours will they be the same height?
link to original post
Dog Hand
Quote:This one should be easy.
We set time=x, that is, in x hours the two candles will be the same height. We have this equation
5-5x/6=3-3x/10.
Solving this, we get x=3.75 hours.
link to original post
I agree!
Quote: acesideOn second thought, I found this puzzle does not have a solution. However, if we change the bottom right corner number to +0, then here is my path to solve this puzzle:
=0, down+1, right x4, right x2, down -2, down x2, left -2, left +2, down +0, right +2, up -2, up +2, right -2, right +2, up -2, right -2, down x2, down +1, down +0 = 21
link to original post
I don't think I'll post the solves to these. Just see what the future brings.
Now use similar logic since the starting position has a similar wall of multipliers (x3 x4 x2) and all the numbers between the two walls are even. Hence you have to come through x3.
Thus the route starts 0 1 x3 and ends x3 3 1 3 1 3 1, so you now need to enter the Southern x3 with 3. Thus you need the same number of +2s as -2s.
One notices that going the direct route (0 1 x3 2 -2 2 -2 2 -2 2) results in 5, so one needs to use the circle of -2s to get a lower number. Since that loop subtracts 4, you now need to add 2. So you also go via (2 0).
Hence the route is
A5 +0 0
B5 +1 1
C5 x3 3
D5 +2 5
E5 -2 -3
E4 -2 -1
D4 -2 -3
D3 +2 -1
C3 -2 -3
B3 +2 -1
A2 +2 1
A1 +0 1
B1 +2 3
C1 x3 9
D1 +3 12
E1 +1 13
D1 +3 16
E1 +1 17
D1 +3 20
E1 +1 21
Quote: charliepatrickAssuming you can go backwards and forwards (otherwise it's impossible). There is a wall of multipliers in the SE corner (x3 x4 x2). You have to go through one (or more) of these. If you come through the x4 or x2 then you'll be even, hence you can only come in via x3. From there you can add multiples of 4 by going to and fro the 3 and 1. To get to 21 you need to find a multiple of 3 that can be turned into 21 by adding a number of 4s. This number is 9. Hence you need to enter the "x3" with 3.
Now use similar logic since the starting position has a similar wall of multipliers (x3 x4 x2) and all the numbers between the two walls are even. Hence you have to come through x3.
Thus the route starts 0 1 x3 and ends x3 3 1 3 1 3 1, so you now need to enter the Southern x3 with 3. Thus you need the same number of +2s as -2s.
One notices that going the direct route (0 1 x3 2 -2 2 -2 2 -2 2) results in 5, so one needs to use the circle of -2s to get a lower number. Since that loop subtracts 4, you now need to add 2. So you also go via (2 0).
Hence the route is
A5 +0 0
B5 +1 1
C5 x3 3
D5 +2 5
E5 -2 -3
E4 -2 -1
D4 -2 -3
D3 +2 -1
C3 -2 -3
B3 +2 -1
A2 +2 1
A1 +0 1
B1 +2 3
C1 x3 9
D1 +3 12
E1 +1 13
D1 +3 16
E1 +1 17
D1 +3 20
E1 +1 21
link to original post
You're hot on the trail with your logic but seem to have missteps. For example, from D5 to E5 you subtracted 8. Also you take an illegal diagonal from B3 to A2.
Quote: GialmereYou're hot on the trail with your logic but seem to have missteps....
| A5 | 0 | 0 |
| B5 | 1 | 1 |
| C5 | x3 | 3 |
| D5 | 2 | 5 |
| E5 | -2 | 3 |
| E4 | -2 | 1 |
| D4 | -2 | -1 |
| D3 | 2 | 1 |
| C3 | -2 | -1 |
| B3 | 2 | 1 |
| B2 | -2 | -1 |
| B1 | 2 | 3 |
| C1 | x3 | 9 |
| D1 | 3 | 12 |
| E1 | 1 | 13 |
| D1 | 3 | 16 |
| E1 | 1 | 17 |
| D1 | 3 | 20 |
| E1 | 1 | 21 |
btw I have two solutions to the first puzzle using 14 moves, but need to check them first!!
The two routes are (i) EastEast to middle, then West and all the way round, SouthEast (ii) South going all the way round, then East (1 2 -5 1), then EastSouth.
| A3 | 0 | 0 |
| B3 | -1 | -1 |
| C3 | x2 | -2 |
| C2 | 2 | 0 |
| B2 | 1 | 1 |
| A2 | 2 | 3 |
| A1 | x3 | 9 |
| B1 | -5 | 4 |
| C1 | 1 | 5 |
| C2 | 2 | 7 |
| C3 | x2 | 14 |
| B3 | -1 | 13 |
| B2 | 1 | 14 |
| B1 | -5 | 9 |
| C1 | 1 | 10 |
| A3 | 0 | 0 |
| A2 | 2 | 2 |
| A1 | x3 | 6 |
| B1 | -5 | 1 |
| C1 | 1 | 2 |
| C2 | 2 | 4 |
| C3 | x2 | 8 |
| B3 | -1 | 7 |
| B2 | 1 | 8 |
| C2 | 2 | 10 |
| C1 | 1 | 11 |
| B1 | -5 | 6 |
| B2 | 1 | 7 |
| C2 | 2 | 9 |
| C1 | 1 | 10 |
(From this Twitter post.)
Quote: MichaelBluejay"A town has only two colours of car: 85% are blue and 15% are green. A person witnesses a hit-and-run and says they saw a green car. If witnesses identify the colour of cars correctly 80% of the time, what are the chances the car is actually green?
link to original post
Quote: MichaelBluejay"A town has only two colours of car: 85% are blue and 15% are green. A person witnesses a hit-and-run and says they saw a green car. If witnesses identify the colour of cars correctly 80% of the time, what are the chances the car is actually green?
(From this Twitter post.)あなたのお母そんはそんなに太っているから、自分の郵便番号があります。
link to original post
There are two possibilities: it was a correctly identified green car, or it was an incorrectly identified blue car.
The probability of it being a green car identified as green = 3/20 x 4/5 = 12/100
The probability of it being a blue car identified as green = 17/20 x 1/5 = 17/100
The probability of it being green = 12 / (12 + 17) = 12/29.


