Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
I show player 1 has an EV of $0.10 and player 2 of $0.15. Thus, player 2 is better off.
I might make a another version of this puzzle where collusion is allowed, but let's wait for this one to be closed first.
Quote: charliepatrickIf a Red card is picked, #1 passes and #2 plays.
If a Black card is picked, #1 plays and #2 (perforce) passes.
As Red and Black cards are picked with equal probability, on average, #1 and #2 play the same number of games. Therefore we only need to look at which, on average, game gives the best return. For simplicity it's easier to sum up the five possible outcomes and see the total profit.
When #1 plays there are 3 Red and 2 Black, thus the profit is (3*$1 - 2*$1) = $1.
When #2 plays there are 2 Red and 3 Black, however the cost to play is 50c so the profit when winning is $1.50. Thus the profit is (2*$1.50 - 3*50c) = $1.50.
Hence #2 is the better off.
link to original post
Quote: gordonm888
Player#1 can play with an EV = $1 if he only play on when he picks up a black card, or an EV of zero if he plays no matter which color he picks up.
Player#2 can play only when Player#1 passes, but then he can make $1.50 when Players#1 picked up a red card and more if Player picks up a black card but passes anyway.
However, Player #2 will never make any money unless palyer#1 passes.
So Player#1 charges Player#2 a fee in order to pass no matter what color card he sees. The fee might reasonably be set at 60% of what player#2 expects to make. Such an arrangement would be a win-win for both players.
So player#1 profits the most.
link to original post
Quote: ThatDonGuy
This assumes that the $2 that a player can win is the entire amount, as opposed to $2 plus the amount bet.
If P1 sees a red card, and:
(a) plays, P1 has a 2/5 chance of winning $2, for an ER of 4/5, and a EV of 4/5 - 1 = -1/5
(b) passes, P2 has a 2/5 chance of winning $2, for an ER of 4/5, and a EV of 4/5 - 1/2 = 3/10
If P1 sees a black card, and:
(a) plays, P1 has a 3/5 chance of winning $2, for an ER of 6/5, and a EV of 6/5 - 1 = 1/5
(b) passes, P2 has a 3/5 chance of winning $2, for an ER of 6/5, and a EV of 6/5 - 1/2 = 7/10
The first card can equally likely be red or black. If it is red, P1's best play is to pass; if it is black, P1's best play is to play.
The EV for each hand is 1/2 x 0 + 1/2 x 1/5 = 1/10 for P1, and 1/2 x 3/10 + 1/2 x 0 = 3/20 for P2.
Player 2 will make more in the long run.
link to original post
Quote: Wizard
I show player 1 has an EV of $0.10 and player 2 of $0.15. Thus, player 2 is better off.
I might make a another version of this puzzle where collusion is allowed, but let's wait for this one to be closed first.
link to original post
Correct!!
Well done.
Gordon makes an interesting point about Player #1 playing hardball. I suppose a mathematician might look at it along the lines of the Nash equilibrium. Other ways to phrase it would be: kickback, shakedown, extortion, racketeering, greasing the wheels, corruption and cost of doing business.
-----------------------------------------
/pic7185433.png)
John must play three singles matches against his parents. If he wins two matches in a row he gets money for a new computer.
His mother says he can play either Mother-Father-Mother, Father-Mother-Father or Father-Father-Mother.
His Father is a better player than his mother.
Which sequence should he play or are all three the same?
:strip_icc()/pic7185458.png)
There are three pucks on the ice. A player shoots one of them between the other two. He repeats the shots never shooting the same puck twice in a row.
What is the minimum number of shots it will take to return the pucks back to their starting positions on the ice, or is that impossible?
Quote: GialmereHappy (U.S.) Thanksgiving! Here's a few easy puzzles to let you escape your in-laws for a few moments...
John must play three singles matches against his parents. If he wins two matches in a row he gets money for a new computer.
His mother says he can play either Mother-Father-Mother, Father-Mother-Father or Father-Father-Mother.
His Father is a better player than his mother.
Which sequence should he play or are all three the same?
link to original post
If the sequence is MFM, his chance of winning is 2mf-fm^2
If the sequence is MFM, his chance of winning is 2mf-mf^2
2mf-fm^2 > 2mf-mf^2
-fm^2 > -mf^2
fm^2 < mf^2
m < f (which we're given)
In more simple English, he must win game #2. Assuming he does, he gets two cracks at the other parent. Better to have to shots at the better player.
By the way, this one was asked in this month's Mensa newsletter. Are you a member, G?
The solution relies on the fact that if all three move then each of them would need to go to somewhere and then back (i.e. six). But it is easier if one of them stays still and so the other two have to go round. The minimum for that is 3-moves each as each of them has to form a triangle.
Quote: WizardQuote: GialmereHappy (U.S.) Thanksgiving! Here's a few easy puzzles to let you escape your in-laws for a few moments...
John must play three singles matches against his parents. If he wins two matches in a row he gets money for a new computer.
His mother says he can play either Mother-Father-Mother, Father-Mother-Father or Father-Father-Mother.
His Father is a better player than his mother.
Which sequence should he play or are all three the same?
link to original postHe should play FMF.
If the sequence is MFM, his chance of winning is 2mf-fm^2
If the sequence is MFM, his chance of winning is 2mf-mf^2
2mf-fm^2 > 2mf-mf^2
-fm^2 > -mf^2
fm^2 < mf^2
m < f (which we're given)
In more simple English, he must win game #2. Assuming he does, he gets two cracks at the other parent. Better to have to shots at the better player.
By the way, this one was asked in this month's Mensa newsletter. Are you a member, G?
link to original post
Quote: charliepatrickI think it can be done with six shots. Consider a six sided star which comprises of two equalateral triangles. A is in the centre and B starts at (say) the SE point with C on the E point. B goes to the NE, C goes to the NW, B goes to the W. B is now opposite where C started, and C is oposite where B started. So continue the next three shots to get back to the original.
The solution relies on the fact that if all three move then each of them would need to go to somewhere and then back (i.e. six). But it is easier if one of them stays still and so the other two have to go round. The minimum for that is 3-moves each as each of them has to form a triangle.
link to original post
Both Correct!!
Well done.
:strip_icc()/pic7185459.png)
-----------------------------------------------
As for Mensa...
Spike in the Hive
:strip_icc()/pic7197580.png)
Two of the regular hexagons are identical; the third has area 10.
Whatís the area of the red triangle?
Quote: Gialmere...Whatís the area of the red triangle?...
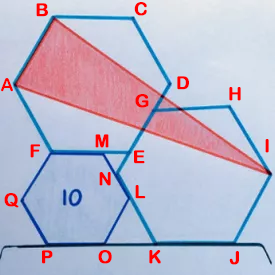
Label the vertices as shown.
Let x be the length of the sides of the two hexagons.
Angles FMN and MEG are 120°, so EMN and MEN are 60°, which means MEN is an equilateral triangle
ME = EF - MF = x - 10, so EM and MN are also x - 10
LN = LM - MN = 10 - (x - 10) = 20 - x
LK = KN - KL = x - (20 - x) = 2x - 20
Angles POL and JKL are 120°, so LOK and LKO are 60°, which means LOK is an equliateral triangle
LO = LK, which means 10 = 2x - 20, which means x = 15
Now, assign coordinates to each point, starting with P being on (0,0)
F is (0, 10 sqrt(3)), so A is (-15/2, 10 sqrt(3) + 15 sqrt(3) / 2), or (-15/2, 35 sqrt(3) / 2), and B is at (0, 25 sqrt(3))
O is at (10, 0), OK = ON = 10, so K is at (20, 0), which means J is at (35, 0), and I is at (85/2, 15 sqrt(3)/2)
Using the "bounding box" method with I in the lower right corner, I get the area of the triangle to be:
(50 x 35 sqrt(3) / 2) - (1/2 x 15/2 x 15 sqrt(3) / 2) - (1/2 x 85/2 x 35 sqrt(3)/2) - (1/2 x 10 sqrt(3) x 50) = 450 sqrt(3)
I have a feeling that's either correct or nowhere near the answer...
That's the answer if the smaller hexagon has side length 10.
A hexagon with side length 10 has area 6 x (1/2 x 10 x 10 sqrt(3) / 2) = 150 sqrt(3), so to find the correct area of the triangle, multiply the area of the "side length 10" triangle by 10 / 150 sqrt(3); the answer = 450 sqrt(3) x 10 / 150 sqrt(3) = 30.
Quote: charliepatrickI haven't checked my arithmetic but it does sound like a nice answer! (I've added the coloured text etc. to explain some of my unstated thoughts.)
link to original post
Correct!!
Excellent.
Now, the red triangle area: Itís half base times height, so itís twice the area of a triangle with the same base and half the height, or twice the area of the same triangle sheared parallel to its base:
:strip_icc()/pic7199904.png)
And that last triangle clearly is 1/3 the area of the hexagon itís inscribed in. So A = 2/3 x 9/4 x 10 = 15.
---------------------------------------------
A quick bad joke.
---------------------------------------------
Shearer is best known for the felt tip marker way she presents her puzzles. Another of her signature moves is neat and tidy answers. Here's another one of her classics. This one called...
Fly the Flags
:strip_icc()/pic7199905.png)
Squares of the same color are the same size.
Whatís the total shaded area?
Quote: Gialmere...Fly the Flags
...
The diagonal of the a blue square is 3, hence each side is 3/2*SQRT(2), hence the area of each blue square is 9/4*2= 4.5.
Areas of two red squares is 4+4=8, areas of two blue squares is 4.5+4.5=9.
Hence total = 17.
The sum of the lengths of the diagonals of the two blue squares = 6, so each blue square has diagonal length 3, which means it has side length 3 sqrt(2) / 2, which means it has area 9/2.
A diagonal of the size 6 square includes a side from each triangle, so you have at least one white triangle with height = the red square's side length and width = (6 - red square side length) / 2; since the angle is 45 degrees, they must be equal, so each red square has side length 2, or area 4.
The total shaded area = 2 (9/2 + 4) = 17.
Quote: charliepatrickThe first thing to notice is the sides of the blue square are 45o to the vertical/horizontal. So you could extend the vertical sides of the red squares to form triangles within the blue squares. These "blue triangles" are identical to the "white" ones. Hence the four triangles form a square which is the same size as a red square. Hence the red squares have sides of length 2 (and hence area of 4).
The diagonal of the a blue square is 3, hence each side is 3/2*SQRT(2), hence the area of each blue square is 9/4*2= 4.5.
Areas of two red squares is 4+4=8, areas of two blue squares is 4.5+4.5=9.
Hence total = 17.
link to original post
Quote: ThatDonGuy
The sum of the lengths of the diagonals of the two blue squares = 6, so each blue square has diagonal length 3, which means it has side length 3 sqrt(2) / 2, which means it has area 9/2.
A diagonal of the size 6 square includes a side from each triangle, so you have at least one white triangle with height = the red square's side length and width = (6 - red square side length) / 2; since the angle is 45 degrees, they must be equal, so each red square has side length 2, or area 4.
The total shaded area = 2 (9/2 + 4) = 17.
link to original post
Correct!!
Good show.
For "Fly the Flags", you either see the key quick or you sit there staring at it for quite some time.
------------------------------------------------------
Here is a joke I'm ashamed to say made me laugh....
------------------------------------------------------
We might as well make it a Catriona Shearer weekend. This one is interesting since at first glance it seems impossible. It's called...
Just One Fact
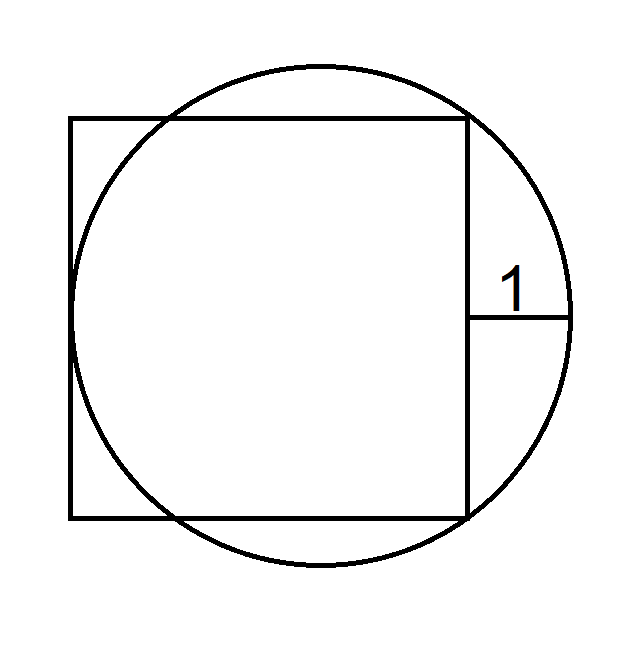
:strip_icc()/pic7201230.png)
Whatís the area of the square?
Let r be the radius of the circle, and s the side length of the square.
Two things we know:
(1) 2r = s + 1
(2) If you draw a line segment from the center of the circle to either point where the circle intersects a vertex of the square, and another from the center of the circle to the midpoint of the side between those two intersection points, then, by the Pythagorean Theorem, (s / 2)^2 = r^2 - (r - 1)^2 = 2r - 1
(2) can be rewritten as 2r = s^2 / 4 + 1
Combining (1) and (2), s^2 / 4 + 1 = 2r = s + 1, so s^2 = 4s, or s = 4
The area of the square is s^2, or 16.
Here are a couple diagrams I'll probably use when I make an Ask the Wizard question out of this one.
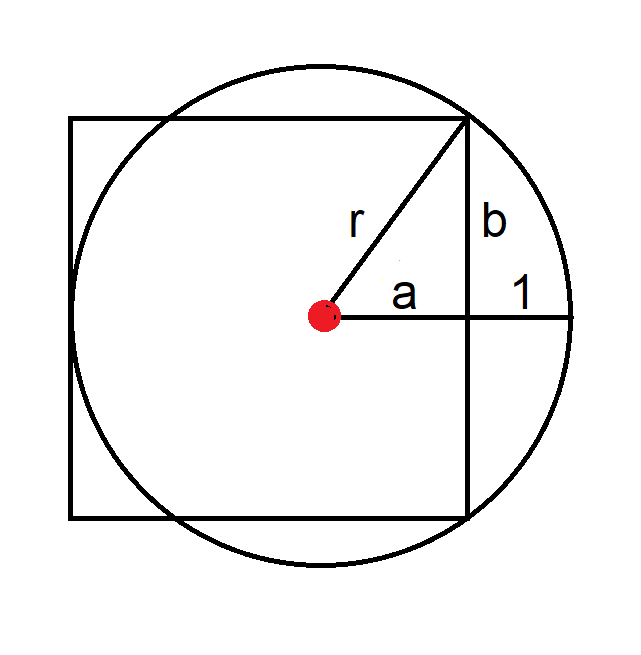
The simplest way is to look at similar triangles. So construct a diameter, which will happen to go across the middle of the square. Then construct two lines, one from each end of the diameter to the NE corner of the square.
Note that one of the triangles (blue) has the base of the size of the square, and the height is half the size of the square. Also it has a right angle and the angle (BWA) as the West end of the diameter.
The triangle (red and blue combined) with a hypoteneuse as the diameter, forms a right angle at the circle. Therefore angle BAE = angle BWA.
So the red triangle with base 1 and height half the square, is similar. Thus it has sizes with ratio of 2 to 1. Hence half the square side is 2.
So the size of the square is 4, and its area is 16.
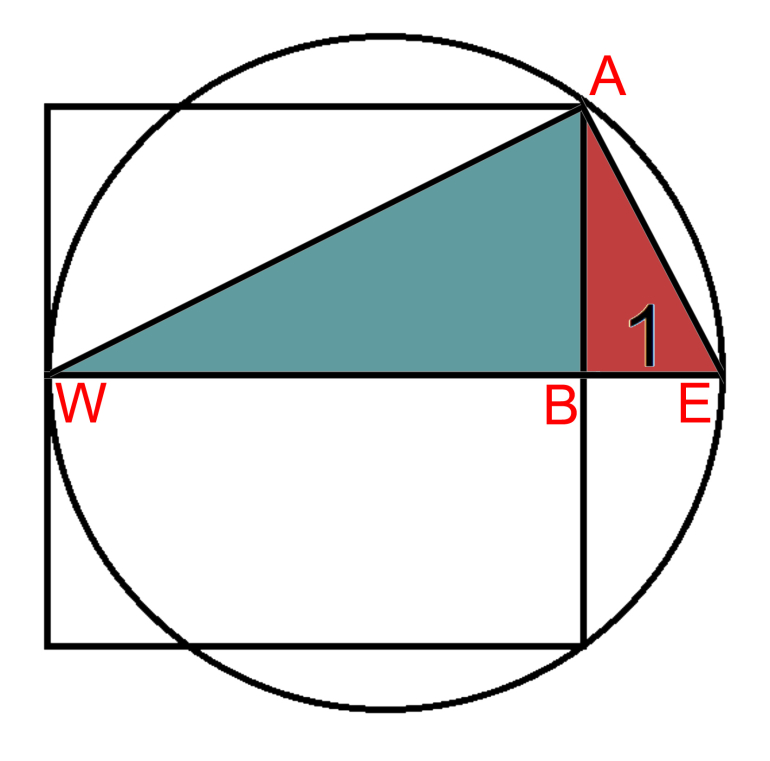
Quote: ThatDonGuy
Let r be the radius of the circle, and s the side length of the square.
Two things we know:
(1) 2r = s + 1
(2) If you draw a line segment from the center of the circle to either point where the circle intersects a vertex of the square, and another from the center of the circle to the midpoint of the side between those two intersection points, then, by the Pythagorean Theorem, (s / 2)^2 = r^2 - (r - 1)^2 = 2r - 1
(2) can be rewritten as 2r = s^2 / 4 + 1
Combining (1) and (2), s^2 / 4 + 1 = 2r = s + 1, so s^2 = 4s, or s = 4
The area of the square is s^2, or 16.
link to original post
Quote: WizardI agree with Don.
link to original post
Quote: charliepatrickAs you say it takes a while and then a penny drops.
The simplest way is to look at similar triangles. So construct a diameter, which will happen to go across the middle of the square. Then construct two lines, one from each end of the diameter to the NE corner of the square.
Note that one of the triangles (blue) has the base of the size of the square, and the height is half the size of the square. Also it has a right angle and the angle (BWA) as the West end of the diameter.
The triangle (red and blue combined) with a hypoteneuse as the diameter, forms a right angle at the circle. Therefore angle BAE = angle BWA.
So the red triangle with base 1 and height half the square, is similar. Thus it has sizes with ratio of 2 to 1. Hence half the square side is 2.
So the size of the square is 4, and its area is 16.
link to original post
Correct!!
Very good.
Not so impossible after all.
--------------------------------------------------

-------------------------------------------------
There's a few other Shearer puzzles I'll post at another time.

Find positive integers a, b, and c, all different, such that a^3 + b^3 = c^4.

Starting in Delaware, you must tour the 48 contiguous United States, visiting each state exactly once.
Where will you finish?
Quote: GialmereIt's easy Monday. Here's another pair of puzzles...
Find positive integers a, b, and c, all different, such that a^3 + b^3 = c^4.
Starting in Delaware, you must tour the 48 contiguous United States, visiting each state exactly once.
Where will you finish?
link to original post
#2 Maine, because if I entered Maine previously, I would have to visit New Hampshire twice.
Buzzzzz!
ding! ding! ding!
Puzzle #2
Quote: ChesterDog#2 Maine, because if I entered Maine previously, I would have to visit New Hampshire twice.
link to original post
Correct!!
Well done.
Quote: Gialmere
While there are many ways to zigzag from sea to shining sea, since Maine uniquely borders only one state it must be either your starting or ending point on such a tour. (Note also that New York guards New England, acting as a sort of one-way gate.)
link to original post
I think you have to get off the interstate highway network several times if you want a reasonably efficient tour route.
Congratulations, ChesterDog.

Last night I sat behind two wizards on the Magical Mystery Tour bus, and overheard the following...
Psychedelic Wizard: I have a positive integral number of children, whose ages are positive integers, the sum of which is the number of this bus, while the product is my own age.
Kaleidoscopic Wizard: How interesting! Perhaps if you told me your age and the number of your children, I could work out their individual ages?
Psychedelic Wizard: No.
Kaleidoscopic Wizard: Aha! AT LAST I know how old you are!
... Did I miss something? Am I tripping? (Admittedly, I did see an elementary penguin singing Hare Krishna a few blocks back.)
How old is the Psychedelic Wizard?

It transpires you can't have only two numbers, since (x-n)*(y+n) does not equal xy.
Similarly you can't have sets of three numbers with any common numbers between them.
Thus the best idea is to look at numbers with lots of factors.
I therefore found 48 which is 1*3*4*4 and 2*2*2*6, each with a product of 48 and total of 12; however that has "twins".
If the ages have to be different then a solution is 96 which is 1 8 12 and 2 3 16, with the bus being #21.
Quote: Gialmere
Starting in Delaware, you must tour the 48 contiguous United States, visiting each state exactly once.
Where will you finish?
link to original post
In order, DE (DC) MD VA NC SC GA FL AL TN MS AR LA TX OK KS NE CO NM AZ UT NV CA OR WA ID MT WY SD ND MN WI IA MO IL KY IN MI OH WV PA NJ NY CT RI MA VT NH ME
This tour misses the UP of Michigan entirely, unless you want to backtrack across the bridge.
I'm curious if someone can land both a UP and LP visit without backtracking.
I don't think the ferries help, as that puts you in Wisconsin twice.
Quote: GialmereIt's easy Monday. Here's another pair of puzzles...
Find positive integers a, b, and c, all different, such that a^3 + b^3 = c^4.
link to original post
Let p, q, r, and x be positive integers such that (ax)^3 + (bx)^3 = (cx)^4
p^3 x^3 + q^3 x^3 = (r^4 x) x^3
x = (p^3 + q^3) / r^4
This provides an infinite number of solutions when r = 1:
p^3 (p^3 + q^3)^3 + q^3 (p^3 + q^3)^3 = (p^3 + q^3) (p^3 + q^3)^3 = (p^3 + q^3)^4
I am attempting a brute force search to see if there are any solutions where a, b, c are relatively prime - for that matter, where just a and b are relatively prime - but have not found any yet.
Quote: DieterQuote: Gialmere
Starting in Delaware, you must tour the 48 contiguous United States, visiting each state exactly once.
Where will you finish?
link to original post
In order, DE (DC) MD VA NC SC GA FL AL TN MS AR LA TX OK KS NE CO NM AZ UT NV CA OR WA ID MT WY SD ND MN WI IA MO IL KY IN MI OH WV PA NJ NY CT RI MA VT NH ME
This tour misses the UP of Michigan entirely, unless you want to backtrack across the bridge.
I'm curious if someone can land both a UP and LP visit without backtracking.
I don't think the ferries help, as that puts you in Wisconsin twice.
link to original post
Quote: charliepatrickWe know there need to be two solutions where you have two sets of numbers which both have the same size (number of elements in the set). They also need to have the same product and same total. (The reason for the latter is you could have a two sets of numbers whose products are the same, but if the totals were different you would know which one corresponded to the bus number.)
It transpires you can't have only two numbers, since (x-n)*(y+n) does not equal xy.
Similarly you can't have sets of three numbers with any common numbers between them.
Thus the best idea is to look at numbers with lots of factors.
I therefore found 48 which is 1*3*4*4 and 2*2*2*6, each with a product of 48 and total of 12; however that has "twins".
If the ages have to be different then a solution is 96 which is 1 8 12 and 2 3 16, with the bus being #21.
link to original post
Correct!!!
We can start by auditioning various bus numbers. For example, the number of the bus cannot have been 5, because in each possible case the wizardís age and the number of his children would then uniquely determine their ages ó if the wizard is 3 years old and has 3 children, then their ages must be 1, 1, and 3 and he cannot have said ďNo.Ē So the bus number cannot be 5.
As we work our way into higher bus numbers this uniqueness disappears, but itís replaced by another problem ó the second wizard must be able to deduce the first wizardís age despite the ambiguity. For example, if the bus number is 21 and the first wizard tells us that heís 96 years old and has three children, then itís true that we canít work out the childrenís ages: They might be 1, 8, and 12 or 2, 3, and 16. But when the wizard informs us of this, we canít declare triumphantly that at last we know how old he is, because we donít ó he might be 96, but he might also be 240, with children aged 4, 5, and 12 or 3, 8, and 10. So the dialogue above cannot have taken place.
But notice that if we increase the bus number by 1, to 22, then all the math above will still work if we give the wizard an extra 1-year-old child: He might now be 96 years old with four children ages 1, 1, 8, and 12 or 1, 2, 3, and 16; or he might be 240 with four children ages 1, 4, 5, and 12 or 1, 3, 8, and 10. The number of children increases by 1, the sum of their ages increases by 1, and the product remains the same. So if bus number b produces two possible ages for Wizard A, then so will bus number b + 1 ó which means that we donít have to check any bus numbers larger than 21.
This limits the problem to a manageable size, and it turns out that the bus number is 12 and Wizard A is 48 ó thatís the only age for which the bus number and the number of children do not uniquely determine the childrenís ages (they might be 2, 2, 2, and 6 or 1, 3, 4, and 4).
(Tanya Khovanova, ďConwayís Wizards,Ē The Mathematical Intelligencer, December 2013.)

---------------------------------------------------------------
Quote: DieterQuote: Gialmere
Starting in Delaware, you must tour the 48 contiguous United States, visiting each state exactly once.
Where will you finish?
link to original post
In order, DE (DC) MD VA NC SC GA FL AL TN MS AR LA TX OK KS NE CO NM AZ UT NV CA OR WA ID MT WY SD ND MN WI IA MO IL KY IN MI OH WV PA NJ NY CT RI MA VT NH ME
This tour misses the UP of Michigan entirely, unless you want to backtrack across the bridge.
I'm curious if someone can land both a UP and LP visit without backtracking.
I don't think the ferries help, as that puts you in Wisconsin twice.
link to original post
Heh. I was going to call the floor moderator over and complain about past posting but, since you are the floor moderator, I'll just quietly place my chips down where you do (except D.C.)
Quote: GialmereQuote: DieterQuote: Gialmere
Starting in Delaware, you must tour the 48 contiguous United States, visiting each state exactly once.
Where will you finish?
link to original post
In order, DE (DC) MD VA NC SC GA FL AL TN MS AR LA TX OK KS NE CO NM AZ UT NV CA OR WA ID MT WY SD ND MN WI IA MO IL KY IN MI OH WV PA NJ NY CT RI MA VT NH ME
This tour misses the UP of Michigan entirely, unless you want to backtrack across the bridge.
I'm curious if someone can land both a UP and LP visit without backtracking.
I don't think the ferries help, as that puts you in Wisconsin twice.
link to original post
Heh. I was going to call the floor moderator over and complain about past posting but, since you are the floor moderator, I'll just quietly place my chips down where you do (except D.C.)
link to original post
No past postings will be honored for prize awards.
No faults there; my schedule just didn't line me up with a slip of paper and an atlas until after that buzzer went off.
The satisfaction comes from working the puzzle, not from beating everyone else to the answer.
Complete this series:
10, 11, 12, 13, 14, 15, 16, 17, 21, 23, 30, 33, Ö
Quote: Gialmere
Complete this series:
10, 11, 12, 13, 14, 15, 16, 17, 21, 23, 30, 33, Ö
link to original post
The remainder of the series is 120, 1111, 111111111111111
Quote: GialmereComplete this series:
10, 11, 12, 13, 14, 15, 16, 17, 21, 23, 30, 33, Ö
link to original post
120, and 1111
The original list is 15 in base 15, 14, 13, ..., 4; 120 in base 3 and 1111 in base 2 = 15
If you want to get pedantic, it's not technically complete; although bases 1, 0, and -1 are undefined, 15 in base -2 = 10011, since (-2)^4 + (-2)^1 + (-2)^0 = 16 - 2 + 1 = 15.
Quote: charliepatrickItís the same number with different bases. Since 30 is divisible by 3 the number must be. One of these is decimal, since 18 isnít there, it must be 15. This gives 120 and 1111 as the last two and F as a giveaway first!
link to original post
Quote: gordonm888The sequence is 15 in base 15-n
The remainder of the series is 120, 1111, 111111111111111
link to original post
Quote: ThatDonGuy
120, and 1111
The original list is 15 in base 15, 14, 13, ..., 4; 120 in base 3 and 1111 in base 2 = 15
If you want to get pedantic, it's not technically complete; although bases 1, 0, and -1 are undefined, 15 in base -2 = 10011, since (-2)^4 + (-2)^1 + (-2)^0 = 16 - 2 + 1 = 15.
link to original post
Correct!!
Well done.
-------------------------------------------

Revised wording: How many distinct combinations of five cards can be made from a five-deck shoe of cards?
Quote: WizardHow many unique five-card stud hands are there in a five-deck shoe?
link to original post
I think the wording is unclear.
Is this: how many distinct 5 card stud hands can be created from 5 decks of cards?
Or:
Is this: given five decks of cards are shuffled and arranged in a shoe, how many unique 5 card stud hands exist as five consecutive cards in the stack?
Quote: gordonm888how many distinct 5 card stud hands can be created from 5 decks of cards?
link to original post
That wording is good.
Revised reply: Please do not think about poker. Rather refer to this revised wording, "How many distinct combinations of five cards can be made from a five-deck shoe of cards?"
5 singletons (includes straights, straight flushes and unpaired flushes)
c(13,5) *45 =1,317,888
1 pair + 3 singletons (includes flushes with 1 pair)
c(13,4)* 45 =732,160
2 pair + 1 singleton (includes flushes with 2 pair)
c(13,3)* 45 = 292,864
3oak +2 singletons (includes flushes with 3oak)
c(13,3)* 45 = 292,864
3oak + 2oak (includes flushes with full houses)
c(13,2)* 45 = 79,872
4oak + 1 singleton (includes flushes with quads)
c(13,2)* 45 = 79,872
5oak (includes flushes with 5oak)
c(13,1)* 45 = 13,312
Summing up the above numbers gives: 2,808,832
I am open to wording suggestions if I ask this one elsewhere.
Quote: WizardMy wording is evidently still unclear. Forget about poker rules. How many distinct sets of five cards can be made? For example, Ah-Ad-As-Ac-Kh is a distinct set from Ah-Ad-As-Ac-Kd.
I am open to wording suggestions if I ask this one elsewhere.
link to original post
5 singletons (includes straights, straight flushes and unpaired flushes)
c(13,5) *45 =1,317,888
1 pair + 3 singletons (includes flushes with 1 pair)
c(13,4)* 43*10 =457,600
2 pair + 1 singleton (includes flushes with 2 pair)
c(13,3)* 41*10*10 = 114,400
3oak +2 singletons (includes flushes with 3oak)
c(13,3)* 42*20 = 91,520
3oak + 2oak (includes flushes with full houses)
c(13,2)* 20*10= 15,600
4oak + 1 singleton (includes flushes with quads)
c(13,2)* 41*35 = 2730
5oak (includes flushes with 5oak)
c(13,1)* 56 = 728
Summing up the above numbers gives: 2,000,466
The numbers 10, 20, 35 and 56 in the above equations are tetrahedral numbers; given 4 suits they are the number of suit combinations for a pair (10), 3oak (20) 4oak (35) and 5oak (56)
Quote: Ace2
link to original post
I agree!
Quote: gordonm888Summing up the above numbers gives: 2,000,466
[/spoiler]
link to original post
I'll take the blame for the bad wording of the problem. Forget about poker rankings. I'm asking about distinct combinations of hands. For example, if there were only one deck, the answer would be combin(52,5)=2,598,960. With five decks and the possibility of 0 to 5 of any one type of card, the total combinations are clearly more.
Quote: Ace2Quote: WizardMy wording is evidently still unclear. Forget about poker rules. How many distinct sets of five cards can be made? For example, Ah-Ad-As-Ac-Kh is a distinct set from Ah-Ad-As-Ac-Kd.
I am open to wording suggestions if I ask this one elsewhere.
link to original postc(52,5) + 4*c(52,4) + 6*c(52,3) + 4*c(52,2) + 52
link to original post
Based on this calculation, the number is 3,819,816.
Quote: acesideBased on this calculation, the number is 3,819,816.
link to original post
I agree!

The year is 1944 and the Germans are rolling out a new and powerful tank, the Uberpanzer. Prominently displayed on the back of each Uberpanzer is its serial number, which is simply the number of tanks that had been built when it rolled off the line. So the first tank built has the serial number 1, the second one built has a 2, and so on.
Recently, a number of these new tanks were spotted by British scouts who recorded the serial numbers that they saw. They immediately sent this information to British intelligence, hoping that the serial number data could be used to estimate the total number of Uberpanzers the Germans have built.
But then the unexpected happened. A German spy intercepted the dossier with the data before it could reach London. By the time the scouts caught up with the spy, most of the data had been destroyed. However, two pieces of information were recovered from the debris.
1) The lowest serial number recorded was 22.
2) The highest serial number recorded was 114.
Assuming that the original data set was a random sample of serial numbers, what is the best estimate of the total number of Uberpanzers the Germans have built?


