Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: ThatDonGuyHere's my problem of the day:
500 men each toss a Ronald Reagan Presidential Dollar Coin.
Simultaneously, 500 women each toss a Sacagawea Dollar Coin.
What is the probability that the number of Reagan coins that come up heads is exactly one more than the number of Sacagawea coins that come up heads?
link to original post
2 .25
3 .234375
4 .21875
5 .205078
10 .160179
50 .078029
100 .055791
500 .025175
1k .017821
c(1000,499) / 2^1000 =~ 0.025174669
A very good approximation is (500π)^(-.5) =~ 0.025231325. Works well for any n over about 30
This works because: if you look at the binomial distribution for p=0.5 for any n, take the products of all the individual probabilities (groups of 2) and then sum them, it comes out to c(2n, n-1) / 2^(2n). Hope I said that right. I just discovered this by trying some low n's and saw that the product-sums all fit into Pascal's triangle
The approximation works due to application of Sterling's formula and cancellation of terms for the probability that a result exactly matches expectations when p=.05. In this case, 499/100 is close enough to 500/1000. Negligible difference
Quote: Ace2My kinda problem
c(1000,499) / 2^1000 =~ 0.025174669
A very good approximation is (500π)^(-.5) =~ 0.025231325. Works well for any n over about 30
This works because: if you look at the binomial distribution for p=0.5 for any n, take the products of all the individual probabilities (groups of 2) and then sum them, it comes out to c(2n, n-1) / 2^(2n). Hope I said that right. The approximation works due to application of Sterling's formula and cancellation of terms for the probability that a result exactly matches expectations when p=.05. In this case, 499/100 is close enough to 500/1000
link to original post
That's very interesting. However, I didn't understand why that approximation works. I don't dispute it does, of course. Can you elaborate on how pi fits into it?
Stirling's approximation says n! =~ (n/e)^n * (2πn)^.5
c(100,50) = 100! / (50!)^2. Use Stirling for those factorials, divide by the 2^100 and the terms cancel out nicely to (50π)^(-.5) = 0.07978 vs the exact answer 0.07958
The problem at hand is answered exactly with: c(1000,499) / 2^1000.<a> This is almost the same as the probability of getting 500 heads in 1000 flips, which would be c(1000,500) / 2^1000 =~ (500π)^(-.5)
Incidentally, Stirling's approximation is already accurate within 1% for 9!, though you wouldn't need to approximate a figure that low
<a>I think so anyway. Answer hasn't been confirmed yet
Quote: ThatDonGuyHere's my problem of the day:
500 men each toss a Ronald Reagan Presidential Dollar Coin.
Simultaneously, 500 women each toss a Sacagawea Dollar Coin.
What is the probability that the number of Reagan coins that come up heads is exactly one more than the number of Sacagawea coins that come up heads?
link to original post
Let N be the number of Reagan coins that come up heads.
This means there are N-1 Sacagawea coins that come up heads, and 500-(N-1) = 501-N Sacagawea coins that come up tails.
Reagan heads + Sacagawea tails = 501.
Thus, each set of tosses where the Reagan heads = 1 + the Sacagawea heads maps to a selection of 501 of the 1000 persons; each man in the selection tossed a head, and each woman tossed a tail. Since the probabilty of tossing a tail = the probability of tossing a head, each of the 2^1000 possible sets of tosses is equally likely.
The solution is C(1000, 501) / 2^1000, or about 1 / 39.7224689 (0.025174669)
Note that this is also C(1001, 499) / 2^1000
Quote: Ace2Do I get a beer ?
link to original post
Wizard, give Ace2 one of my accumulated beers at the next WoV gathering
Quote: ThatDonGuy
Wizard, give Ace2 one of my accumulated beers at the next WoV gathering
link to original post
I would be proud to.

A local newspaper is made of 16 large sheets of paper folded in half and has 64 pages altogether. The first sheet contains pages 1, 2, 63, 64.
If you pick up a sheet containing page number 45. What are the other pages that the sheet contains?
What's a simple formula to quickly get the answer?

There are three hockey pucks on the ice in a rink. A player shoots one of them between the two others. He continues shooting one between the other two but never shoots the same puck twice in a row.
What's the minimum number of shots it'll take him to return the pucks to their original positions on the ice?
Somebody puts a hose into the tank, supplying it with one gallon of pure water per second. At the same time, water flows out of the tank at the same rate. The pure water is instantly mixed with the seawater.
How long will it take for the concentration of salt in the tank to reach 0.1%?

This fits the equation of d(salt)/dt = -(lambda) (salt). Thus lambda = 1/1000 and the amount of salt left is given by T(t) = T(0) * e(-(lambda) t).
So the half-life is -1000*ln(1/2) = 693.147... and the time from 35 to 1 is -1000*ln(1/35) = 3555.348..., just under an hour.
Quote: rsactuaryAh, a good old first year college calculus question.. that I totally don't remember how to do.
link to original post
I like to ask variants of it once in a while, just to keep my differential equations from getting too rusty.
Quote: charliepatrickI think it's similar to half-life ideas. The salt is removed from the tank in the ratio of x/1000 per second. (Initially there are 35 gallons of salt, and as one gallon is removed from 1000 tank, the rate of extraction is 35/1000 of the total.) As the salt percentage in the tank reduces the rate of extraction reduces.
This fits the equation of d(salt)/dt = -(lambda) (salt). Thus lambda = 1/1000 and the amount of salt left is given by T(t) = T(0) * e(-(lambda) t).
So the half-life is -1000*ln(1/2) = 693.147... and the time from 35 to 1 is -1000*ln(1/35) = 3555.348..., just under an hour.
link to original post
I agree! I'd say that one is beer worthy.
Consider a semicircle, of radius 1, with two stacked rectangles inside. What is the maximum combined area of the two rectangles?
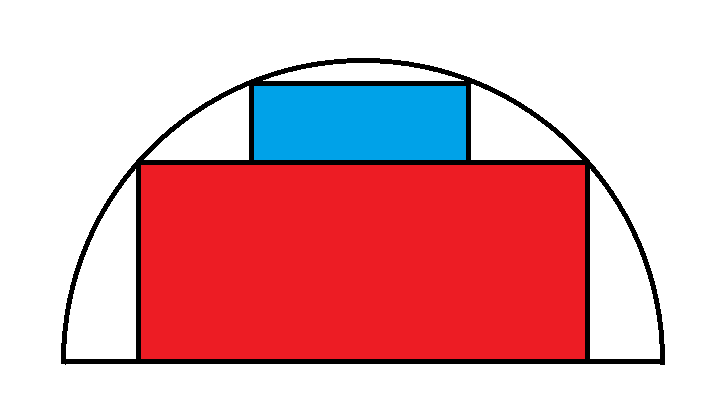
For now, I'll accept a numeric answer to six decimal places.
The first rectangle is SIN(x) * 2*COS(x) (because you have two halves either side of the X axis).
Similar a second rectangle is SIN(90-x) * 2*COS(90-x). The area that overlaps has height SIN (x) and width 2*COS(90-x). So take this away from the other two rectangles.
(Essentially extend the blue rectangle down to the diameter and consider the additional area covering the red rectangle.)
(I originally started with a list of sines for each 0.1 degree from 0 to 90 and was using OFFSET($B$1,10*J1,0). I'm guessing you eventually get something like 31.899999999 and when this get multiplies by 10, it no longer gets to 319 but 318.999999.)
Quote: WizardHere is another beer worthy puzzle.
Consider a semicircle with two stacked rectangles inside. What is the maximum combined area of the two rectangles?
For now, I'll accept a numeric answer to six decimal places.
link to original post
After quite a few attempts to calculate it "directly" which wasn't going to come up with a solution that didn't require at least some approximation, and then three or four attempts on a spreadsheet, I get this:
You didn't specify the radius of the semicircle, so I am assuming it is 1, in which case, the maximum combined area is 1.236068.
This has a red rectangle width of about 1.7 and a blue rectangle width of about 1.05.
Quote: ThatDonGuy
You didn't specify the radius of the semicircle, so I am assuming it is 1, in which case, the maximum combined area is 1.236068.
This has a red rectangle width of about 1.7 and a blue rectangle width of about 1.05.
link to original post
Yes, I forgot to state the radius of the semicircle. is 1. Given that, I agree with your answer.
Now the challenge is to put it in a closed form, which I think will necessitate taking some very ugly derivatives.
Quote: WizardNow the challenge is to put it in a closed form, which I think will necessitate taking some very ugly derivatives.
link to original post
Here's what I have so far:
Let a be the height of the red rectangle, and b the height of the blue rectangle
Area(red) = 2 a sqrt(1 - a^2)
Area(blue) = 2 b sqrt(1 - (a+b)^2)
First, assume a is fixed, and find the value of b that maximizes the total area; since the red area is also fixed, find the value of b that maximizes A(blue)
dA(blue)/db = 2 sqrt(1 - (a+b)^2) + 2 b (-2a - 2b) / 2 sqrt(1 - (a+b)^2)
= 2 sqrt(1 - (a+b)^2) - 2 b (a+b) / sqrt(1 - (a+b)^2)
This is 0 when sqrt(1 - (a+b)^2) = b (a+b) / sqrt(1 - (a+b)^2)
1 - a^2 - 2ab - b^2 = b^2 + ab
2b^2 + 3ab + a^2 - 1 = 0
b = -3/4 a +/- sqrt(9a^2 - 8a^2 + 8)/4
= (-3a +/- sqrt(a^2 + 8)) / 4
The negative sign results in b < 0
b = (sqrt(a^2 + 8) - 3a) / 4
Total area = A(red) + A(blue) = 2a sqrt(1 - a^2) + 2b sqrt(1 - (a+b)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - (a + (sqrt(a^2 + 8) - 3a) / 4)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - ((a + sqrt(a^2 + 8)) / 4)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - (a + sqrt(a^2 + 8))^2 / 16)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(16 - (a + sqrt(a^2 + 8))^2) / 4
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) sqrt(16 - (a + sqrt(a^2 + 8))^2) / 8
Now, just calculate d(Area)/da and find its zeroes...
Quote: ThatDonGuyTotal area = A(red) + A(blue) = 2a sqrt(1 - a^2) + 2b sqrt(1 - (a+b)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - (a + (sqrt(a^2 + 8) - 3a) / 4)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - ((a + sqrt(a^2 + 8)) / 4)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - (a + sqrt(a^2 + 8))^2 / 16)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(16 - (a + sqrt(a^2 + 8))^2) / 4
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) sqrt(16 - (a + sqrt(a^2 + 8))^2) / 8
Now, just calculate d(Area)/da and find its zeroes...
link to original post
Good work. I went part way down this rabbit hole this morning and my expression was much messier.
I put that into a derivative calculator, which gave a derivative as:
-((a^2-1)*sqrt(-2*a*sqrt(a^2+8)-2*a^2+8)+(4-8*a^2)*sqrt(1-a^2))/(2*a^2-2)
When I clicked to find roots, it said "No roots/zeros found! Please note that the calculator is not able to find all types of roots/zeros." I've had this problem before when it couldn't solve an equation this complicated.
Quote: WizardQuote: ThatDonGuyTotal area = A(red) + A(blue) = 2a sqrt(1 - a^2) + 2b sqrt(1 - (a+b)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - (a + (sqrt(a^2 + 8) - 3a) / 4)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - ((a + sqrt(a^2 + 8)) / 4)^2)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(1 - (a + sqrt(a^2 + 8))^2 / 16)
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) / 2 * sqrt(16 - (a + sqrt(a^2 + 8))^2) / 4
= 2a sqrt(1 - a^2) + (sqrt(a^2 + 8) - 3a) sqrt(16 - (a + sqrt(a^2 + 8))^2) / 8
Now, just calculate d(Area)/da and find its zeroes...
link to original post
Good work. I went part way down this rabbit hole this morning and my expression was much messier.
I put that into a derivative calculator, which gave a derivative as:
-((a^2-1)*sqrt(-2*a*sqrt(a^2+8)-2*a^2+8)+(4-8*a^2)*sqrt(1-a^2))/(2*a^2-2)
When I clicked to find roots, it said "No roots/zeros found! Please note that the calculator is not able to find all types of roots/zeros." I've had this problem before when it couldn't solve an equation this complicated.
link to original post
Wolfram Alpha can handle this one -
Zeroes of derivative
Plug back in to get solution (nice form is under Alternate forms)
The area of the lower rectangle is 2 SIN(t) COS(t) = SIN(2t). Similarly the area of the top rectangle is the same. The overlap is 2*SIN(t)*SIN(t).
The derivitave of 2*lower-overlap is 4*COS(2t)-4*SIN(t)COS(t).
https://www.wolframalpha.com/input?i=2SIN%282t%29-2SIN%28t%29*SIN%28t%29 suggests a root is tan-1(2)/2, (spreadsheet confirms TAN(2t)=2).
This leads to the 2SIN(2t) = 4/SQRT(5). Now if someone can work out that taking away 2*SIN(t)*SIN(t) results in SQRT(5)-1, then you have the solution!!!
Quote: charliepatrickI think all you have to do is work out the value of t=theta where COS(2t)=SIN(t)COS(t), and then work out 2SIN(2t)-2SIN2(t).
The area of the lower rectangle is 2 SIN(t) COS(t) = SIN(2t). Similarly the area of the top rectangle is the same. The overlap is 2*SIN(t)*SIN(t).
The derivitave of 2*lower-overlap is 4*COS(2t)-4*SIN(t)COS(t).
https://www.wolframalpha.com/input?i=2SIN%282t%29-2SIN%28t%29*SIN%28t%29 suggests a root is tan-1(2)/2, (spreadsheet confirms TAN(2t)=2).
This leads to the 2SIN(2t) = 4/SQRT(5). Now if someone can work out that taking away 2*SIN(t)*SIN(t) results in SQRT(5)-1, then you have the solution!!!
link to original post
I can get this:
Given: 2 sin 2t = 4 / sqrt(5)
2 sin 2t = 4 sqrt(5) / 5
Substitute sin 2t = 2 sin t cos t:
4 sin t cos t = 4 sqrt(5) / 5
Square both sides:
16 sin^2 t cos^2 t = 16/5
16 sin^2 t (1 - sin^2 t) = 16/5
sin^2 t (1 - sin^2 t) = 1/5
(sin^2 t)^2 - sin^2 t + 1/5 = 0
(sin^2 t)^2 - (sin^2 t) + 1/4 = 1/4 - 1/5 = 1/20
(sin^2 t - 1/2)^2 = 1/20
sin^2 t = 1/2 +/- sqrt(1/20) = 1/2 +/- sqrt(5)/10
2 sin^2 t = 1 +/- sqrt(5)/5
Using the minus, you have 4/5 sqrt(5) - (1 - sqrt(5)/5) = sqrt(5) - 1.
Using the plus, you have 4/5 sqrt(5) - (1 + sqrt(5)/5) = 3/5 sqrt(5) - 1
Quote: djtehch34tWolfram Alpha can handle this one
link to original post
That is amazing the solution works out to something as simple as sqrt(5)-1!
Quote: charliepatrickI think all you have to do is work out the value of t=theta where COS(2t)=SIN(t)COS(t), and then work out 2SIN(2t)-2SIN2(t).
The area of the lower rectangle is 2 SIN(t) COS(t) = SIN(2t). Similarly the area of the top rectangle is the same. The overlap is 2*SIN(t)*SIN(t).
The derivitave of 2*lower-overlap is 4*COS(2t)-4*SIN(t)COS(t).
https://www.wolframalpha.com/input?i=2SIN%282t%29-2SIN%28t%29*SIN%28t%29 suggests a root is tan-1(2)/2, (spreadsheet confirms TAN(2t)=2).
This leads to the 2SIN(2t) = 4/SQRT(5). Now if someone can work out that taking away 2*SIN(t)*SIN(t) results in SQRT(5)-1, then you have the solution!!!
link to original post
Outstanding post!
You guys probably already know thisÖQuote: Wizard
Where φ is the golden ratio of 1.618, the long side (A) of the large rectangle is: 2*(φ^-2 + 1)^-0.5 = 1.7013. The short side (B) is: A / (2φ) = 0.52573.
The long side of the small rectangle is: A / φ = 1.0515. The short side is: B / φ = 0.32492
- Voters rank their choices from first to last.
- If any candidate gets over 50% of the first place vote, they win.
- Otherwise, the candidate with the least votes is eliminated. The second choice votes on those ballots are assigned to those candidates as first place votes.
- There is a second round of ballot counting, based on the reallocated votes from the first round. If any candidate gets over 50% of the first place vote, they win.
- Otherwise, the candidate with the least votes in the second round is eliminated. The second place votes on those ballots are assigned to those candidates as first place votes. However, if any of these second choice votes were to the candidate who lost in the first round, then the third choice votes are assigned to those candidates as first place votes.
- There is a third round of ballot counting, based on the reallocated votes from the second round. If any candidate gets over 50% of the first place vote, they win.
- Otherwise, the candidate with the least votes in the third round is eliminated. The second place votes on those ballots are assigned to those candidates as first place votes. However, if any of these second choice votes were to the candidate who lost in the first or second rounds, then the third choice votes are assigned to those candidates as first place votes. If the second and third choices were the two candidates who got eliminated in the first and second rounds, then the fourth choice votes are assigned to those candidates as first place votes.
- This process keeps repeating until a winner is found.
Here was the voting in Alaska for congress.
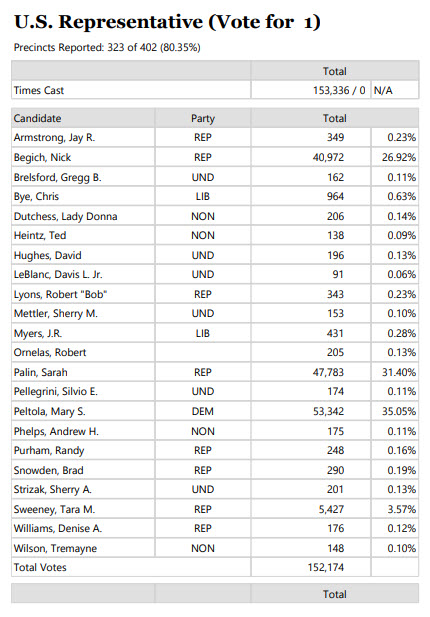
Source: https://www.elections.alaska.gov/results/22PRIM/ElectionSummaryReportRPT.pdf (see page 2).
You can see there were 22 total candidates and 152,174 votes cast. However, not every precinct has reported at the time of this writing, so let's say the total votes are 200,000.
Assuming the same 22 candidates and 200,000 votes, what is the fewest first-choice votes a candidate can get and still win?
Let's ignore ties for the winner, to keep things simple. Let's assume if there is a tie for loser, then all the next choice votes among the candidates in a tie for last get redistributed at the same time.
Quote: Wizard...Assuming the same 22 candidates and 200,000 votes, what is the fewest first-choice votes a candidate can get and still win?...
This is single tranferable vote under another name. Let's assume the winner has everyone's second vote. Working backwards the winner needs to land up with 100001 votes to 99999. Thus candidate #2 had 99999 votes.
Prior to that round the winner needed 50001 and candidate #3 had 50000 votes.
The previous round winner needed 25001 and candidate #4 had 25000 votes.
Continuing this process (nearly halving each round) enables the winner to have started with 2 votes. Roughly the winner votes goes 2x-1 on each round, picking up all the votes of the lowest candidate. For simplicity assume some cadndidates had no votes (otherwise have them having 1 each taken from #2.)
The starting values for each candidate could have been something like 99999, 50000, 25000, 12500, 6250, 3125, 1562, 781, 391, 195, 98, 49, 24, 12, 6, 3, 2, 1, with the winner starting with 2. So the winner wins each round 2-1, 3-2, 5-3, 8-6 etc.
There is a sidebet that is based on the Blackjack total of three cards (probably from one standard deck given the base game!) using the Blackjack rule that all Aces count as 1, except the first Ace counts as 11 if the total would have 11 or less. Using this rule which total is most common. (Hint: this landed up being the sidebet!)
Quote: charliepatrickSimple problem based on an interesting side bet I stumbled across while looking for something. I've assumed infinite decks but suspect the answer's the same for finite ones.
There is a sidebet that is based on the Blackjack total of three cards (probably from one standard deck given the base game!) using the Blackjack rule that all Aces count as 1, except the first Ace counts as 11 if the total would have 11 or less. Using this rule which total is most common. (Hint: this landed up being the sidebet!)
link to original post
Quote: charliepatrickJust two votes!
This is single tranferable vote under another name. Let's assume the winner has everyone's second vote. Working backwards the winner needs to land up with 100001 votes to 99999. Thus candidate #2 had 99999 votes.
Prior to that round the winner needed 50001 and candidate #3 had 50000 votes.
The previous round winner needed 25001 and candidate #4 had 25000 votes.
Continuing this process (nearly halving each round) enables the winner to have started with 2 votes. Roughly the winner votes goes 2x-1 on each round, picking up all the votes of the lowest candidate. For simplicity assume some cadndidates had no votes (otherwise have them having 1 each taken from #2.)
The starting values for each candidate could have been something like 99999, 50000, 25000, 12500, 6250, 3125, 1562, 781, 391, 195, 98, 49, 24, 12, 6, 3, 2, 1, with the winner starting with 2. So the winner wins each round 2-1, 3-2, 5-3, 8-6 etc.
link to original post
I agree!
Quote: charliepatrickSimple problem based on an interesting side bet I stumbled across while looking for something. I've assumed infinite decks but suspect the answer's the same for finite ones.
There is a sidebet that is based on the Blackjack total of three cards (probably from one standard deck given the base game!) using the Blackjack rule that all Aces count as 1, except the first Ace counts as 11 if the total would have 11 or less. Using this rule which total is most common. (Hint: this landed up being the sidebet!)
link to original post
Doing a brute force number-crunching search, I get 21 for any number of decks in the shoe from 1 to 100, with 20 being the second most likely result each time.
Note that the result is 22, with 23 the second most likely, if the first Ace counts as 11 even if the total would be more than 11 if all of the Aces counted as 1.
Good thing I donít gamble for a livingÖ
Agree - I just thought it was an interesting feature and clever sidebet.Quote: ThatDonGuy...
Doing a brute force number-crunching search, I get 21 for any number of decks in the shoe from 1 to 100, with 20 being the second most likely result each time.
Note that the result is 22, with 23 the second most likely, if the first Ace counts as 11 even if the total would be more than 11 if all of the Aces counted as 1.
You decide to create your own cylinder-shaped duffel bag, with the intent to maximize the volume, subject to the size restriction above. You assume the airline will count the diameter of duffel bag as both the height and width.
How many cubic inches will your bag hold?

Quote: WizardYour airline restricts the size of luggage to a combined height+width+length = 62 inches.
You decide to create your own cylinder-shaped duffel bag, with the intent to maximize the volume, subject to the size restriction above. You assume the airline will count the diameter of duffel bag as both the height and width.
How many cubic inches will your bag hold?
link to original post
Formula for area of a cylinder = pi*(D/2)^2*L
L = 62 - 2D
Take the derivative to find the max.
d/dD pi*(D/2)^2 * (62 - 2D) = 1/2 pi *(62-3D)*D= 0
D = 62/3
Area equals = 62/3 * pi * (62/6)^2 = 6,932.675
What if you made it a square instead?
62/3 ^ 3 = 8,826.963 for an extra 27.324% more volume!
Quote: unJonIím assuming the diameter gets counted twice, once for height and once for width. Which makes a cylinder or sphere shape less than optimal.
Formula for area of a cylinder = pi*(D/2)^2*L
L = 62 - 2D
Take the derivative to find the max.
d/dD pi*(D/2)^2 * (62 - 2D) = 1/2 pi *(62-3D)*D= 0
D = 62/3
Area equals = 62/3 * pi * (62/6)^2 = 6,932.675
What if you made it a square instead?
62/3 ^ 3 = 8,826.963 for an extra 27.324% more volume!
link to original post
I agree!
There are 50 rolls of 50 pennies. Labeled Roll 1 to Roll 50. Assume all 50 wrappers have the exact same weight (the lettering on the roll doesnít affect the weight). 49 of the rolls contain real pennies, each with the exact same weight. Letís say 0.000012 grams per penny. 1 roll contains 50 fake pennies. The 50 fake pennies differ in weight from the real pennies by an imperceptible amount. Letís say 0.000011 grams per penny. Thereís no way you could tell by look or holding in your hand which was the fake roll of pennies. You have a scale. It is precise enough that it can accurately measure weights down to a billionth of a billionth of a gram. You canít place objects on the scale sequentially. That is, you must state exactly which objects are going on the scale in advance and then those items will be placed on the scale at the same time. The scale will give a precise number each time, but the scale canít distinguish location on the scale (that is, it canít say objects on the left side are heavier than objects on the right). This isnít a balance. Itís more like a super precise bathroom scale. Basically you tell the judge what goes on the scale and youíll get a number back. You can use the scale as many times as you want but you strive for efficiency.
(A) whatís the minimum number of times youíd need to use the scale to guarantee youíve identified the fake roll of pennies?
(B) Explain.
Quote: unJonQuote: WizardYour airline restricts the size of luggage to a combined height+width+length = 62 inches.
You decide to create your own cylinder-shaped duffel bag, with the intent to maximize the volume, subject to the size restriction above. You assume the airline will count the diameter of duffel bag as both the height and width.
How many cubic inches will your bag hold?
link to original postIím assuming the diameter gets counted twice, once for height and once for width. Which makes a cylinder or sphere shape less than optimal.
Formula for area of a cylinder = pi*(D/2)^2*L
L = 62 - 2D
Take the derivative to find the max.
d/dD pi*(D/2)^2 * (62 - 2D) = 1/2 pi *(62-3D)*D= 0
D = 62/3
Area equals = 62/3 * pi * (62/6)^2 = 6,932.675
What if you made it a square instead?
62/3 ^ 3 = 8,826.963 for an extra 27.324% more volume!
link to original post
Quote: TinManThis is my all time favorite puzzle. I saw it on YouTube. I didnít create it.
There are 50 rolls of 50 pennies. Labeled Roll 1 to Roll 50. Assume all 50 wrappers have the exact same weight (the lettering on the roll doesnít affect the weight). 49 of the rolls contain real pennies, each with the exact same weight. Letís say 0.000012 grams per penny. 1 roll contains 50 fake pennies. The 50 fake pennies differ in weight from the real pennies by an imperceptible amount. Letís say 0.000011 grams per penny. Thereís no way you could tell by look or holding in your hand which was the fake roll of pennies. You have a scale. It is precise enough that it can accurately measure weights down to a billionth of a billionth of a gram. You canít place objects on the scale sequentially. That is, you must state exactly which objects are going on the scale in advance and then those items will be placed on the scale at the same time. The scale will give a precise number each time, but the scale canít distinguish location on the scale (that is, it canít say objects on the left side are heavier than objects on the right). This isnít a balance. Itís more like a super precise bathroom scale. Basically you tell the judge what goes on the scale and youíll get a number back. You can use the scale as many times as you want but you strive for efficiency.
(A) whatís the minimum number of times youíd need to use the scale to guarantee youíve identified the fake roll of pennies?
(B) Explain.
link to original post
Once
Number the rolls from 1 to 50.
Weigh, at the same time, 1 penny from roll 1, 2 from roll 2, ... 50 from roll 50.
The total number of pennies weighed is 1+2+3+...+50 = 50*51/2 = 1,275.
If they were all real, the total weight would be 1275*0.000012 = 0.0153 grams.
Let w = actual weight
Roll with the fake pennies = (0.0153 - w)/0.000001
Quote: WizardQuote: TinManThis is my all time favorite puzzle. I saw it on YouTube. I didnít create it.
There are 50 rolls of 50 pennies. Labeled Roll 1 to Roll 50. Assume all 50 wrappers have the exact same weight (the lettering on the roll doesnít affect the weight). 49 of the rolls contain real pennies, each with the exact same weight. Letís say 0.000012 grams per penny. 1 roll contains 50 fake pennies. The 50 fake pennies differ in weight from the real pennies by an imperceptible amount. Letís say 0.000011 grams per penny. Thereís no way you could tell by look or holding in your hand which was the fake roll of pennies. You have a scale. It is precise enough that it can accurately measure weights down to a billionth of a billionth of a gram. You canít place objects on the scale sequentially. That is, you must state exactly which objects are going on the scale in advance and then those items will be placed on the scale at the same time. The scale will give a precise number each time, but the scale canít distinguish location on the scale (that is, it canít say objects on the left side are heavier than objects on the right). This isnít a balance. Itís more like a super precise bathroom scale. Basically you tell the judge what goes on the scale and youíll get a number back. You can use the scale as many times as you want but you strive for efficiency.
(A) whatís the minimum number of times youíd need to use the scale to guarantee youíve identified the fake roll of pennies?
(B) Explain.
link to original post
Once
Number the rolls from 1 to 50.
Weigh, at the same time, 1 penny from roll 1, 2 from roll 2, ... 50 from roll 50.
The total number of pennies weighed is 1+2+3+...+50 = 50*51/2 = 1,275.
If they were all real, the total weight would be 1275*0.000012 = 0.0153 grams.
Let w = actual weight
Roll with the fake pennies = (0.0153 - w)/0.000001
link to original post
That is correct! The answer to this question blew my mind. When I heard this riddle I thought of broadly similar puzzles that involved racing horses and dropping eggs from various heights. The goal of those puzzles also involved trying to find a minimum number of trials. Both of those had clever solutions but the answers were not nearly as elegant to me.
Yes it's a good puzzle; there was a variant of it on one of the Columbo episodes.Quote: TinManThis is my all time favorite puzzle...There are 50 rolls of 50 pennies...
The 62" cyclinder. You don't have to use trig to get the size, but you do to get the volume.
Quote: TinManThat is correct! The answer to this question blew my mind. When I heard this riddle I thought of broadly similar puzzles that involved racing horses and dropping eggs from various heights. The goal of those puzzles also involved trying to find a minimum number of trials. Both of those had clever solutions but the answers were not nearly as elegant to me.
link to original post
You might like this one, which I think I asked a long time ago.
You have 25 racehorses. Each runs at a unique and consistent speed. You also have a track that can accommodate five horses at a time. From a race, you learn only the order the horses finish, but nothing about the exact time to finish. It is your task to determine the fastest three horses, in order. You are allowed to use the track for seven races only. How do you do it?
Quote: WizardYou might like this one, which I think I asked a long time ago.
You have 25 racehorses. Each runs at a unique and consistent speed. You also have a track that can accommodate five horses at a time. From a race, you learn only the order the horses finish, but nothing about the exact time to finish. It is your task to determine the fastest three horses, in order. You are allowed to use the track for seven races only. How do you do it?
link to original post
I donít believe Iím citing the solution from memory, as it took me some time to sort it outÖ
Quote: Wizard
Who is she, and where shall I inquire as to hire her to carry my bags?


