Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: Gialmere
How did he do it?
link to original post
If the answer is more complicated than the statement of the problem, then it will make beggars of us all.
Quote: Gialmere...How did he do it?...
The top 12 are dealt face down, leaving 40 cards. Thus at this stage the 5h is the 40th card. After the spectator picks the four cards, the magician puts the eight cards underneath, so the 5h is still the 40th card (but now hidden from view).
For the first part he deals out 10-N cards for each card picked by the spectator (e.g. 3 deals 7 at this stage, 10 deals 0). The total number of cards will be 40-(n1+n2+n3+n4).
For the second part, by adding up the total, the spectator effectively deals out N=n1+n2+n3+n4 cards for each card picked (e.g. 3 deals 3, 10 deals 10), and the spectator turns over the last card. This will always be the 40th card - i.e. 5h.
Quote: charliepatrickHe writes down the card that is on the bottom of the deck after the spectator has shuffled the cards.
The top 12 are dealt face down, leaving 40 cards. Thus at this stage the 5h is the 40th card. After the spectator picks the four cards, the magician puts the eight cards underneath, so the 5h is still the 40th card (but now hidden from view).
For the first part he deals out 10-N cards for each card picked by the spectator (e.g. 3 deals 7 at this stage, 10 deals 0). The total number of cards will be 40-(n1+n2+n3+n4).
For the second part, by adding up the total, the spectator effectively deals out N=n1+n2+n3+n4 cards for each card picked (e.g. 3 deals 3, 10 deals 10), and the spectator turns over the last card. This will always be the 40th card - i.e. 5h.
link to original post
Correct!!
Abra Cadabra
It is interesting to note that in this trick, as well as in others based on the same principle, you may permit the spectator to assign any value, from 1 to 10, to the jacks, kings, and queens. For example, he may decide to call each jack a 3, each queen a 7, and each king a 4. This has no effect whatever on the working of the trick, but it serves to make it more mysterious. Actually, the trick requires only that the deck consist of 52 cards - it matters not in the least what these cards are. If they were all deuces the trick would work just as well. This means that a spectator can arbitrarily assign a new value to any card he wishes without affecting the success of the trick!
Further mystification may be added by stealing two cards from the pack before showing the trick. In this case ten cards are dealt on the table instead of twelve. After the trick is over, the two cards are secretly returned to the pack. Now if a spectator tries to repeat the trick exactly as he saw it, it will not work.
---------------------------------------------------------------

------------------------------------------------------------------
I think this one is still in play...
Quote: Ace2Letís say there is an electronic version of craps. The pass/DP rules are the same as standard craps but there is one difference in probabilities: all six point numbers are equally weighted at 4/36 for every roll instead of 3/36, 4/36 and 5/36
Whatís the probability of winning the fire bet (all six points won)?
Hint: no calculus required
link to original post
Quote: Ace2Letís say there is an electronic version of craps. The pass/DP rules are the same as standard craps but there is one difference in probabilities: all six point numbers are equally weighted at 4/36 for every roll instead of 3/36, 4/36 and 5/36
Whatís the probability of winning the fire bet (all six points won)?
Hint: no calculus required
link to original post
If N points have alread been made, the probability of rolling a "new" point and then making it is (6 - N) / 6 x 2/5,
and the probability of missing is 3/5, so the probability of making a new point before missing it is
((6-N)/6) x 2/5 / ((6-N)/6 x 2/5 + 3/5), or (6 - N) / (15 - N).
For N = 0: 2 / 5
N = 1: 5 / 14
N = 2: 4 / 13
N = 3: 1 / 4
N = 4: 2 / 11
N = 5: 1 / 10
The product is 1 / 5005.
Oops - (4/30)/(4/30+18/30) = 2/11. You aren't the first person in this conversation to make easy math errors here...Quote: TorghattenThen we look at 4 points:
2/6*2/5 = 4/30 vs 18/30
(4/30)/(4/30+18/30) = 2/9
Correct. 1 / 5,005 = 1 / combin(15,6)Quote: ThatDonGuyQuote: Ace2Letís say there is an electronic version of craps. The pass/DP rules are the same as standard craps but there is one difference in probabilities: all six point numbers are equally weighted at 4/36 for every roll instead of 3/36, 4/36 and 5/36
Whatís the probability of winning the fire bet (all six points won)?
Hint: no calculus required
link to original post
If N points have alread been made, the probability of rolling a "new" point and then making it is (6 - N) / 6 x 2/5,
and the probability of missing is 3/5, so the probability of making a new point before missing it is
((6-N)/6) x 2/5 / ((6-N)/6 x 2/5 + 3/5), or (6 - N) / (15 - N).
For N = 0: 2 / 5
N = 1: 5 / 14
N = 2: 4 / 13
N = 3: 1 / 4
N = 4: 2 / 11
N = 5: 1 / 10
The product is 1 / 5005.Oops - (4/30)/(4/30+18/30) = 2/11. You aren't the first person in this conversation to make easy math errors here...Quote: TorghattenThen we look at 4 points:
2/6*2/5 = 4/30 vs 18/30
(4/30)/(4/30+18/30) = 2/9
link to original post

Every week you play the lottery and you always play the same number. To play you pick six integers between 1 and 49, inclusive.
The numbers you pick have these properties:
The difference between any two of the six numbers is different from the difference between any other pair.
Due to a childhood trauma, you have a fear of prime numbers, consequently
None of the six numbers is prime.
None of the digits in the six numbers is prime.
None of the differences between any two of the six numbers is prime.
The number 1, of course, is not prime.
What six numbers do you play?
Quote: GialmereIt's easy Monday...What six numbers do you play?
The first thing to notice is if the gaps are X X+2 then (X+2)+4 then you have gaps of 2 4 and 6 used. However if it's 2,6 then 8 enabling 4,10 then 14 at the other end. This gives 4 8 18 as the low numbers and 40 46 and 48 being the high ones.
Quote: Gialmere
Due to a childhood trauma, you have a fear of prime numbers, consequently . . .
link to original post
LOL, extra credit should be assigned to whoever can conjure up a trauma that would provoke a "fear of prime numbers"
Further to previous post I've now found out more about what I had stumbled across - the link below explains "B-2 sequences", which I've never heard of, and also contains the answer to my puzzle.Quote: charliepatrick...Variant puzzle which I noticed as interesting, assuming there are no restrictions, except the difference of any two must be different, and the lowest two numbers are 1 and 2, what are the smallest next numbers in the sequence? I think you can work this one out using logic....
https://mathworld.wolfram.com/B2-Sequence.html
Also I never have heard about "Happy" numbers - https://mathworld.wolfram.com/HappyNumber.html
https://en.wikipedia.org/wiki/List_of_prime_numbers#Happy_primes
Quote: gordonm888Quote: Gialmere
Due to a childhood trauma, you have a fear of prime numbers, consequently . . .
link to original post
LOL, extra credit should be assigned to whoever can conjure up a trauma that would provoke a "fear of prime numbers"
link to original post
Primonumerophobia is real and no laughing matter . . .
Quote: charliepatrickQuote: GialmereIt's easy Monday...What six numbers do you play?
The logic I used was to list the numbers and noticed there was a gap between 18 and 40. So it seemed best to have three small and three large. If one of the gaps was (say) 1, then it seemed one of the others would fall onto a prime, so I looked at evens only.
The first thing to notice is if the gaps are X X+2 then (X+2)+4 then you have gaps of 2 4 and 6 used. However if it's 2,6 then 8 enabling 4,10 then 14 at the other end. This gives 4 8 18 as the low numbers and 40 46 and 48 being the high ones.
Oops. My bad. I didn't notice someone had answered this.
Unfortunately an evil prime number has snuck into your grouping. As a chronic sufferer of Primonumerophobia, you would never pick this particular set of numbers.
Quote: Gialmere..Unfortunately an evil prime number has snuck into your grouping...
Quote: charliepatrickI now see that you can't have all even numbers so tried to have one odd number such that the differences between it and the others happened to have no prime. You also need three numbers at the top, so the only odd differences that aren't prime are 1 and 9. So the numbers at the top must be 40 48 and 49. By elimination the lower numbers are 4 10 and 14.
link to original post
Correct!!
Well done.
The solution is unique.
-------------------------------------------------------

There are six civil service job openings. Thirteen candidates passed the civil service exam with equally high scores. So the administrators gave them all a second test. This one had only five questions, each with a Yes/No answer.
The test results of the candidates had thirteen different answer sequences. The top six had the same number of correct answers and were all hired.
Three of those who were not hired had these answer sequences:
--No, No, Yes, No, No
--Yes, No, No, Yes, Yes
--Yes, Yes, Yes, No, Yes
What was the correct sequence of answers?
0 - 1 way
1 - 5 ways
2 - 10 ways
3 - 10 ways
4 - 5 ways
5 - 1 way
Thus it is impossible for the six winners to have a score of 4 as only 5 ways to get that.
Similarly it is impossible for the winners to have a score of 2 correct and only 6 ways for 0/1 scores
Hence winners had a score of 3 correct
So the examples shown cannot have 3 correct.
(Person A) N N Y N N
(Person B) Y N N Y Y
(Person C) Y Y Y N Y
Consider the answers to the first two questions
If it was "N N" then A has to get rest wrong, so the 5=NNNYY, but this means B gets >2 correct.
If it was "Y N" then B has to get rest wrong, so the 5=YNYNN, but this means C gets >2 correct.
If it was "Y Y" then C has to get rest wrong, so the 5=YYNYN, but this means A gets >2 correct.
Hence the first two have to be "N Y".
Let's look at the last two in a similar manner (now knowing the first two are NY).
It can't be "N N" as A would have >2 correct.
It can't be "N Y" as C would have >2 correct.
If it was "Y Y" then B has to get the rest wrong, so the 5=NYYYY, but this means C gets >2 correct.
So the last two are "Y N".
So the five are "NY?YN".
C is indifferent to the third answer as only has one correct so far.
B is similarly indifferent to the third answer.
A requires the middle answer to be N, otherwise would have >2 correct.
Hence the five are "NYNYN"
Double check
A has answers 1 and 5 correct.
B has answers 3 and 4 correct.
C has answer 2 correct.
Quote: charliepatrickPerms of correct answers are as follows
0 - 1 way
1 - 5 ways
2 - 10 ways
3 - 10 ways
4 - 5 ways
5 - 1 way
Thus it is impossible for the six winners to have a score of 4 as only 5 ways to get that.
Similarly it is impossible for the winners to have a score of 2 correct and only 6 ways for 0/1 scores
Hence winners had a score of 3 correct
So the examples shown cannot have 3 correct.
(Person A) N N Y N N
(Person B) Y N N Y Y
(Person C) Y Y Y N Y
Consider the answers to the first two questions
If it was "N N" then A has to get rest wrong, so the 5=NNNYY, but this means B gets >2 correct.
If it was "Y N" then B has to get rest wrong, so the 5=YNYNN, but this means C gets >2 correct.
If it was "Y Y" then C has to get rest wrong, so the 5=YYNYN, but this means A gets >2 correct.
Hence the first two have to be "N Y".
Let's look at the last two in a similar manner (now knowing the first two are NY).
It can't be "N N" as A would have >2 correct.
It can't be "N Y" as C would have >2 correct.
If it was "Y Y" then B has to get the rest wrong, so the 5=NYYYY, but this means C gets >2 correct.
So the last two are "Y N".
So the five are "NY?YN".
C is indifferent to the third answer as only has one correct so far.
B is similarly indifferent to the third answer.
A requires the middle answer to be N, otherwise would have >2 correct.
Hence the five are "NYNYN"
Double check
A has answers 1 and 5 correct.
B has answers 3 and 4 correct.
C has answer 2 correct.
link to original post
Correct!!
Very good.
-------------------------------------------------------
A recent census came up with some surprising numbers.
For all positive integers N, if you look at all of the families with N children, it turns out that the number of families with 0, 1, 2, ..., N boys is proportional to what it would be if the probability of any particular child being a boy was 1/2 (which, theoretically, it is, at least if you assume that all of the males are XY).
For example, among all of the families with 4 children, 1/16 of them have four boys, 1/4 have three boys and a girl, 3/8 have two boys and two girls, 1/4 have one boy and three girls, and 1/16 have four girls.
For any particular value of N, do more of the boys in N-child familes or more of the girls in those families have any sisters?
Quote: ThatDonGuyFor any particular value of N, do more of the boys in N-child familes or more of the girls in those families have any sisters?
link to original post
Interestingly, I find the probability the same for both genders.
In other words, boys are equally likely to have a sister as girls, regardless of the family size.
For two-child families, 50% of children have a sister.
For three-child families, 75% of children have a sister.
For four-child families, 80% of children have a sister.
Quote: ThatDonGuySince nobody else has published one today, here's a (relatively) easy one for Monday:
A recent census came up with some surprising numbers.
For all positive integers N, if you look at all of the families with N children, it turns out that the number of families with 0, 1, 2, ..., N boys is proportional to what it would be if the probability of any particular child being a boy was 1/2 (which, theoretically, it is, at least if you assume that all of the males are XY).
For example, among all of the families with 4 children, 1/16 of them have four boys, 1/4 have three boys and a girl, 3/8 have two boys and two girls, 1/4 have one boy and three girls, and 1/16 have four girls.
For any particular value of N, do more of the boys in N-child familes or more of the girls in those families have any sisters?
link to original post
Thanks for Mondayís question, although Iím answering on Tuesday!

The cross section of a shed is a 10 foot by 10 foot square. The shed is located in the center of an open, level field.
A goat is tethered to one corner of the shed by a forty foot rope. The goat cannot enter the shed.
What is the area over which the goat can graze?
:strip_icc()/pic6968503.png)
Picture not to scale.
Quote: GialmereIt's toughie Tuesday. Back to goats...
The cross section of a shed is a 10 foot by 10 foot square. The shed is located in the center of an open, level field.
A goat is tethered to one corner of the shed by a forty foot rope. The goat cannot enter the shed.
What is the area over which the goat can graze?
Picture not to scale.
link to original post
I get about 4,847.07 square feet.
This is the result of the following expression:
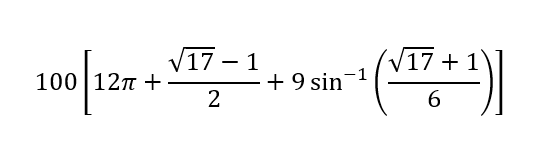
Quote: GialmereWhat is the area over which the goat can graze?
link to original post
I'm getting the answer below, but my confidence is not very high. If I'm right, I'll provide a solution.
Hoping to get a reply to my reply to my reply on the probability of a sister problem.
Quote: camaplQuote: ThatDonGuySince nobody else has published one today, here's a (relatively) easy one for Monday:
A recent census came up with some surprising numbers.
For all positive integers N, if you look at all of the families with N children, it turns out that the number of families with 0, 1, 2, ..., N boys is proportional to what it would be if the probability of any particular child being a boy was 1/2 (which, theoretically, it is, at least if you assume that all of the males are XY).
For example, among all of the families with 4 children, 1/16 of them have four boys, 1/4 have three boys and a girl, 3/8 have two boys and two girls, 1/4 have one boy and three girls, and 1/16 have four girls.
For any particular value of N, do more of the boys in N-child familes or more of the girls in those families have any sisters?
link to original post
Thanks for Mondayís question, although Iím answering on Tuesday!Considering your example, where N = 4, as youíve already done the math, boys have a sister 1/4 + 3/8 + 1/4 = 7/8 or 14/16 of the time, and girls have a sister 3/8 + 1/4 + 1/16 = 11/16 of the time. If you prefer a simpler example, consider N = 2. You only have 2 girls (girl with a sister) 1/2 * 1/2 = 1/4 of the time, while a boy has a sister (1/2 * 1/2) + (1/2 * 1/2) = 1/2 of the time. Answer: more boys than girls have a sister. Consequently, more girls than boys have a brother.
link to original post
You are counting how many families with boys versus how families with girls have sisters. I am looking for the actual numbers of boys and girls with sisters.
For example, your 1/16 value for the girls forgets that this is four girls that have one or more sisters.
Quote: ChesterDog
I get about 4,847.07 square feet.
This is the result of the following expression:
link to original post
I see we're a little off. For now, let me throw out this diagram for purposes of discussion.
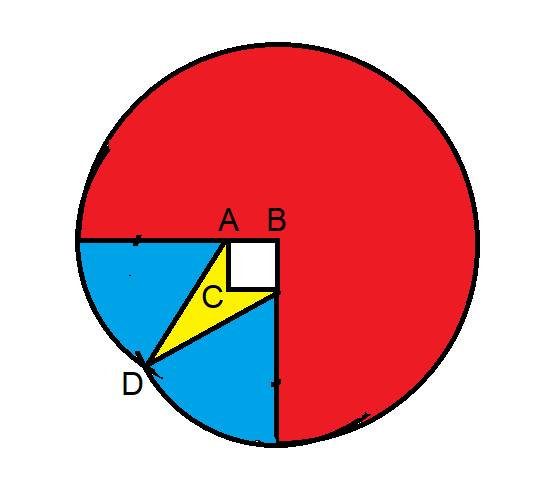
Here is some breakdown of my answer.
| Area | Size | qty | Total |
|---|---|---|---|
| Big quarter slices | 1256.637061 | 3 | 3769.911184 |
| Small slices | 457.5939873 | 2 | 915.187975 |
| Triangle | 103.0776406 | 2 | 206.155281 |
| Total | 4891.254440 |
Quote: WizardQuote: ChesterDog
I get about 4,847.07 square feet.
This is the result of the following expression:
link to original post
I see we're a little off. For now, let me throw out this diagram for purposes of discussion.
Here is some breakdown of my answer.
Area Size qty Total Big quarter slices 1256.637061 3 3769.911184 Small slices 457.5939873 2 915.187975 Triangle 103.0776406 2 206.155281 Total 4891.254440
link to original post
That's a good diagram!
I found the area of the upper yellow triangle by doing half the product of its base and height. I used 10 feet as the base.
To calculate its height, I used point A as the origin and found the intersection of the line y = x - 10 with the circle x2 + y2 = 900.
For the intersection point at point D I got x = -15.615528 and y = -25.615528. I used 15.615528 as the yellow triangle's height. So, I found one yellow triangle's area is (1/2)(10)(15.615528) = 78.077641
Quote: ChesterDog
That's a good diagram!
I found the area of the upper yellow triangle by doing half the product of its base and height. I used 10 feet as the base.
To calculate its height, I used point A as the origin and found the intersection of the line y = x - 10 with the circle x2 + y2 = 900.
For the intersection point at point D I got x = -15.615528 and y = -25.615528. I used 15.615528 as the yellow triangle's height. So, I found one yellow triangle's area is (1/2)(10)(15.615528) = 78.077641
link to original post
Here's what I get:
AC = 10, AD = 30, and angle ACD = 135 degrees
Law of Sines: (sin ADC) / 10 = (sin ACD) / 30, so sin ADC = (sin ACD) / 3 = sqrt(2) / 6; also, cos^2 ACD = 1 - sin^2 ACD = 17/18, so cos ACD = sqrt(34) / 6
Angle CAD = 180 - (ACD + 135) = 45 - ACD, so sin CAD = sin 45 cos ACD - cos 45 sin ACD = (sqrt(2) / 2) (cos ACD - sin ACD)
= (sqrt(2) / 2) (sqrt(34) - sqrt(2)) / 6
= (2 sqrt(17) - 2) / 12 = (sqrt(17) - 1) / 6
Area of CAD = 1/2 AC AD sin CAD = 150 (sqrt(17) - 1) / 6 = 25 (sqrt(17) - 1), which matches ChesterDog's number
Quote: ThatDonGuyQuote: camaplQuote: ThatDonGuySince nobody else has published one today, here's a (relatively) easy one for Monday:
A recent census came up with some surprising numbers.
For all positive integers N, if you look at all of the families with N children, it turns out that the number of families with 0, 1, 2, ..., N boys is proportional to what it would be if the probability of any particular child being a boy was 1/2 (which, theoretically, it is, at least if you assume that all of the males are XY).
For example, among all of the families with 4 children, 1/16 of them have four boys, 1/4 have three boys and a girl, 3/8 have two boys and two girls, 1/4 have one boy and three girls, and 1/16 have four girls.
For any particular value of N, do more of the boys in N-child familes or more of the girls in those families have any sisters?
link to original post
Thanks for Mondayís question, although Iím answering on Tuesday!Considering your example, where N = 4, as youíve already done the math, boys have a sister 1/4 + 3/8 + 1/4 = 7/8 or 14/16 of the time, and girls have a sister 3/8 + 1/4 + 1/16 = 11/16 of the time. If you prefer a simpler example, consider N = 2. You only have 2 girls (girl with a sister) 1/2 * 1/2 = 1/4 of the time, while a boy has a sister (1/2 * 1/2) + (1/2 * 1/2) = 1/2 of the time. Answer: more boys than girls have a sister. Consequently, more girls than boys have a brother.
link to original post
You are counting how many families with boys versus how families with girls have sisters. I am looking for the actual numbers of boys and girls with sisters.
For example, your 1/16 value for the girls forgets that this is four girls that have one or more sisters.
link to original post
For N=2, boys have a sister 1/2 the time (no change), while girls have a sister 2 * 1/2 * 1/2 = 1/2 the time as well.
| Area | Size | qty | Total |
|---|---|---|---|
| Big quarter slices | 1256.637061 | 3 | 3769.911184 |
| Small slices | 460.5026797 | 2 | 921.005359 |
| Triangle | 103.0776406 | 2 | 206.155281 |
| Less quarter square | -25 | 2 | -50.000000 |
| Total | 4847.071825 |
I also computed angle ADC incorrectly. It is atan(sqrt(2)/sqrt(34)).
The area is symmetrical with respect to line BC (i.e. the line that goes through B and C), so only half of it needs to be calculated, and that value doubled.
Half of the area can be divided into three sections:
1 - the red area, which is 3/8 of a circle of radius 40; this is area 3/8 x PI x 40^2 = 600 PI (it is 3/8 because 1/4 of the circle centered at A is taken up by the white square, and half of the remainder is 3/8)
2 - the yellow triangle, which, as I have already shown, is 25 (sqrt(17) - 1)
3 - the blue area; note it is a portion of a circle of radius 30, so the area is 900 PI x the measure (in radians) of the angle at A divided by 2 PI = 450 x the measure of the angle at A.
Let t be the measure of angle CAD; the measure of the angle at A is (PI/2 - t) radians.
In the solution to the yellow triangle area, sin t = (sqrt(17) - 1) / 6; sin (PI/2 - t) = cos t = sqrt(1 - sin^2 t) = sqrt(1 - (sqrt(17) - 1)^2 / 36) = sqrt(1 - (18 - 2 sqrt(17)) / 36) = sqrt(18 + 2 sqrt(17)) / 6 = (sqrt(17) + 1) / 6, so the area = 450 sin^(-1) ((sqrt(17) + 1) / 6)
The area of the entire field covered by the goat = 2 (600 PI + 25 (sqrt(17) - 1) + 900 sin^(-1) ((sqrt(17) + 1) / 6)
= 1200 PI + 50 (sqrt(17) - 1) + 900 sin^(-1) ((sqrt(17) + 1) / 6)
= 100 (12 PI + (sqrt(17) - 1) / 2 + 9 sin^(-1) ((sqrt(17) + 1) / 6))

Quote: ChesterDog
I get about 4,847.07 square feet.
This is the result of the following expression:
link to original post
Quote: ThatDonGuyHere's what I get:
AC = 10, AD = 30, and angle ACD = 135 degrees
Law of Sines: (sin ADC) / 10 = (sin ACD) / 30, so sin ADC = (sin ACD) / 3 = sqrt(2) / 6; also, cos^2 ACD = 1 - sin^2 ACD = 17/18, so cos ACD = sqrt(34) / 6
Angle CAD = 180 - (ACD + 135) = 45 - ACD, so sin CAD = sin 45 cos ACD - cos 45 sin ACD = (sqrt(2) / 2) (cos ACD - sin ACD)
= (sqrt(2) / 2) (sqrt(34) - sqrt(2)) / 6
= (2 sqrt(17) - 2) / 12 = (sqrt(17) - 1) / 6
Area of CAD = 1/2 AC AD sin CAD = 150 (sqrt(17) - 1) / 6 = 25 (sqrt(17) - 1), which matches ChesterDog's number
link to original post
Quote: WizardAs to the goat problem, I now agree with CD. I had a couple of mistakes, including not subtracting out half the size of the shed.
Area Size qty Total Big quarter slices 1256.637061 3 3769.911184 Small slices 460.5026797 2 921.005359 Triangle 103.0776406 2 206.155281 Less quarter square -25 2 -50.000000 Total 4847.071825
I also computed angle ADC incorrectly. It is atan(sqrt(2)/sqrt(34)).
link to original post
Correct!!!
Very good.
One of many classic tethered goat puzzles.
There are a few ways to solve this. Here is a pdf of one.
------------------------------------------------------------------


If you're clever though, you shouldn't have too much trouble.
Quote: GialmereThis one went viral a few years back and is already considered a classic. It was given to 9 year old students in Taiwan. Understandably, the kids couldn't solve it. Neither could their teachers...
If you're clever though, you shouldn't have too much trouble.
link to original post
Quote: Wizard
79385 * 7 = 555555
link to original post
Wizard's answer was: 79385 * 7 = 555555.
But 79385 * 7 = 555695
I think the answer was meant to be: 79365 * 7 = 555555
Quote: gordonm888
Wizard's answer was: 79385 * 7 = 555555.
But 79385 * 7 = 555695
I think the answer was meant to be: 79365 * 7 = 555555
link to original post
Do'h! Typo. My handwritten work does show the correct number, I just typed one incorrect digit.
Quote: Wizard79385 * 7 = 555555
link to original post
Quote: gordonm888
Wizard's answer was: 79385 * 7 = 555555.
But 79385 * 7 = 555695
I think the answer was meant to be: 79365 * 7 = 555555
link to original post
Quote: WizardDo'h! Typo. My handwritten work does show the correct number, I just typed one incorrect digit.
link to original post
Correct!!
Well done. (It was an obvious typo.)
-----------------------------------------------------------
Quote: ThatDonGuySince nobody else has published one today, here's a (relatively) easy one for Monday:
A recent census came up with some surprising numbers.
For all positive integers N, if you look at all of the families with N children, it turns out that the number of families with 0, 1, 2, ..., N boys is proportional to what it would be if the probability of any particular child being a boy was 1/2 (which, theoretically, it is, at least if you assume that all of the males are XY).
For example, among all of the families with 4 children, 1/16 of them have four boys, 1/4 have three boys and a girl, 3/8 have two boys and two girls, 1/4 have one boy and three girls, and 1/16 have four girls.
For any particular value of N, do more of the boys in N-child familes or more of the girls in those families have any sisters?
link to original post
Quote: Wizard
Interestingly, I find the probability the same for both genders.
In other words, boys are equally likely to have a sister as girls, regardless of the family size.
For two-child families, 50% of children have a sister.
For three-child families, 75% of children have a sister.
For four-child families, 80% of children have a sister.
Quote: camaplFor N = 4, boys have a sister 3 * 1/4 + 2 * 3/8 + 1 * 1/4 = 1-3/4 of the time, and girls have a sister 2 * 3/8 + 3 * 1/4 + 4 * 1/16 = 1-3/4 of the time. Thus, an equal number of boys and girls have a sister, as Mr. Wizard answered first.
For N=2, boys have a sister 1/2 the time (no change), while girls have a sister 2 * 1/2 * 1/2 = 1/2 the time as well.
link to original post
Both of you are correct.
For any given N, there are, in proportion:
C(N,0) / 2^N = 1 / 2^N families with no girls - nobody here has any sisters
C(N,1) / 2^N = N / 2^N with one girl - the (N-1) boys in each one have a sister, but the one girl in each one does not
C(N,2) / 2^N with two girls - the (N-2) boys and 2 girls in each one all have at least one sister
C(N,3) / 2^N with three girls - the (N-3) boys and 3 girls in each one all have at least one sister
...
C(N,N-1) / 2^N = N / 2^N with N-1 girls - the 1 boy and (N-1) girls in each one all have at least one sister
C(N,N) / 2^N = 1 / 2^N with N girls - all N girls have at least one sister
The total number of boys is:
(N-1) N / 2^N + (N-2) C(N,2) / 2^N + (N-3) C(N,3) / 2^N + ... + 2 C(N,N-2) / 2^N + C(N,N-1) / 2^N
The total number of girls is:
2 C(N,2) / 2^N + 3 C(N,3) / 2^N + ... + (N-1) C(N,N-1) / 2^N + N C(N,N) / 2^N
Noting that C(N,K) = C(N,N-K) and rewriting the terms, each term in the boys' total is in the girls' total, except that the boys' total includes C(N,N-1) / 2^N, which is N / 2^N, and the girls' total includes N C(N,N) / 2^N, which is also N / 2^n, so the two sums are equal; the number of girls who have sisters equals the number of boys who do.
Three points are chosen randomly along the circumference of a unit circle. What is the mean of the shortest distance among any two of the three points?
Distances should be taken along the circumference, as opposed to taking a shortcut across the interior of the circle (that would be a tough problem).
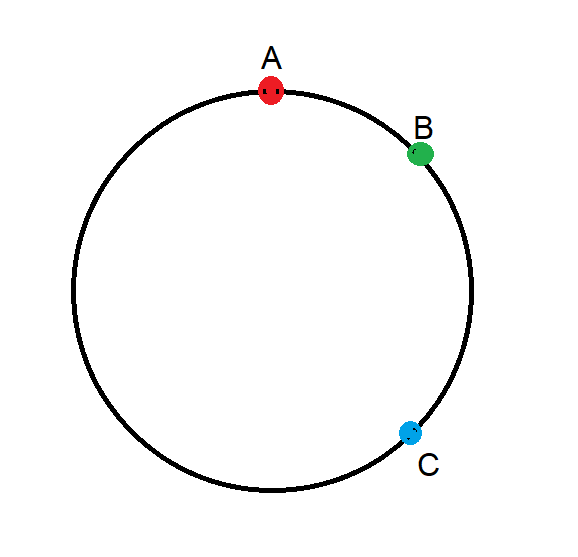
Example: Let's say the circle is a clock. The three points are the 12:00, 1:00, and 3:00 positions. The three distances would be pi/6, pi/3, and 3*pi/2. The minimum of these is pi/6.
Quote: Wizard...Three points...randomly...circumference of...circle. ...mean distance of the shortest distance...
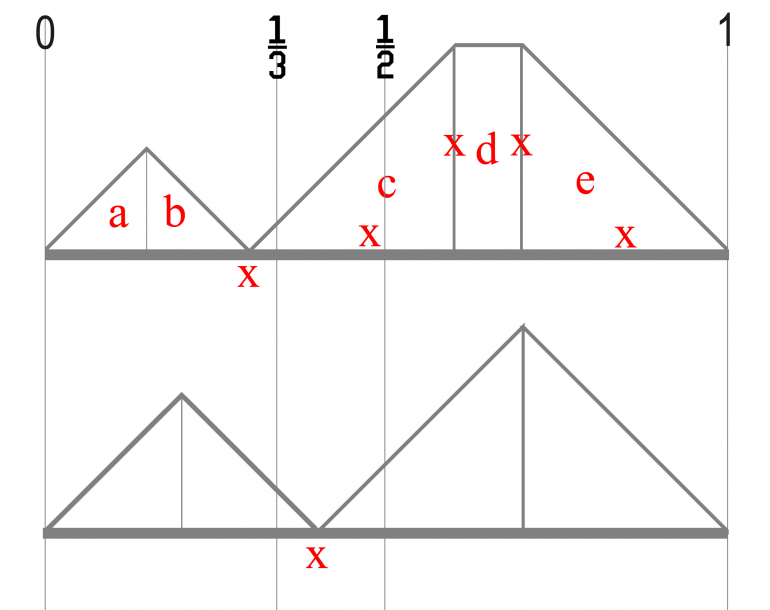
There are two scenarios; the first is that B is with 1/3 of "0", hence that might be the shortest; the second is that B is within [1/3 to 1/2].
In each situation C can now be anywhere along the [0,1] and the problem is to work out the average the shortest distance based on where it falls.
In the first case
(i) if C is left of B, then the shortest distance is either (a) 0 to C or (b) C to B.
(ii) if C is right of B, then the shortest distance is either (c) B to C, (d) 0 to B (e) C to 1.
Thus you need to look at the five places C could fall,
(a) Chances are x/2 - average distance is x/4
(b) same logic as (a)
(c) Chances are x - average distance is x/2.
(d) Chances are (1-3x) - average distance is x.
(e) same logic as (c).
Thus you can add all these chances up. x=[0,1/3].
In the second case where B lies in [1/3,1/2] then it's similar logic except there isn't a (d). x = [1/3,1/2].
For all of these you need to integrate for the various ranges of x.
Quote: WizardYou are on the same path to how I did it, Charlie. I think you're close, just need to integrate properly.
link to original post
Using Charlie's and your method, I get a distance of twice π over nine, which corresponds to an angle of 40 degrees.
I had to evaluate nine integrals. To make the limits on the integrals easier, I used a circle of circumference 6 instead of 2π. At the end, I then multiplied my answer 2/3 by 2π/6 to get 2π/9.
Is there a shortcut method to avoid so many integrals?
Quote: ChesterDog
Using Charlie's and your method, I get a distance of twice π over nine, which corresponds to an angle of 40 degrees.
I had to evaluate nine integrals. To make the limits on the integrals easier, I used a circle of circumference 6 instead of 2π. At the end, I then multiplied my answer 2/3 by 2π/6 to get 2π/9.
Is there a shortcut method to avoid so many integrals?
link to original post
I agree!
I did by that method too, but I had only two easy expressions to integrate. One if the distance between the first two points was less than 1/3 and the other more.
I plan to write up my solution properly.
Quote: WizardHere is my solution (PDF) to the three points on a circle problem.
link to original post
Label the three points A, B, C such that arc lengths AB <= BC <= AC.
Let a and b be the lengths of arcs AB and BC; AC has length (2 PI - a - b)
BC <= AC, so b <= 2 PI - a - b -> b <= PI - a/2
AB <= BC, so a <= b -> a <= PI - a/2 -> a <= 2/3 PI
For any particular value of a, b can be anything from a to PI - a/2. which is a range of size PI - 3/2 a.
The sum of all of these ranges over all a from 0 to 2/3 PI is
INTEGRAL (0, 2/3 PI) {(PI - 3/2 x) dx}
= PI x - 3/4 x^2 | [0, 2/3 PI]
= PI (2/3 PI) - 3/4 (2/3 PI)^2
= 2/3 PI^2 - (3/4 x 4/9) PI^2
= PI^2 / 3
Since a is always the smallest value, the sum of all of the smallest values is:
INTEGRAL (0, 2/3 PI) {x (PI - 3/2 x) dx}
= INTEGRAL (0, 2/3 PI) {(PI x - 3/2 x^2) dx}
= PI/2 x^2 - 1/2 x^3 | [0, 2/3 PI]
= PI/2 (2/3 PI)^2 - 1/2 (2/3 PI)^3
= 2/9 PI^3 - 4/27 PI^3
= 2/27 PI^3
The mean value = (2/27 PI^3) / (1/3 PI^2) = 2/9 PI

I have an unlabeled, six-sided die. I make a single mark on the middle of each face that is parallel to one pair of that faceís four edges.
How many unique ways are there for me to mark the die? (Note: If two ways can be rotated so that they appear the same, then they are considered to be the same marking.)
Extra credit: Suppose you can also mark a face along one of its two diagonals. Now how many unique ways are there to mark the die?
Note: If you're wondering, the "mark" is a small dash like ---
Choose any four connected faces (i.e. where the two unchosen faces) are opposite each other.
Assuming the cube is oriented so that the "top" and "bottom" are the two unchosen faces, the ways to place the marks on the other four faces are:
1. | | | |
2. | | | -
3. | | - -
4. | - | -
5. | - - -
6. - - - -
Normally, there are two ways to orient the top and bottom lines; either they are parallel to each other, or they are perpendicular to each other.
For 1, 3, and 6, the two ways to place the top line result in rotations; for 2, 4, and 5, they represent different placements.
The total is 3 x 2 + 3 x 4 = 18 ways.
Quote: ThatDonGuy
Choose any four connected faces (i.e. where the two unchosen faces) are opposite each other.
Assuming the cube is oriented so that the "top" and "bottom" are the two unchosen faces, the ways to place the marks on the other four faces are:
1. | | | |
2. | | | -
3. | | - -
4. | - | -
5. | - - -
6. - - - -
Normally, there are two ways to orient the top and bottom lines; either they are parallel to each other, or they are perpendicular to each other.
For 1, 3, and 6, the two ways to place the top line result in rotations; for 2, 4, and 5, they represent different placements.
The total is 3 x 2 + 3 x 4 = 18 ways.
link to original post
A good start but incorrect.
Quote: Gialmere
Buzzzzzzzzzzzzzzzz!!
How many unique ways were there for me to mark the die? (Note: If two ways could be rotated so that they appeared the same, then they were considered to be the same marking.)
The three-dimensional cube, as well as its many rotations, was rather hard to visualize. Nevertheless, a few solvers were able to do so. Q. P. Liu carefully counted up the number of unique ways you could mark the die, organized by whether the markings on opposite faces were parallel or perpendicular.
If the markings on opposite faces are all parallel to each other, then there was one way to mark it so that two pairs were parallel to each other and another way to mark it so that each pair was perpendicular to the two other pairs.
Next, if the two markings of each pair of opposite faces were perpendicular to each other, then there were two ways to mark the cube that were mirror images of each other. (Remember, while a rotation from one set of markings to another meant they were equivalent, the same was not true for reflections.)
When one pair of markings on opposite faces were parallel and the other two were perpendicular, there was one unique configuration. And when one pair was perpendicular and the other two were parallel, there were three unique configurations: (1) the parallel pairs were both also parallel to the faces with the perpendicular marks; (2) the parallel pairs were both perpendicular to the faces with the perpendicular marks; and (3) one parallel pair was parallel to and one parallel pair was perpendicular to the faces with the perpendicular marks.
In total, that meant there were eight unique ways to mark the die. In the (likely) event the descriptions of the eight configurations arenít totally clear, hereís an animation showing all of them:

A few solvers, including Emma Knight, recalled their days of studying group theory, the study of algebraic groups along with their symmetries and operators. A particular theorem from group theory known as Burnsideís lemma was especially useful in solving this problem. Let G represent the group of rotations on the unit cube, while X is the set of 26, or 64, markings on the cube (many of which are equivalent by rotation).
Burnsideís lemma provides a formula for calculating the number of ďorbitsĒ ó that is, the number of distinct sets of elements within X that can be reached via the elements of G (i.e., rotations). This number of orbits can be found by averaging (over all the elements of G) the number of elements of X that are unchanged by that particular element of G. For this particular problem, Burnsideís lemma confirmed that the number of orbits was indeed eight.
For extra credit, you had to consider the case where the markings on each face could not only be parallel to the edges of that face, but also along either of the faceís two diagonals. For this version of the puzzle, the rotation group G was the same, but X went from having 26 elements to now having 46, or 4,096, elements, since each face could now be marked in one of four ways. Applying Burnsideís lemma once more, Emma and others found that there were 224 unique ways to mark the die.
(I have a truly marvelous animation of these 224 unique markings which this column is too narrow to contain.)
500 men each toss a Ronald Reagan Presidential Dollar Coin.
Simultaneously, 500 women each toss a Sacagawea Dollar Coin.
What is the probability that the number of Reagan coins that come up heads is exactly one more than the number of Sacagawea coins that come up heads?


