Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: Gialmere
Correct!!
He lives.
link to original post
I think that's what people were waving at me in traffic, anyway.
:strip_icc()/pic6925800.png)
A farmer has three daughters. He is getting old and decides to split his 1-mile-by-1-mile farm equally among his daughters using fencing.
What is the shortest length of fence he needs to divide his square farm into three sections of equal area?
Quote: ThatDonGuyI didn't want to answer this one, as I have seen it before - a variation is in Smullyan's The Riddle of Scheherazade:
You will not keep both bills, nor will you pay me $100.
If the statement is true, then the student keeps both bills - but that makes the statement false. Therefore, the statement must be false.
This means that the student did keep both bills, or paid the professor $100. However, since the statement is false, the student had to give the professor one of the bills, so the only way the statement can be false is if the student pays the $100.
link to original post
Sorry for the tardy reply to this one. Since this one is getting old, I'll dispense with the spoiler tags.
Your answer looks correct. Would you agree the following, which I think is simpler, also works:
"You will give me $1 back or give me $100."
Quote: GialmereIt's toughie Tuesday. Let's go a little bit country...
A farmer has three daughters. He is getting old and decides to split his 1-mile-by-1-mile farm equally among his daughters using fencing.
What is the shortest length of fence he needs to divide his square farm into three sections of equal area?
link to original post
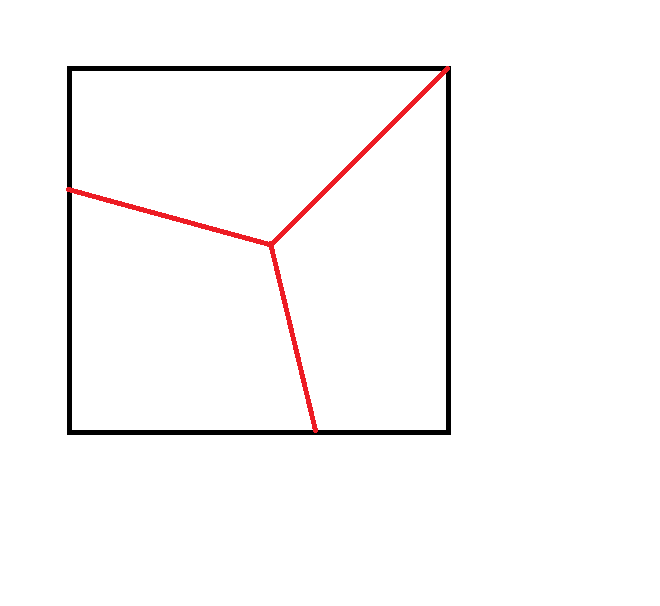
I don't claim any of these is optimal.
My first thought was the following type of borders.
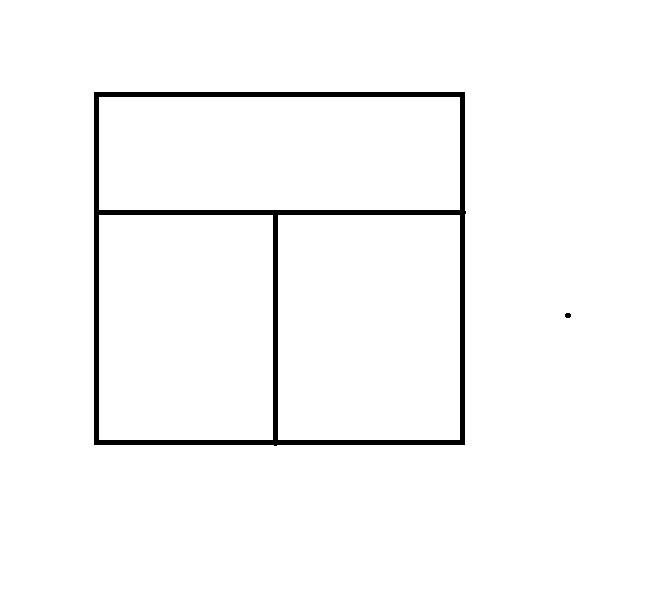
I find the fencing required here is 5/3.
Next, I thought of these diagonal fences:
Here, I get an answer of sqrt(3)=~ 1.7321, which is worse than the first idea.
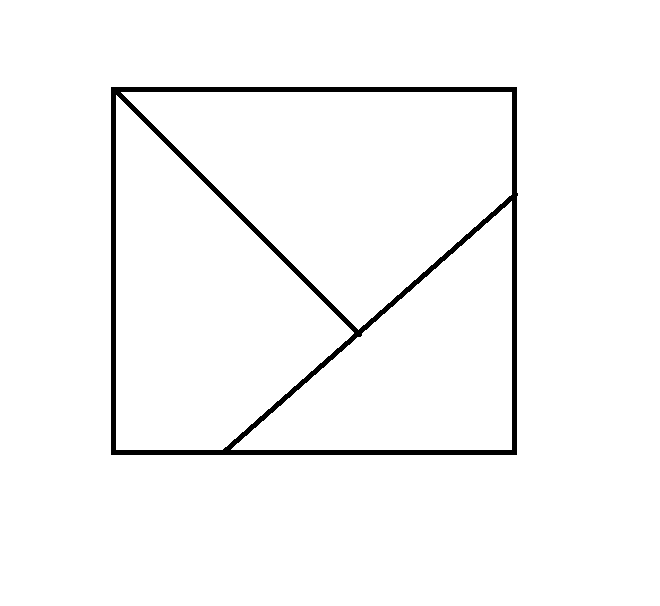
Next, I went with fencing like this:
I'll just say, for now, the total fencing with the optimal measurements is 1.634912503, which is better than 5/3. If this deemed correct, I'll provide my solution.
Nice idea - but WRONG ANSWER - but leads to the second idea!
Applying the same logic here I'm guessing it's similar to the "T" but then you alter the top of the T so the lines are at 120o. I haven't checked the maths but let's assume the height to the junction is y, and the points on the edge are x further up.
The area for each of the lower parts is y/2+x/4 = 1/3. The area for the top is 1-y-x/2. Also you know the Hypotenuse of the "triangle" is 2x, so the base is SQRT(3*)x. I think y=2/3-1/(4*SQRT(3) and x=1/(2*SQRT(3))
The total length of fences is y+4x = 2/3 + SQRT(3)*(2/3-1/12) = 2/3 + SQRT(3)*7/12. = 1.677.
SECOND IDEA
However this leads to considering a similar idea, draw a line up the middle and then create the triangles to give each person an area of 1/3. For instance if y=.6 then x=.133333, this isn't a 90/60/30 so the fence isn't 2x, in fact the total length of the fences is 1.6349. It transpires y=0.6022 gives 1.634913. I don't know why this isn't the 120o solution above or an elegant mathematical expression for it.
A farmer has a square piece of land. Somewhere under his land, an underground straight pipe crosses it. The farmer is tasked with finding this pipe. He decides to dig ditches until he finds it. What is the least amount of ditch length that will guarantee finding it?
Quote: WizardHere is a variant I've heard of the Three Daughters problem.
A farmer has a square piece of land. Somewhere under his land, an underground straight pipe crosses it. The farmer is tasked with finding this pipe. He decides to dig ditches until he finds it. What is the least amount of ditch length that will guarantee finding it?
link to original post
Does “crosses it” mean the straight pipe intersects any two sides of the square? Or must it intersect to parellel sides?
Quote: unJonDoes “crosses it” mean the straight pipe intersects any two sides of the square? Or must it intersect to parellel sides?
link to original post
The former. It may intersect adjacent or opposite sides. For example, both the red and blue pipes in the image below are possible.
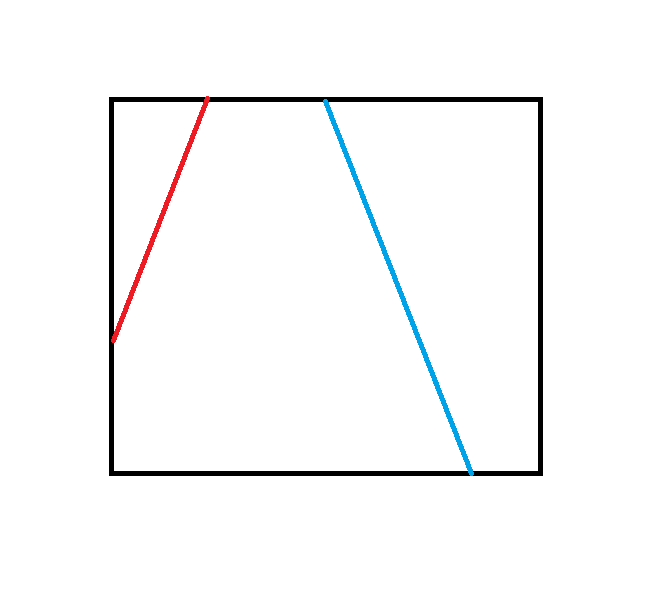
sqrt(15)/4 + 2/3 =~ 1.634912503
I will give a solution upon confirmation this answer is correct.
Quote: Wizard
I don't claim any of these is optimal.
My first thought was the following type of borders.
I find the fencing required here is 5/3.
Next, I thought of these diagonal fences:
Here, I get an answer of sqrt(3)=~ 1.7321, which is worse than the first idea.
Next, I went with fencing like this:
I'll just say, for now, the total fencing with the optimal measurements is 1.634912503, which is better than 5/3. If this deemed correct, I'll provide my solution.
link to original post
Quote: charliepatrickThere's an associated problem of joining three towns with roads; it transpires that roads need to meet at 120o to each other.
Nice idea - but WRONG ANSWER - but leads to the second idea!
Applying the same logic here I'm guessing it's similar to the "T" but then you alter the top of the T so the lines are at 120o. I haven't checked the maths but let's assume the height to the junction is y, and the points on the edge are x further up.
The area for each of the lower parts is y/2+x/4 = 1/3. The area for the top is 1-y-x/2. Also you know the Hypotenuse of the "triangle" is 2x, so the base is SQRT(3*)x. I think y=2/3-1/(4*SQRT(3) and x=1/(2*SQRT(3))
The total length of fences is y+4x = 2/3 + SQRT(3)*(2/3-1/12) = 2/3 + SQRT(3)*7/12. = 1.677.
SECOND IDEA
However this leads to considering a similar idea, draw a line up the middle and then create the triangles to give each person an area of 1/3. For instance if y=.6 then x=.133333, this isn't a 90/60/30 so the fence isn't 2x, in fact the total length of the fences is 1.6349. It transpires y=0.6022 gives 1.634913. I don't know why this isn't the 120o solution above or an elegant mathematical expression for it.
link to original post
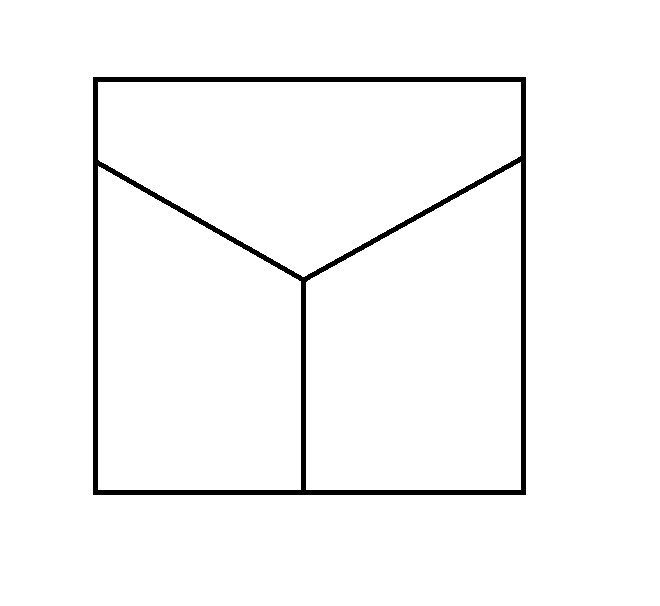
The Y fence configuration earns you both a half point. There is, however, room for tweaking.
Quote: GialmereThe Y fence configuration earns you both a half point. There is, however, room for tweaking.
link to original post
I think I'm going to have to settle upon the half point. However, I'm interested in a hint or the outright answer.
Quote: WizardQuote: GialmereThe Y fence configuration earns you both a half point. There is, however, room for tweaking.
link to original post
I think I'm going to have to settle upon the half point. However, I'm interested in a hint or the outright answer.
link to original post
My speculation:
Quote: GialmereThe Y fence configuration earns you both a half point. There is, however, room for tweaking.
link to original post
As a reminder, the number to beat is 1.634912503.
Quote: charliepatrickSadly it's by trial and error, so I haven't got a formula for the lengths.My arc method, via a spreadsheet, gets 1.63223813 using Y=.530196478. You can work out the hypotenuse and hence the angle, this gives the length of the arc and the area of the slice.
link to original post
You're hot on the trail but missing something. You can still squeeze a little more juice (i.e. a little less fence) out of it.
Quote: GialmereQuote: charliepatrickSadly it's by trial and error, so I haven't got a formula for the lengths.My arc method, via a spreadsheet, gets 1.63223813 using Y=.530196478. You can work out the hypotenuse and hence the angle, this gives the length of the arc and the area of the slice.
link to original post
You're hot on the trail but missing something. You can still squeeze a little more juice (i.e. a little less fence) out of it.
link to original post
Total guess:
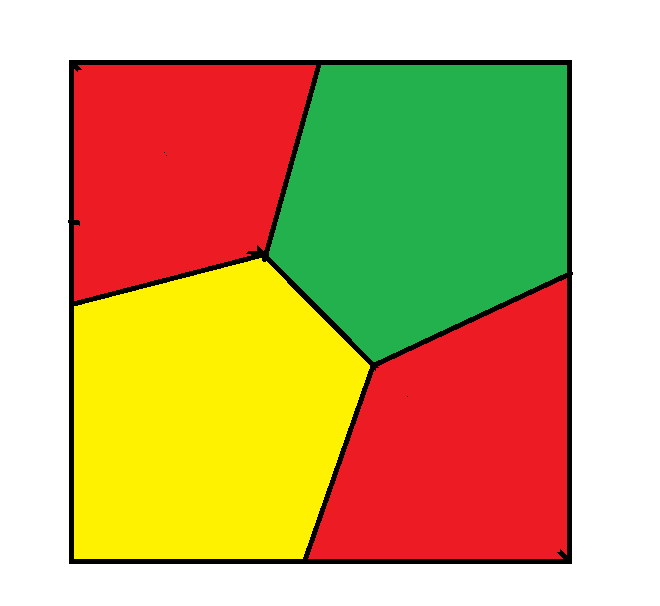
Note that one daughter gets both red pieces.
However, the minimum I can get the fencing is 1.711195869.
Quote: WizardHere is a variant I've heard of the Three Daughters problem.
A farmer has a square piece of land. Somewhere under his land, an underground straight pipe crosses it. The farmer is tasked with finding this pipe. He decides to dig ditches until he finds it. What is the least amount of ditch length that will guarantee finding it?
link to original post
I cannot think of a better answer than this:
In order to be sure to find the intersecting pipe, trenches need to be dug that block each side from each other side. So digging a trench around the perimeter works but has a length of 4. You can save by digging around just three sides for a length of 3. Better still you can start in each corner and make two trenches along the diagonal for a length of 2 * sqrt(2) = 2.828427
I think you could do best though by modifying the X diagonals by having a straight line in the middle connecting the left half > and right half < (or top and bottom). So think of four diagonal lines connecting two halves of the X. Like this:
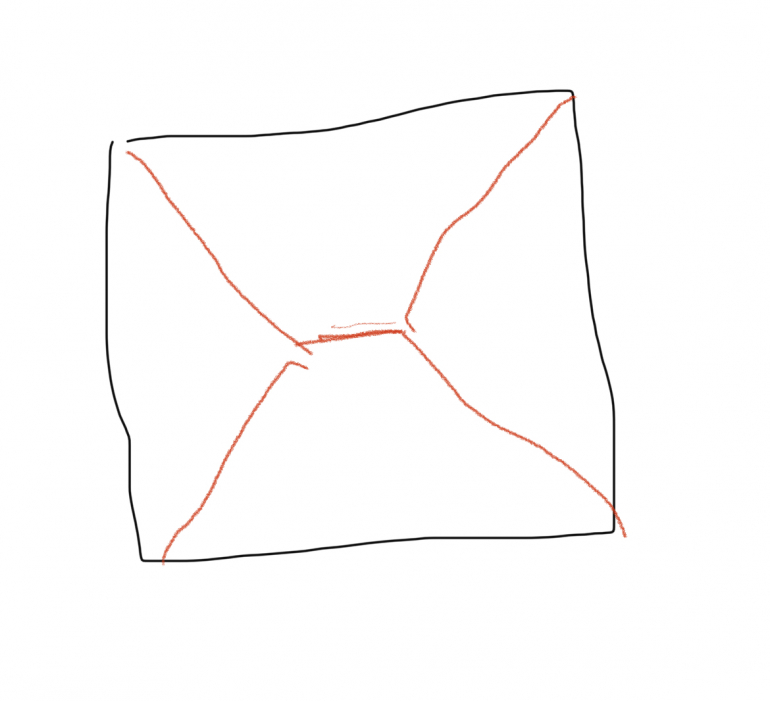
As the length of the middle connecting line (call it X) increases, each of the four diagonal lines (call it Y) shrinks.
The length of the trench is L = X + 4 Y.
The formula between X and Y is based on the Pythagorean formula.
f(X) = Y = sqrt( 1/2 ^ 2 + (1/2 - X/2)^2 )
Simplify to Y = sqrt(1/2 - X/2 + (X^2)/4)
Substitute in for Y in the length formula.
L = X + 4 * sqrt(1/2 - X/2 + (X^2)/4)
Take the derivative to find the minimum of L. (I used Wolfram Alpha) to get the minimum at X = 1 - 1/sqrt(3).
With L = 1 + sqrt(3) = 2.732051
Quote: unJonI cannot think of a better answer than this:
In order to be sure to find the intersecting pipe, trenches need to be dug that block each side from each other side. So digging a trench around the perimeter works but has a length of 4. You can save by digging around just three sides for a length of 3. Better still you can start in each corner and make two trenches along the diagonal for a length of 2 * sqrt(2) = 2.828427
I think you could do best though by modifying the X diagonals by having a straight line in the middle connecting the left half > and right half < (or top and bottom). So think of four diagonal lines connecting two halves of the X. Like this:
As the length of the middle connecting line (call it X) increases, each of the four diagonal lines (call it Y) shrinks.
The length of the trench is L = X + 4 Y.
The formula between X and Y is based on the Pythagorean formula.
f(X) = Y = sqrt( 1/2 ^ 2 + (1/2 - X/2)^2 )
Simplify to Y = sqrt(1/2 - X/2 + (X^2)/4)
Substitute in for Y in the length formula.
L = X + 4 * sqrt(1/2 - X/2 + (X^2)/4)
Take the derivative to find the minimum of L. (I used Wolfram Alpha) to get the minimum at X = 1 - 1/sqrt(3).
With L = 1 + sqrt(3) = 2.732051
link to original post
I agree!
Quote: WizardHere is a variant I've heard of the Three Daughters problem.
A farmer has a square piece of land. Somewhere under his land, an underground straight pipe crosses it. The farmer is tasked with finding this pipe. He decides to dig ditches until he finds it. What is the least amount of ditch length that will guarantee finding it?
link to original post
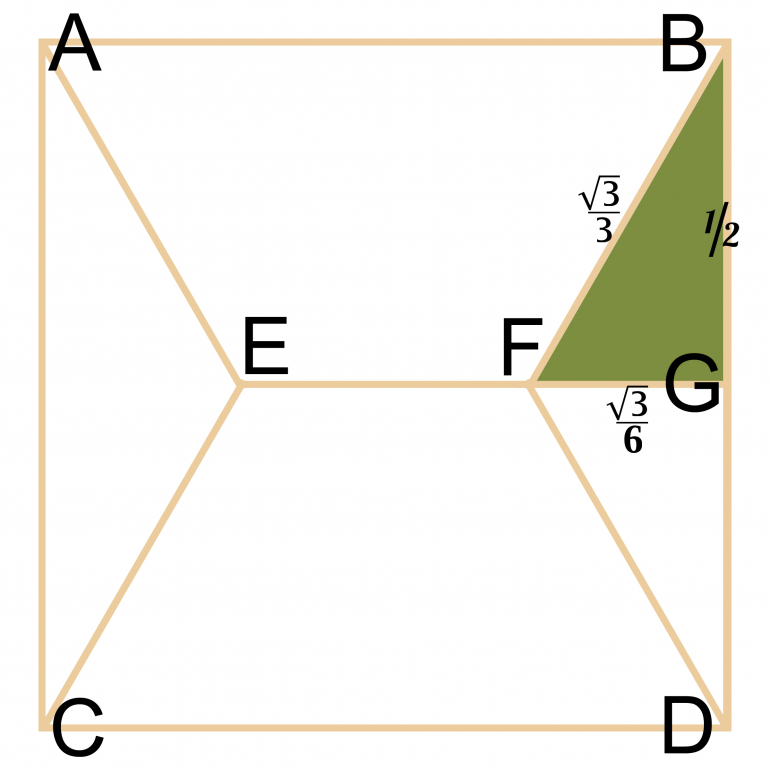
Quote: charliepatrickConsider the square ABCD and the middle line (EFG) As has been shown (you have to cover all the corners and create lines) the objective is to join ABCD with roads. Without going into the proof it transpires when connecting three points with the shortest length the roads have to meet at 120o. Therefore FBG (and the other similar triangles) are 30/60/90, hence FB = SQRT(3)/3. The total roads are four lines similar to FB and EF, which is 1 - 2*FG. This is 4*[SQRT(3)/3]+[1-2*SQRT(3)/6] = 1 + SQRT(3).
link to original post
Kudos to Charlie and UnJon for the correct answer!
Quote: GialmereIt's toughie Tuesday. Let's go a little bit country...
A farmer has three daughters. He is getting old and decides to split his 1-mile-by-1-mile farm equally among his daughters using fencing.
What is the shortest length of fence he needs to divide his square farm into three sections of equal area?
Buzzz
Semi-solve by Wizard and charliepatrick with a correct guess from unJon.
Here is the official solve at Riddler...

You start off simple, just planning to build two plain old east-to-west fences across the farm. These divide your farm into three identically shaped horizontal slices, giving you the equal areas you desire. This first arrangement uses 2 miles of fence.

But nothing is forcing you to go east to west. So you draw a blueprint where a vertical fence line meets a horizontal fence line, as shown in the second diagram. Again, you’ve divided your farm into three regions of equal area, although this time not identically shaped. This arrangement uses 1+2/3 or about 1.67 miles of fence. Much better! If you made it this far, you are a conscientious and efficient farmer and have done the agricultural sector of Riddler Nation proud.

But then you have an epiphany: There’s no reason the fences need to be east-west or north-south at all — they could be diagonal! So you sketch out a blueprint like the third diagram, where fences meet in a Y shape to split up the farm. But now things get a little more complicated because you need to figure out where exactly to put the diagonal lines and how much fence this’ll take. You’ll need a little algebra and a touch of calculus. First you figure out what the distances x and y must be.2 You know each region must have an area of 1/3, so you know, using the formulas for the area of a rectangle (base times height) and a triangle (one-half base times height), that y/2+x/4= 1/3. In other words, y=2/3−x/2
So how much fence does this arrangement use? It uses one vertical piece (length 2/3−x/2
) and two diagonal pieces. The diagonal pieces are the hypotenuses of right triangles, so we can get their length from the Pythagorean theorem: x2+(1/2)2= that length of fence squared. Then we take the square root of that (which is the length of one diagonal) and add two of them to y, which gets us the total length of fence in this arrangement. (Call it L.)
:strip_icc()/pic6928579.png)
Your job as super-efficient farmer is to select the x that minimizes that total length L. You can do this by taking the derivative of L with respect to x and setting it equal to zero. That gives x=1/(2√15). Plugging that back into our equation for L, this arrangement uses about 1.635 miles of fence. Even better than our second fence! If you made it this far, you earned a blue ribbon in the Riddler Nation agricultural expo.

But then you have another epiphany and nearly pass out: There’s no reason the fences need to be straight — they could be curved! So you sketch a blueprint like the fourth diagram. It’s similar to the third, except the “arms” of your fence arrangement are bits of larger circles.
The math here gets more complicated still. But in the end it turns out that z, the “stem” of your fence arrangement, is about 0.576 miles long, the circle itself has radius one, the angle pictured is 30 degrees, and the entire thing takes about 1.623 miles of fence. Our best result yet! If you made it this far, congratulations: You’re Riddler Nation’s new minister of agriculture.
Quote: GialmereYou're hot on the trail but missing something. You can still squeeze a little more juice (i.e. a little less fence) out of it.
link to original post
There is a mathematical expression (if you go through the steps you could work it out) for this number.
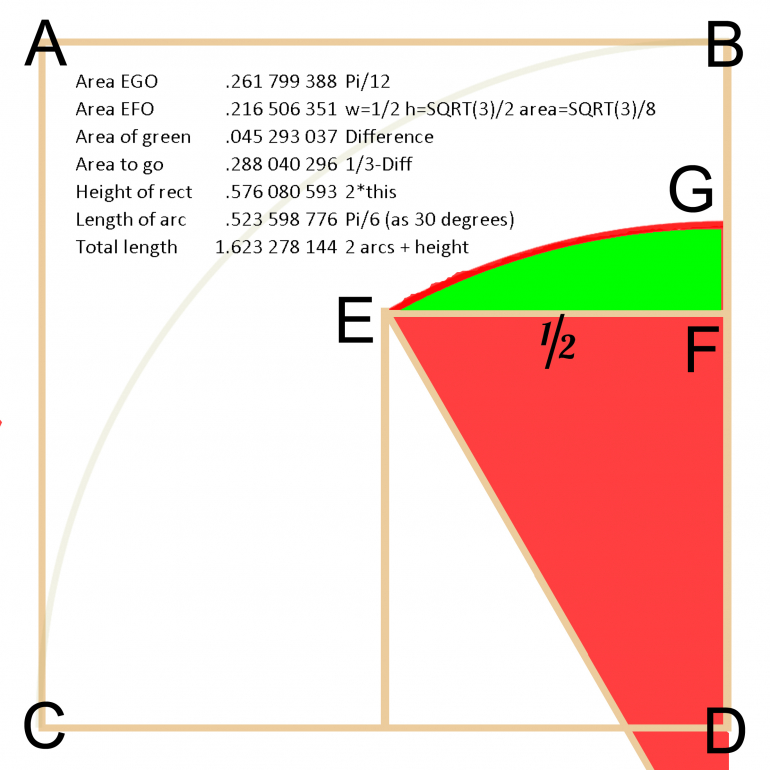
Quote: charliepatrickQuote: GialmereYou're hot on the trail but missing something. You can still squeeze a little more juice (i.e. a little less fence) out of it.
link to original postPlease see enclosed picture. Essentially construct a circle of unit radius - point O is the centre just off the picture (I've included another unit circle CB, so just slid it down to point E). This way the angle of FEG is 30 degrees, thus ensuring the angles of the lines meet at 120 degrees (which is what I was hoping for).
There is a mathematical expression (if you go through the steps you could work it out) for this number.
link to original post
Correct!
Shoot. I knew I should have given you more time.
--------------------------------------------

Quote: GialmereQuote: GialmereIt's toughie Tuesday. Let's go a little bit country...
A farmer has three daughters. He is getting old and decides to split his 1-mile-by-1-mile farm equally among his daughters using fencing.
What is the shortest length of fence he needs to divide his square farm into three sections of equal area?
Buzzz
Semi-solve by Wizard and charliepatrick with a correct guess from unJon.
Here is the official solve at Riddler...As you begin to plan your fence-building, you might sketch out a few blueprints and measure how much fence you’d need.
You start off simple, just planning to build two plain old east-to-west fences across the farm. These divide your farm into three identically shaped horizontal slices, giving you the equal areas you desire. This first arrangement uses 2 miles of fence.
But nothing is forcing you to go east to west. So you draw a blueprint where a vertical fence line meets a horizontal fence line, as shown in the second diagram. Again, you’ve divided your farm into three regions of equal area, although this time not identically shaped. This arrangement uses 1+2/3 or about 1.67 miles of fence. Much better! If you made it this far, you are a conscientious and efficient farmer and have done the agricultural sector of Riddler Nation proud.
But then you have an epiphany: There’s no reason the fences need to be east-west or north-south at all — they could be diagonal! So you sketch out a blueprint like the third diagram, where fences meet in a Y shape to split up the farm. But now things get a little more complicated because you need to figure out where exactly to put the diagonal lines and how much fence this’ll take. You’ll need a little algebra and a touch of calculus. First you figure out what the distances x and y must be.2 You know each region must have an area of 1/3, so you know, using the formulas for the area of a rectangle (base times height) and a triangle (one-half base times height), that y/2+x/4= 1/3. In other words, y=2/3−x/2
So how much fence does this arrangement use? It uses one vertical piece (length 2/3−x/2
) and two diagonal pieces. The diagonal pieces are the hypotenuses of right triangles, so we can get their length from the Pythagorean theorem: x2+(1/2)2= that length of fence squared. Then we take the square root of that (which is the length of one diagonal) and add two of them to y, which gets us the total length of fence in this arrangement. (Call it L.)
Your job as super-efficient farmer is to select the x that minimizes that total length L. You can do this by taking the derivative of L with respect to x and setting it equal to zero. That gives x=1/(2√15). Plugging that back into our equation for L, this arrangement uses about 1.635 miles of fence. Even better than our second fence! If you made it this far, you earned a blue ribbon in the Riddler Nation agricultural expo.
But then you have another epiphany and nearly pass out: There’s no reason the fences need to be straight — they could be curved! So you sketch a blueprint like the fourth diagram. It’s similar to the third, except the “arms” of your fence arrangement are bits of larger circles.
The math here gets more complicated still. But in the end it turns out that z, the “stem” of your fence arrangement, is about 0.576 miles long, the circle itself has radius one, the angle pictured is 30 degrees, and the entire thing takes about 1.623 miles of fence. Our best result yet! If you made it this far, congratulations: You’re Riddler Nation’s new minister of agriculture.
link to original post
Hmmm. I’m too lazy to calculate it, but I do wonder if the below two arcs would be even better. Both red lines are arcs of a unit circle.
To show the practicality of curved fencing, consider a very large square island. A farmer is given pi/2 miles of fence and told he can fence off as much land as he wishes at a corner of the island. By making a quarter of a circle, he can fence off pi/4 = 0.7854 square miles of land.
However, if he goes for a 45-45-90 triangle, he gets only 0.5554 square miles.
I don't suppose there is any way to improve upon the quarter circle.
Quote: unJonHmmm. I’m too lazy to calculate it, but I do wonder if the below two arcs would be even better. Both red lines are arcs of a unit circle.
link to original post
It seems unlikely. Notice that if you rotate the drawing 90 degrees clockwise you get the Y again but with a curved base which would probably add to the length.
:strip_icc()/pic6928824.png)
You have two faucets for your shower, one that releases hot water and one that releases cold water, but at varying pressures.
If the hot water is 105 degrees Fahrenheit and the cold water is 45 degrees Fahrenheit, and you could rotate the faucet at most 360 degrees, how much would you have to rotate the cold water faucet to get the temperature to be 98.6 degrees Fahrenheit, if the hot water is turned on all the way, and could not be turned down?
Quote: Gialmere
You have two faucets for your shower, one that releases hot water and one that releases cold water, but at varying pressures.
If the hot water is 105 degrees Fahrenheit and the cold water is 45 degrees Fahrenheit, and you could rotate the faucet at most 360 degrees, how much would you have to rotate the cold water faucet to get the temperature to be 98.6 degrees Fahrenheit, if the hot water is turned on all the way, and could not be turned down?
link to original post
Turn the cold water faucet on by an angle of 43 degrees.
Call the hot water flow H. With respect to the cold temperature, the energy supplied to the shower is proportional to (H)(105 - 45).
The cold water flow is some fraction (f) of the hot water flow. With respect to the cold water temperature, the energy supplied to the shower by the cold water is proportional to (fH)(45 - 45) = 0.
The total flow of 98.6F water is H + fH. The energy of the 98.6F water with respect to 45F is (H + fH)(98.6 - 45).
Then: (105 - 45)H = (98.6 - 45)( H + fH).
Solve for f: f = 8 / 67.
Then the angle for the cold water would be: 360(8/67) ≈ 43 degrees.
Quote: ChesterDogTurn the cold water faucet on by an angle of 43 degrees.
Call the hot water flow H. With respect to the cold temperature, the energy supplied to the shower is proportional to (H)(105 - 45).
The cold water flow is some fraction (f) of the hot water flow. With respect to the cold water temperature, the energy supplied to the shower by the cold water is proportional to (fH)(45 - 45) = 0.
The total flow of 98.6F water is H + fH. The energy of the 98.6F water with respect to 45F is (H + fH)(98.6 - 45).
Then: (105 - 45)H = (98.6 - 45)( H + fH).
Solve for f: f = 8 / 67.
Then the angle for the cold water would be: 360(8/67) ≈ 43 degrees.
link to original post
Correct!!
Very good.
(105(360)+(45)(x))/(360+x)=98.6
Solving for x:
x = 42.985 degrees
--------------------------------------------------
"You go get that," her husband says and hops into the shower.
Sighing the woman went to the door still wrapped in her towel. She opens the door expecting the mailman but instead sees her neighbor, Aaron standing there.
They stare shocked at each other when Aaron says "I'll pay you 800 dollars to drop that towel"
Thinking for a second the woman drops her towel. Aaron looks for a minute, pays her 800 dollars, and then leaves.
The woman goes back past the bathroom when her husband calls out: "Hey honey, who was at the door?"
"Oh just Aaron from next door" she answers
"Great!" Her husband replied. "Did he mention the 800 dollars he owes me?"

Use each digit 1-9 only once each, so that one number multiplied by another equals the third. One example is 12*483=5796.
How many more of these can you find?
Quote: Gialmere
Use each digit 1-9 only once each, so that one number multiplied by another equals the third. One example is 12*483=5796.
How many more of these can you find?
link to original post
This one seems to allow diagonal moves, which is different than its predecessor puzzle.
Quote: GialmereUse each digit 1-9 only once each, so that one number multiplied by another equals the third. One example is 12*483=5796.
How many more of these can you find?
Buuuzzzzzzz...
18 , 297 , 5346
27 , 198 , 5346
28 , 157 , 4396
39 , 186 , 7254
42 , 138 , 5796
48 , 159 , 7632
-----------------------------------------------
Quote: GialmereUse each digit 1-9 only once each, so that one number multiplied by another equals the third. One example is 12*483=5796.
How many more of these can you find?
link to original post
Solved with brute force:
28 x 157 = 4396
18 x 297 = 5346
27 x 198 = 5346
12 x 483 = 5796
42 x 138 = 5796
4 x 1738 = 6952
48 x 159 = 7632
39 x 186 = 7254
4 x 1963 = 7852
- The first digit of the number is the number of 0's in the entire number.
- The second digit of the number is the number of 1's in the entire number.
- The third digit of the number is the number of 2's in the entire number.
- The 4th digit of the number is the number of 3's in the entire number.
- The 5th digit of the number is the number of 4's in the entire number.
- The 6th digit of the number is the number of 5's in the entire number.
- The 7th digit of the number is the number of 6's in the entire number.
- The 8th digit of the number is the number of 7's in the entire number.
- The 9th digit of the number is the number of 8's in the entire number.
- The 10th digit of the number is the number of 9's in the entire number.
Quote: WizardFind a ten-digit number such that:
- The first digit of the number is the number of 0's in the entire number.
- The second digit of the number is the number of 1's in the entire number.
- The third digit of the number is the number of 2's in the entire number.
- The 4th digit of the number is the number of 3's in the entire number.
- The 5th digit of the number is the number of 4's in the entire number.
- The 6th digit of the number is the number of 5's in the entire number.
- The 7th digit of the number is the number of 6's in the entire number.
- The 8th digit of the number is the number of 7's in the entire number.
- The 9th digit of the number is the number of 8's in the entire number.
- The 10th digit of the number is the number of 9's in the entire number.
link to original post
7,210,000,100
Seven 0s, two 1s, one 2, and one 7
Quote: ThatDonGuy
7,210,000,100
Seven 0s, two 1s, one 2, and one 7
link to original post
I count only six 0's
Quote: WizardQuote: ThatDonGuy
7,210,000,100
Seven 0s, two 1s, one 2, and one 7
link to original post
I count only six 0's
link to original post
It's 6,210,001,000
Six 0s, two 1s, one 2, and one 6
Quote: WizardFind a ten-digit number such that:
- The first digit of the number is the number of 0's in the entire number.
- The second digit of the number is the number of 1's in the entire number.
- The third digit of the number is the number of 2's in the entire number.
- The 4th digit of the number is the number of 3's in the entire number.
- The 5th digit of the number is the number of 4's in the entire number.
- The 6th digit of the number is the number of 5's in the entire number.
- The 7th digit of the number is the number of 6's in the entire number.
- The 8th digit of the number is the number of 7's in the entire number.
- The 9th digit of the number is the number of 8's in the entire number.
- The 10th digit of the number is the number of 9's in the entire number.
link to original post
Let’s do it iteratively from a number that’s all 0s.
Start with 0,000,000,000.
Go to: 9,000,000,000.
Next: 8,000,000,010.
Next: 6,210,001,000.
Done.
Is that the only one?
Quote: ThatDonGuy
It's 6,210,001,000
Six 0s, two 1s, one 2, and one 6
link to original post
Quote: unJon
Let’s do it iteratively from a number that’s all 0s.
Start with 0,000,000,000.
Go to: 9,000,000,000.
Next: 8,000,000,010.
Next: 6,210,001,000.
Done.
Is that the only one?
link to original post
I agree! That is the same answer I came up with. I do not know if there are other answers. One could also ask the same question, but with other ten-digit numbers.
(i) There's a pattern 3211000, 42101000, 521001000, 6210001000
(ii) There's a solution 21200.
That's as far as I got (except perhaps 21200 turns into x21...)
Quote: Wizard
I agree! That is the same answer I came up with. I do not know if there are other answers.
link to original post
There "should be" a way to prove this without using brute force, but a brute force search shows that this is the only 10-digit solution.
A few notes, if anyone is trying to do an analytical proof:
"Obviously," the sum of the digits is 10
The digits in the 5-9 positions must be 0 or 1 (as a 2 would require more than 10 digits)
The first digit (the number of 0s) cannot be 0, as then there would be one 0 in the number

During a game of five card draw poker, played with a standard deck, you are dealt a hand with the following characteristics:
--It contains no aces or face cards.
--No two cards have the same value.
--All four suits are present.
--The total value of the odd cards equals the total value of the even cards.
--There are no three card straights.
--The total value of the black cards is 10.
--The total value of the hearts is 14.
--The card with the lowest value is a spade.
Exactly what are the five cards in your hand?
Quote: GialmereIt's easy Monday. Let's play poker...
During a game of five card draw poker, played with a standard deck, you are dealt a hand with the following characteristics:
--It contains no aces or face cards.
--No two cards have the same value.
--All four suits are present.
--The total value of the odd cards equals the total value of the even cards.
--There are no three card straights.
--The total value of the black cards is 10.
--The total value of the hearts is 14.
--The card with the lowest value is a spade.
Exactly what are the five cards in your hand?
link to original post
Quote: GialmereIt's easy Monday....Exactly what are the five cards in your hand?...
The Hearts have to be 9h and 5h to get to 14. The Blacks, so they can't form a straight or be a 4, are 2 and 8, with the lowest being 2s, gives 8c .
Quote: rsactuaryI think 9 hearts, 5 hearts, 4 diamonds, 8 clubs and 2 spades satisfies the requirements
link to original post
Quote: charliepatrickBlack=10, Hearts=14, these both use up two cards so the diamond is a 4d. The Blacks or Hearts are either both odd or both even. Because of the 4d, the Blacks also have to be even; and the total of even=odd=14.
The Hearts have to be 9h and 5h to get to 14. The Blacks, so they can't form a straight or be a 4, are 2 and 8, with the lowest being 2s, gives 8c .
link to original post
Correct!!
Good show (although I recommend you fold that hand).
Since the hearts total 14 and there are no aces or face cards and all cards have a different value, the heart combination can only be (4, 10), (5, 9) or (6, 8).
The sum of the odd cards equals the sum of the even cards, therefore, there must be two odd and three even cards. The maximum of the odd cards is 7 + 9 = 16. The minimum of the even cards is 2 + 4 + 6 = 12. Therefore, the sums must be 12, 14, or 16.
Only one hand meets the criteria.
-------------------------------------------------------
Quote: ThatDonGuyQuote: Wizard
I agree! That is the same answer I came up with. I do not know if there are other answers.
link to original post
There "should be" a way to prove this without using brute force, but a brute force search shows that this is the only 10-digit solution.
A few notes, if anyone is trying to do an analytical proof:
"Obviously," the sum of the digits is 10
The digits in the 5-9 positions must be 0 or 1 (as a 2 would require more than 10 digits)
The first digit (the number of 0s) cannot be 0, as then there would be one 0 in the number
link to original post
Notice that there cannot be more than one 5, more than one 6, more than one 7, more than one 8, or more than one 9.
If there were, say, two 5s, then the 5s digit would be at least 2, but that is already more than 10 - unless one of the 5s is the 5s digit itself, but then there would have to be five 5.
If the 0s digit is 9, then you have 9,000,000,000, but this is incorrect as the 9s digit has to be 1.
If the 0s digit is 8, then the 8s digit is 1, so the 1s digit is (at least) 1; however, if both are 1, then the 1s digit would have to be 2.
If the 0s digit is 7, then the 7s digit is 1, so the 1s digit is (at least) 1; again, the 1s digit cannot be 1 in this case, so it would have to be 2, which means another digit is 1. This is 7 0s, 2 1s, 1 2, and 1 7, which is 11 digits.
If the 0s digit is 6, then the 6s digit is 1, so the 1s digit is (at least) 1; again, the 1s digit cannot be 1 in this case, so it would have to be 2, which means another digit is 2. If it is the 2s digit, you have 6,210,001,000.
If it is, say, the 3s digit, then there have to be two 3s in the number, but this is more than 10 digits.
If the 0s digit is 5 or less, then there must be at least 4 digits from among the 1s, 2s, ..., 9s that are 1 or more. Even if the 1s, 2s, 3s, and 4s digits could all be 1s (which they can't, as if the 2s and 3s digits are 1s, then the 1s digit has to be at least 2), that is 10 digits, plus the 0s digit, which is more than 10.
Therefore, 6,210,001,000 is the only solution.

Suppose you have a shuffled deck containing 13 cards. Each card has a number from 1 to 13 and each number appears on exactly one card. You look at the number on the first card — suppose it’s k — and then you reverse the order of the first k cards. You continue this procedure — reading the first card’s number and then reversing the order of the corresponding number of cards — until the first card reads 1. Clearly, the number of reversals depends on the initial order of the cards.
What is the largest number of reversals that you might have to do?
You then draw the new top card, say, the jack (which equals 11), you put it back on top and lift up the top eleven cards. Again you reverse them by placing the jack back on top of the stack, then the card that was beneath the jack etc. You continue reversals until you draw the ace thus ending the sequence.
If you start with the cards in order 13, 11, 9, 7, 5, 3, 1, 2, 4, 6, 8, 10, 12, it requires 12 reversals.
I don't think more than that is possible without getting into an infinite loop.


