Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Doesn't this work?
exp( ln(x) + ln(y) ) = x * y
The left side of the equation can be entered using exp and ln keys on the broken calculator.
Where x and y are positive integers
Take 1/(1/x + 1/y) and add it to itself x+y times to get the product xy
For 3 * 7:
1 / (1/3 + 1/7) = 2.1.
2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 = 21 = 3 * 7
Quote: Ace2
Where x and y are positive integers
Take 1/(1/x + 1/y) and add it to itself x+y times to get the product xy
For 3 * 7:
1 / (1/3 + 1/7) = 2.1.
2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 = 21 = 3 * 7
link to original post
The solution that I saw is more involved, but I *think* ultimately it comes down to exactly what you've posted. ETA: But this wouldn't work if you wanted to find Pi*e
Note that (x+y)^2 = x^2 + y^2 +2xy
So therefore xy = [(x+y)^2 -x^2 – y^2]/2
To calculate the square of a number (let’s call it z):
enter z and take the reciprocal
Enter z+1 and take the reciprocal
Note that 1/z - 1/(z+1) with a common denominator equals 1/(z^2 + z)
So take 1/z and subtract 1/(z+1) and then take the reciprocal again
The amount in the calculator will be z^2+z. Subtracting z gives the value of z^2
So you will do that procedure three times to get the numerator of our solution, let’s call that “w”.
So then the last step is to take 1/w and then add to it another 1/w to get 2/w.
Take reciprocal of 2/w and you will have the solution for x times y.
Please show an exampleQuote: rsactuaryHere is the solution as presented on YouTube:
Note that (x+y)^2 = x^2 + y^2 +2xy
So therefore xy = [(x+y)^2 -x^2 – y^2]/2
To calculate the square of a number (let’s call it z):
enter z and take the reciprocal
Enter z+1 and take the reciprocal
Note that 1/z - 1/(z+1) with a common denominator equals 1/(z^2 + z)
So take 1/z and subtract 1/(z+1) and then take the reciprocal again
The amount in the calculator will be z^2+z. Subtracting z gives the value of z^2
So you will do that procedure three times to get the numerator of our solution, let’s call that “w”.
So then the last step is to take 1/w and then add to it another 1/w to get 2/w.
Take reciprocal of 2/w and you will have the solution for x times y.
link to original post
Quote: Ace2Please show an exampleQuote: rsactuaryHere is the solution as presented on YouTube:
Note that (x+y)^2 = x^2 + y^2 +2xy
So therefore xy = [(x+y)^2 -x^2 – y^2]/2
To calculate the square of a number (let’s call it z):
enter z and take the reciprocal
Enter z+1 and take the reciprocal
Note that 1/z - 1/(z+1) with a common denominator equals 1/(z^2 + z)
So take 1/z and subtract 1/(z+1) and then take the reciprocal again
The amount in the calculator will be z^2+z. Subtracting z gives the value of z^2
So you will do that procedure three times to get the numerator of our solution, let’s call that “w”.
So then the last step is to take 1/w and then add to it another 1/w to get 2/w.
Take reciprocal of 2/w and you will have the solution for x times y.
link to original post
link to original post
How about this:
In other words, the solution is:
1 / (1 / (c - a - b) + 1 / (c - a - b)) = xy
where a = 1 / (1/x - 1/(x+1)),
b = 1 / (1/y - 1/(y+1)),
and c = 1 / (1/(x+y) - 1/(x+y+1))
Proof:
(a) 1 / (1/x - 1/(x+1)) = x^2 + x
(b) 1 / (1/y - 1/(y+1)) = y^2 + y
(c) 1 / (1/(x+y) - 1/(x+y+1)) = (x+y)^2 + x + y
(c - a - b) = 2xy
Note that 1 / 2xy + 1 / 2xy = 2 / 2xy = 1 / xy, so 1 / (1 / 2xy + 1 / 2xy) = xy
As an example, choose x = 6 and b = 9
I am assuming the calculator includes parentheses
[(] [6] [1/x] [-] [7] [1/x] [)] [1/x] is 42; this is (a)
[(] [9] [1/x] [-] [10] [1/x] [)] [1/x] is 90; this is (b)
[(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] is 240; this is (c)
[(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] [-] [(] [6] [1/x] [-] [7] [1/x] [)] [1/x] [-] [(] [9] [1/x] [-] [10] [1/x] [)] [1/x] is 240 - 42 - 90 = 108, which is 1 / (c - a - b) and also 2xy
[(] [(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] [-] [(] [6] [1/x] [-] [7] [1/x] [)] [1/x] [-] [(] [9] [1/x] [-] [10] [1/x] [)] [1/x] [)] [1/x] is 1 / 108
[(] [(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] [-] [(] [6] [1/x] [-] [7] [1/x] [)] [1/x] [-] [(] [9] [1/x] [-] [10] [1/x] [)] [1/x] [)] [1/x] + [(] [(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] [-] [(] [6] [1/x] [-] [7] [1/x] [)] [1/x] [-] [(] [9] [1/x] [-] [10] [1/x] [)] [1/x] [)] [1/x] is 1/54
[(] [(] [(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] [-] [(] [6] [1/x] [-] [7] [1/x] [)] [1/x] [-] [(] [9] [1/x] [-] [10] [1/x] [)] [1/x] [)] [1/x] + [(] [(] [1] [5] [1/x] [-] [1] [6] [1/x] [)] [1/x] [-] [(] [6] [1/x] [-] [7] [1/x] [)] [1/x] [-] [(] [9] [1/x] [-] [10] [1/x] [)] [1/x] [)] [1/x] [)] [1/x] is 54 = 6 x 9
Here's an easy broken calculator question:
The Enter key on my friend's Hewlett Packard calculator (which uses RPN.) What key(s) does he now use instead of Enter?
Quote: Ace2Please show an exampleQuote: rsactuaryHere is the solution as presented on YouTube:
Note that (x+y)^2 = x^2 + y^2 +2xy
So therefore xy = [(x+y)^2 -x^2 – y^2]/2
To calculate the square of a number (let’s call it z):
enter z and take the reciprocal
Enter z+1 and take the reciprocal
Note that 1/z - 1/(z+1) with a common denominator equals 1/(z^2 + z)
So take 1/z and subtract 1/(z+1) and then take the reciprocal again
The amount in the calculator will be z^2+z. Subtracting z gives the value of z^2
So you will do that procedure three times to get the numerator of our solution, let’s call that “w”.
So then the last step is to take 1/w and then add to it another 1/w to get 2/w.
Take reciprocal of 2/w and you will have the solution for x times y.
link to original post
link to original post
It's a theoretical proof. Try it yourself.
Quote: ChesterDogWow! I'd put that math question in the Hard Math Puzzle category.
Here's an easy broken calculator question:
The Enter key on my friend's Hewlett Packard calculator (which uses RPN.) What key(s) does he now use instead of Enter?
link to original post
Press the 1/x key twice
RPN? That takes me back...
Quote: ChesterDogWow! I'd put that math question in the Hard Math Puzzle category.
Here's an easy broken calculator question:
The Enter key on my friend's Hewlett Packard calculator (which uses RPN.) What key(s) does he now use instead of Enter?
link to original post
I think your friend should repair their calculator rather than suffering the slings and arrows of outrageous infix, certainly.
My solution, though much more efficient, will only work for integers. If you try it for 3.2 * 7, the last step is to add 2.19608 to itself 10.2 times. Not sure how you would add that to itself 10.2 times with only +, - and 1/x.Quote: Ace2
Where x and y are positive integers
Take 1/(1/x + 1/y) and add it to itself x+y times to get the product xy
For 3 * 7:
1 / (1/3 + 1/7) = 2.1.
2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 + 2.1 = 21 = 3 * 7
Agreed. It's just theory if you haven't worked it out yourself. So you just assume it works?Quote: rsactuaryQuote: Ace2Please show an exampleQuote: rsactuaryHere is the solution as presented on YouTube:
Note that (x+y)^2 = x^2 + y^2 +2xy
So therefore xy = [(x+y)^2 -x^2 – y^2]/2
To calculate the square of a number (let’s call it z):
enter z and take the reciprocal
Enter z+1 and take the reciprocal
Note that 1/z - 1/(z+1) with a common denominator equals 1/(z^2 + z)
So take 1/z and subtract 1/(z+1) and then take the reciprocal again
The amount in the calculator will be z^2+z. Subtracting z gives the value of z^2
So you will do that procedure three times to get the numerator of our solution, let’s call that “w”.
So then the last step is to take 1/w and then add to it another 1/w to get 2/w.
Take reciprocal of 2/w and you will have the solution for x times y.
link to original post
link to original post
It's a theoretical proof. Try it yourself.
link to original post
Quote: ThatDonGuyQuote: ChesterDogWow! I'd put that math question in the Hard Math Puzzle category.
Here's an easy broken calculator question:
The Enter key on my friend's Hewlett Packard calculator (which uses RPN.) What key(s) does he now use instead of Enter?
link to original post
Press the 1/x key twice
RPN? That takes me back...
link to original post
Your method works for almost every number. For 0, I would press the square root key to avoid an error and save one key stroke.
My friend presses the Swap x,y key twice every time he needs an Enter.
What is the largest integer you can form using four 2's and no other letter, mark or mathematical symbol of any type?
2222
That was my answer too, but doesn't preclude someone else's brilliance.Quote: ThatDonGuy
2222
link to original post
Mike owes you another beer.
Okay ... I edited this. I was thinking of another problem, where the answer involved Knuth's arrow notation. I can't get it to work.
Quote: teliotMike owes you another beer.
I learned a lesson the last time I was at a Spring Fling - I can't tell beers apart. They all taste like alcohol.

There is a square of side length 1. Each corner of the square is the center of a circle of radius one. What is the area of the red region, where all four circles overlap?
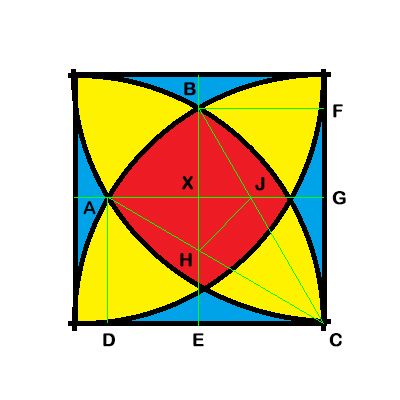
AC = BC = 1
AD = 1/2
This means CAD is a 30-60-90 right triangle, and CD = sqrt(3)/2
Similarly, BCF is also 30 degrees, so ACB = 90 - 30 - 30 = 30 degrees
This means sector AB is 1/12 of a unit circle, so its area is PI/12
The area of the sector inside of the upper left quadrant = PI/12 - AXH - BXJ - HXJ - HCJ
AG = sqrt(3)/2, so AX = BX = (sqrt(3) - 1)/2
CHE is a 30-60-90 triangle; CE = 1/2, so HE = 1 / 2 sqrt(3) = sqrt(3) / 6, and the area = 1/2 * 1/2 * sqrt(3)/6 = sqrt(3)/24
HXJ + HCJ = 1/4 - CEH - CGJ = 1/4 - 2 CEH = 1/4 - sqrt(3)/12
BXJ = AXH = 1/2 * AX * HX = 1/2 * AX * (AX / sqrt(3)) = (AX)^2 / (2 sqrt(3)) = (sqrt(3)-1)^2 / (8 sqrt(3))
= (2 - sqrt(3)) / (4 sqrt(3)) = (2 sqrt(3) - 3) / 12
Sector area inside the quadrant = PI/12 - (2 sqrt(3) - 3) / 6 - (1/4 - sqrt(3)/12)
= PI/12 - sqrt(3)/3 + 1/2 - 1/4 + sqrt(3)/12
= PI/12 + 1/4 - sqrt(3)/4
The total area = 4x the area inside the quadrant = PI/3 + 1 - sqrt(3) = about 0.31515
Quote: Wizard
There is a square of side length 1. Each corner of the square is the center of a circle of radius one. What is the area of the red region, where all four circles overlap?
link to original post
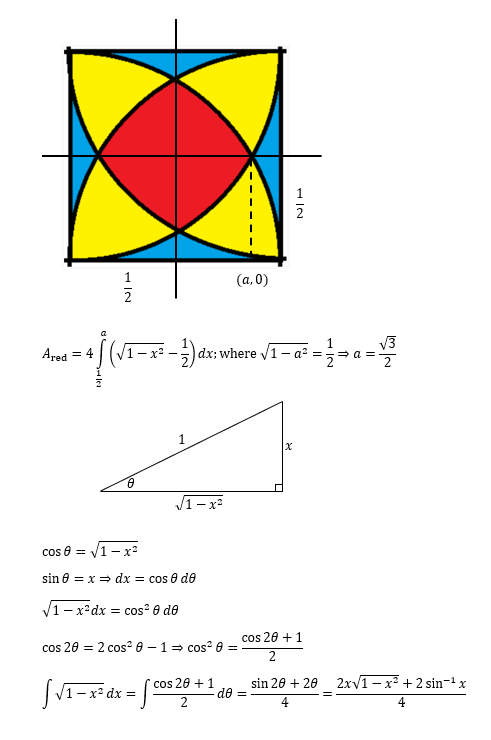
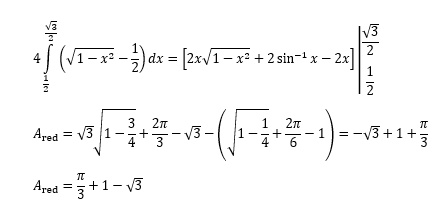
Quote: ChesterDog
link to original post
I agree! I see you used calculus in your solution. Mine was brute force geometry.
Wizard solution (PDF).
Quote: WizardQuote: ChesterDog
link to original post
I agree! I see you used calculus in your solution. Mine was brute force geometry.
Wizard solution (PDF).
link to original post
I would also have used a geometric method as did Don and you if I had thought of it.
Quote: ThatDonGuyHere's my solution, ...
link to original post
Well done Don! I overlooked this post before. I think this one was beer worthy.

While killing some time at your desk one afternoon, you fire up a new game of Solitaire on your computer (specifically the version where you deal out three cards from the deck at a time). But your boredom quickly turns to rage because your game is unplayable — there's nothing you can do on the board and you can flip through your deck, but you never have any legal moves!
Rounded to the nearest quarter percent, what is the probability of being dealt such a nightmare scenario?
Quote: WikipediaThe probability of being able to win a game of Klondike with best-possible play is not known, although Hoyle's Rules of Games suggests the chances of winning as being 1 in 30 games. The inability of theoreticians to precisely calculate these odds has been referred to by mathematician Persi Diaconis as "one of the embarrassments of applied probability".
The game enjoyed a surge in popularity when it was included as part of the Windows operating package. The idea was to get users comfortable using a mouse by dragging and dropping red 6s onto black 7s. The result was workers wasting endless hours playing the game. But hey, it was worth all that losing to see those cards fly around the screen when you finally won right? According to Microsoft, Solitaire was its most popular program for many years.
Klondike was also called Canfield in America, perhaps because it was once a casino game at the Canfield Casino in Saratoga Springs, New York. I've heard of Solitaire in casinos but have never seen it myself. I do think that the reason "Las Vegas Scoring" is so popular on computer versions is that you can lose the game but still claim a minor victory if you got enough cards up top to end with a positive cash amount.
Anyways, although we may never know the true odds of winning Klondike, the above puzzle (from the Riddler) is solvable (but not a cakewalk).
Quote: Ace2For a bet that follows the normal distribution exactly, the risk of ruin for a given bankroll and playing time is exactly double the probability of ending the session with a busted bankroll. For example, if you have a 63 unit bankroll and bet on 1,000 fair coin flips with an even money payout, your RoR is 4.62912 %. If you have unlimited bankroll, the probability of ending the session down more than 62 units is 2.31456%. Incidentally, a z-score calculator approximates the latter as 2.31726%
Can someone prove why the RoR is double?
link to original post
I think the RoR is double ONLY when μ = 0 and σ = 1, am I correct ?
The first thing is to remember the pack can be considered as two of 26 different cards, as red Kings are different from black Kings. So consider the deck as 26x2. For convenience alternate the colours and use
1+2 Red/Black Kings
3+4 Black/Red/Queens
...
25+26 Aces (the colour of these doesn't really matter as they can go to the top)
To enable a card to be played either it is an Ace (25/26) or the card two greater than it is visible, e.g. 5 - Red Queen, 7 = Black Jack.
Therefore stage one is to look at the original seven visible cards, these are all permutations of seven of the numbers 1 thru 26 (allowing for duplicates) where there are no possible movements (you probably do this with distributions of 2221 22111 211111 1111111).
The next thing to notice is after dealing out the board, this leaves 24 cards for the "pack", so if there are no possible movements only eight of these will be looked at.
For each combination in phase 1, work out how many possible cards left could cause a movement (i.e. be an Ace or two more than a visible card) and how many don't. Work out how often the eight are solely in the don't category.
(In practice the eight will be a random selection from the remaining pack of 45. The important feature of 24 is only eight cards can ever be seen if there are no movements.)
Quote: charliepatrickI haven't managed to work it out but here is a thought and possible approach (which would eventually give an exact answer).
The first thing is to remember the pack can be considered as two of 26 different cards, as red Kings are different from black Kings. So consider the deck as 26x2. For convenience alternate the colours and use
1+2 Red/Black Kings
3+4 Black/Red/Queens
...
25+26 Aces (the colour of these doesn't really matter as they can go to the top)
To enable a card to be played either it is an Ace (25/26) or the card two greater than it is visible, e.g. 5 - Red Queen, 7 = Black Jack.
Therefore stage one is to look at the original seven visible cards, these are all permutations of seven of the numbers 1 thru 26 (allowing for duplicates) where there are no possible movements (you probably do this with distributions of 2221 22111 211111 1111111).
The next thing to notice is after dealing out the board, this leaves 24 cards for the "pack", so if there are no possible movements only eight of these will be looked at.
For each combination in phase 1, work out how many possible cards left could cause a movement (i.e. be an Ace or two more than a visible card) and how many don't. Work out how often the eight are solely in the don't category.
(In practice the eight will be a random selection from the remaining pack of 45. The important feature of 24 is only eight cards can ever be seen if there are no movements.)
Keep in mind that there are only 15 cards you need to worry about; the 7 you see in the initial deal, and the 8 you will see in the 24 cards in the deck.
It is a "bad deal" only if all three of these conditions are true:
1. None of the 15 are Aces
2. None of the 7 visible cards are one rank lower than, and the opposite color of, another visible card
3. None of the 8 cards in the deck that you will see are one rank lower than, and the opposite color of, any of the 7 initially visible cards.
Quote: GialmereIt's Toughie Tuesday. Let's waste time playing...
While killing some time at your desk one afternoon, you fire up a new game of Solitaire on your computer (specifically the version where you deal out three cards from the deck at a time). But your boredom quickly turns to rage because your game is unplayable — there's nothing you can do on the board and you can flip through your deck, but you never have any legal moves!
Rounded to the nearest quarter percent, what is the probability of being dealt such a nightmare scenario?In America, Klondike is so popular that if you simply say you're playing Solitaire it's assumed that's the game you're playing. This is somewhat baffling since Klondike has a very low win ratio compared to most other solitaire card games. What are the odds that you'll win? Well, according to Wikipedia...Quote: WikipediaThe probability of being able to win a game of Klondike with best-possible play is not known, although Hoyle's Rules of Games suggests the chances of winning as being 1 in 30 games. The inability of theoreticians to precisely calculate these odds has been referred to by mathematician Persi Diaconis as "one of the embarrassments of applied probability".
The game enjoyed a surge in popularity when it was included as part of the Windows operating package. The idea was to get users comfortable using a mouse by dragging and dropping red 6s onto black 7s. The result was workers wasting endless hours playing the game. But hey, it was worth all that losing to see those cards fly around the screen when you finally won right? According to Microsoft, Solitaire was its most popular program for many years.
Klondike was also called Canfield in America, perhaps because it was once a casino game at the Canfield Casino in Saratoga Springs, New York. I've heard of Solitaire in casinos but have never seen it myself. I do think that the reason "Las Vegas Scoring" is so popular on computer versions is that you can lose the game but still claim a minor victory if you got enough cards up top to end with a positive cash amount.
Anyways, although we may never know the true odds of winning Klondike, the above puzzle (from the Riddler) is solvable (but not a cakewalk).
link to original post
Let’s lay out the things we need to consider to tackle this problem. The first thing is the board of cards we’ve arranged on the table to begin the game. That board includes seven face-up cards (and 21 face-down cards). The second thing is the deck that we’ll deal from during the game. That deck includes the 24 remaining cards, but because we’re dealing three cards at a time, we only care about eight of them (the ones that will appear at the top of the three-card draws). These two sets — the seven face-up cards and eight in the deck — will determine whether we’ll play a nightmare game of Solitaire in which we have no legal moves.
What’s left to do is an intricate counting problem involving some very big numbers. In what follows, I’ve adapted the approach of solver Jacob Kes, who was kind enough to provide the code he used for counting card combinations.
Brute force is always the most elegant solution! The key criteria in this problem are a card’s rank (that is, whether it’s a number or a face card) and its color (red or black). You can use a computer script to find all the possible combinations for the seven face-up cards by rank and color only — for example, a red five, a black seven, a red jack, etc.3 But we can’t forget the suits!
For each set of seven number-and-color combinations, there’s a corresponding number M of possible combinations of seven cards (now taking suit into account). For each of these combinations, you can calculate how many of the remaining cards (of which there are 45 and might end up in the deck) wouldn’t allow us any legal Solitaire moves — let’s call this number N. That’s how many are neither aces, which can be moved to a designated area on the Solitaire table, nor are cards that can be moved onto a face-up card.
This means that, for a given seven cards, our chance of a nightmare deal is of P = (N choose 8)/(45 choose 8). Each face-up card combination has a 1/(52 choose 7) chance of occurring, so for a total probability, you just need to sum M*P/(52 choose 7) over all of the face-up number-and-color combinations. This winds up being 643,746,385,468/257,479,369,193,475, or about 0.0025, or about 1/400.
In addition to walking through the intricate math to arrive at this number, Laurent Lessard calculated the probability of a nightmare game in the version where you deal one card at a time. It’s significantly lower: about 1.8⋅10^−7
Good luck avoiding a nightmare game, you brave, solitary warriors.
----------------------------------------------------------------
Henry and Tom decide to bet on a coin flip. Henry wins on heads, Tom wins on tails.
It’s $1 per flip and they are really bored, so they decide to do one million flips. After each flip, the loser pays the winner $1. The players may bring any bankroll they want, but if a player goes bankrupt he automatically loses the game. Tom is very wealthy and tells Henry he's bringing a million dollars to the game. Henry is not rich and decides to bring an amount that will give him 50% confidence of not going bankrupt. How much should Henry bring?
I get the same answer*** as the Wizard above
***: $337 when rounded
Formula used:
~0.67449σ = "50% of proportion within"
n = "number of coin flips" = 1 million
~0.67449 x0.5 x (n^0.5) = 0.337245 x (1,000,000^0.5) = 0.337245 x 1000 = 337.245
Note: I don't use this (or a variation of this formula) very often, so I could have used it incorrectly / applied it wrong.
Quote: Ace2I respectfully disagree and suggest that you double (cough, cough) check your answers
link to original post
Because I am a relative beginner at this, can you give me a hint? (in spoilers if you like)
Something like, "the formula you used was correct in this situation, but the numbers are wrong", thanks
Quote: Ace2This hint was in my last reply!
link to original post
Thanks.
But when I looked up the SD for a single coin flip online, I found it was 0.5 from multiple sources (the above figure assumes 1 for the SD).
If 674 is closer to correct, please explain why my original POSTED answer was wrong.
Edited (about 455pm, Pac time): In the spoiler see word in capitals, for the edit.
Quote: ksdjdjQuote: Ace2This hint was in my last reply!
link to original post
Thanks.
.~674.
But when I looked up the SD for a single coin flip online, I found it was 0.5 from multiple sources (the above figure assumes 1 for the SD).
If 674 is closer to correct, please explain why my original answer was wrong.
link to original post
...the formula you are using may be trying to calculate the probability of finishing at or below your bankroll point after 1,000,000 tosses. This doesn't take into account the possibility that you can go through your bankroll before 1,000,000 tosses, but then finish with a positive bankroll value.
In effect, the question is this:
What is the smallest positive integer N such that, if you toss a coin 1 million times, the probability that you will never, at any point, have at least N more tails than heads is 1/2 or less?
First, let me refer to what I'll call the Ace2 conjecture.
This says that the probability of ruin at any point is double that of after the million flips, where the game goes on even if one player goes negative. Please note this holds true only in games with 0 EV.
Thus, we want to first find a bankroll where the probability Henry loses all of it or more after the million flips is 25%. The probability the standard normal variable is under -0.674 is about 25%.
The standard deviation of the million flips is 1000.
A bankroll of 674 will give us a Z statistic of -0.674: z=(-674-0)/1000.
Per the Ace2 conjecture, we double that to get our desired 50%.
Though the Ace2 conjecture only works exactly for an even money coin flip (standard normal distribution), it is a good approximation for similar bets like pass line and baccarat. It even works fairly well for blackjack or any bet that has a low edge and a standard deviation close to 1.
Quote: Ace2Though the Ace2 conjecture only works exactly for an even money coin flip (standard normal distribution), it is a good approximation for similar bets like pass line and baccarat. It even works fairly well for blackjack or any bet that has a low edge and a standard deviation close to 1.
link to original post
I find the ratio is closer to 1.7, based on the Player bet in baccarat, but am still working on it. This ratio seems to get lower as the number of trials goes up. For example, at 5000 trials it looks closer to 1.4, but that would be a pretty big "session."
Perhaps your comment was directed at bets much closer to an EV of 0.
For now, I'm trying to find a formula that works for bets like the Player bet that is not as long as Schlesinger's (from page 132 of BJA), but have not been successful.
Quote: ThatDonGuy
...the formula you are using may be trying to calculate the probability of finishing at or below your bankroll point after 1,000,000 tosses. This doesn't take into account the possibility that you can go through your bankroll before 1,000,000 tosses, but then finish with a positive bankroll value.
In effect, the question is this:
What is the smallest positive integer N such that, if you toss a coin 1 million times, the probability that you will never, at any point, have at least N more tails than heads is 1/2 or less?
link to original post
Based on the effective question, doesn't that mean the bankroll requirement needs to be rounded up, never down?
I have a hunch that $674 leaves Henry short just slightly more than half of the time.
Please be more more specific. What bankroll for 5000 trials and what ratio does 1.7 pertain to?Quote: WizardQuote: Ace2Though the Ace2 conjecture only works exactly for an even money coin flip (standard normal distribution), it is a good approximation for similar bets like pass line and baccarat. It even works fairly well for blackjack or any bet that has a low edge and a standard deviation close to 1.
link to original post
I find the ratio is closer to 1.7, based on the Player bet in baccarat, but am still working on it. This ratio seems to get lower as the number of trials goes up. For example, at 5000 trials it looks closer to 1.4, but that would be a pretty big "session."
Perhaps your comment was directed at bets much closer to an EV of 0.
For now, I'm trying to find a formula that works for bets like the Player bet that is not as long as Schlesinger's (from page 132 of BJA), but have not been successful.
link to original post
Here's an example I just ran:
For 900 passline bets (about 30 hours of play), your expectation is -12.7 units +/- 30. With a 60 unit bankroll, your exact RoR is 9.95% (obtained via Markov chain). Using a normal distribution, the chance of finishing 900 bets with a loss of >=60 is 5.75%, which is (60 - 12.7) / 30 = 1.577 SDs to the left of expectations. Therefore, according to the Ace2 conjecture, the chance of falling below 60 units at any time during the 900 bets is 5.75% * 2 = 11.5%, within 1.6% absolute of the exact answer.
Quote: WizardThis topic has inspired me to create my new Session Risk of Ruin Calculator. It took the good part of two days to do, which means nobody will probably ever use it.
link to original post
I just used it! Was cool. I found it confusing at first as the directions say “put the bet amount” in, but then the entry said “bankroll.” It took me a few minutes to realize this was number of betting units. Consider making two entries for “base bet amount” and “bankroll” in dollars to idiot proof it.
On another topic, I've been asked about a probability for a bad-beat jackpot promotion. I think it's pretty easy to do by direct math and the situation is so unlikely, I don't think a simulation would likely ever come across it, even if run for years.
This is for a paying client, so I hate to just throw it out there and ask you guys to work for nothing. If you like straight combinatorial math/poker problems, send me a PM. I imagine this will take any of the math wizard on the forum only about 5-10 minutes, so compensation would be only a free dinner or something like that.

In the three-player Game of Mediocrity, you win by not winning too much.
Each round, every player secretly picks a number from 0 to 10. The numbers are simultaneously revealed, and the median number wins that number of points. (If two or more players pick the same number, then the winner is randomly selected from among them.)
After five rounds, the winner is whoever has the median number of points. (Again, if two or more players have the same score, then the winner is randomly selected from among them.)
With one round remaining, players A, B and C have 6, 8 and 10 points, respectively. Player A sighs and writes down “3,” but fails to do so in secret. Players B and C both see player A’s number (and both see that the other saw A’s number), and will take care to write their own numbers in secret.
Assuming everyone plays to win, what numbers should B and C choose?


