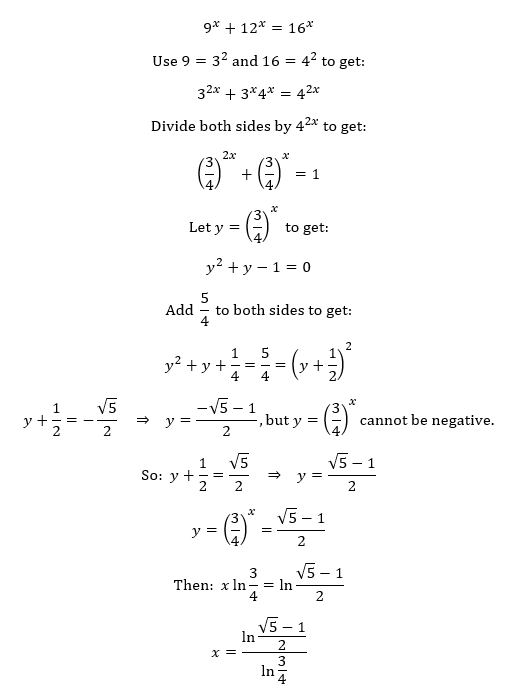Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
6 is divisible by 1, 2 and 3. 1 + 2 + 3 = 6
28 is divisible by 1, 2, 4, 7 and 14. 1 + 2 + 4 + 7 + 14 = 28.
For any rational number a/b, a number is a/b-perfect if the sum of the proper divisors equals to the original number multiplied by (a/b). For example 10 is 4/5-perfect since 1 + 2 + 5 = 8 = (4/5)*10. The normal definition of a perfect number is when this fraction a/b = 1.
Given we are in the year 2022, what is the smallest 20/22-perfect number? The sum of the proper divisors is equal to (20/22)*(the number)?
Can you find a second such number? (I don't know).
Quote: ThatDonGuyI have a feeling this answer earns the QI Klaxon, but the "obvious" answer is...
If you start with the cards in order 13, 11, 9, 7, 5, 3, 1, 2, 4, 6, 8, 10, 12, it requires 12 reversals.
I don't think more than that is possible without getting into an infinite loop.
link to original post
Sorry, incorrect.
I'll let this ride another day although a solve would be surprising, shocking really.
Quote: GialmereQuote: ThatDonGuyI have a feeling this answer earns the QI Klaxon, but the "obvious" answer is...
If you start with the cards in order 13, 11, 9, 7, 5, 3, 1, 2, 4, 6, 8, 10, 12, it requires 12 reversals.
I don't think more than that is possible without getting into an infinite loop.
link to original post
Sorry, incorrect.For 13 cards, there are 13! = 6,227,020,800 decks you might need to consider. Computer assistance advised.
I'll let this ride another day although a solve would be surprising, shocking really.
link to original post
I discovered that even if you limit it to the numbers 1-7, you need 16
Quote: teliotHappy "Perfect Number Day" everyone! It's 6/28.
6 is divisible by 1, 2 and 3. 1 + 2 + 3 = 6
28 is divisible by 1, 2, 4, 7 and 14. 1 + 2 + 4 + 7 + 14 = 28.
For any rational number a/b, a number is a/b-perfect if the sum of the proper divisors equals to the original number multiplied by (a/b). For example 10 is 4/5-perfect since 1 + 2 + 5 = 8 = (4/5)*10. The normal definition of a perfect number is when this fraction a/b = 1.
Given we are in the year 2022, what is the smallest 20/22-perfect number? The sum of the proper divisors is equal to (20/22)*(the number)?
Can you find a second such number? (I don't know).
link to original post
While we're waiting, here are some Perfect Number facts:
Easy enough to prove: the sum of the integers from 1 to any prime number that is one less than a power of 2 (a "Mersenne prime") is a perfect number.
Examples: 1 + 2 + (2^2 - 1) = 6; 1 + 2 + ... + (2^3 - 1) = 28; 1 + 2 + ... + (2^5 - 1) = 496.
Slightly harder to prove: these are the only even perfect numbers.
Conjectured, but not proven (nor disproven) yet: there are no odd perfect numbers.
Quote: Gialmere...I'll let this ride another day although a solve would be surprising, shocking really...
Using brute force, I agree that with seven numbers - e.g. starting with 4762153 - it can take 16 turns. This one takes 6 turns to get the 7 into last position. I can't imagine doing 13 numbers (6Bn of them) in a similar fashion!
Quote: teliotHappy "Perfect Number Day" everyone! It's 6/28.
6 is divisible by 1, 2 and 3. 1 + 2 + 3 = 6
28 is divisible by 1, 2, 4, 7 and 14. 1 + 2 + 4 + 7 + 14 = 28.
For any rational number a/b, a number is a/b-perfect if the sum of the proper divisors equals to the original number multiplied by (a/b). For example 10 is 4/5-perfect since 1 + 2 + 5 = 8 = (4/5)*10. The normal definition of a perfect number is when this fraction a/b = 1.
Given we are in the year 2022, what is the smallest 20/22-perfect number? The sum of the proper divisors is equal to (20/22)*(the number)?
Can you find a second such number? (I don't know).
link to original post
Quote: Gialmere...I'll let this ride another day although a solve would be surprising, shocking really...
This shows where I essentially gave in! I couldn't see an obvious pattern emerging and could see myself putting together a tree almost by hand. While that may eventually show the largest route for 7 numbers, I couldn't see how to shorten the process for the next levels. I was looking for an answer based on loops as there was a puzzle previously on this topic and suspect this is similar or related logic.
However this method would only show there was a maximum while trying to move from level N to N-1. I'm pure guessing it's aboput N or N-1, which would give an upper bound but not an actual maximum. Saying it was less, than say 78 (12+...+1) or 91, doesn't really add any value, especially as we know it's 16 for 7 numbers!
I think you mean 13! permutations not 13! ďdecksĒ. If I understand the problem correctly there is only one deck of 13 cardsQuote: Gialmere
For 13 cards, there are 13! = 6,227,020,800 decks you might need to consider. Computer assistance advised.
Quote: teliotCan you find a second such number? (I don't know).
link to original post
At first, I had problems finding the first number, but then I discovered I was about 200 years before my time - I was looking for 18/22 numbers.
I have checked every number up to 4 million (so far), and have found no other numbers. That doesn't mean they don't exist; after all, there are no perfect numbers between 8128 and 33,550,336.
Quote: GialmereQuote: ThatDonGuyI have a feeling this answer earns the QI Klaxon, but the "obvious" answer is...
If you start with the cards in order 13, 11, 9, 7, 5, 3, 1, 2, 4, 6, 8, 10, 12, it requires 12 reversals.
I don't think more than that is possible without getting into an infinite loop.
link to original post
Sorry, incorrect.For 13 cards, there are 13! = 6,227,020,800 decks you might need to consider. Computer assistance advised.
I'll let this ride another day although a solve would be surprising, shocking really.
link to original post
I was surprised to find that there is no "easy" way to solve this one
The answer is 80; it is sequence A000375 in the Online Encyclopedia of Integer Sequences.
Apparently, these numbers have a name - "Topswops" (note the spelling; it's not "Topswaps") - and they have something to do with John Conway, who apparently didn't stop with (Conway's) Life.
Quote: GialmereIt's toughie Tuesday. Another card conundrum...
Suppose you have a shuffled deck containing 13 cards. Each card has a number from 1 to 13 and each number appears on exactly one card. You look at the number on the first card ó suppose itís k ó and then you reverse the order of the first k cards. You continue this procedure ó reading the first cardís number and then reversing the order of the corresponding number of cards ó until the first card reads 1. Clearly, the number of reversals depends on the initial order of the cards.
What is the largest number of reversals that you might have to do?Suppose you remove the club suit from a deck of cards, shuffle them, and then place them in a stack in front of you. You draw the top card which is, say, the 4. You place the 4 back on top and lift up, in order, the top four cards. You reverse them by placing the top card (the 4) back on top of the stack, then the card that was beneath the 4, then the next card down and finally the last card.
You then draw the new top card, say, the jack (which equals 11), you put it back on top and lift up the top eleven cards. Again you reverse them by placing the jack back on top of the stack, then the card that was beneath the jack etc. You continue reversals until you draw the ace thus ending the sequence.
Buzzzzz...
This problem was developed by the mathematician John Conway in the 1970s ó he called it topswops. Itís essentially a programming problem and has garnered attention from prominent computer scientists including Donald Knuth. But itís a tough programming problem. For the 13-card example, there are 13! = 6,227,020,800 decks you might need to consider. Thatís manageable for a computer to search through, but if the deck starts to grow, the problem becomes unwieldy.
Solver Thad Beier animated one series of 80 reversals:
You can also find the answers for decks of various sizes in the On-Line Encyclopedia of Integer Sequences, but even that only goes up to a deck of 17 cards.
For extra credit, I asked what the maximum number of reversals was for a deck of 53 cards. Thatís roughly 4x10^69
possible decks, and the answer to this question is unknown. Thad estimated that his program wouldnít finish for about a trillion years, and Chris Bergman answered simply ďlol.Ē The best known lower bound on the true answer is 3,185, established in 2011 by Jarek Wroblewski during a three-month computer programming contest. Solver Hector Pefo offered the following proof that the answer is 4,012 ó however it still awaits peer review.
Quote: Ace2I think you mean 13! permutations not 13! ďdecksĒ. If I understand the problem correctly there is only one deck of 13 cardsQuote: Gialmere
For 13 cards, there are 13! = 6,227,020,800 decks you might need to consider. Computer assistance advised.
link to original post
Good point. I just cut and pasted from the above solve.
---------------------------------------------------------------

Quote: ThatDonGuyQuote: GialmereQuote: ThatDonGuyI have a feeling this answer earns the QI Klaxon, but the "obvious" answer is...
If you start with the cards in order 13, 11, 9, 7, 5, 3, 1, 2, 4, 6, 8, 10, 12, it requires 12 reversals.
I don't think more than that is possible without getting into an infinite loop.
link to original post
Sorry, incorrect.For 13 cards, there are 13! = 6,227,020,800 decks you might need to consider. Computer assistance advised.
I'll let this ride another day although a solve would be surprising, shocking really.
link to original post
I was surprised to find that there is no "easy" way to solve this one
The answer is 80; it is sequence A000375 in the Online Encyclopedia of Integer Sequences.
Apparently, these numbers have a name - "Topswops" (note the spelling; it's not "Topswaps") - and they have something to do with John Conway, who apparently didn't stop with (Conway's) Life.
link to original post
Correct!!
Wow! Talk about under the wire.
I checked up to 4.5m and found no others.Quote: ThatDonGuyQuote: teliotCan you find a second such number? (I don't know).
link to original post
At first, I had problems finding the first number, but then I discovered I was about 200 years before my time - I was looking for 18/22 numbers.
I have checked every number up to 4 million (so far), and have found no other numbers. That doesn't mean they don't exist; after all, there are no perfect numbers between 8128 and 33,550,336.
link to original post
I think there is an open problem related to these a/b-perfect numbers, whether for any a/b < 1 there is a solution. Foggy memory here.

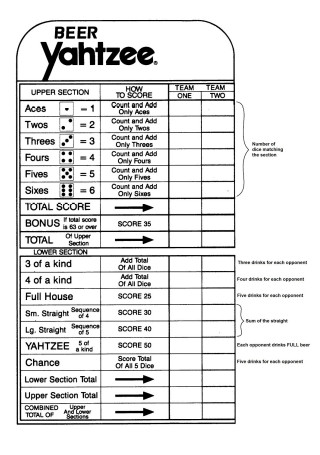
For these puzzles it's assumed you know the rules of Yahtzee. A scorecard for point consultation is provided if needed (just ignore the beer drinking).
a) Keep the 4s and reroll the 5s.
b) Keep all five dice.
c) Keep one 4 and one 5 and reroll the rest.
1) Whatís the best strategy for maximizing your expected score?
2) What's the second best strategy?
Whatís the best strategy for hitting a large straight and winning the game?
1) Should you keep the 2s and reroll the other dice, keep both pairs and reroll the other die, or reroll all the dice looking for a higher scoring 3 of a kind?
2) What if it's actually the first turn of the game and all categories are open. What's the best play?
Quote: teliotI checked up to 4.5m and found no others.
None found (besides the first one) through 100 million
Quote: ThatDonGuyQuote: teliotI checked up to 4.5m and found no others.
None found (besides the first one) through 100 million
link to original post
Wow, thank you!
Quote: GialmereIt's family game night. Let's play...
For these puzzles it's assumed you know the rules of Yahtzee. A scorecard for point consultation is provided if needed (just ignore the beer drinking).Suppose that youíre playing a one-turn game of Yahtzee in which your only consideration is maximizing your score on this single turn. After your second roll your five dice show 4, 4, 4, 5, 5. Should you...
a) Keep the 4s and reroll the 5s.
b) Keep all five dice.
c) Keep one 4 and one 5 and reroll the rest.
1) Whatís the best strategy for maximizing your expected score?
2) What's the second best strategy?Itís your final turn in a heated game of Yahtzee, and the only combination of dice you still need to score is a large straight. On the first of your three possible rolls during your final turn, you roll 1, 2, 4, 5 and X (where X is not a 3). You're gutshot. You could reroll the X in hopes of getting a 3. Or you could reroll the 1 and the X in hopes that they eventually land in some combination of 3 and 6. Or perhaps something completely different!
Whatís the best strategy for hitting a large straight and winning the game?Once again it's your final turn in a heated game but this time you need 3 of a kind. Your first roll yields 1, 1, 2, 2, 3.
1) Should you keep the 2s and reroll the other dice, keep both pairs and reroll the other die, or reroll all the dice looking for a higher scoring 3 of a kind?
2) What if it's actually the first turn of the game and all categories are open. What's the best play?
link to original post
Answers:
#2: Roll the X; the Large Straight probability is 11/36
#3: Keep just the 2's
Dog Hand
1.1 With 4,4,4,5,5 you should (b) Keep all five dice. Your score is 25 points. You can only be beaten by a small or large straight or Yahtzee or by a hand that totals 26 or higher.
1.2 Your second best option is (a) keep the 3 fours and roll for 4oaK or Yahtzee.
2. With a 1-2-4-5-X (X not a three) you should reroll the die with X. This gives you 2 rolls to hit a 3, you miss 25,36 of the time and make it 11/36 = 0.305556 of the time.
If you retain 2-4-5, your total probability of a large straight is 0.24537 in this way:
Roll a 3 + (1 or 6) and stop. P= 4/36 = 0.111111
Roll 3 + (2,4,5),reroll one die and make (1,6) P=6/36*2/6=0.055556
Roll two 3s, reroll one die and make (1,6) P= 1/36*2/6= 0.009259
Roll a (1,6) + (2,4,5), reroll one die and make a 3 P= 9/36*1/6=0.055556
Roll a (2,4,5) + (2,4,5), reroll both dice and make a 3 + (1,6) P= 9/36* 2/36= 0.013889
Total chance of Large Straight = 0.24537
3a) Keeping the pair of 2s is better than keeping 1-1-2-2.
With a pair of 2-2, you have three chances to roll a 2, twice.
With 1-1,2-2 you have one chance to roll a either a 1 or 2, twice.
3*1*2 > 1*2*2 so keep the 2-2 and reroll 3 dice.
3b) With a 1-1-2-2-3 at the beginning of the game you should roll for a full house both times, because its worth 25 points. If you miss, you should count your hand as 2 points in the ONEs category
9^x + 12^x = 16^x
Quote: WizardFind x:
9^x + 12^x = 16^x
link to original post
Answer:
9^x + 12^x = 16^x
;-)
Dog Hand
Quote: teliotGiven we are in the year 2022, what is the smallest 20/22-perfect number? The sum of the proper divisors is equal to (20/22)*(the number)?
Going off on a slight tangent, the remaining years this century that have corresponding numbers (well, numbers < 4 million - that's all that I have checked so far) are:
2025 (10 is a 2025 number)
2028 (14)
2034 (34)
2036 (117)
2044 (33)
2045 (9)
2076 (95)
You should have asked this in 2013; 1,444,352 is a 2013 number.
This is fabulous! I love it.Quote: ThatDonGuyQuote: teliotGiven we are in the year 2022, what is the smallest 20/22-perfect number? The sum of the proper divisors is equal to (20/22)*(the number)?
Going off on a slight tangent, the remaining years this century that have corresponding numbers (well, numbers < 4 million - that's all that I have checked so far) are:
2025 (10 is a 2025 number)
2028 (14)
2034 (34)
2036 (117)
2044 (33)
2045 (9)
2076 (95)
You should have asked this in 2013; 1,444,352 is a 2013 number.
link to original post
Quote: teliotHappy "Perfect Number Day" everyone! It's 6/28.
6 is divisible by 1, 2 and 3. 1 + 2 + 3 = 6
28 is divisible by 1, 2, 4, 7 and 14. 1 + 2 + 4 + 7 + 14 = 28.
For any rational number a/b, a number is a/b-perfect if the sum of the proper divisors equals to the original number multiplied by (a/b). For example 10 is 4/5-perfect since 1 + 2 + 5 = 8 = (4/5)*10. The normal definition of a perfect number is when this fraction a/b = 1.
Given we are in the year 2022, what is the smallest 20/22-perfect number? The sum of the proper divisors is equal to (20/22)*(the number)?
Can you find a second such number? (I don't know).
link to original post
I have checked up to 109 and I have only found one.
I have an idea for doing something more scientific than just searching through billions of numbers. Let n=p1a1⋅⋅⋅pkak be the prime factorization of n (the primes are distinct and all the exponents are at least 1). Let σ(n) be the sum of the divisors of n, including n itself. It is well-known that σ(n)=Π(piai+piai-1+...+1)=Π((piai+1-1)/(pi-1)) (all products run from i=1 to k),
so σ(n)/n=Π((piai+1-1)/(piai+1(pi-1))).
We want this product to be equal to 1+(20/22)=21/11, because we included n among the divisors.
The factor corresponding to the prime p is always at least 1+1/p and less than 1+1/(p-1). 11 must be among the primes dividing n, so the product of the factors corresponding to the other primes is at most (21/11)/(12/11)=21/12=7/4. This implies that n cannot be divisible by 8, because then the factor corresponding to p=2 alone would be greater than 7/4, and if n is divisible by 4, then it is equal to
You could try choosing some primes including 11 such that the product of 1+1/p over these primes is less than 21/11, but the product of 1+1/(p-1) is greater than 21/11 and then play around with the exponents. However, it would require some remarkable cancellation and sometimes remarkable cancellation happens, for example,
σ(197064960)/197064960=8/3 or σ(42990848)/42990848=4 (this means that the sum of the divisors of 42990848, excluding 42990848, is 3*42990848), but the examples I have found where n is large but σ(n)/n is a fraction with relatively small denominator and denominator tend to be divisible by a high power of 2 and have σ(n)/n>2. There is only one number between 107 and 108 such that σ(n)/n<2 and the denominator of σ(n)/n in its lowest terms is less than 100, σ(14381055)/14381055=128/65.
Thank you for this excellent analysis (as usual) and opening this topic up to a theoretical conversation. It is similar to some of the first arguments for conditions that must be placed on an odd perfect number.Quote: GM
I have checked up to 109 and I have only found one.
I have an idea for doing something more scientific than just searching through billions of numbers. Let n=p1a1⋅⋅⋅pkak be the prime factorization of n (the primes are distinct and all the exponents are at least 1). Let σ(n) be the sum of the divisors of n, including n itself. It is well-known that σ(n)=Π(piai+piai-1+...+1)=Π((piai+1-1)/(pi-1)) (all products run from i=1 to k),
so σ(n)/n=Π((piai+1-1)/(piai+1(pi-1))).
We want this product to be equal to 1+(20/22)=21/11, because we included n among the divisors.
The factor corresponding to the prime p is always at least 1+1/p and less than 1+1/(p-1). 11 must be among the primes dividing n, so the product of the factors corresponding to the other primes is at most (21/11)/(12/11)=21/12=7/4. This implies that n cannot be divisible by 8, because then the factor corresponding to p=2 alone would be greater than 7/4, and if n is divisible by 4, then it is equal toFurthermore, if n is even, then it cannot be divisible by either 3 or 5.44.
You could try choosing some primes including 11 such that the product of 1+1/p over these primes is less than 21/11, but the product of 1+1/(p-1) is greater than 21/11 and then play around with the exponents. However, it would require some remarkable cancellation and sometimes remarkable cancellation happens, for example,
σ(197064960)/197064960=8/3 or σ(42990848)/42990848=4 (this means that the sum of the divisors of 42990848, excluding 42990848, is 3*42990848), but the examples I have found where n is large but σ(n)/n is a fraction with relatively small denominator and denominator tend to be divisible by a high power of 2 and have σ(n)/n>2. There is only one number between 107 and 108 such that σ(n)/n<2 and the denominator of σ(n)/n in its lowest terms is less than 100, σ(14381055)/14381055=128/65.
link to original post
Is there a typo in your formula for σ(n)/n in the denominator?
Do you know anything about the (a/b)-perfect question I asked? I just have this vague memory. I'm trying to follow your logic to show there is no solution when a/b = 1/4 (my program found no solutions), but even that leads to issues.
Quote: teliot
Is there a typo in your formula for σ(n)/n in the denominator?
Do you know anything about the (a/b)-perfect question I asked?
Indeed, there is a typo. The correct formula is σ(n)/n=Π((piai+1-1)/(piai(pi-1))).
I don't know anything about (a/b)-perfect numbers. After finding σ(42990848)/42990848=4, I discovered that if the sum of the divisors is is a proper multiple of the number then the number is called multiply perfect, here is a webpage about them: http://wwwhomes.uni-bielefeld.de/achim/mpn.html.
Okay, I think I've proved there is no solution when a/b = 1/4, 1/8, 1/16, ... and it's fairly trivial using the formula above. Next up, a/b = 1/6.Quote: GMQuote: teliot
Is there a typo in your formula for σ(n)/n in the denominator?
Do you know anything about the (a/b)-perfect question I asked?
Indeed, there is a typo. The correct formula is σ(n)/n=Π((piai+1-1)/(piai(pi-1))).
I don't know anything about (a/b)-perfect numbers. After finding σ(42990848)/42990848=4, I discovered that if the sum of the divisors is is a proper multiple of the number then the number is called multiply perfect, here is a webpage about them: http://wwwhomes.uni-bielefeld.de/achim/mpn.html.
link to original post
Many years ago I published a paper on perfect numbers reproving a theorem of Lehmer, that there are only finitely many perfect numbers for any fixed limit on the number of primes the number could have. My co-author Walter Carlip dutifully obfuscated what is a fairly easy argument. In that paper, I make the comment that, "H.-J. Kanold [6] has studied σ(N) = kN for k rational, and proved that there are only finitely many primitive (and hence only finitely many odd) solutions N with a fixed number of prime factors." So, yes, somewhere in my distant past ...
Here it is
Quote: DogHandAnswers:
#1: (b) is best, followed by (a)
#2: Roll the X; the Large Straight probability is 11/36
#3: Keep just the 2's
Dog Hand
link to original post
Quote: gordonm888
1.1 With 4,4,4,5,5 you should (b) Keep all five dice. Your score is 25 points. You can only be beaten by a small or large straight or Yahtzee or by a hand that totals 26 or higher.
1.2 Your second best option is (a) keep the 3 fours and roll for 4oaK or Yahtzee.
2. With a 1-2-4-5-X (X not a three) you should reroll the die with X. This gives you 2 rolls to hit a 3, you miss 25,36 of the time and make it 11/36 = 0.305556 of the time.
If you retain 2-4-5, your total probability of a large straight is 0.24537 in this way:
Roll a 3 + (1 or 6) and stop. P= 4/36 = 0.111111
Roll 3 + (2,4,5),reroll one die and make (1,6) P=6/36*2/6=0.055556
Roll two 3s, reroll one die and make (1,6) P= 1/36*2/6= 0.009259
Roll a (1,6) + (2,4,5), reroll one die and make a 3 P= 9/36*1/6=0.055556
Roll a (2,4,5) + (2,4,5), reroll both dice and make a 3 + (1,6) P= 9/36* 2/36= 0.013889
Total chance of Large Straight = 0.24537
3a) Keeping the pair of 2s is better than keeping 1-1-2-2.
With a pair of 2-2, you have three chances to roll a 2, twice.
With 1-1,2-2 you have one chance to roll a either a 1 or 2, twice.
3*1*2 > 1*2*2 so keep the 2-2 and reroll 3 dice.
3b) With a 1-1-2-2-3 at the beginning of the game you should roll for a full house both times, because its worth 25 points. If you miss, you should count your hand as 2 points in the ONEs category
link to original post
Correct!
For the most part
Letís walk carefully through two possible strategies.
First, suppose you keep all your dice. This oneís easy: Youíll score 25 points for sure for your full house. For the other strategy to be preferable, it needs to net more than 25 points, on average.
So suppose you risk it and reroll your two 5s. There are 36 (or 6×6) ways those two dice could fall. In only one of those cases will they both land as 4s, giving you your 50-point Yahtzee. In five other cases, where your two rerolled dice match, youíll have another full house and earn 25 points. In the other 30 cases, youíll wind up with a three- or four-of-a-kind, which is worth only the sum your five dice. The average of the sum of your dice in those 30 cases is 19. So, putting this all together, your expected score when rerolling your two 5s is (1/36)(50) + (5/36)(25) + (30/36)(19) ≈ 20.69 points.
In fact, youíre better off keeping the numbers you have in front of you than you are rerolling any combination of your dice. A handful of solvers wrote programs to calculate the expected score of possible rerolls. Every option, from rerolling a single die to rerolling all five, scores less than 25 points in expectation. But surprisingly to me, if you were forced to reroll, your best bet would be to keep one 4 and one 5 and just let the other three rip. Youíd score an average of 22.76 points in that case, since you can catch a few straights that way.
Why? There are two future rolls ó your second and third rolls ó we need to consider. If we reroll just the X, there is a 1/6 chance we complete our large straight with the first roll, and a 5/6 chance that we donít. If we still need another roll, there is again a 1/6 chance we complete our large straight and a 5/6 chance that we donít. Overall, thatís a (1/6) + (5/6)(1/6) = 11/36 ≈ .306 chance you complete your large straight using this strategy.
If we reroll the 1 and the X ó keeping 2, 4 and 5 ó itís a little more complicated. For your first reroll, solver Guy Moore explained, there are four outcomes, each of which has an optimal next step for the second reroll.
--On the first reroll, thereís a 1/4 chance that you get two ďuselessĒ numbers ó 2, 4 or 5. If you do get one of those useless numbers, the best thing to do is reroll each die, with a 1/9 chance of completing the large straight.
--On the first reroll, thereís a 7/36 chance to get one 3 and another useless number. If that happens, you should keep the 3 and throw the remaining die, which has a 1/3 chance of getting your remaining 1 or 6.
--On the first reroll, thereís a 4/9 chance to get at least one 1 or 6 and no 3. In that event, you should keep either the 1 or the 6 and reroll the remaining die, which has a 1/6 chance of hitting your remaining 3.
--And, finally, thereís a 1/9 chance to get a 3 and a 1 or a 6 on the first reroll. That completes our large straight, so thereís nothing to do next!
Putting those probabilities together, you have a (1/4)(1/9) + (7/36)(1/3) + (4/9)(1/6) + (1/9)(1) ≈ 27.8 percent chance to hit that large straight. Thatís less than the 30.6 chance you had rerolling just one die. In other words, the strategies succeed with 11/36 and 10/36 probabilities, respectively.
For Part #2, you should keep the 2s and reroll the other three dice after your first roll. Surprisingly, the second best option is to keep only the 3. The third is to reroll all the dice.
If it's after your second roll you should keep both pairs and reroll the 3. If it's after your third roll, score the aces.

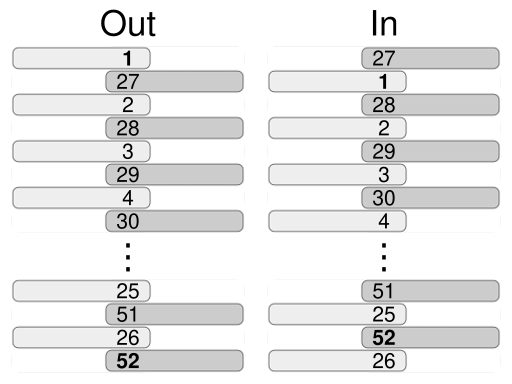
The faro shuffle is also called a perfect shuffle. With a standard deck, the cards are divided into two piles of 26 cards. The two piles are then shuffled together in such a way that they perfectly interlace with a card from one pile followed by a card from the other pile followed by a card from the first pile and so on with no clumps of two or three cards from the same pile.
Since the way the cards are combined is known, it is possible to track and/or manipulate the position of cards in the deck. Because of this, the faro shuffle is studied by a motley assortment of card cheats, magicians and mathematicians.
A faro shuffle where the top card of the deck remains on top is called an "out-shuffle". If the top card becomes the second from the top, it's called an "in-shuffle". (See diagram.)
How many faro out-shuffles in a row are required to cycle the deck back to its original sequence?
How many in-shuffles would it take?
The second case takes all 52 permutations to get back to the starting position, after 26 shuffles it has reversed the pack.
Quote: Gialmere
The faro shuffle is also called a perfect shuffle. With a standard deck, the cards are divided into two piles of 26 cards. The two piles are then shuffled together in such a way that they perfectly interlace with a card from one pile followed by a card from the other pile followed by a card from the first pile and so on with no clumps of two or three cards from the same pile.
Since the way the cards are combined is known, it is possible to track and/or manipulate the position of cards in the deck. Because of this, the faro shuffle is studied by a motley assortment of card cheats, magicians and mathematicians.
A faro shuffle where the top card of the deck remains on top is called an "out-shuffle". If the top card becomes the second from the top, it's called an "in-shuffle". (See diagram.)
How many faro out-shuffles in a row are required to cycle the deck back to its original sequence?
How many in-shuffles would it take?
link to original post
I agree wth charliepatrick's reply above.
It is interesting to consider this problem for a deck consisting of 2n cards. The number of out-shuffles required for 2n cards is the same as the number of in-shuffles required for 2n-2 cards, because an out-shuffle is the same as keeping the top and bottom cards fixed and doing an in-shuffle of the remaining 2n-2 cards. The number of shuffles required does not follow an obvious pattern, but https://mathweb.ucsd.edu/~ronspubs/83_05_shuffles.pdf contains the formula and a proof of the fact that the number of in-shuffles required is always at most 2n.
Anyway...
Using only a straightedge and compass, construct an angle:
(a) of 18 degrees;
(b) whose sine is 3/10.
Note that (a) and (b) are different angles.
Bonus points if you can tell me what upcoming event involves an angle whose sine is 3/10 - actually, it's an angle twice that large.
Interesting! Very related to gambling. Let me use one deck of card to verify this.
The number of out-shuffles required for 2x26 cards is 8;
The number of in-shuffles required for 2x26 cards is 52;
The number of in-shuffles required for 2x26-2=50 cards is 8.
Quote: ThatDonGuySpeaking of Toughie Tuesdays, I've got a couple, including one for the real math boffins as I am not sure a solution even exists.
Anyway...
Using only a straightedge and compass, construct an angle:
(a) of 18 degrees;
(b) whose sine is 3/10.
Note that (a) and (b) are different angles.
Bonus points if you can tell me what upcoming event involves an angle whose sine is 3/10 - actually, it's an angle twice that large.
link to original post
Are you British? Why do I see so many British words in your question?
For your question (a), Iíve looked into my compass on my iPhone and found all 360-degree marks on it, so you can just easily draw a 18 degree angle using these marks.
Quote: ThatDonGuySpeaking of Toughie Tuesdays, I've got a couple, including one for the real math boffins as I am not sure a solution even exists.
Anyway...
Using only a straightedge and compass, construct an angle:
(a) of 18 degrees;
(b) whose sine is 3/10.
Note that (a) and (b) are different angles.
Bonus points if you can tell me what upcoming event involves an angle whose sine is 3/10 - actually, it's an angle twice that large.
link to original post
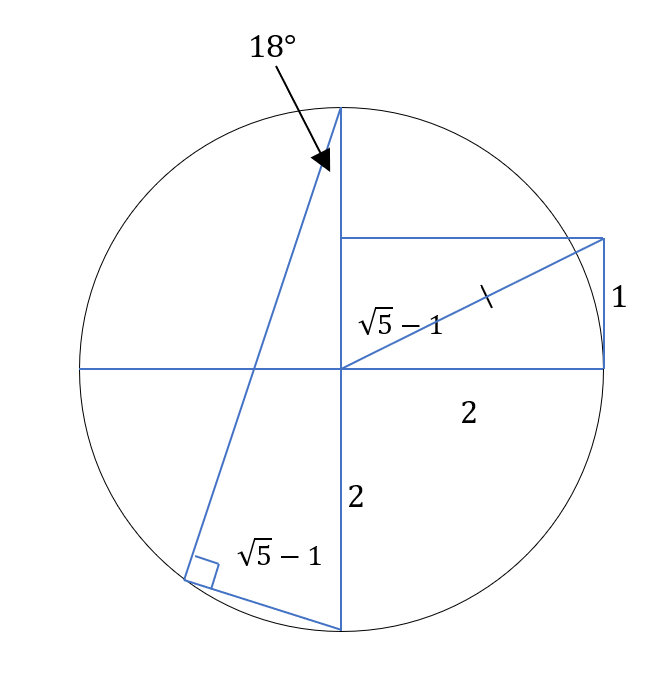
Here's a way to find the sine of 18 degrees, which is one fourth of the quantity of the square root of five minus one.
And the second picture roughly shows the compass and straightedge construction of that angle.
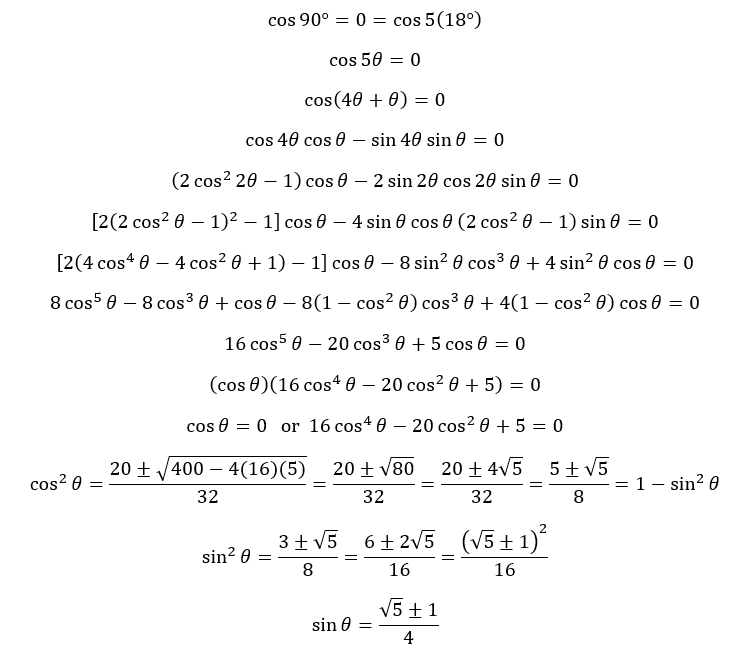
To construct an angle whose sine is 3/10, first make a circle of diameter 10. Then place the compass's point on an end (A) of a diameter and draw an arc of radius 3 intersecting the circle at B. Then connect B to the other end (C) of the diameter. The sine of angle ACB is 3/10.
Which event has a connection of that angle? Is it MLB's All Star Game?
Quote: charliepatrick^I'm not sure how to do it without resorting to brute force, or in my case a spreadsheet!
The first case sorts itself out after 8 iterations, #2 moves to position 3, 5, 9, 17, 33, 14, 27, 2.
The second case takes all 52 permutations to get back to the starting position, after 26 shuffles it has reversed the pack.
link to original post
Quote: GMI agree with charliepatrick's reply above.
It is interesting to consider this problem for a deck consisting of 2n cards. The number of out-shuffles required for 2n cards is the same as the number of in-shuffles required for 2n-2 cards, because an out-shuffle is the same as keeping the top and bottom cards fixed and doing an in-shuffle of the remaining 2n-2 cards. The number of shuffles required does not follow an obvious pattern, but https://mathweb.ucsd.edu/~ronspubs/83_05_shuffles.pdf contains the formula and a proof of the fact that the number of in-shuffles required is always at most 2n.
link to original post
Correct!!
Good show.
Note that by combining in and out shuffles many card tricks can be created. Of course, learning how to accurately faro shuffle while appearing to be casually shuffling a deck all while keeping up a conversation (perhaps telling jokes to an audience) would be a time consuming task to say the least.
------------------------------------------------------
Quote: acesideQuote: ThatDonGuySpeaking of Toughie Tuesdays, I've got a couple, including one for the real math boffins as I am not sure a solution even exists.
Anyway...
Using only a straightedge and compass, construct an angle:
(a) of 18 degrees;
(b) whose sine is 3/10.
Note that (a) and (b) are different angles.
Bonus points if you can tell me what upcoming event involves an angle whose sine is 3/10 - actually, it's an angle twice that large.
link to original post
Are you British? Why do I see so many British words in your question?
For your question (a), Iíve looked into my compass on my iPhone and found all 360-degree marks on it, so you can just easily draw a 18 degree angle using these marks.
link to original post
aceside,
In geometry, a "compass" is the device on the right in the picture below:

It is used to draw arcs or full circles.
Hope this helps!
Dog Hand
Quote: GMQuote: Gialmere
The faro shuffle is also called a perfect shuffle. With a standard deck, the cards are divided into two piles of 26 cards. The two piles are then shuffled together in such a way that they perfectly interlace with a card from one pile followed by a card from the other pile followed by a card from the first pile and so on with no clumps of two or three cards from the same pile.
Since the way the cards are combined is known, it is possible to track and/or manipulate the position of cards in the deck. Because of this, the faro shuffle is studied by a motley assortment of card cheats, magicians and mathematicians.
A faro shuffle where the top card of the deck remains on top is called an "out-shuffle". If the top card becomes the second from the top, it's called an "in-shuffle". (See diagram.)
How many faro out-shuffles in a row are required to cycle the deck back to its original sequence?
How many in-shuffles would it take?
link to original post
I agree wth charliepatrick's reply above.
It is interesting to consider this problem for a deck consisting of 2n cards. The number of out-shuffles required for 2n cards is the same as the number of in-shuffles required for 2n-2 cards, because an out-shuffle is the same as keeping the top and bottom cards fixed and doing an in-shuffle of the remaining 2n-2 cards. The number of shuffles required does not follow an obvious pattern, but https://mathweb.ucsd.edu/~ronspubs/83_05_shuffles.pdf contains the formula and a proof of the fact that the number of in-shuffles required is always at most 2n.
link to original post
I looked up Faro Shuffle on Wikipedia. It says:
For a deck size of N = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, and 52,
the number of in-shuffles needed are
2, 4, 3, 6, 10, 12, 4, 8, 18, 6, 11, 20, 18, 28, 5, 10, 12, 36, 12, 20, 14, 12, 23, 21, 8, and 52, respectively;
the number of out-shuffles needed are
1, 2, 4, 3, 6, 10, 12, 4, 8, 18, 6, 11, 20, 18, 28, 5, 10, 12, 36, 12, 20, 14, 12, 23, 21, and 8, respectively;
Whatís the probability of winning the fire bet (all six points won)?
Hint: no calculus required
1/6 * 2/5 = 2/30, chance of loosing is 3/5=18/30 so not counting ties the chance of making it not counting ties* is (2/30)/(2/30+18/30) = 1/10
Then we look at 4 points:
2/6*2/5 = 4/30 vs 18/30
(4/30)/(4/30+18/30) = 2/9
3 Points:
3/6*2/5 = 6/30 = 1/5 vs 3/5
(1/5) / (1/5+3/5) = 1/4
2 Points:
(4/6)*(2/5) = 8/30 vs 18/30
(8/30) / (8/30+18/30) = 8/26
1 Point
(5/6)*(2/5) = (10/30) vs 18/30
(10/30) / (10/30 + 18/30) = 10/28
0 points = 2/5
multiplies all those together: 2/5 * 10/28 * 8/26 * 1/4 * 2/9 * 1/10 = 480/1965600
*Tie = making a point you already have
Quote: ChesterDogQuote: ThatDonGuySpeaking of Toughie Tuesdays, I've got a couple, including one for the real math boffins as I am not sure a solution even exists.
Anyway...
Using only a straightedge and compass, construct an angle:
(a) of 18 degrees;
(b) whose sine is 3/10.
Note that (a) and (b) are different angles.
Bonus points if you can tell me what upcoming event involves an angle whose sine is 3/10 - actually, it's an angle twice that large.
link to original post
Here's a way to find the sine of 18 degrees, which is one fourth of the quantity of the square root of five minus one.
And the second picture roughly shows the compass and straightedge construction of that angle.
To construct an angle whose sine is 3/10, first make a circle of diameter 10. Then place the compass's point on an end (A) of a diameter and draw an arc of radius 3 intersecting the circle at B. Then connect B to the other end (C) of the diameter. The sine of angle ACB is 3/10.
Which event has a connection of that angle? Is it MLB's All Star Game?
link to original post
Your second answer is invalid as you have no way of "making a circle of diameter 10" as your straightedge is unmarked. Even if you make a circle and say that its diameter is 10, you need to find a way to determine what, exactly, is a "length of 3" for the arc radius.
The event in question is the upcoming World Track & Field Championships - the "wedge" that is the legal landing area for the throwing events has an angle twice the one of the angle whose sine is 3/10 (it's the smallest angle in a 5-3-5 triangle).
Here's how I solved the first one:
Let O be the center of a circle of arbitrary radius; call the radius 1
Draw a line through O; label the two points where it intersects the circle A and C - this is a diameter of the circle
Construct a perpendicular to AC through O; label the two points where it intersects the circle B and D - this is also a diameter of the circle
OA = OB = OC = OD = 1
Let M be the midpoint of OB; MB = OB = 1/2, and MA = sqrt(5) / 2
Construct the point N on BD such that MN = MA; ON = (sqrt(5) - 1) / 2
(NA)^2 = 1^2 + ((sqrt(5) - 1) / 2)^2 = 1 + (6 - 2 sqrt(5)) / 4 = (5 - sqrt(5)) / 2
Construct point X on the circumference of the circle such that AX = AN
AOX is a triangle with OA = OX = 1 and AX = sqrt((5 - sqrt(5)) / 2)
Let Z be the midpoint of AX; sin AOZ = AZ / AO = 1/2 sqrt((5 - sqrt(5)) / 2) = sqrt((5 - sqrt(5) / 8) = sin 36
AOZ is 36 degrees; bisect it to get an angle (well, two) of 18 degrees.
Proof that sin 36 = sqrt((5 - sqrt(5)) / 8):
sin 36 = 2 sin 18 cos 18
sin 36 = 2 sin 18 sin 72
sin 36 = 2 sin 18 x 2 sin 36 cos 36
1/4 = sin 18 cos 36
1/4 = sin 18 sin 54
1/4 = sin (36 - 18) sin (36 + 18)
1/4 = (sin 36 cos 18 - cos 36 sin 18)(sin 36 cos 18 + cos 36 sin 18)
1/4 = (sin 36 cos 18)^2 - (cos 36 sin 18)^2
1/4 = sin^2 36 cos^2 18 - cos^2 36 sin^2 18
1/4 = sin^2 36 cos^2 18 - (1 - sin^2 36) sin^2 18
1/4 = sin^2 36 cos^2 18 - sin^2 18 + sin^2 36 sin^2 18
1/4 = sin^2 36 (cos^2 18 + sin^2 18) - sin^2 18
1/4 = sin^2 36 - sin^2 18
1/4 = 4 sin^2 18 cos^2 18 - sin^2 18
1/4 = 4 sin^2 18 (1 - sin^2 18) - sin^2 18
1/4 = 3 sin^2 18 - 4 sin^4 18
Let t = sin^2 18:
4 t^2 - 3 t + 1/4 = 0
t = (3 +/- sqrt(5)) / 8
(3 + sqrt(5)) / 8 > 1/4, but sin^2 18 < sin^2 30, which is 1/4, so t = (3 - sqrt(5)) / 8
sin 18 = sqrt((3 - sqrt(5)) / 8)
sin^2 36 = sin^2 18 + 1/4 = (5 - sqrt(5)) / 8
Quote: ThatDonGuyQuote: ChesterDogQuote: ThatDonGuySpeaking of Toughie Tuesdays, I've got a couple, including one for the real math boffins as I am not sure a solution even exists.
Anyway...
Using only a straightedge and compass, construct an angle:
(a) of 18 degrees;
(b) whose sine is 3/10.
Note that (a) and (b) are different angles.
Bonus points if you can tell me what upcoming event involves an angle whose sine is 3/10 - actually, it's an angle twice that large.
link to original post
Here's a way to find the sine of 18 degrees, which is one fourth of the quantity of the square root of five minus one.
And the second picture roughly shows the compass and straightedge construction of that angle.
To construct an angle whose sine is 3/10, first make a circle of diameter 10. Then place the compass's point on an end (A) of a diameter and draw an arc of radius 3 intersecting the circle at B. Then connect B to the other end (C) of the diameter. The sine of angle ACB is 3/10.
Which event has a connection of that angle? Is it MLB's All Star Game?
link to original post
Your second answer is invalid as you have no way of "making a circle of diameter 10" as your straightedge is unmarked. Even if you make a circle and say that its diameter is 10, you need to find a way to determine what, exactly, is a "length of 3" for the arc radius.
The event in question is the upcoming World Track & Field Championships - the "wedge" that is the legal landing area for the throwing events has an angle twice the one of the angle whose sine is 3/10 (it's the smallest angle in a 5-3-5 triangle).
Here's how I solved the first one:
Let O be the center of a circle of arbitrary radius; call the radius 1
Draw a line through O; label the two points where it intersects the circle A and C - this is a diameter of the circle
Construct a perpendicular to AC through O; label the two points where it intersects the circle B and D - this is also a diameter of the circle
OA = OB = OC = OD = 1
Let M be the midpoint of OB; MB = OB = 1/2, and MA = sqrt(5) / 2
Construct the point N on BD such that MN = MA; ON = (sqrt(5) - 1) / 2
(NA)^2 = 1^2 + ((sqrt(5) - 1) / 2)^2 = 1 + (6 - 2 sqrt(5)) / 4 = (5 - sqrt(5)) / 2
Construct point X on the circumference of the circle such that AX = AN
AOX is a triangle with OA = OX = 1 and AX = sqrt((5 - sqrt(5)) / 2)
Let Z be the midpoint of AX; sin AOZ = AZ / AO = 1/2 sqrt((5 - sqrt(5)) / 2) = sqrt((5 - sqrt(5) / 8) = sin 36
AOZ is 36 degrees; bisect it to get an angle (well, two) of 18 degrees.
Proof that sin 36 = sqrt((5 - sqrt(5)) / 8):
sin 36 = 2 sin 18 cos 18
sin 36 = 2 sin 18 sin 72
sin 36 = 2 sin 18 x 2 sin 36 cos 36
1/4 = sin 18 cos 36
1/4 = sin 18 sin 54
1/4 = sin (36 - 18) sin (36 + 18)
1/4 = (sin 36 cos 18 - cos 36 sin 18)(sin 36 cos 18 + cos 36 sin 18)
1/4 = (sin 36 cos 18)^2 - (cos 36 sin 18)^2
1/4 = sin^2 36 cos^2 18 - cos^2 36 sin^2 18
1/4 = sin^2 36 cos^2 18 - (1 - sin^2 36) sin^2 18
1/4 = sin^2 36 cos^2 18 - sin^2 18 + sin^2 36 sin^2 18
1/4 = sin^2 36 (cos^2 18 + sin^2 18) - sin^2 18
1/4 = sin^2 36 - sin^2 18
1/4 = 4 sin^2 18 cos^2 18 - sin^2 18
1/4 = 4 sin^2 18 (1 - sin^2 18) - sin^2 18
1/4 = 3 sin^2 18 - 4 sin^4 18
Let t = sin^2 18:
4 t^2 - 3 t + 1/4 = 0
t = (3 +/- sqrt(5)) / 8
(3 + sqrt(5)) / 8 > 1/4, but sin^2 18 < sin^2 30, which is 1/4, so t = (3 - sqrt(5)) / 8
sin 18 = sqrt((3 - sqrt(5)) / 8)
sin^2 36 = sin^2 18 + 1/4 = (5 - sqrt(5)) / 8
link to original post
Thanks for an explanation of the use of that angle whose sine is 3/10!
Here's a picture of my compass and straightedge construction, which is probably self-explanatory. But afterwards is a description in words.
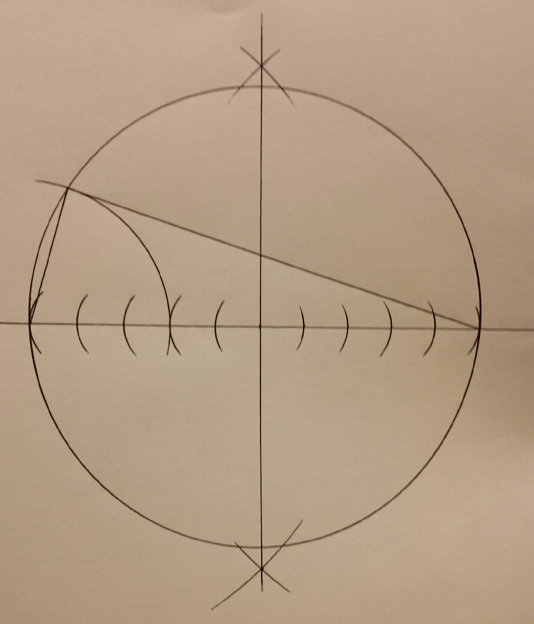
The construction started with one point and a line through that point.
Then I set my compass with a small separation, which I called 1 unit, and drew five arcs to the right of the center point and five to the left. The center of each arc is the intersection between the previous arc and the diameter. I then drew a circle of diameter 10 units about the center point.
Finally, I made an arc of radius 3 units about the left end of the diameter. I drew a line from the circle's and arc's intersection to the other end of the diameter.
By the way, I see that I didn't have to make the perpendicular bisector of the diameter.
Disagree. You are calculating for all six points won, correct ?Quote: Torghatten480/1965600 = 1/4095I assume you have won 5 points. Odds for first rolling correct point and then making it is
1/6 * 2/5 = 2/30, chance of loosing is 3/5=18/30 so not counting ties the chance of making it not counting ties* is (2/30)/(2/30+18/30) = 1/10
Then we look at 4 points:
2/6*2/5 = 4/30 vs 18/30
(4/30)/(4/30+18/30) = 2/9
3 Points:
3/6*2/5 = 6/30 = 1/5 vs 3/5
(1/5) / (1/5+3/5) = 1/4
2 Points:
(4/6)*(2/5) = 8/30 vs 18/30
(8/30) / (8/30+18/30) = 8/26
1 Point
(5/6)*(2/5) = (10/30) vs 18/30
(10/30) / (10/30 + 18/30) = 10/28
0 points = 2/5
multiplies all those together: 2/5 * 10/28 * 8/26 * 1/4 * 2/9 * 1/10 = 480/1965600
*Tie = making a point you already have
link to original post
Next time there are five points to make, so the odds of proceeding is 20/(20+6)=10/13.
Continue this process to get 8/11, 2/3, 4/7, 2/5.
The chances of getting all six before a seven is the product of these which is 1024/15015, or about 6.82%.
DisagreeQuote: charliepatrickWhen you have no points made there are 24 ways to make your first point (6 points left to make * 4 ways per point) versus 6 ways to make the 7-out. Thus the chances of getting to one down, five to go is 24/(24+6) = 4/5.
Next time there are five points to make, so the odds of proceeding is 20/(20+6)=10/13.
Continue this process to get 8/11, 2/3, 4/7, 2/5.
The chances of getting all six before a seven is the product of these which is 1024/15015, or about 6.82%.
link to original post
I think my solution assumed you just needed to roll the six numbers before a seven; rather than the shooter, before a 7-out, has to establish six different points (perhaps amongst others) and win those. In the latter case the fractions would be lower, but the principle the same.Quote: Ace2]Disagree
link to original post
[

During a magic show a magician opens a brand new pack of cards and removes the jokers and extras. He then thumb fans the deck showing the audience all 52 cards and hands it to a randomly selected spectator who thoroughly shuffles it. The volunteer hands the deck back to the magician who places it on a table, calls for silence to concentrate and then writes something down on a piece of paper which he also places face down on the table near the deck and in full view of the audience.
The magician then deals out twelve cards face down on the table and instructs the spectator to select and turn over any four of them. The remaining cards are returned to the bottom of the deck. The cards selected are the 3 of diamonds, the 6 and 10 of spades and the king of clubs.
The magician states that he will deal cards on top of each of the four, dealing enough cards to bring the total of each pile up to ten. For example, he deals seven cards face down onto the three, counting each of them off "4, 5, 6, 7, 8, 9, 10." Then onto the six "7, 8, 9, 10." No cards are needed on the ten. Each face card counts as ten (a la blackjack), so no cards are placed on the king.
The magician has the spectator add up the values of the original four cards: 3 + 6 + 10 + 10 = 29. He hands the volunteer the deck and tells her to count out and turn over the 29th card. It's the 5 of hearts. Finally, to the oohs and ahhs of the audience, the magician picks up the sheet of paper showing he had written a large 5 and a heart on it. Amazing!
How did he do it?