Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: camapl
Divide the 25 racehorses into 5 groups. Each group in turn will comprise 5 heats. The winner from each heat will comprise the 6th race. The 7th, and last, race will include 2 horses from race 6 (the second and third fastest), 2 horses from the heat of the fastest in race 6 (the second and third fastest from that heat), and 1 horse from the heat of the second fastest in race 6 (the second fastest from that heat). The fastest 3 horses, in order are (1) the winner of race 6, (2) the winner of race 7, (3) the runner up of race 7.
link to original post
Correct!
Quote: camaplWho is she, and where shall I inquire as to hire her to carry my bags?
link to original post
She is a Victoria's Secret model.
Sorry I don't know the answer to these puzzles, the basis of it came in a dream last night and I thought it an interesting puzzle.
Dream Version
The initial version had a pack of 100 cards numbered 1 to 100. The aim was to collect cards with the largest total but they either had to be all odd or all even. You drew four random cards and could elect to keep any or none. If you kept any odd cards, all cards kept had to be odd, you could not keep any even ones. Similarly for even cards. Also once any cards were selected you had to keep them, unlike Yangzte.
The game consisted of two draws. Obviously in the second draw, if you had kept some from the first draw, you would pick either all the odd or even cards as appropriate. If not you would keep the highest total. You add up all the cards you managed to collect.
Dice Version
I think it makes the maths easier, since each roll can be independent from the others and there's no question about replacement for the second round, if you assume you roll 100-sided dice (or 6-sided dice) i.e. numbered 1 to N. (Sadly this makes the maths slightly difficult as the average of the even numbers is greater than the odd ones, so if it's easier assume an infinite dice where the average is N/2 for both!)
So the question is what is your best strategy/approach and the expected outcome?
Sorry for such a hard problem, please ignore it as I've given in, especially if the discarded cards stay out (as it's rather like trying to work out all the combos for draw poker). I have worked out the average before the draw and that if they're all the same type you keep any 74 or greater. Also if they all add up to more than 148 and are all larger than 25, I think you keep them all (it happens to beat the average from redrawing the lot).Quote: charliepatrick...Rolling dice and either keeping odd or even...
Here's an easier one from today's paper.
If you reverse the two digits of Adam's age, add one and divide by two, you'll end up with Adam's age. How old is Adam?
Quote: WizardQuote: camaplWho is she, and where shall I inquire as to hire her to carry my bags?
link to original post
She is a Victoria's Secret model.
link to original post
Well, considering what Victoria's Secret clothing looks like, couldn't she get by with just a large business envelope? ;-)
Dog Hand
Correct - well done!Quote: ksdjdj37
link to original post
This puzzle was just played in the latest season of survivor (seasons 37, episode 1).
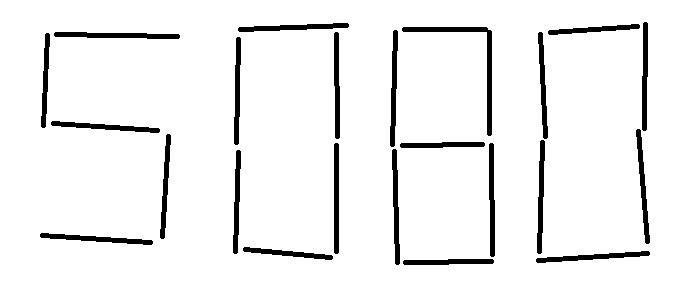
Moving two of these lines only (they used bones on the show), make the largest whole number you can.
It depends on what they accept as a number.
Solution 1, which is questionable:
Move the bottom line of the 5 to the upper right of the 5, making it a 9
Move the center line of the 8 to the left of the 5 and rotate it 90 degrees, making it a 1 - a small 1, mind you, but a 1
The result is 19,000
Solution 2:
Move the bottom line of the 5 to the upper right of the 5, making it a 9
Move the lower left line of the first 0 to the center of the first 0, making it an 8
The result is 9980
This is why I rarely win arguments with her.
Quote: ThatDonGuy
It depends on what they accept as a number.
Solution 1, which is questionable:
Move the bottom line of the 5 to the upper right of the 5, making it a 9
Move the center line of the 8 to the left of the 5 and rotate it 90 degrees, making it a 1 - a small 1, mind you, but a 1
The result is 19,000
Solution 2:
Move the bottom line of the 5 to the upper right of the 5, making it a 9
Move the lower left line of the first 0 to the center of the first 0, making it an 8
The result is 9980
link to original post
They never said on the show what counts as a number, but I will say that the correct answer expresses numbers the way calculators did in the 1970's.
The correct answer is greater than both your solutions.
Quote: charliepatrickThe best I can see is from the first zero, take off the top and bottom lines, (thus 0 becomes 11 and the capability to add a 1 somewhere) and then create a 1 at the front. Thus it becomes 151180. If you were allowed to move them or you could squeeze it imbetween to create 5 111 8 0, that would be even better!
link to original post
The correct answer is greater than your solution.
However, after looking at Charlie's solution it occurs to me that by combining his approach with hers
Quote: Wizard...The correct answer is greater than your solution...
Quote: charliepatrickQuote: Wizard...The correct answer is greater than your solution...
I can see you can create 5E88 by taking the two right bones from the first 0 and using one to create "E" and the other to convert the second "0" into "8".
link to original post
I get E980.
Quote: charliepatrickI can see you can create 5E88 by taking the two right bones from the first 0 and using one to create "E" and the other to convert the second "0" into "8".
link to original post
No letters are allowed. Just 0 to 9.
Quote: TumblingBonesHowever, after looking at Charlie's solution it occurs to me that by combining his approach with hers
can be created.511,801
link to original post
Quote: TumblingBonesOops... I misquoted the wife (not the first time).
should have been 50001 instead of 59801. It's the 8 that gets modified
However, after looking at Charlie's solution it occurs to me that by combining his approach with herscan be created.511,801
link to original post
Quote: unJonQuote: TumblingBonesOops... I misquoted the wife (not the first time).
should have been 50001 instead of 59801. It's the 8 that gets modified
However, after looking at Charlie's solution it occurs to me that by combining his approach with herscan be created.511,801
link to original postDo a bit better by adding the new 1 before the last 0 for 511,810
link to original post
As an idea, although I can't see it works, it to look at it from the other side, so it starts out 0805.
Quote: unJonDo a bit better by adding the new 1 before the last 0 for 511,810
link to original post
That is correct! I think that one is beer worthy.
Quote: WizardQuote: unJonDo a bit better by adding the new 1 before the last 0 for 511,810
link to original post
That is correct! I think that one is beer worthy.
link to original post
How about...
Take the top and bottom sticks from the left zero (which converts the zero into 11) and move them to the end.
By the way, I assumed the rules do not allow us to use a stick to "rearrange" the others.
Dog Hand
Quote: DogHandQuote: WizardQuote: unJonDo a bit better by adding the new 1 before the last 0 for 511,810
link to original post
That is correct! I think that one is beer worthy.
link to original post
How about...5,118,011?
Take the top and bottom sticks from the left zero (which converts the zero into 11) and move them to the end.
By the way, I assumed the rules do not allow us to use a stick to "rearrange" the others.
Dog Hand
link to original post
If that works, and I think it doesn’t because it takes 2 sticks to make a one, then you still can do better with;
Quote: DogHand5,118,011?
Take the top and bottom sticks from the left zero (which converts the zero into 11) and move them to the end.
By the way, I assumed the rules do not allow us to use a stick to "rearrange" the others.
Dog Hand
link to original post
I have to assume that wouldn't be allowed, because a 1 must be made with two sticks.
If I ask this puzzle again, I'll make it clear the numbers must be made in the way classic calculators from the 70's.

Dog Hand
Direct: https://www.youtube.com/watch?v=Kov2G0GouBw
Here is a summary of the rules:
Paper covers rock
Rock crushes lizard
Lizard poisons Spock
Spock smashes scissors
Scissors cuts paper
Lizard eats paper
Spock vaporizes rock
Scissors decapitates lizard
Paper disproves Spock
Rock crushes scissors
I got to wondering what other numbers of symbols besides 3 and 5 does this work for?
It seems the answer is any odd number. With an even number, the game would either be unbalanced or you would have to add a lot of tying combinations that are not the same symbol.
What is an automated way to establish rules for any odd number of symbols?
Here is just one answer, for n symbols.
1. Number the symbols from 1 to n.
2. The players play. Assuming they throw x and y.
3. If abs(x-y) is odd, then the lower number wins.
4. If abs(x-y) is even, then the higher number wins.
If the case of the the Lizard Spock Expansion, their rules can be attained by numbering the symbols as follows:
1=paper
2=rock
3=lizard
4=Spock
5=scissors
Any comments or suggestions for improvement?
To find the rule for any given symbol, turn the circle so the symbol is at 12 o'clock (or consider all the symbols going round the circle like runners at the race track, except they are going round clockwise). Now consider you are looking forward, i.e. towards 1 o'clock. If you were in a race you'd be losing to all those infront of you, and beating all those behind you. (Due to it being a circle, one only considers half a lap as the maximum distance you can lead or trail someone else.) Thus you would lose to any at 1 o'clock, 2 o'clock...5, and beat any at 11 o'clock, 10 o'clock...7.
By construction you beat half and lose to half. Also if you beat someone (you are between zero and half a lap ahead of them) then their logic (they are less than half a lap behind you) shows they lose. Similarly for your losses and their wins.
In your 5-way example, using X mod N, you can see that 1 is trailing 2 and 3, but leading 0 and -1 (being equivalent to 5 and 4).
For any odd n, you can do the following. Arrange the symbols at the vertices of a regular n-gon. For each k, 1≤k≤(n-1)/2, you can decide either that all symbols beat the symbol k steps clockwise from them, or that all symbols are beaten by the symbol k steps clockwise from them, and these choices are independent.
In terms of graph theory, you have a complete graph on n vertices, and you want to make the edges directed in such a way that every vertex has indegree (n-1)/2 and outdegree (n-1)/2. There must be lots and lots of ways of doing this, and it looks like a problem that someone must have studied before.
Quote: charliepatrickPut the symbols on a circle with the one you're considering placed at at 12 o'clock; and make the rule you are losing to the ones in front of you and beating the ones behind you.
link to original post
I considered doing it that way too. However, I didn't want to add the step about deciding who is at 12:00.
One hundred people answer two math questions. 75% get the first question right and 75% get the second question right.
(1) What's the highest number of people who could have answered both questions correctly?
(2) What's the lowest number of people who could have answered both questions correctly?
(3) Which number is more likely, and why?
(4) What's the highest number of people who could have answered both questions incorrectly?
(5) What's the lowest number of people who could have answered both questions incorrectly?
Exactly!Quote: unJonNumber three needs an assumption about correlation.
link to original post
Quote: charliepatrickPut the symbols on a circle with the one you're considering placed at at 12 o'clock; and make the rule you are losing to the ones in front of you and beating the ones behind you.
To find the rule for any given symbol, turn the circle so the symbol is at 12 o'clock (or consider all the symbols going round the circle like runners at the race track, except they are going round clockwise). Now consider you are looking forward, i.e. towards 1 o'clock. If you were in a race you'd be losing to all those infront of you, and beating all those behind you. (Due to it being a circle, one only considers half a lap as the maximum distance you can lead or trail someone else.) Thus you would lose to any at 1 o'clock, 2 o'clock...5, and beat any at 11 o'clock, 10 o'clock...7.
By construction you beat half and lose to half. Also if you beat someone (you are between zero and half a lap ahead of them) then their logic (they are less than half a lap behind you) shows they lose. Similarly for your losses and their wins.
In your 5-way example, using X mod N, you can see that 1 is trailing 2 and 3, but leading 0 and -1 (being equivalent to 5 and 4).
link to original post
I was thinking about this post last night in bed while I was trying to fall asleep.
It occurred to me that my method would work for a prime number (greater than 2) of symbols only. Your would work for any odd number.
I think the way I might express the same principle is you draw a the shortest arc between the two choices on the circle. Then rotate that arc so it looks like a rainbow, with the ends at the bottom. If player x's choice is on the right end of the rainbow, then x wins. Otherwise, y does. Of course, you have to decide who is x and who is y, a step I prefer to avoid.
Quote: MichaelBluejayOn Alexa's "Question of the Day" today, about 75% of people got the first question right, and about 75% got the second question right. That got me thinking of this series of questions, which would seem to be good for a middle school math class:
One hundred people answer two math questions. 75% get the first question right and 75% get the second question right.
(1) What's the highest number of people who could have answered both questions correctly?
(2) What's the lowest number of people who could have answered both questions correctly?
(3) Which number is more likely, and why?
(4) What's the highest number of people who could have answered both questions incorrectly?
(5) What's the lowest number of people who could have answered both questions incorrectly?
link to original post
(1) 75 - 75 is possible if everybody that got the first one right got the second one right, and 76 is impossible as that would mean that more than 75 got the first one right.
(2) 50 - 25 got the first one wrong, and 25 got the second one wrong, so at most 50 got any wrong, which means at least 50 got both right.
(3) From a mathematical standpoint, 50 - given 25 people that got the first one wrong, it is more likely to have 25 of the remaining 75 get the second one right than for all 25 right answers to come from the same 25.
Of course, it actually depends on the people and the questions.'
(4) 25 - it can't be more as only 25 got the first question wrong.
(5) Zero, in, for example, the case where 25 people got the first one right and a different 25 got the second one right.
A new casino game consists of the following:
There are 50 discs on the table, numbered 1, 2, 3, ..., 49, 50. On one side of the discs is a large red area, and on the other is a large black area.
The game is played with a dealer and one player.
Starting with the dealer and alternating, the two choose a disc and place it in either the red or black areas.
For example, the game may begin with the dealer placing disc 25 in Red, then the player placing disc 50 in Red, then the dealer placing disc 49 in Black, and so on until all 50 discs are placed. There is no restriction as to where any of the discs can be played (e.g. there do not have to be 25 in each color at the end).
The player wins the difference between the sums of the numbers in the two areas. For example, if Red's total is 650 and Black's is 625, then the player wins 25.
Assuming the player is trying to maximize the final difference and the dealer is trying to minimize it, what is the expected result?
I agree with you, except:Quote: ThatDonGuy
(1) 75 - 75 is possible if everybody that got the first one right got the second one right, and 76 is impossible as that would mean that more than 75 got the first one right.
(2) 50 - 25 got the first one wrong, and 25 got the second one wrong, so at most 50 got any wrong, which means at least 50 got both right.
(3) From a mathematical standpoint, 50 - given 25 people that got the first one wrong, it is more likely to have 25 of the remaining 75 get the second one right than for all 25 right answers to come from the same 25.
Of course, it actually depends on the people and the questions.'
(4) 25 - it can't be more as only 25 got the first question wrong.
(5) Zero, in, for example, the case where 25 people got the first one right and a different 25 got the second one right.
link to original post
Person A gets the 1st math question right and Person B gets it wrong. Person A is more likely to get the 2nd question right than Person B, because Person A showed math superiority on question 1. In other words, the correct answers are correlated. So, it's more likely that 75 people answered both questions correctly than that 50 answered both questions correctly.
Quote: ThatDonGuyHere's one, straight out of the first round (recently ended) of this year's USA Mathematical Talent Search, slightly modified to fit this forum....
link to original post
If the dealer picks 50, the player is gonna pick 1, to maximize the difference.
But if the dealer picks 1, then the player can pick 50, because it's the same difference in the other direction.
So it seems the dealer should pick a number in the middle, to limit how far the player can play from the first disc.
So if the dealer picks 25, then the player picks 50. (Or if the dealer picks 26, then the player picks 1.)
In either case, the difference after the first round is 25.
For the second round, the dealer can play ±1 to the current difference, to reduce the difference to 1, so the dealer plays 26.
This is also keeping with the idea of playing in the middle so the player can't go for an extreme.
Discs played = (25,26) (50), difference is 1.
Interestingly, the play is now flipped: When the game started, the dealer was the one to deviate from 0 or 1, but now the player gets to do that.
The player plays 49 to maximize the difference.
The dealer plays 48 to take the difference back down to 1, and the player plays 47 to maximize the difference.
From here, on each turn the dealer plays the largest number available to minimize the diff., and the player plays the largest available to maximize the diff. So for the dealer, 46, 44, 42, 40, etc., and for the player 45, 43, 41, 39, etc.
Summing all those, I get a difference of 25. But I'm not confident about either the expected strategy or the final result.
FWIW, the sum of 1-50 is 1275, and the average is 25.5.
Quote: MichaelBluejayQuote: ThatDonGuyHere's one, straight out of the first round (recently ended) of this year's USA Mathematical Talent Search, slightly modified to fit this forum....
link to original postThat's an interesting problem.
If the dealer picks 50, the player is gonna pick 1, to maximize the difference.
But if the dealer picks 1, then the player can pick 50, because it's the same difference in the other direction.
So it seems the dealer should pick a number in the middle, to limit how far the player can play from the first disc.
So if the dealer picks 25, then the player picks 50. (Or if the dealer picks 26, then the player picks 1.)
In either case, the difference after the first round is 25.
For the second round, the dealer can play ±1 to the current difference, to reduce the difference to 1, so the dealer plays 26.
This is also keeping with the idea of playing in the middle so the player can't go for an extreme.
Discs played = (25,26) (50), difference is 1.
Interestingly, the play is now flipped: When the game started, the dealer was the one to deviate from 0 or 1, but now the player gets to do that.
The player plays 49 to maximize the difference.
The dealer plays 48 to take the difference back down to 1, and the player plays 47 to maximize the difference.
From here, on each turn the dealer plays the largest number available to minimize the diff., and the player plays the largest available to maximize the diff. So for the dealer, 46, 44, 42, 40, etc., and for the player 45, 43, 41, 39, etc.
Summing all those, I get a difference of 25. But I'm not confident about either the expected strategy or the final result.
FWIW, the sum of 1-50 is 1275, and the average is 25.5.
link to original post
No; the actual answer is quite a bit higher.
I had a strategy similar to yours: the player should always play in the color with the higher sum, to increase the difference, and the dealer should always play in the color with the lower sum, to decrease it if possible.
The dealer starts with 1 in Red; the player plays 50 in Red. (51, 0 - that is, 51 Red, 0 Black)
The dealer then plays 49 in Black (51, 49); the player plays 48 Red (99, 49)
The dealer and player then continue 47, 46, 45, and so on down to 1, with the dealer always playing Black and the player always playing Red. Each pair of plays reduces the difference by 1; there were 24 pairs after the first pair, so the final result difference would be 51 - 24 = 27.
That is also not close to the correct answer.
Quote: ThatDonGuyHere's one, straight out of the first round (recently ended) of this year's USA Mathematical Talent Search, slightly modified to fit this forum....50 discs...
After thought - I did wonder whether it was better for you to pick 48 if the dealer didn't, but your aim is to keep the difference small until the [50,49] is played. For instance it might start R1 B48, R 50 R49, B47 and now your advantage is lost. So I suspect you're best to stick with the dealer's pair.
Quote: MichaelBluejay@charliepatrick, starting with the second sentence in your first paragraph, I didn't understand that sentence or any that followed it.
link to original post
it seems counter intutivie but in the early stages the Player is trying to keep the difference to a minimum until the Dealer picks either 49 or 50. This is because when the [49,50] pair is breached it will add 99 to one of the colours. The Player doesn't want the other colour to have much of a lead.
The suggested strategy to achieve this is always pick a number adjacent to the Dealer and choose the other colour. The method of splitting the numbers into pairs ([1,2] [3,4]...[47,48]) and picking the other number in the pair ensures this. The best the Dealer can do is pick all the even numbers, whereby you pick the odd ones. Thus this eventually creates a difference of 24 in the favour, of say, Red. (e.g. 1 Black, 2 Red = +1 Red). (If the Dealer deviates from choosing even numbers, you can pick the even number and reduce the difference.)
When 49 or 50 is chosen it would be in the interests of the Dealer to pick the colour that trails, in this case, Black.
So at the end the numbers 1-48 create +24 Red, and 49-50 create +99 Black. This leads to a difference of 75.
Quote: charliepatrickQuote: ThatDonGuyHere's one, straight out of the first round (recently ended) of this year's USA Mathematical Talent Search, slightly modified to fit this forum....50 discs...
Consider the discs in pairs [1,2] [3,4]...[49,50] etc. Your strategy is if the Dealer picks any one of the pairs you will always pick the other number in the pair trying to keep the current average of those pairs down. The only exception is if the dealer ever picks 49 or 50, then you pick the other with the same colour. The best the dealer can do is, say, pick 50 Black and then always pick even numbers Red. This will create "+99" black in the top pair and "+1" red in the others, leading to a net 99-24=75. The reason the Player can win is because the Dealer always has to place first, thus has to open up every pair allowing the Player to adopt the strategy.
After thought - I did wonder whether it was better for you to pick 48 if the dealer didn't, but your aim is to keep the difference small until the [50,49] is played. For instance it might start R1 B48, R 50 R49, B47 and now your advantage is lost. So I suspect you're best to stick with the dealer's pair.
link to original post
It turns out that...this is the correct idea, which surprised me.
Note that, in the competition, to get the "full points," you also had to show that any other strategy by the Dealer would result in the difference being more than 75.
In my second post, elaborating the initial idea, I did mention that the Dealer had to stick to the Even numbers (except for 49/50), otherwise you grabbed them! I'll have another splash of gin with my tonic (Southampton FC won vs Bournemouth earlier this evening) to celebrate!Quote: ThatDonGuy....to get the "full points," you also had to show that any other strategy by the Dealer would result in the difference being more than 75...
Assuming the player never folds, what is the probability of a tie in Three Card Poker? I have seen such a bet on a game I'm analyzing and looking for a confirmation on my number.
Thank you.
Quote: WizardAssuming the player never folds, what is the probability of a tie in Three Card Poker? I have seen such a bet on a game I'm analyzing and looking for a confirmation on my number.
Thank you.
link to original post
Here's what I get: of the 22,100 possible player hands, there are:
48 straight flushes - each has 3 hands that tie it (e.g. KQJ of spades is tied by KQJ of hearts, clubs, or diamonds)
52 threes of a kind - these cannot be tied as there aren't three of that rank remaining
720 straights - there are 3 cards of each of the 3 ranks, but that includes 3 sets that make a straight flush, so 24 hands tie each one
1096 flushes - each has 3 hands that tie it, similar to straight flushes (e.g. 642 of spades is tied by 642 of hearts, clubs, or diamonds)
3744 pairs - there is only one set of two cards that match the pair, and 3 cards that match the third card, so 3 hads tie each one (e.g. 2s 2h 6s is tied with 2c 2d and any of 6h, 6c, or 6d)
16,440 garbage hands - like with straights, 3 cards of each of the 3 ranks, but that includes 3 flushes, so 24 hands tie each one
The total number of ties is (48 x 3) + (52 x 0) + (720 x 24) + (1096 x 3) + (3744 x 3) + (16,440 x 24) = 426,504
There are a total of C(52,3) x C(49,3) = 407,170,400 deals
The probability of a tie = 426,504 / 407,174,000 = 4101 / 3,915,100, or about 1 / 954.67.
Quote: ThatDonGuy16,440 garbage hands - like with straights, 3 cards of each of the 3 ranks, but that includes 3 flushes, so 24 hands tie each one
link to original post
Here is our point of departure, the 3 flushes.
If the three singletons were all of different suits, wouldn't there be one possible flush only?
Likewise, if the three singletons had two different suits, there would be two possible flushes.
Thus, I submit for your consideration there are 25 or 26 possible ways to arrange the suits, depending on the nature of the suit configuration in the garbage hand.


