Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
If die1 would be ABCccc and die2 EFGeee then you could only create nine different numbers; thus you need at least three different numbers on one die and four on the other. Once you've done this, e.g. ABCDdd EFGggg such that d+g=7 you have at least 12 sevens. ABCD and EFG create twelve permutations, so ideally you'd like them to create 7s via DG but also one other. You can't have three ways to make 7 as you need to create 11 different totals.
Thus the puzzle boils down to finding ABCD and EFG (obviously ABCD are all different, so are EFG, and A=1, E=1, and D+G=12) so that they create all the numbers 2-12 and 7 twice. If you can, the probability of a 7 would be 13/36 rather than the value I found. If not, then I'm happy with my solution, although there may be more than one possibility.
(I feel a spreadsheet is about to be created!!)
Quote: GialmereWhat is the largest possible probability of rolling a 7?
I also could not come up with anything better than .3333.
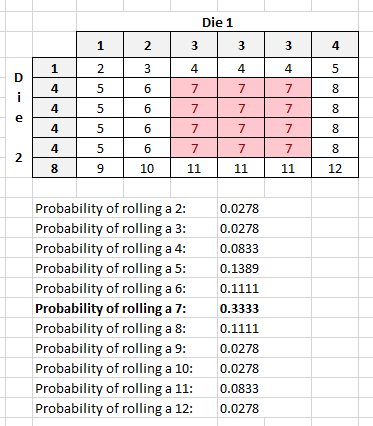
Quote: GialmereGood stuff so far, but nothing correct.
link to original post
Oh, my gosh.
This dice arrangement seems to satisfy all of the criteria.
I agree...Quote: EdCollins...Oh, my gosh...
1 2 3 3 3 3
1 2 3 4 .. .. ..
4 5 6 7 .. ... .
6 7 8 9 .. .. ..
9 10 11 12 .. .. ..
4 .. .. .. .. .. ..
4 .. .. .. .. .. ..
Initial 4x3 has all the numbers 2 thru 12 including two Sevens.
1 2 3 3 3 3
1 2 3 4 .. .. ..
4 5 6 7 +7 +7 +7
6 7 8 9 .. .. ..
9 10 11 12 .. .. ..
4 .. .. +7 +7 +7 +7
4 .. .. +7 +7 +7 +7
Adding more 3s and 4s, create another eleven Sevens.
Quote: EdCollinsOh, my gosh.
This dice arrangement seems to satisfy all of the criteria.
link to original post
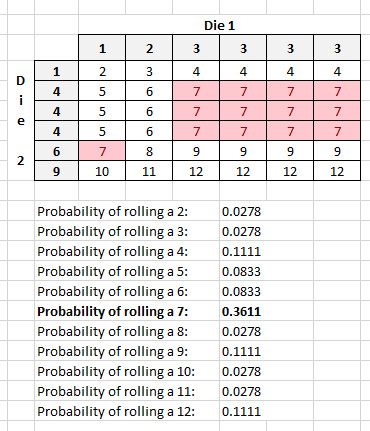
Quote: charliepatrickI agree...Quote: EdCollins...Oh, my gosh...
It's obvious once you see it - well spotted!! Using 123 as EFG it would enable the other numbers of 1 4 7 10 to create all the numbers 2 thru 13. However by using 1469 instead means you can include two sevens.
1 2 3 3 3 3
1 2 3 4 .. .. ..
4 5 6 7 .. ... .
6 7 8 9 .. .. ..
9 10 11 12 .. .. ..
4 .. .. .. .. .. ..
4 .. .. .. .. .. ..
Initial 4x3 has all the numbers 2 thru 12 including two Sevens.
1 2 3 3 3 3
1 2 3 4 .. .. ..
4 5 6 7 +7 +7 +7
6 7 8 9 .. .. ..
9 10 11 12 .. .. ..
4 .. .. +7 +7 +7 +7
4 .. .. +7 +7 +7 +7
Adding more 3s and 4s, create another eleven Sevens.
link to original post
Correct!!!
Excellent. In fact, that set of dice isn't included in the official solve. (We'll call it the EdCollins special "come out roll" dice.)
If the first die has five different numbers, with one appearing twice, the second die must have at least three different numbers. There is only one possible number on the second die which totals a 7 with the duplicated number on the first die. The second die has at most four copies of the number which totals a 7 with the duplicated number and has two ways to roll a 7; all other numbers on the second die have only one way to roll a 7. This is a maximum total of 10 rolls for a probability of 10/36.
If each die has four different numbers, they can be split 2,2,1,1 or 3,1,1,1. Each number on each die can pair with at most one number on the other die to make a 7. The largest possible sum of products, which gives the number of ways to roll a 7, is 3 × 3 + 1 × 1 + 1 × 1 + 1 × 1 = 12. The maximum probability is thus 12/36.
If the first die has four different numbers and the second has three, there are only 12 different pairs of values, and thus there must be at most two different value pairs which total 7 in order to have 11 possible totals.
Therefore, the largest possible sum of products is 3 × 4 + 1 × 1 = 13, not 3 × 4 + 1 × 1 + 1 × 1 = 14. And 13 is possible, with one die having 1,2,6,6,6,7 and the other having 1,1,1,1,3,5 (or 1,2,2,2,6,7 and 1,3,5,5,5,5); this gives a probability of 13/36.
--------------------------------------------

1267 135 have 1+7=2+6, and 2-1=7-6=1, 6-2=4, 5-3=3-1=2 (i.e. not 1 nor 4). Also the average of the first die is 4 and the second 3, 4+3=7.
1469 123 have 1+9=4+6, 4-1=9-6=3, 6-4=2, 3-2=2-1=1 (i.e. not 2 nor 3). The average of the first die is 5 and the second 2, 5+2=7.

Is it obvious or a coincidence that the average of ABCD and average of EFG add up to 7, that A+D must equal B+C, and EFG have equal spacing? Not at the time!!

Paint the outside of an n × n × n cube red, then chop it into n^3 unit cubes. Put the unit cubes in a box, mix them up thoroughly, withdraw one at random and throw it across a table.
Whatís the probability that it comes to rest with a red face on top?
Quote: GialmereWhatís the probability that it comes to rest with a red face on top?
* - j/k!
Quote: JoemanHaving brute-forced n=1 through n=4 (including taking apart my Rubik's Cube at n=3*), it appears that the probability of a red face is 1/n.
* - j/k!
link to original post
The number of red squares is 6n2.
The number of squares is 6n3.
So, the probability of a red square is 6n2 / (6n3) = 1/n.
Quote: JoemanHaving brute-forced n=1 through n=4 (including taking apart my Rubik's Cube at n=3*), it appears that the probability of a red face is 1/n.
* - j/k!
link to original post
Yep, I knew my answer wasn't the best way to express it. Thanks.
| 1 | 2 | 3 | 3 | 3 | 4 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 4 | 4 | 5 |
| 3 | 4 | 5 | 6 | 6 | 6 | 7 |
| 4 | 5 | 6 | 7 | 7 | 7 | 8 |
| 4 | 5 | 6 | 7 | 7 | 7 | 8 |
| 5 | 6 | 7 | 8 | 8 | 8 | 9 |
| 9 | 10 | 11 | 12 | 12 | 12 | 13 |
Quote: WizardI hope nobody minds me saying the best I can do with the two dice problem is eight sevens. I haven't looked at any spoilers on this. G, can you tell me if it's possible to do better than 8?
1 2 3 3 3 4 1 2 3 4 4 4 5 3 4 5 6 6 6 7 4 5 6 7 7 7 8 4 5 6 7 7 7 8 5 6 7 8 8 8 9 9 10 11 12 12 12 13
link to original post
Yes it is.
Quote: Gialmere
Yes it is.
link to original post
Thanks. How about ten sevens?
| 1 | 2 | 3 | 3 | 3 | 4 | |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 4 | 4 | 5 |
| 4 | 5 | 6 | 7 | 7 | 7 | 8 |
| 4 | 5 | 6 | 7 | 7 | 7 | 8 |
| 4 | 5 | 6 | 7 | 7 | 7 | 8 |
| 5 | 6 | 7 | 8 | 8 | 8 | 9 |
| 8 | 9 | 10 | 11 | 11 | 11 | 12 |
Quote: WizardQuote: Gialmere
Yes it is.
link to original post
Thanks. How about ten sevens?
1 2 3 3 3 4 1 2 3 4 4 4 5 4 5 6 7 7 7 8 4 5 6 7 7 7 8 4 5 6 7 7 7 8 5 6 7 8 8 8 9 8 9 10 11 11 11 12
link to original post
Getting warmer.
Of the n^3 cubes, the (n-2)^3 cubes in the interior have zero red faces, the 6 (n-2)^2 cubes on a face but not an edge/corner each have one, the 12 (n-2) on an edge each have 2, and the 8 on the corners each have 3.
The probability of a red face = ((n-2)^3 x 0/6 + 6 (n-2)^2 x 1/6 + 12 (n-2) x 2/6 + 8 x 3/6) / n^3
= (6n^2 - 24n + 24 + 24n - 48 + 24) / (6 n^3)
= 6n^2 / (6 n^3)
= 1 / n
Quote: JoemanHaving brute-forced n=1 through n=4 (including taking apart my Rubik's Cube at n=3*), it appears that the probability of a red face is 1/n.
* - j/k!
link to original post
Quote: ChesterDog
The number of red squares is 6n2.
The number of squares is 6n3.
So, the probability of a red square is 6n2 / (6n3) = 1/n.
link to original post
Quote: ThatDonGuy
Of the n^3 cubes, the (n-2)^3 cubes in the interior have zero red faces, the 6 (n-2)^2 cubes on a face but not an edge/corner each have one, the 12 (n-2) on an edge each have 2, and the 8 on the corners each have 3.
The probability of a red face = ((n-2)^3 x 0/6 + 6 (n-2)^2 x 1/6 + 12 (n-2) x 2/6 + 8 x 3/6) / n^3
= (6n^2 - 24n + 24 + 24n - 48 + 24) / (6 n^3)
= 6n^2 / (6 n^3)
= 1 / n
link to original post
Correct!!
Very good.
----------------------------------------------
:strip_icc()/pic7266039.png)
She has randomly chosen two of the cartons and hidden an Easter egg inside each of them, leaving the remaining ten cartons empty. She gives the dozen cartons to Bob, who opens them in the order A, B, C, D, E, F, G, H, I, J, K, L until he finds one of the Easter eggs, whereupon he stops. The number of cartons that he opens is his score. Alice then reseals the cartons, keeping the eggs where they are, and presents the cartons to Chris, who opens the cartons in the order A, E, I, B, F, J, C, G, K, D, H, L, again stopping as soon as one of the Easter eggs is found, and scoring the number of opened cartons. Whoever scores lower wins the game; if they score the same then itís a tie.
For example, suppose Alice hides the Easter eggs in cartons H and K. Then Bob will stop after reaching the egg in carton H and will score 8, while Chris will stop after reaching the egg in carton K and will score 9. So Bob wins in this case.
Who is more likely to win this game, Bob or Chris? Or are they equally likely to win?
Quote: GialmereWho is more likely to win this game, Bob or Chris? Or are they equally likely to win?
I think Bob is more likely to win this interesting game.
Bob should win the game approximately 42.36% of the time.
Chris should win the game approximately 37.49% of the time.
Approximately 20.15% of the time the game should end in a tie.
Bob wins with a probability of .42424
Chris wins with a probability of .37879
The probability of a tie is .19697
Quote: GialmereAlice has a dozen cartons, arranged in a 3×4 grid, which for convenience we'll labeled A through L:
She has randomly chosen two of the cartons and hidden an Easter egg inside each of them, leaving the remaining ten cartons empty. She gives the dozen cartons to Bob, who opens them in the order A, B, C, D, E, F, G, H, I, J, K, L until he finds one of the Easter eggs, whereupon he stops. The number of cartons that he opens is his score. Alice then reseals the cartons, keeping the eggs where they are, and presents the cartons to Chris, who opens the cartons in the order A, E, I, B, F, J, C, G, K, D, H, L, again stopping as soon as one of the Easter eggs is found, and scoring the number of opened cartons. Whoever scores lower wins the game; if they score the same then itís a tie.
For example, suppose Alice hides the Easter eggs in cartons H and K. Then Bob will stop after reaching the egg in carton H and will score 8, while Chris will stop after reaching the egg in carton K and will score 9. So Bob wins in this case.
Who is more likely to win this game, Bob or Chris? Or are they equally likely to win?
link to original post
I couldnít think of a clever way so used excel for Brute force.
Extra credit, if Chris gets to know Bobís choosing order and then decide how to open the cartons, how often should Chris win.
ETA: fixed names
Edit: Yep. Found my mistake. I agree with your answer.
Quote: unJonI couldnít think of a clever way so used excel for Brute force.
I get a tie 26/132 (19.70%) of the time, Bob wins 54/132 (40.91%) of the time and Chris wins 52/132 (39.39%) of the time.
Extra credit, if Chris gets to know Bobís choosing order and then decide how to open the cartons, how often should Chris win.Chris should skip Bobís first carton and then do Bobís order of opening beginning with the second carton she opened. Chris would win unless the first crate Bob opened had an Easter egg. So Chris would win 110/132 (83.33%) of the time, and tie 2/132 (1.52%) of the time.
ETA: fixed names
link to original post
Quote: EdCollinsUnjon, you have Bob winning one less time (and Chris winning one more time) than I do... which means I likely made a mistake. Darn for me.
Edit: Yep. Found my mistake. I agree with your answer.
link to original post
Quote: acesideMy calculation numbers agree with unJon.
link to original post
Correct!!
Well done. (I wasn't sure what order to place you guys, so I settled on the last three posts.)
We obtain:
xx b2 b3 b4
c2 c5 b7 b8
c3 c6 c9 xx
Note that there are five b cartons and five c cartons. So the cases in which Alice selects carton A or carton L are equally split between Bob and Chris. Similarly if Alice selects two b cartons then Bob necessarily wins, but these are balanced out by an equal number of cases in which Alice selects two c cartons and C necessarily wins.
The crucial cases occur when Alice selects one b carton and one c carton. Bob wins if the b carton has a lower score than the c carton:
b2 and (c3 or c5 or c6 or c9)
b3 and (c5 or c6 or c9)
b4 and (c5 or c6 or c9)
b7 and c9
b8 and c9
Chris wins if the c carton has a lower score than the b carton:
c2 and (b3 or b4 or b7 or b8)
c3 and (b4 or b7 or b8)
c5 and (b7 or b8)
c6 and (b7 or b8)
Since this yields 12 cases in Bobís favor and only 11 cases in Chrisís favor, Bob has the advantage.
------------------------------------------
Box Jokes...
A - 1st round
B or E - 2nd round
C or I - 3rd round (so CI is a tie, C but not ABEI is a win, I but not ABCE is a win).
D - 4th round (Chris can't win in the 4th round as A would have won if there was a B)
etc.
XY NN Bb Ti Ch
Ax 11 .. 11 ..
BE 1 .. .1 ..
B2 9 9 .. ..
E2 9 .. .. 9
CI 1 .. 1 ..
C4 7 7 .. ..
I4 7 .. .. 7
D5 6 6 .. ..
F6 5 .. .. 5
J7 4 .. .. 4
G8 3 3 .. ..
H9 2 2 .. ..
KL 1 .. .. 1
Total 27 13 26
------------------------------------------
/pic5045763.png)
Chip Chase
Well, viva Las Vegas. You've made it to Cutting Edge and are attending a meet-and-greet for designers. To your surprise, your name is called out as a possible door prize winner. You are taken to a table that has five boxes (numbered 1-5) placed in a line and told that one of the boxes contains a $5000 casino chip.
/pic5045745.png)
Also on the table is a bag containing ten keno balls (numbered 1-10). You need to draw a ball from the bag to indicate how many guesses you get at which box contains the five grand cheque. The catch is, after each incorrect guess, you must turn your back and the chip is moved to an adjacent box before you can guess again.
Fortunately, being a game designer, you've seen this sort of mechanic before and realize that the game is beatable. You just need to get lucky with the draw.
What is the lowest numbered keno ball you can draw that guarantees you'll find the $5000 chip?
/pic5045762.png)
Can the host move the money to same box it has been before?
Can the host move the money to a box that has been picked before?
Quote: GialmereYes, yes and yes.
link to original post
Is box 1 adjacent to box 5?
Quote: GialmereNo. A chip at the end has only one legal move.
link to original post
In that case you can win with:
Round 1: box 2
Round 2: box 2
You will have won if the chip started in either box 1 or 2. So you now know the chip is either in box 3, 4 or 5.
Round 3: box 4
Round 4: box 4
You will have won if the chip was either in box 4 or 5 at the start of round 3. That means the chip must have started round 3 in box 3 and then moved to box 2 at the start of round 4. So at the start of round 5 the chip is either in box 1 or 3.
Round 5: box 3
If you havenít won they means the chip was in box 1 so is now in box 2
Round 6: box 2
Winner for sure. I donít think you can do better than that, but maybe I havenít thought of a more efficient sorting method.
Quote: unJonQuote: GialmereNo. A chip at the end has only one legal move.
link to original post
In that case you can win with:6 guesses.
Round 1: box 2
Round 2: box 2
You will have won if the chip started in either box 1 or 2. So you now know the chip is either in box 3, 4 or 5.
Round 3: box 4
Round 4: box 4
You will have won if the chip was either in box 4 or 5 at the start of round 3. That means the chip must have started round 3 in box 3 and then moved to box 2 at the start of round 4. So at the start of round 5 the chip is either in box 1 or 3.
Round 5: box 3
If you havenít won they means the chip was in box 1 so is now in box 2
Round 6: box 2
Winner for sure. I donít think you can do better than that, but maybe I havenít thought of a more efficient sorting method.
link to original post
You open an empty box.
1) you 2, chip 4
2) you 2, chip 3
3) you 4, chip 2
4) you 4, chip 3
5) you 3, chip 4
6) you 2, chip 3 or 5
(I guess you don't remember this one.)
Quote: GialmereWhat is the lowest numbered keno ball you can draw that guarantees you'll find the $5000 chip?
Keno Ball 6.
The trick is to narrow down where the chip is as much as possible with each guess.
1st guess: Box 4
2nd guess: Box 3
If I haven't found it, I know the chip cannot be in Box 5 right now. (Why? Because if it IS in 5, it had in 4 on the prior turn, but that was my first guess which obviously came up empty.)
3rd guess: Box 2
Right now we know the chip isn't in Box 4 because a turn earlier we eliminated it being in 5. (It can only move from 5 to 4.) However, I think I can make a case that right now it COULD be in all of the others. So my 3rd guess was Box 2 and if not right...
4th guess: Box 2
...I'll chose Box 2 again! If it's not here, I think I can now eliminate the chip is not in Boxes 1, 2, 3, or 5! (Not in 1 because it wasn't in 2 a turn earlier. Not in Box 5 because it wasn't in Box 4 a turn earlier. Not in Box 3 because it wasn't in Box 2 or Box 4 earlier.) So if Box 2 isn't correct, I found the chip... it's in Box 4 right now! However, we know it could move adjacently to 3 or 5 next time. So, I will then guess...
5th guess: Box 3!
... and if that's not correct it MUST be in Box 5 right and can only move adjacently to Box 4. (This is why we don't guess Box 5 here, because if we are wrong, sure it was in Box 3 but now COULD move to 2 OR 4.)
6th guess: Box 4. The chip has to be here.
So I think it's possible I might need as many as six guesses to select a box that I know for sure the chip is in, and thus I hope I draw Keno Ball #6 or higher. It does seem if I guess in this specific order each time (4-3-2-2-3-4) I will have tracked it down by Guess #6 for sure.
(I haven't figured out a way yet, to guarantee I will always get it in 5 turns.)
Quote: EdCollinsQuote: GialmereWhat is the lowest numbered keno ball you can draw that guarantees you'll find the $5000 chip?
Keno Ball 6.
The trick is to narrow down where the chip is as much as possible with each guess.
1st guess: Box 4
2nd guess: Box 3
If I haven't found it, I know the chip cannot be in Box 5 right now. (Why? Because if it IS in 5, it had in 4 on the prior turn, but that was my first guess which obviously came up empty.)
3rd guess: Box 2
Right now we know the chip isn't in Box 4 because a turn earlier we eliminated it being in 5. (It can only move from 5 to 4.) However, I think I can make a case that right now it COULD be in all of the others. So my 3rd guess was Box 2 and if not right...
4th guess: Box 2
...I'll chose Box 2 again! If it's not here, I think I can now eliminate the chip is not in Boxes 1, 2, 3, or 5! (Not in 1 because it wasn't in 2 a turn earlier. Not in Box 5 because it wasn't in Box 4 a turn earlier. Not in Box 3 because it wasn't in Box 2 or Box 4 earlier.) So if Box 2 isn't correct, I found the chip... it's in Box 4 right now! However, we know it could move adjacently to 3 or 5 next time. So, I will then guess...
5th guess: Box 3!
... and if that's not correct it MUST be in Box 5 right and can only move adjacently to Box 4. (This is why we don't guess Box 5 here, because if we are wrong, sure it was in Box 3 but now COULD move to 2 OR 4.)
6th guess: Box 4. The chip has to be here.
So I think it's possible I might need as many as six guesses to select a box that I know for sure the chip is in, and thus I hope I draw Keno Ball #6 or higher. It does seem if I guess in this specific order each time (4-3-2-2-3-4) I will have tracked it down by Guess #6 for sure.
(I haven't figured out a way yet, to guarantee I will always get it in 5 turns.)
link to original post
...if it was in Box 5 originally, it moves to Box 4 after the first incorrect guess (by the way, now it cannot be in box 5), so if the second guess is 3, it can move from 4 to 3 or 5. It cannot be in 4, as it was not in 5, and if it was in 3, then you would have found it, but it can be in 1, 2, 3, or 5.
Apologies if I solved this one the first time, but I don't remember it
...6 notes
Guess 1: #4 - 1 moves to 2; 2 moves to 1 or 3; 3 moves to 2 or 4; 5 moves to 4 - the chip can be moved to 1, 2, 3, or 4
Guess 2: #3 - 1 moves to 2; 2 moves to 1 or 3; 4 moves to 3 or 5; it cannot be in 5 - the chip can be moved to 1, 2, 3, or 5
Guess 3: #4 - 1 moves to 2; cannot be in 2; 3 moves to 2 or 4; 5 moves to 4 - the chip can be moved to 2 or 4
Guess 4: #2 - if the chip is in 4, it can be moved to 3 or 5
Guess 5: #3 - if the chip is in 5, it has to be moved to 4
Guess 6: #4
Hmmm.... Not sure I'm following you. I'll check again, but if it was in 5 originally, I still think I find it no matter where it ends up.
If it always alternates between 4 and 5, I find it on Guess #5.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 5
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 5
6th guess: Box 4 / It's in 4 Found
If it stops at Box 3 for a moment, but still ends up in 5 at my 5th guess, I'll again find it on Guess #6.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 3
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 5
6th guess: Box 4 / It's in 4 Found
If it stops at Box 2 from Box 3, I'll find it on Guess #4.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 3
4th guess: Box 2 / It's in 2 Found
If it stops at Box 3 from Box 4, I'll find it on Guess #5.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 3
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 3 Found
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 5
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 3 Found
Which travel path by the chip am I missing, where I don't find it with 4-3-2-2-3-4?
Don's Guess 1: #4 / Chip is in #2
Don's Guess 2: #3 / Chip is in #1
Don's Guess 3: #4 / Chip is in #2
Don's Guess 4: #2 / Chip is in #3
Don's Guess 5: #3 / Chip is in #4
Don's Guess 6: #4 / Chip is in #3 or #5
Quote: EdCollinsDon, thanks for responding.
Hmmm.... Not sure I'm following you. I'll check again, but if it was in 5 originally, I still think I find it no matter where it ends up.
If it always alternates between 4 and 5, I find it on Guess #5.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 5
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 5
6th guess: Box 4 / It's in 4 Found
If it stops at Box 3 for a moment, but still ends up in 5 at my 5th guess, I'll again find it on Guess #6.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 3
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 5
6th guess: Box 4 / It's in 4 Found
If it stops at Box 2 from Box 3, I'll find it on Guess #4.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 3
4th guess: Box 2 / It's in 2 Found
If it stops at Box 3 from Box 4, I'll find it on Guess #5.
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 3
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 3 Found
1st guess: Box 4 / It's in 5
2nd guess: Box 3 / It's in 4
3rd guess: Box 2 / It's in 5
4th guess: Box 2 / It's in 4
5th guess: Box 3 / It's in 3 Found
Which travel path by the chip am I missing, where I don't find it with 4-3-2-2-3-4?
link to original post
I checked all six possible first moves where the box is not in 4; all six can be solved with 4,3,2,2,3,4 in six or fewer guesses
Quote: EdCollinsDon, does this chip path refute your solution?
Don's Guess 1: #4 / Chip is in #2
Don's Guess 2: #3 / Chip is in #1
Don's Guess 3: #4 / Chip is in #2
Don's Guess 4: #2 / Chip is in #3
Don's Guess 5: #3 / Chip is in #4
Don's Guess 6: #4 / Chip is in #3 or #5
link to original post
I'll have to check my answer again...
I think I now found four possible solutions which also guarantee a find in six moves.
The first one I listed earlier... 4-3-2-2-3-4
I just realized there's the mirror of that, of course, which should also work: 2-3-4-4-3-2
However, I believe 2-3-4-2-3-4 and its mirror, 4-3-2-4-3-2 also work.
Quote: EdCollinsQuote: GialmereWhat is the lowest numbered keno ball you can draw that guarantees you'll find the $5000 chip?
Keno Ball 6.
The trick is to narrow down where the chip is as much as possible with each guess.
1st guess: Box 4
2nd guess: Box 3
If I haven't found it, I know the chip cannot be in Box 5 right now. (Why? Because if it IS in 5, it had in 4 on the prior turn, but that was my first guess which obviously came up empty.)
3rd guess: Box 2
Right now we know the chip isn't in Box 4 because a turn earlier we eliminated it being in 5. (It can only move from 5 to 4.) However, I think I can make a case that right now it COULD be in all of the others. So my 3rd guess was Box 2 and if not right...
4th guess: Box 2
...I'll chose Box 2 again! If it's not here, I think I can now eliminate the chip is not in Boxes 1, 2, 3, or 5! (Not in 1 because it wasn't in 2 a turn earlier. Not in Box 5 because it wasn't in Box 4 a turn earlier. Not in Box 3 because it wasn't in Box 2 or Box 4 earlier.) So if Box 2 isn't correct, I found the chip... it's in Box 4 right now! However, we know it could move adjacently to 3 or 5 next time. So, I will then guess...
5th guess: Box 3!
... and if that's not correct it MUST be in Box 5 right and can only move adjacently to Box 4. (This is why we don't guess Box 5 here, because if we are wrong, sure it was in Box 3 but now COULD move to 2 OR 4.)
6th guess: Box 4. The chip has to be here.
So I think it's possible I might need as many as six guesses to select a box that I know for sure the chip is in, and thus I hope I draw Keno Ball #6 or higher. It does seem if I guess in this specific order each time (4-3-2-2-3-4) I will have tracked it down by Guess #6 for sure.
(I haven't figured out a way yet, to guarantee I will always get it in 5 turns.)
link to original post
Correct!!
Good show.
Although I gave this puzzle a Vegas theme, it comes in various guises. Sometimes it's a gopher popping up from holes in the ground. The last time I saw it, the puzzle was to find a princess in (no less than) 17 rooms with doors opening to the same hallway! To me that seems like overkill.
-----------------------------------------------------
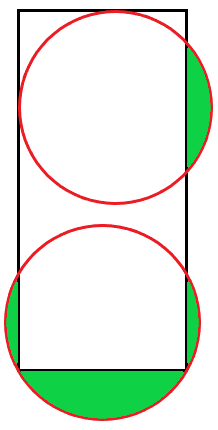
The rectangle is 8 x 20, and the circles each have diameter 10.
To make it clear, the top circle is tangent to the top and left sides of the rectangle, and the bottom circle goes through both of the rectangle's bottom corners.
What is the combined area of the green sections?
Total area = 25 Pi -48 ~ 30.54.
If you draw straight lines from each circle center to its intersection points, and then draw lines toward the arc midpoint, all of the angles are formed by right triangles of sides (3, 4, 5). Each shaded area is just the area of the big fan formed by 2x the angle subtracted by 2x the triangle area. I just add all of them up.
It's easy Monday. Here's another trilogy of tiny teasers...

You're shopping for a doohickey online. You find four similar doohickeys that have the same price, the same functions, the same look, but different ratings.
Based on the ratings, which doohickey should you buy?
A. 177 positive ratings (198 total ratings)
B. 90 positive ratings (98 total ratings)
C. 45 positive ratings (48 total ratings)
D. 8 positive ratings (8 total ratings)

The Red Sox beat the Orioles 9 to 4 in 17 innings.
Where was the game played?
:strip_icc()/pic7274372.png)
Who moved last?
Quote: Gialmere
The Red Sox beat the Orioles 9 to 4 in 17 innings.
Where was the game played?
Oddly enough, if the home team batter hits a bases-loaded ground-rule double, only the first run counts.


