Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: Gialmere1) During what phases of the lunar cycle do solar and lunar eclipses take place?
2) Solar eclipses are more common than lunar eclipses*, but we tend to have the opposite impression. Why?
*This stat includes all types of solar and lunar eclipses except for penumbral lunar eclipses.
link to original post
1. Solar eclipses occur during new moons; lunar eclipses occur during full moons.
2. I think it is because lunar eclipses last longer - the moon is in the earth's shadow longer than it is in front of the sun - so they are more "obvious" to the casual viewers, who then get the impression that they are more frequent.
Quote: JoemanLunar eclipses happen during a full moon; solar eclipses occur during a new moon.Hmmm... I didn't know that, but my guess would be that solar eclipses are only visible to relatively small portions of the planet, while lunar eclipses are visible to just about anyone in the hemisphere that is in darkness. So, an individual is likely to personally experience more lunar eclipses than solar eclipses in his lifetime, and thus conclude that lunar eclipses are more common.
link to original post
Quote: ThatDonGuy
1. Solar eclipses occur during new moons; lunar eclipses occur during full moons.
2. I think it is because lunar eclipses last longer - the moon is in the earth's shadow longer than it is in front of the sun - so they are more "obvious" to the casual viewers, who then get the impression that they are more frequent.
link to original post
Correct!!
Very good.
Also, if you add in the (usually never noticed) penumbral lunar eclipses, the number of solar and lunar eclipses is roughly equal (and just slightly favors lunar).
-----------------------------------------
If the earth is between the sun and the moon, it's called a lunar eclipse.
And if the sun is between the moon and the earth, it's called an apoc eclipse.

Andre Agassi and Boris Becker are playing tennis. Agassi wins the first set 6-3.
If there were 5 service breaks in the set, did Becker serve the first game?

You’ve just won a set of singles tennis.
What’s the least number of times your racket can have struck the ball?
[Note: If you don't know the rules of tennis, you should probably skip this post.]
Quote: GialmereTennis anyone?
Andre Agassi and Boris Becker are playing tennis. Agassi wins the first set 6-3.
If there were 5 service breaks in the set, did Becker serve the first game?
You’ve just won a set of singles tennis.
What’s the least number of times your racket can have struck the ball?
[Note: If you don't know the rules of tennis, you should probably skip this post.]
link to original post
This would assume that all your service points were first service aces/service winners (4 points per gams X 3 games = 12 strikes), and your opponent double-faulted all of his serves. Actually, he could have mixed in a few aces along the way, but winning these game in this fashion doesn't require you to touch the ball.

For those interested, the Lazy Tennis puzzle remains unsolved.
Assuming the answers so far given are wrong, as on the surface I tend to agree with them except...Quote: Gialmere...For those interested, the Lazy Tennis puzzle remains unsolved..
However I suspect the penalties are such that after a while there would have been a match penalty for repeated violations.
Let's assume that penalties are given in staggered stages and can happen without you having made a serve in your game.
The first game is lost by your opponent double faluting. So you are 1-0 up.
In the second game the opponent, say, goes for a long toilet break and gets a one game penalty. 2-0 up.
I'm not sure whether this is "your" game that is awarded or an extra one. Let's assume it's the one (just about to be) in progress.
Opponent double faults to 3-0.
Now your opponent repeats the earlier issue, and you get awarded two games. At this stage the opponent has run out of options to give you games, as the next one will result in the match. So it's 5-0 with you about to serve.
Thus I think you have to create a penalty on your own game, to lose it. 5-1.
Finally the opponent double-faults to give you the set (6-1).
Therefore it seems possible you can win the set by never hitting the ball.
Quote: charliepatrickAssuming the answers so far given are wrong, as on the surface I tend to agree with them except...Quote: Gialmere...For those interested, the Lazy Tennis puzzle remains unsolved..
The opponent can lose games through penalties, as can you. So technically you could both lose games and, say, get to 5-5 (or even so there's a tie break). Then your opponent has a penalty. Thus it's possible for neither player to have hit the ball.
However I suspect the penalties are such that after a while there would have been a match penalty for repeated violations.
Let's assume that penalties are given in staggered stages and can happen without you having made a serve in your game.
The first game is lost by your opponent double faluting. So you are 1-0 up.
In the second game the opponent, say, goes for a long toilet break and gets a one game penalty. 2-0 up.
I'm not sure whether this is "your" game that is awarded or an extra one. Let's assume it's the one (just about to be) in progress.
Opponent double faults to 3-0.
Now your opponent repeats the earlier issue, and you get awarded two games. At this stage the opponent has run out of options to give you games, as the next one will result in the match. So it's 5-0 with you about to serve.
Thus I think you have to create a penalty on your own game, to lose it. 5-1.
Finally the opponent double-faults to give you the set (6-1).
Therefore it seems possible you can win the set by never hitting the ball.
link to original post
I like your "out of the box" thinking, but it's a little too far out. Assume you and your opponent are both on the court the whole time playing "by the book" tennis.
Quote: GialmereFor those interested, the Lazy Tennis puzzle remains unsolved.
I guess my 1st answer was a fault!
Second service:

Technically, zero - your opponent serves an ace to open the set, but pulls a hamstring doing so and has to default.
If the standard penalty system is in play, but the opponent was not disqualified, it is 7 - your opponent serves first, gets a penalty during their first game (a warning), a second penalty on your serve (a point, so you only served three times in the second game), and just before your first serve when up 5-0, a third penalty, which is a game penalty.
Something tells me there's another way to score a point on your serve without hitting the ball.
Suppose instead that you were standing still. The ones going in your direction are headed toward you at 10 mph, and the ones going in the opposite direction are going at 20 mph, so there will be twice as many going toward you as going with you, which is 2/3.
Suppose I am bicycling west. Relative to the joggers running west, my speed is 15 - 5 = 10 MPH.
And relative to the joggers running east, my speed is 15 + 5 = 20 MPH.
So, I would encounter twice as many eastbound joggers as westbound joggers.
I assumed the path to be 15 miles long.
I would encounter joggers who started from the other side anywhere from 3 hours before I started to 1 hour after, for a total of 4 hours of joggers encountered.
Going the same direction, I would encounter joggers who left anywhere from 2 hours before me to the same time, for a total of 2 hours.
4 to 2 = 2 to 1 ratio.

Some solves for the tennis puzzles are...
Correct!!
Well done.
But we know that Agassi won 6 games, so this is a contradiction. Hence Agassi must really have served 5 rather than 4 games, and therefore he served the first game.
---------------------------------------------------
Once. You swing and miss [a fault] each time you serve, and your opponent commits a double fault each time he serves. Eventually you find yourself serving at 6-5 or 7-6 in the tiebreak [because service order changes], and then you heroically serve an ace.
From Dick Hess, All-Star Mathlete Puzzles, 2009.
UPDATE: A reader points out that a superlatively lazy player can win a set without ever hitting the ball, thanks to the hindrance rule:
26. HINDRANCE
If a player is hindered in playing the point by a deliberate act of the opponent(s), the player shall win the point.
“On the crucial tie-break point, your opponent dashes across the net and tackles you, awarding you the point and the set.”
---------------------------------------------

Andre has shorter hair now.

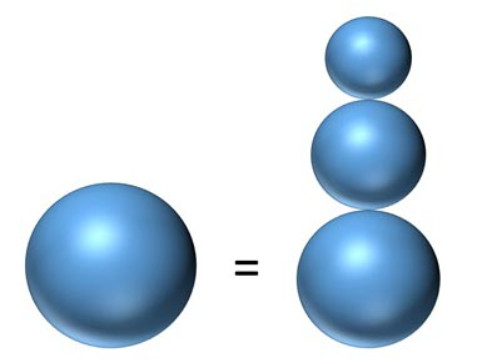
Frosty the Snowman wants to create a small snowman friend for himself. The new snowman needs a base, torso, and a head, all three of which should be spheres. The torso should be no larger than the base and the head should be no larger than the torso.
For building material, Frosty has a spherical snowball with a 6-inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer.
Can Frosty accomplish this?
Quote: Gialmere
Frosty the Snowman wants to create a small snowman friend for himself. The new snowman needs a base, torso, and a head, all three of which should be spheres. The torso should be no larger than the base and the head should be no larger than the torso.
For building material, Frosty has a spherical snowball with a 6-inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer.
Can Frosty accomplish this?
link to original post
Aside it’s interesting that 3/4/5 is also a right triangle.
Quote: GialmereFrosty the Snowman wants to create a small snowman friend for himself. The new snowman needs a base, torso, and a head, all three of which should be spheres. The torso should be no larger than the base and the head should be no larger than the torso.
For building material, Frosty has a spherical snowball with a 6-inch radius. Since Frosty likes to keep things simple, he also wants the radius of each of the three pieces to be a positive integer.
Can Frosty accomplish this?
link to original post
Yes.
The problem is simple enough: let a, b and c be the three radii.
4/3 PI a^3 + 4/3 PI b^3 + 4/3 PI c^3 = 4/3 PI x 6^3.
a^3 + b^3 + c^3 = 216, where a, b, and c are distinct positive integers.
Brute force checking shows the only solution is 5, 4, 3.
Bonus Math: "But doesn't that violate Fermat's Last Theorem?" No, as Fermat's Last Theorem only applies to a^n + b^n = c^n, and not, for example, a^n + b^n + c^n = d^n.
Bonus Bonus Math: Here are all of the solutions where the base is limited by some strange building code to a maximum radius of 100:
3, 4, 5 (6)
1, 6, 8 (9)
6, 8, 10 (12)
9, 12, 15 (18)
2, 12, 16 (18)
3, 10, 18 (19)
7, 14, 17 (20)
12, 16, 20 (24)
4, 17, 22 (25)
3, 18, 24 (27)
18, 19, 21 (28)
11, 15, 27 (29)
15, 20, 25 (30)
18, 24, 30 (36)
4, 24, 32 (36)
6, 20, 36 (38)
14, 28, 34 (40)
6, 32, 33 (41)
2, 17, 40 (41)
21, 28, 35 (42)
16, 23, 41 (44)
5, 30, 40 (45)
27, 30, 37 (46)
3, 36, 37 (46)
24, 32, 40 (48)
8, 34, 44 (50)
29, 34, 44 (53)
27, 36, 45 (54)
6, 36, 48 (54)
12, 19, 53 (54)
36, 38, 42 (56)
9, 30, 54 (57)
15, 42, 49 (58)
22, 30, 54 (58)
30, 40, 50 (60)
21, 42, 51 (60)
7, 42, 56 (63)
33, 44, 55 (66)
22, 51, 54 (67)
36, 38, 61 (69)
7, 54, 57 (70)
14, 23, 70 (71)
36, 48, 60 (72)
8, 48, 64 (72)
34, 39, 65 (72)
38, 43, 66 (75)
12, 51, 66 (75)
31, 33, 72 (76)
12, 40, 72 (76)
39, 52, 65 (78)
28, 56, 68 (80)
9, 54, 72 (81)
25, 48, 74 (81)
12, 64, 66 (82)
19, 60, 69 (82)
4, 34, 80 (82)
54, 57, 63 (84)
42, 56, 70 (84)
28, 53, 75 (84)
50, 61, 64 (85)
26, 55, 78 (87)
38, 48, 79 (87)
20, 54, 79 (87)
33, 45, 81 (87)
32, 46, 82 (88)
21, 43, 84 (88)
25, 31, 86 (88)
17, 40, 86 (89)
58, 59, 69 (90)
45, 60, 75 (90)
10, 60, 80 (90)
25, 38, 87 (90)
54, 60, 74 (92)
6, 72, 74 (92)
32, 54, 85 (93)
15, 50, 90 (95)
48, 64, 80 (96)
19, 53, 90 (96)
45, 69, 79 (97)
11, 66, 88 (99)
35, 70, 85 (100)
16, 68, 88 (100)
51, 68, 85 (102)
33, 70, 92 (105)
58, 68, 88 (106)
15, 82, 89 (108)
54, 72, 90 (108)
12, 72, 96 (108)
29, 75, 96 (110)
72, 76, 84 (112)
50, 74, 97 (113)
57, 76, 95 (114)
23, 86, 97 (116)
30, 84, 98 (116)
18, 96, 99 (123)
86, 95, 97 (134)
94, 96, 99 (139)
60, 80, 100 (120)
Quote: WizardIn the Cash 5 game of the Texas Lottery, the player picks 5 numbers from 1 to 37. The state does the same via a random draw. If the two or more match, the player wins. What is the least number of tickets you need to buy to ensure a win? You may choose your own numbers.
The analogous problem for the UK National Lottery (choose 6 numbers from 1 to 59) was solved this year by two mathematicians in Manchester. The answer is that the minimum is 27. They describe how you can choose the numbers on 27 tickets to guarantee a win (not a profit, of course), and they also prove 26 tickets are not enough. It was reported quite widely in the mainstream media, e.g., https://www.itv.com/news/granada/2023-08-03/how-many-lottery-tickets-do-you-need-to-guarantee-a-win.
The paper is at https://pure.manchester.ac.uk/ws/portalfiles/portal/272368587/2307.12430v1.pdf.
Quote: unJonvolume of a sphere equals 4pi(r)^3. So this question comes down to whether 6^3 = 216 is the sum of three cubes. Turns out it is the sum of 3^3 + 4^3 + 5^3 = 27 + 64 + 125 = 216.
Aside it’s interesting that 3/4/5 is also a right triangle.
link to original post
Quote: ThatDonGuy
Yes.
The problem is simple enough: let a, b and c be the three radii.
4/3 PI a^3 + 4/3 PI b^3 + 4/3 PI c^3 = 4/3 PI x 6^3.
a^3 + b^3 + c^3 = 216, where a, b, and c are distinct positive integers.
Brute force checking shows the only solution is 5, 4, 3.
Bonus Math: "But doesn't that violate Fermat's Last Theorem?" No, as Fermat's Last Theorem only applies to a^n + b^n = c^n, and not, for example, a^n + b^n + c^n = d^n.
Bonus Bonus Math: Here are all of the solutions where the base is limited by some strange building code to a maximum radius of 100:
3, 4, 5 (6)
1, 6, 8 (9)
6, 8, 10 (12)
9, 12, 15 (18)
2, 12, 16 (18)
3, 10, 18 (19)
7, 14, 17 (20)
12, 16, 20 (24)
4, 17, 22 (25)
3, 18, 24 (27)
18, 19, 21 (28)
11, 15, 27 (29)
15, 20, 25 (30)
18, 24, 30 (36)
4, 24, 32 (36)
6, 20, 36 (38)
14, 28, 34 (40)
6, 32, 33 (41)
2, 17, 40 (41)
21, 28, 35 (42)
16, 23, 41 (44)
5, 30, 40 (45)
27, 30, 37 (46)
3, 36, 37 (46)
24, 32, 40 (48)
8, 34, 44 (50)
29, 34, 44 (53)
27, 36, 45 (54)
6, 36, 48 (54)
12, 19, 53 (54)
36, 38, 42 (56)
9, 30, 54 (57)
15, 42, 49 (58)
22, 30, 54 (58)
30, 40, 50 (60)
21, 42, 51 (60)
7, 42, 56 (63)
33, 44, 55 (66)
22, 51, 54 (67)
36, 38, 61 (69)
7, 54, 57 (70)
14, 23, 70 (71)
36, 48, 60 (72)
8, 48, 64 (72)
34, 39, 65 (72)
38, 43, 66 (75)
12, 51, 66 (75)
31, 33, 72 (76)
12, 40, 72 (76)
39, 52, 65 (78)
28, 56, 68 (80)
9, 54, 72 (81)
25, 48, 74 (81)
12, 64, 66 (82)
19, 60, 69 (82)
4, 34, 80 (82)
54, 57, 63 (84)
42, 56, 70 (84)
28, 53, 75 (84)
50, 61, 64 (85)
26, 55, 78 (87)
38, 48, 79 (87)
20, 54, 79 (87)
33, 45, 81 (87)
32, 46, 82 (88)
21, 43, 84 (88)
25, 31, 86 (88)
17, 40, 86 (89)
58, 59, 69 (90)
45, 60, 75 (90)
10, 60, 80 (90)
25, 38, 87 (90)
54, 60, 74 (92)
6, 72, 74 (92)
32, 54, 85 (93)
15, 50, 90 (95)
48, 64, 80 (96)
19, 53, 90 (96)
45, 69, 79 (97)
11, 66, 88 (99)
35, 70, 85 (100)
16, 68, 88 (100)
51, 68, 85 (102)
33, 70, 92 (105)
58, 68, 88 (106)
15, 82, 89 (108)
54, 72, 90 (108)
12, 72, 96 (108)
29, 75, 96 (110)
72, 76, 84 (112)
50, 74, 97 (113)
57, 76, 95 (114)
23, 86, 97 (116)
30, 84, 98 (116)
18, 96, 99 (123)
86, 95, 97 (134)
94, 96, 99 (139)
60, 80, 100 (120)
link to original post
Correct!!
Good show.
------------------------------------
An oldie I couldn't resist...
The first part is neat as It is based on being able to cover 14 numbers with 7 tickets.
Consider the 14 numbers arranged into seven pairs aa bb cc dd ee ff gg. Then the objective is to cover every combination of two of the seven pairs.
Suppose the first ticket is A B C (i.e. aa bb cc) then that covers AB AC and BC. So each ticket covers three of the combinations of pairs.
In total there are 21 possible pairs from A-G. Thus seven carefully picked entries (each comprising of three pairs) could (and do) cover all 21. They use ABE ACG ADF BCF BDG CDE EFG, and have a neat triangle to show the logic.
That uses 21 entries, and now you know if those don't find a pair of drawn numbers, then there must be three in the 1-17 range. This can be covered (as I think could 1-18) with six tickets (using the three triple idea) as xxx yyy zzz can be covered with XY XZ YZ).
Quote: Wizard
Andre has shorter hair now.
link to original post
How old is that picture? The Wizard looks much younger there.
I used to see Andre and Steffi at the Original Pancake House on the weekends.
Quote: ThatDonGuyOkay, time for me to ask another one...
This time, it is a classic problem and two variations, in increasing order of difficulty; solving either of the harder ones also provides a solution to the easier problem(s).
Easiest version:
You have 12 coins, each with a unique integer mint mark from 2001 through 2012, so you can identify any particular coin by sight.
11 of the coins weigh the same; the other one is either lighter or heavier by the others by a small amount, so you cannot distinguish it by feel or sight.
You do have a balance scale that can take up to four coins on each side. Note that the balance scale cannot tell you by how much one side weighs more than the other - just which side, if either, is heavier.
In three usages of the scale, identify the "off" coin, and whether it his heavier or lighter than the others.
You are allowed to make each weighing conditional on the previous one(s).
Moderate version:
You are too busy working on other "easy" math problems, so you have your assistant do it.
However, you don't trust your assistant to be able to handle complex conditions, so you specify all three weighings in advance (e.g. "weighing 1 is 2001, 2002, 2003, 2004 against 2005, 2006, 2007, 2008; weighing 2 is 2001, 2002, 2005, 2006 against 2003, 2004, 2011, 2012; weighing 3 is 2009, 2010, 2005, 2006 against 2007, 2008, 2011, 2012"); the assistant will write down the results of the three weighings, and from that, you can solve the problem.
Hardest version:
First, there is the possibility that all 12 coins weigh the same.
Second, did I say those were mint marks? My mistake - the numbers indicate what each coin is supposed to weigh, in mg. The "off" coin is off by about 0.5 mg. You have to take this into account when determine the weighings for your assistant.
For example, if you put coins 2001-2004 on one side and 2005-2008 on the other, the 2001-2004 side weighs 8010 +/- 0.5 mg, while the 2005-2008 side weight 8026 +/- 0.5 mg. You need to have the sum of the coin numbers on each side of a particular weighing be the same.
link to original post
Here are the Medium and Hard solutions:
Start with ABCD / EFGH, then ABGI / CEJK, then AECL / DFIJ
| ABCD / EFGH | ABGI / CEJK | AECL / DFIJ | Result |
|---|---|---|---|
| Left | Left | Left | A heavy |
| Left | Left | Same | B heavy |
| Left | Left | Right | E light |
| Left | Same | Left | F light |
| Left | Same | Same | H light |
| Left | Same | Right | D heavy |
| Left | Right | Left | C heavy |
| Left | Right | Same | G light |
| Left | Right | Right | (impossible) |
| Same | Same | Left | L heavy |
| Same | Same | Same | all 12 the same |
| Same | Same | Right | L light |
| Same | Left | Left | J light |
| Same | Left | Same | K light |
| Same | Left | Right | I heavy |
| Same | Right | Left | I light |
| Same | Right | Same | K heavy |
| Same | Right | Right | J heavy |
| Right | Same | Left | D light |
| Right | Same | Same | H heavy |
| Right | Same | Right | F heavy |
| Right | Left | Left | (impossible) |
| Right | Left | Same | G heavy |
| Right | Left | Right | C light |
| Right | Right | Left | E heavy |
| Right | Right | Same | B light |
| Right | Right | Right | A light |
For the hard problem, there are over 20,000 solutions - here are 12:
| A | B | C | D | E | F | G | H | I | J | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7 | 8 | 10 | 2 | 3 | 9 | 12 | 4 | 5 | 6 | 11 |
| 2 | 4 | 10 | 12 | 5 | 8 | 6 | 9 | 7 | 1 | 3 | 11 |
| 3 | 2 | 7 | 8 | 4 | 1 | 10 | 5 | 11 | 6 | 9 | 12 |
| 4 | 2 | 12 | 7 | 5 | 9 | 8 | 3 | 10 | 6 | 1 | 11 |
| 5 | 1 | 8 | 12 | 4 | 3 | 9 | 10 | 6 | 7 | 2 | 11 |
| 6 | 1 | 10 | 7 | 4 | 9 | 3 | 8 | 11 | 5 | 2 | 12 |
| 7 | 1 | 3 | 12 | 8 | 2 | 4 | 9 | 10 | 5 | 6 | 11 |
| 8 | 1 | 3 | 12 | 6 | 7 | 9 | 2 | 5 | 4 | 10 | 11 |
| 9 | 1 | 6 | 5 | 2 | 3 | 12 | 4 | 7 | 10 | 11 | 8 |
| 10 | 1 | 2 | 9 | 4 | 8 | 7 | 3 | 5 | 6 | 11 | 12 |
| 11 | 2 | 9 | 6 | 5 | 12 | 8 | 3 | 4 | 10 | 1 | 7 |
| 12 | 1 | 2 | 11 | 9 | 3 | 4 | 10 | 7 | 8 | 5 | 6 |
Quote: Gialmere
Can Frosty accomplish this?
link to original post
Quote: DRichHow old is that picture? The Wizard looks much younger there.
link to original post
It was taken in 2008, so 15 years ago. It was taken at the Mini Grand Prix. Both our kids were celebrating birthdays there at the same time.
Quote: ThatDonGuyQuote: ThatDonGuyOkay, time for me to ask another one...
This time, it is a classic problem and two variations, in increasing order of difficulty; solving either of the harder ones also provides a solution to the easier problem(s).
Easiest version:
You have 12 coins, each with a unique integer mint mark from 2001 through 2012, so you can identify any particular coin by sight.
11 of the coins weigh the same; the other one is either lighter or heavier by the others by a small amount, so you cannot distinguish it by feel or sight.
You do have a balance scale that can take up to four coins on each side. Note that the balance scale cannot tell you by how much one side weighs more than the other - just which side, if either, is heavier.
In three usages of the scale, identify the "off" coin, and whether it his heavier or lighter than the others.
You are allowed to make each weighing conditional on the previous one(s).
Moderate version:
You are too busy working on other "easy" math problems, so you have your assistant do it.
However, you don't trust your assistant to be able to handle complex conditions, so you specify all three weighings in advance (e.g. "weighing 1 is 2001, 2002, 2003, 2004 against 2005, 2006, 2007, 2008; weighing 2 is 2001, 2002, 2005, 2006 against 2003, 2004, 2011, 2012; weighing 3 is 2009, 2010, 2005, 2006 against 2007, 2008, 2011, 2012"); the assistant will write down the results of the three weighings, and from that, you can solve the problem.
Hardest version:
First, there is the possibility that all 12 coins weigh the same.
Second, did I say those were mint marks? My mistake - the numbers indicate what each coin is supposed to weigh, in mg. The "off" coin is off by about 0.5 mg. You have to take this into account when determine the weighings for your assistant.
For example, if you put coins 2001-2004 on one side and 2005-2008 on the other, the 2001-2004 side weighs 8010 +/- 0.5 mg, while the 2005-2008 side weight 8026 +/- 0.5 mg. You need to have the sum of the coin numbers on each side of a particular weighing be the same.
link to original post
Here are the Medium and Hard solutions:
Start with ABCD / EFGH, then ABGI / CEJK, then AECL / DFIJ
ABCD / EFGH ABGI / CEJK AECL / DFIJ Result Left Left Left A heavy Left Left Same B heavy Left Left Right E light Left Same Left F light Left Same Same H light Left Same Right D heavy Left Right Left C heavy Left Right Same G light Left Right Right (impossible) Same Same Left L heavy Same Same Same all 12 the same Same Same Right L light Same Left Left J light Same Left Same K light Same Left Right I heavy Same Right Left I light Same Right Same K heavy Same Right Right J heavy Right Same Left D light Right Same Same H heavy Right Same Right F heavy Right Left Left (impossible) Right Left Same G heavy Right Left Right C light Right Right Left E heavy Right Right Same B light Right Right Right A light
For the hard problem, there are over 20,000 solutions - here are 12:
A B C D E F G H I J K L 1 7 8 10 2 3 9 12 4 5 6 11 2 4 10 12 5 8 6 9 7 1 3 11 3 2 7 8 4 1 10 5 11 6 9 12 4 2 12 7 5 9 8 3 10 6 1 11 5 1 8 12 4 3 9 10 6 7 2 11 6 1 10 7 4 9 3 8 11 5 2 12 7 1 3 12 8 2 4 9 10 5 6 11 8 1 3 12 6 7 9 2 5 4 10 11 9 1 6 5 2 3 12 4 7 10 11 8 10 1 2 9 4 8 7 3 5 6 11 12 11 2 9 6 5 12 8 3 4 10 1 7 12 1 2 11 9 3 4 10 7 8 5 6
link to original post
I read the third question several times but still haven’t figured out what the question is. The solution to this question is not easy to understand either. Actually, all these three puzzles are very complicated.

It's Easy Monday. Time for more minor mysteries...

Ten senators are about to enter Congress when a barrage of snowballs knocks off their top hats. Each retrieves a hat at random.
What is the probability that exactly nine of them receive their own hats?
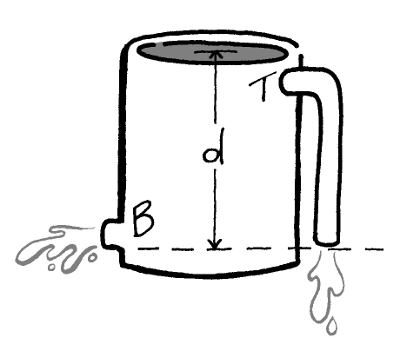
A tank of water has two holes of equal area, one at top and one at bottom. The top one leads to a downspout, so that both holes discharge their water at the same level.
Ignoring friction, which hole produces the faster flow of water?

What were the last moves by White and Black?
Hats: 0% probability that exactly nine of ten receive their own hats. Because if 9/10 have their own hat then the tenth must have their own hat as well. In which case the requirement that "exactly nine of ten receive their own hats" is not fulfilled.
Water: Hole B produces faster flowing water, because there is more water pressure, known as 'head' working to force water through the hole. The force of gravity is working equally on both holes.
Quote: gordonm888
Hats: 0% probability that exactly nine of ten receive their own hats. Because if 9/10 have their own hat then the tenth must have their own hat as well. In which case the requirement that "exactly nine of ten receive their own hats" is not fulfilled.
Water: Hole B produces faster flowing water, because there is more water pressure, known as 'head' working to force water through the hole. The force of gravity is working equally on both holes.
link to original post
On the other hand, if the outlet is big enough in diameter to allow incoming air to overcome surface tension, then the siphon is broken and there will be a no siphon suction on the upper outlet, so the flow will be less.
Further complicating matters, in the absence of friction, the fluid flow is dictated by the detailed shape of the outlets. We are not given the detailed shape of the outlets. Even if there is a siphon and the shape of the effluent jets are equal, the flow will not be identical unless the outlet angles are both horizontal.
Another issue is the height of the water above the T outlet. There will be a depression in the surface of the water above T which will reduce the head on that side of the tank. The size of this effect depends on the height of the water above T relative to the diameter of T. It also depends on viscosity (which may or may not be considered as friction).
Hats: 0
Water: The same -- I see others say the bottom hole. However, I think they are the same because of the syphon effect.
Quote: aceside
I read the third question several times but still haven’t figured out what the question is. The solution to this question is not easy to understand either. Actually, all these three puzzles are very complicated.
link to original post
The difference between the "moderate" and "hard" questions is, in the moderate (and easy) questions, 11 of the 12 coins are the same weight, but in the hard one, the coin marked 2001 weighs 2001 mg, the one marked 2002 weighs 2002 mg, and so on, except that possibly one of the 12 is 0.5 mg off. If 2012 is the "off-weight" coin and you put, say, 2001, 2002, 2003, and 2004 on one side and 2005, 2006, 2007, and 2008 on the other, then in the moderate question, the two sides balance, but in the hard problem, the right side weighs a total of 8026 mg while the left side weighs only 8010, so the scale shows that the right side is heavier. You have to arrange the three weighings so the sum of the numbers on each side is the same, and only an off-weight coin will tip the scale either way.
1+7+8+10 = 2+3+9+12= 4+5+6+11.
This should be a lot shorter, but this is hard.
However, I notice
3+2+7+8= 4+1+10+5 <11+6+9+12.
It’s not consistent

Two of the three puzzles have been solved and are ...
Correct!
Very good.

The water flows from both openings at the same rate. If it didn’t, we could connect the two to create a perpetual-motion machine.
[Mental does, however, make some good points. I'm thinking he moonlights as a hydraulic engineer.]
No takers on the chess puzzle yet so I'll just...

-----------------------------------------------
Therefore, the Earth is flat.
Quote: Gialmere
What were the last moves by White and Black?
link to original post
Black's last move then was not a king move, as all of the squares surrounding the Black king were either under attack or are occupied by a White pawn. This means Black's last move was with a piece no longer on the board, so the piece had to move to a2 and was subsequently captured by the White knight. The captured piece cannot have been a pawn, since White has a pawn on a3, nor a knight, since it would have had to have started on b4, but that's where the White knight was. We can rule out a rook or queen, since either would have moved from the first rank, so White would have been in check with Black to move. Thus, to quote Monty Python, "It's the Bishop!", whose only starting square was b1.
The last two moves were thus
1. ... Bb1-a2
2. Nb4xa2
Dog Hand
Quote: acesideIt looks like you are saying that arrange these 12 integers from 1 to 12 so that this three way equation satisfies,
1+7+8+10 = 2+3+9+12= 4+5+6+11.
This should be a lot shorter, but this is hard.
However, I notice
3+2+7+8= 4+1+10+5 <11+6+9+12.
It’s not consistent
link to original post
You don't have to divide them into four equal groups of 3.
What you have to do is, for each row in the grid, assign the letter for 1 to coin 2001, the letter for 2 to coin 2002, and so on.
For example, the first row is:
A = 1, B = 7, C = 8, D = 10, E = 2, F = 3
G = 9, H = 12, I = 4, J = 5, K = 6, L = 11
Your first weighing, going by the Moderate solution, is A,B,C,D on one side, and E,F,G,H on the other
If none of those coins are the "bad" one, both sides weigh 8026 mg, so the scale will balance. If you replace H with L, then, even if L is also good, the ABCD side weighs 8026, but the EFGL side weighs only 8025, so the scale will show that ABCD is heavier, even though none of the coins on the scale are bad.
Note that, if both sides each weigh 8026, then the remaining four coins, if good, would also weigh 8026.
Your second weighing is A,B,G,I on one side, and C,E,J,K on the other; if all of these coins are good, both sides weigh 8021.
However, in this case, the four remaining coins weigh 8036, as the total weight of the 12 coins is 24,078.
Your third weighing is A,E,C,L on one side, and D,F,I,J on the other; if all of these coins are good, both sides weigh 8022.
However, here, the four remaining coins weigh 8034.
Suppose the first weighing showed that A,B,G,I was heavier, the second showed that D,F,I,J was heavier, and the third showed that A,B,G,I was heavier. The only way this is possible is if coin C - in this case, coin 8 - is heavier than it should be. (Look up "left, right, left" on the moderate solutions table.)
Quote: Gialmere
The water flows from both openings at the same rate. If it didn’t, we could connect the two to create a perpetual-motion machine.
Speaking of a perpetual motion machine, I bought one of these recently. A great desk ornament that attracts lots of attention.
Quote: DRichSpeaking of a perpetual motion machine, I bought one of these recently. A great desk ornament that attracts lots of attention.
link to original post
Can you save us all the trouble and tell us how it works?
Quote: DogHandBlack is in check, so White moved last, placing Black in check. This means White's last move was moving the knight from b4 to a2.
Black's last move then was not a king move, as all of the squares surrounding the Black king were either under attack or are occupied by a White pawn. This means Black's last move was with a piece no longer on the board, so the piece had to move to a2 and was subsequently captured by the White knight. The captured piece cannot have been a pawn, since White has a pawn on a3, nor a knight, since it would have had to have started on b4, but that's where the White knight was. We can rule out a rook or queen, since either would have moved from the first rank, so White would have been in check with Black to move. Thus, to quote Monty Python, "It's the Bishop!", whose only starting square was b1.
The last two moves were thus
1. ... Bb1-a2
2. Nb4xa2
Dog Hand
link to original post
Correct!!
Well done.
(Consider Dog Hand's solution to be official.)
-----------------------------------
Quote: WizardQuote: DRichSpeaking of a perpetual motion machine, I bought one of these recently. A great desk ornament that attracts lots of attention.
link to original post
Can you save us all the trouble and tell us how it works?
link to original post
I watched the video. Seems straightforward to me that the balls when dropped in have enough starting velocity to make the loop back. I assume they lose energy to friction every transit and will eventually not make it back the full loop anymore. DRich, how many times have you seen the ball travel the loop before it can’t make it?
Quote: unJon
DRich, how many times have you seen the ball travel the loop before it can’t make it?
It is perpetual. I have watched hundreds of circuits of it.
Quote: WizardQuote: DRichSpeaking of a perpetual motion machine, I bought one of these recently. A great desk ornament that attracts lots of attention.
link to original post
Can you save us all the trouble and tell us how it works?
link to original post
There is a magnet in the base that accelerates the ball each time. A fun little desk toy for about $40.
Quote: GialmereThere's a clue to how it's done in the video. I've seen these before, but it's a fun puzzle so I'll say no more.
link to original post
If the ball is steel, then it would be easy to rig a magnetic sensor to detect when the ball is arriving. Then simply sequence a set of electromagnets in the base of the toy to provide the impulse.


Mount Everest rises 29,029 feet above sea level, and Ecuador’s volcano Chimborazo rises only 20,702 feet. But because Earth bulges at the equator, Chimborazo is actually farther from the center of the planet.
If we could connect the two peaks with a water pipe, in which direction would the water flow?

You walk into Arlington, Virginia. As the Pentagon comes into view, you’ll be able to see either two or three sides of the building.
Which is more likely?

White to play and checkmate all six black kings simultaneously with his second move.
Quote: Gialmere
Quote:Mount Everest rises 29,029 feet above sea level, and Ecuador’s volcano Chimborazo rises only 20,702 feet. But because Earth bulges at the equator, Chimborazo is actually farther from the center of the planet.
If we could connect the two peaks with a water pipe, in which direction would the water flow?
Because both heights are referenced to sea level, the centrifugal effects of the earth's rotation are already zeroed out. A sea-level pipe between the bases of the mountains would not flow in either direction. A pair of vertical pipes from sea level to the tops of each mountain would have a 3600 psi difference in pressure if filled with fresh water. Water would flow from Mount Everest to Chimborazo.Gambling is a math contest where the score is tracked in dollars. Try not to get a negative score.
The answer depends on the radius of your movement. When the radius is small, you will see only two sides or one side, no three sides. When the radius the medium, you will more likely to see two sides. When the radius is infinite, they are equally likely.
What "water"? At that altitude, doesn't the pressure cause a direct conversion from steam to ice, or vice versa?
This question appears in my copy of Lytton's Problematical Recreations, with what I am pretty sure is an incorrect answer: "If you draw any line through the center of the Pentagon, and select the two points equidistant from the center, then you can see two sides from one point and three from the other, so the two possibilities are equal."
Draw the five lines that are extensions of the five sides. If you select a point that is inside the region bounded by two lines outside of where they meet, you can see three sides from there; otherwise, you can see only two. The two-point zones are much larger than the three-point ones, so the most likely number is two.
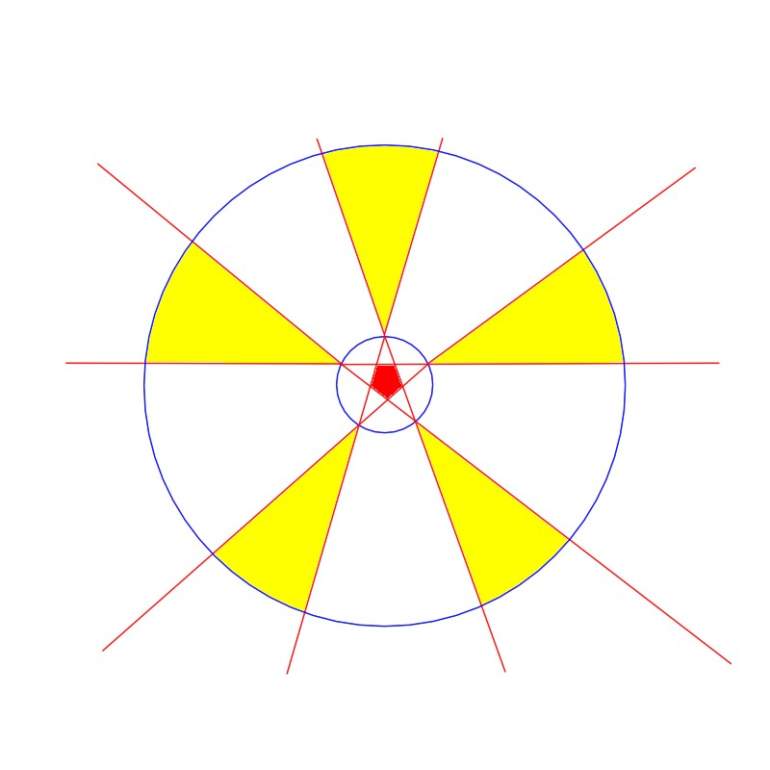
The Pentagon is in red, in the center.
The areas in yellow are where you can see three sides; the areas in white inside the same circle are where you can see two.
Quote: GialmereIt's Easy Monday. Time for another selection of small secrets...
Mount Everest rises 29,029 feet above sea level, and Ecuador’s volcano Chimborazo rises only 20,702 feet. But because Earth bulges at the equator, Chimborazo is actually farther from the center of the planet.
If we could connect the two peaks with a water pipe, in which direction would the water flow?
You walk into Arlington, Virginia. As the Pentagon comes into view, you’ll be able to see either two or three sides of the building.
Which is more likely?
White to play and checkmate all six black kings simultaneously with his second move.
link to original post
Quote: Mental
Because both heights are referenced to sea level, the centrifugal effects of the earth's rotation are already zeroed out. A sea-level pipe between the bases of the mountains would not flow in either direction. A pair of vertical pipes from sea level to the tops of each mountain would have a 3600 psi difference in pressure if filled with fresh water. Water would flow from Mount Everest to Chimborazo.
link to original post
But:


