Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: unJonQuote: Mental
Because both heights are referenced to sea level, the centrifugal effects of the earth's rotation are already zeroed out. A sea-level pipe between the bases of the mountains would not flow in either direction. A pair of vertical pipes from sea level to the tops of each mountain would have a 3600 psi difference in pressure if filled with fresh water. Water would flow from Mount Everest to Chimborazo.
link to original post
But:A sea level pipe connecting the two mountains would be curved matching the curvature of the earth. A straight line pipe connecting the peaks I think goes “down” from both ends to some point in the middle.
link to original post
Water can exist in equilibrium in liquid form down to 0.006 bar. The pressure on Everest is about 0.33 bar. The boiling point of water on top of Everest is about 70C. The problem with finding liquid water on Everest is not the pressure, it is the temperature. It never gets above freezing, so the water would need to be warmed/kept above ambient temperature.
Quote: Gialmere<snip>
White to play and checkmate all six black kings simultaneously with his second move.
link to original post
2. cxd++,++,++,++,++,++
Dog Hand
However, to answer the question, probably incorrectly, if you poured water down either end, it would go down the hole due to gravity. I think it would end up a the spot closest to the center of the earth.
Somebody mentioned the water vaporizing, but mountaineers at these altitudes melt snow all the time to liquid water to drink.
Quote: WizardWhat you asked makes for a good trivia question. Another good one is "What was the name of Mount Everest before it was discovered?
link to original post
Er, before it was discovered, nobody knew it was there, so obviously it didn't have a name yet.
By any chance, are you thinking of the question, "Before Mount Everest was discovered, what was the tallest mountain in the world?"
Quote: ThatDonGuy
By any chance, are you thinking of the question, "Before Mount Everest was discovered, what was the tallest mountain in the world?"
link to original post
Yes, that is the correct wording. Thank you.

Responses for the three Monday puzzles are...
Correct!
Sea level gives us a convenient equilibrium water level. Since Everest rises higher, the water would flow toward Chimborazo.
As you can see from the responses, however, there are several ways to consider this one. I confess to thinking of every thing from a flat earth, to a pipe taking the proverbial hole to China, to a rain gutter suspended 20k+ feet in the air following the surface curvature. So, solver's choice as to what's correct.
They’re equally likely. Imagine someone approaching the building from the opposite side. If you can see two sides, she can see three, and vice versa. Because these are the only two possibilities, the probability of each must be 1/2.
As aceside mentions above, however, the solve also adds this caveat...
(Strictly speaking, the two probabilities are perfectly equal only if you’re approaching an abstract pentagonal building from an infinite distance. But you get the point.)
1. Bb3+ d5 (forced) 2. cxd6 e.p.######

I like this one but note that the pawn now attacking the two kings is overworked. Either king might be killed or not killed. Call it a Schrödinger's Mate I guess.

This design is made of three 2 x 1 rectangles.
What fraction of it is shaded?
I'm getting 1/7.
I originally made an error and then I misunderstood the question, thinking it was asking the area of the shaded regions, which I get as 3/4.
(3/4)/(6-3/4) = (3/4)/(21/4) = 1/7
Note: Answer updated 8:05 PST
Quote: GialmereIt's Toughie Tuesday. Time for another evil Catriona Shearer puzzle...
This design is made of three 2 x 1 rectangles.
What fraction of it is shaded?
link to original post
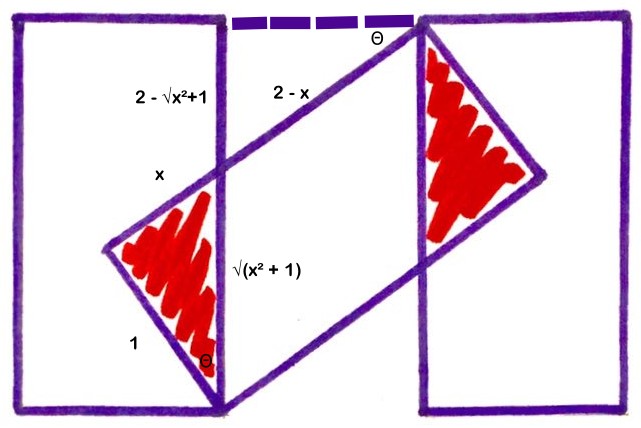
Note that the upper dotted line does not necessarily connect the corners of two rectangles; it is perpendicular to the right side of the left triangle and extends from its upper right corner.
Let x be the distance marked.
Similar triangles: sqrt(x^2 + 1) / x = (2 - x) / (2 - sqrt(x^2 + 1))
x (2 - x) = 2 sqrt(x^2 + 1) - (x^2 + 1)
2x + 1 = 2 sqrt(x^2 + 1)
4 x^2 + 4 x + 1 = 4 x^2 + 4
x = 3/4
The shaded area = 2 * (1/2 * 1 * 3/4) = 3/4
The total area = the area of three triangles minus the shaded area, which is counted twice
= 3 x 2 x 1 - 3/4
= 21 / 4
The fraction that is shaded is (3/4) / (21/4) = 1 / 7.
1/3
The shaded triangle is the same as the lower triangle in the center. (the central strip has same height=2 and diagonal=sqrt(5), so must have the same width=1 as the slanted rectangle)
So the two triangles are same (similar angles and one side the same)
Call the height of the lower center triangle x, and the hypotenuse is sqrt(x^2+1)
x+sqrt(x^2+1)=2
sqrt(x^2+1) = 2-x
x^2+1 = 4-4x+x^2
4x=3
x=3/4
So shaded triangle area = x * 1 = 3/4
Two shaded triangles have area 2*3/4 = 3/2
Total area = 2+2+2 - 3/2 (since the shaded region is doubled up) = 9/2
fraction shaded = (3/2)/(9/2) = 1/3
Which fits your description that "evil Catriona Shearer puzzle"s have clean answers
------------------------------------------------
EDIT: Doh......area of triangle is 1/2 * b * h......
shaded = (3/4) / (21/4) = 1/7
Credit to @ThatDonGuy.....as usual
Dog Hand

Quote: ThatDonGuy
Note that the upper dotted line does not necessarily connect the corners of two rectangles; it is perpendicular to the right side of the left triangle and extends from its upper right corner.
Let x be the distance marked.
Similar triangles: sqrt(x^2 + 1) / x = (2 - x) / (2 - sqrt(x^2 + 1))
x (2 - x) = 2 sqrt(x^2 + 1) - (x^2 + 1)
2x + 1 = 2 sqrt(x^2 + 1)
4 x^2 + 4 x + 1 = 4 x^2 + 4
x = 3/4
The shaded area = 2 * (1/2 * 1 * 3/4) = 3/4
The total area = the area of three triangles minus the shaded area, which is counted twice
= 3 x 2 x 1 - 3/4
= 21 / 4
The fraction that is shaded is (3/4) / (21/4) = 1 / 7.
link to original post
Quote: chevy
1/3
The shaded triangle is the same as the lower triangle in the center. (the central strip has same height=2 and diagonal=sqrt(5), so must have the same width=1 as the slanted rectangle)
So the two triangles are same (similar angles and one side the same)
Call the height of the lower center triangle x, and the hypotenuse is sqrt(x^2+1)
x+sqrt(x^2+1)=2
sqrt(x^2+1) = 2-x
x^2+1 = 4-4x+x^2
4x=3
x=3/4
So shaded triangle area = x * 1 = 3/4
Two shaded triangles have area 2*3/4 = 3/2
Total area = 2+2+2 - 3/2 (since the shaded region is doubled up) = 9/2
fraction shaded = (3/2)/(9/2) = 1/3
Which fits your description that "evil Catriona Shearer puzzle"s have clean answers
------------------------------------------------
EDIT: Doh......area of triangle is 1/2 * b * h......
shaded = (3/4) / (21/4) = 1/7
Credit to @ThatDonGuy.....as usual
link to original post
Quote: DogHandI agree with ThatDonGuy... He beat me by an hour, and has a much simpler solution.
Dog Hand
link to original post
Quote: Wizard
I'm getting 1/3.
I originally made an error and then I misunderstood the question, thinking it was asking the area of the shaded regions, which I get as 3/4.
(3/4)/(6-3/4) = (3/4)/(21/4) = 1/7
Note: Answer updated 8:05 PST
link to original post
Correct!!!
Very good.
Label vertices and draw in a couple line segments:
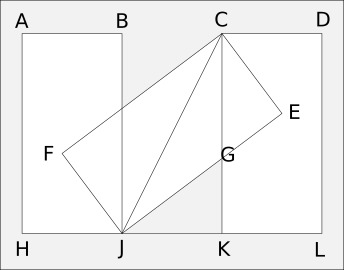
Considering triangles CFJ and CKJ, angles CFJ and CKJ are right, line segment CJ is common, and CF = CK = 2, so the two triangles are congruent and FJ = JK = 1. But then angles CGE and JGK are equal, angles CEG and GKJ are right, and CE = JK, so those triangles are congruent and CG = GJ.
So JK = 1, and if KG = x, GJ = CG = 2-x, so 1²+x² = (2-x)². The solution is x = 3/4. The area of each shaded triangle is 3/8. The area of the whole pattern is three rectangles minus the shaded area: 6-3/4 = 21/5. The shaded area is 1/7 of the area of the whole pattern.
Notice the shaded triangles are 3:4:5.
-----------------------------------------------
Works well in a classroom or seminar setting.
Proof by forward reference:
Reference is usually to a forthcoming paper of the author, which is often not as forthcoming as at first.
Proof by funding:
How could three different government agencies be wrong?
Proof by example:
The author gives only the case n = 2 and suggests that it contains most of the ideas of the general proof.

You know there's Dasher and Dancer and Prancer and Vixen, Comet and Cupid and Donner and Blitzen." But what the song doesn't reveal is that the ordering of the reindeer is determined by how they placed in this year's Reindeer Games, with the winner going first (behind Rudolph, of course) and the last place finisher coming in 8th.
This year, Santa Claus didn't get the full results from the Reindeer Games, since he was busy supervising the elves.
Clues:
Santa has only this information:
1) Prancer finished three spots behind Dasher, which was better than Blitzen can say;
2) Donner had his strongest showing ever, but hopes to place higher next year;
3) Vixen just barely beat out Cupid in the closest finish of the competition;
4) Comet, Dancer, and Dasher all hoped to finish in the top three; with only Dasher disappointed in the outcome;
5) Only one reindeer finished between Donner and Dancer.
Reader, with your brain so bright, won't you help Santa sort his reindeer tonight?
Quote: Gialmere
You know there's Dasher and Dancer and Prancer and Vixen, Comet and Cupid and Donner and Blitzen." But what the song doesn't reveal is that the ordering of the reindeer is determined by how they placed in this year's Reindeer Games, with the winner going first (behind Rudolph, of course) and the last place finisher coming in 8th.
This year, Santa Claus didn't get the full results from the Reindeer Games, since he was busy supervising the elves.
Clues:
Santa has only this information:
1) Prancer finished three spots behind Dasher, which was better than Blitzen can say;
2) Donner had his strongest showing ever, but hopes to place higher next year;
3) Vixen just barely beat out Cupid in the closest finish of the competition;
4) Comet, Dancer, and Dasher all hoped to finish in the top three; with only Dasher disappointed in the outcome;
5) Only one reindeer finished between Donner and Dancer.
Reader, with your brain so bright, won't you help Santa sort his reindeer tonight?
link to original post
Rudolph
Comet
Dancer
Donner
Dasher
Vixen
Cupid
Prancer
Blitzen
ETA: I misread one of them. Ignore this I agree with Charlie and Don
The logic is
(1) DAS - - PRA (4) DAS not in top 3, so must be 4th or 5th
(1) As BLI is behind PRA, DAS=4th, PRA=7th, BLI=8th
(3)(4) {VIX CUP} cannot be in top 3 so must occupy 5th and 6th
(5) Top 3 are now {COM,DAN,DON}, and so COM=2nd (as between the other two)
(2) DON didn't win, as otherwise couldn't do better next year, so DON=3rd DAN=1st.
Quote: GialmereReader, with your brain so bright, won't you help Santa sort his reindeer tonight?
link to original post
(1) Blitzen finished at least four spots behind Prancer, so Prancer finished 4th or better; Dasher did not finish in the top 3 nor 8th, and Prancer did not finish in the top 4.
(2) Donner did not finish 1st or 8th.
(3) Vixen finished one place ahead of Cupid, so Vixen did not finish 8th, and Cupid did not finish 1st.
(4) Comet and Dancer finished in the top 3; Dancer did not.
(a) Since Prancer finished ahead of Blitzen, Prancer was not 8th, so Dasher was 4th or better (1); Dasher did not finish in the top 3 (4), so Dasher finished 4th, which means Prancer finished 7th (1) and Blitzen 8th (1).
(b) Vixen could not have finished 6th, as Cupid did not finish 7th (3), so Cupid finished 6th (3), which means Vixen finished 5th.
(c) Since neither Donner nor Dasher finished fourth, neither finished second (5), which means Comet finished 2nd, which means Dancer finished 1st, which means Donner finished 3rd.
The final finishing order: Dancer, Comet, Donner, Dasher, Vixen, Cupid, Prancer, Vixen
Quote: charliepatrickDancer Comet Donner Dasher Vixen Cupid Prancer Blitzen.
The logic is
(1) DAS - - PRA (4) DAS not in top 3, so must be 4th or 5th
(1) As BLI is behind PRA, DAS=4th, PRA=7th, BLI=8th
(3)(4) {VIX CUP} cannot be in top 3 so must occupy 5th and 6th
(5) Top 3 are now {COM,DAN,DON}, and so COM=2nd (as between the other two)
(2) DON didn't win, as otherwise couldn't do better next year, so DON=3rd DAN=1st.
link to original post
Quote: ThatDonGuy
(1) Blitzen finished at least four spots behind Prancer, so Prancer finished 4th or better; Dasher did not finish in the top 3 nor 8th, and Prancer did not finish in the top 4.
(2) Donner did not finish 1st or 8th.
(3) Vixen finished one place ahead of Cupid, so Vixen did not finish 8th, and Cupid did not finish 1st.
(4) Comet and Dancer finished in the top 3; Dancer did not.
(a) Since Prancer finished ahead of Blitzen, Prancer was not 8th, so Dasher was 4th or better (1); Dasher did not finish in the top 3 (4), so Dasher finished 4th, which means Prancer finished 7th (1) and Blitzen 8th (1).
(b) Vixen could not have finished 6th, as Cupid did not finish 7th (3), so Cupid finished 6th (3), which means Vixen finished 5th.
(c) Since neither Donner nor Dasher finished fourth, neither finished second (5), which means Comet finished 2nd, which means Dancer finished 1st, which means Donner finished 3rd.
The final finishing order: Dancer, Comet, Donner, Dasher, Vixen, Cupid, Prancer, Vixen
link to original post
Quote: unJonETA: I misread one of them. Ignore this I agree with Charlie and Don
link to original post
Correct!!
A holly jolly good show.
By statement 4, Dasher finished no better than 4th. Thus Dasher finished exactly 4th.
Now statement 1 implies Prancer finished 7th and Blitzen must be 8th.
Statement 3 means Vixen finished one spot ahead of Cupid. But from statement 4, Comet and Dancer occupy 2 of the top 3 spots. So the only two adjacent positions remaining are 5 and 6. Therefore, Vixen finished 5th and Cupid was 6th.
We now know the top three finishers include Donner, Dancer, and Comet. Statement 5 implies Comet must come in 2nd place between Donner and Dancer.
Finally, statement 2 implies Donner did not win, so he came in 3rd, leaving the top spot for Dancer!
The Reindeer Games finishers following Rudolph are:
1) Dancer
2) Comet
3) Donner
4) Dasher
5) Vixen
6) Cupid
7) Prancer
8) Blitzen
----------------------------------------
Kid: What about Donner?
Santa (frowning): The year was 1847, snowfall had trapped us in the Sierra Nevada...
:strip_icc()/pic7925333.png)
This classic holiday puzzle asks you to convert its six straight rows each containing four mince pies, into seven straight rows each containing four mince pies, by moving just four pies.
The mince pie puzzle is almost 120 years old and still boggles the mind. I'll let it ride...
-----------------------------------

Meanwhile, here is some Hollywood Christmas trivia...
1) In "Home Alone," where are the McCallisters going on vacation when they leave Kevin behind?
2) The movie "Miracle on 34th Street" (1947) is based on a real-life department store. What is it?
3) In "A Christmas Story" what gift does Ralphie receive from his aunt?
4) What was the name of the character Tim Allen plays in "The Santa Clause?"
5) In "The Muppet Christmas Carol" who played Scrooge?
6) In the movie "Elf" what was the third rule of The Code of Elves?
7) In the movie "It’s A Wonderful Life" what happens every time a bell rings?
8) In the 1964 TV movie "Rudolph the Red-Nosed Reindeer" what was the name of Rudolph’s elf friend?
9) How many lights were on the Griswold’s house in "National Lampoon's Christmas Vacation?"
10) What does the Peanuts gang sing at the end of “A Charlie Brown Christmas?”
----------------------------------------
Poll
Is "Die Hard" a Christmas movie?
2. Macy's
7. An angel gets its wings
8. Hermie
10. Hark, the Herald Angels Sing
Twice, a contestant on What's My Line? was the Santa at Macy's at Herald Square (on 34th Street)...despite the fact that Macy's goes to reasonably great pains to claim that this store has the real Santa.
Quote: Gialmere
Poll
Is "Die Hard" a Christmas movie?
link to original post
I was going to link the Star Wars Holiday Special as an example of "if this, then that", but after several minutes of Wookiee grunting (without subtitles), I've had a rare moment of clarity. (It seems to be on Youtube, if you wish to enjoy endure it.)
I'm more likely to watch Love, Actually or Life of Brian.
2) The movie "Miracle on 34th Street" (1947) is based on a real-life department store. What is it?
I'll go with Macy's, but I have a feeling it's a trick question.
7) In the movie "It’s A Wonderful Life" what happens every time a bell rings?
An Angel get's its wings!
10) What does the Peanuts gang sing at the end of “A Charlie Brown Christmas?”
Joy to the World
Quote:Poll
Is "Die Hard" a Christmas movie?
No! Christmas is not germane to the story. To those who vote "yes," was Rocky IV a Christmas movie (the final fight was on Dec 25).
95% played in the casino
90% went to a show
85% played golf
80% went shopping
What is the least percentage that did all four?
Quote: WizardOf visitors to Las Vegas:
95% played in the casino
90% went to a show
85% played golf
80% went shopping
What is the least percentage that did all four?
link to original post
Quote: aceside
50%
link to original post
I agree!
Quote: WizardOf visitors to Las Vegas:
95% played in the casino
90% went to a show
85% played golf
80% went shopping
What is the least percentage that did all four?
link to original post
5% did not play in the casino; 10% did not go to a show; 15% did not play golf; 20% did not go shopping.
If each person that did not do something did do all of the other three, then 5% + 10% + 15% + 20% = 50% did not do something, so 50% did all three.
If anybody did do more than one thing, then there has to be at least one more person that did do all four, so the minimum is 50%.
That reminds me of a similar problem: of the people that did play in the casino:
90% played slots
80% played roulette
70% played blackjack
60% played poker
If nobody played all four, what is the minimum percentage that played at least one card game?
Without loss of generality, assume there are 300 people.
The number of games played = 90 + 80 + 70 + 60 = 300.
Since nobody played all four games, the only way 300 games could have been played is if all 100 people played three.
Since it is impossible to play three games without playing either blackjack or poker, everybody played a card game, so the answer is 100%.
Say players 95-100 didn't do #1.
Say players 85-95 didn't do #2.
Say players 70-85 didn't do #3.
Say players 50-70 didn't do #4.
Then that leaves 50% of players who played all four.
Quote: Wizard
Quote:Poll
Is "Die Hard" a Christmas movie?
No! Christmas is not germane to the story. To those who vote "yes," was Rocky IV a Christmas movie (the final fight was on Dec 25).
link to original post
I would argue that travelling across the country to spend a little time with estranged family members is a very "because it's Christmas" thing to do, and without this plot device, there would be nobody to thwart the dastardly plans of Hans Gruber & Co.
No idea about Rocky IV. Haven't seen it, I might check it out after I finish travelling across the country to spend a few days with strange family members...
Quote: DieterI would argue that travelling across the country to spend a little time with estranged family members is a very "because it's Christmas" thing to do, and without this plot device, there would be nobody to thwart the dastardly plans of Hans Gruber & Co.
link to original post
Good point. You might also argue that a Christmas party was the reason so many people were still in the building at night.

:strip_icc()/pic7925334.png)
2) Macy's (Although the real R.H. Macy died in 1877.)
3) A pink bunny suit
4) Scott Calvin (Initials S.C. were a minor plot point.)
5) Michael Caine
6) "Let's recite The Code of the Elves, shall we? #1: Treat every day like Christmas. #2: There's room for everyone on the nice list. #3: The best way to spread Christmas cheer is singing loud for all to hear."
7) An angel gets his wings.
8) Hermey (the wannabe dentist.)
9) In the film, Clark proclaims the house is decked out with "25,000 imported Italian twinkle lights."
10) Hark! The Herald Angels Sing
1 yes vote
1 no vote
The heated debate continues.
Tune in next year.
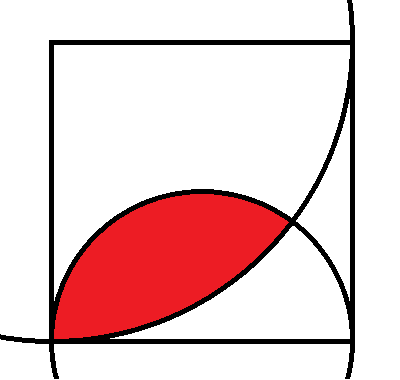
The square above has side length 2. One arc is of a circle of radius 1 and the other radius 2. What is the area of the red region? It is allowed to express your answer in trig functions.
For purposes of discussion, feel free to use...
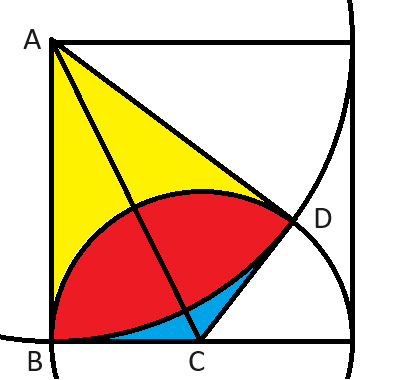
Note that tan BAC = 1/2, and tan BCA = 2
The area of ABC = 1/2 x 2 x 1 = 1
AB = AD, BC = DC, and AC = AC, so triangles ABC and ADC are SSS-congruent, which means tan DAC = 1/2, tan DCA = 2, and the area of triangle ADC = 1.
The area of "pie slice" DAB = 4 PI x 2 arctan 1/2 / (2 PI) = 4 arctan 1/2
The area of pie slice DCB = PI x 2 arctan 2 / (2 PI) = 1/2 arctan 2
The shaded area = pie slice DAB + pie slice DCB - (triangle ABC + triangle ADC) = 4 arctan 1/2 + 1/2 arctan 2 - 2
Admin note: I'm sorry, but I screwed up your post. I meant to quote it, but hit "edit" by mistake.
Quote: ThatDonGuy
Note that tan BAC = 1/2, and tan BCA = 2
The area of ABC = 1/2 x 2 x 1 = 1
AB = AD, BC = DC, and AC = AC, so triangles ABC and ADC are SSS-congruent, which means tan DAC = 1/2, tan DCA = 2, and the area of triangle ADC = 1.
The area of "pie slice" DAB = 4 PI x 2 arctan 1/2 / (2 PI) = 4 arctan 1/2
The area of pie slice DCB = PI x 2 arctan 2 / (2 PI) = 1/2 arctan 2
The shaded area = pie slice DAB + pie slice DCB - (triangle ABC + triangle ADC) = 4 arctan 1/2 + 1/2 arctan 2 - 2
link to original post
Quote: WizardThree logicians are asleep under a tree. While asleep, a mischievous boy draws an illustration of a penis on the forehead of each of them. Later, they wake up the same time. Each being able to see the other two, but not himself, break out laughing. However, after the initial laughter, they all suddenly stop. Why?
link to original post
Label the logicians A, B, and C.
C thinks, "Suppose I don't have one. B would reason that A must be laughing at B, and immediately stop laughing. Using similar reasoning, A would realize that B is laughing at A, and also stop. Since neither of them stopped right away, I must have one." Using similar reasoning, A and B come to the conclusion that each of them has one as well.
Quote: ThatDonGuy
Label the logicians A, B, and C.
C thinks, "Suppose I don't have one. B would reason that A must be laughing at B, and immediately stop laughing. Using similar reasoning, A would realize that B is laughing at A, and also stop. Since neither of them stopped right away, I must have one." Using similar reasoning, A and B come to the conclusion that each of them has one as well.
link to original post
You're absolutely right! Very good explanation too.
Quote: WizardQuote: ThatDonGuy
Label the logicians A, B, and C.
C thinks, "Suppose I don't have one. B would reason that A must be laughing at B, and immediately stop laughing. Using similar reasoning, A would realize that B is laughing at A, and also stop. Since neither of them stopped right away, I must have one." Using similar reasoning, A and B come to the conclusion that each of them has one as well.
link to original post
You're absolutely right! Very good explanation too.
link to original post
ThatDonGuy's answer assumes that the logicians will stop laughing at a guy with a penis on his forehead just because they realize they have one, too.
What assumptions can we make about the kind of person who laughs at another person having a vulgar practical joke played on them?
If they think it is funny that two people have a penis on their forehead, logically, it should be 50% funnier when they realize they all have one.
Even if they don't feel this way, they cannot logically deduce that the other two logicians feel the same way.
If they are superb logicians, they should figure this out before they start laughing in the first place.
Quote: Mental
ThatDonGuy's answer assumes that the logicians will stop laughing at a guy with a penis on his forehead just because they realize they have one, too.
What assumptions can we make about the kind of person who laughs at another person having a vulgar practical joke played on them?
If they think it is funny that two people have a penis on their forehead, logically, it should be 50% funnier when they realize they all have one.
Even if they don't feel this way, they cannot logically deduce that the other two logicians feel the same way.
If they are superb logicians, they should figure this out before they start laughing in the first place.
link to original post
I think this puzzle is old enough to not need spoiler tags anymore, so will reply openly.
I like this puzzle, but have struggled how to phrase the wording. I used to phrase it involving a game show with black and white hats, but I found most people found it difficult to understand what was being asked. The sleeping logicians phrasing I find the most simple and Don at least understood it.
Before I said the boy painted the foreheads red, but I think some people evidently didn't get why that would be funny, so changed it to a penis.
Personally, I think it can be inferred from context they find the penis drawings funny.
I am very open to how to word this one better, but I hate to add a lot of rules about what logicians find funny. It's my goal to keep the wording to a minimum.

Yes, this is an easy inference, but you have to further assume they stop thinking it is funny once they deduce that they themselves are similarly affected.Quote: Wizard
Personally, I think it can be inferred from context they find the penis drawings funny.
link to original post
If you add too much explanation of the assumptions, you give away the answer.
Yes, I know I overthink everything, but sometimes puzzles are based on faulty assumptions.
There are plenty of alternative methods for stating logical rules. Setting up a story about "cruel tyrants with captive logicians who will be killed unless . . .' seems better because you don't need to establish the fact that the logicians desire to live.*
*Although, if the logician oversees a forum full of quarrelsome nitpickers perhaps death might seem preferable.
Three logicians are on a game show. The host puts blindfolds on them and then place a black hat on each person. He then asks them to remove the blindfolds. Each logician can see the hat of the other two, but not his own.
The host explains that if, when asked, if any logician can figure out the color of his hat, he should immediately blurt it out or stay quiet. If he is right, they each win $1,000,000. If he is wrong, they all get nothing.
The host then says, "Raise your hand if you see at least one black hat." All three raise their hands.
The host then immediately says, "Do any of you know the color of your hat?" None of them say anything.
Then several minutes go by and he asks again. All of them immediately raise their hands.
How did they know?
Quote: WizardHere is the wording I used to use, which I felt was too long. I don't know that anyone had the patience to read the whole thing. Here is goes. I would be interested to know which wording you like better or feel free to use your own wording.
Three logicians are on a game show. The host puts blindfolds on them and then place a black hat on each person. He then asks them to remove the blindfolds. Each logician can see the hat of the other two, but not his own.
The host explains that if, when asked, if any logician can figure out the color of his hat, he should immediately blurt it out or stay quiet. If he is right, they each win $1,000,000. If he is wrong, they all get nothing.
The host then says, "Raise your hand if you see at least one black hat." All three raise their hands.
The host then immediately says, "Do any of you know the color of your hat?" None of them say anything.
Then several minutes go by and he asks again. All of them immediately raise their hands.
How did they know?
link to original post
I once saw a variation on this, where only the first person to give the correct answer won the million.
The minute all three hands went up, one of them said, "My hat is black."
Any other result, and it would not have been equally fair to all three of them.
Quote: Wizard
The square above has side length 2. One arc is of a circle of radius 1 and the other radius 2. What is the area of the red region? It is allowed to express your answer in trig functions.
For purposes of discussion, feel free to use...
link to original post
What is the answer?
Note that tan BAC = 1/2, and tan BCA = 2
The area of ABC = 1/2 x 2 x 1 = 1
AB = AD, BC = DC, and AC = AC, so triangles ABC and ADC are SSS-congruent, which means tan DAC = 1/2, tan DCA = 2, and the area of triangle ADC = 1.
The area of "pie slice" DAB = 4 PI x 2 arctan 1/2 / (2 PI) = 4 arctan 1/2
The area of pie slice DCB = PI x 2 arctan 2 / (2 PI) = 1/2 arctan 2 oops = arctan 2
Also note that arctan 1/x = PI/2 - arctan x
The shaded area = pie slice DAB + pie slice DCB - (triangle ABC + triangle ADC) = 4 arctan 1/2 + PI/2 - arctan 1/2 - 2 = 3 arctan 1/2 + PI/2 - 2
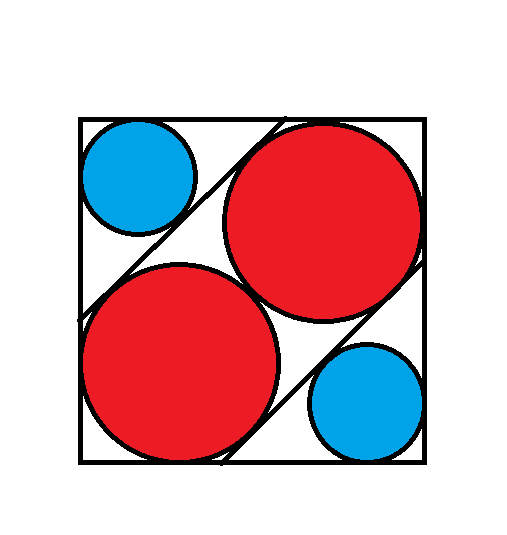
In the diagram above, the red circles have radius of 1. What is the radius of the blue circles?
Source: Nov/Dec 2023 Mensa Bulletin
Since the red circles have radius 1, the diagonal of the square = 2 + 2 sqrt(2).
The distance between the two lines inside the square is 2, so the distance from each line to the nearer corner with a blue circle is sqrt(2).
The radius of a blue circle = sqrt(2) / (1 + sqrt(2)) = 2 - sqrt(2).
Quote: ThatDonGuy
Since the red circles have radius 1, the diagonal of the square = 2 + 2 sqrt(2).
The distance between the two lines inside the square is 2, so the distance from each line to the nearer corner with a blue circle is sqrt(2).
The radius of a blue circle = sqrt(2) / (1 + sqrt(2)) = 2 - sqrt(2).
link to original post
I agree!
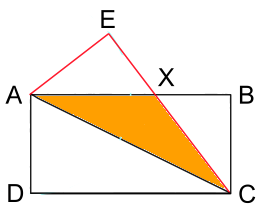
ABCD is a rectangle with AB = 2 and AD = 1
AE = AD, CE = CD, and AEC is a right angle
AB intersects CE at X
What is the area of triangle AXC?



