Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
January 20th, 2024 at 4:06:21 PM
permalink
Quote: ThatDonGuyWhat is the area of triangle AXC?
link to original post
I get 5*sqrt(5)/16 =~ 0.698771
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 22nd, 2024 at 4:36:47 PM
permalink
Quote: acesideLet AX=x, then the yellow area is x/2.
Apply Pythagorean theorem to the triangle on the upper right corner,
(2-x)^2 + 1^2 = x^2.
Thus, x=5/4
Then, the area of the triangle AXC is 5/8=0.625.
link to original post
Quote: WizardQuote: ThatDonGuyWhat is the area of triangle AXC?
link to original post
I get 5*sqrt(5)/16 =~ 0.698771
link to original post
Aceside is correct.
Let x be the length of BX, and t the measure of angle ACD
Since ADC is a right angle, angle DAC = 90 - t; since DAB is also a right angle, angle CAB = t
AD = AE and CD = CE, so DAC and EAC are SSS-congruent, which means angle CAE = angle CAD = 90 - t, so angle EAX = 90 - 2t
Angle AEX = 90, so angle AXE = 2t, which means angle BXC = 2t
tan 2t = 1 / x = 2 tan t / (1 - tan^2 t)
tan t = AD / CD = 1/2, so tan 2t = 1 / (1 - 1/4) = 4/3, and x = 1 / (4/3) = 3/4
I could have used the method Aceside used to calculate the area, but instead I used:
AXC = ABC - XBC = 1/2 x 1 x 2 - 1/2 x 1 x 3/4 = 1 - 3/8 = 5/8.
I have a tough one, courtesy of the 2023 Stanford High School Math Tournament, ready for Toughie Tuesday, if I remember to post it...
January 22nd, 2024 at 5:18:51 PM
permalink
There is a 10x10 grid. Two random walkers start at opposite corners diagonally from each other. Every minute each takes a step towards the opposite corner, randomly in either direction that brings the walker closer.
For example, if Adam starts at the south-west corner, his goal is the north-east corner. Every step he would either go north or east, except if he were at the north or east end of the grid, he could only go one way, as he can't leave the grid.
What is the probability both meet at the same point at the same time?
For example, if Adam starts at the south-west corner, his goal is the north-east corner. Every step he would either go north or east, except if he were at the north or east end of the grid, he could only go one way, as he can't leave the grid.
What is the probability both meet at the same point at the same time?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 22nd, 2024 at 6:03:30 PM
permalink
Quote: WizardThere is a 10x10 grid. Two random walkers start at opposite corners diagonally from each other. Every minute each takes a step towards the opposite corner, randomly in either direction that brings the walker closer.
For example, if Adam starts at the south-west corner, his goal is the north-east corner. Every step he would either go north or east, except if he were at the north or east end of the grid, he could only go one way, as he can't leave the grid.
What is the probability both meet at the same point at the same time?
link to original post
46,189 / 262,144
January 22nd, 2024 at 6:41:27 PM
permalink
Quote: ChesterDogQuote: WizardThere is a 10x10 grid. Two random walkers start at opposite corners diagonally from each other. Every minute each takes a step towards the opposite corner, randomly in either direction that brings the walker closer.
For example, if Adam starts at the south-west corner, his goal is the north-east corner. Every step he would either go north or east, except if he were at the north or east end of the grid, he could only go one way, as he can't leave the grid.
What is the probability both meet at the same point at the same time?
link to original post
46,189 / 262,144
link to original post
I get the same answer
They will only meet on the 10th move.
The number of south moves made by the one in the NE corner must equal the number of east moves made by the one in the SW corner.
The probability is (C(10,0)^2 + C(10,1)^2 + C(10,2)^2 + ... + C(10,10)^2) / (2^10)^2 = 46,189 / 262,144.
January 22nd, 2024 at 7:21:00 PM
permalink
Quote: ChesterDog
46,189 / 262,144
link to original post
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 23rd, 2024 at 4:16:27 PM
permalink
As promised, here is my Toughie Tuesday problem:
Let f(x) = 2^(2x) - 2^(x+1) + 1 - 1 / N^2 for some integer N >= 2.
Each N has two real roots for its corresponding f(x).
The sum of the roots for all N from 2 to 1000 can be expressed as the base 2 logarithm of S.
What is S?
Let f(x) = 2^(2x) - 2^(x+1) + 1 - 1 / N^2 for some integer N >= 2.
Each N has two real roots for its corresponding f(x).
The sum of the roots for all N from 2 to 1000 can be expressed as the base 2 logarithm of S.
What is S?
January 23rd, 2024 at 5:41:46 PM
permalink
1001/2000
Last edited by: aceside on Jan 23, 2024
January 26th, 2024 at 9:13:07 AM
permalink
A normal 52-card deck is shuffled. Cards are dealt until a red card is seen. What is the expected number of black cards dealt?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 26th, 2024 at 3:59:51 PM
permalink
Quote: WizardA normal 52-card deck is shuffled. Cards are dealt until a red card is seen. What is the expected number of black cards dealt?
link to original post
Sum for k = 0 to 26 of k * 26! / (26 - k)! * 26 / ( 52! / (51 - k)!)
Excel did the sum and got 0.962962962962963, which I assumed to be 26 / 27.
January 26th, 2024 at 4:27:44 PM
permalink
Quote: ChesterDogQuote: WizardA normal 52-card deck is shuffled. Cards are dealt until a red card is seen. What is the expected number of black cards dealt?
link to original post
Sum for k = 0 to 26 of k * 26! / (26 - k)! * 26 / ( 52! / (51 - k)!)
Excel did the sum and got 0.962962962962963, which I assumed to be 26 / 27.
link to original post
I did a brute force calculation with rational numbers, and got what ChesterDog got.
January 26th, 2024 at 4:40:20 PM
permalink
Quote: ChesterDog
Sum for k = 0 to 26 of k * 26! / (26 - k)! * 26 / ( 52! / (51 - k)!)
Excel did the sum and got 0.962962962962963, which I assumed to be 26 / 27.
link to original post
I agree! I didn't see that about the fraction. Interesting!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
January 26th, 2024 at 4:49:32 PM
permalink
Quote: WizardQuote: ChesterDog
Sum for k = 0 to 26 of k * 26! / (26 - k)! * 26 / ( 52! / (51 - k)!)
Excel did the sum and got 0.962962962962963, which I assumed to be 26 / 27.
link to original post
I agree! I didn't see that about the fraction. Interesting!
link to original post
How did you calculate it?
I think I found a non-force solution that returns the exact number, but it's not as elegant as I would like.
The probability of having B black cards before the first red is
26/52 x 25/51 x 24/50 x ... x (27-B)/(53-B) x 26/(52-B)
(the last term is the probability that the (B+1)th card is red).
To get the expected number, multiply the B probability by B - skipping B = 0, the values to sum are:
1 x 26/52 x 26/51
2 x 26/52 x 25/51 x 26/50
3 x 26/52 x 25/51 x 24/50 x 26/49
4 x 26/52 x 25/51 x 24/50 x 23/49 x 26/48
...
26 x 26/52 x 25/51 x 24/50 x ... x 2/28 x 1/27 x 26/26
Separate this sum into 26 groups; group 1 has one of each line, group 2 has one of each line for B = 2 to 26,
and so on, with group N having one of each line for B = N to 26.
Sum Group 1's lines, going from B = 26 to B = 1:
26/52 x 25/51 x ... x 2/28 x 26/27
26/52 x 25/51 x ... x 2/28 x 1/27 x 26/26
This sums to 26/52 x 25/51 x ... x 3/29 x 2/28
Add the line 26/52 x 25/51 x ... x 3/29 x 26/28
This sums to 26/52 x 25/51 x ... x 4/30 x 3/29
If you keep going, eventually the sum of 26/52, which is 1/2.
For group 2, if you stop the sum at B = 2, it is 1/2 x 25/51.
For group 3, if you stop the sum at B = 3, it is 1/2 x 25/51 x 24/50.
The sums of the 26 groups are:
1/2
1/2 x 25/51
1/2 x 25/51 x 24/50
1/2 x 25/51 x 24/50 x 23/49
...
1/2 x 25/51 x 24/50 x ... x 3/29
1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28
1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28 x 1/27
Sum the last two terms to get 1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28 x (1 + 2/27),
which is 1/2 x 25/51 x 24/50 x ... x 3/29 x 2/27
Add the next term to get 1/2 x 25/51 x 24/50 x ... x 3/29 x (1 + 2/27),
which is 1/2 x 25/51 x 24/50 x ... x 3/28.
Continuing in this fashion, the result is 26/52 x (1 + 25/27) = 26/27.
January 26th, 2024 at 7:19:47 PM
permalink
The above question is purely mathematical, not of practical applications. I can just guess an answer of 1, and it’s not too off.
Let me change it a bit. A normal 52-card deck is shuffled. Cards are dealt until an Ace card is seen. What is the expected number of cards dealt?
Let me change it a bit. A normal 52-card deck is shuffled. Cards are dealt until an Ace card is seen. What is the expected number of cards dealt?
January 28th, 2024 at 7:59:17 AM
permalink
Quote: ThatDonGuyQuote: WizardQuote: ChesterDog
Sum for k = 0 to 26 of k * 26! / (26 - k)! * 26 / ( 52! / (51 - k)!)
Excel did the sum and got 0.962962962962963, which I assumed to be 26 / 27.
link to original post
I agree! I didn't see that about the fraction. Interesting!
link to original post
How did you calculate it?
I think I found a non-force solution that returns the exact number, but it's not as elegant as I would like.
The probability of having B black cards before the first red is
26/52 x 25/51 x 24/50 x ... x (27-B)/(53-B) x 26/(52-B)
(the last term is the probability that the (B+1)th card is red).
To get the expected number, multiply the B probability by B - skipping B = 0, the values to sum are:
1 x 26/52 x 26/51
2 x 26/52 x 25/51 x 26/50
3 x 26/52 x 25/51 x 24/50 x 26/49
4 x 26/52 x 25/51 x 24/50 x 23/49 x 26/48
...
26 x 26/52 x 25/51 x 24/50 x ... x 2/28 x 1/27 x 26/26
Separate this sum into 26 groups; group 1 has one of each line, group 2 has one of each line for B = 2 to 26,
and so on, with group N having one of each line for B = N to 26.
Sum Group 1's lines, going from B = 26 to B = 1:
26/52 x 25/51 x ... x 2/28 x 26/27
26/52 x 25/51 x ... x 2/28 x 1/27 x 26/26
This sums to 26/52 x 25/51 x ... x 3/29 x 2/28
Add the line 26/52 x 25/51 x ... x 3/29 x 26/28
This sums to 26/52 x 25/51 x ... x 4/30 x 3/29
If you keep going, eventually the sum of 26/52, which is 1/2.
For group 2, if you stop the sum at B = 2, it is 1/2 x 25/51.
For group 3, if you stop the sum at B = 3, it is 1/2 x 25/51 x 24/50.
The sums of the 26 groups are:
1/2
1/2 x 25/51
1/2 x 25/51 x 24/50
1/2 x 25/51 x 24/50 x 23/49
...
1/2 x 25/51 x 24/50 x ... x 3/29
1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28
1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28 x 1/27
Sum the last two terms to get 1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28 x (1 + 2/27),
which is 1/2 x 25/51 x 24/50 x ... x 3/29 x 2/27
Add the next term to get 1/2 x 25/51 x 24/50 x ... x 3/29 x (1 + 2/27),
which is 1/2 x 25/51 x 24/50 x ... x 3/28.
Continuing in this fashion, the result is 26/52 x (1 + 25/27) = 26/27.
link to original post
I thought about this again and see a problem. Did you include the probability of having 0 black card before the first red is dealt? My intuition tells me the answer is 0.5?
January 28th, 2024 at 9:06:32 AM
permalink
Quote: acesideQuote: ThatDonGuyQuote: WizardQuote: ChesterDog
Sum for k = 0 to 26 of k * 26! / (26 - k)! * 26 / ( 52! / (51 - k)!)
Excel did the sum and got 0.962962962962963, which I assumed to be 26 / 27.
link to original post
I agree! I didn't see that about the fraction. Interesting!
link to original post
How did you calculate it?
I think I found a non-force solution that returns the exact number, but it's not as elegant as I would like.
The probability of having B black cards before the first red is
26/52 x 25/51 x 24/50 x ... x (27-B)/(53-B) x 26/(52-B)
(the last term is the probability that the (B+1)th card is red).
To get the expected number, multiply the B probability by B - skipping B = 0, the values to sum are:
1 x 26/52 x 26/51
2 x 26/52 x 25/51 x 26/50
3 x 26/52 x 25/51 x 24/50 x 26/49
4 x 26/52 x 25/51 x 24/50 x 23/49 x 26/48
...
26 x 26/52 x 25/51 x 24/50 x ... x 2/28 x 1/27 x 26/26
Separate this sum into 26 groups; group 1 has one of each line, group 2 has one of each line for B = 2 to 26,
and so on, with group N having one of each line for B = N to 26.
Sum Group 1's lines, going from B = 26 to B = 1:
26/52 x 25/51 x ... x 2/28 x 26/27
26/52 x 25/51 x ... x 2/28 x 1/27 x 26/26
This sums to 26/52 x 25/51 x ... x 3/29 x 2/28
Add the line 26/52 x 25/51 x ... x 3/29 x 26/28
This sums to 26/52 x 25/51 x ... x 4/30 x 3/29
If you keep going, eventually the sum of 26/52, which is 1/2.
For group 2, if you stop the sum at B = 2, it is 1/2 x 25/51.
For group 3, if you stop the sum at B = 3, it is 1/2 x 25/51 x 24/50.
The sums of the 26 groups are:
1/2
1/2 x 25/51
1/2 x 25/51 x 24/50
1/2 x 25/51 x 24/50 x 23/49
...
1/2 x 25/51 x 24/50 x ... x 3/29
1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28
1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28 x 1/27
Sum the last two terms to get 1/2 x 25/51 x 24/50 x ... x 3/29 x 2/28 x (1 + 2/27),
which is 1/2 x 25/51 x 24/50 x ... x 3/29 x 2/27
Add the next term to get 1/2 x 25/51 x 24/50 x ... x 3/29 x (1 + 2/27),
which is 1/2 x 25/51 x 24/50 x ... x 3/28.
Continuing in this fashion, the result is 26/52 x (1 + 25/27) = 26/27.
link to original post
I thought about this again and see a problem. Did you include the probability of having 0 black card before the first red is dealt? My intuition tells me the answer is 0.5?
link to original post
Yes, I did. If you want to include it in the solution, add "0 x 26/52" to the expected value sum.
1/2 x 26/51 of the time, there will be 1 black card; 1/2 x 25/51 x 26/50 of the time, there will be 2; 1/2 x 25/51 x 24/50 of the time, there will be 3 or more. That alone adds up to almost 7/8.
Quote: acesideThe above question is purely mathematical, not of practical applications. I can just guess an answer of 1, and it’s not too off.
Let me change it a bit. A normal 52-card deck is shuffled. Cards are dealt until an Ace card is seen. What is the expected number of cards dealt?
link to original post
Simulating gets a result of 53 / 5.
It appears that, if you want the total number of cards dealt, including the stopping point card, the expected number is 53 / (the number of stopping cards + 1).
February 3rd, 2024 at 9:13:55 PM
permalink
I don't think this qualifies as "easy", but The Password Game is interesting. I made it to step #25 of 35, then gave up, because I don't know how to find a YouTube video of a specific length.
I run Easy Vegas ( https://easy.vegas )
February 5th, 2024 at 8:31:36 AM
permalink
Allow me to propose Monday's easy problem.
A casino has a 5% free play rebate promotion in slots, based on play. Free play can generate more free play at the same 5% rate, infinitely. What is the value, as a percentage, of this promotion. You may assume that fractional points are allowed.
A casino has a 5% free play rebate promotion in slots, based on play. Free play can generate more free play at the same 5% rate, infinitely. What is the value, as a percentage, of this promotion. You may assume that fractional points are allowed.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 5th, 2024 at 4:05:59 PM
permalink
I have an easy problem. (Not easy for me or I wouldn’t ask!)
10 line Jacks or Better game. All with leftover multiple on my Ult X scavenge.
Dealt K 8 6 4 2. Kept the K. The K was spade; none of the other 4 were spades. What are the odds of not winning even ONE line?
It seemed like very bad luck……
10 line Jacks or Better game. All with leftover multiple on my Ult X scavenge.
Dealt K 8 6 4 2. Kept the K. The K was spade; none of the other 4 were spades. What are the odds of not winning even ONE line?
It seemed like very bad luck……
February 5th, 2024 at 4:27:56 PM
permalink
Quote: WizardAllow me to propose Monday's easy problem.
A casino has a 5% free play rebate promotion in slots, based on play. Free play can generate more free play at the same 5% rate, infinitely. What is the value, as a percentage, of this promotion. You may assume that fractional points are allowed.
link to original post
If I am understanding the problem right, the value of the free play is
0.05 + 0.05^2 + 0.05^3 + ...
= 0.05 (1 + 0.05 + 0.05^2 + 0.05^3 + ...)
= 0.05 / (1 - 0.05)
= 0.05 / 0.95
= 1/19 = 100 / 19 %
Quote: SOOPOOI have an easy problem. (Not easy for me or I wouldn’t ask!)
10 line Jacks or Better game. All with leftover multiple on my Ult X scavenge.
Dealt K 8 6 4 2. Kept the K. The K was spade; none of the other 4 were spades. What are the odds of not winning even ONE line?
It seemed like very bad luck……
link to original post
It looks easy, but I don't think there's a way to calculate it other than...
to count the number of paying hands you can get, divide by 178,365 (the number of ways you can get 4 cards from 47), subtract this fraction from 1 (to determine the probability of one hand not being a winner), and raise that to the tenth power.
February 5th, 2024 at 4:44:22 PM
permalink
Quote: ThatDonGuy
If I am understanding the problem right, the value of the free play is
0.05 + 0.05^2 + 0.05^3 + ...
= 0.05 (1 + 0.05 + 0.05^2 + 0.05^3 + ...)
= 0.05 / (1 - 0.05)
= 0.05 / 0.95
= 1/19 = 100 / 19 %
link to original post
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 5th, 2024 at 5:21:38 PM
permalink
If Y is a discrete random variable with a geometric distribution in which
P(Y = i) = p(1 - p)^i-1, i=1,2,...
Assume that P {Y=2 } = 9 * P {Y=4}. Find P {Y is odd} ?
P(Y = i) = p(1 - p)^i-1, i=1,2,...
Assume that P {Y=2 } = 9 * P {Y=4}. Find P {Y is odd} ?
Last edited by: gerback123 on Feb 5, 2024
February 5th, 2024 at 6:19:45 PM
permalink
Quote: gerback123Assume that P {Y=i } = 9 * P {Y=4}.
link to original post
You're going to have to explain that one to me. P(Y = i) is different for each i.
Should that be P{Y = 1} = 9 P{Y = 4} instead?
February 5th, 2024 at 6:21:27 PM
permalink
Yes, that is my mistake, sorry about that Y=2
Last edited by: gerback123 on Feb 5, 2024
February 5th, 2024 at 6:35:06 PM
permalink
Quote: gerback123Yes, that is my mistake, sorry about that Y=1
link to original post
P{y = 4} = p (1 - p)^4
P{y = 1} = p (1 - p) = 9 p (1 - p)^4
1/9 = (1 - p)^3
1 - p = (1/9)^(1/3)
P{y is odd} = p (1 - p) (1 + (1 - p)^2 + (1 - p)^4 + (1 - p)^6 + ...)
= p (1 - p) (1 + (1 - p)^2 + ((1 - p)^2)^2 + ((1 - p)^2)^3 + ...)
= p (1 - p) / (1 - (1 - p)^2)
= p (1 - p) / (p (2 - p))
= (1 - p) / (2 - p)
= (1/9)^(1/3) / (1 + (1/9)^(1/3))
= 1 / (1 + 9^(1/3))
Is there a way to get the radical out of the denominator?
February 5th, 2024 at 7:30:12 PM
permalink
Quote: ThatDonGuyQuote: Wizard
Quote: SOOPOOI have an easy problem. (Not easy for me or I wouldn’t ask!)
10 line Jacks or Better game. All with leftover multiple on my Ult X scavenge.
Dealt K 8 6 4 2. Kept the K. The K was spade; none of the other 4 were spades. What are the odds of not winning even ONE line?
It seemed like very bad luck……
link to original post
It looks easy, but I don't think there's a way to calculate it other than...
to count the number of paying hands you can get, divide by 178,365 (the number of ways you can get 4 cards from 47), subtract this fraction from 1 (to determine the probability of one hand not being a winner), and raise that to the tenth power.
link to original post
I know that’s a ‘brute’ way to figure it out. But I was hoping it would be easier than me trying to manually figure out how many of those 178,365 hands are winners.
February 5th, 2024 at 7:45:12 PM
permalink
Very good! I totally messed the question up, twice actually. First, with Y=i (bad typo) should have been Y=2, but then you asked if it was Y=1, but it was 2, but you still solved it correctly, and I'm sure you could do with the original question I had intended.
February 6th, 2024 at 2:10:24 PM
permalink
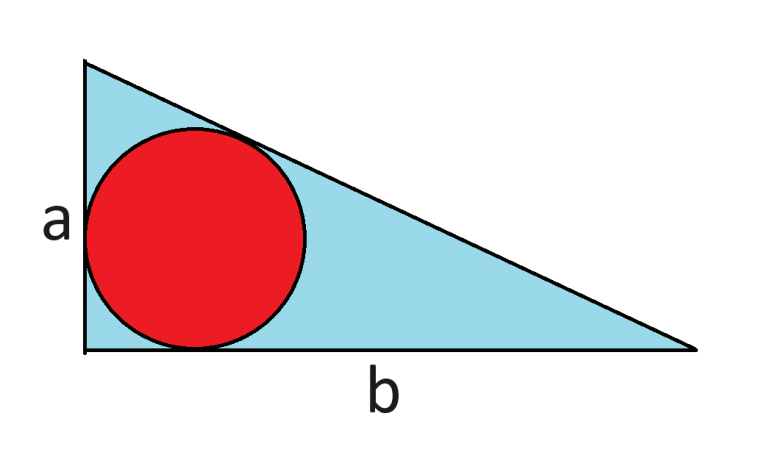
A circle is inscribed in a right triangle with legs of length a and b. What is the radius of the circle? For credit, show your work.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 6th, 2024 at 3:04:55 PM
permalink
Quote: ThatDonGuy
P{y = 4} = p (1 - p)^4
P{y = 1} = p (1 - p) = 9 p (1 - p)^4
1/9 = (1 - p)^3
1 - p = (1/9)^(1/3)
P{y is odd} = p (1 - p) (1 + (1 - p)^2 + (1 - p)^4 + (1 - p)^6 + ...)
= p (1 - p) (1 + (1 - p)^2 + ((1 - p)^2)^2 + ((1 - p)^2)^3 + ...)
= p (1 - p) / (1 - (1 - p)^2)
= p (1 - p) / (p (2 - p))
= (1 - p) / (2 - p)
= (1/9)^(1/3) / (1 + (1/9)^(1/3))
= 1 / (1 + 9^(1/3))
Is there a way to get the radical out of the denominator?
link to original post
To remove the cube root from the denominator, multiply top and bottom by 1 - x^(1/3) + x^(2/3).
February 6th, 2024 at 3:45:55 PM
permalink
r=radius of circle.
a-r = top portion of left side
drop perpendicular radii to the left side and hypotenuse. The similar triangles in upper left gives
a-r = left portion of the hypotenuse
similarly
b-r = right side of bottom
b-r = right portion of hypotenuse
So sqrt (a^2 + b^2) = hypotenuse = (a-r) + (b-r) = a+b - 2r
r = 0.5*(a+b - sqrt(a^2+b^2))
February 6th, 2024 at 4:00:17 PM
permalink
Quote: Wizard
A circle is inscribed in a right triangle with legs of length a and b. What is the radius of the circle? For credit, show your work.
link to original post
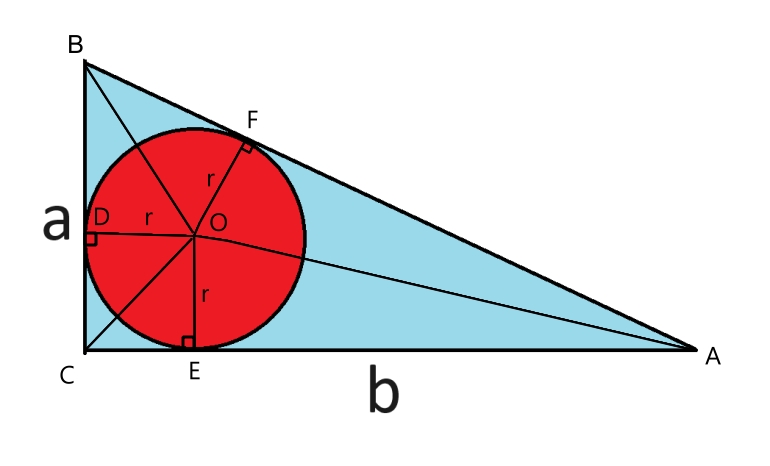
OE = OF and OA = OA, so AOE and AOF are HL-congruent, which means AE = AF
OD = OF and OB = OB, so BOD and BOF are HL-congruent, which means BE = BF
OD || CE and OE || CD, so ODCE is a rectangle; since OD = OE, ODCE is a square, which means CD = CE = r, so BF = BD = a - 4 and AF = AE = b - r
Pythagorean Theorem: (a - r + b - r)^2 = a^2 + b^2
a^2 + b^2 + 4 r^2 + 2 ab - 4 ar - 4 br = a^2 + b^2
4 r^2 + 2 ab - 4 ar - 4 br = 0
r^2 - r (a + b) + ab / 2 = 0
r = (a + b) / 2 +/- sqrt(a^2 + 2ab + b^2 - 2ab) / 2
= (a + b +/- sqrt(a^2 + b^2)) / 2
However, r < a/2 as otherwise the diameter of the circle would be longer than one of the sides
Therefore, r = (a + b - sqrt(a^2 + b^2)) / 2
Note that this is always positive because of the triangle inequality, as a and b are the lengths of two sides of the triangle and sqrt(a^2 + b^2) is the length of the third side
February 6th, 2024 at 6:40:51 PM
permalink
Quote: chevy
r=radius of circle.
a-r = top portion of left side
drop perpendicular radii to the left side and hypotenuse. The similar triangles in upper left gives
a-r = left portion of the hypotenuse
similarly
b-r = right side of bottom
b-r = right portion of hypotenuse
So sqrt (a^2 + b^2) = hypotenuse = (a-r) + (b-r) = a+b - 2r
r = 0.5*(a+b - sqrt(a^2+b^2))
link to original post
I agree!
Same credit to ThatDonGuy.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 6th, 2024 at 7:08:51 PM
permalink
Quote: WizardI agree!
Same credit to ThatDonGuy.
link to original post
And now, for bonus points:
Suppose it isn't a right triangle, and the third side has length c.
In terms of a, b, and c, what is the radius of the inscribed circle (i.e. the circle internal to the triangle that is tangent to all three sides)?
February 6th, 2024 at 9:08:50 PM
permalink
Showoff.Quote: ThatDonGuy
OE = OF and OA = OA, so AOE and AOF are HL-congruent, which means AE = AF
OD = OF and OB = OB, so BOD and BOF are HL-congruent, which means BE = BF
OD || CE and OE || CD, so ODCE is a rectangle; since OD = OE, ODCE is a square, which means CD = CE = r, so BF = BD = a - 4 and AF = AE = b - r
Pythagorean Theorem: (a - r + b - r)^2 = a^2 + b^2
a^2 + b^2 + 4 r^2 + 2 ab - 4 ar - 4 br = a^2 + b^2
4 r^2 + 2 ab - 4 ar - 4 br = 0
r^2 - r (a + b) + ab / 2 = 0
r = (a + b) / 2 +/- sqrt(a^2 + 2ab + b^2 - 2ab) / 2
= (a + b +/- sqrt(a^2 + b^2)) / 2
However, r < a/2 as otherwise the diameter of the circle would be longer than one of the sides
Therefore, r = (a + b - sqrt(a^2 + b^2)) / 2
Note that this is always positive because of the triangle inequality, as a and b are the lengths of two sides of the triangle and sqrt(a^2 + b^2) is the length of the third side
link to original post
I run Easy Vegas ( https://easy.vegas )
February 7th, 2024 at 3:41:11 AM
permalink
Quote: ThatDonGuySuppose it isn't a right triangle, and the third side has length c.
In terms of a, b, and c, what is the radius of the inscribed circle (i.e. the circle internal to the triangle that is tangent to all three sides)?
link to original post
I admit I had to use Heron's formula for this one. As a reminder, it says the area of the triangle is sqrt(S*(S-A)*(S-B)*(S-C)), where S=(A+B+C)/2.
Let's call that area x.
Let's call the radius of the inscribed circle r.
x = Ar/2 + Br/2 + Cr/2
r = 2x/(A+B+C)
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 7th, 2024 at 12:58:31 PM
permalink
Your wife is mad 10% of the time.
When asked "Are you mad?" she will answer "no" 100% of the time when not mad and "no" 80% of the time when mad.
You ask her if she is mad and she says "no." What is the probability she is mad?
Image source: https://www.focusonthefamily.com/marriage/dont-let-your-spouse-make-you-angry/
When asked "Are you mad?" she will answer "no" 100% of the time when not mad and "no" 80% of the time when mad.
You ask her if she is mad and she says "no." What is the probability she is mad?
Image source: https://www.focusonthefamily.com/marriage/dont-let-your-spouse-make-you-angry/
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 7th, 2024 at 2:34:06 PM
permalink
In this case there are no false results when not mad, so we can consider the chances of three things.
(a) Is "not mad" (90%), says "not mad" (all the time) = 90%
(b) is "mad" (10%), says "not mad" (80% of these) = 8%
(c) is "mad" (10%), says "mad" (20% of these) = 2%.
So there are 90 + 8 occcasions when she says she is not mad. 90 of the time she is correct, 8 she is mad.
So the chances of being mad = 8/98 (and being fine is 90/98).
In normal similar cases you're using a test to see whether a patient has a disease. You know the test will give both false positives and false negatives. So the problem for a doctor is how much useful informaton does the test give. Typically the chances of having the problem is low so, unless the test is very good, the result isn't that useful because the chances of getting a false positive is similar to that of a true positive.
(a) Is "not mad" (90%), says "not mad" (all the time) = 90%
(b) is "mad" (10%), says "not mad" (80% of these) = 8%
(c) is "mad" (10%), says "mad" (20% of these) = 2%.
So there are 90 + 8 occcasions when she says she is not mad. 90 of the time she is correct, 8 she is mad.
So the chances of being mad = 8/98 (and being fine is 90/98).
In normal similar cases you're using a test to see whether a patient has a disease. You know the test will give both false positives and false negatives. So the problem for a doctor is how much useful informaton does the test give. Typically the chances of having the problem is low so, unless the test is very good, the result isn't that useful because the chances of getting a false positive is similar to that of a true positive.
February 7th, 2024 at 6:50:36 PM
permalink
Quote: charliepatrickIn this case there are no false results when not mad, so we can consider the chances of three things.
(a) Is "not mad" (90%), says "not mad" (all the time) = 90%
(b) is "mad" (10%), says "not mad" (80% of these) = 8%
(c) is "mad" (10%), says "mad" (20% of these) = 2%.
So there are 90 + 8 occcasions when she says she is not mad. 90 of the time she is correct, 8 she is mad.
So the chances of being mad = 8/98 (and being fine is 90/98).
In normal similar cases you're using a test to see whether a patient has a disease. You know the test will give both false positives and false negatives. So the problem for a doctor is how much useful informaton does the test give. Typically the chances of having the problem is low so, unless the test is very good, the result isn't that useful because the chances of getting a false positive is similar to that of a true positive.
link to original post
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 8th, 2024 at 8:46:30 AM
permalink
The following is a follow-up on my circle in a right triangle puzzle a few days ago.
The square has sides of length 1. All the triangles are the same size. All the circles have the same size. What is the radius of each circle?
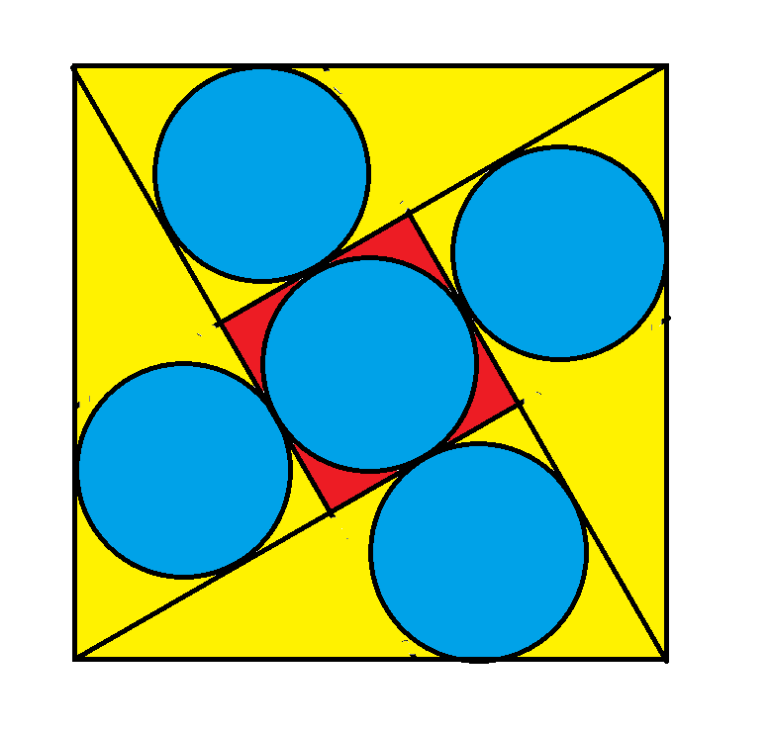
The square has sides of length 1. All the triangles are the same size. All the circles have the same size. What is the radius of each circle?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 8th, 2024 at 11:14:45 AM
permalink
Quote: WizardThe following is a follow-up on my circle in a right triangle puzzle a few days ago.
The square has sides of length 1. All the triangles are the same size. All the circles have the same size. What is the radius of each circle?
link to original post
r=(sqrt(3)-1)/4 ??(changed it 4 times, so probably still wrong)??
a = short side of triangle
b = long leg of triangle
1 = hypotenuse of triangle = side of big square
a^2 + b^2 = 1^2
From last problem
r = (a+b-sqrt(a^2+b^2)) /2 = (a+b-1)/2
2r+1 = a+b
4r^2+4r+1 = a^2+2ab+b^2 = 2ab+1
so
2ab = 4r^2+4r
From total area= 4*Area triangle + area of square
1^2 = 4 * (.5ab) + (2r)^2
1 = 2ab+4r^2
1=(4r^2+4r) +4r^2
8r^2+4r-1=0
r = (-4 +/- sqrt (4^2 - 4(8)(-1)))/(2*8)
positive root
r=(-4+sqrt(48))/16
r=(-1+sqrt(3))/4
maybe????
February 8th, 2024 at 12:21:41 PM
permalink
Quote: chevy
r=(-1+sqrt(3))/4
maybe????
link to original post
I agree!!!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 8th, 2024 at 4:14:05 PM
permalink
Quote: WizardQuote: ThatDonGuySuppose it isn't a right triangle, and the third side has length c.
In terms of a, b, and c, what is the radius of the inscribed circle (i.e. the circle internal to the triangle that is tangent to all three sides)?
link to original post
I admit I had to use Heron's formula for this one. As a reminder, it says the area of the triangle is sqrt(S*(S-A)*(S-B)*(S-C)), where S=(A+B+C)/2.
Let's call that area x.
Let's call the radius of the inscribed circle r.
x = Ar/2 + Br/2 + Cr/2
r = 2x/(A+B+C)
link to original post
That is correct. I actually got the answer expressed differently:
r = (b + c + a) / 2 * sqrt(a^2 - (b - c)^2) / sqrt((b + c)^2 - a^2)
Proof that the two answers are the same:
((b + c - a) / 2 * sqrt((a^2 - (b - c)^2) / ((b + c)^2 - a^2)))^2
= (b + c - a)^2 * (a^2 - (b - c)^2) / (4 ((b + c)^2 - a^2))
= (b + c - a)^2 * (a^2 - (b - c)^2) / (4 (b + c + a)(b + c - a)
= (b + c - a) * (a^2 - (b - c)^2) / (4 (a + b + c))
= (b + c - a) * (a - (b - c)) * (a + (b - c)) / (4 (a + b + c))
= (b + c - a) * (a + c - b) * (a + b - c) / (4 (a + b + c))
= (a + b + c - 2a) * (a + b + c - 2b) * (a + b + c - 2c) / (4 (a + b + c))
= (2S - 2a) (2S - 2b) (2S - 2c) / (8S), where S = (a + b + c) / 2
= (S - a) (S - b) (S - c) / S
= S (S - a) (S - b) (S - c) / S^2
= (sqrt(S (S - a)(S - b)(S - c)) / S)^2
= (Area / ((A + B + C) / 2))^2
= (2 * Area / (A + B + C))^2
February 8th, 2024 at 5:23:47 PM
permalink
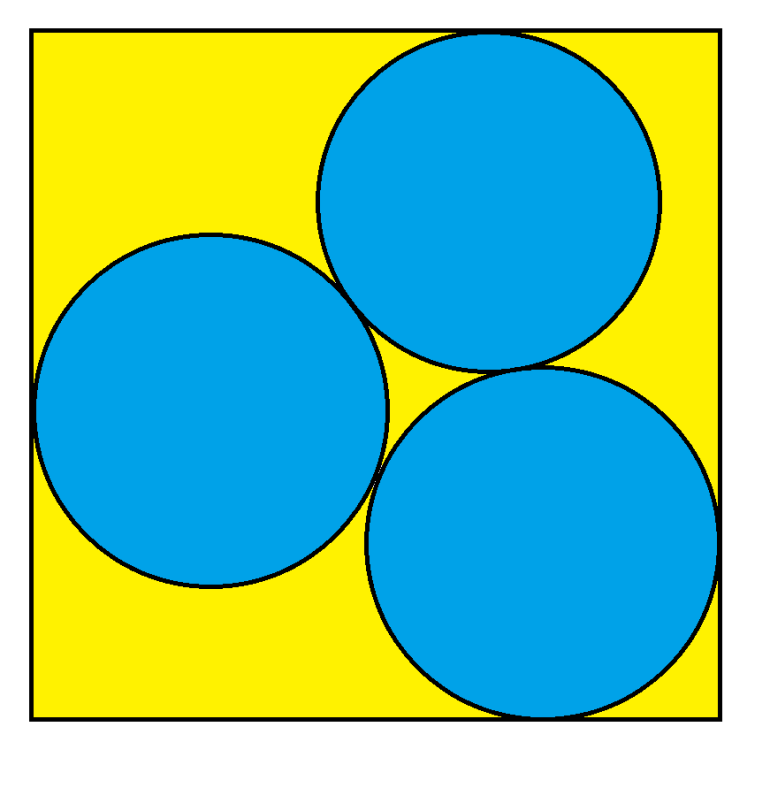
What is the side length of the minimum size square that can fit three circles of radius 1? I am not saying they have to be arranged as in the picture above, but I can't immediately think of a better way.
Hint: cos(x+y)=cos(x)*cos(y)-sin(x)*sin(y)
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 8th, 2024 at 7:24:19 PM
permalink
Quote: Wizard
What is the side length of the minimum size square that can fit three circles of radius 1? I am not saying they have to be arranged as in the picture above, but I can't immediately think of a better way.
Hint: cos(x+y)=cos(x)*cos(y)-sin(x)*sin(y)
link to original post
I think it does have to be with the three circles symmetric about the diagonal.
Start with two circles stacked on top (e.g. 2&3 in my pic) - need square of height 4r=4*1=4
then rotate the three circle arrangement counterclockwise, the height gets smaller
Eventually when you cross the diagonal the width starts to get wider until the case where two circles are side by side (1&3 in my pic).....so square is 4r = 4 wide.
That is process is symmetric, so the midpoint is the min.....(unless it hits a min, increases to the diagonal, then back to a min, before increasing to the max).....Handwaving says it isn't.
Then
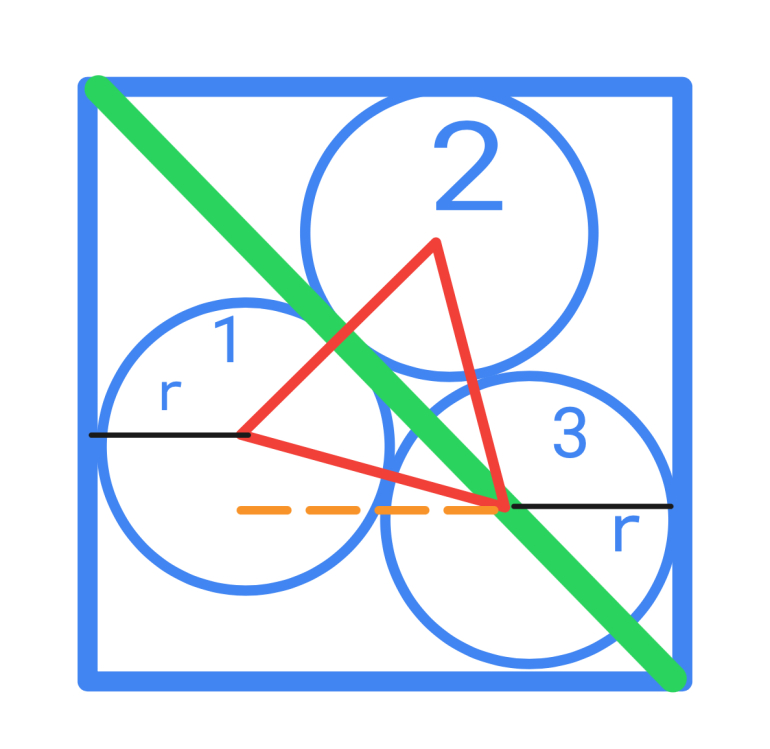
Green diagonal at 45 degrees above horizontal
red equilateral triangle connecting centers has side 2r = 2 and lower side is at 30 degrees below green. Or 15 degrees above orange dashed line
Orange dashed line is (red side) * cos(15) = 2 cos(15)
half angle formula....
cos(15)= sqrt((1+cos(30))/2) = sqrt ( (1+ sqrt(3)/2)/2) = sqrt((2+sqrt(3))/4) = sqrt(2+sqrt(3)) / 2
So orange dashed = sqrt(2+sqrt(3))
and width of square is
black + orange dashed + black
1+sqrt(2+sqrt(3))+1
2+sqrt(2+sqrt(3)) or about 3.93185165258
PS: I am embarrassed just how sloppy this is, but a it is an attempt
February 8th, 2024 at 7:43:30 PM
permalink
Quote: chevy
I think it does have to be with the three circles symmetric about the diagonal.
Start with two circles stacked on top (e.g. 2&3 in my pic) - need square of height 4r=4*1=4
then rotate the three circle arrangement counterclockwise, the height gets smaller
Eventually when you cross the diagonal the width starts to get wider until the case where two circles are side by side (1&3 in my pic).....so square is 4r = 4 wide.
That is process is symmetric, so the midpoint is the min.....(unless it hits a min, increases to the diagonal, then back to a min, before increasing to the max).....Handwaving says it isn't.
Then
Green diagonal at 45 degrees above horizontal
red equilateral triangle connecting centers has side 2r = 2 and lower side is at 30 degrees below green. Or 15 degrees above orange dashed line
Orange dashed line is (red side) * cos(15) = 2 cos(15)
half angle formula....
cos(15)= sqrt((1+cos(30))/2) = sqrt ( (1+ sqrt(3)/2)/2) = sqrt((2+sqrt(3))/4) = sqrt(2+sqrt(3)) / 2
So orange dashed = sqrt(2+sqrt(3))
and width of square is
black + orange dashed + black
1+sqrt(2+sqrt(3))+1
2+sqrt(2+sqrt(3)) or about 3.93185165258
PS: I am embarrassed just how sloppy this is, but a it is an attempt
link to original post
We are close, but I don't quite agree. I could be the one in error.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 9th, 2024 at 10:37:28 AM
permalink
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
February 9th, 2024 at 11:42:27 AM
permalink
In 10 minutes someone doing 60mph does 10 miles, and doing 30mph does 5 miles. Hence Jack has covered 10 and Joe 5, so they must have been either 15 (heading towards each other as requested here) or 5 (Jack catching up) miles apart. It's the former, 15 miles, because of the wording of the puzzle. (It's an interesting mathematical puzzle if you don't specifiy they cross/towards each other but just meet to see whether people spot both answers.)
February 9th, 2024 at 12:28:40 PM
permalink
Quote: Wizard
We are close, but I don't quite agree. I could be the one in error.
link to original post
I looked over mine and while certainly can expect I am wrong, I at least right now am not seeing my mistake. If nobody else chimes in, feel free to share yours in spoilers and maybe I can see where I went astray.
February 9th, 2024 at 1:26:09 PM
permalink
Quote: Wizard...We are close, but I don't quite agree. I could be the one in error.
It seemed obvious the first circle was in the SE corner and the other two would be symmetrically arranged. Since the centres of the three circles form an equilateral triangle, one can see the width is 2 + 2*cos(15 degrees).
There is a method of calculating cos(15) via cos(30/2), SQRT((1+cos(30)/2) which gives SQRT((2+SQRT(3))/2.
Thus the answer required is 2+SQRT((2+SQRT(3)). A calculator gives this as 3.93185... .
There is a method of calculating cos(15) via cos(30/2), SQRT((1+cos(30)/2) which gives SQRT((2+SQRT(3))/2.
Thus the answer required is 2+SQRT((2+SQRT(3)). A calculator gives this as 3.93185... .
