Easy math puzzles

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

February 22nd, 2024 at 5:11:37 PM permalink

Quote: ThatDonGuy

Apply L'Hopital's Rule:

d/dx of ln (1-x) = -1 / (1-x)
d/dx of sin x = cos x
The answer is the limit as x approaches 0 of -1 / ((1 - x) cos x) = -1

link to original post

I agree!

L'Hopital's Rule would have been an applicable rule in the Mean Girls calculus competition.

Direct: https://www.youtube.com/watch?v=oDAKKQuBtDo

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

DogHand

DogHand

Threads: 2
Posts: 1840

Joined: Sep 24, 2011

February 23rd, 2024 at 2:00:47 AM permalink

Quote: Wizard
Quote: ThatDonGuy

Apply L'Hopital's Rule:

d/dx of ln (1-x) = -1 / (1-x)
d/dx of sin x = cos x
The answer is the limit as x approaches 0 of -1 / ((1 - x) cos x) = -1

link to original post

I agree!

L'Hopital's Rule would have been an applicable rule in the Mean Girls calculus competition.

Direct: https://www.youtube.com/watch?v=oDAKKQuBtDo
link to original post

Wiz,

Speaking of L'Hopital, (or more correctly, L'Hôpital), how would you like to have the "correct" spelling of your name changed retroactively?

Back when I took calculus, we spelled his name "L'Hospital" (which is how he himself spelled his name) and generally referred to him jokingly as "the Hospital guy".

According to Wikipedia:

"In the 17th and 18th centuries, the name was commonly spelled "l'Hospital", and he himself spelled his name that way. Since then, French spellings have changed: the silent 's' has been removed and replaced with a circumflex over the preceding vowel."

This whole "change the spelling" business reminds me of an old Dolton Edwards science fiction short story, "Meihem in ce Klasrum": read it here.

Dog Hand

Wizard
Administrator

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

February 23rd, 2024 at 4:18:57 AM permalink

Quote: DogHand
Wiz,

Speaking of L'Hopital, (or more correctly, L'Hôpital), how would you like to have the "correct" spelling of your name changed retroactively?

Back when I took calculus, we spelled his name "L'Hospital" (which is how he himself spelled his name) and generally referred to him jokingly as "the Hospital guy".

According to Wikipedia:

"In the 17th and 18th centuries, the name was commonly spelled "l'Hospital", and he himself spelled his name that way. Since then, French spellings have changed: the silent 's' has been removed and replaced with a circumflex over the preceding vowel."

This whole "change the spelling" business reminds me of an old Dolton Edwards science fiction short story, "Meihem in ce Klasrum": read it here.

Dog Hand
link to original post

Nobody has ever asked me that before. I think I favor changing the spelling to conform with the way language changes.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

gerback123

Threads: 4
Posts: 21

Joined: May 13, 2020

February 27th, 2024 at 2:47:19 PM permalink

In the state lottery, a person selects a 3 digit number and wins $500 if that number is drawn from a box containing tickets labeled 000,···,999. If it costs $1 to play the game, what is the player's expected gain?
If 1000 people play the game each day, find the state lottery expected gain and describe its distribution?

Let S denote the state lottery total gain in 100 days, assuming that 1000 people play on each day.
Find ν:= E(S) and a value of c for which P {ν − c < S ≤ ν + c} ≈ .95

ChesterDog

ChesterDog

Threads: 9
Posts: 1730

Joined: Jul 26, 2010

Thanked by

February 27th, 2024 at 6:10:10 PM permalink

The player's expected gain on a $1 ticket is exactly -$0.50. (That's 0.001 * 499.00 + 0.999 * (-1.00).)

If 1000 people play the lottery each day, the state lottery's expected gain is 1000 * $0.50 = $500 per day. If the people select their numbers randomly (or if the lottery assigns the numbers randomly), the distribution of the lottery's gain per day is a binomial distribution with a standard deviation of 500 * sqrt(1000 * 0.001 * 0.999) ≈ $499.75.

S, the lottery's total gain in 100 days at 1000 tickets per day, would have the same distribution as selling 100,000 tickets. The distribution for S would be a binomial distribution with a standard deviation of 500 * sqrt(100,000 * 0.001 * 0.999) ≈ $4,997.50.

To find the value of c, I would use a normal distribution with mean of $50,000 and standard deviation of $4,997.50. I find that c is about 1.96 * $4,997.50 ≈ $9,795.

Edit: S would have to be a multiple of $500, so a better distribution to use would be Poisson's. I find that with c = 19 * $5,000 = $9,500, Poisson's distribution gives P {ν − c < S ≤ ν + c} = 94.9%.

Another edit: Better yet, we can use the binomial distribution directly with n = trials = 100*1000 and p = probability of success = 1 / 1000 to get c = $9,500. The probability of having fewer than 120 winners but more 80 is 94.9% as in the Poisson result.

(I welcome any corrections to my answers.)

Last edited by: ChesterDog on Feb 28, 2024

gerback123

Threads: 4
Posts: 21

Joined: May 13, 2020

Thanked by

February 28th, 2024 at 9:11:48 AM permalink

You're very close to what I had
Answers: −$0.50; 500; 1000 − 500X, where X ∼ Poisson(λ = 1)
Since
P {v - c < S <= v + c} = P{|S - v| / 5000 <= 5000 }
and the upper 0.025 quantile of N(0,1) is about 1.96, we have
c/5000 = 1.96 which is c=9800

Wizard
Administrator

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

March 4th, 2024 at 4:44:27 PM permalink

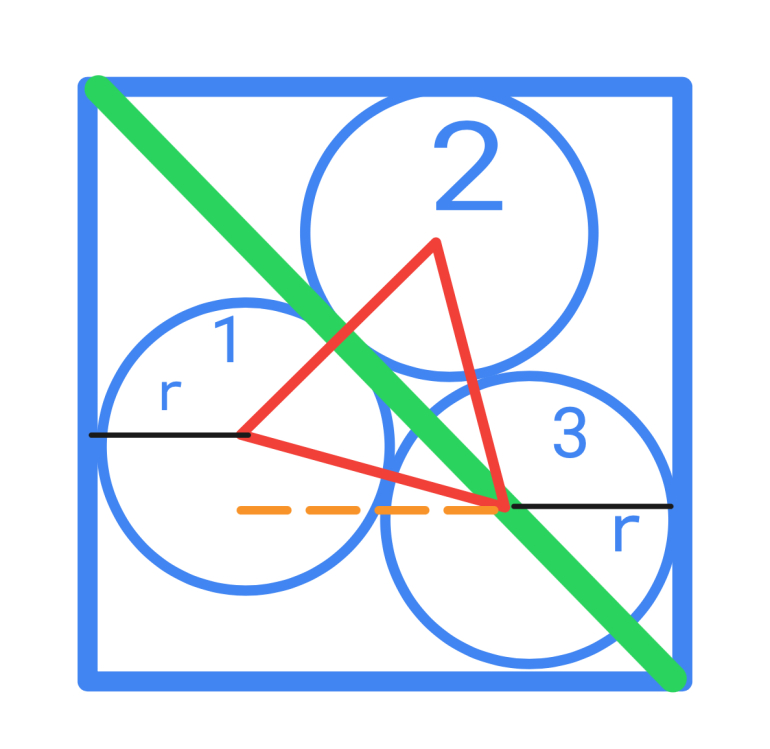
Quote: chevy

I think it does have to be with the three circles symmetric about the diagonal.
Start with two circles stacked on top (e.g. 2&3 in my pic) - need square of height 4r=4*1=4
then rotate the three circle arrangement counterclockwise, the height gets smaller
Eventually when you cross the diagonal the width starts to get wider until the case where two circles are side by side (1&3 in my pic).....so square is 4r = 4 wide.

That is process is symmetric, so the midpoint is the min.....(unless it hits a min, increases to the diagonal, then back to a min, before increasing to the max).....Handwaving says it isn't.

Then

Green diagonal at 45 degrees above horizontal
red equilateral triangle connecting centers has side 2r = 2 and lower side is at 30 degrees below green. Or 15 degrees above orange dashed line

Orange dashed line is (red side) * cos(15) = 2 cos(15)

half angle formula....
cos(15)= sqrt((1+cos(30))/2) = sqrt ( (1+ sqrt(3)/2)/2) = sqrt((2+sqrt(3))/4) = sqrt(2+sqrt(3)) / 2

So orange dashed = sqrt(2+sqrt(3))

and width of square is

black + orange dashed + black
1+sqrt(2+sqrt(3))+1

2+sqrt(2+sqrt(3)) or about 3.93185165258

PS: I am embarrassed just how sloppy this is, but a it is an attempt

link to original post

I finally got back to this one and agree. Very clever solution. Mine was much more complicated and error prone.

Here is my solution (PDF), which is the same as Chevy's. Note that I express is without the cosine function.

Last edited by: Wizard on Mar 4, 2024

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

chevy

chevy

Threads: 3
Posts: 151

Joined: Apr 15, 2011

March 4th, 2024 at 6:37:16 PM permalink

Quote: Wizard
Quote: chevy

I think it does have to be with the three circles symmetric about the diagonal.
Start with two circles stacked on top (e.g. 2&3 in my pic) - need square of height 4r=4*1=4
then rotate the three circle arrangement counterclockwise, the height gets smaller
Eventually when you cross the diagonal the width starts to get wider until the case where two circles are side by side (1&3 in my pic).....so square is 4r = 4 wide.

That is process is symmetric, so the midpoint is the min.....(unless it hits a min, increases to the diagonal, then back to a min, before increasing to the max).....Handwaving says it isn't.

Then

Green diagonal at 45 degrees above horizontal
red equilateral triangle connecting centers has side 2r = 2 and lower side is at 30 degrees below green. Or 15 degrees above orange dashed line

Orange dashed line is (red side) * cos(15) = 2 cos(15)

half angle formula....
cos(15)= sqrt((1+cos(30))/2) = sqrt ( (1+ sqrt(3)/2)/2) = sqrt((2+sqrt(3))/4) = sqrt(2+sqrt(3)) / 2

So orange dashed = sqrt(2+sqrt(3))

and width of square is

black + orange dashed + black
1+sqrt(2+sqrt(3))+1

2+sqrt(2+sqrt(3)) or about 3.93185165258

PS: I am embarrassed just how sloppy this is, but a it is an attempt

link to original post

I finally got back to this one and agree. Very clever solution. Mine was much more complicated and error prone.

Here is my solution (PDF), which is the same as Chevy's. Note that I express is without the cosine function.
link to original post

That means

mine =?= yours
sqrt(2+sqrt(3)) = (sqrt(6) + sqrt(2))/2
2+sqrt(3) = (6 + 2sqrt(12) + 2)/4
2+sqrt(3) = (8 + 4sqrt(3))/4
2+sqrt(3) = 2+sqrt(3)

YEP, checks out.....though I don't see a simplification I remember from algebra that converts one to the other.

gerback123

Threads: 4
Posts: 21

Joined: May 13, 2020

March 4th, 2024 at 6:53:21 PM permalink

Here's a joint probability density function (PDF) problem:
Let fX,Y(x,y) be the joint PDF of two random variables X and Y, defined as follows:

fX,Y(x,y) = {cxy^2 for 0< x < 1 and 0< y < 2
{0 otherwise

Find the constant c such that fX,Y(x,y) is a valid joint PDF.
Then, compute the marginal PDFs of X and Y, denoted as fX(x) and fY(y), respectively.
Finally, compute P(X < 0.5 and Y > 1).

Jimmy2Times

Jimmy2Times

Threads: 2
Posts: 66

Joined: Nov 28, 2018

March 5th, 2024 at 3:47:35 PM permalink

If assistance is needed in solving this problem I would suggest: Montgomery, D. C & Runger, G. C. (1999) Applied Statistics and Probability for Engineers, Section 6-3 (pages 218 - 224) - the steps are nicely shown and explained for this type of problem.

I 'm gonna go get the papers, get the papers.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 14th, 2024 at 5:01:24 AM permalink

Presenting a plethora of pi perplexities...

Pictured above are three identical boxes packed with pies.

Which box contains the most pie?

Assume all pies are the same height.

You have a pizza with crust thickness 'a' and radius 'z'.

What's the volume of the pizza?

Assume a perfect, flat circle.

P = ?
I = ?
E= ?

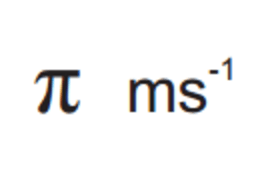
Riddle me this Rebus riddle.

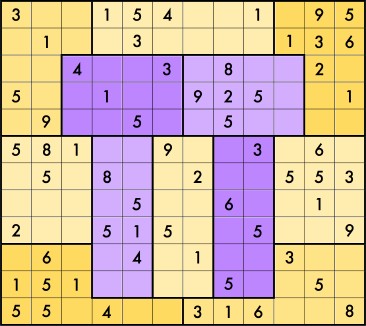
For those of you with some time on this Pi Day, try solving this sudoku. The rules are the same as regular sudoku except...

--The grid is 12x12.

--Each row, column, and colored block contains the first 12 digits of pi

3 1 4 1 5 9 2 6 5 3 5 8

in some order. In particular, there are two 1s, one 2, two 3s, one 4, three 5s, one 6, no 7s one 8, and one 9.

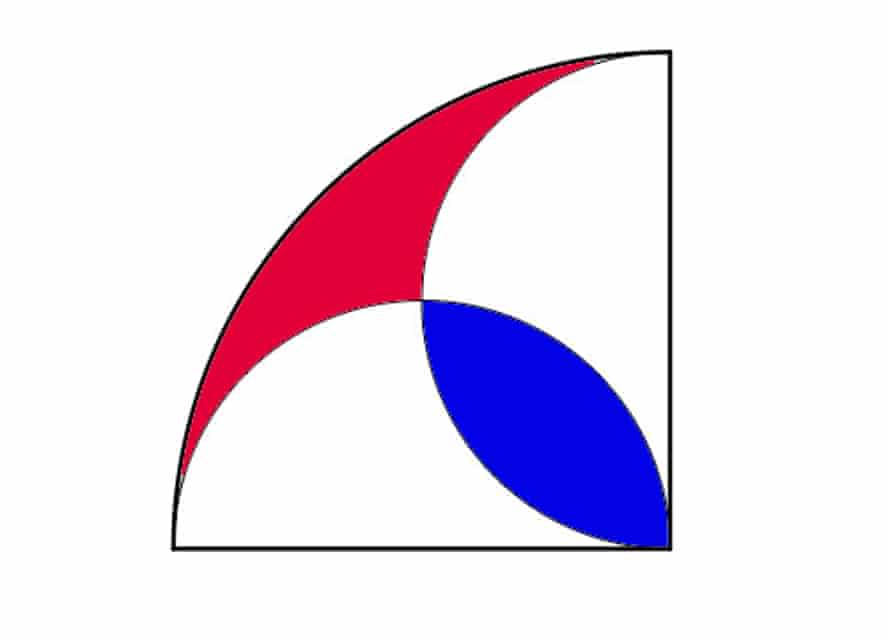
Illustrated above is a quarter-circle, containing two semicircles of smaller circles.

Prove that the red segment has the same area as the blue.

Have you tried 22 tonight? I said 22.

gerback123

Threads: 4
Posts: 21

Joined: May 13, 2020

March 14th, 2024 at 5:43:56 AM permalink

Solution to my earlier problem

chevy

chevy

Threads: 3
Posts: 151

Joined: Apr 15, 2011

Thanked by

March 14th, 2024 at 6:51:23 AM permalink

picking the low hanging fruit

all the same
if D is side of box
(pi/4) D^2 = 4 * (pi/4) (D/2)^2 = 16 * (pi/4) (D/4)^2

pizza volume = pizza

PIE = 169
sqrt(16) + 9 = 4+9 = 13 = sqrt(169)

?? pi-rate = pirate ??

Call the side of the big quarter circle = r

Area of quarter circle = (1/4) pi * r^2
Area of small semicircle = (1/2) pi (r/2)^2 = (1/8) pi * r^2

Then (area of quarter circle = { 2 * area of semicircle - BlueArea } + RedArea ...... (blue is counted twice in semicircles, so take one out)

(1/4) pi * r^2 = {2 * (1/8) pi * r^2 - BlueArea } + RedArea
0= - BlueArea + RedArea
BlueArea=RedArea

Last edited by: chevy on Mar 14, 2024

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 14th, 2024 at 4:28:41 PM permalink

Quote: chevy
picking the low hanging fruit

all the same
if D is side of box
(pi/4) D^2 = 4 * (pi/4) (D/2)^2 = 16 * (pi/4) (D/4)^2

pizza volume = pizza

PIE = 169
sqrt(16) + 9 = 4+9 = 13 = sqrt(169)

?? pi-rate = pirate ??

Call the side of the big quarter circle = r

Area of quarter circle = (1/4) pi * r^2
Area of small semicircle = (1/2) pi (r/2)^2 = (1/8) pi * r^2

Then (area of quarter circle = { 2 * area of semicircle - BlueArea } + RedArea ...... (blue is counted twice in semicircles, so take one out)

(1/4) pi * r^2 = {2 * (1/8) pi * r^2 - BlueArea } + RedArea
0= - BlueArea + RedArea
BlueArea=RedArea

link to original post

Correct!

Well done.
---------------------------------------------

...it would never end.

Backwards

Cake

Have you tried 22 tonight? I said 22.

terapined

terapined

Threads: 95
Posts: 6576

Joined: Dec 1, 2012

Thanked by

March 14th, 2024 at 5:24:18 PM permalink

Quote: Gialmere
Quote: chevy
picking the low hanging fruit

all the same
if D is side of box
(pi/4) D^2 = 4 * (pi/4) (D/2)^2 = 16 * (pi/4) (D/4)^2

pizza volume = pizza

PIE = 169
sqrt(16) + 9 = 4+9 = 13 = sqrt(169)

?? pi-rate = pirate ??

Call the side of the big quarter circle = r

Area of quarter circle = (1/4) pi * r^2
Area of small semicircle = (1/2) pi (r/2)^2 = (1/8) pi * r^2

Then (area of quarter circle = { 2 * area of semicircle - BlueArea } + RedArea ...... (blue is counted twice in semicircles, so take one out)

(1/4) pi * r^2 = {2 * (1/8) pi * r^2 - BlueArea } + RedArea
0= - BlueArea + RedArea
BlueArea=RedArea

link to original post

Correct!

Well done.
---------------------------------------------

...it would never end.

Backwards

Cake

link to original post

Love Chuck Jokes
Chuck doesn't do push ups, he pushes the earth down
He can judge a book by its cover
He doesn't sleep, he waits
When he jumps in the water, he doesn't get wet, the water gets Chuck Norris
Chuck counted to infinity, twice
Chuck can divide by zero

When somebody doesn't believe me, I could care less. Some get totally bent out of shape when not believed. Weird. I believe very little on all forums

DogHand

DogHand

Threads: 2
Posts: 1840

Joined: Sep 24, 2011

Thanked by

March 16th, 2024 at 12:06:28 PM permalink

Pi-Doku Answer

That was fun!

Dog Hand

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 17th, 2024 at 11:11:24 PM permalink

Quote: DogHand
Pi-Doku Answer

That was fun!

Dog Hand
link to original post

Correct!!

Well done. (As a bonus, you have now memorized the first 12 digits of pi. Watch the girls in the math club swoon.)

Consider Dog Hand's response to be official.
------------------------------------------

Magnum PI

Fat. You get fat.

I've heard them all like 3.14 million times already.

Have you tried 22 tonight? I said 22.

rackuun

rackuun

Threads: 0
Posts: 6

Joined: Jan 24, 2023

March 18th, 2024 at 8:57:14 AM permalink

I don't know if this one was posted before:

There are N people in a room. For any pair of people in the room, the two of them are either friends with each other or not. Friendship is always reciprocal and people cannot be friends with themselves. Prove there are at least two people in the room who have the same number of room-friends.

aceside

aceside

Threads: 2
Posts: 589

Joined: May 14, 2021

March 18th, 2024 at 9:31:46 AM permalink

If N=2, they are either friends or not. There are at least two people who have the same number of room-friends.

When N=n, we assume there are at least 2m people who have the same number, x, of room-friends.

By math deduction, when N=n+1, �.

Last edited by: aceside on Mar 18, 2024

ThatDonGuy

Threads: 122
Posts: 6737

Joined: Jun 22, 2011

Thanked by

March 18th, 2024 at 4:37:08 PM permalink

Quote: rackuun
I don't know if this one was posted before:

There are N people in a room. For any pair of people in the room, the two of them are either friends with each other or not. Friendship is always reciprocal and people cannot be friends with themselves. Prove there are at least two people in the room who have the same number of room-friends.
link to original post

Assume that each person has a different number of friends.
This is possible only if one has no friends, one has 1 friend, one has 2 friends, and so on, with the last one having N-1 friends.
This means the person with N-1 friends is friends with everyone else in the room, which is impossible as the person with no friends is not friends with this person.
Therefore, the assumption that each person has a different number of friends is false.

rackuun

rackuun

Threads: 0
Posts: 6

Joined: Jan 24, 2023

March 18th, 2024 at 6:50:06 PM permalink

Quote: ThatDonGuy
Quote: rackuun
I don't know if this one was posted before:

There are N people in a room. For any pair of people in the room, the two of them are either friends with each other or not. Friendship is always reciprocal and people cannot be friends with themselves. Prove there are at least two people in the room who have the same number of room-friends.
link to original post

Assume that each person has a different number of friends.
This is possible only if one has no friends, one has 1 friend, one has 2 friends, and so on, with the last one having N-1 friends.
This means the person with N-1 friends is friends with everyone else in the room, which is impossible as the person with no friends is not friends with this person.
Therefore, the assumption that each person has a different number of friends is false.

link to original post

👍 Nice

aceside

aceside

Threads: 2
Posts: 589

Joined: May 14, 2021

March 19th, 2024 at 11:33:00 AM permalink

I tried to prove this statement by mathematical induction but could not. This part is confusing:

If N=2 and they are not friends, is this true that there are at least two people who have the same number, 0, of room-friends?

Wizard
Administrator

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

March 25th, 2024 at 7:58:03 PM permalink

The question was asked in this post on the average number of spins to see every number appear at least twice in double-zero roulette?

234.8326629288898

Integrate from 0 to infinity of 1-(1-exp(-x/38)*(1+x/38))^38 dx

Recommended integral calculator: https://www.integral-calculator.com/

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ThatDonGuy

Threads: 122
Posts: 6737

Joined: Jun 22, 2011

March 26th, 2024 at 5:59:55 PM permalink

Quote: Wizard
The question was asked in this post on the average number of spins to see every number appear at least twice in double-zero roulette?

234.8326629288898

Integrate from 0 to infinity of 1-(1-exp(-x/38)*(1+x/38))^38 dx

Recommended integral calculator: https://www.integral-calculator.com/

link to original post

The exact answer, calculated through a Markov chain process, is


                                               2,458,532,792
,431,545,299,268,331,086,172,570,342,312,718,399,986,188,067
,613,993,736,050,899,703,294,263,621,414,373,376,335,532,123
,938,814,367,114,586,068,064,224,623,137,338,487,255,215,140
,008,621,838,160,580,491,305,106,138,247,464,350,795,459,486
,531,836,562,054,491,448,024,234,478,387,675,642,506,165,051
,266,071,873,671,771,900,922,226,332,086,888,171,157,513,993
,773,263,459,648,019,582,058,157,468,484,735,864,723,796,556
,010,777,275,053,180,121,803,203,922,520,306,071,448,436,764
,103,411,971,842,531,832,013,580,185,101,482,792,146,107,877
,371,534,984,353,278,390,414,808,452,594,198,307,228,367,261
over                                              10,469,296
,569,600,366,313,766,776,904,675,214,787,660,719,539,249,122
,838,110,753,732,469,863,621,352,350,201,672,413,287,522,823
,017,184,089,776,680,121,455,346,561,472,842,277,765,179,834
,313,091,454,122,181,241,307,952,873,173,734,004,633,490,787
,983,474,048,654,417,920,804,096,222,705,207,398,226,915,954
,866,956,131,936,567,944,994,893,548,485,765,436,847,000,729
,947,022,400,734,253,517,093,794,023,492,037,172,521,077,848
,152,918,335,557,895,072,383,721,878,928,916,078,101,947,708
,069,094,178,209,223,588,432,334,788,347,805,884,617,850,880
,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000

which is about 234.83266292891, although I am not sure how many decimal places of accuracy Visual C# floating point division has

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 29th, 2024 at 12:36:28 PM permalink

With the Monty Hall Problem returning to the forum for contemplation, here is a pair of puny puzzles to ponder...

For these variations, it's the 70s and you love watching "Let's Make A Deal." In fact, you watch it so much you begin to notice things.

You notice that when Hall has a choice between opening doors #2 or #3 to reveal a goat, he more often opens door #2 because he�s usually standing closer to it. In fact, this happens 3/4 of the time. Perhaps he's lazy.

Eventually you become a contestant on the show and confront the three doors yourself. You pick door #1. Monty then walks to door #2 and opens it to reveal a goat.

What is the probability that switching to door #3 wins?

Being a gambler, in this variation you notice that when a contestant has initially chosen the car door, Hall often subtly arches his left eyebrow at least three times between revealing the goat and offering the option to switch. Hall gives this tell 95% of the time the car door is chosen.

On the other hand, he sometimes gives false tells�i.e., arches his left eyebrow in this way when a contestant has chosen a goat door. He does this 10% of the time a goat door is chosen.

Now, you're on the show and have selected a door. You then see Monty's left eyebrow arch three times after he opens another door to reveal a goat. He asks if you wish to switch doors.

What is the probability you'll win the car if you don't switch and stick with your initial door choice?

Have you tried 22 tonight? I said 22.

Wizard
Administrator

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

Thanked by

March 29th, 2024 at 1:06:42 PM permalink

80% chance to win by staying, 20% by switching.

Pr(win if you don't switch)=19/23

Last edited by: Wizard on Mar 30, 2024

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Wizard
Administrator

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

March 30th, 2024 at 3:56:34 PM permalink

Waiting to get graded...

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

ThatDonGuy

Threads: 122
Posts: 6737

Joined: Jun 22, 2011

March 30th, 2024 at 4:05:34 PM permalink

Quote: Wizard
Waiting to get graded...
link to original post

If he is waiting to get more answers, here are mine:

The probability that door 3 is shown if door 1 has the prize is 1/4
The probability that door 3 is shown if door 2 has the prize is 1
The probability that door 3 is shown if door 3 has the prize is 0

The probability of winning by switching = (1/4) / (1 + 1/4 + 0) = 1 / 5

The probability that Monty twitches if the prize is selected is 19/20
The probability that Monty twitches if a goat is selected is 1/10

The probability of winning by not switching = (19/20) / (19/20 + 1/10) = 19 / 21

Wizard
Administrator

Threads: 1520
Posts: 27117

Joined: Oct 14, 2009

March 30th, 2024 at 6:03:48 PM permalink

Quote: ThatDonGuy

If he is waiting to get more answers, here are mine:
link to original post

I see we have a small difference on Monty's Tell. Of course, I could easily be the one in error.

"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 30th, 2024 at 10:04:17 PM permalink

Apologies for my tardiness. This holiday weekend has gotten much busier than anticipated.

So far, the Wizard is correct about Monty's Tell.

Lazy Monty, however, remains unsolved.

Have you tried 22 tonight? I said 22.

unJon

unJon

Threads: 16
Posts: 4806

Joined: Jul 1, 2018

Thanked by

March 31st, 2024 at 6:44:24 AM permalink

Quote: Gialmere
Apologies for my tardiness. This holiday weekend has gotten much busier than anticipated.

So far, the Wizard is correct about Monty's Tell.

Lazy Monty, however, remains unsolved.
link to original post

In that case I�ll try:

I read the assumption as saying if the contestant picks door #1 and the car is behind door #1, so Monty is free to choose to open either door 2 or 3, then 75% of the time he chooses door 2.

In that case now that I have picked door #1, Monty chooses door 2 one-third of the time when the car is in door #3 and one-third times three-quarters of the time when the car is in door #1.

So 1/3 * 3/4 / (1/3 + 1/3 * 3/4) = 3/7 chance that door #1 has the car.

Better off switching to win 4/7 of the time.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

ThatDonGuy

Threads: 122
Posts: 6737

Joined: Jun 22, 2011

Thanked by

March 31st, 2024 at 12:10:21 PM permalink

Quote: ThatDonGuy
Quote: Wizard
Waiting to get graded...
link to original post

If he is waiting to get more answers, here are mine:

The probability that door 3 is shown if door 1 has the prize is 1/4
The probability that door 3 is shown if door 2 has the prize is 1
The probability that door 3 is shown if door 3 has the prize is 0

The probability of winning by switching = (1/4) / (1 + 1/4 + 0) = 1 / 5

link to original post

...that Monty opens door 2.

The probability that door 2 is shown if door 1 has the prize is 3/4
The probability that door 2 is shown if door 2 has the prize is 0
The probability that door 2 is shown if door 3 has the prize is 1

The probability of winning by switching = 1 / (3/4 + 0 + 1) = 4 / 7

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

March 31st, 2024 at 11:18:53 PM permalink

Quote: Wizard
Pr(win if you don't switch)=19/23

link to original post

Quote: unJon
I read the assumption as saying if the contestant picks door #1 and the car is behind door #1, so Monty is free to choose to open either door 2 or 3, then 75% of the time he chooses door 2.

In that case now that I have picked door #1, Monty chooses door 2 one-third of the time when the car is in door #3 and one-third times three-quarters of the time when the car is in door #1.

So 1/3 * 3/4 / (1/3 + 1/3 * 3/4) = 3/7 chance that door #1 has the car.

Better off switching to win 4/7 of the time.

link to original post

Quote: ThatDonGuy

...that Monty opens door 2.

The probability that door 2 is shown if door 1 has the prize is 3/4
The probability that door 2 is shown if door 2 has the prize is 0
The probability that door 2 is shown if door 3 has the prize is 1

The probability of winning by switching = 1 / (3/4 + 0 + 1) = 4 / 7

link to original post

Correct!!

Good show.

In the classic Monty Hall problem, you'll often hear arguments about whether or not Monty knows which door the car is behind. You hardly ever hear talk about a door selection being biased in a way that, say, the locations of Daily Doubles on a Jeopardy! board are biased. What's interesting about these variations is that they show how even a little bias can go a long way in changing probability.

Or consider an extreme case. Suppose that lazy Monty is so lazy that, after you pick door #1, he will always show you a goat behind door #2 ... unless he can't. If he shows you a goat behind door #3, you know with 100% certainty that the car is behind door #2.

--------------------------------------

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

April 4th, 2024 at 9:55:05 AM permalink

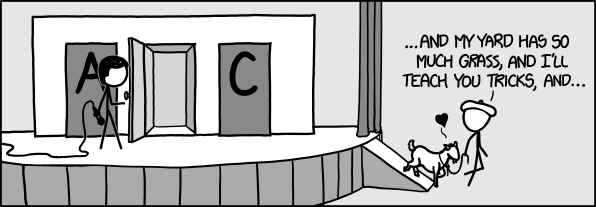
There sits before you a standard, well-shuffled deck of 52 playing cards. I remove a card and look at it without showing it to you. I set the card aside and truthfully inform you that it is not the A♦. I point back at the deck and tell you to draw a card.

What, from your perspective, is the probability of drawing the 9♣?

Have you tried 22 tonight? I said 22.

ChesterDog

ChesterDog

Threads: 9
Posts: 1730

Joined: Jul 26, 2010

Thanked by

April 4th, 2024 at 11:23:07 AM permalink

Quote: Gialmere

There sits before you a standard, well-shuffled deck of 52 playing cards. I remove a card and look at it without showing it to you. I set the card aside and truthfully inform you that it is not the A♦. I point back at the deck and tell you to draw a card.

What, from your perspective, is the probability of drawing the 9♣?
link to original post

Assuming you intended to check if the first card was the A♦ before you looked at it, I get a probability of 50 / 51² of my drawing the 9♣.

ThatDonGuy

Threads: 122
Posts: 6737

Joined: Jun 22, 2011

April 4th, 2024 at 3:35:31 PM permalink

Quote: Gialmere
There sits before you a standard, well-shuffled deck of 52 playing cards. I remove a card and look at it without showing it to you. I set the card aside and truthfully inform you that it is not the A♦. I point back at the deck and tell you to draw a card.

What, from your perspective, is the probability of drawing the 9♣?
link to original post

Knowing nothing else about your statement (e.g. would you have said "It is the Ace of Diamonds" if it was), this sounds like a variation on the Monty Hall problem; I think the answer is 1/52.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

Thanked by

April 4th, 2024 at 6:35:30 PM permalink

Quote: ChesterDog

Assuming you intended to check if the first card was the A♦ before you looked at it, I get a probability of 50 / 51² of my drawing the 9♣.

link to original post

Correct!

Well done.
---------------------------------

And yes, it's as easy as you'd think.

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

Thanked by

May 4th, 2024 at 9:18:35 AM permalink

May the 4th be with you...

You are a rebel agent overseeing shipments at a cargo warehouse. You secretly ship supplies to fellow agents who arrange to have the crates smuggled to a hidden rebel base. To get past Imperial customs all packages must follow a strict protocol...

--If a box is marked with an even number on the bottom side, the top side must be colored red.--

You are nervously watching a shipment of four crates head towards the transport ship when you receive an urgent message from a rebel spy. One of the boxes was packaged incorrectly and they lost track of which one it is. All four boxes are still on the conveyor belt. Two of them are facing down: one showing a 4 on the bottom and the other showing a 7. The other two are facing up: one with red top and the other with a black top.

You know that if any box is mislabeled the entire shipment will be seized and searched. You run towards the conveyor belt. The transport is about leave and you realize that any box you pull off for inspection won't make it onto this delivery run. On the other hand, the rebel base is in desperate need of supplies.

What box or boxes (if any) must you remove to insure some supplies are shipped? Or, is it safer to grab them all?

You are leading an imperial detachment in pursuit of rebel spies who have stolen the plans for the empire's new battle station. You have tracked them to a cluster of seven planets and must apprehend them quickly before their reinforcements arrive.

Of course, the rebels won't just stay put. They'll try to dodge you by moving from planet to planet. But you have a huge advantage. Every hour, your state-of-the-art cruiser can warp to any planet in the system, while their beat up smuggling transport can only jump to an adjacent planet in that same time.The rebels know they're being pursued and will always jump to an adjacent planet every hour.

Imperial scouts are now signaling you that a rebel fleet has gone into hyperspace and will arrive at your cluster system in ten hours. You can't risk letting the spies escape. Lord Vader does not take such failures well.

Can you devise a search pattern that will find the rebels in ten warps or less?

Rules
1) The rebels may start on any of the seven planets.
2) Every hour you MAY warp to any of the seven planets.
3) Starting after your first search, the rebels MUST move every hour to an adjacent planet.
4) You must find the rebels in ten moves or less. Assume you both jump/warp at the same time.
5) Your sequence must be capable of finding the rebels in every possible scenario.

1) What year did the original Star Wars movie (aka Episode 4) hit theaters?

2) Who's the only actor to perform in all 12 Star Wars movies?

3) In an animated sequence, bounty hunter Boba Fett first appeared in what Star Wars production?

4) In the Mel Brooks comedy "Spaceballs," what was the name of the character spoofing the Star Wars character Jabba?

5) George Lucas had an Alaskan Malamute that became the inspiration for the Star Wars character Chewbacca. What was the name of this famous dog?

Have you tried 22 tonight? I said 22.

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

Thanked by

May 4th, 2024 at 9:30:02 AM permalink

The rule is if even then must be red. Thus if it is red is it safe, since it could be odd or even and still be OK. Similarly if it is odd it is safe (as it doesn't have to be red). However if you only know it's black, or you only know it's even, then you can't be sure of the package (as you don't know the other side). Hence you leave the one showing "7" and the one showing "red", and remove the "4" and "black".
edit: got my red and black confused!!

Last edited by: charliepatrick on May 4, 2024

charliepatrick

charliepatrick

Threads: 39
Posts: 3017

Joined: Jun 17, 2011

Thanked by

May 4th, 2024 at 10:25:03 AM permalink

This is a variant of the 5-in a row and relies on trying to pin them down to even or odd numbers. For instance if you start at 4, you only know they didn't start at 4, but if on the second turn you try 3, then you also know they can't be at 5 (since they would have needed to have been at 4, which you know they weren't). Thus this logic is used...
4 : 1 2 3 x 5 6 7
3 : 1 2 x 4 x 6 7 (can't be at 5, as per above)
2 : 1 x 3 x 5 6 7 (can't be at 4, as needed 3 or 5 previous turn)
3 : x 2 x 4 x 6 7 (can't be at 1 or 5, as needed 2 or 4 previous turn)
6 : 1 x 3 x 5 x 7 (caught the one at 7 last time, so all the others were even last time, so must be odd now)
6 : x 2 x 4 x x x (must now be even, so only leaves 2 and 4)
3 : 1 x x x 5 x x (from 2 or 4, can only go to 1 3 or 5, hence only leaves 1 or 5)
2 : x x x 4 x x x (this catches 1 to 2, but leaves 5 to 4)
3 : x x x x 5 x x (from 4 can only go to 3 or 5, so catch the one at 3, so for next turn we now know at 5...)
4 : x x x X x x x (hence now catch them going from 5 to 4).

ThatDonGuy

Threads: 122
Posts: 6737

Joined: Jun 22, 2011

Thanked by

May 4th, 2024 at 10:43:58 AM permalink

"If the box has an even number, it needs a red side" means that a box is bad only if it has both an even number and a non-red side.
The 7 box and the red-side box are good.
The black-side box is bad if it has an even number hidden.
The 4 box is bad if it has a black side hidden.
Remove the box with the 4 and the box with the black side.

1. I think 1976.

2. Anthony Daniels (C-3PO)

3. I don't know what you're talking about - there is no "Star Wars Holiday Special." Fighting the frizzies, at 11.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

May 5th, 2024 at 12:25:40 AM permalink

Quote: charliepatrick
The rule is if even then must be red. Thus if it is red is it safe, since it could be odd or even and still be OK. Similarly if it is odd it is safe (as it doesn't have to be red). However if you only know it's black, or you only know it's even, then you can't be sure of the package (as you don't know the other side). Hence you leave the one showing "7" and the one showing "red", and remove the "4" and "black".
edit: got my red and black confused!!

link to original post

Quote: charliepatrick
This is a variant of the 5-in a row and relies on trying to pin them down to even or odd numbers. For instance if you start at 4, you only know they didn't start at 4, but if on the second turn you try 3, then you also know they can't be at 5 (since they would have needed to have been at 4, which you know they weren't). Thus this logic is used...
4 : 1 2 3 x 5 6 7
3 : 1 2 x 4 x 6 7 (can't be at 5, as per above)
2 : 1 x 3 x 5 6 7 (can't be at 4, as needed 3 or 5 previous turn)
3 : x 2 x 4 x 6 7 (can't be at 1 or 5, as needed 2 or 4 previous turn)
6 : 1 x 3 x 5 x 7 (caught the one at 7 last time, so all the others were even last time, so must be odd now)
6 : x 2 x 4 x x x (must now be even, so only leaves 2 and 4)
3 : 1 x x x 5 x x (from 2 or 4, can only go to 1 3 or 5, hence only leaves 1 or 5)
2 : x x x 4 x x x (this catches 1 to 2, but leaves 5 to 4)
3 : x x x x 5 x x (from 4 can only go to 3 or 5, so catch the one at 3, so for next turn we now know at 5...)
4 : x x x X x x x (hence now catch them going from 5 to 4).

link to original post

Quote: ThatDonGuy

"If the box has an even number, it needs a red side" means that a box is bad only if it has both an even number and a non-red side.
The 7 box and the red-side box are good.
The black-side box is bad if it has an even number hidden.
The 4 box is bad if it has a black side hidden.
Remove the box with the 4 and the box with the black side.

1. I think 1976.

2. Anthony Daniels (C-3PO)

3. I don't know what you're talking about - there is no "Star Wars Holiday Special." Fighting the frizzies, at 11.

link to original post

Correct!!

The force is strong with these two.

These both came from Ted-Ed.

1) 1977
And Sci-Fi movies, in terms of special effects, would never be the same. The jaw dropping opening scene when the Imperial cruiser enters from the top of the screen and goes on and on overhead had audiences thinking that no matter how bad this film might turn out to be, they've already gotten their money's worth.

2) Anthony Daniels
He played C-3P0 onscreen in ten movies, did the voice of C-3P0 in the animated Clone Wars film, and played a human slave in the spice mines of Kessel for the (Han) Solo movie. The latter role was sort of an inside joke about the first Star Wars film in which C-3P0 was concerned about being sent to the spice mines of Kessel.

3) The Star Wars Holiday Special (1978)
Yes, Boba Fett first appeared in the notorious, aired only once, Holiday Special. If you've never seen it, and you hate what Disney has done to Star Wars, you should watch it just to see what levels of cringey embarrassment George Lucas once pushed the franchise to. As an asterisk, Star Wars uber fanatics will point out that a production worker dressed up as Boba Fett for a local parade that took place a few months before the special was aired. He walked down the route next to Darth Vader. The character was so new that, when prompted for an autograph, he had to ask another employee how the name was spelled. (Two Ts.)

4) Pizza the Hutt
Pizza was voiced by Dom DeLuise. Spaceballs is not a great movie but, if you enjoy Sci-Fi films, it does have a few yuks.

5) Indiana
Thus the dog gave his looks to Star Wars and his name to Raiders of the Lost Ark.

------------------------------------------------

Have you tried 22 tonight? I said 22.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

May 8th, 2024 at 10:13:19 AM permalink

You have 16 motorbikes gathered together at the edge of a desert plain. Each bike has a rider and a full tank of gas. A bike can travel 100 kilometers on a full tank.

Using all 16 bikes as a team, how far can you get one of the bikes to travel across the desert?

Have you tried 22 tonight? I said 22.

Joeman

Joeman

Threads: 36
Posts: 2454

Joined: Feb 21, 2014

May 8th, 2024 at 11:04:59 AM permalink

Assuming you can't stack or tow bikes, I would say 300km:

After 50 km, have half of the riders riders transfer their gas to the other half of the remaining bikes, yielding 8 bikes with full tanks. Every 50 km after that, do the same until you have 1 bike with a full tank at a distance of 200 km from the start. He can get another 100 km for a total of 300 km.

Also, from this past weekend...

Quote: Gialmere
3) In an animated sequence, bounty hunter Boba Fett first appeared in what Star Wars production?

Quote: ThatDonGuy
3. I don't know what you're talking about - there is no "Star Wars Holiday Special." Fighting the frizzies, at 11.

Quote: Gialmere
3) The Star Wars Holiday Special (1978)
Yes, Boba Fett first appeared in the notorious, aired only once, Holiday Special. If you've never seen it, and you hate what Disney has done to Star Wars, you should watch it just to see what levels of cringey embarrassment George Lucas once pushed the franchise to. As an asterisk, Star Wars uber fanatics will point out that a production worker dressed up as Boba Fett for a local parade that took place a few months before the special was aired. He walked down the route next to Darth Vader. The character was so new that, when prompted for an autograph, he had to ask another employee how the name was spelled. (Two Ts.)

I meant to mention this before, but for those curious about the Star Wars Holiday Special, there is a 2-hour documentary (well, actually 1-1/2 hours without commercials) about it called A Disturbance in the Force . They were airing it on the Vice channel pretty much non-stop on Saturday. I had not really known anything about the SWHS. It was pretty interesting.

"Dealer has 'rock'... Pay 'paper!'"

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

May 8th, 2024 at 2:31:10 PM permalink

Quote: Joeman
Assuming you can't stack or tow bikes, I would say 300km:

After 50 km, have half of the riders riders transfer their gas to the other half of the remaining bikes, yielding 8 bikes with full tanks. Every 50 km after that, do the same until you have 1 bike with a full tank at a distance of 200 km from the start. He can get another 100 km for a total of 300 km.

Also, from this past weekend...

Quote: Gialmere
3) In an animated sequence, bounty hunter Boba Fett first appeared in what Star Wars production?

Quote: ThatDonGuy
3. I don't know what you're talking about - there is no "Star Wars Holiday Special." Fighting the frizzies, at 11.

Quote: Gialmere
3) The Star Wars Holiday Special (1978)
Yes, Boba Fett first appeared in the notorious, aired only once, Holiday Special. If you've never seen it, and you hate what Disney has done to Star Wars, you should watch it just to see what levels of cringey embarrassment George Lucas once pushed the franchise to. As an asterisk, Star Wars uber fanatics will point out that a production worker dressed up as Boba Fett for a local parade that took place a few months before the special was aired. He walked down the route next to Darth Vader. The character was so new that, when prompted for an autograph, he had to ask another employee how the name was spelled. (Two Ts.)

I meant to mention this before, but for those curious about the Star Wars Holiday Special, there is a 2-hour documentary (well, actually 1-1/2 hours without commercials) about it called A Disturbance in the Force . They were airing it on the Vice channel pretty much non-stop on Saturday. I had not really known anything about the SWHS. It was pretty interesting.

link to original post

A good guess but not optimal.

And yes, assume stacking or towing would increase the weight and reduce the mileage.

P.S. Thank you for the documentary tip. I definitely gotta see it.

Have you tried 22 tonight? I said 22.

unJon

unJon

Threads: 16
Posts: 4806

Joined: Jul 1, 2018

May 8th, 2024 at 5:44:40 PM permalink

Quote: Gialmere

You have 16 motorbikes gathered together at the edge of a desert plain. Each bike has a rider and a full tank of gas. A bike can travel 100 kilometers on a full tank.

Using all 16 bikes as a team, how far can you get one of the bikes to travel across the desert?
link to original post

Not sure this is optimal as feels like the kind of thing that should go to 1/e as bikes go to infinity but:

If you ditch a bike every time there is enough for that bike to fill up the remaining bikes you can go:

100*(1/15 + 1/14 + 1/13 + . . . + 1/2 + 1) = 331.823km.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere

Threads: 45
Posts: 3047

Joined: Nov 26, 2018

May 8th, 2024 at 8:10:43 PM permalink

Quote: unJon
Not sure this is optimal as feels like the kind of thing that should go to 1/e as bikes go to infinity but:

If you ditch a bike every time there is enough for that bike to fill up the remaining bikes you can go:

100*(1/15 + 1/14 + 1/13 + . . . + 1/2 + 1) = 331.823km.

link to original post

Good logic, but you're missing something.

Have you tried 22 tonight? I said 22.

unJon

unJon

Threads: 16
Posts: 4806

Joined: Jul 1, 2018

Thanked by

May 8th, 2024 at 9:50:39 PM permalink

Quote: Gialmere
Quote: unJon
Not sure this is optimal as feels like the kind of thing that should go to 1/e as bikes go to infinity but:

If you ditch a bike every time there is enough for that bike to fill up the remaining bikes you can go:

100*(1/15 + 1/14 + 1/13 + . . . + 1/2 + 1) = 331.823km.

link to original post

Good logic, but you're missing something.
link to original post

Oh I started the series too soon. So add :

1/16*100 = 6.25 miles to make a total of 338.07 miles.

The race is not always to the swift, nor the battle to the strong; but that is the way to bet.

Gialmere