Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
June 10th, 2024 at 5:45:05 PM
permalink
Quote: djtehch34tQuote: ThatDonGuyHere's a new problem - bad news: it's a "proof" problem.
Interplanetary Express serves 65 different locations throughout the solar system. Every pair of locations is served by a route that is one of four colors - red, blue, green, or yellow. It turns out that, given any three locations, the three routes that connect them to each other are not all the same color.
Somebody wants to add a 66th location, with routes to each of the other 65, and maintaining the "no single-color triangles" policy.
Prove that this is impossible.
(Hint: the fact that you can with 65 is irrelevant; in fact, I am not entirely sure that such a mapping exists.)
link to original postAssume we have a graph that satisfies the condition (call this 4-colorable). Take the 66th vertex and look at its edges. The color C1 that has the maximum number of edges must have at least ceiling(65/4) = 17 edges. Look at the subgraph with the vertices we get from those edges. This must not have any edges with C1 (aka be 3-colorable), or else we get a cycle with color C1.
Pick an arbitrary vertex in the subgraph of size 17 and repeat the argument. Color C2 must have ceiling(16/3) = 6 edges. So, this creates a 2-colorable subgraph of size 6. Repeat the argument once more to get a 1-colorable subgraph of size ceiling(5/2) = 3. But, this is a contraction, as that's the same as a cycle of the same color.
link to original post
Exactly.
Call the three paths that connect three locations to each other a "red triangle" if they are all red; similarly for any other color.
Choose a location; call it Location A.
There are 65 paths from A to the other locations. If there were only 16 of each color, that would be only 64 paths; therefore, there must be at least one color with 17 paths from A. Let's assume it is red.
If any of the paths between any of the 17 locations are also red, then those two locations and A form a red triangle; therefore, they can only be blue, green, or yellow.
Choose one of these 17 locations; call it Location B.
There are 16 paths from B to the other locations of these 17; if there were only 5 of each color, that would be only 15 paths, so there must be at least one color with 6 paths from B to the other 16 locations. Let's assume it is blue.
If any of the paths between any of the 6 locations are also blue, then those two locations and B form a blue triangle; therefore, they can only be green or yellow.
Choose one of these 6 locations; call it Location C.
There are 5 paths from C to these five locations; if there were only 2 of each color, that would be only 4 paths, so there must be at least one color with 3 paths from C to these 5 locations. Let's assume it is green, and let CD, CE, and CF all be green.
If DE is green, then CDE is a green triangle; if DF is green, then CDF is a green triangle; if CEF is green, then CEF is a green triangle; if none of them are green, then DEF is a yellow triangle.
For those of you interested in such things, the principle that, if you have N items and each is one of K types, then there must be at least N/K rounded up items of at least one type is called the Pigeonhole Principle (because you are trying to put N pigeons into K pigeonholes).
June 10th, 2024 at 7:58:22 PM
permalink
To reply to all posts since my puzzle on the 13 cards, I can't give anyone credit for a proper answer yet.
To clarify, yes, both players may look at their cards.
To clarify, yes, both players may look at their cards.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 11th, 2024 at 4:37:04 AM
permalink
Either you simply don't like the form of my answer or there is something missing from your description.Quote: WizardTo reply to all posts since my puzzle on the 13 cards, I can't give anyone credit for a proper answer yet.
To clarify, yes, both players may look at their cards.
link to original post
There are 13*12 ways the cards can be chosen. L1 wins 78 of these matchups and L2 wins the other 78 when no exchange is ever offered. If L1 offers to exchange any card but a deuce, L2 will always accept if L2 is holding a deuce. L2 can sit pat in any other situation. This will give L2 an advantage in what was otherwise a fair game. So, L1 can only offer to exchange when holding a deuce. There is no way for L1 to force L2 into a disadvantage and vice versa.
Since L2 should be able to deduce all of this, L1 knows it is futile to offer to exchange any other card but a deuce to a logical opponent. The logical opponent will always refuse any exchange unless they are holding a deuce.
Am I missing something?
Since L2 should be able to deduce all of this, L1 knows it is futile to offer to exchange any other card but a deuce to a logical opponent. The logical opponent will always refuse any exchange unless they are holding a deuce.
Am I missing something?
This forum is more enjoyable after I learned how to use the 'Block this user' button.
June 11th, 2024 at 6:08:17 AM
permalink
Quote: MentalEither you simply don't like the form of my answer or there is something missing from your description.
link to original post
Sorry, I missed your answer. Credit given for being correct.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 14th, 2024 at 1:47:39 PM
permalink
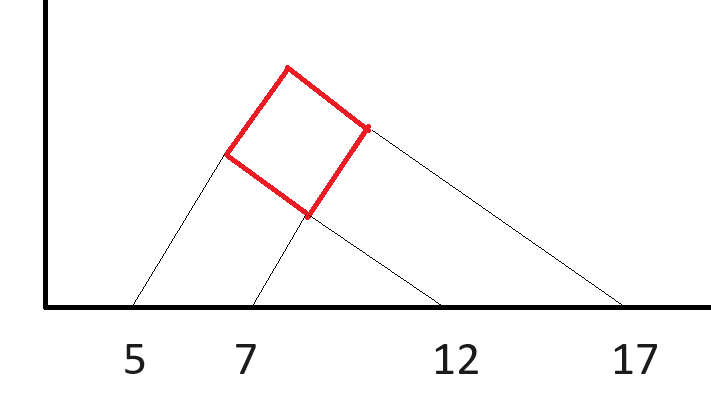
The red figure is a square. If you extend its sides, they cross the x-axis at points 5, 7, 12, and 17.
What is the area of the square?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 14th, 2024 at 1:58:43 PM
permalink
the triangle hitting 7 & 12 is 3-4-5
So right side (from square to 12) is 4
The triangle hitting 5&12 is similar,
so side from (leftmost) square corner to 12 is. 7*(4/5) = 5.6
So side of square is 5.6-4 = 1.6
Area = 2.56
Hmmm
Same method for triangle hitting 7&17
Side is 10*(3/5)=6
side of square is 6-3 = 3
area = 9
I am going something wrong
Never mind…. Doesn’t have to be 3-4-5 triangle
Will look at it further
June 14th, 2024 at 2:41:28 PM
permalink
Similar triangles…y is side of square
7&12 to 7&17
X/5= (x+y)/10…..x=y
5&12to 5&17
Z/7 = (z+y)//12….z=7y/5
Small triangle x^2 + z^2 = 5^2
Y^2 + (49/25* y^2) =25
Wrong again
Trying to do on phone is not helping
……..
Need
Z^2 + (y+(sqrt (25-x^2))^2 = 7^2
Sub in z and x from above…. Solve with paper and pen….. later
Areas of square =Y^2= __________
June 14th, 2024 at 3:27:40 PM
permalink
Note that the lines touching x = 5 and x = 7 are parallel, and the lines touching x = 12 and x = 17 are parallel, so the four triangles that are visible are all similar.
Let x be the length of the side of the square, a the distance from the square to (5,0), and b the distance from the square to (17,0)
(12 - 5) / a = (17 - 5) / (a + x) => 7 a + 7 x = 12 a => a = 7/5 x
(17 - 7) / b = (17 - 5) / (b + x) => 10 b + 10 x = 12 b => b = 5 x
Pythagorean Theorem: (a + x)^2 + (b + x)^2 = (17 - 5)^2
(12/5 x)^2 + (6 x)^2 = 144
1044/25 x^2 = 144
x^2 = 144 * 25 / 1044 = 100 / 29
Since x is a side of the square, the area is x^2, or 100 / 29
June 14th, 2024 at 7:15:52 PM
permalink
Quote: ThatDonGuy
Note that the lines touching x = 5 and x = 7 are parallel, and the lines touching x = 12 and x = 17 are parallel, so the four triangles that are visible are all similar.
Let x be the length of the side of the square, a the distance from the square to (5,0), and b the distance from the square to (17,0)
(12 - 5) / a = (17 - 5) / (a + x) => 7 a + 7 x = 12 a => a = 7/5 x
(17 - 7) / b = (17 - 5) / (b + x) => 10 b + 10 x = 12 b => b = 5 x
Pythagorean Theorem: (a + x)^2 + (b + x)^2 = (17 - 5)^2
(12/5 x)^2 + (6 x)^2 = 144
1044/25 x^2 = 144
x^2 = 144 * 25 / 1044 = 100 / 29
Since x is a side of the square, the area is x^2, or 100 / 29
link to original post
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 25th, 2024 at 3:42:19 PM
permalink
There are ten lillipad (is that the right spelling?) in a row. A frog is sitting on the first one from one side. He can hop to the next pad or jump over it to the next one. How many ways can he get to the last lillipad? Note, he must land on the last one, no jumping over it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 25th, 2024 at 4:02:01 PM
permalink
Quote: WizardThere are ten lillipad (is that the right spelling?) in a row. A frog is sitting on the first one from one side. He can hop to the next pad or jump over it to the next one. How many ways can he get to the last lillipad? Note, he must land on the last one, no jumping over it.
link to original post
There are an infinite number of ways, if the frog can jump in either direction.
If all jumps must be from one side to the other, this is the Fibonacci sequence.
June 25th, 2024 at 4:26:09 PM
permalink
Let me add that the frog may NOT jump backwards.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 26th, 2024 at 3:58:39 AM
permalink
55.
I think you can prove it's a fibonacci series...
Let's assume the starting position is called #9, and the home called #0.
Firstly consider the number of ways of getting from #1 to #0, we'll call this f(1) - obviously there is only one way. So f(1)=1.
Next consider getting from #2 to #0. You can either go #2>#1, then f(1), or #2>#0 = 1. So f(2)=f(1)+1 = 2.
Next consider getting from #3 to #0. You can either go from #3 to #2, then f(2); or #3 to #1, then f(1). So f(3)=f(2)+f(1)
I think you can prove it's a fibonacci series...
Let's assume the starting position is called #9, and the home called #0.
Firstly consider the number of ways of getting from #1 to #0, we'll call this f(1) - obviously there is only one way. So f(1)=1.
Next consider getting from #2 to #0. You can either go #2>#1, then f(1), or #2>#0 = 1. So f(2)=f(1)+1 = 2.
Next consider getting from #3 to #0. You can either go from #3 to #2, then f(2); or #3 to #1, then f(1). So f(3)=f(2)+f(1)
| f(1) | 1 |
| f(2) | 2 |
| f(3) | 3 |
| f(4) | 5 |
| f(5) | 8 |
| f(6) | 13 |
| f(7) | 21 |
| f(8) | 34 |
| f(9) | 55 |
June 26th, 2024 at 6:39:56 AM
permalink
Quote: charliepatrick55.
I think you can prove it's a fibonacci series...
Let's assume the starting position is called #9, and the home called #0.
Firstly consider the number of ways of getting from #1 to #0, we'll call this f(1) - obviously there is only one way. So f(1)=1.
Next consider getting from #2 to #0. You can either go #2>#1, then f(1), or #2>#0 = 1. So f(2)=f(1)+1 = 2.
Next consider getting from #3 to #0. You can either go from #3 to #2, then f(2); or #3 to #1, then f(1). So f(3)=f(2)+f(1)
f(1) 1 f(2) 2 f(3) 3 f(4) 5 f(5) 8 f(6) 13 f(7) 21 f(8) 34 f(9) 55
link to original post
Agreed!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 26th, 2024 at 1:53:58 PM
permalink
There are four camels at an oasis. Each camel may carry up to a five-day supply of water. An urgent letter must be delivered to an outpost a four-day journey away. There is no supply of water in the desert or the outpost. Transferring of water is allowed. Leaving unattended caches of water is not allowed. Camels do not require water at the oasis. How can a letter be delivered with 20 days supply of water?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 26th, 2024 at 2:11:16 PM
permalink
Let's call the camels A B C and D and, to help describe things, assume there are "mile markers" at 1-day, 2-days, 3-days, 4 days from the oasis.
(i) Camel A goes to MM4, delivers the message and returns to MM3 (at the end of day 5).
(ii) After two days have passed, Camel B goes to MM3 (to reach it at the end of of day 5). Since there are now 2 units of water left, this enables A and B to return (from MM3) to MM2 (at the end of day 6).
(iii) Similarly Camel C goes to MM2 to meet A and B; this uses up 2 units, so they have 3 units to allow A, B and C to travel to MM1 (at the end of day 7).
(iv) Similarly Camel D goes to MM1 to meet A, B and C; this uses up 1 unit, so they have 4 units to allow all four to travel back to the oasis.
(i) Camel A goes to MM4, delivers the message and returns to MM3 (at the end of day 5).
(ii) After two days have passed, Camel B goes to MM3 (to reach it at the end of of day 5). Since there are now 2 units of water left, this enables A and B to return (from MM3) to MM2 (at the end of day 6).
(iii) Similarly Camel C goes to MM2 to meet A and B; this uses up 2 units, so they have 3 units to allow A, B and C to travel to MM1 (at the end of day 7).
(iv) Similarly Camel D goes to MM1 to meet A, B and C; this uses up 1 unit, so they have 4 units to allow all four to travel back to the oasis.
June 26th, 2024 at 9:11:28 PM
permalink
Quote: charliepatrickLet's call the camels A B C and D and, to help describe things, assume there are "mile markers" at 1-day, 2-days, 3-days, 4 days from the oasis.
(i) Camel A goes to MM4, delivers the message and returns to MM3 (at the end of day 5).
(ii) After two days have passed, Camel B goes to MM3 (to reach it at the end of of day 5). Since there are now 2 units of water left, this enables A and B to return (from MM3) to MM2 (at the end of day 6).
(iii) Similarly Camel C goes to MM2 to meet A and B; this uses up 2 units, so they have 3 units to allow A, B and C to travel to MM1 (at the end of day 7).
(iv) Similarly Camel D goes to MM1 to meet A, B and C; this uses up 1 unit, so they have 4 units to allow all four to travel back to the oasis.
link to original post
Well done Charlie! I worked out your solution and agree it work. Mine is different, as below.
Day 1: All four camels advance to point 1. Camel A gives camels B, C, D one day of water each. At this point the locations of the four camels are (1,1,1,1). The water supply of each is (1,5,5,5).
Day 2: Camel A returns home. B, C, D advance to 2. B gives C and D one day of water each. At this point the locations are (0,2,2,2). The water supply of each is (0,2,5,5)
Day 3: Camel B goes back to 1. C and D advance to 3. C gives D one day of water. At this point the locations are (0,1,3,3). The water supply of each is (0,1,3,5)
Day 4: Camel B returns home. Camel C returns to 2. Camel D advances to 4 and delivers the letter. At this point the locations are (0,0,2,4). The water supply of each is (0,0,2,4)
Day 5: Camel C returns to 1. Camel D returns to 3. At this point the locations are (0,0,1,3). The water supply of each is (0,0,1,3).
Day 6: Camel C returns home. Camel D returns to 2. At this point the locations are (0,0,0,2). The water supply of each is (0,0,0,2).
Day 7: Camel D returns to 1. After arrival he has one day of water left.
Day 8: Camel D returns to 0 with no water.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 26th, 2024 at 9:14:06 PM
permalink
There is a one-meter rubber band, with an ant on one end. Each day the ant travels one centimeter. At the end of the day, the rubber band is expanded by one meter. How long will it take for the ant to reach the other side?
I do not require an exact answer. An expression for the answer or to six significant digits will suffice.
You probably will need to be familiar with Euler's Constant (not to be confused with Euler's Number) to solve this one.
I do not require an exact answer. An expression for the answer or to six significant digits will suffice.
You probably will need to be familiar with Euler's Constant (not to be confused with Euler's Number) to solve this one.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 27th, 2024 at 1:31:26 AM
permalink
I think both solutions require
(i) Camel A goes from 0 to 4 and back, so uses 8 units of water.
(ii) Camel B goes from 0 to 3 and back, so uses 6 units of water.
(iii) Camel C goes from 0 to 2 and back, so uses 4 units of water.
(iv) Camel D goes from 0 to 1 and back, so uses 2 units of water.
Both solutions engineer how the water is delivered to other camels to enable them to finish their journey.
I think my solution meets returning camels and yours lets each camel complete the return/second part of the journey unaided.
Thus in your solution when A and B leave MM2, together they have 10 units of water, and at MM3, A lands up with 5 units and B 3 units; so B can get home and A can deliver the letter and then get home.
Similarly at MM1 ABC together had 15 units of water, so could get 12 units to MM2, allowing C to get home and AB to continue.
(i) Camel A goes from 0 to 4 and back, so uses 8 units of water.
(ii) Camel B goes from 0 to 3 and back, so uses 6 units of water.
(iii) Camel C goes from 0 to 2 and back, so uses 4 units of water.
(iv) Camel D goes from 0 to 1 and back, so uses 2 units of water.
Both solutions engineer how the water is delivered to other camels to enable them to finish their journey.
I think my solution meets returning camels and yours lets each camel complete the return/second part of the journey unaided.
Thus in your solution when A and B leave MM2, together they have 10 units of water, and at MM3, A lands up with 5 units and B 3 units; so B can get home and A can deliver the letter and then get home.
Similarly at MM1 ABC together had 15 units of water, so could get 12 units to MM2, allowing C to get home and AB to continue.
June 28th, 2024 at 6:00:15 AM
permalink
On the first day the ant walks 1 centimeter (of the 1m long band), and before the second day the band is enlarged to 2m. So on the second day the ant walks 1 centimeter (of the 2m long band). This is equivilant to walking 1/2 centimeter on a 1m long band. Similarly on other days the ant can be considered as walking 1/N centimeters on a 1m long band.
Thus the question changes to how long does the series 1 + 1/2 + 1/3 ... need to get to 100cm.
Well this is a very large number!! (e.g. End after 10000000000 numbers PrevTot = 23.603066594897502 ThisTot = 23.6030665949975 , so a simple program isn't going to find the answer)
Your hint suggests googling the Euler constant and I saw ( https://en.wikipedia.org/wiki/Harmonic_series_(mathematics) ) a formula.
H(n) = ln (n) + Euler's constant + 1/2n - e(n) (where e(n)<1/8n2).
Using excel and assuming e(n)=the value, this gives 15 092 688 622 100 000 000 000 000 000 000 000 000 000 000 (or about 1.5E43)
Thus the question changes to how long does the series 1 + 1/2 + 1/3 ... need to get to 100cm.
Well this is a very large number!! (e.g. End after 10000000000 numbers PrevTot = 23.603066594897502 ThisTot = 23.6030665949975 , so a simple program isn't going to find the answer)
Your hint suggests googling the Euler constant and I saw ( https://en.wikipedia.org/wiki/Harmonic_series_(mathematics) ) a formula.
H(n) = ln (n) + Euler's constant + 1/2n - e(n) (where e(n)<1/8n2).
Using excel and assuming e(n)=the value, this gives 15 092 688 622 100 000 000 000 000 000 000 000 000 000 000 (or about 1.5E43)
June 28th, 2024 at 7:12:54 AM
permalink
After day 1, the ant has 99 cm to go - at least before the rubber band's length is expanded by 2/1
After day 2, after the ant moves and the rubber band is then expanded by 3/2, the ant has (99 x 2 - 1) x 3/2 cm to go
After day 3, it is ((99 x 2 - 1) x 3/2 - 1) x 4/3
...
After day N, the value is 99 N - (N + 1) (1/2 + 1/3 + ...+ 1/N); the solution is the value of N for which this = 0
The answer is the value N where (N + 1) (1/2 + 1/3 + ...+ 1/N) / N = 99
I am working on a numeric approximation, but it appears to be well over 20 billion.
June 28th, 2024 at 8:42:37 AM
permalink
Quote: charliepatrickOn the first day the ant walks 1 centimeter (of the 1m long band), and before the second day the band is enlarged to 2m. So on the second day the ant walks 1 centimeter (of the 2m long band). This is equivilant to walking 1/2 centimeter on a 1m long band. Similarly on other days the ant can be considered as walking 1/N centimeters on a 1m long band.
Thus the question changes to how long does the series 1 + 1/2 + 1/3 ... need to get to 100cm.
Well this is a very large number!! (e.g. End after 10000000000 numbers PrevTot = 23.603066594897502 ThisTot = 23.6030665949975 , so a simple program isn't going to find the answer)
Your hint suggests googling the Euler constant and I saw ( https://en.wikipedia.org/wiki/Harmonic_series_(mathematics) ) a formula.
H(n) = ln (n) + Euler's constant + 1/2n - e(n) (where e(n)<1/8n2).
Using excel and assuming e(n)=the value, this gives 15 092 688 622 100 000 000 000 000 000 000 000 000 000 000 (or about 1.5E43)
link to original post
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 28th, 2024 at 8:44:32 AM
permalink
Next, a twist on the same puzzle, where the rubber band is stretched all the time...
There is a one-meter rubber band, with an ant on one end. Each day, the ant travels one centimeter. The rubber band is continuously stretched at a rate of one meter per day. How long will it take for the ant to reach the other side?
An expression for the answer or to six significant digits will suffice.
There is a one-meter rubber band, with an ant on one end. Each day, the ant travels one centimeter. The rubber band is continuously stretched at a rate of one meter per day. How long will it take for the ant to reach the other side?
An expression for the answer or to six significant digits will suffice.
Last edited by: Wizard on Jul 9, 2024
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 5th, 2024 at 3:49:53 PM
permalink
I was hoping for more traction on the previous puzzle, but maybe integral calculus isn't everybody's cup of tea. So, let's try one that requires only logic.
There are five gopher holes in a row. A gopher is in one of them. It is your task to find the gopher. Every day you may pick one hole to search. If you pick incorrectly, the gopher will move to a neighboring hole, in either direction at night.
What strategy will allow you to find the gopher in the least number of days for certain?
For extra credit, what is the strategy for n gopher holes?
There are five gopher holes in a row. A gopher is in one of them. It is your task to find the gopher. Every day you may pick one hole to search. If you pick incorrectly, the gopher will move to a neighboring hole, in either direction at night.
What strategy will allow you to find the gopher in the least number of days for certain?
For extra credit, what is the strategy for n gopher holes?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 10th, 2024 at 8:26:35 PM
permalink
I was watching jeopardy the other day and the contestant rang in and answered magic triangle and was called wrong. They were looking for magic square. Later in the show they corrected the answer and said magic triangle was acceptable. I had never heard of a magic triangle before 
this just kind of strikes me as the type of question you would see on are you smarter than 5th grader. Also don't forget alextrebek stamp being issued July 22
this just kind of strikes me as the type of question you would see on are you smarter than 5th grader. Also don't forget alextrebek stamp being issued July 22Last edited by: avianrandy on Jul 10, 2024
July 11th, 2024 at 3:50:37 PM
permalink
Quote: avianrandyAlso don't forget alextrebek stamp being issued July 22
link to original post
I am still trying to find the last time before Trebek that USPS issued a stamp commemorating a person that did not have the person's image on it.
July 12th, 2024 at 12:46:17 AM
permalink
More about magic triangles
I googled the triangle and stumbled across an interesting article with some triangles length 3 (e.g. 162,243,351) and others length 4. Apparently they normalise solutions so the lowest tip is North and the next SE (otherwise you have six ways for each solution).
One interesting length 4 solution had the property that the numbers were a triangle, and also if you squared the numbers they were. I'll leave it to the reader to work it out. (Note the 3 length triangles use the numbers 1 to 6, and the 4 length 1 to 9.)
This page I read has the solution https://www.cuemath.com/learn/do-you-want-to-know-the-secrets-of-the-magic-triangle/
I googled the triangle and stumbled across an interesting article with some triangles length 3 (e.g. 162,243,351) and others length 4. Apparently they normalise solutions so the lowest tip is North and the next SE (otherwise you have six ways for each solution).
One interesting length 4 solution had the property that the numbers were a triangle, and also if you squared the numbers they were. I'll leave it to the reader to work it out. (Note the 3 length triangles use the numbers 1 to 6, and the 4 length 1 to 9.)
This page I read has the solution https://www.cuemath.com/learn/do-you-want-to-know-the-secrets-of-the-magic-triangle/
July 12th, 2024 at 1:38:37 AM
permalink
Quote: WizardI was hoping for more traction on the previous puzzle, but maybe integral calculus isn't everybody's cup of tea.
link to original post
(snip)
I'm assuming that's deliberate, and I feel I must groan.
May the cards fall in your favor.
July 25th, 2024 at 2:32:43 PM
permalink
You have a flashlight that requires two batteries. You also have eight batteries, of which four are good and four are bad. As usual, you can't tell the good from the bad ones by appearance. The flashlight requires two good batteries to work.
What is the least number of tests required to ensure you have two good batteries in the flashlight?
What is the least number of tests required to ensure you have two good batteries in the flashlight?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 25th, 2024 at 3:04:03 PM
permalink
I have a feeling I could do it in eight.
The logic I used was similar to picking numbers for a lottery so you can ensure one ticket is a winner. In this case we have eight batteries and have to find a pair of batteries where both are good.
Let's call the batteries AB CD EF GH and initially try those four pairings. If we don't have a winning pair then it means in each pair there is one good battery. (For instance if both GH were bad, then there would be four good ones in AB CD EF which can only be distributed 220 or 211. Hence one of the pairs would have worked. Similar logic applies to AB, CD and EF.)
So the second stage is try all combinations of picking one of AB and one of CD (i.e. AC AD BC BD). One of these will work.
Hence four to try AB CD EF and GH; followed by four AC AD BC BD = 8.
The logic I used was similar to picking numbers for a lottery so you can ensure one ticket is a winner. In this case we have eight batteries and have to find a pair of batteries where both are good.
Let's call the batteries AB CD EF GH and initially try those four pairings. If we don't have a winning pair then it means in each pair there is one good battery. (For instance if both GH were bad, then there would be four good ones in AB CD EF which can only be distributed 220 or 211. Hence one of the pairs would have worked. Similar logic applies to AB, CD and EF.)
So the second stage is try all combinations of picking one of AB and one of CD (i.e. AC AD BC BD). One of these will work.
Hence four to try AB CD EF and GH; followed by four AC AD BC BD = 8.
July 25th, 2024 at 3:42:23 PM
permalink
6
Call the batteries 1-8:
Try 12. 13. 23
If those dosent work try
45, 46, 56
If i still dosent work, each group of 3 have 2 non-working batteries, and you know without testing that 7-8 work,
Call the batteries 1-8:
Try 12. 13. 23
If those dosent work try
45, 46, 56
If i still dosent work, each group of 3 have 2 non-working batteries, and you know without testing that 7-8 work,
July 25th, 2024 at 3:46:33 PM
permalink
The best I can come up with is 7.
Label the batteries A, B, C, D, E, F, G, H.
#1: check A, B
#2: check C, D
#3: check E, F
#4: check G, H
If none of those worked, then each pair consisted of one good battery and one bad one.
#5: check A, C
#6: check A, D
#7: check B, C
If none of those worked either, then B and D are both good.
July 25th, 2024 at 4:13:18 PM
permalink
^ Don't forget you have to finish with the torch having two good batteries inside. So I agree that my earlier answer wasn't optimal!!
I agree that the best way is to split the batteries into ABC DEF and GH. You can test AB AC BC to show that there aren't two good ones in ABC, similarly in DEF; but you then have to put G and H into the torch. This gives 7.
The logic here is to split the 8 batteries into groups of 3 3 and 2 and once you have proved there aren't two good ones in either ABC or DEF then you know GH will work, but you still have to put them in. My mistake was using pairs rather than triples, this wasn't optimal.
The logic here is to split the 8 batteries into groups of 3 3 and 2 and once you have proved there aren't two good ones in either ABC or DEF then you know GH will work, but you still have to put them in. My mistake was using pairs rather than triples, this wasn't optimal.
July 25th, 2024 at 5:02:12 PM
permalink
I forgot to say that you must actually turn the flashlight on, which counts as a turn. That said, my spoiler below shows the minimum required. I would like to give Torghatten credit for the first correct answer, although we should add one to his count for actually turning the flashlight on.
7
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 25th, 2024 at 8:04:11 PM
permalink
- There's a room with 3 lights inside. Outside the room there are 3 switches. One switch for each light. If you can only walk in to room once, how do know which switch is for which light?
- There's a boat in a lake with a bowling ball on it. The ball rolls off the boat into the lake. What happens to the level of the lake? Does it go up,down or stay the same?
-psg
- There's a boat in a lake with a bowling ball on it. The ball rolls off the boat into the lake. What happens to the level of the lake? Does it go up,down or stay the same?
-psg
July 26th, 2024 at 2:08:34 AM
permalink
Quote: WizardYou have a flashlight that requires two batteries. You also have eight batteries, of which four are good and four are bad. As usual, you can't tell the good from the bad ones by appearance. The flashlight requires two good batteries to work.
What is the least number of tests required to ensure you have two good batteries in the flashlight?
link to original post
What flashlight?!?
It’s a dog eat dog world.
…Or maybe it’s the other way around!
July 26th, 2024 at 7:41:41 AM
permalink
Quote: PowerSupplyGuy- There's a room with 3 lights inside. Outside the room there are 3 switches. One switch for each light. If you can only walk in to room once, how do know which switch is for which light?
- There's a boat in a lake with a bowling ball on it. The ball rolls off the boat into the lake. What happens to the level of the lake? Does it go up,down or stay the same?
-psg
link to original post
Turn on two switches, wait a few minutes, then turn off ORANGE ATTACK
Er...you can't - at least, not that everybody has switched to LED bulbs, which don't get hot when you turn them on.
The level drops down. This is because, while the ball is in the boat, the boat/ball combination is less dense than water, so the displacement = the volume of water with the same mass as the boat and ball combined. When the ball is released, the displacement is reduced by the volume of water with the same mass as the ball, but increased by the volume of the ball itself - but as the ball is more dense, the volume of water is greater, so the displacement decreases.
July 26th, 2024 at 8:01:37 AM
permalink
Method 1: Before walking into the room see if you can find a way to keep the door ajar. Then walk into the room and leave the door open. Return to the switches and see which lights go off and on as you turn switches off and on.
Method 2: This method is used for some coin tricks and relies on the bulbs getting hot when turned on. I suspect this is the mathematical answer.
(a) Turn one of the switches and leave it on a while. The plan is the bulb gets hot. Then, sometime later, turn that off and turn a different one on. Thus you will know (i) which one was turned on, (ii) which one is turned on, and (iii) which one was never turned on. Enter the room, the one that is off but warm is (i) , the one on is (ii) and the cold one is (iii).
Method 3: naughty, so not recommended. Turn one of the bulbs on and also find a bit of wire. Enter the room, this will determine the one that's on. Put a short in one of the others. Go back outside and when the fuse goes bang you know which was the one you put the short in!
Method 2: This method is used for some coin tricks and relies on the bulbs getting hot when turned on. I suspect this is the mathematical answer.
(a) Turn one of the switches and leave it on a while. The plan is the bulb gets hot. Then, sometime later, turn that off and turn a different one on. Thus you will know (i) which one was turned on, (ii) which one is turned on, and (iii) which one was never turned on. Enter the room, the one that is off but warm is (i) , the one on is (ii) and the cold one is (iii).
Method 3: naughty, so not recommended. Turn one of the bulbs on and also find a bit of wire. Enter the room, this will determine the one that's on. Put a short in one of the others. Go back outside and when the fuse goes bang you know which was the one you put the short in!
July 26th, 2024 at 9:58:49 AM
permalink
Turn on two switches for about a minute. Then turn one off and immediately go into the other room. In the other room, the bulb that is warm but off will be the one you turned off. The other two will be obvious.
Down. Because the density of the bowling ball is greater than water. It displaced more water pushing the boat down, due to its weight, than by being in the water, due to its volume.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
July 26th, 2024 at 11:23:15 AM
permalink
In the northern hemisphere, say around 40DEGN, which day of the year does the sun set the earliest? Is it:
Dec 7th
Dec 14th
Dec 21st
Why?
-psg
Dec 7th
Dec 14th
Dec 21st
Why?
-psg
July 26th, 2024 at 1:48:07 PM
permalink
There's a nice description of Solar Noon which explains that only four times a year does the sun actually reach its highest point at noon (or the equivalent if you're not on the meridian of the time zone). This explains why the latest sunrise isn't at the solstice.... ( https://www.timeanddate.com/astronomy/equation-of-time.html )
....the latest sunrise comes after the winter solstice, while the earliest sunset comes before it. So December 12th has the earliest sunset.
