Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
2. Select two opposite holes. Flip any down switches up. If the tomb doesn't open, you will know there are three up and one down.
3. Select two opposite holes. If one switch is down, flip it up and you're done. If both are up, switch one down. The switches will now be two up and two down, with the up and down switches in adjacent positions.
4. Select two opposite holes. They will be set the same way. Flip both the opposite way you found them and you will be done.
Quote: WizardCharlie, that is a very impressive graphic you created! I hope you will forgive me if I don't follow down every possible situation and just post my solution below.
1. Select two adjacent holes. Flip any down switches up. If the tomb doesn't open, you will know there are one or two switches in the down position.
2. Select two opposite holes. Flip any down switches up. If the tomb doesn't open, you will know there are three up and one down.
3. Select two opposite holes. If one switch is down, flip it up and you're done. If both are up, switch one down. The switches will now be two up and two down, with the up and down switches in adjacent positions.
4. Select two opposite holes. They will be set the same way. Flip both the opposite way you found them and you will be done.
link to original post
I may be lost but donít see how your step 4 works.
By step three you have set it up so that the switches are
DDUU
So when you stick your hand in opposite holes the switches will definitely not be the same. It will be one D and one U.
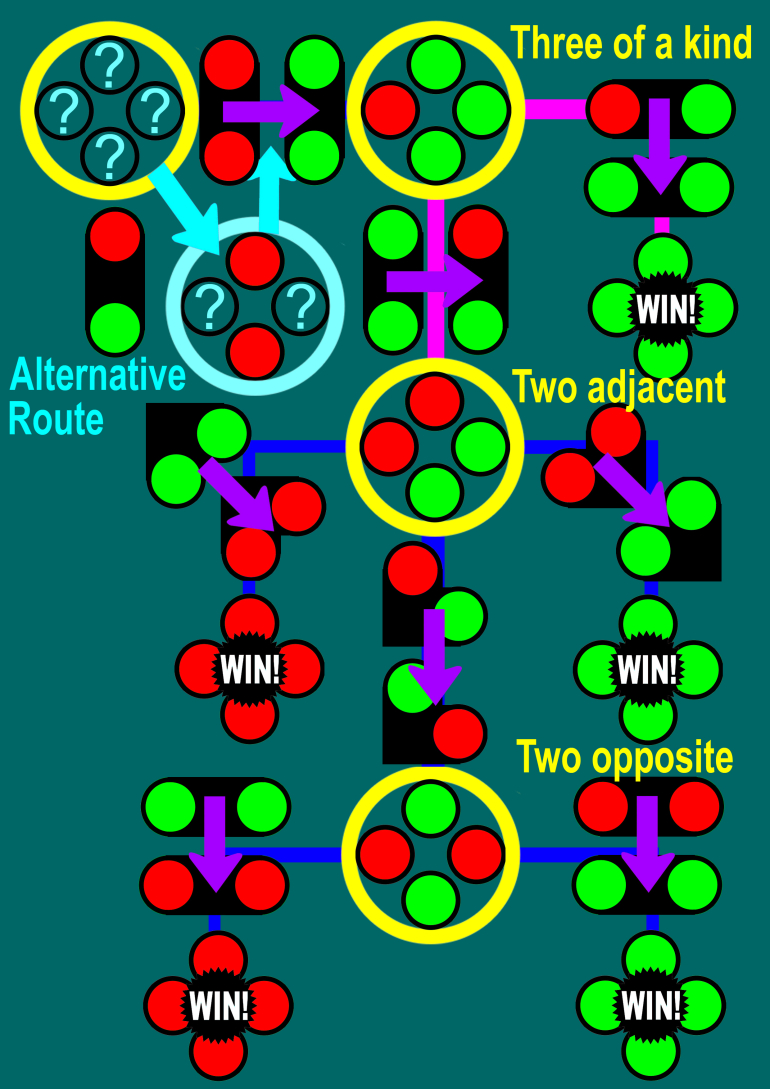 (The "alternative route" means for the second step, if you find a red-green or green-green, then set them to red-red for a win; otherwise you find red-red and can set them to green-green to ensure the other two are red-green.)
(The "alternative route" means for the second step, if you find a red-green or green-green, then set them to red-red for a win; otherwise you find red-red and can set them to green-green to ensure the other two are red-green.)Quote: unJonI may be lost but donít see how your step 4 works.
link to original post
You're right. I'm just spent an hour on a revised solution and see that it fails.
Quote: WizardQuote: Gialmere
Above are six pieces of rope. Imagine that you grasp the two ends of the rope and pull until the rope is straight.
Which of the six ropes will end up with a knot in them, and which ones just form loops that can be pulled out?
link to original post
A -- No loop
B -- No loop
C -- Loops
D -- Loop (figure 8 knot)
E -- No loop
F -- No loop
I must admit I got a piece of rope, mimicked these diagrams and pulled on the ends. It's possible I didn't construct some correctly.
I'd be interested to know the method to solve such puzzles mentally. I have a feeling it's some kind of odd/even thing to do with the rope going over/under itself.
link to original post
Hmm, I'm not sure what your answer is saying but...
Apologies for the delay. I'm having terrible computer issues and can only use my phone these days.
-----------------------------------------

Here is my revised solution to the four switch puzzle.
Key:
U = Switch in up position
D = Switch in down position.
Since this one is rather stale, I'm not putting it in spoiler tags.
1. For turn 1, choose opposite switches. If the same, flip both switches. If opposite, flip the D switch.
2. For turn 2, choose opposite switches.
3. If the turn 1 switches were originally in the same position, and the turn 2 switches are in the same position, then flip either switch on turn 2. This will result in either the puzzle being solved or switches in an UUDD configuration.
4. If the turn 1 switches were originally both up, and the turn 2 switches are in opposite positions, then flip the up switch. This will result in the puzzle being solved in a DDDD configuration.
5. If the turn 1 switches were originally both down, and the turn 2 switches are in opposite positions, then flip the down switch. This will result in the puzzle being solved in the UUUU configuration.
6. If the turn 1 switches were opposite, and the turn 2 switches are in the same position, then flip either switch. This will either result in a solved puzzle or an UUDD configuration.
7. If the turn 1 switches were opposite, and the turn 2 switches are in opposite positions, then flip the D switch. This will either result in a solved puzzle in the UUUU configuration.
8. For turn 3, if the puzzle isn't solved yet, it must be in a UUDD configuration. Pick adjacent switches and flip both. This will result in the puzzle being solved or a UDUD configuration.
9. For turn 4, pick opposite switches and flip both. This will solve the puzzle.
0) This is where you finid opposites so U?D? is turned to U?U? (all you now know at this stage is that ?? cannot be UU).
6) You're starting with U?U? and picking opposites
(a) obviously if you see any D, then you're looking at ?? and can win by turning them both to UU.
(b) however if you see UU then you must have picked the same two again. Even if you turn them to UD you're left with U?D?; you have no further information. So my proposed solution is to turn them to D?D?. You know ?? is not UU and now you know ?? is not DD; hence you know ?? = UD so must have UDDD. (On the next move you can turn UDDD into UUDD by flipping opposite DD to UD.)
8) I agree on "Turn 3" if you're in a UUDD configuration you can force a win in two moves by picking adjacent switches. If you see UU turn them to DD for DDDD; if you see DD turn them to UU for UUUU; if you see UD (or DU) swap them around to get UDUD.
Quote: charliepatrickI'm not sure about 0) then 6) (this is where I couldn't do it in four moves).
0) This is where you finid opposites so U?D? is turned to U?U? (all you now know at this stage is that ?? cannot be UU).
6) You're starting with U?U? and picking opposites
(a) obviously if you see any D, then you're looking at ?? and can win by turning them both to UU.
(b) however if you see UU then you must have picked the same two again. Even if you turn them to UD you're left with U?D?; you have no further information. So my proposed solution is to turn them to D?D?. You know ?? is not UU and now you know ?? is not DD; hence you know ?? = UD so must have UDDD. (On the next move you can turn UDDD into UUDD by flipping opposite DD to UD.)
8) I agree on "Turn 3" if you're in a UUDD configuration you can force a win in two moves by picking adjacent switches. If you see UU turn them to DD for DDDD; if you see DD turn them to UU for UUUU; if you see UD (or DU) swap them around to get UDUD.
link to original post
Thank you for your comments. I agree I screwed up, again.
You can only have a handful of positions as many are rotations or mirror of the others.
(a) 4-0 : UUUU or DDDD (these are winners)
(b) 3-1 : UDDD or DUUU
(c) 2-2 adjacent : UUDD (which is the same as DDUU, DUUD, UDDU)
(d) 2-2 opposite : UDUD (which is the same as DUDU)
The starting position cannot be (a)
Letís assume your first move is to pick opposite
1A U?U? : you change this to D?D?
(i) uuud/uduu goes to dudd/dddu = (b)
(ii) udud goes to dddd = win
(iii) uudd : this cannot create the case where you see U?U?.
In this case you know you have (b) (or have won)
1B U?D? : you change this to D?D?
(i) uddd goes to dddd = win
(ii) uudu goes to dudu = (d)
(iii) uddu/uudd goes to dddu/dudd = (b)
The problem is that after 1B, you donít know whether you are (b) or (d), see (e) below.
(b) (assuming you are starting with DDDU, pick opposite)
(i) D?U? : since you have found the only U, change it to D and win
(ii) D?D? : if you change it to d?u? then you must have duud or dduu = (c)
(c) (starting with DDUU or equivalent, pick adjacent)
(i) DD?? : since the other two are Us, flip DD to UU to win.
(ii) UU?? : since the other two are Ds, flip UU to DD to win.
(iii) DU : since you have DU from DUud, swap them to create UDUD =(d)
(d) (starting with DUDU or equivalent, pick opposite)
(i) D?D? : since the other two are Us, flip the Ds to Us to win
(ii) U?U? : since the other two are Ds, flip the Us to Ds to win
Now 1A U?U? can go via (b) (c) and (d) to win in four moves or fewer
The problem with 1B is you donít know whether you have (d) or (b).
(I suspect this is where we still need to find a four move solution, but I canít see it!)
(e) (starting with 1B U?D? and converting it to D?D, not pick opposite)
One way is to pick opposite
(x) U?U? : since you know there are two Ds, you change the two Us to Ds (D?D?)
(i) udud goes to dddd = win
(y) D?D? : you donít know the other two, this is equivalent to 1A, so change to U?U?
(i) dudu goes to uuuu = win
(ii) dudd goes to uuud = (b)
(z) U?D? : this can only happen if you had uddd
(i) uddd goes to dddd = win
So 1B can either win or go to (b) (which via (c) and (d) can be solved, but it takes five turns).
Summary : 1A goes to (b) (c) and (d) (or wins earlier) and 1B goes to (e) before (b) (c) and (d) (or wins earlier).

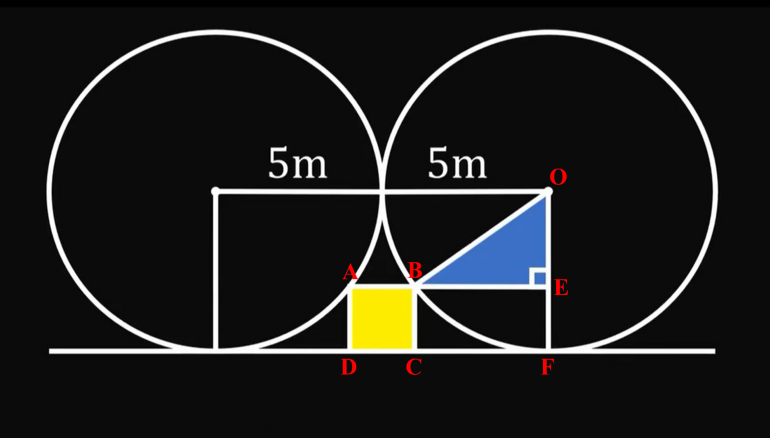
Using the diagram, let P be the point where the line segment connecting the two circles' centers intersects the circles.
Let x be the length of the side of the square.
OP = OB = OF = 5; EF = x, so OE = 5 - x
Note that BE = AB / 2 = 5; since AB / 2 = x / 2, BE = 5 - x / 2
Pythagorean Theorem on OEB: (5 - x)^2 + (5 - x/2)^2 = 25
25 - 10 x + x^2 + 25 - x^2 + x^2 / 4 = 25
5/4 x^2 - 15 x + 50 = 25
x^2 - 12 x + 20 = 0
x = 2 or 10, but x < 5 as otherwise BC > OF.
The area of the square = x^2 = 4.
Check: BE = 5 - 1 = 4 and OE = 5 - 2 = 3; OEB is a 3-4-5 right triangle.
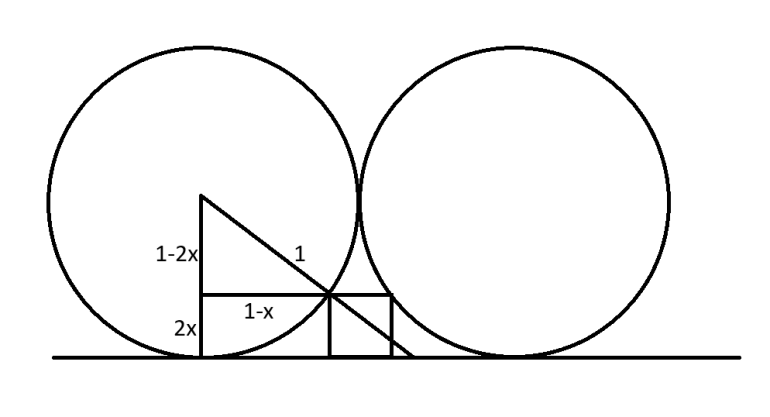
Here is my solution if the radius of the circles were 1:
(1-2x)^2 + (1-x)^2 = 1
5x^5 - 6x + 1 = 0
x = (3+/-2)/5
The only one that makes sense is x=1/5.
So, if the radius of the circles were 1, the area of the square would be (2/5)^2 = 4/25.
Then multiply by 5^2 = 25 if the circles have radius 5: (4/25)*25 = 4
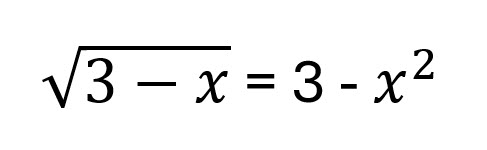
I hate to ask a question I can't solve, but this is one of those times. I wrote it in my notes for future "ask the wizard" questions. I put down the answer, but forgot how I solved it. I have a feeling there is some trig substation involved. This one beer worth for an answer in pure form with solution.
Quote: Wizard
I hate to ask a question I can't solve, but this is one of those times. I wrote it in my notes for future "ask the wizard" questions. I put down the answer, but forgot how I solved it. I have a feeling there is some trig substation involved. This one beer worth for an answer in pure form with solution.
link to original post
I can solve it. But only by that method I used in high school algebra class, that would earn me a disdainful frown from the teacher and to be called lazy and a waste of great potential.
(He was only half right. I have worked very hard at being a waste of great potential.)
Quote: AutomaticMonkeyQuote: Wizard
I hate to ask a question I can't solve, but this is one of those times. I wrote it in my notes for future "ask the wizard" questions. I put down the answer, but forgot how I solved it. I have a feeling there is some trig substation involved. This one beer worth for an answer in pure form with solution.
link to original post
I can solve it. But only by that method I used in high school algebra class, that would earn me a disdainful frown from the teacher and to be called lazy and a waste of great potential.
(He was only half right. I have worked very hard at being a waste of great potential.)
link to original post
Square both sides: 3 - x = 9 - 6 x^2 + x^4, limited to x <= 3 (as otherwise the square root is imaginary)
x^4 - 6 x^2 + x + 6 = 0
(x + 1) (x - 2) (x^2 + x - 3) = 0
This has solutions -1, 2, -1/2 - sqrt(13)/2, and -1/2 + sqrt(13)/2, but I think only x = -1 is valid for the original equation

x^4 - 6 x^2 + x + 6 = (x + 1) (x - 2) (x^2 + x - 3)?
Quote: WizardWell done, Don and CD. However how did you easily factor:
x^4 - 6 x^2 + x + 6 = (x + 1) (x - 2) (x^2 + x - 3)?
link to original post
I should have mentioned that if x^4 - 6 x^2 + x + 6 has rational solutions, they must be either -6, -3, -2, -1, 1, 2, 3, or 6.
I used "synthetic division" to find that x = -1 is a solution. So, x + 1 is a factor of x^4 - 6 x^2 + x + 6.
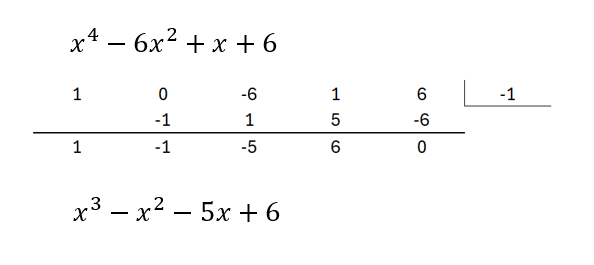
I forgot about the rational root formula. I probably haven't used it since high school.
A well-earned beer to both of you!

Quote: WizardThank you to both of you!
I forgot about the rational root formula. I probably haven't used it since high school.
A well-earned beer to both of you!
link to original post
Tomorrow is my 11th birthday in sobrietyÖ I might have to rethink that now - Oktoberfest, here I come! (I know, itís already over!)
Quote: WizardYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups?
link to original post
Edit to addÖ I misread the OP. My optic nerves mustíve been on a break! My calculations consider distinct cups AND ballsÖ
Four identical cups, six unique items: how many arrangements
For arguments sake put (1) into a cup, and see how many are in the main cup.
1 (i) 6-0 Only one way of having six in the main cup
5 (ii) 5-1 Five ways to pick the one that isn't in main cup
10 (iii) 4 - 2 (10 ways to pick the two that will not be in the main cup)
10 (iv) 4 - 1 - 1 (10 ways to pick the two that will not be in the main cup)
10 (v) 3 - 3 (10 ways to pick the two to accompany the main cup)
30 (vi) 3 - 2 - 1 (10 ways to pick the two for the main cup, then 3 ways to pick the solo)
10 (vii) 3 - 1 - 1 - 1 (10 ways to pick the two for the main cup)
5 (vii) 2 - 4 (5 ways to pick the ball to accompany the main cup)
20 (viii) 2 - 3 - 1 (5 ways to pick the ball to accompany the main cup, 4 ways to pick the odd ball)
15 (ix) 2 - 2 - 2 (5 ways to pick the ball to accompany the main cup, 3 ways to organise the rest into pairs)
30 (x) 2 - 2 - 1 - 1 (5 ways to pick the ball to accompany the main cup, 6 ways to pick the pair)
1 (xi) 1 -5 (Only one way of having the others in another cup)
5 (xii) 1 - 4 -1 (5 ways to pick the solo, leaving the other four to go into a cup)
10 (xiii) 1 - 3 - 2 (10 ways to pick the pair, leaving the triple to go into a cup)
10 (xiv) 1 - 3 - 1 - 1 (10 ways to pick the two solos, similar to picking the pair)
15 (xv) 1 - 2 - 2 - 1 (5 ways to pick the solo, 3 ways to organise the rest into pairs)
0 (xvi) 0 - ? (by definition the main cup must have the (1) ball, so impossible.
187
Quote:5 (ii) 5-1 Five ways to pick the one that isn't in main cup
Aren't there six ways to pick the singleton ball?
I've got another approach that I'll be looking at, so hopefully can post that later.
Then for each of these possibilities look at how the other three might fit in.
(a) All three balls can go into one cup (1 way) (ABC) (empty) (empty) (empty)
(b) Two balls in one cup, and one in another (3 ways) (AB) (C) (empty) (empty) (or AC B, BC A)
(c) One ball in each of three cups (1 way) (A) (B) (C) (empty)
Now for each of these options see how the other three balls might fit in.
(i) All three balls into one cup (1 way) DEF
(ii) Two balls in one cup, one in another (3 ways) DE F
(iii) One ball in each of three cups (1 way) D E F
(a)(i) Same cup (ABC+DEF) or different cup (ABC,DEF) (2 ways) total = 2 ways
(a)(ii) ABC+DE,F / ABC+F,DE / ABC,DE,F (3 ways) total = 9 ways
(a)(iii) ABC+D,E,F / ABC+E,D,F / ABC+F,D,E / ABC,D,E,F (4 ways) total = 4 ways
(b)(i) AB+DEF,C / AB,C+DEF / AB,C,DEF (3 ways) total = 9 ways
(b)(ii) AB+DE,C+F / AB+DE,C,F / AB+F,C+DE / AB+F,C,DE / AB,C+DE,F / AB,C+F,DE / AB,C,DE,F (7 ways) total = 63 ways
(b)(iii) AB+D,C+E,F / AB+D,C+F,E / AB+D,C,E,F / AB+E,C+D,F / AB+E,C+F,D / AB+E,C,D,F / AB+F,C+D,E / AB+F,C+E,D / AB+F,C,D,E / AB,C+D,E,F / AB,C+E,D,F / AB,C+F,D,E (12 ways) total = 36 ways
(c)(i) A+DEF,B,C / A,B+DEF,C / A,B,C+DEF / A,B,C,DEF (4 ways) total = 4 ways
(c)(ii) A+DE,B+F,C / A+DE,B,C+F / A+DE,B,C,F / A+F,B+DE,C / A+F,B,C+DE / A+F,B,C,DE / A,B+DE,C+F / A,B+DE,C,F / A,B+F,C+DE / A,B+F,C,DE / A,B,C+DE,F / A,B,C+F,DE (12 ways) total = 36 ways
(c)(iii) Ax,Bx,Cx (6 ways) / Ax,Bx,C,x (6 ways) / Ax,B,Cx,x (6 ways) / A,Bx,Cx,x (6 ways) total = 24 ways
2+9+4+9+63+36+4+36+24 = 187
Quote: WizardYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups?
link to original post
The problem is not worded clearly. What is a "distinguishable way," especially if the cups are identical?
Since the cups are identical, does any "order" in which they are arranged important?
Also, does there have to be a ball in every cup?
Assuming (a) order is unimportant - e.g. placing "red, blue, green, and yellow balls" in cups is a single "distinguishable way" regardless of which balls go into which cups, and (b) you can leave some, or even all, of the cups empty:
There are C(6,1) = 6 ways to use 1 ball
There are C(6,2) = 15 ways to use 2 balls
There are C(6,3) = 20 ways to use 3 balls
There are C(6,4) = 15 ways to use 4 balls
The total is 57, or 56 if you have to put at least one ball underneath a cup
^ I have assumed you have to place each of the six balls into a cup, but that cups can land up unused and empty. The reply above addresses a different puzzle where a cup can contain a maximum of one ball and asks how many ways the cups could land up from 6 different balls. Perhaps this is why I have a different answer.
Quote: ThatDonGuySince the cups are identical, does any "order" in which they are arranged important?
No. The order does not matter.
Quote:Also, does there have to be a ball in every cup?
No.
Also, every ball must be used.
Quote: charliepatrick^^ If the balls were A B C D E and F, then I have assumed that AB CD E F is the same as F AB E CD
This is correct.
Quote:Similarly ABCDE F is different from ABCDF E or A BCDEF.
That is correct.
Quote:I have assumed you have to place each of the six balls into a cup, but that cups can land up unused and empty.
That is true.
Quote:The reply above addresses a different puzzle where a cup can contain a maximum of one ball and asks how many ways the cups could land up from 6 different balls. Perhaps this is why I have a different answer.
Each cup can contain any number of balls, from 0 to 6.
Quote: WizardYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups?
link to original post
I got complaints this puzzle wasn't worded clearly. How would you have worded it?
You have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups, such that each ball is under a cup?Quote: WizardQuote: WizardYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups?
link to original post
I got complaints this puzzle wasn't worded clearly. How would you have worded it?
link to original post
You may put more than one ball under a particular cup, and one or cups may be empty.
Two ways are "distinguishable" if they cannot be made the same merely by moving the cups around.
Quote: WizardNathan buys 100 pounds of beans. The beans consist of 99% water by weight. She leaves them in the sun to let them dry out. The next day, she finds they consist of 98% water. What is their new weight?
link to original post
Originally, the beans consist of 99 pounds of water and 1 pound of "bean."
Assuming the amount of actual bean is unaffected by the drying, there is still 1 pound of bean, so there must be 49 pounds of water.
The new weight is 50 pounds.
Quote: ThatDonGuyYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups, such that each ball is under a cup?
You may put more than one ball under a particular cup, and one or cups may be empty.
Thank you. That seems rather wordy. How about: "You have four identical cups and six distinct balls. How many ways can all six balls be placed in the cups?
Note I removed the word "distinguishable" as that seemed to cause more confusion than clarity.
Quote:
Originally, the beans consist of 99 pounds of water and 1 pound of "bean."
Assuming the amount of actual bean is unaffected by the drying, there is still 1 pound of bean, so there must be 49 pounds of water.
The new weight is 50 pounds.
link to original post
Correct!
Quote: WizardNathan buys 100 pounds of beans. The beans consist of 99% water by weight. She leaves them in the sun to let them dry out. The next day, she finds they consist of 98% water. What is their new weight?
link to original post
Is the answer 198 pounds? 🤔💡
Quote: NathanIs the answer 198 pounds? 🤔💡
link to original post
Where did the additional 98 pounds come from?
Quote: WizardQuote: NathanIs the answer 198 pounds? 🤔💡
link to original post
Where did the additional 98 pounds come from?
link to original post
I doubled the weight of the beans and erased 2 pounds, because of the 98/99 percent water thing. 💡

Two circles of radius 1 overlap such that the edge of one touches the center of the other. What is the area of the overlapping region?
Let P and Q be the centers of the two circles, and A and B the points where they intersect.
Let X be the point where PQ intersects AB.
PA and PB are both radii of circle P, so they have length 1.
PQ is also a radius, so its length is 1; AB divides PQ into two equal pieces, so PX = 1/2.
Pythagorean Theorem: AX = BX = sqrt(3) / 2, so AB = sqrt(3).
The area of the overlap = 2 x the area of the overlap to the right of AB
= 2 x (the area of the wedge APB of circle P - the area of triangle APB)
PXA is a right triangle with right angle at X, PX = 1/2, and PA = 1, so angle APX = cos^(-1) 1/2 = 60 degrees.
BPX = APX, so angle APB = 120 degrees, and wedge APB is 1/3 of the circle, so its area = 1/3 (PI x 1^2) = PI / 3.
The area of triangle APB = 1/2 x sqrt(3) x 1/2 = sqrt(3) / 4
Therefore, the area of the overlap to the right of AB = PI / 3 - sqrt(3) / 4.
The total overlap = 2 (PI / 6 - sqrt(3) / 4) = 2 PI / 3 - sqrt(3) / 2.
Quote: WizardNathan buys 100 pounds of beans. The beans consist of 99% water by weight. She leaves them in the sun to let them dry out. The next day, she finds they consist of 98% water. What is their new weight?
link to original post
let n= the non-hydrous weight of the bean
let w= the initial weight of water in the beans
let x = the weight of water in the beans the next day
Initially
w=99n
100 pounds = n+w; 99 pounds of water, 1 pound of solid bean
After one day, the non-hydrous weight of the bean is 2% of the total weight
x = 49n = 49 pounds
So the new weight is x+n = 50 pounds.
Quote: gordonm888Quote: WizardNathan buys 100 pounds of beans. The beans consist of 99% water by weight. She leaves them in the sun to let them dry out. The next day, she finds they consist of 98% water. What is their new weight?
link to original post
let n= the non-hydrous weight of the bean
let w= the initial weight of water in the beans
let x = the weight of water in the beans the next day
Initially
w=99n
100 pounds = n+w; 99 pounds of water, 1 pound of solid bean
After one day, the non-hydrous weight of the bean is 2% of the total weight
x = 49n = 49 pounds
So the new weight is x+n = 50 pounds.
link to original post
Uhhh.. I don't think I agree.
edit: nevermind. I just saw my logic error.
Quote: gordonm888
let n= the non-hydrous weight of the bean
let w= the initial weight of water in the beans
let x = the weight of water in the beans the next day
Initially
w=99n
100 pounds = n+w; 99 pounds of water, 1 pound of solid bean
After one day, the non-hydrous weight of the bean is 2% of the total weight
x = 49n = 49 pounds
So the new weight is x+n = 50 pounds.
link to original post
Correct!
Quote: WizardHow about: "You have four identical cups and six distinct balls. How many ways can all six balls be placed in the cups?
link to original post
I think this is pretty good, but should still add "The order of the cups does not matter". I don't think "identical" is sufficient for the cups.
There are five bowls, numbered 1, 2, 3, 4, and 5.
Each bowl begins with a number of balls equal to the number on the bowl - for example, bowl 4 begins with 4 balls.
You have a 10-sided die; the sides are numbered 12, 13, 14, 15, 23, 24, 25, 34, 35, and 45.
Roll the die. If the bowls identified by the two digits on the die have the same number of balls, then do nothing; otherwise, remove balls from whichever of the two bowls has more balls until they have the same number.
(Clarification: when you remove balls from a bowl, you do not put them into any of the other bowls.)
For example, if your first roll is 25, since bowl 2 has 2 balls and bowl 5 has 5, remove 3 balls from bowl 5, so that bowls 2 and 5 now each have 2 balls.
What is the expected number of die rolls needed before all five bowls have the same number of balls?
Quote: ThatDonGuyHere's a new one you can think about later this week while digesting your Thanksgiving dinner:
There are five bowls, numbered 1, 2, 3, 4, and 5.
Each bowl begins with a number of balls equal to the number on the bowl - for example, bowl 4 begins with 4 balls.
You have a 10-sided die; the sides are numbered 12, 13, 14, 15, 23, 24, 25, 34, 35, and 45.
Roll the die. If the bowls identified by the two digits on the die have the same number of balls, then do nothing; otherwise, remove balls from whichever of the two bowls has more balls until they have the same number.
(Clarification: when you remove balls from a bowl, you do not put them into any of the other bowls.)
For example, if your first roll is 25, since bowl 2 has 2 balls and bowl 5 has 5, remove 3 balls from bowl 5, so that bowls 2 and 5 now each have 2 balls.
What is the expected number of die rolls needed before all five bowls have the same number of balls?
link to original post
Why think, when you can use a Monkey Carlo simulation?
Interesting result. I don't think I could do the math to get it.
'program bowlbuster
Dim bowl(5) As _Unsigned _Byte
Dim sumofrolls As Long
Dim l As Long
Dim equality As _Unsigned _Bit
Dim rolls As _Unsigned _Byte
Randomize Timer
sumofrolls = 0
For l = 1 To 10000000
equality = 0
rolls = 0
bowl(1) = 1
bowl(2) = 2
bowl(3) = 3
bowl(4) = 4
bowl(5) = 5
Do Until equality = 1
dieroll = Int(Rnd * 10) 'roll the bones!
rolls = rolls + 1
Select Case dieroll
Case Is = 0 '12
If bowl(1) > bowl(2) Then
bowl(1) = bowl(2)
Else
bowl(2) = bowl(1)
End If
Case Is = 1 '13
If bowl(1) > bowl(3) Then
bowl(1) = bowl(3)
Else
bowl(3) = bowl(1)
End If
Case Is = 2 '14
If bowl(1) > bowl(4) Then
bowl(1) = bowl(4)
Else
bowl(4) = bowl(1)
End If
Case Is = 3 '15
If bowl(1) > bowl(5) Then
bowl(1) = bowl(5)
Else
bowl(5) = bowl(1)
End If
Case Is = 4 '23
If bowl(2) > bowl(3) Then
bowl(2) = bowl(3)
Else
bowl(3) = bowl(2)
End If
Case Is = 5 '24
If bowl(2) > bowl(4) Then
bowl(2) = bowl(4)
Else
bowl(4) = bowl(2)
End If
Case Is = 6 '25
If bowl(2) > bowl(5) Then
bowl(2) = bowl(5)
Else
bowl(5) = bowl(2)
End If
Case Is = 7 '34
If bowl(3) > bowl(4) Then
bowl(3) = bowl(4)
Else
bowl(4) = bowl(3)
End If
Case Is = 8 '35
If bowl(3) > bowl(5) Then
bowl(3) = bowl(5)
Else
bowl(5) = bowl(3)
End If
Case Is = 9 '45
If bowl(4) > bowl(5) Then
bowl(4) = bowl(5)
Else
bowl(5) = bowl(4)
End If
End Select
'test for equality
If bowl(1) = bowl(2) And bowl(2) = bowl(3) And bowl(3) = bowl(4) And bowl(4) = bowl(5) Then
sumofrolls = sumofrolls + rolls
equality = 1
If Int(l / 1000) = l / 1000 Then
Cls
Print sumofrolls / l, sumofrolls, l
End If
End If
Loop
Next l
End
Therefore we only need to track how many bowls now contain one ball and how many rolls are needed (on average) to get another bowl set to one ball. At various times in the game there will be N bowls with 1, and 5-N bowls with >1.
Stage 1 : 2.5
Initially only bowl 1 has 1, so picking 12, 13, 14 or 15 will set another bowl to 1, while the other six possibilities (23 24 25 34 35 45) will have no effect. This is 4 out of 10; so takes on average 10 / 4 rolls to occur, i.e. 2.5.
Stage 2 : 1.666..
Now there are two bowls, say {1,2}, with 1 ball, and three others. Thus 13 14 15 23 24 25 are good and 12 34 35 45 no good. This is 6 out of 10, so takes on average 10/6 = 1.666...
Stage 3 : 1.666..
Similarly {1,2,3} giving 14 15 24 25 34 35 and 1.666...
Stage 4 : 2.5
Now {1,2,3,4} with only 5 not having 1. So similar logic to Stage 1 = 10/4 = 2.5
Thus the answer is 8 1/3.
btw I have confirmed this via simulation.
Rolls: 4 games: 576163
Rolls: 5 games: 1151611
Rolls: 6 games: 1452112
Rolls: 7 games: 1472264
Rolls: 8 games: 1320544
Rolls: 9 games: 1089969
Rolls: 10 games: 849252
Rolls: 11 games: 632688
Rolls: 12 games: 458568
Rolls: 13 games: 323296
Rolls: 14 games: 224001
Rolls: 15 games: 151968
Rolls: 16 games: 102432
Rolls: 17 games: 67831
Rolls: 18 games: 45093
Rolls: 19 games: 29298
Rolls: 20 games: 19023
Rolls: 21 games: 12121
Rolls: 22 games: 7698
Rolls: 23 games: 5175
Rolls: 24 games: 3284
Rolls: 25 games: 2052
Rolls: 26 games: 1307
Rolls: 27 games: 829
Rolls: 28 games: 511
Rolls: 29 games: 346
Rolls: 30 games: 224
Rolls: 31 games: 122
Rolls: 32 games: 87
Rolls: 33 games: 44
Rolls: 34 games: 39
Rolls: 35 games: 20
Rolls: 36 games: 15
Rolls: 37 games: 5
Rolls: 38 games: 3
Rolls: 40 games: 2
Rolls: 41 games: 3
Overall Result: Avg: 8.3340972
xi=1; pick1[xi]=1; pick2[xi]=2;
xi++; pick1[xi]=1; pick2[xi]=3;
xi++; pick1[xi]=1; pick2[xi]=4;
xi++; pick1[xi]=1; pick2[xi]=5;
xi++; pick1[xi]=2; pick2[xi]=3;
xi++; pick1[xi]=2; pick2[xi]=4;
xi++; pick1[xi]=2; pick2[xi]=5;
xi++; pick1[xi]=3; pick2[xi]=4;
xi++; pick1[xi]=3; pick2[xi]=5;
xi++; pick1[xi]=4; pick2[xi]=5;
function playgame()
{
for (xi=1; xi<=5; xi++) {whatsin[xi]=xi;};
for (roll=1; roll<1000000; roll++)
{
thispick = Math.floor(10*(getarand(seed)+poweroftwo)/(poweroftwo*2))+1;
pot1=pick1[thispick];
pot2=pick2[thispick];
mininpot=whatsin[pot1];
if (whatsin[pot2]<mininpot) {mininpot=whatsin[pot2];};
whatsin[pot1]=mininpot;
whatsin[pot2]=mininpot;
if (whatsin[1]+whatsin[2]+whatsin[3]+whatsin[4]+whatsin[5]==5)
{
gameresult[roll]++;
roll=9999999;
};
};
return (true);
};
theaverage=0;
totalrolls=0;
for (ii=0; ii<=999999; ii++)
{
if (gameresult[ii]>0)
{
totalrolls+=gameresult[ii]*ii;
countline = "Rolls: "+ii+" ";
countline+= "games: "+gameresult[ii]+" ";
countline+= "<BR>";
document.write(countline);
};
};
theaverage=totalrolls/noofshoes;
countline = "Overall Result:";
countline = countline + " Avg: " + theaverage;
countline = countline + "<BR>";
document.write(countline);
Quote: charliepatrickSince Bowl 1 contains 1 ball, for them all to be the same they must all eventually contain one ball. Thus any rolls including bowls which both have > 1 ball can be ignored; similarly any which include two bowls already set to 1 can be ignored.
Therefore we only need to track how many bowls now contain one ball and how many rolls are needed (on average) to get another bowl set to one ball. At various times in the game there will be N bowls with 1, and 5-N bowls with >1.
Stage 1 : 2.5
Initially only bowl 1 has 1, so picking 12, 13, 14 or 15 will set another bowl to 1, while the other six possibilities (23 24 25 34 35 45) will have no effect. This is 4 out of 10; so takes on average 10 / 4 rolls to occur, i.e. 2.5.
Stage 2 : 1.666..
Now there are two bowls, say {1,2}, with 1 ball, and three others. Thus 13 14 15 23 24 25 are good and 12 34 35 45 no good. This is 6 out of 10, so takes on average 10/6 = 1.666...
Stage 3 : 1.666..
Similarly {1,2,3} giving 14 15 24 25 34 35 and 1.666...
Stage 4 : 2.5
Now {1,2,3,4} with only 5 not having 1. So similar logic to Stage 1 = 10/4 = 2.5
Thus the answer is 8 1/3.
btw I have confirmed this via simulation.
Rolls: 4 games: 576163
Rolls: 5 games: 1151611
Rolls: 6 games: 1452112
Rolls: 7 games: 1472264
Rolls: 8 games: 1320544
Rolls: 9 games: 1089969
Rolls: 10 games: 849252
Rolls: 11 games: 632688
Rolls: 12 games: 458568
Rolls: 13 games: 323296
Rolls: 14 games: 224001
Rolls: 15 games: 151968
Rolls: 16 games: 102432
Rolls: 17 games: 67831
Rolls: 18 games: 45093
Rolls: 19 games: 29298
Rolls: 20 games: 19023
Rolls: 21 games: 12121
Rolls: 22 games: 7698
Rolls: 23 games: 5175
Rolls: 24 games: 3284
Rolls: 25 games: 2052
Rolls: 26 games: 1307
Rolls: 27 games: 829
Rolls: 28 games: 511
Rolls: 29 games: 346
Rolls: 30 games: 224
Rolls: 31 games: 122
Rolls: 32 games: 87
Rolls: 33 games: 44
Rolls: 34 games: 39
Rolls: 35 games: 20
Rolls: 36 games: 15
Rolls: 37 games: 5
Rolls: 38 games: 3
Rolls: 40 games: 2
Rolls: 41 games: 3
Overall Result: Avg: 8.3340972
link to original post
Correct - and just as good of an explanation as to why as I can give



