Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Assume the radius of the earth is 4000 miles
You start walking northeast from a point on the equator. How far do you travel until you reach the north pole?
Fair warning that I do not claim to know the answer, but think mine is close.
Assuming the radius of the earth is 4000, then this gives the straight line distance between the equator and pole as Pi/2*4000.
Hence the length walked is 2000*SQRT(2)*Pi.
I then did some googling and found out about loxodromes aka Rhumb lines.
http://www.clowder.net/hop/Riemann/Riemann.html
https://en.wikipedia.org/wiki/Rhumb_line
This gives the equation as sec(angle), which is our case confirms the SQRT(2) idea.
Quote: charliepatrickMy immediate reaction was using derivative ideas looking at a series of very small squares. You start in the South-West corner of one and travel North-East to the opposite corner. Assume the side of the square is dx, then you get dx nearer the North Pole but have to walk SQRT(2) dx. You repeat the process with a series of smaller and smaller squares (at the pole you go round and round but for a finite distance).
Assuming the radius of the earth is 4000, then this gives the straight line distance between the equator and pole as Pi/2*4000.
Hence the length walked is 2000*SQRT(2)*Pi.
I then did some googling and found out about loxodromes aka Rhumb lines.
http://www.clowder.net/hop/Riemann/Riemann.html
https://en.wikipedia.org/wiki/Rhumb_line
This gives the equation as sec(angle), which is our case confirms the SQRT(2) idea.
link to original post
I agree!
What is the appropriate formula to solve this using a loxodrome?
Quote: charliepatrick^ If you used a different angle than 45 degress, the square would be a rectangle. Thus the distance covered, compared to getting nearer the pole, would be secant of the angle. At the limit, the equator (angle-90 degrees to meridien) never reaches the pole.
link to original post
Question 2: That leads to the following follow-up question. How long would it take if you always walked ENE?
Let me try another one.
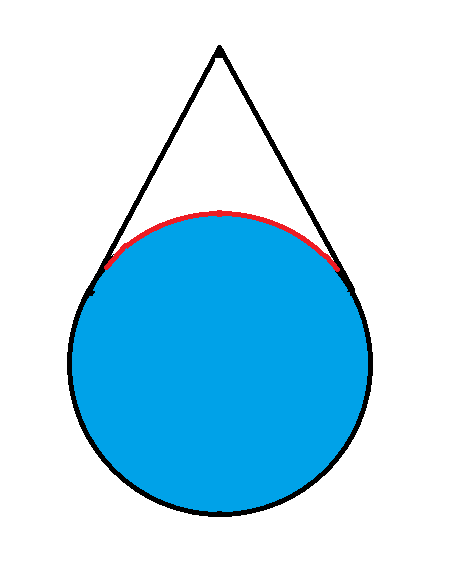
A point in Flatland outside of a circle, can see 1/3 of the circle. How far away is it?
For purposes of discussion, feel free to use this diagram...
Quote: Wizard
Let me try another one.
A point in Flatland outside of a circle, can see 1/3 of the circle. How far away is it?
For purposes of discussion, feel free to use this diagram...
link to original post
Wiz,
Proof:
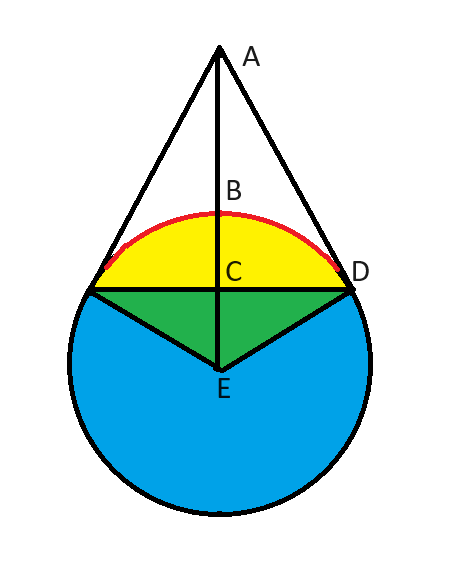
The sight line AD is tangent to the circle at point D, so the angle ADE is 90°.
ED is a radius so its length is r.
Since the point sees ⅓ of the circle, the red arc angle is ⅓*360° = 120°. Because of symmetry around the line AE, the angle AED is ½*120° = 60°. That means the angle EAD is 30°, so the three angles of the triangle AED sum to 180°.
Thus, AED is a 30°-60°-90° right triangle, so the ratio of the sides EA/ED is 2/1. Since the length of ED is r, the length of EA is 2*r.
Since EB has a length of r, the length of AB is also r.
Dog Hand
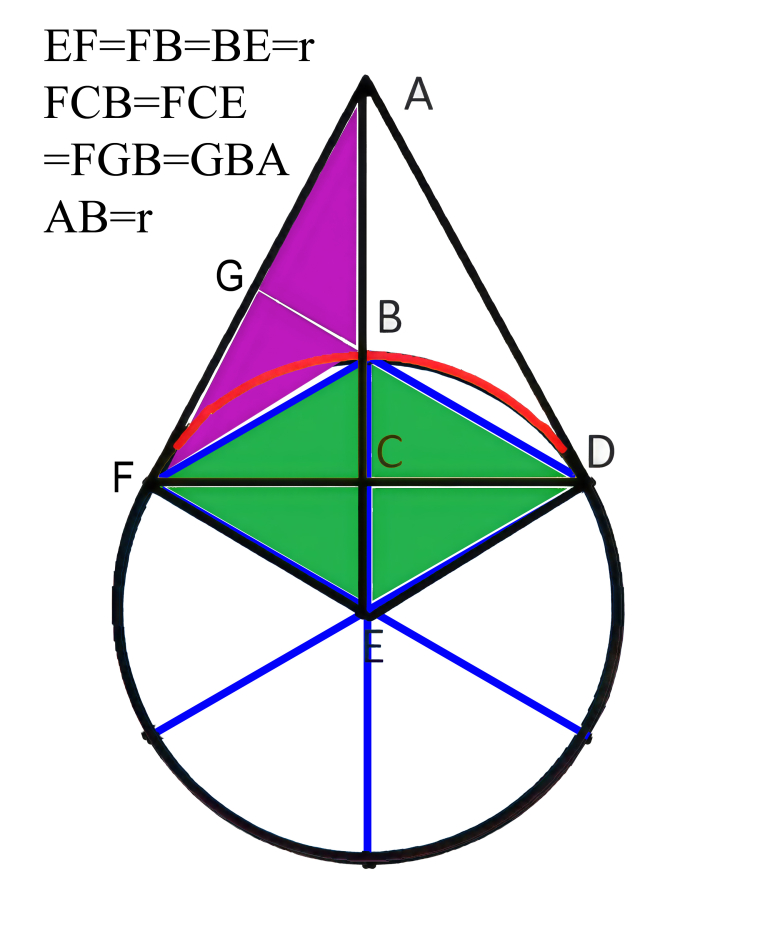
Note that an external tangent line to a circle is perpendicular to the radius of the circle at the point of tangency - in this case, AD is perpendicular to DE.
Since 1/3 of the circle can be seen, DAE is half of 1/3 of 360 degrees = 60 degrees
ADE is a right angle, so AED = 30 degrees
ACD is also a right angle, so ADC = 60 degrees, which means CDE = 30 degrees
Let r be the radius of the circle; BE = DE = r
AD / DE = sqrt(3), so AD = sqrt(3) r
AD / AE = sqrt(3) / 2, so AE = 3/2 r
The distance to the circle from A = AB = AE - BE = 3/2 r - r = 1/2 r = half of the radius of the circle
From ThatDonGuy Answer
...
AD / DE = sqrt(3), so AD = sqrt(3) r
AD / AE = sqrt(3) / 2, so AE = 3/2 r
***I think should be***
AD/AE = sqrt(3)r / AE = sqrt(3)/2
r/AE = 1/2
2r = AE
So
The distance to the circle from A = AB = AE - BE = 2r - r = r = radius of the circle
***
- How many marks can you put on a tic tac toe board without forming a line?
- How can you put the ten pennies shown above into the three glasses in such a way that each glass contains an odd number of pennies?
- How can you arrange ten marbles so that they form five lines for four marbles each?
- In front of you are 12 pearls, 11 being real and one fake. The real ones all weigh the same and the fake one differs in weight from the real ones (may weigh more or less). With a balance scale and three weighings how can you weed out the fake one and determine whether it is too heavy or too light?
- You are blindfolded and seated at a table. You are informed that the table contains 25 coins, 10 heads up 15 tails up. Your task is to create two piles that contail the same number of heads face up. How can you do it?

Draw a regular 5-pointed star; place a marble on each of the star's points, and a marble on each of the five points where two lines of the star intersect.
Form two piles, one with 10 and the other with 15.
Turn all of the coins in the pile with 10 over.
If there are H heads in the pile with 15, then there were H tails and 10-H heads in the pile with 10; when you turned them over, there are now H heads in that pile.
There's a problem with #2: what three glasses?
...and the answer is usually to put 2 pennies into glass A, 3 into glass B, 5 into glass C, then stick glass B into glass A so glass A now has a total of 5 pennies
Clarification needed on #1: are standard tic-tac-toe rules used, and what is meant by "a line"?
The max numbers of marks without making a line on a standard tic-tac -toe board is 6.
XX-
X-X
-XX
Quote: ThatDonGuyClarification needed on #1: are standard tic-tac-toe rules used, and what is meant by "a line"?
link to original post
Yes, standard rules, except there is no opponent and the object is to NOT get three in a row. Don got the right answer. I am struggling with the wording of this puzzle and could use suggestions.
I do not claim to have the right answer, but did figure a way to deliver it in 15 days. Can anyone beat that?
Update: I got my solution down to 11.8 days.
If you can get a full camel (with 60g) at MM20 and 20g at MM40, then the camel can now get to MM100.
This can be achieved with 20g at MM20, 20g at MM40 and (setting out with a full) camel at MM0.
(0 - 6 days)
A trip from MM0 to MM20 and back can deliver 20g to MM20 (and each trip takes 2 days). Call this ABA.
Three of these deliveries cn leave 60g at MM20. Call this aBABABA. MM20 now has 60g.
(6 - 10 days)
A trip from MM0 via MM20 (picking up 20g) to MM40, back to MM20 (picking up 20g) and back to MM0, delivers 20g to MM40 using up 40g from MM20. Call this aBCBA. MM20 now only has 20g, but we have C at MM0, 20g at MM20, 20g at MM40.
(10 - 15 days).
This final trip uses 20g to get to MM20, picks up 20g (so full again), and goes onto MM40, picks up 20g (so full again) so can make it to MM100. Call this aBCDE.
Hence I agree with the toal of 15 days.
(Technically one can flip the order of the first ABA trip to after ABCBA, but this is easier to explain.)
I think 15 is the best you can do if you make 24-hour trips. However, you don't have to. Trips can be any distance, subject to not running out of water.
There will be three trips from the base and back to increasingly distant places. The camel is refuelled at the internediate places.
For the last trip the camel fills up at each of the points to keep going all the way to MM100.
The places I have picked (there may be others) are at MM8, MM20, MM40 (although it might be better to have the first one closer, I don't know - see last comment). (There's no mathematical logic excet it added up to your figure and I felt it had to be MM20.)
First trip 0-8, drop 44g, return. Distance = 16 miles, so time = 0.8 days. (44 - 0 - 0)
Second trip, 0-20, drop 36g. Distance = 40 miles, so time = 2 days. The camel picks up 8g on way out, and 8g on way back. So MM8 now has 44-16=28g. (28 - 36 - 0)
Third trip, 0-40, drop 20g. Distance = 80 miles, so time = 4 days. The camel picks up 8g each way at MM8, and 12g each way at MM20. (12 - 12 - 20)
Fourth trip 0-100. At each place the camel can fill up, so is full at MM40, so makes MM100. Time = 5 days.
The reason it might not be optimal is that there were 44g. There needs to be 12 at MM20 (to fill up and reach MM40) and 20 at MM40 (to fill up and reach MM100), but not 12 at MM8 (since the camel has only used 8g).
Total time = 0.8 + 2 + 4 + 5 = 11.8.
(Having q quick look at, say, 7.5, it fails because there isn't enough water left at MM20 for the final trip, so I think this is why it's 8 20 40.)
Now consider the trip that managed to drop off z gallons at D.
In general on any run as you head out, you start with 60g and then fill up at each depot. The last section, in this case CDC, you lose z gallons each way (2z) and want to leave z gallons at the depot to support the last run. As the maximum you can have is 60 gallons as you leave C, it seems optimal to have z=20 gallons. This also means C is at MM20 (and cannot be earlier, otherwise one can't get 20g to D to support the last run.)
On the way back you'll be empty as you reach each depot, and take just enough to get you to the next depot (or home). This means prior to the D run, B and C need to have have 3x and 3y.
Now consider the trip that manages to drop off 3y gallons to C.
Similar to the previous trip, when leaving B you need 2y for the trip and 3y to drop off. The maximum you can set off from B is 60 gallons. So y=12. This also means B is at MM8 (and cannot be earlier, otherwise one can't get 36g to C).
Finally you do the logic for leaving 5x at B and work out that you need 7x. Since x=8, this explains why for the 8 12 20 solution you have 4 gallons left over (7*8=56 but you have 60). (I think I got the 8 could be 8 4/7 so you could get to MM100+ using three depots.)
Now I'm probably missing something and am guessng from your solution it has B at MM 7 5/7; however this doesn't leave enough water at C (10 6/7g) to make the final trip. I can see you want to minimise the earlier routes, since you do them multiple times; but my feeling is CD can't be more than 20, and BC can't be more than 12, and adding any route other than AB just takes longer. On the other hand it does seem unfortunate to have water lying around. While playing around I did find shorter times, but they left negative numbers of water or broke the 60 rule.
By rulling out things with anything with N thousand
so nine hundred and ???
By rulling out 90,80,70,60,50,40,30,20,19-12, leaving eleven.
Of course you could have things like nine hundred and eleven squared or one million less one or even ..less a half.
Quote: charliepatrickIt reminds me of one on the 1% club which asked for the first number with a "b" in it.911.
By rulling out things with anything with N thousand
so nine hundred and ???
By rulling out 90,80,70,60,50,40,30,20,19-12, leaving eleven.
Of course you could have things like nine hundred and eleven squared or one million less one or even ..less a half.
link to original post
I think that's correct. It's weird that the next integer with no 't' after that is one million.
What is the lowest number which, when spelled out, has its letters in alphabetical order?
(edit: This was asked on the (UK) 1% Club, where 1% of the population managed to get it right in 30 seconds. You can see the question, and then the 30 seconds while to contestant can think. followed by the correct answer here >> https://www.tiktok.com/@kazusername/video/7287552163348270369 )
You may stick both your hands in any two holes at the same time and switch the switches at the same time. You must then take your hands out. If the switches are then all in the same position, then a door will open leading to freedom. Otherwise, the pilar will spin around randomly, but without changing the switches.
You are allowed up to four attempts. If you fail, you will be trapped in the tomb forever. How can you guarantee your freedom?
Let me know if you don't understand what is being asked.
Quote: WizardYou are trapped in a tomb. Inside the tomb there is a pillar about 1 foot in diameter. About a shoulder-high height from the floor are four holes in the pillar that are evenly spaced around the column. The holes are barely big enough to fit your hand in. Inside each hole is a switch that can either be in the up or down position. The goal is to get all the switches in the same position.
You may stick both your hands in any two holes at the same time and switch the switches at the same time. You must then take your hands out. If the switches are then all in the same position, then a door will open leading to freedom. Otherwise, the pilar will spin around randomly, but without changing the switches.
You are allowed up to four attempts. If you fail, you will be trapped in the tomb forever. How can you guarantee your freedom?
Let me know if you don't understand what is being asked.
link to original post
Questions in spoilers just to be safe.
Do you have to switch both switches when you stick in your hands in? Or could you choose to just switch one or zero?
If you switch one or zero does the pillar still spin after you remove your arms? [
Do you have to stick your hands in at the same time or can you stick in one hand and then choose which hole to stick the second hand into?
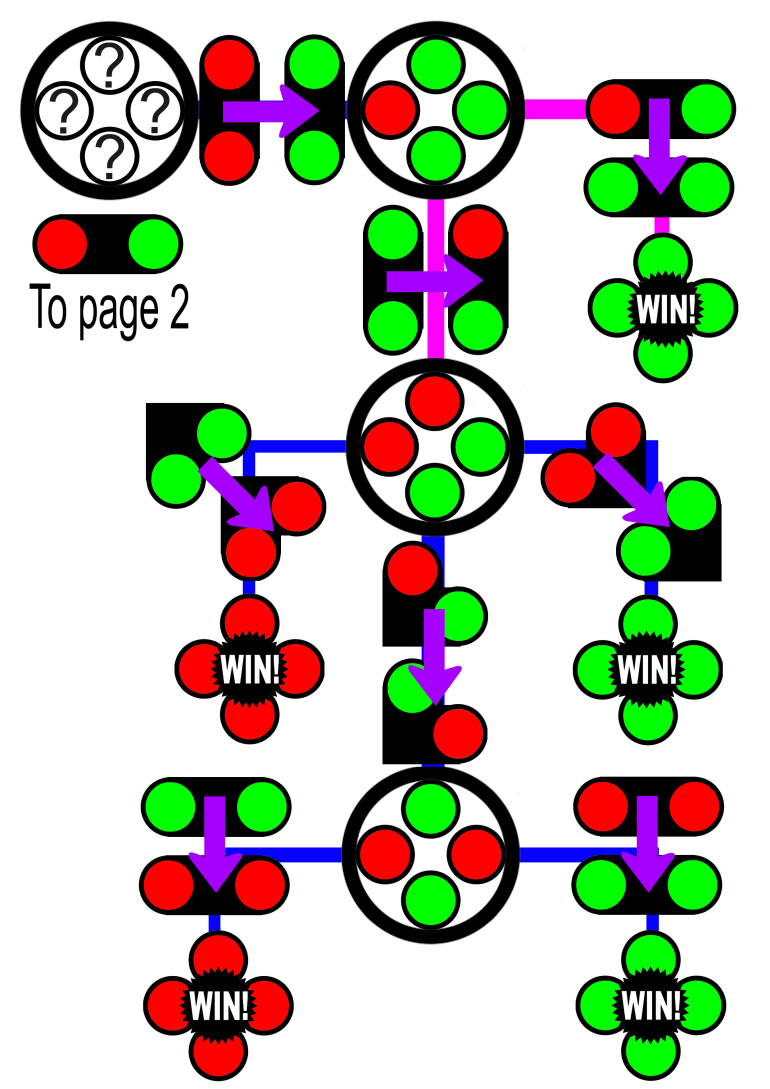
Note you can guarantee a win next move from E=W and N=S (xyxy) and a win in two from N=E S=W (xxyy). I think this is what you're aiming towards, but perhaps there's another way by elimination after 1b 2b.
| 1a) | x | y | |||||
| N S | ? | ? | If the same then flip, you know now the other two are different (as they can't be xx or yy) | x | y | ||
| same | x | Thus you know the EW pair are xy (or yx) | y | ||||
| 2a) | y | If you choose (EW) x y then you can win by setting them to y y | x | ||||
| N S | x | y | If you choose (NS) y y then set them to x y, this creates x x y y | x | y | ||
y | y | ||||||
| 3a) | x | If you choose (NW) xx or (SE) yy then you flip them to win e.g .(x x y y -> y y y y) | x | ||||
| N E | x | y | If you choose (NE SW) xy (or yx) then flip them to create EW and NS pairs | y | y | ||
y | x | ||||||
| 4a) | x | You will either pick xx or yy, just flip them to create a winner e.g. (x y x y -> y y y y) | |||||
| N S | y | y | |||||
x | |||||||
x | y | ||||||
| 1b) | ? | ? | If they are different, then the best you can do is set them to (say) y | ? | ? | ||
| N S | y | All you now know is EW are not yy | y | ||||
y | You will either pick yy or x?. If you pick x? then set to yy to win. | x | |||||
| 2b) | ? | ? | Otherwise set yy to xx. Now you know EW must be xy (as can't be xx) | x | y | ||
| N S | y | You can now proceed as above (except it takes five moves to force a win). | x |
Quote: unJonDo you have to switch both switches when you stick in your hands in? Or could you choose to just switch one or zero?
No. You can switch whatever you want once you put your hands in.
Quote:If you switch one or zero does the pillar still spin after you remove your arms?
Yes.
Quote:Do you have to stick your hands in at the same time or can you stick in one hand and then choose which hole to stick the second hand into?
link to original post
Must be at the same time.
Quote: charliepatrickI'm assuming you have to put your hands in two pre-determined holes and can then investigate the current settings and then set none, one or both of them to your choice.I am also assuming that the four do not start all in the same position.
link to original post
Yes, that is correct.
ABC is a triangle with AB = 13, BC = 14, and AC = 15
D is on side BC such that AD is perpendicular to BC
The circle inside triangle ABD that is tangent to all three sides is tangent to AB at E, to BD at P, and to AD at X; label its center J
The circle inside triangle ACD that is tangent to all three sides is tangent to AC at F, to CD at Q, and to AD at Y; label its center K
Lines PX and QY meet at R (indicated in the image by where the two blue lines meet)
What is the area of triangle PQR?
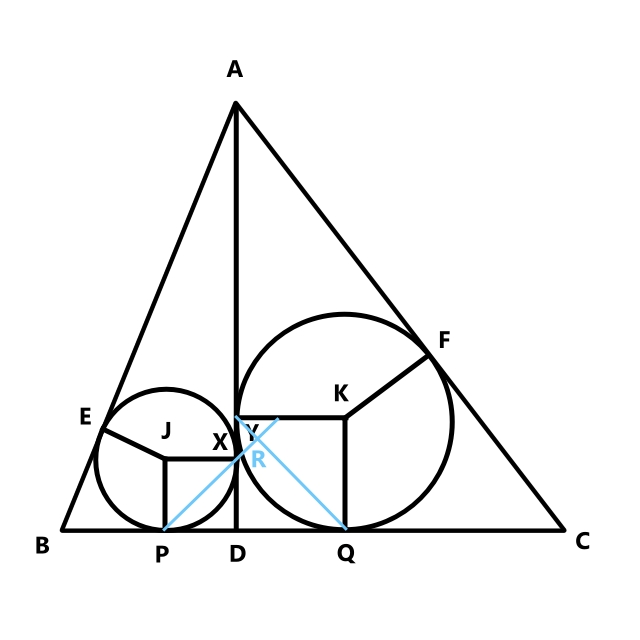
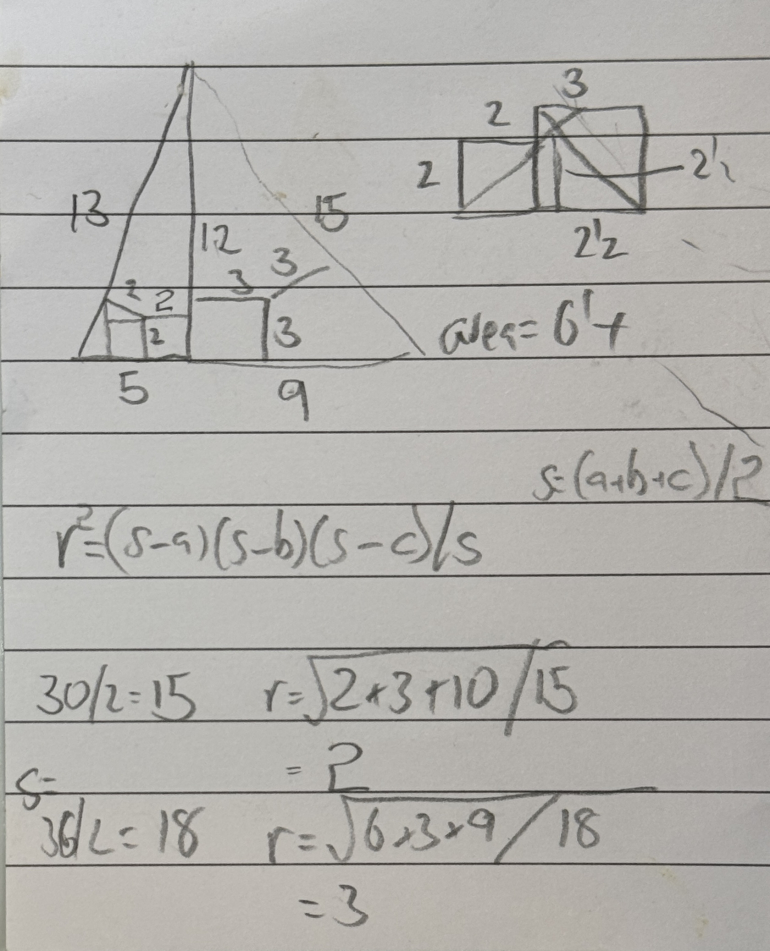
First, determine the lengths of BD, DC, and AD
Let x be the length of BD; DC = 14 - x
Pythagorean Theorem (twice): (AD)^2 = 169 - x^2 = 225 - (14 - x)^2
169 - x^2 = 225 - 196 + 28 x - x^2
x = (169 + 196 - 225) / 28 = 5
BD = 5, DC = 9, and AD = 12
Let p and q be the radii of the circles centered at J and K, respectively
BP = 5 - p
Construct BJ; JE = JP and JEB and JPB are both right angles, so triangles JEB and JPB are congruent (Hypotenuse-Leg)
BE = BP = 5 - p; AE = 13 - (5 - p) = 8 + p
Construct AJ; JE = JX and JEA and JXA are both right angles, so triangles AJE and AJX are congruent
AX = AE = 8 + p; XD = JP = p, so 8 + 2p = 12, which means p = 2
FC = CQ = 9 - q, so AF = 6 + q
AY = AF = 6 + q; AY + AD = 6 + 2q = 12, so q = 6
Let P be at point (0,0); PD + DQ = 5, so let Q be at (5,0)
Line PX is y = x; line QY is y = 5 - x; the lines intersect at (5/2, 5/2)
Area of PQR = 1/2 x 5 x 5/2 = 25/4

Six players with equal stacks go all in pre flop...
Player #1: QQ
Player #2: QQ
Player #3: KK
Player #4: AA
Player #5: AK suited
Player #6: AK offsuit
1) Do pocket queens have any chance of winning the whole pot?
2) Do pocket kings have any chance of winning the whole pot?
Suppose players #1 and #2 are always dealt pocket queens, but players #3, #4, #5 and #6 always randomly receive either AA, KK or AK. Obviously bullets would be the best starting hand.
3) What would be the second best starting hand?
1) Yes
2) No
Even a hand like 27o can win a pot against any pocket pair. They just need to be suited on the river and have the highest card in that suit or have a straight flush. The trick to this puzzle is that all of the queens, kings, and aces are accounted for. Any ordinary flush with the queens will not win the whole pot (there is a higher card of that rank among opponents hands). Any straight with a queen will chop the pot (same for other lesser rank winning hands). Only the Q-high SF can scoop the pot. There cannot be a K-high SF or even a straight. Any other hand KK can make (2-pair or FH, for example) will lose to AA.
Part three is not well defined. If it was totally random, then all four other players could receive AA. What is meant by part three?
1) Do pocket queens have any chance of winning the whole pot?
Yes? Q-high straight Flush.....has to be straight flush to avoid split on Q-high straight
2) Do pocket kings have any chance of winning the whole pot?
No? Straights are out because of Q's. Flush is beater by A-high flush, anything involving board beaten by AA
3) What would be the second best starting hand?
AK (either one?) - Can win a A-high flush. K-high flush would always lose to A-high....in one case it is another player (offsuit) and the other it is the player's own hand (suited)
Quote: MentalPart three is not well defined. If it was totally random, then all four other players could receive AA. What is meant by part three?
link to original post
The 4 aces and 4 kings are randomly distributed to players 3-6. Assume this scenario is repeated one million times.
Quote: Mental
1) Yes
2) No
Even a hand like 27o can win a pot against any pocket pair. They just need to be suited on the river and have the highest card in that suit or have a straight flush. The trick to this puzzle is that all of the queens, kings, and aces are accounted for. Any ordinary flush with the queens will not win the whole pot (there is a higher card of that rank among opponents hands). Any straight with a queen will chop the pot (same for other lesser rank winning hands). Only the Q-high SF can scoop the pot. There cannot be a K-high SF or even a straight. Any other hand KK can make (2-pair or FH, for example) will lose to AA.
Part three is not well defined. If it was totally random, then all four other players could receive AA. What is meant by part three?
link to original post
Quote: chevy
1) Do pocket queens have any chance of winning the whole pot?
Yes? Q-high straight Flush.....has to be straight flush to avoid split on Q-high straight
2) Do pocket kings have any chance of winning the whole pot?
No? Straights are out because of Q's. Flush is beater by A-high flush, anything involving board beaten by AA
3) What would be the second best starting hand?
AK (either one?) - Can win a A-high flush. K-high flush would always lose to A-high....in one case it is another player (offsuit) and the other it is the player's own hand (suited)
link to original post
Correct!
Very good.
2) No. KK's only hope is a straight or straight flush on the board that is neither queen-high nor a wheel. Thus the pot would chop six ways.
3) Somewhat surprisingly, it's QQ. The aces and kings will end up in one of three ways: AK, AK, AK, AK, or AA. AA, KK, KK, or AA, KK, AK, AK. For the latter two cases, AA is practically guaranteed to either win or (in case #2) chop the pot. For case #1, however, it's QQ that's practically guaranteed to win or (most likely) chop the pot. Despite all the chopping, case #1 happens frequently enough for QQ to edge out AKs as second best, while AKo and the hapless KK are just there for the very occasional bad beat or lucky push.
-----------------------------------

Above are six pieces of rope. Imagine that you grasp the two ends of the rope and pull until the rope is straight.
Which of the six ropes will end up with a knot in them, and which ones just form loops that can be pulled out?
Quote: Gialmere
Above are six pieces of rope. Imagine that you grasp the two ends of the rope and pull until the rope is straight.
Which of the six ropes will end up with a knot in them, and which ones just form loops that can be pulled out?
link to original post
A -- No loop
B -- No loop
C -- Loops
D -- Loop (figure 8 knot)
E -- No loop
F -- No loop
I must admit I got a piece of rope, mimicked these diagrams and pulled on the ends. It's possible I didn't construct some correctly.
I'd be interested to know the method to solve such puzzles mentally. I have a feeling it's some kind of odd/even thing to do with the rope going over/under itself.
Bus A comes exactly every 60 minutes.
Bus B comes on average every 60 minutes, but has a memoryless property in that no matter how long you wait, the bus is no closer to arriving (in other words, the actual waiting time has an exponential distribution with a mean of one hour).
You do not have a watch and have no idea how long it has been since either bus has arrived. You must choose a bus to wait for and can't switch. What is the average waiting for each?
Quote: WizardThere are two busses that will take you to the airport.
Bus A comes exactly every 60 minutes.
Bus B comes on average every 60 minutes, but has a memoryless property in that no matter how long you wait, the bus is no closer to arriving (in other words, the actual waiting time has an exponential distribution with a mean of one hour).
You do not have a watch and have no idea how long it has been since either bus has arrived. You must choose a bus to wait for and can't switch. What is the average waiting for each?
link to original post
The average waiting time for bus B is one hour because the mean, which is the average, is given as one hour.
If I waited for bus A, I would have to wait anywhere from 0 minutes to 60 minutes with all times equally likely. The mean for this uniform distribution is 30 minutes.
Quote: ChesterDog
The average waiting time for bus B is one hour because the mean, which is the average, is given as one hour.
If I waited for bus A, I would have to wait anywhere from 0 minutes to 60 minutes with all times equally likely. The mean for this uniform distribution is 30 minutes.
link to original post
I agree!
Interesting how the average time between buses is the same, but the average waiting times are not.
I've been stuck on this problem so felt it was time to explain where I am upto. I'm sure I'm missing something. btw I get the same blockage if I pick two adjacent rather than two opposite. I suspect it's to do with knowing something that can't have happened.Quote: WizardYou are trapped in a tomb. Inside the tomb there is a pillar about 1 foot in diameter. About a shoulder-high height from the floor are four holes in the pillar that are evenly spaced around the column. The holes are barely big enough to fit your hand in. Inside each hole is a switch that can either be in the up or down position. The goal is to get all the switches in the same position.
You may stick both your hands in any two holes at the same time and switch the switches at the same time. You must then take your hands out. If the switches are then all in the same position, then a door will open leading to freedom. Otherwise, the pilar will spin around randomly, but without changing the switches.
You are allowed up to four attempts. If you fail, you will be trapped in the tomb forever. How can you guarantee your freedom?
Let me know if you don't understand what is being asked.
link to original post
The problem if the first move has one of each colour is the best you can do is make them both (say) green. Thus the other two could be red-red or red-green. Your second move is also opposite and if you get green-green then you've found the initial two, so turning them both red leads you to the situation at the top middle of page 1. Thus this route takes five turns to solve. Obviously if you find red-green or red-red you can turn them both green to force a win.