Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
"You have sealed the ninth of nine boxes that weigh about the same, only to discover that your diamond ring has accidentally fallen into one of the packages. You don't want to unwrap every box. Can you work out how to find the box containing the ring by using the balance scale just twice?"
I failed.
solution
Quote: MichaelBluejayFrom the weekly Math column in my local paper:
"You have sealed the ninth of nine boxes that weigh about the same, only to discover that your diamond ring has accidentally fallen into one of the packages. You don't want to unwrap every box. Can you work out how to find the box containing the ring by using the balance scale just twice?"
I failed.
solution
link to original post
Number the boxes 1-9
Weigh 1, 2, 3 on one side and 4, 5, 6 on the other
If the sides don't balance, the heavier side has the ring; if they do, then one of 7, 8, 9 does
For the second weighing, put one of the three boxes in the "heavy three" on one side, and another on the other
If they don't balance, the heavier side has the ring; if they do, the box you didn't weigh does
Quote: MichaelBluejayFrom the weekly Math column in my local paper:
"You have sealed the ninth of nine boxes that weigh about the same, only to discover that your diamond ring has accidentally fallen into one of the packages. You don't want to unwrap every box. Can you work out how to find the box containing the ring by using the balance scale just twice?"
I failed.
solution
link to original post
MichaelBluejay,
The adverb that gave me pause is "about":
"... nine boxes that weigh about the same... "
If the eight non-ring boxes do not have EXACTLY the same weight, the solution fails.
In real life, variations in the amount of tape used to seal each box will invalidate the given solution anyway. After all, how much does a diamond ring actually weigh?
Dog Hand
P.S. I enjoyed the puzzle anyway and had no trouble finding the solution, despite my qualms ;-)
(2A) If they balance out, balance 7 vs 8. If they balance out, 9 has the ring. If they donít balance, the heavier one has the ring.
(2B) If they donít balance, take the 3 cans on the heavy side. Letís say itís 123. Balance 1 vs 2. If they balance 3 has the ring. If one is heavier that has the ring.
Use this:
[spoiler=Spoiler Button Text]
Spoiler Goes here
[/spoiler]
to create this:
Spoiler goes here
Quote: DogHand
After all, how much does a diamond ring actually weigh?
link to original post
(snip!)
The diamonds don't weigh much (often less than half a gram, unless... but if you have a diamond boulder on your finger, are you really sealing packages?)
The diamonds usually come attached to several grams of gold.
Here is my next puzzle.
sqrt(1-x) = 1-x2
Find x.
Quote: WizardI would like to wish all my math puzzle friends a happy Thanksgiving! May we all be thankful for the good things and people we have.
Here is my next puzzle.
sqrt(1-x) = 1-x2
Find x.
link to original post
Subtracting (1-x) from both sides and simplifying gives x(x3-2x+1)=0=x(x-1)(x2+ax-1) and it transpires a=1.
So the solutions are 0, 1, (SQRT(5)-1)/2, (-SQRT(5)-1)/2.
Quote: charliepatrickSquaring gives (1-x)=(1-x2)2=1-2x2+x4
Subtracting (1-x) from both sides and simplifying gives x(x3-2x+1)=0=x(x-1)(x2+ax-1) and it transpires a=1.
So the solutions are 0, 1, (SQRT(5)-1)/2, (-SQRT(5)-1)/2.
link to original post
Correct!

My grandfatherís papers included an old invoice:
72 turkeys $-67.9-
The first and last digits are illegible.
What are the missing digits, and what was the price of one turkey?
Quote: Gialmere
My grandfatherís papers included an old invoice:
72 turkeys $-67.9-
The first and last digits are illegible.
What are the missing digits, and what was the price of one turkey?
link to original post
A multiple of 72 is also a multiple of 8 and 9.
Multiples of 8 have their last three digits as multiples of 8; the only multiple of 8 between 790 and 799 inclusive is 792, so the last digit is 2.
Multiples of 9 have the sum of their digits be a multiple of 9; 6 + 7 + 9 + 2 = 24, so the first digit has to be 3.
The missing digits are 3 (first digit) and 2 (last digit), and the price of one turkey is $367.92 / 72 = $5.11.
There are four players. All make $1 pass, don't pass, come and don't come bets and back them up the full way on the odds.
- Alice makes one pass bet only
- Bob makes one don't pass bet only
- Cathy makes a pass or don't pass bet every roll
- David makes a don't pass or don't come bet every
What is the average wager resolved per throw of each player?
Quote: WizardCathy makes a pass or don't pass bet every roll link to original post
Should that be, "Cathy makes a pass or come bet every roll"? How can Cathy make a pass or don't pass bet on "every roll"?
Also, for Cathy and David, should I only be counting the rolls until their original comeout is resolved, or keep going until they seven out and have to pass the dice?
Quote: charliepatrickA turkey is $5.11 costing $367.92. Personally I just divided n6790 by 72 until it was just under a whole number.
link to original post
Quote: ThatDonGuyQuote: Gialmere
My grandfatherís papers included an old invoice:
72 turkeys $-67.9-
The first and last digits are illegible.
What are the missing digits, and what was the price of one turkey?
link to original post
A multiple of 72 is also a multiple of 8 and 9.
Multiples of 8 have their last three digits as multiples of 8; the only multiple of 8 between 790 and 799 inclusive is 792, so the last digit is 2.
Multiples of 9 have the sum of their digits be a multiple of 9; 6 + 7 + 9 + 2 = 24, so the first digit has to be 3.
The missing digits are 3 (first digit) and 2 (last digit), and the price of one turkey is $367.92 / 72 = $5.11.
link to original post
Correct!!
Good show.
---------------------------------------
---------------------------------------
Still in play...
Quote: WizardA craps electronic table game awards points upon bets resolved, including the odds. The game has double odds. As usual, when laying odds, the player may lay up to the amount that would result in a win 2x the don't pass/come bet (in other words 4x on a 4 or 10, 3x on a 5 or 9, and 2.4x on a 6 or 8).
There are four players. All make $1 pass, don't pass, come and don't come bets and back them up the full way on the odds.
- Alice makes one pass bet only
- Bob makes one don't pass bet only
- Cathy makes a pass or don't pass bet every roll
- David makes a don't pass or don't come bet every
What is the average wager resolved per throw of each player?
link to original post
Should be
A) (1/3 + 2/3 * 3) * 165/557 =~ 0.691
B) (1/3 + 1/6 * 5 + 2/9 * 4 + 5/18 * 3.4) * 165/557 =~ 0.889
C) (1/3 + 2/3 * 3) = 7/3
D) 1/3 + 1/6 * 5 + 2/9 * 4 + 5/18 * 3.4) = 3
Quote: Ace2
Should be
A) (1/3 + 2/3 * 3) * 165/557 =~ 0.691
B) (1/3 + 1/6 * 5 + 2/9 * 4 + 5/18 * 3.4) * 165/557 =~ 0.889
C) (1/3 + 2/3 * 3) = 7/3
D) 1/3 + 1/6 * 5 + 2/9 * 4 + 5/18 * 3.4) = 3
link to original post
Thank for working these out. We agree on C and D. I'm not saying you're wrong on the other two. I think I'll run a simulation to get a third opinion. I'm not sure where you get the fraction in your answer for A and B.
1 + 1/6 * 4 + 2/9 * 3.6 + 5/18 * 36/11 = 557/165 which is the average number of rolls to resolve a Pass/DP betQuote: WizardQuote: Ace2
Should be
A) (1/3 + 2/3 * 3) * 165/557 =~ 0.691
B) (1/3 + 1/6 * 5 + 2/9 * 4 + 5/18 * 3.4) * 165/557 =~ 0.889
C) (1/3 + 2/3 * 3) = 7/3
D) 1/3 + 1/6 * 5 + 2/9 * 4 + 5/18 * 3.4) = 3
link to original post
Thank for working these out. We agree on C and D. I'm not saying you're wrong on the other two. I think I'll run a simulation to get a third opinion. I'm not sure where you get the fraction in your answer for A and B.
link to original post
165/557 is a fraction used so often in craps problems that I have it memorized. If, for instance, you bet DP only and assume 100 rolls per hour then you can expect 100 * 165/557 =~ 30 bets resolved per hour. I just use 0.3 for calculations in my head
Quote: Ace2165/557 is a fraction used so often in craps problems that I have it memorized. If, for instance, you bet DP only and assume 100 rolls per hour then you can expect 100 * 165/557 =~ 30 bets resolved per hour. I just use 0.3 for calculations in my head
link to original post
Ah, thank you. That helped me find a mistake in my work. We now agree.
May I suggest the following extra credit problems.Quote: WizardA craps electronic table game awards points upon bets resolved, including the odds. The game has double odds. As usual, when laying odds, the player may lay up to the amount that would result in a win 2x the don't pass/come bet (in other words 4x on a 4 or 10, 3x on a 5 or 9, and 2.4x on a 6 or 8).
There are four players. All make $1 pass, don't pass, come and don't come bets and back them up the full way on the odds.
- Alice makes one pass bet only
- Bob makes one don't pass bet only
- Cathy makes a pass or don't pass bet every roll
- David makes a don't pass or don't come bet every
What is the average wager resolved per throw of each player?
link to original post
Cathy plays 3-point Molly instead of always coming. What is her average wager resolved per roll?
What is her per-roll expectation and standard deviation?
*3-point Molly means you play the passline and make come bets until you have wagers on three numbers total, including the passline point
Add three + symbols and one - symbol for this equation to be true:
9 8 7 6 5 4 3 2 1 = 100
9 8 -7 6 +5 4 +3 +2 1 = 100
6 min
Quote: Ace2
Cathy plays 3-point Molly instead of always coming. What is her average wager resolved per roll?
What is her per-roll expectation and standard deviation?
*3-point Molly means you play the passline and make come bets until you have wagers on three numbers total, including the passline point
link to original post
I get 1.668579 unit wagers resolved per throw. I admit this was done by simulation. I'd be very interested in your method of an exact calculation.
Quote: WizardThis was a puzzle on the last Survivor episode. Players had 3 minutes to do it. I didn't time it, but I think it took me about double that. On the show one of three players solved it in time.
Add three + symbols and one - symbol for this equation to be true:
9 8 7 6 5 4 3 2 1 = 100
link to original post
Took me about 90 seconds, but then again, I have seen my share of these type of problems:
98 - 76 + 54 + 3 + 21 = 100
On average, a shooter takes 1.5 rolls to establish a point and then 6 rolls to roll a seven. If playing a 2-point molly, heíd always have 2 bets on the table (pass + come or point) except for come out rolls. So wagers increase by 6 / (1.5 + 6) = 80% relative to betting PL only.Quote: WizardQuote: Ace2
Cathy plays 3-point Molly instead of always coming. What is her average wager resolved per roll?
What is her per-roll expectation and standard deviation?
*3-point Molly means you play the passline and make come bets until you have wagers on three numbers total, including the passline point
link to original post
I get 1.668579 unit wagers resolved per throw. I admit this was done by simulation. I'd be very interested in your method of an exact calculation.
link to original post
For a 3-point molly, we need to calculate how often the shooter, after establishing a point, will roll (not necessarily make) at least one additional point before sevening out. If, for example, he establishes a point of 5 or 9, then there is a (24-4)/(30-4) = 10/13 chance he will roll at least one additional point during his turn. The probabilities for points 4&10 and 6&8 are 7/9 and 19/25 respectively. Therefore, that weighed probability is 1/4 * 7/9 + 1/3 * 10/13 + 5/12 * 19/25 = 449/585.
As previously shown, 6 of 7.5 bets will make it to a 2-point molly. Of those 6, 449/585 will make it to a 3-point molly. Therefore, ((449/585 + 1) * 6) / 7.5 = 4,136 / 2,925 =~ 141% increase in wagers relative to betting PL only
So playing double odds and 3-point Molly, Cathyís average wager per roll will be 7/3 * 165/557 * (4136/2925 + 1) = 543697 / 325845 =~ 1.6686 units
Note, I previously posted the 3-point Molly increase calculation here: https://wizardofvegas.com/forum/off-topic/general/34651-craps-3-point-molly/#post768558
Quote: Ace2On average, a shooter takes 1.5 rolls to establish a point and then 6 rolls to roll a seven. If playing a 2-point molly, heíd always have 2 bets on the table (pass + come or point) except for come out rolls. So wagers increase by 6 / (1.5 + 6) = 80% relative to betting PL only.
For a 3-point molly, we need to calculate how often the shooter, after establishing a point, will roll (not necessarily make) at least one additional point before sevening out. If, for example, he establishes a point of 5 or 9, then there is a (24-4)/(30-4) = 10/13 chance he will roll at least one additional point during his turn. The probabilities for points 4&10 and 6&8 are 7/9 and 19/25 respectively. Therefore, that weighed probability is 1/4 * 7/9 + 1/3 * 10/13 + 5/12 * 19/25 = 449/585.
As previously shown, 6 of 7.5 bets will make it to a 2-point molly. Of those 6, 449/585 will make it to a 3-point molly. Therefore, ((449/585 + 1) * 6) / 7.5 = 4,136 / 2,925 =~ 141% increase in wagers relative to betting PL only
So playing double odds and 3-point Molly, Cathyís average wager per roll will be 7/3 * 165/557 * (4136/2925 + 1) = 543697 / 325845 =~ 1.6686 units
Note, I previously posted the 3-point Molly increase calculation here: https://wizardofvegas.com/forum/off-topic/general/34651-craps-3-point-molly/#post768558
link to original post
That is very good stuff, thank you! You have humbled me once again.
p.s. At least my simulator worked properly.
0X Odds
| Points | Do | Donít |
|---|---|---|
| 1 | 0.296230 | 0.296230 |
| 2 | 0.533214 | 0.533214 |
| 3 | 0.715104 | 0.715104 |
| Max | 1.000000 | 1.000000 |
1X Odds
| Points | Do | Donít |
|---|---|---|
| 1 | 0.493716 | 0.592460 |
| 2 | 0.888689 | 1.066427 |
| 3 | 1.191840 | 1.430208 |
| Max | 1.666667 | 2.000000 |
2X Odds
| Points | Do | Donít |
|---|---|---|
| 1 | 0.691203 | 0.888689 |
| 2 | 1.244165 | 1.599641 |
| 3 | 1.668576 | 2.145311 |
| Max | 2.333333 | 3.000000 |
3-4-5X Odds
| Points | Do | Donít |
|---|---|---|
| 1 | 1.036804 | 1.481149 |
| 2 | 1.866248 | 2.666068 |
| 3 | 2.502863 | 3.575519 |
| Max | 3.500000 | 5.000000 |

It's Easy Monday. Here's another trilogy of tiny teasers...

What is the best full house? Suppose you are playing poker and a genie offers to arrange the deal so that you receive the full house of your choice.
What hand should you specify?

Youíre about to roll five regular dice.
Which is more likely, rolling no sixes or rolling exactly one six?
:strip_icc()/pic7877285.png)
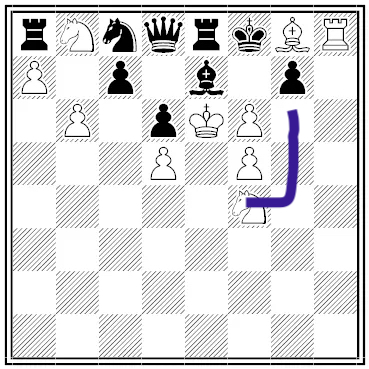
Who mates in 1?
Quote: Gialmere
It's Easy Monday. Here's another trilogy of tiny teasers...
What is the best full house? Suppose you are playing poker and a genie offers to arrange the deal so that you receive the full house of your choice.
What hand should you specify?
Youíre about to roll five regular dice.
Which is more likely, rolling no sixes or rolling exactly one six?
Who mates in 1?
link to original post
A, A, A, 10, 10. where one of the 10's is the suit of the missing Ace? to minimize on hands that will beat this full house?
The same?
no 6.....(5/6)^5
exactly one 6.......5 * (1/6) * (5/6)^4
White?
One die being six works out as four die (non-sixes) which each have the five options, but there's the possibility of five die that could have been the six. So it's also 3125.
Five sixes = 1
Four sixes = 25
Three sixes = 250
Two sixes = 1250
One six = 3125
No sixes = 3125
Total = 7776.
White can win by either moving his knight to G6, directly attacking Black's king, or by moving his bishop either way for a discovered checkmate.
Black can win by taking White's pawn with his bishop for a discovered checkmate.
You can't do anything about quads, since any rank of quad will beat you and you have to leave eleven, but you can reduce the number of possible straight flushes.
The Aces have removed AKQJT and A2345 in three of the suits. Therefore your best chances are now to remove as many others as possible. I get it that any pair, 9 thru 6, would get rid of five, in their suit, so are most useful. (e.g. 9 KQJT9 QJT98 JT987 T9876 98765.) (A ten or five of the same suit as an Ace would only manage four, since one has already been eliminated from the Ace.)
What is interesting in whether something like TTT55, which gets rid of more SFs, would let in too many Full Houses. The answer is yes because there are, for instance, 4*6 ways to get AAAKK. Thus the primary aim is to have AAAxx.
So the answer is AAAxx where x is 9 8 7 or 6, the actual suits used being irrelevant.
The key is to understand that:
1. with 9 numbers and 4 digits you are mostly adding or subtracting two-digit numbers
2. The high digits at the beginning of the sequence cannot be added, i.e., 98+77 yields a sum too high to be reduced to a number that can reach 100. Thus, one should explore sequences in which the minus sign is used first to reduce 4 high digits to a relatively small sum.
Therefore:
98 - 76 + 54 + 3 + 21 = 100
Both can mate in one move.
White: N to G6 mate
Black: BxF6 mate
Quote: acesideI havenít fully understood the best full house question. Do you mean Texas HoldíEm poker or the Mississippi Stud type of poker. The former has five community cards for every player to share.
link to original post
I don't think it matters, but assume you're playing simple 5-card draw.
-------------------------
In other news...
The Chess puzzle remains unsolved.
Quote: GialmereQuote: acesideI havenít fully understood the best full house question. Do you mean Texas HoldíEm poker or the Mississippi Stud type of poker. The former has five community cards for every player to share.
link to original post
I don't think it matters, but assume you're playing simple 5-card draw.
-------------------------
In other news...
The Chess puzzle remains unsolved.
link to original post
Clever re chess:
I don't see any possible way that this chess configuration could exist. Specifically, it is almost impossible for the White King to have moved into its position on E6 -where it is now incapable of moving.
Also, why hasn't White checkmated Black on its previous move by either N-F6 or B|G8-H7? One of those Mate possibilities must have existed on the prior move, right?
Also, Black must have been able to CheckMate White on its previous move with BxP.
So, the situation is impossible/
No sixes = (5/6)^5 = 40.1878%
One six = 5*5^4/6^5 = 40.1878%
Interesting. I would have expected that with six dice, but not five.
Both.
White plays Ng6.
Black plays g6.
This question was poorly phrased, if I may say so. It depends on what form of poker.
My interpretation is that it's simple five-card stud. Your opponents gets five random cards and that's it.
That said, my answer is aces high full house, including a pair of 6's to 9's. For example AAA77.
The only hands that will beat you are a four of a kind and straight flush. Nothing you can do about the four of a kinds. However, the middle pairs serve as a blocker to straight flushes.
Quote: Gialmere
It's Easy Monday. Here's another trilogy of tiny teasers...
What is the best full house? Suppose you are playing poker and a genie offers to arrange the deal so that you receive the full house of your choice.
What hand should you specify?
Youíre about to roll five regular dice.
Which is more likely, rolling no sixes or rolling exactly one six?
Who mates in 1?
link to original post
You might be thinking in terms of a Poisson distribution.Quote: Wizard
No sixes = (5/6)^5 = 40.1878%
One six = 5*5^4/6^5 = 40.1878%
Interesting. I would have expected that with six dice, but not five.
link to original post
If, for instance, you receive an average of four spams per day (one every six hours) then the probability of receiving both zero spams and one spam in any six-hour period is 1/e
In a binomial distribution, such as rolling these dice, that equilibrium is attained at 1/p - 1 rolls, not 1/p rolls
Quote: Ace2You might be thinking in terms of a Poisson distribution.
If, for instance, you receive an average of four spams per day (one every six hours) then the probability of receiving both zero spams and one spam in any six-hour period is 1/e
In a binomial distribution, such as rolling these dice, that equilibrium is attained at 1/p - 1 rolls, not 1/p rolls
link to original post
Indeed, I was thinking of Poisson. I didn't know that about discrete events.
There are 10 keys on his keyring and only 1 fits. He randomly pulls a key and tries to open the door.
If it doesn't fit he returns the key to the ring and randomly pulls another key again and again until he finds the one that fits.
Under these circumstances, on which try is he most likely to open the door?
How drunk?Quote: rawtuffA drunken person arrives at home and wants to get in.
There are 10 keys on his keyring and only 1 fits. He randomly pulls a key and tries to open the door.
If it doesn't fit he returns the key to the ring and randomly pulls another key again and again until he finds the one that fits.
Under these circumstances, on which try is he most likely to open the door?
link to original post


