Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Quote: charliepatrickI think the trick here is to consider A at (0,2) but B at (5,-3) rather than (5,3). Where the line between A and B meets the X asis (2,0) is where the river is. Since the horizontal and vertical lengths are each 5, the length of the pipe is 5 SQRT(2).
As I'm away the Y solution, for three points, usually requires the three pipes to be at 120 degrees to each other, thus you would construct two lines at 120o connecting to A and B such that, a third line 120o to those, was vertically down to the river.
link to original post
the 120 degree solution does match what I got finding intersection (x,y) that minimizes pipe distance numerically.
Quote: unJonSolving the two simultaneous equations:
Hits/ABs = 0.274
(Hits + 3) / (ABs + 4) = 0.289
Gives hits of 33.683
With rounding you get the right answer with 34 Hits and 124 At Bats before the current game.
link to original post
Correct!!
Well done.
------------------------------------------
Patient: Baseball.
Doctor: Don’t you dream about anything else?
Patient: What, and miss my turn at bat?
Here is the diagram again.
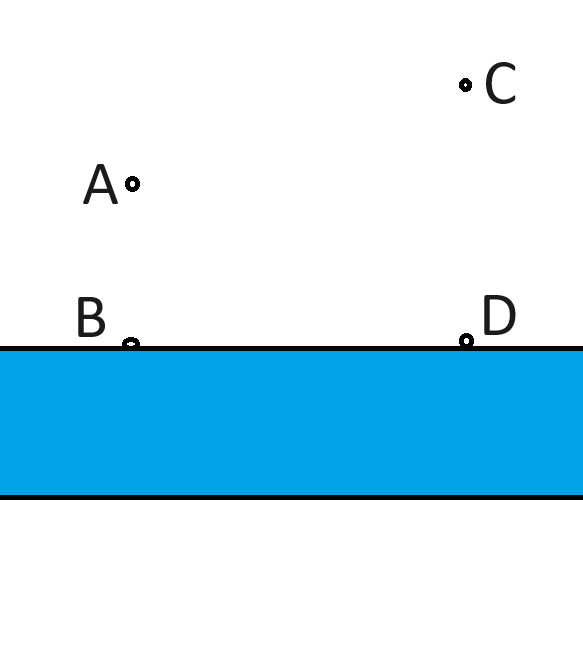
If we say point B is at (0,0) and point D is at (5,0), then I find the point where the three points meet to be at (1.633971768, 1.056623499).
This results in total pipe length of 6.830127019. Can anyone do better?
I admit the calculus got too messy and I used the "solver" feature in Excel to get those coordinates. If you don't have that add-on, then I highly recommend you do.
I'd be very interested to see a closed-form solution, if anyone is up to the challenge.
Quote: WizardTo follow up on the water pipe problem -- it's tough because there are two things to solve, the x and y coordinates of where to split off from the main pipe to the river to the two houses.
Here is the diagram again.
If we say point B is at (0,0) and point D is at (5,0), then I find the point where the three points meet to be at (1.633971768, 1.056623499).
This results in total pipe length of 6.830127019. Can anyone do better?
I admit the calculus got too messy and I used the "solver" feature in Excel to get those coordinates. If you don't have that add-on, then I highly recommend you do.
I'd be very interested to see a closed-form solution, if anyone is up to the challenge.
link to original post
I agree with your (x,y). I had numerically solved on a 0.01x0.01 size grid getting (1.63, 1.06). So yours is more precise. And it does give the 120 degree spacing @charliepatrick mentions.
Didn't work out closed form yet....I too gave up on the calculus.....got as far as
x=5*(2-y) / (5-2*y) from partial deriv wrt x set = 0.....it works for your solution, so plenty confident in your numbers
Quote: chevyI agree with your (x,y). I had numerically solved on a 0.01x0.01 size grid getting (1.63, 1.06). So yours is more precise. And it does give the 120 degree spacing @charliepatrick mentions.
Didn't work out closed form yet....I too gave up on the calculus.....got as far as
x=5*(2-y) / (5-2*y) from partial deriv wrt x set = 0.....it works for your solution, so plenty confident in your numbers
link to original post
Thank you for the confirmation. That is interesting about the 120 angles.
Quote: WizardQuote: chevyI agree with your (x,y). I had numerically solved on a 0.01x0.01 size grid getting (1.63, 1.06). So yours is more precise. And it does give the 120 degree spacing @charliepatrick mentions.
Didn't work out closed form yet....I too gave up on the calculus.....got as far as
x=5*(2-y) / (5-2*y) from partial deriv wrt x set = 0.....it works for your solution, so plenty confident in your numbers
link to original post
Thank you for the confirmation. That is interesting about the 120 angles.
link to original post
Still can't get calculus to work, but using @charliepatrick's 120 degree theorem (maybe he can chime in on why)....
then just use geometry....calling intersection F
AF is 30 degrees above horizontal.........(2-y)/x = tan(30) = 1/sqrt(3)
CF is 30 degrees above horizontal.........(3-y)/(5-x) = tan (30) = 1/sqrt(3)
Solving these two equations for x,y....making several algebra mistakes in the process, I get
setting the two equal yields x=5(y-2)/(2y-5)......mention it as it matches the local min in x dir from calc)
plugging in to AF equation gives
y=(5/2) * (1 - 1/sqrt(3)) = 1.05662432703
Plugging back in gives
x=(5/2) * (1-sqrt(3) / 5) = 1.63397459622

One sunny day four young boys began following the train tracks out of town in search of a dead body. They had begun crossing a high railroad bridge spanning a gorge when, to their horror, they heard a train coming from behind them. Two of the boys were up ahead and easily made it to the other side. But, the other two were only 3/7 of the way across the bridge. As their friends screamed for them to hurry, they began running for their lives to the far side, only just reaching it and jumping off the tracks before the train roared by.
Later, when they had time to think about it, they realized they had been less than halfway across the bridge. They wondered if they could have run back toward the train and still gotten off the tracks in time.
What's the minimum distance away the train would of had to have been in order for the two boys to have escaped in either direction?
If D = length of bridge
They run at speed (4/7)*D / T
Running other way a distance (3/7)*D takes (3/4)*T
If just barely making it to safety either way is required, then the train is at the start of the bridge at t=(3/4)*T and end of bridge at time t=T. It travels the length of the bridge in (1/4)*T.
So if train starting at distance of 4D (from the end of bridge or 3D from start of bridge) they should just barely jump to safety
Quote: chevyStill can't get calculus to work, but using @charliepatrick's 120 degree theorem (maybe he can chime in on why)....
link to original post
I too would be interested to see a proof or a citation of the 120-degree theorem.
Quote: GialmereWhat's the minimum distance away the train would of had to have been in order for the two boys to have escaped in either direction?
link to original post
I get the train is 3/4 the length of the bridge away from the entrance to it.
If the question is asking the distance from the boys, that would then be 3/4 + 3/7 = 33/28 the length of the bridge.
Quote: WizardQuote: chevyStill can't get calculus to work, but using @charliepatrick's 120 degree theorem (maybe he can chime in on why)....
link to original post
I too would be interested to see a proof or a citation of the 120-degree theorem.
link to original post
Some googling suggests It seems to be a variant of what is called the Fermat Point. (I will now think of it as the Fermat-CharliePatrick point)
https://en.wikipedia.org/wiki/Fermat_point#:~:text=In%20Euclidean%20geometry%2C%20the%20Fermat,median%20of%20the%20three%20vertices.
For the ring to be in equilibrium the net force must be zero. Therefore thinking along one of the lines, the forces from either side must be equal. Since the weights are equal, the angles must be. Use this for all three lines shows they must be at 120 (assuming the interior angles of the "triangle" are less than 120.) (Remember it's all about the potential energy, so this means the weights being as low as possible, which means the total length of string above the table.)
I did do a mathematical solution ages ago, probably based on the fact that any deviation from 120 will increase the length of one string more than the other one decreases, but if you can visualise the above it is possibly clearer to see.
Quote: charliepatrickThe easiest way to think of it is to consider a flat table with three holes drilled. Then a ring with three pieces of string attached, such that a string goes through each hole, each string having an equal weight hung from it.
For the ring to be in equilibrium the net force must be zero. Therefore thinking along one of the lines, the forces from either side must be equal. Since the weights are equal, the angles must be. Use this for all three lines shows they must be at 120 (assuming the interior angles of the "triangle" are less than 120.) (Remember it's all about the potential energy, so this means the weights being as low as possible, which means the total length of string above the table.)
I did do a mathematical solution ages ago, probably based on the fact that any deviation from 120 will increase the length of one string more than the other one decreases, but if you can visualise the above it is possibly clearer to see.
link to original post
Very nice....Thanks
Quote: MichaelBluejayWhy did the obtuse angle jump in the pool?
link to original post

Quote: chevy
If D = length of bridge
They run at speed (4/7)*D / T
Running other way a distance (3/7)*D takes (3/4)*T
If just barely making it to safety either way is required, then the train is at the start of the bridge at t=(3/4)*T and end of bridge at time t=T. It travels the length of the bridge in (1/4)*T.
So if train starting at distance of 4D (from the end of bridge or 3D from start of bridge) they should just barely jump to safety
link to original post
Quote: Wizard
I get the train is 3/4 the length of the bridge away from the entrance to it.
If the question is asking the distance from the boys, that would then be 3/4 + 3/7 = 33/28 the length of the bridge.
link to original post
Correct!!
Good show.
------------------------------------
I said, "God loves you. Do you believe in God?"
He said, "Yes." I said, "Are you a Christian or a Jew?" He said, "A Christian." I said, "Me, too! Protestant or Catholic?" He said, "Protestant." I said, "Me, too! What franchise?" He said, "Baptist." I said, "Me, too! Northern Baptist or Southern Baptist?" He said, "Northern Baptist." I said, "Me, too! Northern Conservative Baptist or Northern Liberal Baptist?"
He said, "Northern Conservative Baptist." I said, "Me, too! Northern Conservative Baptist Great Lakes Region, or Northern Conservative Baptist Eastern Region?" He said, "Northern Conservative Baptist Great Lakes Region." I said, "Me, too!"
Northern Conservative†Baptist Great Lakes Region Council of 1879, or Northern Conservative Baptist Great Lakes Region Council of 1912?" He said, "Northern Conservative Baptist Great Lakes Region Council of 1912." I said, "Die, heretic!" And I pushed him over.
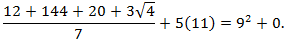
The numerical expression above is actually the mathematical representation of a limerick. Translate the numbers and symbols into the English words they commonly represent, and the expression will scan perfectly into the rhythm of a limerick. There are several possibilities for translating so try being fussy to make it work.
Can you translate it?
I'm not saying you need to be a Baptist to get into heaven ... Buy why take any chances?
Quote: chevySome googling suggests It seems to be a variant of what is called the Fermat Point. (I will now think of it as the Fermat-CharliePatrick point)
link to original post
The Wikipedia page does indeed say 120-degree angles are formed between the center point and the three corners of a triangle.
Quote: Gialmere
The numerical expression above is actually the mathematical representation of a limerick. Translate the numbers and symbols into the English words they commonly represent, and the expression will scan perfectly into the rhythm of a limerick. There are several possibilities for translating so try being fussy to make it work.
Can you translate it?
link to original post
It's in Lytton's Problematical Recreations:
A dozen, a gross, and a score
Plus three times the square root of four
Divided by seven
Plus five times eleven
Is nine squared and not a bit more
Quote: ThatDonGuyQuote: Gialmere
The numerical expression above is actually the mathematical representation of a limerick. Translate the numbers and symbols into the English words they commonly represent, and the expression will scan perfectly into the rhythm of a limerick. There are several possibilities for translating so try being fussy to make it work.
Can you translate it?
link to original post
It's in Lytton's Problematical Recreations:
A dozen, a gross, and a score
Plus three times the square root of four
Divided by seven
Plus five times eleven
Is nine squared and not a bit more
link to original post
Correct!!
Very good.
-----------------------------------------
A mathematician confided
That the M"obius band is one-sided
And you'll get quite a laugh
If you cut one in half
'Cause it stays in one piece when divided.
----------
'Tis a favorite project of mine
A new value of pi to assign.
I would fix it at 3
For it's simpler, you see,
Than 3 point 1 4 1 5 9
----------
Integral z-squared dz
from 1 to the cube root of 3
times the cosine
of three pi over 9
equals log of the cube root of 'e'.
(And it's correct, too)
Quote: Gialmere<snip>
Very good.
-----------------------------------------
A mathematician confided
That the M"obius band is one-sided
And you'll get quite a laugh
If you cut one in half
'Cause it stays in one piece when divided.
----------
'Tis a favorite project of mine
A new value of pi to assign.
I would fix it at 3
For it's simpler, you see,
Than 3 point 1 4 1 5 9
----------
Integral z-squared dz
from 1 to the cube root of 3
times the cosine
of three pi over 9
equals log of the cube root of 'e'.
(And it's correct, too)
link to original post
Gialmere,
I remember that first limerick somewhat differently:
A mathematician confided,
That a Möbius strip is one-sided,
You'll get quite a laugh,
If you cut it in half,
'Cause it's twice as long when divided.
How about:
A burlesque dancer, a pip,
Named Virginia, could peel in a zip,
But she read science fiction,
And died of constriction,
Attempting a Möbius strip.
Another favorite:
Equations, when spoken aloud,
To children in class sound profound,
But you'll get quite a stare,
When you say "Pi r square",
For they all know that Mom's pies are round.
Dog Hand
Quote: chevyStill can't get calculus to work, but using @charliepatrick's 120 degree theorem (maybe he can chime in on why)....
then just use geometry....calling intersection F
AF is 30 degrees above horizontal.........(2-y)/x = tan(30) = 1/sqrt(3)
CF is 30 degrees above horizontal.........(3-y)/(5-x) = tan (30) = 1/sqrt(3)
Solving these two equations for x,y....making several algebra mistakes in the process, I get
setting the two equal yields x=5(y-2)/(2y-5)......mention it as it matches the local min in x dir from calc)
plugging in to AF equation gives
y=(5/2) * (1 - 1/sqrt(3)) = 1.05662432703
Plugging back in gives
x=(5/2) * (1-sqrt(3) / 5) = 1.63397459622
link to original post
I independently had the same idea.
A 30-60-90 triangle has sides proportional to 1, sqrt(3) and 2.
The equations of the two pipes would be:
From left house: y = -x/sqrt(3) + 2
From right house: y = +x/(sqrt(3) + (9-5*sqrt(3))/3
Solving for x gives us x = (5-sqrt(3))/2 =~ 1.633975
Express 1 / (x^8 - 1) as the sum of five fractions of the form (a / (x + b)) and/or (ax + b) / (x^2 + cx + d), where all a, b, c, d are real numbers.
x^4 + 1 = (x^2 + sqrt(2) x + 1) (x^2 - sqrt(2) x + 1)
I agree with this - it's 5/2 (1 + SQRT(3) ).Quote: WizardTo follow up on the water pipe problem...This results in total pipe length of 6.830127019. Can anyone do better?...
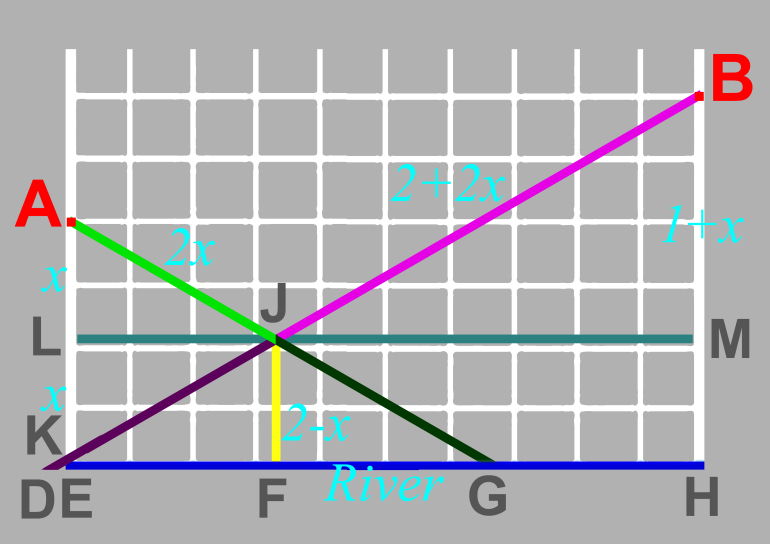
Construct lines down from A and B so they meet at 120 degrees, and extend these to the river. Construct other lines as shown.
BH=3, so BD=6 (D is beyond E), so DH=3*SQRT(3) (about 5.196).
Note AJ=AK so BJ+AJ=BK. This is therefore 6 * 5 / (3 SQRT(3) = 10/SQRT(3).
So let AL=x and so JF=2-x. Similarly BM=1+x giving BJ=2*(1+x).
Using BK=2+4x, this gives 4x=10/SQRT(3)-2 or x=5/(2 SQRT(3)) - 1/2.
The total required is 2 + 2x +2x+2 - x = 4+3x = 4 + 3(above) = 4-3/2+5*SQRT(3)/2 = 5/2(1+SQRT(3))
This is about 6.830127 and as BK was 5.773503 gives the y-coordinate as about 1.056624.
What was interesting is I think you get the same result if both A and B were 2.5 away from the river, so I'm guessing this is where the 5/2 comes from.
edit Further thoughts, an easier approach. If you consider two squares, size SQRT(3), you get the lengths would be 2+2+(SQRT(3)-1) = 3 + SQRT(3). So if it had been unit squares it would have been SQRT(3)+1. In our puzzle it is 5/2 sides, hence 5/2 (SQRT(3)+1).

In a non sequitur, today is both Hump Day and the middle of the Dia de los Muertos festivities. Here are three puzzles...

A nasty number is a positive integer having at least four different factors such that the difference between one pair of factors equals the sum of another pair of factors. For instance,
6 is nasty because 6 – 1 = 2 + 3
24 is nasty because 12 – 2 = 4 + 6
30 is nasty because 15 – 2 = 10 + 3.
Find the other six nasty numbers that are less than 180.

What is the closest planet to Earth on average?

Up in a forest fire lookout tower in California’s Sierra Nevada, two watchers need supplies. Three mules, led by a ranch hand, can carry supplies up to them.
The mules are named Geranium, Delphinium, and Ammonium. Geranium can carry 200 pounds, Delphinium can carry 190 pounds, and Ammonium can carry 180 pounds.
What supplies should each mule carry so that everything fits?
Drinking water 28 lb
Ice 35 lb
Kitty litter 42 lb
Camera Equipment 44 lb
Backup Telescope 48 lb
Batteries 61 lb
Detective Novels 63 lb
Window Glass Cleaner 77 lb
Ping Pong Table 84 lb
Mountain Dew 88 lb

Just work through using 61 with each of the other odd numbers in turn...
61 63 (124) 28 48 = 200
35 77 (112) 88 = 200 (no good as already got a 200)
61 35 (96) 84 = 180
63 77 (140) now impossible
61 77 (138) 42 = 180
35 63 (98) 42 48 = 190
leaves 28 84 88 = 200.
At three o'clock and nine o'click the distance to the "12" is least for the shortest hour hand. At 12 o'clock and 6 o'clock (combined) it's the same. At times imbetween, the total distance of (say) 1 o'clock and 5 o'clock is least with the smallest hands.
Thus the average is smallest for the smallest hour hand.
Thus the answer is Mercury.
Drinking Water + Ping Pong Table + Mountain Dew = 200 lbs for Geranium.
Ice + Camera Equipment + Backup Telescope + Detective Novels = 190 lbs for Delphinium.
Kitty Litter + Batteries + Window Glass Cleaner = 180 lbs for Ammonium.
Also, I see the question should read "less than or equal to 180".
Quote: unJonMercury. I’ve always liked this question. Venus and Mars would seem to be correct until you realize they are very far away for half the time or so that they are across the Sun from Earth.
link to original post
Quote: charliepatrickThe trick seems to be to realise the total of the numbers means there's no slack. Hence the odd numbers have to be divided 2-2-0 or 4-0-0. Since all four add up to more than 200, it's 2-2-0. Thus just work through all the permutations of two pairs.
Just work through using 61 with each of the other odd numbers in turn...
61 63 (124) 28 48 = 200
35 77 (112) 88 = 200 (no good as already got a 200)
61 35 (96) 84 = 180
63 77 (140) now impossible
61 77 (138) 42 = 180
35 63 (98) 42 48 = 190
leaves 28 84 88 = 200.
link to original post
Quote: charliepatrickAssuming all the planets have circular motion it's easier to think of the Earth and Sun not moving and look at how the other planets go round the sun (rather like being on a clock at the "12" and watching the tip of an hour hand go round). In this case consider the effects of having longer or shorter hour hands.
At three o'clock and nine o'click the distance to the "12" is least for the shortest hour hand. At 12 o'clock and 6 o'clock (combined) it's the same. At times imbetween, the total distance of (say) 1 o'clock and 5 o'clock is least with the smallest hands.
Thus the average is smallest for the smallest hour hand.
Thus the answer is Mercury.
link to original post
Quote: unJonI thought this would be trickier:
Drinking Water + Ping Pong Table + Mountain Dew = 200 lbs for Geranium.
Ice + Camera Equipment + Backup Telescope + Detective Novels = 190 lbs for Delphinium.
Kitty Litter + Batteries + Window Glass Cleaner = 180 lbs for Ammonium.
link to original post
Quote: WizardMercury
link to original post
Correct!!
Well done.
54 is nasty because 18 – 3 = 6 + 9
60 is nasty because 20 – 3 = 12 + 5
96 is nasty because 24 – 4 = 12 + 8
120 is nasty because 30 – 4 = 20 + 6
150 is nasty because 30 – 5 = 10 + 15
180 is nasty because 45 – 4 = 36 + 5
I have no idea why "nasty" is used to describe these numbers.
------------------------------------------
No joke today. Instead here's a link to an article at "Physics Today" discussing calculations and computer data on Mercury's proximity to other planets.
Venus is not Earth’s closest neighbor
The funny part is the comments at the end. If you think a gambling forum is filled with piss and vinegar, you should see astronomers going at it.
--------------------------------------------
Still in play but got lost amongst the limericks...
Quote: ThatDonGuyOkay, back to the "easy" math puzzles...
Express 1 / (x^8 - 1) as the sum of five fractions of the form (a / (x + b)) and/or (ax + b) / (x^2 + cx + d), where all a, b, c, d are real numbers.
x^4 + 1 = (x^2 + sqrt(2) x + 1) (x^2 - sqrt(2) x + 1)
link to original post
Quote: Gialmere
Still in play but got lost amongst the limericks...Quote: ThatDonGuyOkay, back to the "easy" math puzzles...
Express 1 / (x^8 - 1) as the sum of five fractions of the form (a / (x + b)) and/or (ax + b) / (x^2 + cx + d), where all a, b, c, d are real numbers.
x^4 + 1 = (x^2 + sqrt(2) x + 1) (x^2 - sqrt(2) x + 1)
Apparently, nobody is interested, so here is the answer
(x^2 + sqrt(2) x + 1)(x^2 - sqrt(2) x + 1)(x^2 + 1)(x + 1)(x - 1)
Let q = sqrt(2):
(ax + b) (x^2 - q x + 1)(x^4 - 1)
(cx + d) (x^2 + q x + 1)(x^4 - 1)
(ex + f) (x^4 + 1)(x^2 - 1)
g (x^4 + 1)(x^2 + 1)(x - 1)
h (x^4 + 1)(x^2 + 1)(x + 1)
a (x^7 - q x^6 + x^5 - x^3 + q x^2 - x)
b (x^6 - q x^5 + x^4 - x^2 + q x - 1)
c (x^7 + q x^6 + x^5 - x^3 - q x^2 - x)
d (x^6 + q x^5 + x^4 - x^2 - q x - 1)
e (x^7 - x^5 + x^3 - x)
f (x^6 - x^4 + x^2 - 1)
g (x^7 - x^6 + x^5 - x^4 + x^3 - x^2 + x - 1)
h (x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1)
a (x^7 - q x^6 + x^5 - x^3 + q x^2 - x)
b ( x^6 - q x^5 + x^4 - x^2 + q x - 1)
c (x^7 + q x^6 + x^5 - x^3 - q x^2 - x)
d ( x^6 + q x^5 + x^4 - x^2 - q x - 1)
e (x^7 - x^5 + x^3 - x)
f ( x^6 - x^4 + x^2 - 1)
g (x^7 - x^6 + x^5 - x^4 + x^3 - x^2 + x - 1)
h (x^7 + x^6 + x^5 + x^4 + x^3 + x^2 + x + 1)
[7] a + c + e + g + h = 0
[6] -q a + b + q c + d + f - g + h = 0
[5] a - q b + c + q d - e + g + h = 0
[4] b + d - f - g + h = 0
[3] -a - c + e + g + h = 0
[2] q a - b - q c - d + f - g + h = 0
[1] -a + q b - c - q d - e + g + h = 0
[0] -b - d - f - g + h = 1
[4] b + d - f - g + h = 0
[0] -b - d - f - g + h = 1
[4-0] 2b + 2d = -1 -> d = -1/2 - b
[4+0] -2f -2g + 2h = 1
[7] a + c + e + g + h = 0
[3] -a - c + e + g + h = 0
[7-3] 2a + 2c = 0 -> c = -a
[7+3] 2e + 2g + 2h = 0 -> e = -g - h
[5] a - q b + c + q d - e + g + h = 0
[1] -a + q b - c - q d - e + g + h = 0
[5+1] -2e + 2g + 2h = 0 -> e = g + h
By [5+1] and [7+3], e = 0 -> h = -g -> f = 2g
Substitute into [4+0]: -4g - 2g - 2g = 1 -> g = -1/8 -> h = 1/8, f = -1/4
[6] -q a + b + q c + d + f - g + h = 0
[2] q a - b - q c - d + f - g + h = 0
[2-6] 2q a - 2 b - 2q c - 2 d = 0
Substitute for e, f, g, h:
[7] c = -a
[6] -q a + b + q c + d = 0
[5] a - q b + c + q d = 0
[4] b + d = -1/2 -> d = -1/2 - b
{[3] is the negative of [7]; [0] is the negative of [4]; [1] is the negative of [5]; [2] is the negative of [6]}
Substitute c = -a in [5]:
- q b + q d = 0 -> d = b = -1/2 - b -> b = -1/4 -> d = -1/4
Substitue for b and d (as well as c = -a) in [6]:
a = b / q = -1 / (4q) -> c = 1 / (4q)
The five fractions are:
(-sqrt(2)/8 x - 1/4) / (x^2 + sqrt(2) x + 1)
(sqrt(2)/8 x - 1/4) / (x^2 - sqrt(2) x + 1)
(-1/4) / (x^2 + 1)
(-1/8) / (x + 1)
(1/8) / (x - 1)
| Planet | AU | Cosest distance | Furthest distance | Average distance |
|---|---|---|---|---|
| Mercury | 0.39 | 0.61 | 1.39 | 1.038401104 |
| Venus | 0.72 | 0.28 | 1.72 | 1.134493617 |
| Earth 2 | 1 | 0 | 2 | 1.273231464 |
| Mars | 1.52 | 0.52 | 2.52 | 1.689508849 |
| Jupiter | 5.2 | 4.2 | 6.2 | 5.24818909 |
| Saturn | 9.54 | 8.54 | 10.54 | 9.566223496 |
| Uranus | 19.2 | 18.2 | 20.2 | 19.21302304 |
| Neptune | 30.06 | 29.06 | 31.06 | 30.06831728 |
As for the Earth 2 row, I am referring to a hypothetical second earth that has the same orbit, but different speed. Yes, I know that violates one of Kepler's laws, so take it as hypothetical only. Interesting that Mercury would be closer than another Earth.
Quote: WizardGetting back to the closest planet puzzle, here are my calculations. All distances are in Astronomical Units (AU).
Planet AU Cosest distance Furthest distance Average distance Mercury 0.39 0.61 1.39 1.038401104 Venus 0.72 0.28 1.72 1.134493617 Earth 2 1 0 2 1.273231464 Mars 1.52 0.52 2.52 1.689508849 Jupiter 5.2 4.2 6.2 5.24818909 Saturn 9.54 8.54 10.54 9.566223496 Uranus 19.2 18.2 20.2 19.21302304 Neptune 30.06 29.06 31.06 30.06831728
As for the Earth 2 row, I am referring to a hypothetical second earth that has the same orbit, but different speed. Yes, I know that violates one of Kepler's laws, so take it as hypothetical only. Interesting that Mercury would be closer than another Earth.
link to original post
I got the same answer for the 2nd earth, which is 4 / pi. And I had the same problem you had about a planet traveling in earth's orbit with a different speed. Also, the planets would have trouble passing each other.
Quote: ChesterDogI got the same answer for the 2nd earth, which is 4 / pi. And I had the same problem you had about a planet traveling in earth's orbit with a different speed. Also, the planets would have trouble passing each other.
link to original post
Interesting about the 4/pi. That must have been some messy integration.
Quote: WizardQuote: ChesterDogI got the same answer for the 2nd earth, which is 4 / pi. And I had the same problem you had about a planet traveling in earth's orbit with a different speed. Also, the planets would have trouble passing each other.
link to original post
Interesting about the 4/pi. That must have been some messy integration.
link to original post
I thought it would be a messy integration (integral from x = 0 to x = pi of sqrt( 2 - 2 cos x ) dx / pi ), so I had WolframAlpha do it.
But just now, I see that the half-angle formulas make it easy.
Your other planet integrations must have been messy.
Quote: ChesterDogYour other planet integrations must have been messy.
link to original post
I was lazy and didn't even try. I used Excel. I put earth at point (1,0) and the other planet at every point around the sun from 0 to 359 degrees, in groups of one degree. It was simple trigonometry to get the coordinates of the other planet and then the Pythagorean formula to find the distance.
You are allowed a total of one square foot of metal to make a can, including the top and bottom. What is the radius of the can that maximizes the volume?

A band is stretched taut over the circumference of the earth. Assume the earths circumference is static. There’s no room between the band and the earth. Treat the earth like a solid spherical object so no issues with oceans/mountains/etc. suddenly, the band increases in size by 1 foot. What does that do to the space between the band and the earth? can you slip a playing card between them? Your hand? Will the difference be indistinguishable from before?
Quote: WizardI may have asked this one before, but here goes:
You are allowed 1 square foot of metal to make a can, including the top and bottom. What is the radius of the can that maximizes the volume?
link to original post
Roll up the metal and join the ends, giving a circumference of 12 inches. Pinch the ends together like this. That makes a can that maximizes volume without wasting metal by cutting.
If you're talking about a traditional can like the one in the picture, I have no idea.
Quote: TigerWuA radius of 1.91 inches.
Roll up the metal and join the ends, giving a circumference of 12 inches. Pinch the ends together like this. That makes a can that maximizes volume without wasting metal by cutting.
If you're talking about a traditional can like the one in the picture, I have no idea.
link to original post
To make it clear, you can form the one square foot of metal any way you like. In other words, you can cut it, melt it, and shape it however you wish. The goal is to make a normal shaped can.
Quote: WizardI may have asked this one before, but here goes:
You are allowed 1 square foot of metal to make a can, including the top and bottom. What is the radius of the can that maximizes the volume?
link to original post
Or maybe rusty calculus...
Area
2*pi*r^2 + 2*pi*r*h=1
h=1/(2*pi*r) - r
Volume
V=pi * r^2 * h = r/2 - pi*r^3
dV/dr = 1/2 - 3*pi*r^2 = 0
r= 1/sqrt(6*pi)
or some typo permutation of that....
Quote: chevy
Or maybe rusty calculus...
Area
2*pi*r^2 + 2*pi*r*h=1
h=1/(2*pi*r) - r
Volume
V=pi * r^2 * h = r/2 - pi*r^3
dV/dr = 1/2 - 3*pi*r^2 = 0
r= 1/sqrt(6*pi)
or some typo permutation of that....
link to original post
I agree! That one is beer worthy. Please add it to my tab.


