Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted

Find the smallest positive integer whose last digit is "6" such that moving the "6" to the beginning of the number increases its value by a factor of 4. For example, the number 1236 would be transformed to 6123, which is more than four times as large, while 3126 becomes 6312, which is less than four times as large.
You are to find a number which is transformed to one exactly four times as large.
Quote: Gialmere
Find the smallest positive integer whose last digit is "6" such that moving the "6" to the beginning of the number increases its value by a factor of 4. For example, the number 1236 would be transformed to 6123, which is more than four times as large, while 3126 becomes 6312, which is less than four times as large.
You are to find a number which is transformed to one exactly four times as large.
link to original post
So the first number I tried was 1546. Didnít work so must have more digits. With 5 digits the closest without going over is 15346. So have to try six digits with some digit inserted before the 3 and 4.
153,846 works. Times 4 is 615,384.
I assume thereís a better way than my trial and error to find the middle digits.
Quote: Gialmere
Find the smallest positive integer whose last digit is "6" such that moving the "6" to the beginning of the number increases its value by a factor of 4. For example, the number 1236 would be transformed to 6123, which is more than four times as large, while 3126 becomes 6312, which is less than four times as large.
You are to find a number which is transformed to one exactly four times as large.
link to original post
153846
153846 * 4 = 615384
Quote: Ace2With the average arrival time of one passenger per minute, the answer is ten minus the integral from zero to ten of x^12 * x / (e^x * 12!) divided by the integral from zero to ten of x^12 / (e^x * 12!). The 12! cancels so we are left with ten minus the gamma function of 14 divided by the gamma function of 13, albeit the lower incomplete gamma function since we are integrating from zero to ten instead of zero to infinity. Therefore the answer can be expressed as:
10 - γ(14,10) / γ(13,10) =
10 - (13! - 118569301068800/e^10) / (12! − 8351484697600/e^10)
=~ 1.547 minutes
link to original post
I'm afraid I haven't seen the Gamma function in almost 40 years and didn't really get what it was for at the time either. So, basically, I couldn't follow this. I would need a lot more steps to follow what you were doing.
Quote: GialmereFind the smallest positive integer whose last digit is "6" such that moving the "6" to the beginning of the number increases its value by a factor of 4. For example, the number 1236 would be transformed to 6123, which is more than four times as large, while 3126 becomes 6312, which is less than four times as large.
You are to find a number which is transformed to one exactly four times as large.
link to original post
Let n be the number of digits
4 (10^(n-1) an-1 + 10^(n-2) an-2 + ... + 10 a1 + 6) = 6 x 10^(n-1) + 10^(n-1) an-2 + 10^(n-2) an-3 + ... + a1
39 (10^(n-2) an-1 + 10^(n-3) an-2 + ... + 10 a2 + a1) = 6 x 10^(n-1) - 24
13 (10^(n-2) an-1 + 10^(n-3) an-2 + ... + 10 a2 + a1) = 2 x 10^(n-1) - 8
The smallest n where 2 x 10^(n-1) - 8 is a multiple of 13 is 6; (2 x 10^5 - 8) / 13 = 15,384, so the original number is 153,846
Quote: unJonThe original number ends in 6 and gets multiplied by 4 so the final number must end in 4. The final number starts with 6 so the original number must start with 15.
So the first number I tried was 1546. Didnít work so must have more digits. With 5 digits the closest without going over is 15346. So have to try six digits with some digit inserted before the 3 and 4.
153,846 works. Times 4 is 615,384.
I assume thereís a better way than my trial and error to find the middle digits.
link to original post
Quote: gordonm888
153846
153846 * 4 = 615384
link to original post
Quote: ThatDonGuy
Let n be the number of digits
4 (10^(n-1) an-1 + 10^(n-2) an-2 + ... + 10 a1 + 6) = 6 x 10^(n-1) + 10^(n-1) an-2 + 10^(n-2) an-3 + ... + a1
39 (10^(n-2) an-1 + 10^(n-3) an-2 + ... + 10 a2 + a1) = 6 x 10^(n-1) - 24
13 (10^(n-2) an-1 + 10^(n-3) an-2 + ... + 10 a2 + a1) = 2 x 10^(n-1) - 8
The smallest n where 2 x 10^(n-1) - 8 is a multiple of 13 is 6; (2 x 10^5 - 8) / 13 = 15,384, so the original number is 153,846
link to original post
Correct!!
Well done.
----------------------------------
The Odor of Operations

Quote: GialmereYou are to find a number which is transformed to one exactly four times as large.
link to original post
I show 153846153846 also works.
I suspect the 153846 can repeated any number of times and it will still work, but more than 2x bumps up against the limits of Excel.
Quote: WizardQuote: GialmereYou are to find a number which is transformed to one exactly four times as large.
link to original post
I show 153846153846 also works.
I suspect the 153846 can repeated any number of times and it will still work, but more than 2x bumps up against the limits of Excel.
link to original post
Break the number up into blocks of 6 digits; when you multiply each 153846 block by 4, you get 615384. In effect, the 6 on the right of each block is "pushed into" the leftmost digit of the block to its right.
Furthermore look at various fractions, such as 1/7, 1/13, 1/17 etc. and these are repeating decimals. So it transpires 999999/7 has one loop of six numbers, and 428571 is 3*142857 and 714285=5*142857.
999...999/17 (0 588 235 294 117 647) has one loop of sixteen numbers. Sadly the latter loop doesn't have the nice property that the 7s or 13s had.
I haven't looked at higher numbers as my simple excel breaks down and it's too late to start a program!

You are given three parallel panes of glass. Each pane will transmit 70%, reflect 20%, and absorb 10% of the light that falls on it.
If a light source is placed on one side of the three panes, what is the total percentage of light that passes through to the other side?
I get 0.73 / 0.962 or about 37.22%.
(Some light transmitted through the first pane will be reflected back and forth between the first and second panes before transmission through the second pane. Likewise, some light transmitted through the second pane will be reflected back and forth between the second pane and third pane before transmission through the third pane.)
I change my answer to 0.380266075388.
Consider the panes labeled A B and C from west to east, with the light initially going east.
Let x = Prob(Light reaches B east gets through) = 0.729166666667
Let y = Prob(Light reaches B west eventually goes from B to C) = 0.302083333333
Let z = Prob(Light reaches C gets through) = 0.745011086475
Answer = 0.7*x*z = 0.380266075388
Please note my two extra digits beyond Don's answer, to show I'm not just copying him.
He should get credit for being first, assuming we're right in the first place.
I get 38.02660754%, but I can't find a "closed form" solution for it.
I do get a Markov-style chain:
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
c(n) be the amount of light between panes 2 and 3, heading toward pane 2,
d(n) be the amount of light between panes 2 and 3, heading toward pane 3,
and e(n) the amount of light that passes through pane 3
I get:
a(n) = 0.2 b(n-1) + 0.7 c(n-1)
b(n) = 0.2 a(n-1)
c(n) = 0.2 d(n-1)
d(n) = 0.7 b(n-1) + 0.2 c(n-1)
e(n) = e(n-1) + 0.7 d(n-1)
With the initial condition that b(0) = 0.7 (representing 70% of the light that entered in the first place) and a(0) = c(0) = d(0) = e(0) = 0.
I would like to see how this can be reduced to a closed form solution, if possible.
I used a spreadsheet and recursion to get my answer.
The solution given from going into A and coming out of B is based on 70% from A into B, then 70% of that from B towards C. This can happen once (i.e. straight through) or be repeated after the light has returned to A from B and then reversed back to B, this is 20%2. The return journey can also continue to happen multiple times. So in essence the first part is 70%*70%*(1+.22+.24+...) which gives the (1-.04)=.96 denominator. Since the same can happen between B and C, this leads to the denominator of .962 and numerator of .73.
Thus I think the factor just needs to be adjusted slightly for the possible return journey of ABCBA. That's where I've got to.
See my comments inserted in your method
I get 38.02660754%, but I can't find a "closed form" solution for it.
I do get a Markov-style chain:
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
c(n) be the amount of light between panes 2 and 3, heading toward pane 2,
d(n) be the amount of light between panes 2 and 3, heading toward pane 3,
and e(n) the amount of light that passes through pane 3
I get:
a(n) = 0.2 b(n-1) + 0.7 c(n-1)**
** isn't light from c(n-1) heading toward 2....so 70% would then be heading toward 1 (i.e. for b(n))?
b(n) = 0.2 a(n-1) + **
c(n) = 0.2 d(n-1)
d(n) = 0.7 b(n-1)**** + 0.2 c(n-1)
**** Isn't light from b(n-1) heading toward 1, so 70% would exit out of 1...should this be a(n-1)?
e(n) = e(n-1) + 0.7 d(n-1)
Basically, I don't know Markov chains, but just from your definitions, it seems it should be
a(n) = 0.2 b(n-1)
b(n) = 0.2 a(n-1). + 0.7 c(n-1)**
c(n) = 0.2 d(n-1)
d(n) = 0.7 a(n-1) **** + 0.2 c(n-1)
e(n) = e(n-1) + 0.7 d(n-1)
link to original post
Quote: chevy
See my comments inserted in your method
I get 38.02660754%, but I can't find a "closed form" solution for it.
I do get a Markov-style chain:
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
c(n) be the amount of light between panes 2 and 3, heading toward pane 2,
d(n) be the amount of light between panes 2 and 3, heading toward pane 3,
and e(n) the amount of light that passes through pane 3
I get:
a(n) = 0.2 b(n-1) + 0.7 c(n-1)**
** isn't light from c(n-1) heading toward 2....so 70% would then be heading toward 1 (i.e. for b(n))?
b(n) = 0.2 a(n-1) + **
c(n) = 0.2 d(n-1)
d(n) = 0.7 b(n-1)**** + 0.2 c(n-1)
**** Isn't light from b(n-1) heading toward 1, so 70% would exit out of 1...should this be a(n-1)?
e(n) = e(n-1) + 0.7 d(n-1)
Basically, I don't know Markov chains, but just from your definitions, it seems it should be
a(n) = 0.2 b(n-1)
b(n) = 0.2 a(n-1). + 0.7 c(n-1)**
c(n) = 0.2 d(n-1)
d(n) = 0.7 a(n-1) **** + 0.2 c(n-1)
e(n) = e(n-1) + 0.7 d(n-1)
link to original post
link to original post
Light from (c) will go through Pane 2 into the area between 2 and 1, headed toward 1, so it will be in (a).
Similarly, light from (b) will go through Pane 2 into the area between 2 and 3, headed toward 3, so it will be in (d).
Note that (a) and (b) are both between Panes 1 and 2, and (c) and (d) are both between Panes 2 and 3. Each has two letters as you have to differentiate in which direction the light is moving.
Quote: ThatDonGuyQuote: chevy
See my comments inserted in your method
I get 38.02660754%, but I can't find a "closed form" solution for it.
I do get a Markov-style chain:
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
c(n) be the amount of light between panes 2 and 3, heading toward pane 2,
d(n) be the amount of light between panes 2 and 3, heading toward pane 3,
and e(n) the amount of light that passes through pane 3
I get:
a(n) = 0.2 b(n-1) + 0.7 c(n-1)**
** isn't light from c(n-1) heading toward 2....so 70% would then be heading toward 1 (i.e. for b(n))?
b(n) = 0.2 a(n-1) + **
c(n) = 0.2 d(n-1)
d(n) = 0.7 b(n-1)**** + 0.2 c(n-1)
**** Isn't light from b(n-1) heading toward 1, so 70% would exit out of 1...should this be a(n-1)?
e(n) = e(n-1) + 0.7 d(n-1)
Basically, I don't know Markov chains, but just from your definitions, it seems it should be
a(n) = 0.2 b(n-1)
b(n) = 0.2 a(n-1). + 0.7 c(n-1)**
c(n) = 0.2 d(n-1)
d(n) = 0.7 a(n-1) **** + 0.2 c(n-1)
e(n) = e(n-1) + 0.7 d(n-1)
link to original post
link to original post
Light from (c) will go through Pane 2 into the area between 2 and 1, headed toward 1, so it will be in (a).
Similarly, light from (b) will go through Pane 2 into the area between 2 and 3, headed toward 3, so it will be in (d).
Note that (a) and (b) are both between Panes 1 and 2, and (c) and (d) are both between Panes 2 and 3. Each has two letters as you have to differentiate in which direction the light is moving.
link to original post
Thanks for the response. You said
Light from (c) will go through Pane 2 into the area between 2 and 1, headed toward 1, so it will be in (a).
But your definition for (a) and (b) is
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
Isn't heading toward pane 1 (b)?
Similarly, you said
light from (b) will go through Pane 2 into the area between 2 and 3, headed toward 3, so it will be in (d).
But your definition for (b) has light heading to pane 1??? So light from (b) will not go through pane 2???
I think maybe it is the definitions that have the typo??? Should it be
Let a(n) be the amount of light between panes 1 and 2, heading toward pane ****1*****,
b(n) be the amount of light between panes 1 and 2, heading toward pane ******2*****,
Then I think I would agree with your original equations and your response to my query?????
And if I am still mixing it up, I accept I am wrong as I am just trying to tag along on your approach, not solve it.
thanks
Quote: chevyQuote: ThatDonGuyQuote: chevy
See my comments inserted in your method
I get 38.02660754%, but I can't find a "closed form" solution for it.
I do get a Markov-style chain:
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
c(n) be the amount of light between panes 2 and 3, heading toward pane 2,
d(n) be the amount of light between panes 2 and 3, heading toward pane 3,
and e(n) the amount of light that passes through pane 3
I get:
a(n) = 0.2 b(n-1) + 0.7 c(n-1)**
** isn't light from c(n-1) heading toward 2....so 70% would then be heading toward 1 (i.e. for b(n))?
b(n) = 0.2 a(n-1) + **
c(n) = 0.2 d(n-1)
d(n) = 0.7 b(n-1)**** + 0.2 c(n-1)
**** Isn't light from b(n-1) heading toward 1, so 70% would exit out of 1...should this be a(n-1)?
e(n) = e(n-1) + 0.7 d(n-1)
Basically, I don't know Markov chains, but just from your definitions, it seems it should be
a(n) = 0.2 b(n-1)
b(n) = 0.2 a(n-1). + 0.7 c(n-1)**
c(n) = 0.2 d(n-1)
d(n) = 0.7 a(n-1) **** + 0.2 c(n-1)
e(n) = e(n-1) + 0.7 d(n-1)
link to original post
link to original post
Light from (c) will go through Pane 2 into the area between 2 and 1, headed toward 1, so it will be in (a).
Similarly, light from (b) will go through Pane 2 into the area between 2 and 3, headed toward 3, so it will be in (d).
Note that (a) and (b) are both between Panes 1 and 2, and (c) and (d) are both between Panes 2 and 3. Each has two letters as you have to differentiate in which direction the light is moving.
link to original post
Thanks for the response. You said
Light from (c) will go through Pane 2 into the area between 2 and 1, headed toward 1, so it will be in (a).
But your definition for (a) and (b) is
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
Isn't heading toward pane 1 (b)?
Similarly, you said
light from (b) will go through Pane 2 into the area between 2 and 3, headed toward 3, so it will be in (d).
But your definition for (b) has light heading to pane 1??? So light from (b) will not go through pane 2???
I think maybe it is the definitions that have the typo??? Should it be
Let a(n) be the amount of light between panes 1 and 2, heading toward pane ****1*****,
b(n) be the amount of light between panes 1 and 2, heading toward pane ******2*****,
Then I think I would agree with your original equations and your response to my query?????
And if I am still mixing it up, I accept I am wrong as I am just trying to tag along on your approach, not solve it.
thanks
link to original post
You are correct; the original directions are incorrect.
a(n) is the amount of light between panes 1 and 2, heading back toward pane 1
b(n) is the amount of light between panes 1 and 2, heading toward pane 2
c(n) is the amount of light between panes 2 and 3, heading back toward pane 2
d(n) is the amount of light between panes 2 and 3, heading toward pane 3
If you calculate every step in terms of the step that was two before it (i.e.. a(n) through e(n) in terms of a(n-2) through e(n-2)), given that a(0) and d(0) = 0, you get a situation where a(0) and d(0) in every even-numbered step, and the equations reduce to:
b(n+2) = 0.04 b(n) + 0.14 c(n)
c(n+2) = 0.14 b(n) + 0.04 c(n)
e(n+2) = e(n) + 0.14 b(n) + 0.04 c(n)
Looks like a matrix algebra problem coming up...
The exact answer that I get is 343 / 902
a(n+1) = 0.2 b(n) + 0.7 c(n)
b(n+1) = 0.2 a(n)
c(n+1) = 0.2 d(n)
d(n+1) = 0.7 b(n) + 0.2 c(n)
e(n+1) = e(n) + 0.7 d(n)
a(n+2) = 0.2 b(n+1) + 0.7 c(n)
b(n+2) = 0.2 a(n+1) = 0.04 b(n) + 0.14 c(n)
c(n+2) = 0.2 d(n+1) = 0.14 b(n) + 0.04 c(n)
d(n+2) = 0.7 b(n+1) + 0.2 c(n)
e(n+2) = e(n+1) + 0.7 d(n+1) = e(n) + 0.7 d(n) + 0.49 b(n) + 0.14 c(n)
The Eigenvector matrix for (b(n), c(n)) is:
[0.04 0.14]
[ ]
[0.14 0.04]
x^2 - 0.08 x + 0.0016 - 0.0196 = 0
x = 0.04 +/- 0.14 = 0.18, -0.1
Eigenvector for x = 0.18:
[-0.14 0.14][a] [0] [1]
[ ][ ] = [ ] -> [ ]
[0.14 -0.14][b] [0] [1]
Eigenvector for x = -0.1:
[0.14 0.14][a] [0] [-1]
[ ][ ] = [ ] -> [ ]
[0.14 0.14][b] [0] [ 1]
[1 -1] [1/2 1/2]
The Eigenvector matrix is [ ], whose inverse is [ ]
[1 1] [-1/2 1/2]
[b(n)] [1 -1] [(0.18)^n 0] [1/2 1/2] [b(0)]
[ ] = [ ] [ ] [ ] [ ]
[c(n)] [1 1] [0 (-0.1)^n] [-1/2 1/2] [c(0)]
[0.18^n -(-0.1)^n] [1/2 1/2] [b(0)]
= [ ] [ ] [ ]
[0.18^n (-0.1)^n] [-1/2 1/2] [c(0)]
[(0.18^n + (-0.1)^n) / 2 (0.18^n - (-0.1)^n) / 2][b(0)]
= [ ][ ]
[(0.18^n - (-0.1)^n) / 2 (0.18^n + (-0.1)^n) / 2][c(0)]
Given b(0) = 0.7 and c(0) = 0:
b(n) = 0.35 (0.18^n + (-0.1)^n)
c(n) = 0.35 (0.18^n - (-0.1)^n)
e(n) = 0.49 b(n) + 0.14 c(n) = 0.18^n (0.49 * 0.35 + 0.14 * 0.35) + (-0.1)^n (0.49 * 0.35 - 0.14 * 0.35)
= 0.18^n * 0.35 * 0.63 + (-0.1)^n * 0.35 * 0.35
The sum over all nonegative integers n is 0.35 * 0.63 / 0.82 + 0.35 * 0.35 / 1.1
= 35/100 * 63/82 + 35/100 * 35/110
= 343 / 902
Quote: WizardI initially didn't use matrices, but Don inspired me to use that approach. That said, here is my solution (PDF).
link to original post
You didn't need matrices.
Your four equations in four unknowns are:
[1] a = 0.7 c + 0.2 b
[2] b = 0.2 a
[3] c = 0.7 + 0.2 d
[4] d = 0.7 b + 0.2 c
Substituting for b in 1:
a = 0.7 c + 0.04 a -> 0.96 a = 0.7 c -> c = (0.96 / 0.7) a = 48/35 a
Substituting for b and c in 4:
d = 0.7 b + 0.14 + 0.04 d -> 0.96 d = 0.7 b + 0.14 = 0.14 a + 0.14 -> d = 7/48 a + 7/48
Substituting for c and d in 3:
48/35 a = 0.7 + 7/240 a + 7/240
(48/35 - 7/240) a = 35/48
(48 x 240 - 35 x 7) / (35 x 240) a = (35 x 35 x 5) / (35 x 240)
(48 x 240 - 35 x 7) a = (35 x 35 x 5)
a = 6125 / 11275 = 245 / 451, or, as you put it, 490 / 902
Thatís what I was going to say. Why not just solve the four equations for a, then multiply by .7Quote: ThatDonGuyQuote: WizardI initially didn't use matrices, but Don inspired me to use that approach. That said, here is my solution (PDF).
link to original post
You didn't need matrices.
Your four equations in four unknowns are:
[1] a = 0.7 c + 0.2 b
[2] b = 0.2 a
[3] c = 0.7 + 0.2 d
[4] d = 0.7 b + 0.2 c
Substituting for b in 1:
a = 0.7 c + 0.04 a -> 0.96 a = 0.7 c -> c = (0.96 / 0.7) a = 48/35 a
Substituting for b and c in 4:
d = 0.7 b + 0.14 + 0.04 d -> 0.96 d = 0.7 b + 0.14 = 0.14 a + 0.14 -> d = 7/48 a + 7/48
Substituting for c and d in 3:
48/35 a = 0.7 + 7/240 a + 7/240
(48/35 - 7/240) a = 35/48
(48 x 240 - 35 x 7) / (35 x 240) a = (35 x 35 x 5) / (35 x 240)
(48 x 240 - 35 x 7) a = (35 x 35 x 5)
a = 6125 / 11275 = 245 / 451, or, as you put it, 490 / 902
link to original post
Quote: ThatDonGuy
I get 38.02660754%, but I can't find a "closed form" solution for it.
I do get a Markov-style chain:
Let a(n) be the amount of light between panes 1 and 2, heading toward pane 2,
b(n) be the amount of light between panes 1 and 2, heading toward pane 1,
c(n) be the amount of light between panes 2 and 3, heading toward pane 2,
d(n) be the amount of light between panes 2 and 3, heading toward pane 3,
and e(n) the amount of light that passes through pane 3
I get:
a(n) = 0.2 b(n-1) + 0.7 c(n-1)
b(n) = 0.2 a(n-1)
c(n) = 0.2 d(n-1)
d(n) = 0.7 b(n-1) + 0.2 c(n-1)
e(n) = e(n-1) + 0.7 d(n-1)
With the initial condition that b(0) = 0.7 (representing 70% of the light that entered in the first place) and a(0) = c(0) = d(0) = e(0) = 0.
I would like to see how this can be reduced to a closed form solution, if possible.
I used a spreadsheet and recursion to get my answer.
link to original post
Quote: ThatDonGuy
The exact answer that I get is 343 / 902
a(n+1) = 0.2 b(n) + 0.7 c(n)
b(n+1) = 0.2 a(n)
c(n+1) = 0.2 d(n)
d(n+1) = 0.7 b(n) + 0.2 c(n)
e(n+1) = e(n) + 0.7 d(n)
a(n+2) = 0.2 b(n+1) + 0.7 c(n)
b(n+2) = 0.2 a(n+1) = 0.04 b(n) + 0.14 c(n)
c(n+2) = 0.2 d(n+1) = 0.14 b(n) + 0.04 c(n)
d(n+2) = 0.7 b(n+1) + 0.2 c(n)
e(n+2) = e(n+1) + 0.7 d(n+1) = e(n) + 0.7 d(n) + 0.49 b(n) + 0.14 c(n)
The Eigenvector matrix for (b(n), c(n)) is:
[0.04 0.14]
[ ]
[0.14 0.04]
x^2 - 0.08 x + 0.0016 - 0.0196 = 0
x = 0.04 +/- 0.14 = 0.18, -0.1
Eigenvector for x = 0.18:
[-0.14 0.14][a] [0] [1]
[ ][ ] = [ ] -> [ ]
[0.14 -0.14][b] [0] [1]
Eigenvector for x = -0.1:
[0.14 0.14][a] [0] [-1]
[ ][ ] = [ ] -> [ ]
[0.14 0.14][b] [0] [ 1]
[1 -1] [1/2 1/2]
The Eigenvector matrix is [ ], whose inverse is [ ]
[1 1] [-1/2 1/2]
[b(n)] [1 -1] [(0.18)^n 0] [1/2 1/2] [b(0)]
[ ] = [ ] [ ] [ ] [ ]
[c(n)] [1 1] [0 (-0.1)^n] [-1/2 1/2] [c(0)]
[0.18^n -(-0.1)^n] [1/2 1/2] [b(0)]
= [ ] [ ] [ ]
[0.18^n (-0.1)^n] [-1/2 1/2] [c(0)]
[(0.18^n + (-0.1)^n) / 2 (0.18^n - (-0.1)^n) / 2][b(0)]
= [ ][ ]
[(0.18^n - (-0.1)^n) / 2 (0.18^n + (-0.1)^n) / 2][c(0)]
Given b(0) = 0.7 and c(0) = 0:
b(n) = 0.35 (0.18^n + (-0.1)^n)
c(n) = 0.35 (0.18^n - (-0.1)^n)
e(n) = 0.49 b(n) + 0.14 c(n) = 0.18^n (0.49 * 0.35 + 0.14 * 0.35) + (-0.1)^n (0.49 * 0.35 - 0.14 * 0.35)
= 0.18^n * 0.35 * 0.63 + (-0.1)^n * 0.35 * 0.35
The sum over all nonegative integers n is 0.35 * 0.63 / 0.82 + 0.35 * 0.35 / 1.1
= 35/100 * 63/82 + 35/100 * 35/110
= 343 / 902
link to original post
Quote: WizardI initially didn't use matrices, but Don inspired me to use that approach. That said, here is my solution (PDF).
link to original post
Correct!!
Nailed it. In ThatDonGuy's case, twice.
I'll post the official solve if anyone wants it, but the above covers all the bases.
------------------------------------------------
b. 100,000 km/s
c.
d. 1,000,000 km/s

Quote: ThatDonGuyYou didn't need matrices.
link to original post
I know. I didn't use them in my first solution, but it took longer and would be harder to explain, as it involves infinite sums.
If anyone caresÖQuote: Ace2Extra credit part 2:Quote: Ace2A study of one billion email accounts shows that they received an average of four spam emails within 24 hours of creating the account, sixteen spams within 48 hours and thirty-six spams within 72 hours.
Assuming the aforementioned growth rate is continuous, starts the instant an account is opened and never ends, whatís the expected waiting time for a new account to receive its first spam ?
link to original post
What is the standard deviation of the expected waiting time?
link to original post
The tricky part is getting the probability p(f) of the first spam occurring at any specific point in time t. Since the probability p(z) of zero cumulative spams at time t is 1/e^(t^2), the derivative of t^2 times p(z) times the spacing used gives us p(f) of 2t/e^(t^2)
We already know the expected value of the first spam is π^.5/2 periods. So we can easily calculate the variance as the integral from zero to infinity of p(f) * (t - π^.5/2)^2 dt, expanded as 2t / e^(t^2) * (t - π^.5/2)^2 dt, which evaluates to: 1 - π/4. Therefore, the standard deviation is (1 - π/4)^.5 periods, multiplied by 12 is ~5.56 hours
Footnote: to calculate the probability of, for example, the first spam arriving between 3 and 3.001 periods, it's exactly: 1/e^3^2 - 1/e^3.001^2 =~ 7.38 * 10^-7. Since the difference between the bases (that e is taken to) is only 1/1000, we can treat the change as continuous and therefore use the derivative of 3^2 = 6 to determine the rate of change at that point. So, 1/e^3 * 6 / 1000 =~ 7.40 * 10^7, quite accurate at 1/1000 spacing and exact as the denominator approaches ♾️. That derivative of 2t allows us to integrate chance of the first spam over all time and calculate the variance.
If anyone cares part twoÖQuote: Ace2Extra credit part 3:Quote: Ace2A study of one billion email accounts shows that they received an average of four spam emails within 24 hours of creating the account, sixteen spams within 48 hours and thirty-six spams within 72 hours.
Assuming the aforementioned growth rate is continuous, starts the instant an account is opened and never ends, whatís the expected waiting time for a new account to receive its first spam ?
link to original post
What is the mode (most common value) of the waiting time to receive the first spam ?
link to original post
The derivative of 2t/e^(t^2) (see above) is: -(4t^2 - 2)/e^(t^2). Setting that to zero and solving for t gives the answer of 1/2^.5 periods, multiplied by 12 is ~8.49 hours
To recap, the expected value, median, standard deviation and mode of the first spam received are (respectively, expressed in 12-hour periods):
√π / 2
sqrt(Ln(2))
(1 - π/4)^.5
1/2^.5
What is the number of positive integer solutions (x, y, z) for the system of simultaneous equations:
xy + yz = 63
xz + yz = 23
Subtract the second equation from the first:
x (y - z) = 40
Since x, y, and z are positive integers, x and (y - z) are both factors of 40, and since x > 0, y > z
Checking each possible factor of x:
x ; y-z ; 23 = z (x + y) = z (x + (z + (y-z))) = z (z + (x + (y-z)))
1 ; 40 ; z (z + 41)
2 ; 20 ; z (z + 22)
4 ; 10 ; z (z + 14)
5 ; 8 ; z (z + 13)
8 ; 5 ; z (z + 13)
10 ; 4 ; z (z + 14)
20 ; 2 ; z (z + 22)
40 ; 1 ; z (z + 41)
Since 23 is prime, one of the two factors of the last number in each line is 1 and the other is 23, so only z = 1 works
The only solutions in positive integers are (2, 21, 1) and (20, 3, 1)
For the first, xy + yz = 42 + 21 = 63
For the second, xy + yz = 60 + 3 = 63
The two solutions are (2, 21, 1) and (20, 3, 1)
Quote: ThatDonGuy
Subtract the second equation from the first:
x (y - z) = 40
Since x, y, and z are positive integers, x and (y - z) are both factors of 40, and since x > 0, y > z
Checking each possible factor of x:
x ; y-z ; 23 = z (x + y) = z (x + (z + (y-z))) = z (z + (x + (y-z)))
1 ; 40 ; z (z + 41)
2 ; 20 ; z (z + 22)
4 ; 10 ; z (z + 14)
5 ; 8 ; z (z + 13)
8 ; 5 ; z (z + 13)
10 ; 4 ; z (z + 14)
20 ; 2 ; z (z + 22)
40 ; 1 ; z (z + 41)
Since 23 is prime, one of the two factors of the last number in each line is 1 and the other is 23, so only z = 1 works
The only solutions in positive integers are (2, 21, 1) and (20, 3, 1)
For the first, xy + yz = 42 + 21 = 63
For the second, xy + yz = 60 + 3 = 63
The two solutions are (2, 21, 1) and (20, 3, 1)
link to original post
(i) (x+y)z=23 and (ii) (x+z)y=63.
Using (i) as 23 is prime z is either 23 or 1, so z=1 (as (x+y) must be 2 or bigger), also note x+y=23.
Using (ii) 63 = 7x9 = 7x3x3. So y is a factor of 63, and (x+1) the other factor
Remember x+y = 23, so neither can be >22.
y = 21 or 9 or 7 or 3 or 1 giving
x = 2 or 6 or 8 or 20 or >22
So 2 21 and 20 3 are the only pair adding up to 23.
This gives the two solutions.
btw I believe there's another method which creates a quadratic equation, but recognising factors seems to be the easiest way.
Quote: charliepatrickbtw I believe there's another method which creates a quadratic equation, but recognising factors seems to be the easiest way.
z (x + y) = 23
z = 1; x + y = 23
y = 23 - x
y (x + z) = 63
(23 - x)(x + 1) = 63
22 x - x^2 + 23 = 63
x^2 - 22 x + 40 = 0
(x - 20)(x - 2) = 0
x = 2, 20

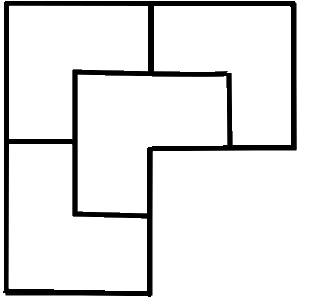
The figure is obtained by joining three squares.
Divide the given region in four congruent pieces.
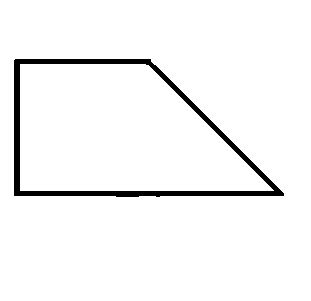
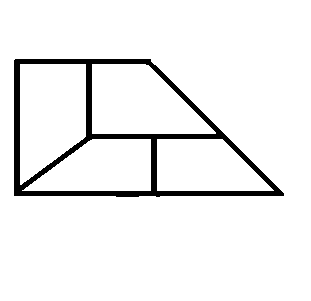
The given figure is a trapezoid obtained by gluing together a square and an isosceles right triangle.
Divide the given region in four congruent pieces.
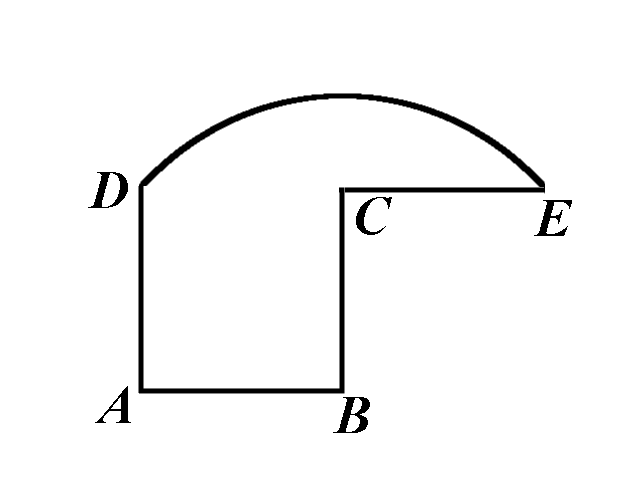
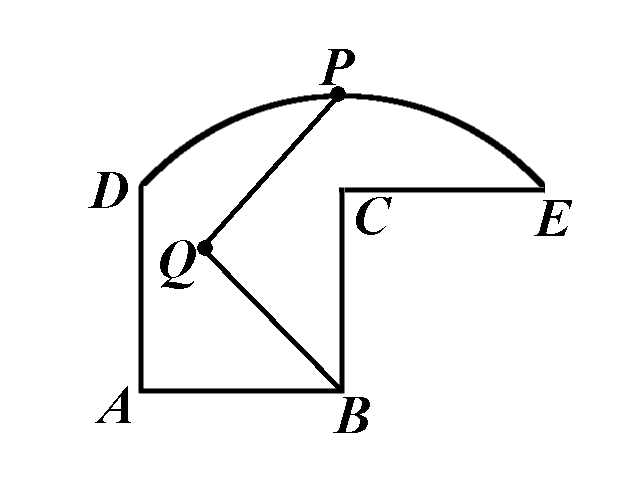
In this figure ABCD is a square, CE = BC, and the arc DE is centered at B.
Divide the given region in two congruent pieces.
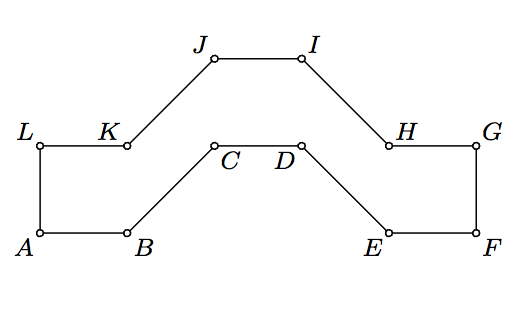
In the figure above ABKL, CDIJ, and EFGH are congruent squares and KBCJ, DEHI are parallelograms with KB = BC = DE = EH.
Divide the given region in five congruent pieces.

The hardest part of some of these solutions is figuring out a way to display or express the solution.
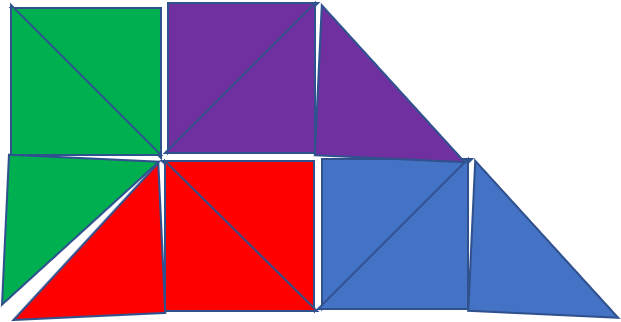
I believe there is no solution to Puzzle #3. The square part of the shape lies entirely to one side of the line of symmetry for dividing the circular segment into two congruent shapes.
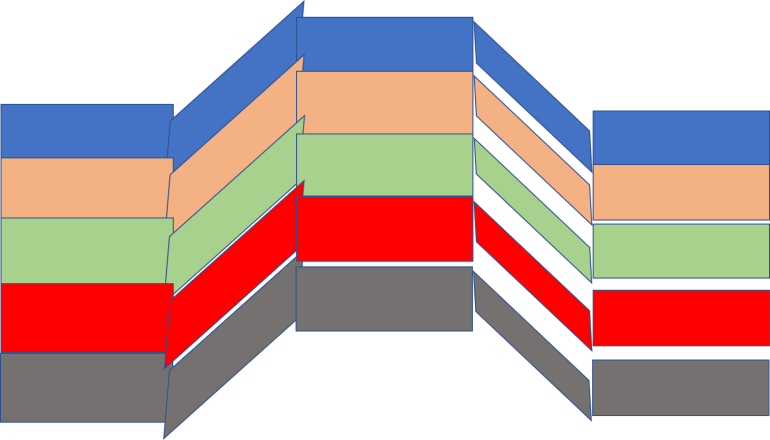
This is a terrible graphic but it gives the basic idea:
Quote: gordonm888
The hardest part of some of these solutions is figuring out a way to display or express the solution.
link to original post
Quote: gordonm888
This is a terrible graphic but it gives the basic idea:
link to original post
Correct!
Very good.
-----------------------------------------------------
Surgeon: "I know, I am."
----------------------------------------------------
Quote: TigerWuSilly me... I came here looking for EASY math puzzles...
link to original post
That's a good point and, in fact, the Wizard on a livestream once said this thread's title was misleading. The trouble is, "easy" is a very relative term. What is an easy math puzzle on a site populated by math geeks, many of whom are professional mathematicians?
If I asked 100 random people how much more likely it is to get a 7 before a 4 if I rolled a pair of dice, I would be shocked if 50% of them could figure it out. It's really not an easy question if you never considered what happens when two dice are rolled. If I presented that puzzle here, however, I'd be laughed off the site for posting something so simplistic. (Wow! Thanks for the challenge Elmo! Okay, Sesame Street is back that way. Move along now.)
Through some trial and error I've concluded that a math puzzle considered challenging to a high school senior is what this board considers "easy". Hard puzzles are from the college level or math competitions. Obviously there are exceptions to this rule, and some "fun" puzzles (such as logic mazes and rebus puzzles) are often only marginally mathematical. One of my favorite puzzles was the Mathematician's License Plates where math skills were needed but was really more of a history quiz.
Still, if the "Easy" was dropped from this thread's title, you'd get no argument from me.

Equilateral triangle EKP with side EK of length 2 inches is placed inside square EAMI with side of length 4 inches so that K is on side EA. The triangle is rotated clockwise about K, then P, and so on along the sides of the square until E, K, and P return to their original positions.
What is the length of the path in inches traversed by vertex P?
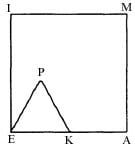
Quote: GialmereIt's Toughie Tuesday. Let's play...
Equilateral triangle EKP with side EK of length 2 inches is placed inside square EAMI with side of length 4 inches so that K is on side EA. The triangle is rotated clockwise about K, then P, and so on along the sides of the square until E, K, and P return to their original positions.
What is the length of the path in inches traversed by vertex P?
link to original post
Just guessing on general principles: π*4 inches
120+30+120+30+120+120+30+30+30+30+120+120+30+120+30+120
=1200 Degree
The length of the path in inches traversed by vertex P,
(1200/360)x2 Pi x2 = 40 Pi/3
The spoiler box shows a way I believe I can do it with x tickets, but maybe you can do better.
x=47
- 1,2,3,4,9
- 1,2,5,6,9
- 1,2,7,8,9
- 3,4,5,6,9
- 3,4,7,8,9
- 5,6,7,8,9
- 1,2,3,4,10
- 1,2,5,6,10
- 1,2,7,8,10
- 3,4,5,6,10
- 3,4,7,8,10
- 5,6,7,8,10
- 11,12,13,14,19
- 11,12,15,16,19
- 11,12,17,18,19
- 13,14,15,16,19
- 1314,,17,18,19
- 15,16,17,18,19
- 11,12,13,14,20
- 11,12,15,16,20
- 11,12,17,18,20
- 13,14,15,16,20
- 1314,,17,18,20
- 15,16,17,18,20
- 21,22,23,24,29
- 21,22,25,26,29
- 21,22,27,28,29
- 23,24,25,26,29
- 2324,,27,28,29
- 25,26,27,28,29
- 21,22,23,24,30
- 21,22,25,26,30
- 21,22,27,28,30
- 23,24,25,26,30
- 2324,,27,28,30
- 25,26,27,28,30
- 31,32,33,34,35
- 31,32,33,34,35
- 31,32,33,34,35
- 31,32,33,34,36
- 31,32,33,34,36
- 31,32,33,34,36
- 31,32,33,34,37
- 31,32,33,34,37
- 31,32,33,34,37
- 9,10,19,20,x
- x,x,35,36,37
Where x = anything
If you think I'm wrong, give me a set of 5 numbers where no ticket matches at least two.
Update: A better answer and solution appear as a response to this post.
Quote: acesideTotal angle of rotation for point P:
120+30+120+30+120+120+30+30+30+30+120+120+30+120+30+120
=1200 Degree
The length of the path in inches traversed by vertex P,
(1200/360)x2 Pi x2 = 40 Pi/3
link to original post
Correct!!
Excellent, and nice graphic.
------------------------------------------
Quote: ThatDonGuyOne small problem with the solution: it's a 5/37 game, but your solution assumes it's a 6/37 one.
link to original post
Well, that's embarrassing.
I just redid my answer to match the five picks. I have a feeling my solution can be improved upon. Let's see.
Quote: WizardI just redid my answer to match the five picks. I have a feeling my solution can be improved upon. Let's see.
link to original post
This sort of thing is a "known problem" in mathematics. I vaguely remember somebody posting a 40-ticket solution to a 6/49 game that guaranteed at least one number would have at least 3 hits.
I am trying a Monte Carlo-style solution (generate random tickets one at a time until all C(37,5) possible number draws match at least two numbers on at least one ticket), but the best I have gotten so far is 65.
Each ticket can contain c(5,2) = 10 unique pairs
So 660/10 = 66 tickets + 1 = 67 total
Just a guess
at first glance, I donít see a ticket containing 29 and 30Quote: WizardIn the Cash 5 game of the Texas Lottery, the player picks 5 numbers from 1 to 37. The state does the same via a random draw. If the two or more match, the player wins. What is the least number of tickets you need to buy to ensure a win? You may choose your own numbers.
The spoiler box shows a way I believe I can do it with x tickets, but maybe you can do better.
x=45
- 1,2,3,4,9
- 1,2,5,6,9
- 1,2,7,8,9
- 3,4,5,6,9
- 3,4,7,8,9
- 5,6,7,8,9
- 1,2,3,4,10
- 1,2,5,6,10
- 1,2,7,8,10
- 3,4,5,6,10
- 3,4,7,8,10
- 5,6,7,8,10
- 11,12,13,14,19
- 11,12,15,16,19
- 11,12,17,18,19
- 13,14,15,16,19
- 1314,,17,18,19
- 15,16,17,18,19
- 11,12,13,14,20
- 11,12,15,16,20
- 11,12,17,18,20
- 13,14,15,16,20
- 1314,,17,18,20
- 15,16,17,18,20
- 21,22,23,24,29
- 21,22,25,26,29
- 21,22,27,28,29
- 23,24,25,26,29
- 2324,,27,28,29
- 25,26,27,28,29
- 21,22,23,24,30
- 21,22,25,26,30
- 21,22,27,28,30
- 23,24,25,26,30
- 2324,,27,28,30
- 25,26,27,28,30
- 31,32,33,34,35
- 31,32,33,34,35
- 31,32,33,34,35
- 31,32,33,34,36
- 31,32,33,34,36
- 31,32,33,34,36
- 31,32,33,34,37
- 31,32,33,34,37
- 31,32,33,34,37
If you think I'm wrong, give me a set of 5 numbers where no ticket matches at least two.
link to original post
Quote: Ace2at first glance, I donít see a ticket containing 29 and 30
link to original post
Dang. I was up at night thinking about this and realized this omission and another one. When I came down to quietly add them I found you called me out on it. I have added two to the number of tickets needed.
The logic is to split the set of numbers into 25s (in this case 1-25 then 26-37 (or 40, as we'll see).
The proposal is to have five horizontal lines (H1-H5), There will also been three additional horizontal lines (H6-H8).
There will be five sets of five lines (i.e. 25 in all) which cover one number in each row, but the offset between one row and the next is +0 (i.e. a vertical line), +1 (i.e. a diagonal line), +2, +3, +4. (Note this is mod 5, so the second diagonal line goes 2, 8, 14, 20, 21 etc.)
Since there are five winning numbers either
(i) Two (or more) are within the range 1-25 OR
(ii) Four (or more) are within the range 26+.
Firstly consider (i): the (1-25) range; this can be divided into 5 horizontal lines/rows.
Either (a) one horizontal line has two winning numbers OR (b) two horizontal lines each have one winning number.
In (a) One of our first five lines will find two winnings numbers.
In (b) The two winning numbers are in different rows.
There will be five lines that go through the higher number. Because they all have different offsets, one of these will also go through the second number.
Thus the first 30 lines will find any pair of numbers in the 1-25 range.
In the second case it is known there are four numbers in the 26-40 range. Thus there must be two, or more, in one of the horizontal lines. Thus one of H6 to H8 will find two winning numbers. (As H6 and H7 would leave out 36 and 37 (e.g. 1 26 31 36 37), there needs to be another line, so it might as well be 36-40. Thus the solution works for 37-40 numbers.)
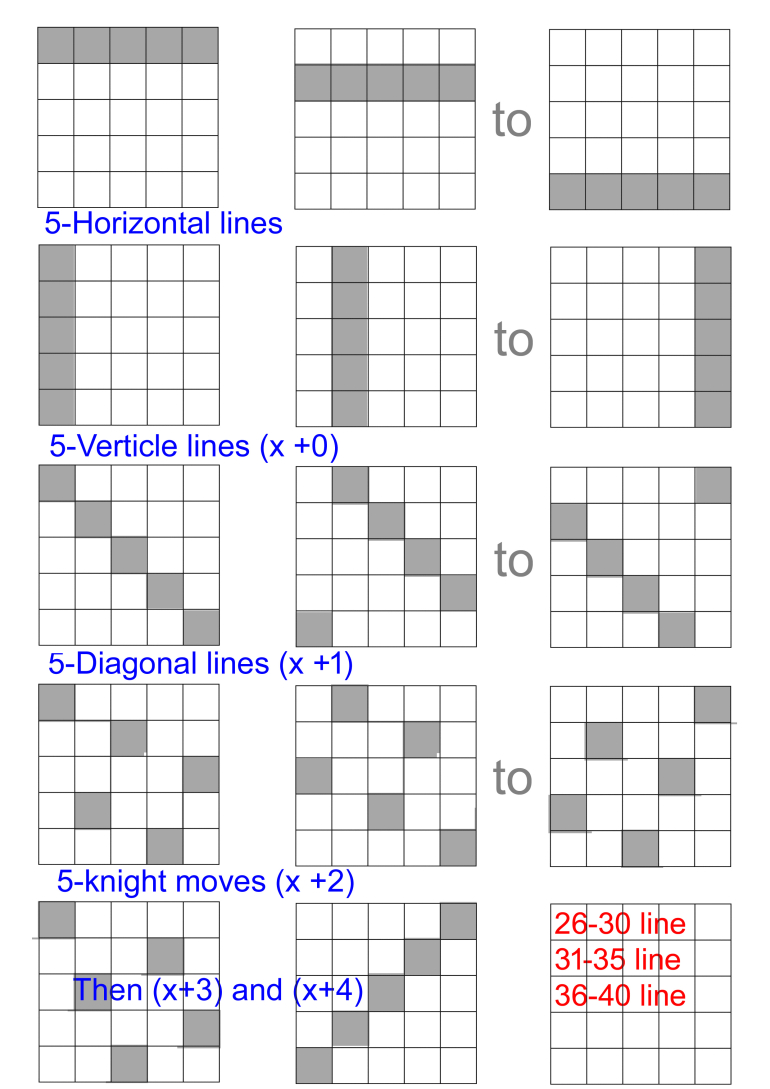
Hence the total number of lines required is 33.


