Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
After proposing my solution I did stumble across a 163-ticket wheel - http://lottery.merseyworld.com/Wheel/Wheel.html but it's confusing as the next page then looks at 57.Quote: ThatDonGuy...I vaguely remember somebody posting a 40-ticket solution to a 6/49 game that guaranteed at least one number would have at least 3 hits....
Is this a bizarre, numerical quirk, or can it be explained?
(i) 1-14 (ii) 15-28 (iii) 28-37.
Thus given there are five winnings numbers there are either two in (i) or two in (ii) or three in (iii).
The latter can be covered by the lines 28-32 and 33-37 since at least one row must have two.
I've yet to check this but the numbers 1 thru 14 can be covered with 13 lines as follows:-
(it uses the logic used above, have 1-2 with all the remaining numbers 3-14, similarly 3-4 with 5 to 14, then 5-6 with 7 to 14, then do the rest somehow. Mirror logic suggests it could start 1-5 and end 10-14, I don't know )
There might be a way to bring this down to twelve lines, for instance 7 8 appear together a lot, but I don't know.
1 2 3 4 5
1 2 6 7 8
1 2 9 10 11
1 2 12 13 14
3 4 6 7 12
3 4 8 9 13
3 4 10 11 14
5 6 7 8 13
5 6 9 10 14
5 6 8 11 12
7 8 10 11 14
7 9 11 12 13
10 12 13 any any
This give 13 lines to find any pair of numbers in 1-14.
Do the same for 15-28 (you probably only need one or two lines fewer as you don't need to cover No 28 but only 15-27; there may also be a smart way to use 10 12 13 any any etc. across the boundary.)
Thus this currently gives 13 (for 1-14) + 13 (for 15-28) + 2 (for 28-32 and 33-37), giving 28. But I suspect a few more lines can be removed.
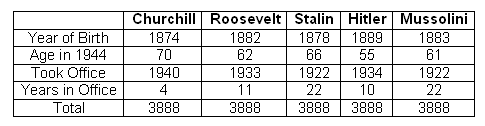
Quote: GialmereNewspapers in 1944 noted a striking coincidence:
Is this a bizarre, numerical quirk, or can it be explained?
link to original post
Quote: GialmereNewspapers in 1944 noted a striking coincidence:
Is this a bizarre, numerical quirk, or can it be explained?
link to original post
There are magic tricks based on this principle.
As was pointed out, the first two numbers will sum to 1944 for everybody who was alive in 1944.
The second two will always sum to 1944 for everyone "in office" at that time.
I personally don't do this magic trick because I find it obvious how it's done, but maybe I should try it and see how it goes.
1 2 3 5 8
1 2 3 6 7
1 2 3 4 9
4 5 6 7 8
5 6 7 8 9
I've quickly look at the last group and get seven lines
28 29 30 31 32
28 29 33 34 35
28 29 xx 36 37
30 31 32 33 34
30 31 35 36 37
xx 32 35 36 37
33 34 35 36 37
Hence this gives 5+5+5+7=22 lines.
(I haven't double checked this covers everything, but I think four blocks is a reasonable plan of attack.)
Quote: WizardQuote: GialmereNewspapers in 1944 noted a striking coincidence:
Is this a bizarre, numerical quirk, or can it be explained?
link to original post
There are magic tricks based on this principle.
As was pointed out, the first two numbers will sum to 1944 for everybody who was alive in 1944.
The second two will always sum to 1944 for everyone "in office" at that time.
I personally don't do this magic trick because I find it obvious how it's done, but maybe I should try it and see how it goes.
link to original post
Good point! Hitler became the chancellor of germany January 30, 1933
Quote: charliepatrickIf one splits the range into 1-9, 10-18, 19-27, 28-37 then there are nine numbers in the first three groups and ten in the last. There must be at least two winning numbers in one of the blocks. Using the same logic there are five lines to cover 9 numbers.
1 2 3 5 8
1 2 3 6 7
1 2 3 4 9
4 5 6 7 8
5 6 7 8 9
I've quickly look at the last group and get seven lines
28 29 30 31 32
28 29 33 34 35
28 29 xx 36 37
30 31 32 33 34
30 31 35 36 37
xx 32 35 36 37
33 34 35 36 37
Hence this gives 5+5+5+7=22 lines.
(I haven't double checked this covers everything, but I think four blocks is a reasonable plan of attack.)
link to original post
Very good work there. It certainly humbles me. I've gone through and can't find a way to do better than 5 tickets with 9 numbers and 7 with 10.
Quote: charliepatrickIt can be explained because the first two numbers (assuming it's 31st December or similar) of your current age and birth year will always add up to the current year. Similarly for something happened (took office) and time since that happened (years in office). And 3888 is twice 1944.
link to original post
Correct!!
Quote: WizardThere are magic tricks based on this principle.
As was pointed out, the first two numbers will sum to 1944 for everybody who was alive in 1944.
The second two will always sum to 1944 for everyone "in office" at that time.
I personally don't do this magic trick because I find it obvious how it's done, but maybe I should try it and see how it goes.
link to original post
Correct!!
Good show.
Their magic total, sure enough, is just twice 2009.
------------------------------------------------
Quote: GialmereGood show.
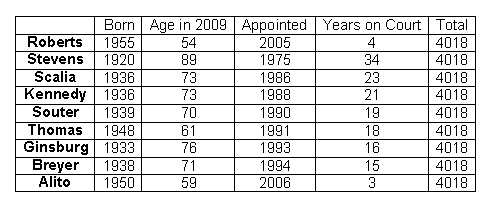
This works for any group of people — as long as they’re all still alive and working, these values will add to a miraculous constant. Here, for example, is the Supreme Court in 2009:
Their magic total, sure enough, is just twice 2009.
It only "always" works on December 31. Otherwise, if at least one person in the group has already had their birthday/anniversary that year and at least one has not, the numbers will differ by one.
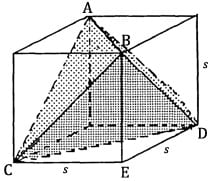
Four of the 8 vertices of a cube are vertices of a regular tetrahedron.
Find the ratio of the surface area of the cube to the surface area of the tetrahedron.

Quote: ChesterDog
link to original post
Correct!!
Well done.
------------------------------------------------------


Take the circumference of the earth at the equator to be 24,000 miles. An airplane taking off at the equator and flying west at 1000 miles an hour would land at exactly the same time that it started. Moreover, the sun would not move in the plane’s sky during the flight.
At what degree of latitude could a plane flying 500 miles per hour keep up with the sun in this way?
Quote: GialmereAt what degree of latitude could a plane flying 500 miles per hour keep up with the sun in this way?
link to original post
As an very unrelated question, how is it that Superman went back in time when he spun around the earth really fast?
Quote: aceside60 degrees
link to original post
Quote: WizardI get 60 degrees north or south latitude. This is where the circumference is half that of the equator.
As an very unrelated question, how is it that Superman went back in time when he spun around the earth really fast?
link to original post
Correct!
Very good.
------------------------------------------
"I'll always remember a certain radio exchange that occurred one day as Walt (my back-seater) and I were screaming across Southern California 13 miles high. We were monitoring various radio transmissions from other aircraft as we entered Los Angeles airspace. Although they didn't really control us, they did monitor our movement across their scope.
I heard a Cessna ask for a readout of its ground speed."90 knots" Center replied. Moments later, a Twin Beech required the same. "120 knots," Center answered. We weren't the only ones proud of our ground speed that day as almost instantly an F-18 smugly transmitted, "Ah, Center, Dusty 52 requests ground speed readout." There was a slight pause, then the response, "525 knots on the ground, Dusty." Another silent pause.
As I was thinking to myself how ripe a situation this was, I heard a familiar click of a radio transmission coming from my back-seater. It was at that precise moment I realized Walt and I had become a real crew, for we were both thinking in unison. "Center, Aspen 20, you got a ground speed readout for us?" There was a longer than normal pause....
"Aspen, I show 1,742 knots." (That's about 2005 mph)
No further inquiries were heard on that frequency.
I'm not great with geometry, but even I got this one right (though I did it by a different method than what's described in the answer).

answer

The revolving portion of a splendid barber pole is a cylinder 4 feet tall and 6 inches in radius. The red stripe is painted in a spiral around the cylinder and makes exactly 8 complete turns around it from bottom to top.
How long is the stripe?
(Ignore its width.)
I get about 25.45 feet.
The trick is to make a vertical cut in the white and red material and flatten it out. And then use the Pythagorean theorem.
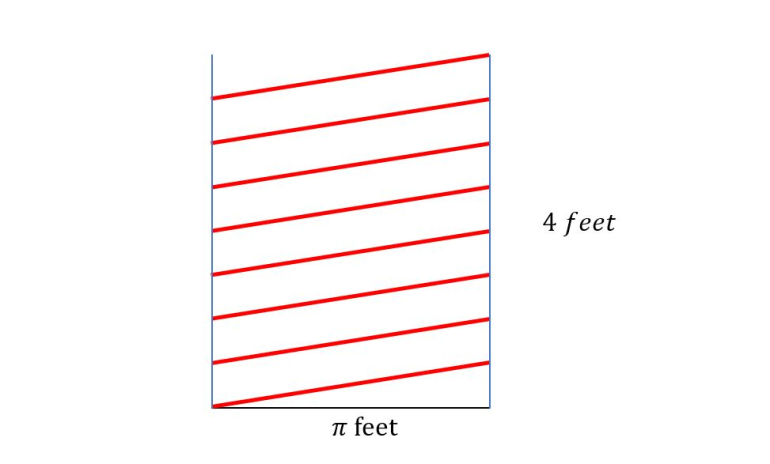
And then rearrange to get:
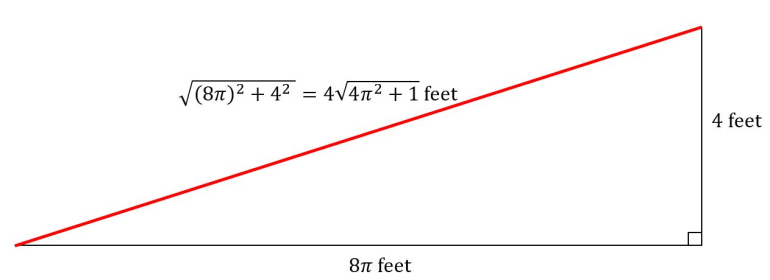
I get ~97.2π inches.
(I seem to remember something about a rope and a cylinder from maybe 3 years ago?)
The ugly bottle makes me seem more attractive.
Quote: ChesterDog
I get about 25.45 feet.
The trick is to make a vertical cut in the white and red material and flatten it out. And then use the Pythagorean theorem.
And then rearrange to get:
link to original post
Quote: Dieter
I get ~97.2π inches.
(I seem to remember something about a rope and a cylinder from maybe 3 years ago?)
The ugly bottle makes me seem more attractive.
link to original post
Correct!!
Very good.
Note, if you're a teacher doing this puzzle you can cut out a paper version of ChesterDog's triangle. Tape the 48" side to a pencil, wrap it around with the red hypotenuse becoming the stripe and then present it as innocent visual aid. If the students have trouble, slowly unravel the right angle triangle and watch their eyes widen.
-----------------------------------

Quote: Gialmere
The revolving portion of a splendid barber pole is a cylinder 4 feet tall and 6 inches in radius. The red stripe is painted in a spiral around the cylinder and makes exactly 8 complete turns around it from bottom to top.
How long is the stripe?
(Ignore its width.)
link to original post
I get sqrt(48^2 + (96*pi)^2) = 305.388726 inches.
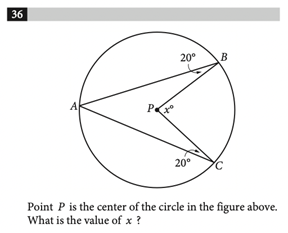
Quote: GialmereHere's one you'll often see on SAT tests...
link to original post
Quote: GialmereHere's one you'll often see on SAT tests...
link to original post
Draw line segment AP
AP, BP, and CP are all radii of the circle, so they have the same length
This means APC and BPC are isosceles triangles; PAC = PCA = 20 degrees, and PAB = PBA = 20 degrees, so APB = 180 - 20 - 20 = 140 and APC = 180 - 20 - 20 = 140, and x = 360 - (140 + 140) = 80 degrees.
The sum of the interior angles of a quadrilateral is 360 degrees. ABPC is a quadrilateral.
The angle at A is x/2, and the interior angle at P is 360 - x.
So, x/2 + 20 + 360 - x + 20 = 360
40 - x/2 = 0
x = 80 degrees.
Quote: Wizard80 degrees
link to original post
Quote: ThatDonGuy
Draw line segment AP
AP, BP, and CP are all radii of the circle, so they have the same length
This means APC and BPC are isosceles triangles; PAC = PCA = 20 degrees, and PAB = PBA = 20 degrees, so APB = 180 - 20 - 20 = 140 and APC = 180 - 20 - 20 = 140, and x = 360 - (140 + 140) = 80 degrees.
link to original post
Quote: ChesterDog
The sum of the interior angles of a quadrilateral is 360 degrees. ABPC is a quadrilateral.
The angle at A is x/2, and the interior angle at P is 360 - x.
So, x/2 + 20 + 360 - x + 20 = 360
40 - x/2 = 0
x = 80 degrees.
link to original post
Correct!!
Well done.
--------------------------------------------------
Quote: Gialmere
Geometry
link to original post
*groan*
Remind me to tell you my rope joke if we ever meet. It's too long to type out.
Quote: Gialmere[
GeometryJust sum.
link to original post
Best two jokes you’ve posted in a while!!
Quote: ChesterDog
The sum of the interior angles of a quadrilateral is 360 degrees. ABPC is a quadrilateral.
The angle at A is x/2, and the interior angle at P is 360 - x.
So, x/2 + 20 + 360 - x + 20 = 360
40 - x/2 = 0
x = 80 degrees.
link to original post
Why is the angle at A equal to x/2? Thanks
Quote: Jimmy2TimesQuote: ChesterDog
The sum of the interior angles of a quadrilateral is 360 degrees. ABPC is a quadrilateral.
The angle at A is x/2, and the interior angle at P is 360 - x.
So, x/2 + 20 + 360 - x + 20 = 360
40 - x/2 = 0
x = 80 degrees.
link to original post
Why is the angle at A equal to x/2? Thanks
link to original post
I used the famous geometry theorem that the measure of an inscribed angle is half the central angle.
Below demonstrates why this theorem is true.
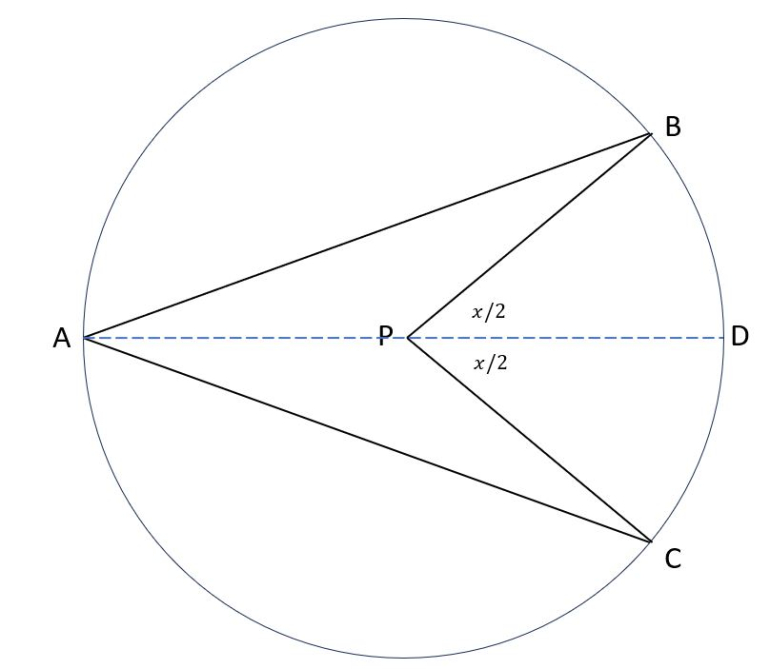
Triangle APB is an isosceles triangle because AP and BP are both radii of the circle. Therefore, angle BAP = angle ABP (∠BAP = ∠ABP).
The angles of a triangle add up to 180 degrees, so ∠BAP + ∠ABP + ∠APB = 180.
∠APD is 180 degrees, so ∠APB = 180 - x/2.
Combining these last three equations yields: ∠BAP + ∠BAP + (180 - x/2) = 180.
Solving yields: ∠BAP = x/4. Therefore, ∠BAC = 2( x/4 ) = x/2.

At what time, exactly, do the two hands of a clock overlap for the first time after 12:00 midnight?
Quote: GialmereAt what time, exactly, do the two hands of a clock overlap for the first time after 12:00 midnight?
link to original post
1:05:27 AM.
In other words 12/11 hours.
I solved it by equating the time of both hands when they meet. Remember time = distance/rate. Let d be the distance from the 12:00 position, where each hour is 1/12, then:
minute hand time = hour hand time
(1+d)/12 = d
1+d = 12d
d = 1/11
Quote: GialmereMore exact please.
link to original post
Oy.
I thought the 12/11 hours was an exact expression, but to put it another way 1 hour, 5 minutes, 27 3/11 seconds.
Quote: Wizard
Oy.
I thought the 12/11 hours was an exact expression, but to put it another way 1 hour, 5 minutes, 27 3/11 seconds.
[/spoiler]
link to original post
Correct!!
Very good.
(Apologies for my laziness. I have the flu.)
----------------------------------
You get mad at me when I work....You get mad at me when I don't work.
Sincerely,
Confused alarm clock.

Mike enters the Vermilion game with a batting average of .274. After going 3-for-4 in the game, his average has gone up to .289.
How many hits did he have for the season before the game started?
Quote: Gialmere
Mike enters the Vermilion game with a batting average of .274. After going 3-for-4 in the game, his average has gone up to .289.
How many hits did he have for the season before the game started?
link to original post
Hits/ABs = 0.274
(Hits + 3) / (ABs + 4) = 0.289
Gives hits of 33.683
With rounding you get the right answer with 34 Hits and 124 At Bats before the current game.
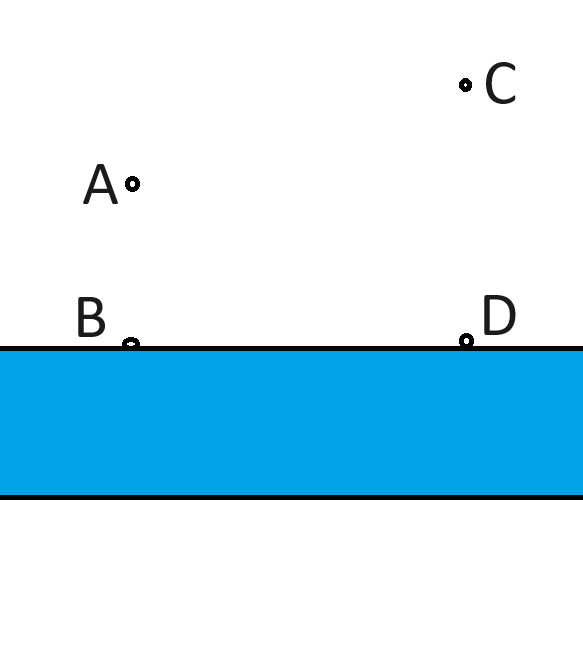
There are two houses, A and C, near a straight river. The closest point to the river from A is point B. The closest point to the river from C is D.
AB = 2
CD = 3
BD = 5
It is desired to build a single pumping station along the river to supply water to both houses. The goal is to minimize the piping required to connect both houses to the pumping station. Where should the pumping station be built and how much piping is required if built there?
Quote: Wizard
There are two houses, A and C, near a straight river. The closest point to the river from A is point B. The closest point to the river from C is D.
AB = 2
CD = 3
BD = 5
It is desired to build a single pumping station along the river to supply water to both houses. The goal is to minimize the piping required to connect both houses to the pumping station. Where should the pumping station be built and how much piping is required if built there?
link to original post
Wiz,
The total length is then 2√2 + 3√2 = 5√2.
Dog Hand
Do you mean that both house are connected directly to the pumping station? If so then I get
****WRONG - can't multiply numbers apparently****
pumping station 1 unit to right of B
pipe required is 5+sqrt(5)=7.236
But building station at B and pipes BA + AC = 2+sqrt(26)=7.099 seems better ......are there others better still?
******EDITED - I agree with Doghand now.....but still unsure it is in fact best??
EDITED mine - I agree with Doghand....but still unsure of actual question.
Quote: DogHand
Wiz,I get a location on the river 2 units from B and 3 units from D.
The total length is then 2√3 + 3√2.
Dog Hand
link to original post
I agree with Dog Hand location, 2 units from B....
I think pipe required is 2sqrt(2) + 3sqrt(2) = 5sqrt(2) = 7.071????
Quote: chevyQuote: DogHand
Wiz,I get a location on the river 2 units from B and 3 units from D.
The total length is then 2√3 + 3√2.
Dog Hand
link to original post
I agree with Dog Hand location, 2 units from B....
I think pipe required is 2sqrt(2) + 3sqrt(2) = 5sqrt(2) = 7.071????
link to original post
Yeah... I fixed my typo.
I agree with your total length.
Dog Hand
Starting with Dog Hand solution (shown in black) and dropping perpendicular AF + EC.....Green < Black
But then starting with Green, and Dropping perpendicular FG +AF + FC..... PINK < Green
Not optimizing the locations, just showing that the two direct connections can be improved. Not sure how to optimize if location on the river is a variable.
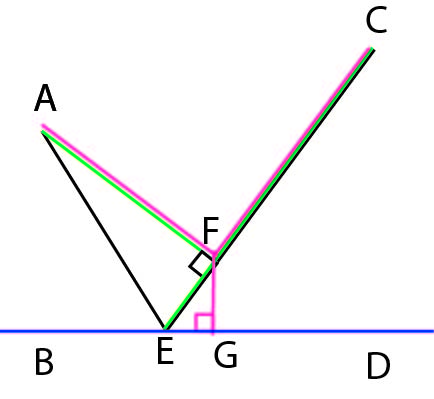
Quote: chevy
Starting with Dog Hand solution (shown in black) and dropping perpendicular AF + EC.....Green < Black
But then starting with Green, and Dropping perpendicular FG +AF + FC..... PINK < Green
Not optimizing the locations, just showing that the two direct connections can be improved. Not sure how to optimize if location on the river is a variable.
link to original post
Oh that’s an interesting question. Are you supposed to make 3 lengths of pipe if equivalent length?
Quote: unJonQuote: chevy
Starting with Dog Hand solution (shown in black) and dropping perpendicular AF + EC.....Green < Black
But then starting with Green, and Dropping perpendicular FG +AF + FC..... PINK < Green
Not optimizing the locations, just showing that the two direct connections can be improved. Not sure how to optimize if location on the river is a variable.
link to original post
Oh that’s an interesting question. Are you supposed to make 3 lengths of pipe if equivalent length?
link to original post
Not sure of correct answer ...but I don't think you can require equal lengths in general.
Call F = the floating intersection....if all three are equal length, then AF = CF and F must be on the line perpendicular to AC.
But imagine stretching the problem horizontally (BD increases to a large amount)...AF and FC increase
The pipe from F to G (The location on the river)will not grow without limit) in fact FG would never be more than 2.5 units (midpoint between heights of A and C)
So for arbitrary case, seems can't require equal lengths.
Need some constraint though, it seems?
If intersection F is at (x,y), the total of the three pipes would be
AF + FC + FG
sqrt(x^2 + (2-y)^2) + sqrt ( (5-x)^2 + (3-y)^2) + y
???
As I'm away the Y solution, for three points, usually requires the three pipes to be at 120 degrees to each other, thus you would construct two lines at 120o connecting to A and B such that, a third line 120o to those, was vertically down to the river.


