Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
November 30th, 2023 at 5:09:36 PM
permalink
Here are the guys you should call to fix your plumbing systems...
System #1) Joeman, Wizard, unJon
System #2) unJon
System #3) Joeman, gordon888
And here is today's chess master: gordon888
Correct!!
Good show.
[Sorry, no video]
Answer of the puzzle Which Tank will be filled first is : K
How : L and G are not possible answer as water supply is blocked from N.
Also there is no water coming from D to I as the supply is blocked.
So the only possible answers are K or N. But N will take more time than K to get filled up.
As we mentioned in the beginning that each tank takes 4 minutes to get filled up completely, so based on that when water will take route A-B-C-I-H-F-K it will take complete 8 minutes to fill up tank K. (1 minute for tank A as the outlet is at the 1/4 level, o minute at tank B and C, 1 minute at tank I, 1 minute at tank H, 1 minute at tank F and 4 minutes at tank K ).
When water will follow path E-D-M-N it will take 9 minutes. 3 minutes at tank E, 2 minutes at tank D, 0 minute at tank M and 4 minutes at tank N. so total 9 minutes.
Answer of the puzzle Which Tank will be filled first is : K
How : L and G are not possible answer as water supply is blocked from N.
Also there is no water coming from D to I as the supply is blocked.
So the only possible answers are K or N. But N will take more time than K to get filled up.
As we mentioned in the beginning that each tank takes 4 minutes to get filled up completely, so based on that when water will take route A-B-C-I-H-F-K it will take complete 8 minutes to fill up tank K. (1 minute for tank A as the outlet is at the 1/4 level, o minute at tank B and C, 1 minute at tank I, 1 minute at tank H, 1 minute at tank F and 4 minutes at tank K ).
When water will follow path E-D-M-N it will take 9 minutes. 3 minutes at tank E, 2 minutes at tank D, 0 minute at tank M and 4 minutes at tank N. so total 9 minutes.
White only has one bad move as every other legal move is immediate checkmate.
1. Rc6+ permits 1. … Rxh7.
----------------------------------------------
...a beautiful conjecture ruined by an ugly fact.
Have you tried 22 tonight? I said 22.
November 30th, 2023 at 5:13:44 PM
permalink
Quote: Ace2link to original post
Agree. However, a more elegant solution is 10% / (100 * 2π)^.5 =~ 0.003989, accurate within 0.3%
The binomial calculation only takes a few minutes set up. It is easy to extend it to dozens or individual numbers.
Your approximation makes it clear that the house edge is inversely related to the square root of the session length. This is something everyone should keep firmly in mind if they play a zero-EV game that is raked on session wins. Want to cut the house edge in half? Just play 4 times longer sessions.
Gambling is a math contest where the score is tracked in dollars. Try not to get a negative score.
November 30th, 2023 at 5:44:57 PM
permalink
Okay, to the nearest power of 10, what is 4^(4^(4^4))).
Not so hard. No calculators allowed.
Not so hard. No calculators allowed.
Climate Casino: https://climatecasino.net/climate-casino/
November 30th, 2023 at 6:10:09 PM
permalink
Binomial expansion is not a closed-form solution.Quote: MentalQuote: Ace2link to original post
Agree. However, a more elegant solution is 10% / (100 * 2π)^.5 =~ 0.003989, accurate within 0.3%
The binomial calculation only takes a few minutes set up. It is easy to extend it to dozens or individual numbers.
Your approximation makes it clear that the house edge is inversely related to the square root of the session length. This is something everyone should keep firmly in mind if they play a zero-EV game that is raked on session wins. Want to cut the house edge in half? Just play 4 times longer sessions.
link to original post
In excel, you can’t run this binomial expansion for any number of bets above 1,030, as the numerator then exceeds 10^300. The approximation formula can be quickly applied for any N no matter how large, and will get even more accurate as N increases, becoming exact for all practical purposes
As you state, the very accurate approximation clearly shows the inverse relationship between increasing n and decreasing house edge
Thinking through problems and using clever formulas (instead of brute forcing) was the way everything was solved until recently. Computers are a relatively new invention
It’s all about making that GTA
November 30th, 2023 at 6:23:26 PM
permalink
Do you mean 4^(4^(4^4)) ?Quote: teliotOkay, to the nearest power of 10, what is 4^(4^(4^4))).
Not so hard. No calculators allowed.
link to original post
It’s all about making that GTA
November 30th, 2023 at 6:46:47 PM
permalink
Yes, I have only been programming for 50-some years. I am embarrassed at being able to get a more exact answer by such a low-brow method. Sometimes I wish I were not so damn good at programming.Quote: Ace2Binomial expansion is not a closed-form solution.Quote: MentalQuote: Ace2link to original post
Agree. However, a more elegant solution is 10% / (100 * 2π)^.5 =~ 0.003989, accurate within 0.3%
The binomial calculation only takes a few minutes set up. It is easy to extend it to dozens or individual numbers.
Your approximation makes it clear that the house edge is inversely related to the square root of the session length. This is something everyone should keep firmly in mind if they play a zero-EV game that is raked on session wins. Want to cut the house edge in half? Just play 4 times longer sessions.
link to original post
In excel, you can’t run this binomial expansion for any number of bets above 1,030, as the numerator then exceeds 10^300. The approximation formula can be quickly applied for any N no matter how large, and will get even more accurate as N increases, becoming exact for all practical purposes
As you state, the very accurate approximation clearly shows the inverse relationship between increasing n and decreasing house edge
Thinking through problems and using clever formulas (instead of brute forcing) was the way everything was solved until recently. Computers are a relatively new invention
link to original post
Gambling is a math contest where the score is tracked in dollars. Try not to get a negative score.
November 30th, 2023 at 6:57:12 PM
permalink
Quote: teliotOkay, to the nearest power of 10, what is 4^(4^(4^4))).
Not so hard. No calculators allowed.
link to original post
x = 4^(4^(4^4)))
log x = 4^256 log 4 = 2^513 log 2
x = 10^(2^513 log 2)
Since log 2 = about 0.3, the answer is about 10^(8/3 x 2^512)
December 1st, 2023 at 4:35:13 AM
permalink
Quote: MentalQuote: Ace2link to original post
Agree. However, a more elegant solution is 10% / (100 * 2π)^.5 =~ 0.003989, accurate within 0.3%
The binomial calculation only takes a few minutes set up. It is easy to extend it to dozens or individual numbers.
Your approximation makes it clear that the house edge is inversely related to the square root of the session length. This is something everyone should keep firmly in mind if they play a zero-EV game that is raked on session wins. Want to cut the house edge in half? Just play 4 times longer sessions.
link to original post
Again showing why house edge is not a great driver of rational play.
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
December 1st, 2023 at 4:35:32 AM
permalink
Yes. And by "nearest" power of 10, I mean as close as you can get without a calculator -- some approximations are needed.Quote: Ace2Do you mean 4^(4^(4^4)) ?Quote: teliotOkay, to the nearest power of 10, what is 4^(4^(4^4))).
Not so hard. No calculators allowed.
link to original post
link to original post
In Knuth's up-arrow notation, I'm asking for an approximation of 4↑↑4
Last edited by: teliot on Dec 1, 2023
Climate Casino: https://climatecasino.net/climate-casino/
December 1st, 2023 at 4:56:20 AM
permalink
Quote: ThatDonGuyQuote: teliotOkay, to the nearest power of 10, what is 4^(4^(4^4))).
Not so hard. No calculators allowed.
link to original post
x = 4^(4^(4^4)))
log x = 4^256 log 4 = 2^513 log 2
x = 10^(2^513 log 2)
Since log 2 = about 0.3, the answer is about 10^(8/3 x 2^512)
link to original post
Not the way I had in mind. I would only ask that you also express 2^512 in powers of 10.
Climate Casino: https://climatecasino.net/climate-casino/
December 1st, 2023 at 5:13:04 AM
permalink
I had got a very rough estimate using...
(i) 210 is about 103 so 2N is roughly 10(N*0.3)
(ii) 44=256 (4 16 64 256)
(iii) 4256 = 2512 about 10153.6=s (this is not a bad estimate as excel says it's 1.3408E154).
(iv) 4s = 22s = 10.6s which is slightly more than 1010153 (10 10 153)
(i) 210 is about 103 so 2N is roughly 10(N*0.3)
(ii) 44=256 (4 16 64 256)
(iii) 4256 = 2512 about 10153.6=s (this is not a bad estimate as excel says it's 1.3408E154).
(iv) 4s = 22s = 10.6s which is slightly more than 1010153 (10 10 153)
December 1st, 2023 at 5:20:23 AM
permalink
Yes! And this answer uses one of my favorite numbers --Quote: charliepatrickI had got a very rough estimate using...
(i) 210 is about 103 so 2N is roughly 10(N*0.3)
(ii) 44=256 (4 16 64 256)
(iii) 4256 = 2512 about 10153.6=s (this is not a bad estimate as excel says it's 1.3408E154).
(iv) 4s = 22s = 10.6s which is slightly more than 1010153 (10 10 153)
link to original post
153 is the smallest 3 digit integer that is the sum of the cubes of its digits.
153 = 1^3 + 5^3 + 3^3.
There are 3 others.
Climate Casino: https://climatecasino.net/climate-casino/
December 1st, 2023 at 5:21:26 AM
permalink
Quote: unJonQuote: MentalQuote: Ace2link to original post
Agree. However, a more elegant solution is 10% / (100 * 2π)^.5 =~ 0.003989, accurate within 0.3%
The binomial calculation only takes a few minutes set up. It is easy to extend it to dozens or individual numbers.
Your approximation makes it clear that the house edge is inversely related to the square root of the session length. This is something everyone should keep firmly in mind if they play a zero-EV game that is raked on session wins. Want to cut the house edge in half? Just play 4 times longer sessions.
link to original post
Again showing why house edge is not a great driver of rational play.
link to original post
Yes, you want to take the totality of the situation into account. For loss rebates, house edge is only a small part of the equation.
This 10% session-rake system has a lot in common with loss rebates. After every win or loss, your EV outlook changes. If you are playing for cash back, this rake system can be +EV. You can quit any session while you are a loser, but you need to stick with winning sessions until your cashback exceeds the rake.
Gambling is a math contest where the score is tracked in dollars. Try not to get a negative score.
December 1st, 2023 at 5:34:05 AM
permalink
Quote: teliotYes! And this answer uses one of my favorite numbers --Quote: charliepatrickI had got a very rough estimate using...
(i) 210 is about 103 so 2N is roughly 10(N*0.3)
(ii) 44=256 (4 16 64 256)
(iii) 4256 = 2512 about 10153.6=s (this is not a bad estimate as excel says it's 1.3408E154).
(iv) 4s = 22s = 10.6s which is slightly more than 1010153 (10 10 153)
link to original post
153 is the smallest 3 digit integer that is the sum of the cubes of its digits.
153 = 1^3 + 5^3 + 3^3.
There are 3 others.
link to original post
combined both methods above and got a little closer:
=10^(2.408x10^153).
=10^(2.408x10^153).
December 1st, 2023 at 6:10:32 AM
permalink
^ Yes I agree that my figure ignored the decimal part, so xxx.6 would become something like xxx.3 or xxx.4 when multiplying by .6 rather than xxx. But then it wouldn't have been a favourite number!
December 1st, 2023 at 6:43:10 AM
permalink
Quote: teliot
153 is the smallest 3 digit integer that is the sum of the cubes of its digits.
153 = 1^3 + 5^3 + 3^3.
There are 3 others.
link to original post
I hope nobody will mind I reply outside of spoiler tags. This number is mentioned in the bible in the story of the second miraculous catch of fish. I find it very interesting this bit of information was retained and later made it into the bible. I speculate somebody who had a hand in the translation, writing or editing also liked math and threw it in as an inside joke to people like you and me.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 1st, 2023 at 7:42:36 AM
permalink
Ive managed to find 407 370 and 371
December 1st, 2023 at 8:52:17 AM
permalink
Okay, time for me to ask another one...
This time, it is a classic problem and two variations, in increasing order of difficulty; solving either of the harder ones also provides a solution to the easier problem(s).
Easiest version:
You have 12 coins, each with a unique integer mint mark from 2001 through 2012, so you can identify any particular coin by sight.
11 of the coins weigh the same; the other one is either lighter or heavier by the others by a small amount, so you cannot distinguish it by feel or sight.
You do have a balance scale that can take up to four coins on each side. Note that the balance scale cannot tell you by how much one side weighs more than the other - just which side, if either, is heavier.
In three usages of the scale, identify the "off" coin, and whether it his heavier or lighter than the others.
You are allowed to make each weighing conditional on the previous one(s).
Moderate version:
You are too busy working on other "easy" math problems, so you have your assistant do it.
However, you don't trust your assistant to be able to handle complex conditions, so you specify all three weighings in advance (e.g. "weighing 1 is 2001, 2002, 2003, 2004 against 2005, 2006, 2007, 2008; weighing 2 is 2001, 2002, 2005, 2006 against 2003, 2004, 2011, 2012; weighing 3 is 2009, 2010, 2005, 2006 against 2007, 2008, 2011, 2012"); the assistant will write down the results of the three weighings, and from that, you can solve the problem.
Hardest version:
First, there is the possibility that all 12 coins weigh the same.
Second, did I say those were mint marks? My mistake - the numbers indicate what each coin is supposed to weigh, in mg. The "off" coin is off by about 0.5 mg. You have to take this into account when determine the weighings for your assistant.
For example, if you put coins 2001-2004 on one side and 2005-2008 on the other, the 2001-2004 side weighs 8010 +/- 0.5 mg, while the 2005-2008 side weight 8026 +/- 0.5 mg. You need to have the sum of the coin numbers on each side of a particular weighing be the same.
This time, it is a classic problem and two variations, in increasing order of difficulty; solving either of the harder ones also provides a solution to the easier problem(s).
Easiest version:
You have 12 coins, each with a unique integer mint mark from 2001 through 2012, so you can identify any particular coin by sight.
11 of the coins weigh the same; the other one is either lighter or heavier by the others by a small amount, so you cannot distinguish it by feel or sight.
You do have a balance scale that can take up to four coins on each side. Note that the balance scale cannot tell you by how much one side weighs more than the other - just which side, if either, is heavier.
In three usages of the scale, identify the "off" coin, and whether it his heavier or lighter than the others.
You are allowed to make each weighing conditional on the previous one(s).
Moderate version:
You are too busy working on other "easy" math problems, so you have your assistant do it.
However, you don't trust your assistant to be able to handle complex conditions, so you specify all three weighings in advance (e.g. "weighing 1 is 2001, 2002, 2003, 2004 against 2005, 2006, 2007, 2008; weighing 2 is 2001, 2002, 2005, 2006 against 2003, 2004, 2011, 2012; weighing 3 is 2009, 2010, 2005, 2006 against 2007, 2008, 2011, 2012"); the assistant will write down the results of the three weighings, and from that, you can solve the problem.
Hardest version:
First, there is the possibility that all 12 coins weigh the same.
Second, did I say those were mint marks? My mistake - the numbers indicate what each coin is supposed to weigh, in mg. The "off" coin is off by about 0.5 mg. You have to take this into account when determine the weighings for your assistant.
For example, if you put coins 2001-2004 on one side and 2005-2008 on the other, the 2001-2004 side weighs 8010 +/- 0.5 mg, while the 2005-2008 side weight 8026 +/- 0.5 mg. You need to have the sum of the coin numbers on each side of a particular weighing be the same.
December 1st, 2023 at 9:38:50 AM
permalink
That is the infamous Simon Peter's catch. I take it that ancient numerologists assigned special powers to certain numbers based on their mathematical properties. 153 is a trinity of trinities, hence being used in the New Testament.Quote: WizardQuote: teliot
153 is the smallest 3 digit integer that is the sum of the cubes of its digits.
153 = 1^3 + 5^3 + 3^3.
There are 3 others.
link to original post
I hope nobody will mind I reply outside of spoiler tags. This number is mentioned in the bible in the story of the second miraculous catch of fish. I find it very interesting this bit of information was retained and later made it into the bible. I speculate somebody who had a hand in the translation, writing or editing also liked math and threw it in as an inside joke to people like you and me.
link to original post
By the way, I first heard about 153 in the book "The Incredible Dr. Matrix" by Martin Gardner. Best book on recreational mathematics ever.
Climate Casino: https://climatecasino.net/climate-casino/
December 1st, 2023 at 10:43:49 AM
permalink
Quote: ThatDonGuyOkay, time for me to ask another one...
This time, it is a classic problem and two variations, in increasing order of difficulty; solving either of the harder ones also provides a solution to the easier problem(s).
Easiest version:
You have 12 coins, each with a unique integer mint mark from 2001 through 2012, so you can identify any particular coin by sight.
11 of the coins weigh the same; the other one is either lighter or heavier by the others by a small amount, so you cannot distinguish it by feel or sight.
You do have a balance scale that can take up to four coins on each side. Note that the balance scale cannot tell you by how much one side weighs more than the other - just which side, if either, is heavier.
In three usages of the scale, identify the "off" coin, and whether it his heavier or lighter than the others.
You are allowed to make each weighing conditional on the previous one(s).
Moderate version:
You are too busy working on other "easy" math problems, so you have your assistant do it.
However, you don't trust your assistant to be able to handle complex conditions, so you specify all three weighings in advance (e.g. "weighing 1 is 2001, 2002, 2003, 2004 against 2005, 2006, 2007, 2008; weighing 2 is 2001, 2002, 2005, 2006 against 2003, 2004, 2011, 2012; weighing 3 is 2009, 2010, 2005, 2006 against 2007, 2008, 2011, 2012"); the assistant will write down the results of the three weighings, and from that, you can solve the problem.
Hardest version:
First, there is the possibility that all 12 coins weigh the same.
Second, did I say those were mint marks? My mistake - the numbers indicate what each coin is supposed to weigh, in mg. The "off" coin is off by about 0.5 mg. You have to take this into account when determine the weighings for your assistant.
For example, if you put coins 2001-2004 on one side and 2005-2008 on the other, the 2001-2004 side weighs 8010 +/- 0.5 mg, while the 2005-2008 side weight 8026 +/- 0.5 mg. You need to have the sum of the coin numbers on each side of a particular weighing be the same.
link to original post
Questions are all long, but first one is easy.
Step 1. Put 4 coins on each side of the scale to check weight.
Step 2. If same weight, unload all coins from the scale and then load 2 of the 4 remaining coins onto each side of the scale; and they must have different weights. If different weights, unload only 2 of the weighted 4 coins from each side of the scale and mark them until different weights appear.
Step 3. Unload 1 of the 2 weighted coins from each side of the scale to check weight again. If same weight, the off coin is one of those two that were just unloaded; if different weights, it’s one of those two that were on the scale.
Step 1. Put 4 coins on each side of the scale to check weight.
Step 2. If same weight, unload all coins from the scale and then load 2 of the 4 remaining coins onto each side of the scale; and they must have different weights. If different weights, unload only 2 of the weighted 4 coins from each side of the scale and mark them until different weights appear.
Step 3. Unload 1 of the 2 weighted coins from each side of the scale to check weight again. If same weight, the off coin is one of those two that were just unloaded; if different weights, it’s one of those two that were on the scale.
Last edited by: aceside on Dec 1, 2023
December 1st, 2023 at 12:11:49 PM
permalink
Quote: acesideQuote: ThatDonGuyOkay, time for me to ask another one...
This time, it is a classic problem and two variations, in increasing order of difficulty; solving either of the harder ones also provides a solution to the easier problem(s).
Easiest version:
You have 12 coins, each with a unique integer mint mark from 2001 through 2012, so you can identify any particular coin by sight.
11 of the coins weigh the same; the other one is either lighter or heavier by the others by a small amount, so you cannot distinguish it by feel or sight.
You do have a balance scale that can take up to four coins on each side. Note that the balance scale cannot tell you by how much one side weighs more than the other - just which side, if either, is heavier.
In three usages of the scale, identify the "off" coin, and whether it his heavier or lighter than the others.
You are allowed to make each weighing conditional on the previous one(s).
Moderate version:
You are too busy working on other "easy" math problems, so you have your assistant do it.
However, you don't trust your assistant to be able to handle complex conditions, so you specify all three weighings in advance (e.g. "weighing 1 is 2001, 2002, 2003, 2004 against 2005, 2006, 2007, 2008; weighing 2 is 2001, 2002, 2005, 2006 against 2003, 2004, 2011, 2012; weighing 3 is 2009, 2010, 2005, 2006 against 2007, 2008, 2011, 2012"); the assistant will write down the results of the three weighings, and from that, you can solve the problem.
Hardest version:
First, there is the possibility that all 12 coins weigh the same.
Second, did I say those were mint marks? My mistake - the numbers indicate what each coin is supposed to weigh, in mg. The "off" coin is off by about 0.5 mg. You have to take this into account when determine the weighings for your assistant.
For example, if you put coins 2001-2004 on one side and 2005-2008 on the other, the 2001-2004 side weighs 8010 +/- 0.5 mg, while the 2005-2008 side weight 8026 +/- 0.5 mg. You need to have the sum of the coin numbers on each side of a particular weighing be the same.
link to original postQuestions are all long, but first one is easy.
Step 1. Put 4 coins on each side of the scale to check weight.
Step 2. If same weight, unload all coins from the scale and then load 2 of the 4 remaining coins onto each side of the scale; and they must have different weights. If different weights, unload only 2 of the weighted 4 coins from each side of the scale and mark them until different weights appear.
Step 3. Unload 1 of the 2 weighted coins from each side of the scale to check weight again. If same weight, the off coin is one of those two that were just unloaded; if different weights, it’s one of those two that were on the scale.
link to original post
For Step 2, what do you mean by "mark them until different weights appear"? You only get three weighings total. Every time you change the coins, that counts as a different weighing.
December 1st, 2023 at 2:26:47 PM
permalink
1. Weighing 1: Take any 8 coins and put 4 each on the balance scale. If they do not balance, go to step 2. If they do balance, go to step 7.
2. Label the 4 coins that weighed heavier from step 1 "H." The four on the light side of the scale label "L." The other four, which you've verified as being fair, label "V." Go to step 3.
3. Weighing 2: Put on the balance scale HHLL vs. HLVV. If the HHLL side goes down, go to step 4. If the HLVV goes down, go to step 5. If they are the same, go to step 6.
4. Weighing 3: You have identified three coins as the culprit two H and one L. Weigh HL vs. VV. If the HL goes down, the H coin on the scale is heavy. If the HL side goes up, the L coin is light. If they balance, the other H coin that wasn't weighed is heavy.
5. Weighing 3: You have identified three coins as the culprit two L and one H. Weigh HL vs. VV. If the HL goes down, the H coin on the scale is heavy. If the HL side goes up, the L coin is light. If they balance, the other L coin that wasn't weighed is light.
6. Weighing 3: You have identified two coins as the culprit, one H and one L. Weigh both against two V. If the HL go down, the H is heavy. If they go up the L is light.
7. Weighing 2: The other four coins that were not weighed are the culprits. We can label the other 8 coins "V" for verified fair. Weigh 3 of the culprits against 3 of the V coins. If the culprits go down, go to step 8. If the culprits go up, go to step 9. If they balance, go to step 10.
8. Weighing 3: You have identified 3 coins as heavy. Label them "H." Weigh an H vs. H. If a side goes down, it has the heavy coin. If it balances, the remaining H coin is the heavy one.
9. Weighing 3: You have identified 3 coins as light. Label them "L." Weigh an L vs. L. If a side goes up, it has the light coin. If it balances, the remaining L coin is the heavy one.
10. Weighing 3: You have one coin left as the culprit, which hasn't been weighed yet. Weigh it against a V coin. If it goes down, it's heavy. If it goes up, it's light.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 1st, 2023 at 4:43:28 PM
permalink
Correction by a picture
I researched Wizard's solution and found this puzzle is complicated. My earlier answer is wrong. Here is a diagram picture for me to understand Wizard's answer. As below:
December 2nd, 2023 at 10:45:36 AM
permalink
I cannot edit the above post, so I post a new picture to correct it.
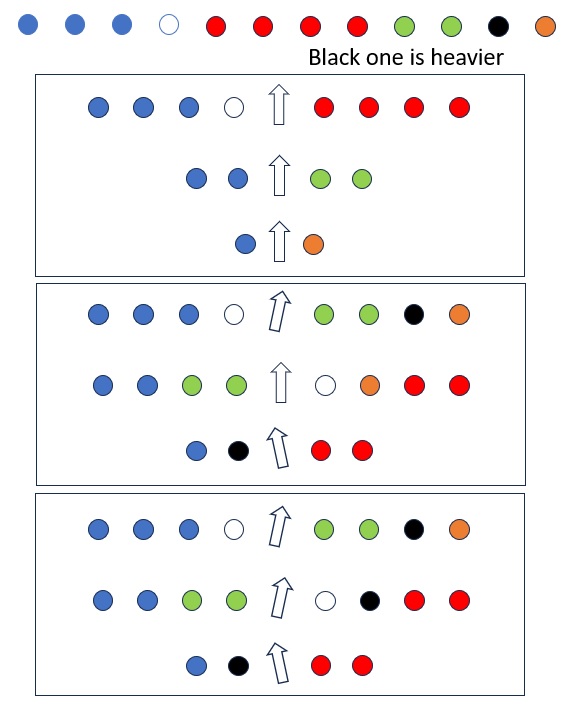
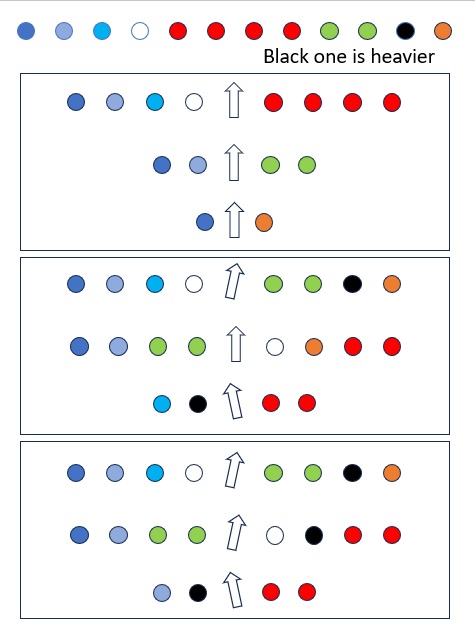
If the black coin is lighter, the logic is the same.
If the black coin is +/- off, we need a little bit more work in the third picture.
If the black coin is lighter, the logic is the same.
If the black coin is +/- off, we need a little bit more work in the third picture.
December 4th, 2023 at 6:59:57 AM
permalink
It's Easy Monday. Time for some more minor mysteries (kind of)...
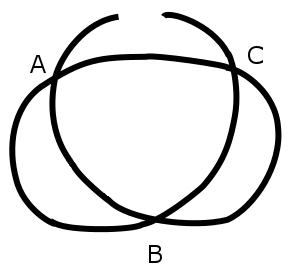
A shoelace is lying on the floor, and I’m too nearsighted to see how the lace crosses itself at points A, B, and C.
If I pull on the ends, what’s the probability that it will produce a knot?
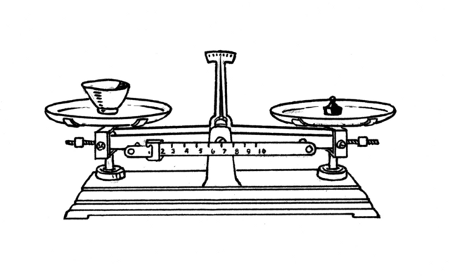
This scale balances a cup of water with a certain weight.
Will the balance be upset if you put your finger in the water, if you’re careful not to touch the glass?
White might capture Black’s queen at this point, but instead can choose to mate on the move.
How?
Have you tried 22 tonight? I said 22.
December 4th, 2023 at 7:37:00 AM
permalink
1/4. I admit I had to play around with some rappelling rope to get at this figure.
I think, yes. The side with the water will go up as you're putting your finger in and will go back down once you stop. The best reason I can give is you feel lighter in an elevator going down and heavier if it goes up.
Qd4
Last edited by: Wizard on Dec 4, 2023
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 4th, 2023 at 7:48:00 AM
permalink
Quote: Gialmere
It's Easy Monday. Time for some more minor mysteries (kind of)...
A shoelace is lying on the floor, and I’m too nearsighted to see how the lace crosses itself at points A, B, and C.
If I pull on the ends, what’s the probability that it will produce a knot?
This scale balances a cup of water with a certain weight.
Will the balance be upset if you put your finger in the water, if you’re careful not to touch the glass?
White might capture Black’s queen at this point, but instead can choose to mate on the move.
How?
link to original post
I think just 2/9 of the time, when it goes up/down/up or down/up/down.. ETA: typo 2/8 not 2/9.
your finger adds downward pressure to the glass even if you only touch the water. The easiest way to see that is to see that putting your finger in the glass raises the water in the glass. So the water side becomes heavier and sinks down.
rotate board counter clockwise 90 degrees. Pawn moves to last row and becomes knight, checkmate.
Last edited by: unJon on Dec 4, 2023
The race is not always to the swift, nor the battle to the strong; but that is the way to bet.
December 4th, 2023 at 7:48:13 AM
permalink
Quote: Gialmere
This scale balances a cup of water with a certain weight.
Will the balance be upset if you put your finger in the water, if you’re careful not to touch the glass?
link to original post
No. I've done this before with my digital scale at home because I wondered the exact same thing, but the weight doesn't change.
December 4th, 2023 at 8:12:09 AM
permalink
I think just 2/8 of the time.
There are 8 up ^ and down ! combinations:
^^^
^^!
^!^ yes
^!!
!^^
!^! Yes
!!^
!!!
Only two of these will make a knot.
There are 8 up ^ and down ! combinations:
^^^
^^!
^!^ yes
^!!
!^^
!^! Yes
!!^
!!!
Only two of these will make a knot.
Water side becomes heavier and will tilt down when finger is stable.
December 4th, 2023 at 9:20:32 AM
permalink
The weight seems to go up. I tried it with a large glass of water and a small empty thermos flask. I had to push the flask down, as it wanted to float; and could see the weight go up accordingly.
So my feeling is the force you need to use to push the finger into the water has to be compensated, and this is done by the weighing machine pushing upwards and recoding a higher weight. I suspect it equals the weight of the displaced water.
So my feeling is the force you need to use to push the finger into the water has to be compensated, and this is done by the weighing machine pushing upwards and recoding a higher weight. I suspect it equals the weight of the displaced water.
December 4th, 2023 at 9:26:06 AM
permalink
Apparently I'm wrong about the weight one.
I need to try it again because I swear the weight didn't change when I stuck my finger in the water. It's been a few months since I did it so I could be remembering incorrectly.
December 4th, 2023 at 1:51:04 PM
permalink
After doing some homework, I believe the water side would go down. This is because the water would push up on your finger. To balance that, it would also push down harder on the bottom of the glass. Something to do with Newton's third law. That's about the best I can do. Where is Doc when you need him?
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 4th, 2023 at 4:31:37 PM
permalink
Our old friend, the "there's a white square on the lower left, so the board is rotated 90 degrees" problem.
Since white moving right to left would have the black king already in check, white's pawns move left to right.
The winning move is:
d8=N #
(i.e. white's pawn to d8, promoted to a knight, checkmate)
It took me a minute to figure out why black couldn't counter with Rxd8.
December 4th, 2023 at 5:13:52 PM
permalink
Too many to quote, but at least one response for each puzzle is...
Correct!
Correct!
One in four. There are three intersections, so there are eight possible ways the lace can cross itself. Of these, only two (over/under/over and under/over/under) will produce a knot.
Yes. The water imparts an upward force on your finger as you immerse it, so you must exert a downward force to overcome it. That force is transferred to the glass and then to the scale, which sinks.
From Yuri B. Chernyak, The Chicken From Minsk, 1995.
From Yuri B. Chernyak, The Chicken From Minsk, 1995.
It’s a trick. The square in the lower right is dark when it should be light, so we must rotate the board 90 degrees. If we turn it to the right then the black king is in check on White’s move, which is illegal. So turn it to the left:
Now White can mate by promoting the d7 pawn to a knight.
[As mentioned, this one is a followup to last week's board orientation puzzle discussion. It has the added twist of a rare pawn to knight promotion. Kudos to unJon and ThatDonGuy for the solve.]
Now White can mate by promoting the d7 pawn to a knight.
[As mentioned, this one is a followup to last week's board orientation puzzle discussion. It has the added twist of a rare pawn to knight promotion. Kudos to unJon and ThatDonGuy for the solve.]
Have you tried 22 tonight? I said 22.
December 5th, 2023 at 7:00:10 AM
permalink
It's Toughie Tuesday. Last week we didn't have much luck with a Catriona Shearer puzzle. So let's try again...
:strip_icc()/pic7894103.png)
The circles each have a radius 1.
What's the area of the rectangle?
The circles each have a radius 1.
What's the area of the rectangle?
Have you tried 22 tonight? I said 22.
December 5th, 2023 at 12:39:44 PM
permalink
Quote: GialmereIt's Toughie Tuesday. Last week we didn't have much luck with a Catriona Shearer puzzle. So let's try again...
The circles each have a radius 1.
What's the area of the rectangle?
link to original post
My answer:
Rectangle area = 2+√3
Let h be the height of the rectangle. If we superimpose a coordinate system with the origin at the lower-left corner, then the center of the yellow circle is at (½, h-½) and the point where the circle touches the diagonal line is at (¾, h-¼(2+√3)). Since the diagonal passes through this point and intersects the vertical line at (1, h/3), by similar triangles we get:
(h/3)/1 = (h-¼(2+√3))/(¾)
Solving gives h = ⅓(2+√3).
The rectangle area is 3*h, so area = 2+√3
Let h be the height of the rectangle. If we superimpose a coordinate system with the origin at the lower-left corner, then the center of the yellow circle is at (½, h-½) and the point where the circle touches the diagonal line is at (¾, h-¼(2+√3)). Since the diagonal passes through this point and intersects the vertical line at (1, h/3), by similar triangles we get:
(h/3)/1 = (h-¼(2+√3))/(¾)
Solving gives h = ⅓(2+√3).
The rectangle area is 3*h, so area = 2+√3
Dog Hand
December 5th, 2023 at 3:14:54 PM
permalink
“The circles each have a radius 1.”
This means each circular disk has an area of pi=3.14?
Three of these is 3 pi= 9.42.
This means each circular disk has an area of pi=3.14?
Three of these is 3 pi= 9.42.
December 5th, 2023 at 3:43:59 PM
permalink
I admit I had to look up the formula for Tan 2 x.
Consider the line from the SW corner to the middle of the RHS circle. The height is 1 (radius of the circle) and the width is 5 (2 diameters plus one radius).
So the Tangent of the angle is 1/5.
Now consider the line which rests on top of the RHS circle. By similar triangles the angle is twice the one just mentioned.
So the tangent of it is tan 2 x = (2*tan)/(1-tan2x) = 2 * 1/5 / (1-1/25) = (2/5)/(24/25) = 10/24.
So the height of the rectangle is 6 * 10 / 24 = 60/24 = 10/4 = 2.5.
The width is 6 (being three diameters)...
So the area is 6 * 2.5 = 15.
Consider the line from the SW corner to the middle of the RHS circle. The height is 1 (radius of the circle) and the width is 5 (2 diameters plus one radius).
So the Tangent of the angle is 1/5.
Now consider the line which rests on top of the RHS circle. By similar triangles the angle is twice the one just mentioned.
So the tangent of it is tan 2 x = (2*tan)/(1-tan2x) = 2 * 1/5 / (1-1/25) = (2/5)/(24/25) = 10/24.
So the height of the rectangle is 6 * 10 / 24 = 60/24 = 10/4 = 2.5.
The width is 6 (being three diameters)...
So the area is 6 * 2.5 = 15.
December 5th, 2023 at 6:10:33 PM
permalink
Quote: aceside“The circles each have a radius 1.”
This means each circular disk has an area of pi=3.14?
Three of these is 3 pi= 9.42.
link to original post
Except that the area of the rectangle > the areas of the circles.
December 5th, 2023 at 6:29:18 PM
permalink
Quote: charliepatrickI admit I had to look up the formula for Tan 2 x.
Consider the line from the SW corner to the middle of the RHS circle. The height is 1 (radius of the circle) and the width is 5 (2 diameters plus one radius).
So the Tangent of the angle is 1/5.
Now consider the line which rests on top of the RHS circle. By similar triangles the angle is twice the one just mentioned.
So the tangent of it is tan 2 x = (2*tan)/(1-tan2x) = 2 * 1/5 / (1-1/25) = (2/5)/(24/25) = 10/24.
So the height of the rectangle is 6 * 10 / 24 = 60/24 = 10/4 = 2.5.
The width is 6 (being three diameters)...
So the area is 6 * 2.5 = 15.
link to original post
Correct!!!
Excellent.
15 is the area. Usually I post the names of the Shearer puzzles but felt this one gave too much away.
It's called: Pythagorean Circles.
It's called: Pythagorean Circles.
----------------------------------------------
...one who talks in someone else's sleep.
Have you tried 22 tonight? I said 22.
December 5th, 2023 at 7:40:18 PM
permalink
Quote: Gialmere
What's the area of the rectangle?
link to original post
15.
I hope I'm right. That took more work than it probably needed to and that isn't to say I'm even right.
Solution available, assuming I'm right.
I see that Charlie beat me to it. Kudos, Charlie.
For what little it's worth, I didn't need to look up any formulas. I had five Pythagorean equations and five unknowns. I thought it would turn into a huge mess, but surprisingly they simplified nicely.
I still have a nagging feeling there is a very simple solution, but I don't see it.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 5th, 2023 at 7:45:51 PM
permalink
Correct. Let's see if your solve is different than charliepatrick's.
Have you tried 22 tonight? I said 22.
December 5th, 2023 at 8:05:17 PM
permalink
As I said in mine I didn’t like the method, except the answer was nice. I suspect there’s a geometrical way to solve it since there could have been a lot of triangles around.
December 5th, 2023 at 9:34:15 PM
permalink
[I don't think Shearer releases "official" solves but here's one from elsewhere.]
Let’s start with a related picture, one with only two circles:
Again, the circles have unit radius. What are the dimensions of the rectangle?
The key to figuring this out is that if you have two lines through a point both tangent to a circle, then the line segments from the intersection point to the tangent points are congruent. We know the distance from the top right corner of the rectangle to the top tangent point on the yellow circle is 3. We don’t know the distance from the bottom right corner of the rectangle to the left tangent point on the yellow circle; call it x. Then the length of the diagonal is 3+x. By Pythagoras,
(3 + x)² = 4² + (1 + x)²
whose solution is x=2. So the height of the rectangle is 3, its width is 4, and its diagonal is 5: the diagonal and two sides make a 3:4:5 triangle, where 3:4:5 is a Pythagorean triple. [And in particular it’s a triple in which the hypotenuse is one greater than the longer side.]
You can do the 3-circle problem the same way; here the length of the diagonal is 5+x, the equation is
(5 + x)² = 6² + (1 + x)²
whose solution is x = 3/2. The rectangle then is 2.5 by 6 with diagonal 6.5. Those three numbers are in the proportion 5:12:13, another Pythagorean triple!
Let’s start with a related picture, one with only two circles:
Again, the circles have unit radius. What are the dimensions of the rectangle?
The key to figuring this out is that if you have two lines through a point both tangent to a circle, then the line segments from the intersection point to the tangent points are congruent. We know the distance from the top right corner of the rectangle to the top tangent point on the yellow circle is 3. We don’t know the distance from the bottom right corner of the rectangle to the left tangent point on the yellow circle; call it x. Then the length of the diagonal is 3+x. By Pythagoras,
(3 + x)² = 4² + (1 + x)²
whose solution is x=2. So the height of the rectangle is 3, its width is 4, and its diagonal is 5: the diagonal and two sides make a 3:4:5 triangle, where 3:4:5 is a Pythagorean triple. [And in particular it’s a triple in which the hypotenuse is one greater than the longer side.]
You can do the 3-circle problem the same way; here the length of the diagonal is 5+x, the equation is
(5 + x)² = 6² + (1 + x)²
whose solution is x = 3/2. The rectangle then is 2.5 by 6 with diagonal 6.5. Those three numbers are in the proportion 5:12:13, another Pythagorean triple!
Last edited by: Gialmere on Dec 5, 2023
Have you tried 22 tonight? I said 22.
December 5th, 2023 at 10:11:12 PM
permalink
Generalize the above to n circles. The Pythagorean equation becomes,
(2n-1+ x)² = (2n)² + (1 + x)².
Then x= n/(n-1).
(2n-1+ x)² = (2n)² + (1 + x)².
Then x= n/(n-1).
December 6th, 2023 at 2:15:28 AM
permalink
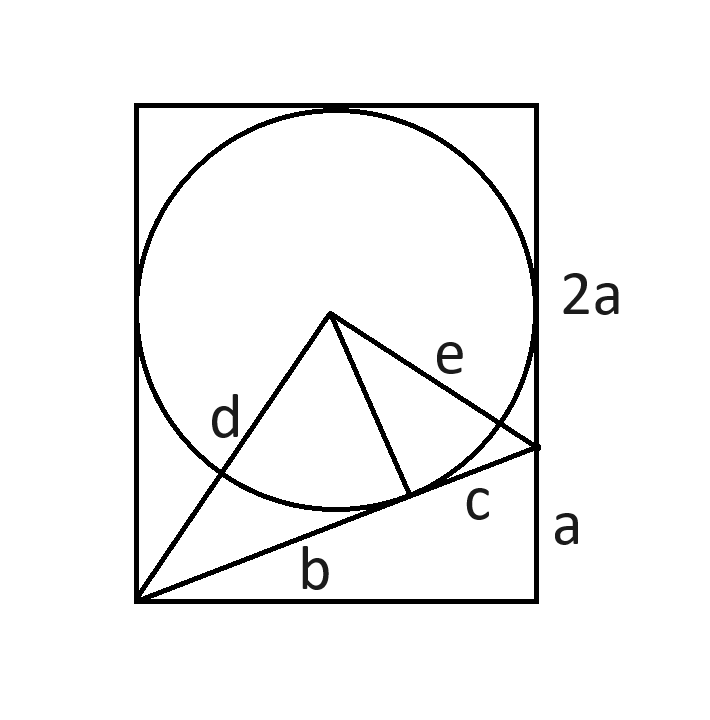
In this figure:
d is the distance from the center of the circle to the lower-left corner of the rectangle.
e is the distance from the center of the circle to the point on the right edge of the rectangle.
From Pythagoreus:
a2 + 4 = (b+c)2
1+b2 = d2
1+(3a-1)2 = d2
1+c2 = e2
1 + (2a-1)2 = e2
Equate d2 and e2:
a2 + 4 = (b+c)2
1+b2 = 1+(3a-1)2
1+c2 = 1 + (2a-1)2
Here we have three equations and three unknowns.
At this point, I thought the algebra would be a mess, but it wasn't. I think anyone reading this could easily solve it from here.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
December 6th, 2023 at 7:00:07 AM
permalink
1) During what phases of the lunar cycle do solar and lunar eclipses take place?
2) Solar eclipses are more common than lunar eclipses*, but we tend to have the opposite impression. Why?
*This stat includes all types of solar and lunar eclipses except for penumbral lunar eclipses.
Have you tried 22 tonight? I said 22.
December 6th, 2023 at 7:16:20 AM
permalink
Quote: Gialmere
2) Solar eclipses are more common than lunar eclipses*, but we tend to have the opposite impression. Why?
link to original post
You have the impression that lunar eclipses are more common?? I feel like I almost never hear about them, whereas it seems someone is talking about a solar eclipse every couple of months.
December 6th, 2023 at 7:20:43 AM
permalink
Quote: TigerWuQuote: Gialmere
2) Solar eclipses are more common than lunar eclipses*, but we tend to have the opposite impression. Why?
link to original post
You have the impression that lunar eclipses are more common?? I feel like I almost never hear about them, whereas it seems someone is talking about a solar eclipse every couple of months.
link to original post
Heh heh. Only because you hang out at this website.
Have you tried 22 tonight? I said 22.
December 6th, 2023 at 7:21:16 AM
permalink
Lunar eclipses happen during a full moon; solar eclipses occur during a new moon.
Hmmm... I didn't know that, but my guess would be that solar eclipses are only visible to relatively small portions of the planet, while lunar eclipses are visible to just about anyone in the hemisphere that is in darkness. So, an individual is likely to personally experience more lunar eclipses than solar eclipses in his lifetime, and thus conclude that lunar eclipses are more common.
"Dealer has 'rock'... Pay 'paper!'"
