Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: MentalHow drunk?Quote: rawtuffA drunken person arrives at home and wants to get in.
There are 10 keys on his keyring and only 1 fits. He randomly pulls a key and tries to open the door.
If it doesn't fit he returns the key to the ring and randomly pulls another key again and again until he finds the one that fits.
Under these circumstances, on which try is he most likely to open the door?
link to original postHe is most likely to succeed on the first try. He always makes the first try. He almost never makes the 100th try. He either gets in or passes out before the later tries.
link to original post
Too smart :)
Quote: rawtuffA drunken person arrives at home and wants to get in.
There are 10 keys on his keyring and only 1 fits. He randomly pulls a key and tries to open the door.
If it doesn't fit he returns the key to the ring and randomly pulls another key again and again until he finds the one that fits.
Under these circumstances, on which try is he most likely to open the door?
link to original post
I assume, he can pick the same key he already tried, since he's drunk. That said, it would be the first try. If he couldn't repeat keys, every try would be equally likely.
The logic is to win on the first time has Pr = p.
To win on any subsequent time = p*qn

Too many posts to quote, but all three Monday teasers have been correctly solved.
Here are the official solves with comments..
Thereís nothing we can do to reduce the possibility that another player holds four of a kind ó if weíre holding a full house then 11 varieties are possible. But by choosing carefully we can minimize the likelihood of a straight flush. Specifically, each of the hands AAA99, AAA88, AAA77, and AAA66 will prevent 13 straight flushes ó each ace prevents one, and each spot card prevents five.
These are thus the best to choose; of the 40 possible straight flushes, each leaves only 40 Ė 13 = 27 straight flushes that can beat us. By contrast, the impressive-looking AAAKK leaves 40 Ė 6 = 34, or even more if we havenít covered all four suits.
From Aaron Friedlandís Puzzles in Math and Logic, via Peter Winklerís Mathematical Mind-Benders.
---------------------------------------------------
Although AAA99, AAA88, AAA77, and AAA66 are the same on paper, Joeman makes a good point about the psychology of the 9s.
Only at a site like this would you have to specify the type of poker being played, but it's also a good point. Although you must choose your full house before seeing any cards, it would certainly be a heartless, almost Monkey's Paw type of genie to give you pocket 9s and then flop three aces for the community.
5/6 × 5/6 × 5/6 × 5/6 × 5/6
The chance of rolling exactly one six is
1/6 × 5/6 × 5/6 × 5/6 × 5/6
Ö times 5, because the six can appear on any one of the five dice. So the probabilities are equal.
--------------------------------------------
Something to think about perhaps when playing Yahtzee.
--------------------------------------------
Many chess puzzles, being puzzles, do not conform to "real" play. Some, for example, use extra pieces or special rules. For this one, you can simply assume it's a game between two beginners, both floundering their way to victory. It reminds me of the saying...
The winner of a game of chess is the person who makes the second to last mistake.
---------------------------------------------
---------------------------------------------
Thread News
The official solve for the keys puzzle will be appearing in about 3 days.
Stay tuned for Toughie Tuesday.
Four Hexagons
:strip_icc()/pic7879641.png)
Four regular hexagons. What's the pink area?
Quote: GialmereFour Hexagons
link to original post
The big one looks like a heptagon.
Quote: WizardQuote: GialmereFour Hexagons
link to original post
The big one looks like a heptagon.
link to original post
I thought that too, but I think the "big one" is the "White hexagon" and the pink and yellow extend outside the white one.
Nowhere in the chess challenge does it say that the position was arrived at in a legal game. The question could have been simply "Which side moved last if this is a legal position?"Quote: Gialmere
Too many posts to quote, but all three Monday teasers have been correctly solved.
Here are the official solves with comments..A full house with three aces will beat any other full house dealt in this hand, because only one hand can have three aces, assuming no cards are wild. But even this can still lose to a superior hand ó four of a kind or a straight flush.
Thereís nothing we can do to reduce the possibility that another player holds four of a kind ó if weíre holding a full house then 11 varieties are possible. But by choosing carefully we can minimize the likelihood of a straight flush. Specifically, each of the hands AAA99, AAA88, AAA77, and AAA66 will prevent 13 straight flushes ó each ace prevents one, and each spot card prevents five.
These are thus the best to choose; of the 40 possible straight flushes, each leaves only 40 Ė 13 = 27 straight flushes that can beat us. By contrast, the impressive-looking AAAKK leaves 40 Ė 6 = 34, or even more if we havenít covered all four suits.
From Aaron Friedlandís Puzzles in Math and Logic, via Peter Winklerís Mathematical Mind-Benders.
---------------------------------------------------
Although AAA99, AAA88, AAA77, and AAA66 are the same on paper, Joeman makes a good point about the psychology of the 9s.
Only at a site like this would you have to specify the type of poker being played, but it's also a good point. Although you must choose your full house before seeing any cards, it would certainly be a heartless, almost Monkey's Paw type of genie to give you pocket 9s and then flop three aces for the community.The chance of rolling no sixes is
5/6 × 5/6 × 5/6 × 5/6 × 5/6
The chance of rolling exactly one six is
1/6 × 5/6 × 5/6 × 5/6 × 5/6
Ö times 5, because the six can appear on any one of the five dice. So the probabilities are equal.
--------------------------------------------
Something to think about perhaps when playing Yahtzee.White could mate in three different ways if it were his turn, but it canít be, as thereís no legal move that Black can just have made. So Black plays Bxf6#.
--------------------------------------------
Many chess puzzles, being puzzles, do not conform to "real" play. Some, for example, use extra pieces or special rules. For this one, you can simply assume it's a game between two beginners, both floundering their way to victory. It reminds me of the saying...
The winner of a game of chess is the person who makes the second to last mistake.
---------------------------------------------How mean.
---------------------------------------------
Thread News
The official solve for the keys puzzle will be appearing in about 3 days.
Stay tuned for Toughie Tuesday.
link to original post
If this game is Texas Holdem, then the answer is going to be different from 5-card stud. If the game is Omaha, the answer is different yet again. If the game is Omaha Hi/Lo 8 the answer is different and more complex.
Quote: WizardQuote: GialmereFour Hexagons
link to original post
The big one looks like a heptagon.
link to original post
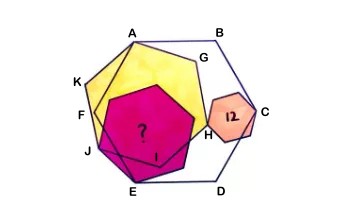
ABCDEF is the big (white) hexagon.
AGHIJK is the yellow one.
Quote: GialmereIt's Toughie Tuesday. Time for another Catriona Shearer puzzle. This one is simply called...
Four Hexagons
Four regular hexagons. What's the pink area?
link to original post
Area=48,
by calculating this particular case in this picture:
Quote: acesideQuote: GialmereIt's Toughie Tuesday. Time for another Catriona Shearer puzzle. This one is simply called...
Four Hexagons
Four regular hexagons. What's the pink area?
link to original postI found the pink
Area=48,
by calculating this particular case in this picture:
link to original post
Correct!!!
Impressive.
----------------------------
...but lacks the personality to be an accountant.
Quote: Gialmere
Who mates in 1?
link to original post
As unJon correctly indicated, in the given position Black must be on move. To see this, assume it is instead White to move and try to determine what Black's previous move could have been.
Black's knight, bishop, and both rooks cannot have just moved, because they have no square from which to move to reach their positions.
The c and g pawns are on their starting squares, so they have not moved.
The king cannot have moved from its only adjacent unoccupied square, f7, because it would have been both in check and adjacent to the White king.
The queen cannot have just moved from d7, because on d7 it would have been checking the White king.
Finally, Black cannot have just played the pawn from d7 to d6, because on d7 it would have been checking the White king.
Thus, we conclude that Black cannot have played the last move, so therefore Black is on move.
This position can be reached legally (though not logically). Here is one possibility:
If we go back a few moves, White's pawn on d5 was back on c4 and his king was on d4 (or e4). Black's "missing" queen's bishop is on f1 (many other starting squares for the QB would also work):
1. Kd5 Bg2+
2. Ke6 Bd5+
3. cxd5
And we arrived at the given position.
This was a fun problem!
Dog Hand
Edit: added Spoiler tag... Sorry!
Quote: DogHandQuote: Gialmere
Who mates in 1?
link to original post
The c and g pawns are on their starting squares, so they have not moved.
Dog Hand
link to original post
Is there a reason Black must be at the top and thus the c & g pawns are in starting position? Are all chess problems presented as that?
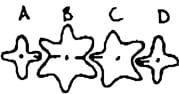
The marks on the faces of these gears are aligned as shown.
What is the least number of rotations that gear A must make so that the marks are all re-aligned as shown?
Quote: chevyIs there a reason Black must be at the top and thus the c & g pawns are in starting position? Are all chess problems presented as that?
link to original post
Black is traditionally at the top of a chess diagram, however, the trick some chess puzzles (including one earlier in this thread) is knowing the correct orientation of the board.
Quote: GialmereQuote: chevyIs there a reason Black must be at the top and thus the c & g pawns are in starting position? Are all chess problems presented as that?
link to original post
Black is traditionally at the top of a chess diagram, however, the trick some chess puzzles (including one earlier in this thread) is knowing the correct orientation of the board.
link to original post
Here's an example...

White to mate on the move.
Quote: Gialmere
The marks on the faces of these gears are aligned as shown.
What is the least number of rotations that gear A must make so that the marks are all re-aligned as shown?
link to original post
The lease number of 360-degree rotations = 4x3x5x4 /(4x4)= 15.
P.S. Itís not clear to me if a rotation is 360 degrees or 90 degrees in this gear A. I looked into other answers and agreed on them. Gears A and D are always in phase, so no need to consider D.
Quote: charliepatrickIs the answer en passant? So the black pawn (in same row/column as rook) has just moved up two spaces, allowing the pawn to take it, so it is now adjacent to the King, giving check, and protected by the rook and King.
link to original post
That would mean the board starts white on left and black on right.......
If so, how did black's black bishop get in the upper left corner? White's pawn must be in starting position???
Or maybe I can't think of a way for white to clear out and then get that position filed again.
Quote: Gialmere
The marks on the faces of these gears are aligned as shown.
What is the least number of rotations that gear A must make so that the marks are all re-aligned as shown?
link to original post
Under these assumptions, I get 60 "rotations."
Gear A will take 4 turns to re-align itself. This would put B's marks 60°/120° out of alignment. If this were to be repeated 2 more times (total of 12 turns), both A & B would be aligned. This whole process will put gear C's mark 144° out of alignment. You'd need to do the 12 turns 4 more times (total of 60 turns) to get A, B, & C back into alignment. D is the mirror image of A, such that whenever A is aligned (i.e., turned a multiple of 4 times), D must also be aligned.
Quote: Gialmere
The marks on the faces of these gears are aligned as shown.
What is the least number of rotations that gear A must make so that the marks are all re-aligned as shown?
link to original post
15?
A and D are back to original on multiples of 4 steps (a step = one tooth advancing = 1/4 turn of A)
B on multiples of 3 (assuming it is symmetric)
C on multiples of 5
So need 4*3*5 steps .... or complete rotations .... 3*5
Quote: chevyQuote: charliepatrickIs the answer en passant? So the black pawn (in same row/column as rook) has just moved up two spaces, allowing the pawn to take it, so it is now adjacent to the King, giving check, and protected by the rook and King.
link to original post
That would mean the board starts white on left and black on right.......
If so, how did black's black bishop get in the upper left corner? White's pawn must be in starting position???
Or maybe I can't think of a way for white to clear out and then get that position filed again.
link to original post
Quote: charliepatrickQuote: chevyQuote: charliepatrickIs the answer en passant? So the black pawn (in same row/column as rook) has just moved up two spaces, allowing the pawn to take it, so it is now adjacent to the King, giving check, and protected by the rook and King.
link to original post
That would mean the board starts white on left and black on right.......
If so, how did black's black bishop get in the upper left corner? White's pawn must be in starting position???
Or maybe I can't think of a way for white to clear out and then get that position filed again.
link to original postI agree it is a problem, but I can only see the pawn move giving mate. So a black pawn could technically have made it (into the to corner) to eighth rank and been promoted to a bishop.
link to original post
Quote: JoemanQuote: charliepatrickQuote: chevyQuote: charliepatrickIs the answer en passant? So the black pawn (in same row/column as rook) has just moved up two spaces, allowing the pawn to take it, so it is now adjacent to the King, giving check, and protected by the rook and King.
link to original post
That would mean the board starts white on left and black on right.......
If so, how did black's black bishop get in the upper left corner? White's pawn must be in starting position???
Or maybe I can't think of a way for white to clear out and then get that position filed again.
link to original postI agree it is a problem, but I can only see the pawn move giving mate. So a black pawn could technically have made it (into the to corner) to eighth rank and been promoted to a bishop.
link to original postI agree with your solve of the bishop issue, but then how did Black's pawns get into that alignment? I can't see how they got there without capturing 9 of White's pieces, but White still has 10 on the board.
link to original post
A highly unrealistic chess configuration, but not impossible,
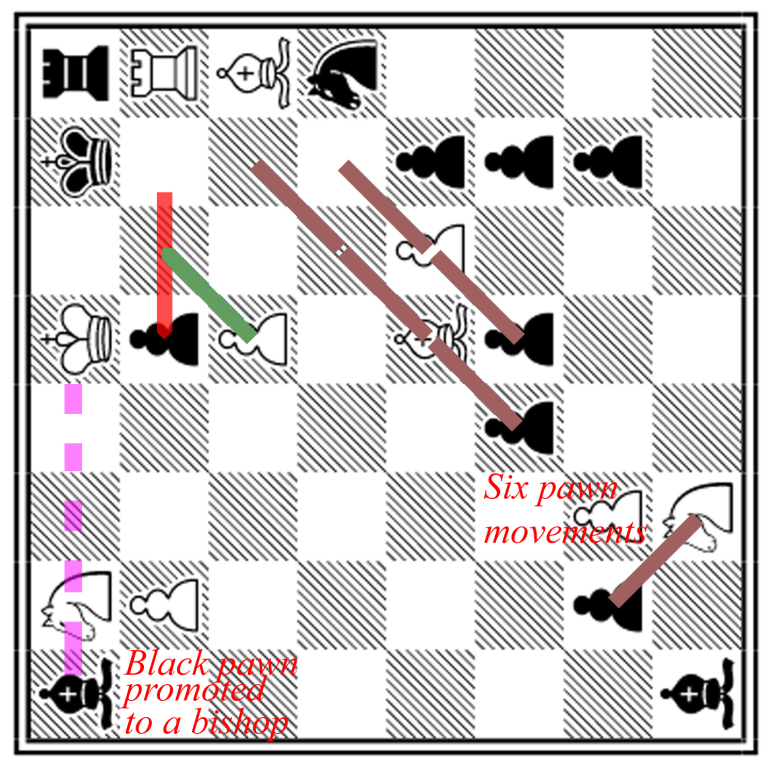 Note: the black bishops prove which way the board is, otherwise how did they get there other than by promotion.
Note: the black bishops prove which way the board is, otherwise how did they get there other than by promotion.Quote: rawtuffA drunken person arrives at home and wants to get in.
There are 10 keys on his keyring and only 1 fits. He randomly pulls a key and tries to open the door.
If it doesn't fit he returns the key to the ring and randomly pulls another key again and again until he finds the one that fits.
Under these circumstances, on which try is he most likely to open the door?
link to original post
I can say for a fact that I know the answer to this one.
In college, after way too many drinks my roommates came home and found me sleeping in the snow on the front porch with the keys in my hand.
This was the house in Iowa City.

And he was successful. I didn't like that last chess problem but I am very impressed with how clever the problem author was in setting that problem up and in deceiving the reader. That had very little to do with chess, and was more of a logic problem that used the rules of chess. Sort or like "seventeen logicians are prisoners in a dungeon with thirteen vestal virgins . . . "
Quote: GialmereWhat is the least number of rotations that gear A must make so that the marks are all re-aligned as shown?
link to original post
LCM(4,3,5,4)=60
Quote: charliepatrickIs the answer en passant? So the black pawn (in same row/column as rook) has just moved up two spaces, allowing the pawn to take it, so it is now adjacent to the King, giving check, and protected by the rook and King.
link to original post
Correct!!
Well done.
The diagram is sideways. Bwahahaha! (ducks)
How should we correct it? Well, if we turn it a quarter turn clockwise, then Blackís light-square bishop is trapped behind an unmoved pawn [the bishop issue], which is impossible. So turn it to the left:

Now, the black pawn on g2 must have started on h7; otherwise Blackís pawns must have devoured an impossible amount of material to reach their present positions [the pawn issue]. That means that the f5, f4, and g2 pawns cannot have moved last, and that means that Blackís last move must have been b7-b5. Thus White can capture the b-pawn en passant, giving mate.
[As mentioned by gordonm888, White has lost enough material to account for the cluster. However, I think that Black's light bishop is simply trying to shepherd the g2 pawn to glory as a promotion would require yet another black pawn on that side of the board.
This puzzle was first published in 1884.]
-------------------------------------------
And now the gears...
Quote: JoemanQuote: Gialmere
The marks on the faces of these gears are aligned as shown.
What is the least number of rotations that gear A must make so that the marks are all re-aligned as shown?
link to original postI'm assuming a "rotation" for gear A constitutes a turn of 90° (the angle to advance the gear 1 tooth). Also, I assume that the marks on gear B are symmetrical and "re-alignment" would be achieved if it were rotated 180°.
Under these assumptions, I get 60 "rotations."
Gear A will take 4 turns to re-align itself. This would put B's marks 60°/120° out of alignment. If this were to be repeated 2 more times (total of 12 turns), both A & B would be aligned. This whole process will put gear C's mark 144° out of alignment. You'd need to do the 12 turns 4 more times (total of 60 turns) to get A, B, & C back into alignment. D is the mirror image of A, such that whenever A is aligned (i.e., turned a multiple of 4 times), D must also be aligned.
link to original post
Quote: chevy
15?
A and D are back to original on multiples of 4 steps (a step = one tooth advancing = 1/4 turn of A)
B on multiples of 3 (assuming it is symmetric)
C on multiples of 5
So need 4*3*5 steps .... or complete rotations .... 3*5
link to original post
Quote: acesideI actually guessed the answer to yesterdayís puzzle but luckily I got it right. For todayís puzzle, Iím a lot more confident with my answer:
The lease number of 360-degree rotations = 4x3x5x4 /(4x4)= 15.
P.S. Itís not clear to me if a rotation is 360 degrees or 90 degrees in this gear A. I looked into other answers and agreed on them. Gears A and D are always in phase, so no need to consider D.
link to original post
Correct!!
Very good.
Let us assume that ďturnsĒ means complete spins, not just moving one notch.
We see that 3 A spins = 2 B spins (12 notches for each).
And 5 Bís = 6 Cís.
But to bring A back, 10 Bís = 12 Cís, and 15 Aís = 10 Bís = 12 Cís.
We see that 4 Cís = 5 Dís, so 12 Cís = 15 Dís.
So it appears that 15 complete A spins [60 teeth] will give 10 Bís, 12 Cís, and 15 Dís, returning all marks to their original positions.
[Note that if the B gear notches were different (say) colors, you'd need 30 "turns."]
---------------------------------------------

A quartet of quizzers...

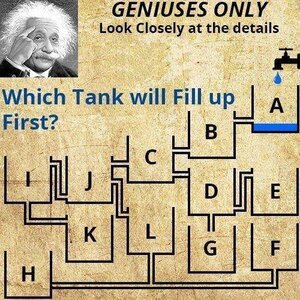

For this one, please note the following points...
1) Force of both the taps is equal.
2) Assume that each tank takes 4 minutes to get filled up fully.
[Fair warning: I make no claims of reality.]

White to move and not checkmate.
Therefore, I will make the assumption that the tank volume, flow rate, and pipe diameter are such that the tanks will drain (assuming the water has somewhere to go) at a rate equal to the rate with which they are filled. I will also assume, as implied by the diagrams, that the pipe diameters and tank volumes are all the same.
Note that without making any assumptions, the variables could be construed such that just about any answers could be correct.
Not to be too pedantic, but for Assumption #1, equal "force" does not necessarily = equal flow rate. Plus, I'm not really sure how to interpret Assumption #2. On it's face, this means either the tanks or the pipes must be different sizes since Tank I, e.g., is receiving twice the flow of either Tank C or Tank D.
Quote: JoemanThe answers for these are dependent on three variables: tank volume, flow rate, and pipe diameter. E.g., for puzzle #1, if the tank was 1 gallon, the flow rate was 10 gal/minute, and the pipe diameter was 1/8", tank #1 would fill first.
Therefore, I will make the assumption that the tank volume, flow rate, and pipe diameter are such that the tanks will drain (assuming the water has somewhere to go) at a rate equal to the rate with which they are filled. I will also assume, as implied by the diagrams, that the pipe diameters and tank volumes are all the same.
Note that without making any assumptions, the variables could be construed such that just about any answers could be correct.Tanks 3 & 4 will be full simultaneously. (assuming no hysteresis)Tank GTank K
Not to be too pedantic, but for Assumption #1, equal "force" does not necessarily = equal flow rate. Plus, I'm not really sure how to interpret Assumption #2. On it's face, this means either the tanks or the pipes must be different sizes since Tank I, e.g., is receiving twice the flow of either Tank C or Tank D.k to f8
link to original post
Two of your answers are correct.
Quote: Joeman#2. On it's face, this means either the tanks or the pipes must be different sizes since Tank I, e.g., is receiving twice the flow of either Tank C or Tank D.
You sure about that?
Quote: GialmereQuote: Joeman#2. On it's face, this means either the tanks or the pipes must be different sizes since Tank I, e.g., is receiving twice the flow of either Tank C or Tank D.
You sure about that?Pretty sure... or am I missing something?
Quote: JoemanQuote: GialmereQuote: Joeman#2. On it's face, this means either the tanks or the pipes must be different sizes since Tank I, e.g., is receiving twice the flow of either Tank C or Tank D.
You sure about that?Pretty sure... or am I missing something?
link to original post
Let's just say that Mario and Luigi have news about that system's waterflow.
Assuming the average player makes 100 bets before withdrawing his entire remaining deposit, what is the house edge?
Also assume the player flat bets even-money bets only and his initial deposit covers at least 100 bets
Incidentally, using the Ace2 Conjecture, an initial deposit of 20 units will have a 99.99% chance of lasting 100 bets
Puzzle #1: Water Tank 3
Puzzle #2: Water Tank G
Puzzle #3: Water Tank K
White: R|G6 - C6 discovered check
Black: R|B7 x H7
1. 3 and 4 tie
2. L
3. N
Note, this assumes the flow rates are the same in #3.
The rake depends on the variance per bet of each session. Longer sessions decrease variance per bet while longer odds increase variance.
Assuming sessions of 100 flat bets on even money props give a house edge of just 0.398%.
Assuming sessions of 100 flat bets on single numbers give a house edge of 2.367%.
Quote: Ace2On the roulette thread, someone recently claimed thereís a ďNo-ZeroĒ roulette game that charges a 10% commission on net wins. I interpret this to be an online game that, when you cash out, withholds 10% of any amount greater than your initial deposit. So if you make a bet on red, for instance, you have an 18/36 chance of winning 2 for 1
Assuming the average player makes 100 bets before withdrawing his entire remaining deposit, what is the house edge?
Also assume the player flat bets even-money bets only and his initial deposit covers at least 100 bets
Incidentally, using the Ace2 Conjecture, an initial deposit of 20 units will have a 99.99% chance of lasting 100 bets
link to original post
Hmmf.........
We don't know whether they take the 10% of difference between buy in and cash out, or whether they take 10% of profit from the winning wagers and tough titty on the losing wagers. I suspect it's the latter.
If it's the former, Being a zero edge game, You might win 50 wagers and lose 50 wagers to end up even.
If they take 10% of net winnings, they take 10% of zero = 0
If it's the latter,
You lose 50 wagers. Tough titty. You win 50 wagers, making a net win of 50 units on those 50 wagers. They take 10% of that 50 = 5.
Total action was 100 wagered once
Hold was 5
House edge = 5% ?
I'll PM a link to the actual casino, so Ace can check the rules.
Ok, I see it now, but I'm going to have to throw a BS flag on the play!Quote: GialmereQuote: JoemanQuote: GialmereQuote: Joeman#2. On it's face, this means either the tanks or the pipes must be different sizes since Tank I, e.g., is receiving twice the flow of either Tank C or Tank D.
You sure about that?Pretty sure... or am I missing something?
link to original post
Let's just say that Mario and Luigi have news about that system's waterflow.
link to original post
P.S., These eyes ain't as young as they used to be!
Quote: Gialmere
A quartet of quizzers...
For this one, please note the following points...
1) Force of both the taps is equal.
2) Assume that each tank takes 4 minutes to get filled up fully.Once again chess fans, have at thee!
[Fair warning: I make no claims of reality.]
White to move and not checkmate.
link to original post
1) 3 and 4
2) F
3) N
Quote: Mental
The rake depends on the variance per bet of each session. Longer sessions decrease variance per bet while longer odds increase variance.
Assuming sessions of 100 flat bets on even money props give a house edge of just 0.398%.
Assuming sessions of 100 flat bets on single numbers give a house edge of 2.367%.
link to original post
workings out?
For now letís assume the rules are how I stated themQuote: OnceDearQuote: Ace2On the roulette thread, someone recently claimed thereís a ďNo-ZeroĒ roulette game that charges a 10% commission on net wins. I interpret this to be an online game that, when you cash out, withholds 10% of any amount greater than your initial deposit. So if you make a bet on red, for instance, you have an 18/36 chance of winning 2 for 1
Assuming the average player makes 100 bets before withdrawing his entire remaining deposit, what is the house edge?
Also assume the player flat bets even-money bets only and his initial deposit covers at least 100 bets
Incidentally, using the Ace2 Conjecture, an initial deposit of 20 units will have a 99.99% chance of lasting 100 bets
link to original post
Hmmf.........
We don't know whether they take the 10% of difference between buy in and cash out, or whether they take 10% of profit from the winning wagers and tough titty on the losing wagers. I suspect it's the latter.
If it's the former, Being a zero edge game, You might win 50 wagers and lose 50 wagers to end up even.
If they take 10% of net winnings, they take 10% of zero = 0
If it's the latter,
You lose 50 wagers. Tough titty. You win 50 wagers, making a net win of 50 units on those 50 wagers. They take 10% of that 50 = 5.
Total action was 100 wagered once
Hold was 5
House edge = 5% ?
I'll PM a link to the actual casino, so Ace can check the rules.
link to original post
Quote: OnceDearQuote: Mental
The rake depends on the variance per bet of each session. Longer sessions decrease variance per bet while longer odds increase variance.
Assuming sessions of 100 flat bets on even money props give a house edge of just 0.398%.
Assuming sessions of 100 flat bets on single numbers give a house edge of 2.367%.
link to original post
workings out?
link to original post
I did it by summing over the binomial distribution but my first try was off by a factor of 2. If you win 51/100, then you net two units of profit, not one. My first try was giving the answer as 0.001989730935 which is half the answer I copied above, 0.003979461869.
I did a quick MC sim to confirm.
Agree. However, a more elegant solution is 10% / (100 * 2π)^.5 =~ 0.003989, accurate within 0.3%Quote: MentalQuote: OnceDearQuote: Mental
The rake depends on the variance per bet of each session. Longer sessions decrease variance per bet while longer odds increase variance.
Assuming sessions of 100 flat bets on even money props give a house edge of just 0.398%.
Assuming sessions of 100 flat bets on single numbers give a house edge of 2.367%.
link to original post
workings out?
link to original post
I did it by summing over the binomial distribution but my first try was off by a factor of 2. If you win 51/100, then you net two units of profit, not one. My first try was giving the answer as 0.001989730935 which is half the answer I copied above, 0.003979461869.
I did a quick MC sim to confirm.
link to original post
This question is unclear. Is this an average player who makes exactly 100 bets, or are you asking what the rake is as a percentage of action will be if the average player makes 100 bets on average?Quote: Ace2On the roulette thread, someone recently claimed thereís a ďNo-ZeroĒ roulette game that charges a 10% commission on net wins. I interpret this to be an online game that, when you cash out, withholds 10% of any amount greater than your initial deposit. So if you make a bet on red, for instance, you have an 18/36 chance of winning 2 for 1
Assuming the average player makes 100 bets before withdrawing his entire remaining deposit, what is the house edge?
Also assume the player flat bets even-money bets only and his initial deposit covers at least 100 bets
Incidentally, using the Ace2 Conjecture, an initial deposit of 20 units will have a 99.99% chance of lasting 100 bets
link to original post
In the latter case, the question cannot be answered. If there are 100 players and 99 players make one bet each and the last player make 9901 bets, the average player is making 100 bets. But the house edge (calculated over the group) will be quite different than if each of them makes exactly 100 bets. In that case, I need the PDF for session length to calculate any answer. Every session length has a different house edge. The one-spin session has the largest house edge and the infinite session has no house edge.
So I am thinking you mean this is an average-height player, and he makes exactly 100 bets.
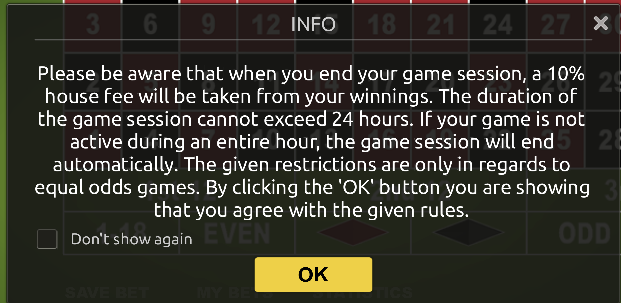
Note that the house makes more money if they time your winning session out rather than let you resume it.
Who knows what happens if you get disconnected.
They have an incentive to disconnect winners.
They seem to realize they are making more rake on the riskier bets, so they don't need to have as many restrictions. If you keep your session open for the rest of your life, then there is no rake. I think the 24-hour restriction is probably still enforced.



:strip_icc()/pic7877285.png)