Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
| Hand type | Perms | Ties | Perms | Comments |
|---|---|---|---|---|
xxx - trips | 52 | 0 | 0 | Not possible |
xxy - pair | 3 744 | 3 | 11 232 | One way for pair, three for odd card |
XYZ - flush | 1 144 | 3 | 3 432 | Any, incl SF, flush, three other suits match |
XYz - two suited | 10 296 | 25 | 257 400 | Any, incl St,; any 3 of each less 2 flushes |
Xyz - rainbow | 6 864 | 26 | 178 464 | Any, incl St,; any 3 of each less 1 flush |
22 100 | 407 170 400 | 450 528 |
Quote: charliepatrick450 528
Thanks Charlie! I agree.
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
Quote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
I get 6 feet + 5 * sqrt(2/pi) inches or about 6'4".
Quote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
I see now the problem is asking for the mean. I knew the median was too easy, which I list below, hopefully correctly.
Median large = 75.37244875"
Median giant = 77.7517469"
Quote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
My previous answer was for L only.
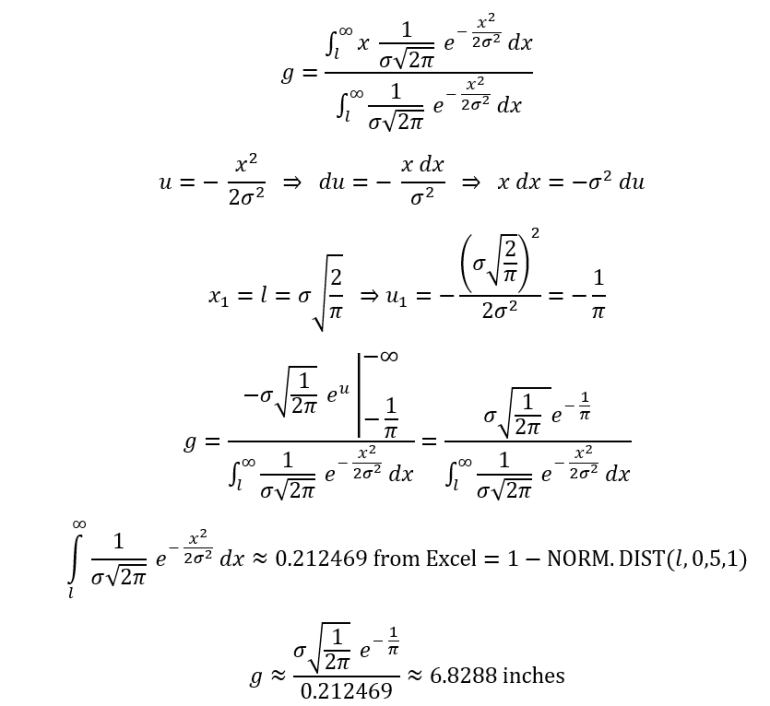
For the average height of giant people, I get approximately 6 feet + 6.8288 inches.
Integral of 0 to infinity of the area under the right side of the bell curve.
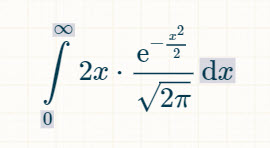
My favorate integral calculator (women didn't speak to me until I was 30) says the answer is sqrt(2)/sqrt(pi).
If CD has a method that uses less cheating, I'd very keen to see it.
Agree with average Large heightQuote: ChesterDogQuote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
I get 6 feet + 5 * sqrt(2/pi) inches or about 6'4".
link to original post
Agree with average Giant height, but please show your method to receive full creditQuote: ChesterDogQuote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
My previous answer was for L only.
For the average height of giant people, I get approximately 6 feet + 6.8288 inches.
link to original post
Quote: Ace2Agree with average Giant height, but please show your method to receive full creditQuote: ChesterDogQuote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
My previous answer was for L only.
For the average height of giant people, I get approximately 6 feet + 6.8288 inches.
link to original post
link to original post
Below is my method. I used g for the number of inches above six feet for the average height of giant people and l for the inches above six feet for large people.
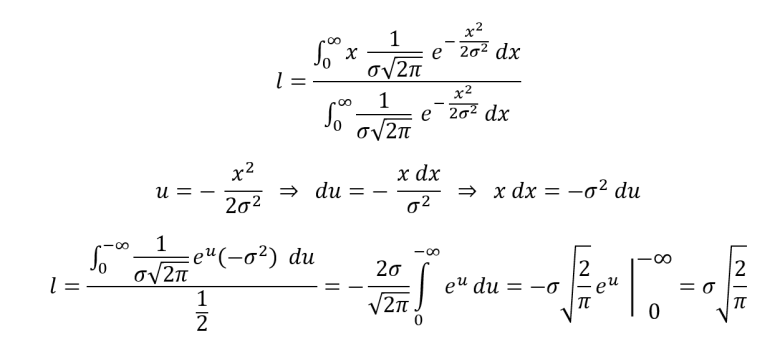
Great write-up of the solution. I agree !Quote: ChesterDogQuote: Ace2Agree with average Giant height, but please show your method to receive full creditQuote: ChesterDogQuote: Ace2Assume the height of the adult population is normally distributed with an average of six feet and a standard deviation of five inches. Everyone over six feet is classified as “Large”
What is the average height of the large people? Call this average “L”
Among the large people, those taller than the average L are classified as “Giant”. What is the average height of the giant people ?
link to original post
My previous answer was for L only.
For the average height of giant people, I get approximately 6 feet + 6.8288 inches.
link to original post
link to original post
Below is my method. I used g for the number of inches above six feet for the average height of giant people and l for the inches above six feet for large people.
link to original post
It’s not too often that both π and e appear in the final solution of a problem. Euler’s identity of e^(i π) = -1 is the only instance I can recall when e is taken to a power of π

You're playing a game where two standard dice are rolled but they produce 21 different outcomes.
How are you reading the dice?
Quote: GialmereHow are you reading the dice?
link to original post
Doubles = Zero.
Quote: DieterSubtracting the smaller value from the larger value.
Doubles = Zero.
link to original post
If I'm reading this correctly, you're coming up with six different outcomes: the numbers 0, 1, 2, 3, 4 and 5.
Apologies if my wording is confusing.
Quote: GialmereQuote: DieterSubtracting the smaller value from the larger value.
Doubles = Zero.
link to original post
If I'm reading this correctly, you're coming up with six different outcomes: the numbers 0, 1, 2, 3, 4 and 5.
Apologies if my wording is confusing.
link to original post
Nobody said I was good at this.
Hopefully some other lucky contestant learns from my mistake.
Quote: Gialmere...How are you reading the dice?...
Quote: GialmereIt's easy Monday. Let's gather 'round the game table...
You're playing a game where two standard dice are rolled but they produce 21 different outcomes.
How are you reading the dice?
link to original post
I have actually played quite a few games that do this.
You are reading them as a 2-digit number, with the lower digit first. For example, a 1 and a 6 is a 16, as is a 6 and a 1, and a pair of 3s is a 33.
6-6 = 12
6-5 = 11
6-4 = 30 5-5 = 10
6-3 = 39 5-4 = 19
6-2 = 48 5-3 = 28 4-4 = 8
6-1 = 57 5-2 = 37 4-3 = 17
and similarly (by symmetry) there are nine options for 6 thru 2.
Total = 9 from 12-8, 3 from 7, 9 from 6-2. Total = 21 ways.
Quote: charliepatrickI used to play that in a pub many years ago, never won!In dominoes there are 28 different pieces, but it includes Blanks. So ignoring those (6-0 thru 0-0) there are 21. This can be achieved by putting the larger dice to the left, and the smaller (or equal) one to the right, and then reading them as a two digit number. That way 6-6 (66) can be formed once, and things like 6-5 (65) 6-4 (64) etc can be formed twice. There are six doubles (66)to(11) and fifteen others (65)to(21); hence 21 different views.
link to original post
Quote: ThatDonGuyI have actually played quite a few games that do this.
You are reading them as a 2-digit number, with the lower digit first. For example, a 1 and a 6 is a 16, as is a 6 and a 1, and a pair of 3s is a 33.
link to original post
Correct!!
Good show.
6-6
5-5, 5-6
4-4, 4-5, 4-6
3-3, 3-4, 3-5, 3-6
2-2, 2-3, 2-4, 2-5, 2-6
1-1, 1-2, 1-3, 1-4, 1-5, 1-6
Also typically the higher the number the better. For example, I have a golf game that uses this method. On a tee shot for a par 4, a roll of 6-6 would indicate you launched a long drive down the center of the fairway. A roll of 1-2. however, would indicate a short drive sliced into the rough.
-------------------------------------------------------
Incidentally, aforementioned figures aren’t much different than those of recent drawings
Here is an easy problem, to wake up the thread.
There is a 5-mile tunnel and a train 1/4 long long, traveling 60 mph towards the tunnel. How much time will any portion of the train be in the tunnel?
For something a little harder -- same question, except the train is accelerating at a rate of 100 mph at the time the engine enters the tunnel.
I assume you mean train is 1/4 mile long....
a) t~0.19hr or 5.25 min........front of engine needs to get from x_i=0mi to x_f=5.25mi and travels at 60mph (x_f=x_i+v_i*t+.5*a*t^2....v_i=60mph and a=0mi/hr^2)
b) There seems to be problem with second question. 100mph is not an acceleration. Do you mean 100mi/hr^2 ? If so, then assuming it enters tunnel at 60mph, it will be completely clear (x=5.25mi) at speed = 68.19mph (v_f^2 = v_i^2 + 2*a*x). And this happens at time t~0.0819hr or 4.91 min (v_f=v_i+a*t).....or solve the quadratic in a) with a=100mi/hr^2
Quote: WizardSorry I didn't see the post above. I am getting rather sick of the Powerball topic, to be honest with you.
Here is an easy problem, to wake up the thread.
There is a 5-mile tunnel and a train 1/4 long long, traveling 60 mph towards the tunnel. How much time will any portion of the train be in the tunnel?
For something a little harder -- same question, except the train is accelerating at a rate of 100 mph at the time the engine enters the tunnel.
link to original post
Let L be the length of the tunnel and l be the length of the train.
Let t = 0 be the moment the front of the train reaches the entrance of the tunnel, and let V be the speed of the train at t = 0. Let T be the moment the end of the train is at the exit of the tunnel.
Let a be the constant acceleration of the train.
At T, the front of the train will be at L + l. Then (1/2)a T2 + V T = L + l.
(1/2) a T2 + V T - L - l = 0
The solution of the above is:
T = { [V2 + 2 a (L + l) ] 1/2 - V} / a
L = 5 miles
l = 0.25 miles
V = 60 mph
If a = 100 miles/hr2, then T is about 4.914545 minutes.
Also, as a approaches 0, T becomes 5.25 minutes.
Quote: WizardAlan and Bob decide to play a tennis until one of them wins two games in a row. The probability of Alan winning any given game is 2/3. What is the probability Alan wins the tournament?
link to original post
Lets define a few situations that may come up
0 - original starting position
A1 - either Alan won the first game or most recent one (i.e. can come from 0 or B1)
B1 - either Bob won the first game or most recent one (i.e. can come from 0 or A1)
A2 - Alan won the second in a row (so must have come from A1)
B2 - Bob won the second in a row (so must have come from B1)
After the first two games it could go
AA - Alan wins - Pr=2/3 * 2/3 = 4/9.
BB - Bob wins : Pr=1/3 * 1/3 = 1/9.
AB - one of each Bob won most recently : Pr = 2/3 * 1/3 = 2/9
BA - one of each Alan won most recently : Pr = 1/3 * 2/3 = 2/9.
So the series could end or it would be equally likel whether Alan or Bob won the most recent game.
Now look at the various outcomes given you could start in A1.
A wins : Pr = 2/3
B wins : Pr = 1/3*1/3 = 1/9
BA i.e. back to same : Pr = 1/3 * 2/3 = 2/9
Similarly if one was in B1
B wins : Pr = 1/3
A wins : Pr = 2/3 * 2/3 = 4/9
AB back to same : Pr = 2/9.
Combining these two gets
A wins = (2/3+4/9) / 2 = 10/18
B wins = (1/9+1/3) / 2 = 4/18
Back to same state = (2/9+2/9)/2 = 4/18
Thus the series can to and fro, after an even number of games it is 50/50 who is leading, until eventually one actually wins the game.
A wins after 2 games = 4/9 = 28/63
B wins after 2 games = 1/9 = 7/63
A wins after to and fro = Pr (into to and fro) * Pr (AWins) 10/14 = 4/9*5/7 = 20/63
B wins after to and fro = 4/14 = 4/9*2/7 = 8/63
So Pr (A wins) = (28+20)/63 and Pr (B wins) = (7+8)/63. i.e. 16/21 and 5/21.
Let p = probability a wins.
Let a = probability Alan wins tournament after Alan wins last game.
Let b = probability Alan wins tournament after Bob wins last game.
(1) a = p + (1-p)*b
(2) b = p*a
Substituting equation (2) into equation (1):
a = p + (1-p)*pa
a = p + pa - p^2*a
a - pa + p^2*a = p
a(1-p+p^2) = p
(3) a = p/(1-p+p^2)
Substituting equation (3) into equation (2):
b = p^2/(1-p+p^2)
The first game will determine whether the probability of a winning the tournament is a or b:
answer = pa + (1-p)b
= p^2/(1-p+p^2) + (1-p)*p^2/(1-p+p^2)
= (2a^2-a^3)/(a^2-a+1)
Plugging a=2/3, gives a probability of winning the tournament of 16/21.
Quote: WizardI agree with Charlie. That one, I think, is beer worthy. Add one to my tab.
Let p = probability a wins.
Let a = probability Alan wins tournament after Alan wins last game.
Let b = probability Alan wins tournament after Bob wins last game.
(1) a = p + (1-p)*b
(2) b = p*a
Substituting equation (2) into equation (1):
a = p + (1-p)*pa
a = p + pa - p^2*a
a - pa + p^2*a = p
a(1-p+p^2) = p
(3) a = p/(1-p+p^2)
Substituting equation (3) into equation (2):
b = p^2/(1-p+p^2)
The first game will determine whether the probability of a winning the tournament is a or b:
answer = pa + (1-p)b
= p^2/(1-p+p^2) + (1-p)*p^2/(1-p+p^2)
= (2a^2-a^3)/(a^2-a+1)
Plugging a=2/3, gives a probability of winning the tournament of 16/21.
link to original post
I agree. I see what I did wrong.
:strip_icc()/pic7185419.png)
The nine red points form a triangle.
What is the minimum number of points that have to be moved to make a square?
:strip_icc()/pic7190282.png)
This is a capital letter of the alphabet that's been folded just once. Which letter is it if you unfold it? Is it...
1) ...a letter in the range from M to R?
2) ...a letter in the range from G to K?
3) ...a letter in the range from A to G?
4) ...a letter in the range from R to Z?
The second one is 3). That was fun!
btw for those who watch Pointless FUN is the airport code for the capital in Tuvalu!
Does moving the interior point south 3 and east 3 work?
Quote: Dieter
Does moving the interior point south 3 and east 3 work?
link to original post
I think you technically end up with a triangle near a point. It's a clever idea though as both these puzzles fall into the "outside the box thinking" category.
Expected number of games for Alan to win two consecutive is 3/2 + (3/2)^2 = 3.75
Expected number of games for Bob to win two consecutive is 3/1 + (3/1)^2 = 12
Chance of Alan winning two consecutive first is 12 / (12 + 3.75) = 16/21
Quote: GialmereQuote: Dieter
Does moving the interior point south 3 and east 3 work?
link to original post
I think you technically end up with a triangle near a point. It's a clever idea though as both these puzzles fall into the "outside the box thinking" category.
link to original post
Fair enough. The definition of "square" varies considerably.

Quote: Ace2Another approach to the Alan/Bob problem
Expected number of games for Alan to win two consecutive is 3/2 + (3/2)^2 = 3.75
Expected number of games for Bob to win two consecutive is 3/1 + (3/1)^2 = 12
Chance of Alan winning two consecutive first is 12 / (12 + 3.75) = 16/21
link to original post
Thanks, good observation. Reminds me of some puzzles we did before with dice, I think. I'm not sure I could explain to someone else why this works, but I'm not questioning it, of course.
Quote: charliepatrickIf the NW point is the origin then move Southernmost and Eastermost dots to (1,1) and (-1,-1) thus forming a square which has been rotated 45o.
The second one is 3). That was fun!
btw for those who watch Pointless FUN is the airport code for the capital in Tuvalu!
link to original post
Correct!!
Very good. Easy puzzles are still puzzles.
:strip_icc()/pic7185420.png)
--------------------------------------------------------------------------------------------
Quote: DieterFair enough. The definition of "square" varies considerably.
I have to give bonus points for this out of the box response. No need to move anything. It reminds me of the classic riddle: When is a door not a door? Here it's: When is a triangle not a triangle? That's some clever "manure".
:strip_icc()/pic7190283.png)
The interesting thing about this simple puzzle (by puzzlemaster Scott Kim) is that you can't just ask pointblank what the letter is. Nor can you clarify what letter it isn't since that would immediately put the solvers outside the box. Instead you give them various ranges of letters and when they realize what's missing the actual puzzle begins.
-------------------------------------------------

You shuffle a standard (28 tile) set of dominos and draw one at random. You carefully uncover one of the sides to reveal a 6.
What is the probability that this is the double 6 tile?
Quote: GialmereYou shuffle a standard (28 tile) set of dominos and draw one at random. You carefully uncover one of the sides to reveal a 6.
What is the probability that this is the double 6 tile?
link to original post
I'd like to dedicate this one to the memory of Alan.
1/4
Quote: WizardI'd like to dedicate this one to the memory of Alan.
1/4
link to original post
Correct!!
Very good.
Heh. I thought someone might pick up on the puzzle's vibe.
--------------------------------------------------------
Quote: Gialmere
...it has a really long setup and in the end it falls flat.
link to original post
Much like the Aristrocrats joke, assuming I even get the point of it.
Somewhat seriously, thanks for waiting for Alan to pass to ask that one. I think he would have argued the answer is 1/7 for years.
:strip_icc()/pic7190281.png)
Three red and three black cards are removed from a standard deck, shuffled thoroughly and spread facedown on the table in front of Players #1 and #2. The dealer picks up one of the cards and shows it only to Player #1. This card is then set aside out of play.
Player #1 may now either play or pass. If he plays he pays the dealer a $1 fee. He then turns over one of the five remaining cards. If the card is red he wins $2. If it's black he gets nothing. Either way, the game ends.
If Player #1 passes then Player #2 must pay the dealer a 50¢ fee and turn over one of the cards. If the card is red he wins $2. If it's black he gets nothing. Either way, the game ends.
Assuming optimal play, which player will make more money at this game in the long run?
If a Black card is picked, #1 plays and #2 (perforce) passes.
As Red and Black cards are picked with equal probability, on average, #1 and #2 play the same number of games. Therefore we only need to look at which, on average, game gives the best return. For simplicity it's easier to sum up the five possible outcomes and see the total profit.
When #1 plays there are 3 Red and 2 Black, thus the profit is (3*$1 - 2*$1) = $1.
When #2 plays there are 2 Red and 3 Black, however the cost to play is 50c so the profit when winning is $1.50. Thus the profit is (2*$1.50 - 3*50c) = $1.50.
Hence #2 is the better off.
Player#1 can play with an EV = $1 if he only play on when he picks up a black card, or an EV of zero if he plays no matter which color he picks up.
Player#2 can play only when Player#1 passes, but then he can make $1.50 when Players#1 picked up a red card and more if Player picks up a black card but passes anyway.
However, Player #2 will never make any money unless palyer#1 passes.
So Player#1 charges Player#2 a fee in order to pass no matter what color card he sees. The fee might reasonably be set at 60% of what player#2 expects to make. Such an arrangement would be a win-win for both players.
So player#1 profits the most.
This assumes that the $2 that a player can win is the entire amount, as opposed to $2 plus the amount bet.
If P1 sees a red card, and:
(a) plays, P1 has a 2/5 chance of winning $2, for an ER of 4/5, and a EV of 4/5 - 1 = -1/5
(b) passes, P2 has a 2/5 chance of winning $2, for an ER of 4/5, and a EV of 4/5 - 1/2 = 3/10
If P1 sees a black card, and:
(a) plays, P1 has a 3/5 chance of winning $2, for an ER of 6/5, and a EV of 6/5 - 1 = 1/5
(b) passes, P2 has a 3/5 chance of winning $2, for an ER of 6/5, and a EV of 6/5 - 1/2 = 7/10
The first card can equally likely be red or black. If it is red, P1's best play is to pass; if it is black, P1's best play is to play.
The EV for each hand is 1/2 x 0 + 1/2 x 1/5 = 1/10 for P1, and 1/2 x 3/10 + 1/2 x 0 = 3/20 for P2.
Player 2 will make more in the long run.


