Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Quote: ThatDonGuyDice where 2s and 5s "don't count" remind me of Scarney Dice (created by John Scarne), where the 2s and 5s actually say "Dead".
Hopefully I avoided any idiot math errors this time; the number appears to be confirmed by simulation.
Let E(n) be the expected score with N dice remaining
E(0) = 0
E(1) = 2/3 (E(1) + 7/2)
= 7
E(2) = 4/9 (E(2) + 7) + 4/9 E(1)
= 4/9 E(2) + 56/9
= 56/5
E(3) = 8/27 (E(3) + 21/2) + 12/27 E(2) + 6/27 E(1)
= 8/27 E(3) + 84/27 + 12/27 x 56/5 + 6/27 x 7
19 E(3) = 84 + 12 x 56/5 + 42
E(3) = (126 + 12 x 56/5) / 19
= (126 x 5 + 12 x 56) / 95
= 1302 / 95
E(4) = 16/81 (E(4) + 14) + 32/81 E(3) + 24/81 E(2) + 8/81 E(1)
= 16/81 E(4) + 224/81 + 32/81 x 1302/95 + 24/81 x 56/5 + 8/81 x 7
65 E(4) = 224 + 32 x 1302 / 95 + 24 x 56 / 5 + 56
E(4) = (280 x 475 + 41,664 x 5 + 1344 x 95) / (95 x 5 x 65)
= (280 x 95 + 41,664 + 1344 x 19) / (95 x 65)
= 3752 / 247
E(5) = 32/243 (E(5) + 35/2) + 80/243 E(4) + 80/243 E(3) + 40/243 E(2) + 10/243 E(1)
243 E(5) = 32 E(5) + 560 + 80 x 3752 / (19 x 13) + 80 x 1302 / (19 x 5) + 448 + 70
211 E(5) = 1078 + 80 x 3752 / (19 x 13) + 80 x 1302 / (19 x 5)
(211 x 19 x 65) E(5) = 1078 x 19 x 65 + 80 x 3752 x 5 + 80 x 1302 x 13
E(5) = 837,242 / 52,117, or about 16.065
Correct!
Very impressive.
-------------------------------
A pun walks into a bar and 10 people drop dead.
Pun in, ten dead.
I agree with the answer as provided.

On his TV show in 2007, comedian David Letterman made the following quip...
"In 1626, we bought Manhattan from the Indians for $24. Today, it would be worth 730 trillion dollars."
At what interest rate would you have to invest $24 in 1626 so that it would be worth $730 trillion in 2007?
Assume that the rate stays constant and that it is compounded annually.
Give your answer as a percent correct to two decimal places (e.g., like 3.74%).
Quote: Gialmere...
On his TV show in 2007, comedian David Letterman made the following quip...
"In 1626, we bought Manhattan from the Indians for $24. Today, it would be worth 730 trillion dollars."
At what interest rate would you have to invest $24 in 1626 so that it would be worth $730 trillion in 2007?
Assume that the rate stays constant and that it is compounded annually.
Give your answer as a percent correct to two decimal places (e.g., like 3.74%).
Solved this equation for x:
$24(1+x)2020-1626=$730 trillion
Edit: Reading Joeman's post, I see my equation should have been:
$24(1+x)2007-1626=$730 trillion for Joeman's correct answer 8.49%.
For annual compounding...
Today's value = Initial principal * (1 + rate) ^ years
--or--
$730 Trillion = $24(1+rate) ^ 381
Dividing both sides by the initial principal and then taking the 381st root, you get:
1 + rate = 1.0849
So the rate = 0.0849 or 8.49%

Quote: Gialmere
On his TV show in 2007, comedian David Letterman made the following quip...
"In 1626, we bought Manhattan from the Indians for $24. Today, it would be worth 730 trillion dollars."
At the risk of making a political comment, that makes the national debt seem not so bad.
Quote: Joeman8.49%
For annual compounding...
Today's value = Initial principal * (1 + rate) ^ years
--or--
$730 Trillion = $24(1+rate) ^ 381
Dividing both sides by the initial principal and then taking the 381st root, you get:
1 + rate = 1.0849
So the rate = 0.0849 or 8.49%
I get the other answer. Think you subtracted wrong. 394 years not 381.
Extra credit, what’s the interest rate if there is continuous compounding?
I read the question as asking about the value in 2007 when the statement was made, not today's value.Quote: unJonI get the other answer. Think you subtracted wrong. 394 years not 381.
If the US were to sell Manhattan at that valuation, the government could pay off all its debts and have enough left over to make each US citizen a millionaire twice over!Quote: WizardAt the risk of making a political comment, that makes the national debt seem not so bad.
Quote: JoemanI read the question as asking about the value in 2007 when the statement was made, not today's value.
Ah. Then I agree with you and see your powers of reading comprehension exceed mine.
True statement! A recreational poker site has the following weird Texas hold-em poker variant.
The deck is 10 to Ace, 4 suits; 20 cards.
1. What is the lowest possible 5-card poker hand that a player can make with his two hole cards and five common cards?
2. Given that hand categories are: Royal Flush, Straight Flush, Quads, etc., which hand category is the most probable and with what probability?
Quote: JoemanIf the US were to sell Manhattan at that valuation, the government could pay off all its debts and have enough left over to make each US citizen a millionaire twice over!
Let's confirm that. The valuation is $730 trillion.
The national debt is $27 trillion (source = debt clock).
That leaves $703 trillion.
The US population is 330 million. (source = census.gov).
If we sold Manhattan that would be:
703,000,000,000,000
----------------------
330,000,000
Dividing each side by 1,000,000:
703,000,000/330 = $2,130,303.
BTW, Bloomberg.com puts the total valuation of Manhattan at $1.74 trillion.
Quote: gordonm888...weird Texas hold-em poker...The deck is 10 to Ace, 4 suits; 20 cards.
1. What is the lowest possible 5-card poker hand that a player can make with his two hole cards and five common cards?
2. Given that hand categories are: Royal Flush, Straight Flush, Quads, etc., which hand category is the most probable and with what probability?
| RF | 420 |
| Quads | 2800 |
| FH | 29280 |
| Straight | 27740 |
| Two Pairs | 17280 |
Quote: charliepatrickQuote: gordonm888...weird Texas hold-em poker...The deck is 10 to Ace, 4 suits; 20 cards.
1. What is the lowest possible 5-card poker hand that a player can make with his two hole cards and five common cards?
2. Given that hand categories are: Royal Flush, Straight Flush, Quads, etc., which hand category is the most probable and with what probability?The lowest hand is Two Pairs, because if before the river you only had one pair then you would have all five ranks making a straight. Similarly Trips makes a straight.So Full House is most likely 29280/77520 ~= 37.77%
RF Quads FH Straight Two Pairs
For question #1, your answer was a hand category and not the lowest possible hand. In normal Texas holdem, the lowest possible 5 card poker hand is 9-8-7-5-4, not "No Pair."
For question#2, I calculate a different number.
Quote: gordonm888Quote: charliepatrickQuote: gordonm888...weird Texas hold-em poker...The deck is 10 to Ace, 4 suits; 20 cards.
1. What is the lowest possible 5-card poker hand that a player can make with his two hole cards and five common cards?
2. Given that hand categories are: Royal Flush, Straight Flush, Quads, etc., which hand category is the most probable and with what probability?The lowest hand is Two Pairs, because if before the river you only had one pair then you would have all five ranks making a straight. Similarly Trips makes a straight.So Full House is most likely 29280/77520 ~= 37.77%
RF Quads FH Straight Two Pairs
For question #1, your answer was a hand category and not the lowest possible hand. In normal Texas holdem, the lowest possible 5 card poker hand is 9-8-7-5-4, not "No Pair."
For question#2, I calculate a different number.
Should be jacks and tens with an ace kicker.
If there are only two pair among the 7 cards, there must also be a straight. So, to get a 5-card hand of two pair, there must be three pair among the 7 cards.
Quote: Joeman8.49%
For annual compounding...
Today's value = Initial principal * (1 + rate) ^ years
--or--
$730 Trillion = $24(1+rate) ^ 381
Dividing both sides by the initial principal and then taking the 381st root, you get:
1 + rate = 1.0849
So the rate = 0.0849 or 8.49%
Correct!
With bonus points for the spoiler joke.
----------------------------------
Did you hear about the banker who's also learning chemistry?
He's got a lot of compound interest.
Quote: JoemanTwo Pair: Queens & Jacks with a King kicker. The combination of hand + board would be: T, T, J, J, Q, Q, K
If there are only two pair among the 7 cards, there must also be a straight. So, to get a 5-card hand of two pair, there must be three pair among the 7 cards.
CORRECT for question#1
Quote: JoemanTwo Pair: Queens & Jacks with a King kicker. The combination of hand + board would be: T, T, J, J, Q, Q, K
If there are only two pair among the 7 cards, there must also be a straight. So, to get a 5-card hand of two pair, there must be three pair among the 7 cards.
Oops. Right.
Quote: gordonm888...For question#2, I calculate a different number.
| C1 | C2 | C3 | C4 | C5 | Combins | Ways | Quads | FullHouse | Straight/SF | TwoPairs | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
4 | 3 | 0 | 0 | 0 | 1 | 4 | 1 | 1 | 1 | 5 | 4 | 1 | 80 | 80 | 0 | 0 | 0 |
4 | 2 | 1 | 0 | 0 | 1 | 6 | 4 | 1 | 1 | 5 | 4 | 3 | 1 440 | 1 440 | 0 | 0 | 0 |
4 | 1 | 1 | 1 | 0 | 1 | 4 | 4 | 4 | 1 | 5 | 4 | 1 | 1 280 | 1 280 | 0 | 0 | 0 |
3 | 3 | 1 | 0 | 0 | 4 | 4 | 4 | 1 | 1 | 10 | 3 | 1 | 1 920 | 0 | 1 920 | 0 | 0 |
3 | 2 | 2 | 0 | 0 | 4 | 6 | 6 | 1 | 1 | 5 | 6 | 1 | 4 320 | 0 | 4 320 | 0 | 0 |
3 | 2 | 1 | 1 | 0 | 4 | 6 | 4 | 4 | 1 | 5 | 4 | 3 | 23 040 | 0 | 23 040 | 0 | 0 |
3 | 1 | 1 | 1 | 1 | 4 | 4 | 4 | 4 | 4 | 5 | 1 | 1 | 5 120 | 0 | 0 | 5 120 | 0 |
2 | 2 | 2 | 1 | 0 | 6 | 6 | 6 | 4 | 1 | 10 | 2 | 1 | 17 280 | 0 | 0 | 0 | 17 280 |
2 | 2 | 1 | 1 | 1 | 6 | 6 | 4 | 4 | 4 | 10 | 1 | 1 | 23 040 | 0 | 0 | 23 040 | 0 |
77 520 | 2 800 | 29 280 | 28 160 | 17 280 |
Quote: charliepatrickI've tried a different method as the distribution of cards leads to a unique category (except Straights may be SFs and there are 420 of those 4*15*14/2).
C1 C2 C3 C4 C5 Combins Ways Quads FullHouse Straight/SF TwoPairs
CORRECT
I see now I made a mistake when calculating Full Houses. I did separate out the "Two 3oaks + singleton" (3+3+1) correctly, but lumped together the 3+2+1+1 with the 3+2+2 and thus ultimately doublecounted some of the 3+2+2 hands.
The reason I shared this game with everyone (as a math puzzle) is because it is such an extreme example of a short-deck game. It has only five possible categories of 5-card poker hands:
Royal Flush
Quads
Full House
Straight
Two Pair (and only as 3-pair within the 7 card hand)
And because the lowest possible 5 card poker hand is so high: QQ-JJ-K.

The high school newspaper seems to be having trouble both with its printer and its editing. The box score for the district hockey league is a confusing mess.
Using the information that was printed, can you fill in the empty boxes and make sense of the current standings?
:strip_icc()/pic5757632.png)
Hockey standings are based on points -- each WIN is 2 points, each LOSS is 0 points, and each TIE is 1 point.
In this local high school league, each team plays each other once, but they have not finished the season.
Quote: Gialmere...can you fill in the empty boxes...
(b) Sum(For)=Sum(Against)
(c) 0 pts -> WA lost all games
(d) J and WI have played everyone, so E has played >1game. Sum(Played) must be even (two teams per game), E = 3
(e) Sum(Points)=Sum(Played), Points€=5
(f) J and WI played everyone, so WA has played them but not played C or E
(g) C's ties are with J WI and E
(h) So WI won 1 and J won 2
8 games: J=C WI=C E=C E>WI W>J J<WA WI>WA J>WI
P W L T F A Points
4 2 1 1 7 1 5
2 0 2 0 2 6 0
4 1 2 1 5 10 3
3 0 0 3 4 4 3
3 2 0 1 5 2 5
Quote: charliepatrick(a) C Played 3, 3 pts with no losses -> all draws and For=Against
(b) Sum(For)=Sum(Against)
(c) 0 pts -> WA lost all games
(d) J and WI have played everyone, so E has played >1game. Sum(Played) must be even (two teams per game), E = 3
(e) Sum(Points)=Sum(Played), Points€=5
(f) J and WI played everyone, so WA has played them but not played C or E
(g) C's ties are with J WI and E
(h) So WI won 1 and J won 2
8 games: J=C WI=C E=C E>WI W>J J<WA WI>WA J>WI
P W L T F A Points
4 2 1 1 7 1 5
2 0 2 0 2 6 0
4 1 2 1 5 10 3
3 0 0 3 4 4 3
3 2 0 1 5 2 5
Correct!
-----------------------------
My local hockey rink just reported their Zamboni driver has gone missing...
They hope he resurfaces soon.

Four honest and hard-working computer engineers were having lunch together when the topic of salaries came up.
They decided they wanted to compute the average of all four of their annual incomes. None of the engineers, however, were willing to disclose how much money they actually made in a year.
How were they able to make the correct calculation?
Quote: Gialmere...How were they able to make the correct calculation?...
Then calculate the difference between the total of "original numbers" and "less two salaries" and divide by 2.
Quote: GialmereIt's easy Monday...
...
Four honest and hard-working computer engineers were having lunch together when the topic of salaries came up.
They decided they wanted to compute the average of all four of their annual incomes. None of the engineers, however, were willing to disclose how much money they actually made in a year.
How were they able to make the correct calculation?
Four playing cards will be prepared, each with a different number on it. For example, the four numbers might be: 5,000; 10,000; 15,000; and 20,000.
The four cards are shuffled and dealt face down to the four engineers. Each adds his salary to the number on his card and announces the sum.
They add the four announced numbers, subtract 50,000 and divide by four to find their average salary.
Quote: charliepatrickJust an idea that seems to work. Using two pieces of paper A writes down the same large value, known to exceed the value of the four salaries, and (can show them to B) and put one in the "original numbers" box and passes the other piece of paper to C. C subtracts their salary, writes the total on another piece of paper and hands it to D. D does the same and now puts their piece of paper in the "less two salaries" box. B, C and D similarly repeat the process. (It is even fairer if they all come up with their initial numbers at the same time and then randomise who gets which one. Another method is for people to come up with two initial random numbers each. Another method is only to use A and C to initiate the process, so divide by 1.)
Then calculate the difference between the total of "original numbers" and "less two salaries" and divide by 2.
Quote: ChesterDog
Four playing cards will be prepared, each with a different number on it. For example, the four numbers might be: 5,000; 10,000; 15,000; and 20,000.
The four cards are shuffled and dealt face down to the four engineers. Each adds his salary to the number on his card and announces the sum.
They add the four announced numbers, subtract 50,000 and divide by four to find their average salary.
All Correct!
Engineer #1 secretly generates a large (say, seven figure) random number and adds his salary to the amount. He writes down the new number and gives it to engineer #2. She, in turn, secretly adds her salary to the number, writes down the new sum and passes it to engineer #3, and so on. When the final number returns to engineer #1, he subtracts from it the original random number and divides the difference by 4.
The engineers can now see how underpaid they are as a group.
-----------------------------
Reaching the end of a job interview, the interviewer asked a young engineer, "What starting salary were you thinking about?"
The Engineer said, "In the neighborhood of $125,000 a year, depending on the benefits package."
The interviewer said, "Well, what would you say to a package of 5 weeks vacation, 14 paid holidays, full medical and dental, company matching retirement fund to 50% of salary, and a company car leased every 2 years - say, a red Corvette?"
The Engineer sat up straight and said, "Wow! Are you kidding?"
The interviewer replied, "Yeah, but you started it."
Quote: Gialmere....
...As you can see, there are actually several ways to solve this puzzle that a clever person might think up. The "official" solve uses probably the simplest technique...
Engineer #1 secretly generates a large (say, seven figure) random number and adds his salary to the amount. He writes down the new number and gives it to engineer #2. She, in turn, secretly adds her salary to the number, writes down the new sum and passes it to engineer #3, and so on. When the final number returns to engineer #1, he subtracts from it the original random number and divides the difference by 4.
The engineers can now see how underpaid they are as a group.

An a × b × c cuboid is constructed out of abc identical unit cubes -- a la Rubik's Cube. Divide the cubes into two mutually exclusive types. External cubes are those that constitute the faces of the cuboid; internal cubes are completely enclosed. For example, the cuboid below has 74 external and 10 internal cubes.
:strip_icc()/pic5807145.png)
Find all cuboids such that the number of external cubes equals the number of internal cubes.
(That is, give the dimensions of all such cuboids.)
8,10,12.
I think any solution must have and odd number of even numbers (either 1 or 3).
It's easy to say that if the sides are x, y, and z, then 4*(xy+xz+yz) +16 = xyz + 8*(x+y+z)
Quote: Wizard
8,10,12.
I think any solution must have and odd number of even numbers (either 1 or 3).
It's easy to say that if the sides are x, y, and z, then 4*(xy+xz+yz) = xyz + 8*(x+y+z)
Not an answer but two other formulae.
(x-2)*(y-2)*(z-2) = xyz/2
That is the number of interior cubes equals half the cubes.
Or
xy + 2y(z-2) + 2(x-2)(z-2) = xyz/2
That is the number of exterior cubes equals half the cubes.
12 x 10 x 8
14 x 9 x 8
16 x 10 x 7
16 x 14 x 6
18 x 8 x 8
20 x 9 x 7
20 x 12 x 6
24 x 11 x 6
24 x 22 x 5
27 x 20 x 5
30 x 8 x 7
32 x 10 x 6
32 x 18 x 5
36 x 17 x 5
42 x 16 x 5
52 x 15 x 5
56 x 9 x 6
72 x 14 x 5
100 x 7 x 7
132 x 13 x 5
Note that, if the dimensions are L x W x H, then LWH = 2 (L - 2) (W - 2) (H - 2)
Quote: ThatDonGuy
Here are the ones I could find where all of the dimensions < 5000:
12 x 10 x 8
14 x 9 x 8
16 x 10 x 7
16 x 14 x 6
18 x 8 x 8
20 x 9 x 7
20 x 12 x 6
24 x 11 x 6
24 x 22 x 5
27 x 20 x 5
30 x 8 x 7
32 x 10 x 6
32 x 18 x 5
36 x 17 x 5
42 x 16 x 5
52 x 15 x 5
56 x 9 x 6
72 x 14 x 5
100 x 7 x 7
132 x 13 x 5
2581 x 2580 x 651
2836 x 2744 x 2218
2951 x 2176 x 1346
2988 x 2550 x 1700
3554 x 3216 x 2264
3570 x 3040 x 2781
4233 x 3222 x 3160
4479 x 2648 x 2182
4580 x 4501 x 1465
4700 x 3586 x 1536
4770 x 4279 x 2112
4831 x 3621 x 1972
4838 x 3606 x 2224
4858 x 4060 x 2840
4866 x 3840 x 3228
4962 x 4736 x 2750
Note that, if the dimensions are L x W x H, then LWH = 2 (L - 2) (W - 2) (H - 2)
I have a feeling there is no maximum solution, but I am still working on the proof (one way or the other)
My gut feeling was that there would be a maximum solution because
5,13,132
5,14,72
5,15,52
5,16,42
5,17,36
5,18,32
5,20,27
6,9,56
6,10,32
6,11,24
6,12,20
6,14,16
7,7,100
7,8,30
7,9,20
7,10,16
8,8,18
8,9,14
8,10,12
Quote: WizardHere are my answers thus far
5, 22, 24
Quote: ThatDonGuyEDIT: My earlier list had answers that were incorrect because of 32-bit integer overflows
12 x 10 x 8
14 x 9 x 8
16 x 10 x 7
16 x 14 x 6
18 x 8 x 8
20 x 9 x 7
20 x 12 x 6
24 x 11 x 6
24 x 22 x 5
27 x 20 x 5
30 x 8 x 7
32 x 10 x 6
32 x 18 x 5
36 x 17 x 5
42 x 16 x 5
52 x 15 x 5
56 x 9 x 6
72 x 14 x 5
100 x 7 x 7
132 x 13 x 5
Note that, if the dimensions are L x W x H, then LWH = 2 (L - 2) (W - 2) (H - 2)
Quote: WizardHere are my answers thus far. I don't think there are more and can't find any connection to them, other than a circular reference to the problem at hand.
5,13,132
5,14,72
5,15,52
5,16,42
5,17,36
5,18,32
5,20,27
6,9,56
6,10,32
6,11,24
6,12,20
6,14,16
7,7,100
7,8,30
7,9,20
7,10,16
8,8,18
8,9,14
8,10,12
Correct!
In an unusual joint solve, kind of, sort of.

--------------------------------

You have a 1x4 rectangular piece of paper. You fold it so that two opposite corners overlap, making a pentagon shape. What is the ratio of the area of that pentagon where the paper overlaps to the entire pentagon?
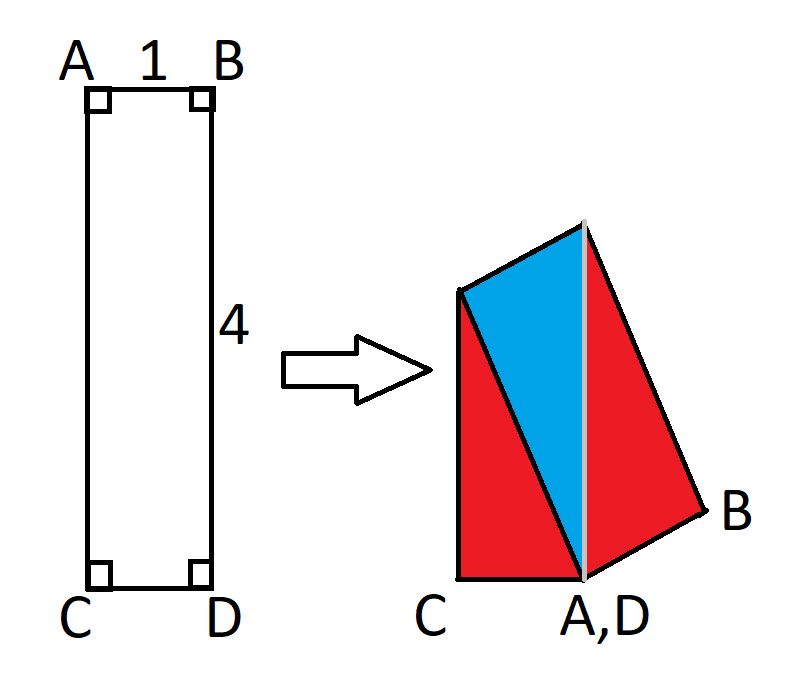
In other words, what is the ratio of the blue area to the total area?
***I "think" the red/blue diagram is not to scale. It makes blue appear as right angle. I "think" the line from A,D to the center of opposite side is the perpendicular.***
Call the center of the rectangle Y. Call the ends of the fold (X,Z). So side of blue triangle opposite A,D is XYZ with Y at midpoint and (A,D) to Y is perpendicular to XZ.
Area of Blue = .5 * XZ * AY = XY * AY
Area of rectangle = 2*Area of Blue + 2* Area of Red = 4
Area of Pentagon = Area of rectangle - Area of Blue = 4-Area of Blue
Ratio = Area of Blue / (4-Area of Blue)
From Trig using the rectangle diagram with XYZ added accordingly....
AD = sqrt(4^2+1^2)=sqrt(17)
AY = AD/2 = sqrt(17)/2
Call theta angle given by CAD, then
tan(theta) = DC/AC = 1/4
Theta is also angle for XAY, so
tan(theta) = XY/AY
XY = AY * tan(theta) = sqrt(17)/2 * (1/4) = sqrt(17)/8
Thus Area of Blue = XY * AY = [sqrt(17)/8] * sqrt(17)/2 = 17/16
And
ratio = Area of Blue / (4-Area of Blue)
= (17/16) / (4 - 17/16)
=17/47
For arbitrary rectangle with Height=H, Width=W......(oriented with H>=W), What range can the area ratio (Blue/Total) of the folded result have? And for what H,W is the Blue area 50%?
Your second set disproves your earlier statement about the permissible number of evens.
Dog Hand
Quote: chevyFollow up question:
For arbitrary rectangle with Height=H, Width=W......(oriented with H>=W), What range can the area ratio (Blue/Total) of the folded result have? And for what H,W is the Blue area 50%?
I get a general equation for the ratio of H/W = sqrt((ratio+1)/(3ratio -1)) .
For a ratio of 0.5, H/W = sqrt(3)
If H=W, ratio = 1 (same as folding a square in half).
If H >> W, the ratio approaches 1/3.
Quote: CrystalMath
I get a general equation for the ratio of H/W = sqrt((ratio+1)/(3ratio -1)) .
For a ratio of 0.5, H/W = sqrt(3)
If H=W, ratio = 1 (same as folding a square in half).
If H >> W, the ratio approaches 1/3.
I agree!
The ratio of the area of that pentagon where the paper overlaps to the entire pentagon is 1/3
Sorry, didn't notice that the problem was a day old.
:strip_icc()/pic5814095.png)
Turkey = ?
Cornucopia = ?
Native American = ?
Mayflower = ?
Pilgrim = ?
Quote: Gialmere
Turkey = ?
Cornucopia = ?
Native American = ?
Mayflower = ?
Pilgrim = ?
Just the numbers this time...
Turkey = 6
Cornucopia = 8
Native American = 7
Mayflower = 11
Pilgrim = 29
Quote: chevy
***I "think" the red/blue diagram is not to scale. It makes blue appear as right angle. I "think" the line from A,D to the center of opposite side is the perpendicular.***
Call the center of the rectangle Y. Call the ends of the fold (X,Z). So side of blue triangle opposite A,D is XYZ with Y at midpoint and (A,D) to Y is perpendicular to XZ.
Area of Blue = .5 * XZ * AY = XY * AY
Area of rectangle = 2*Area of Blue + 2* Area of Red = 4
Area of Pentagon = Area of rectangle - Area of Blue = 4-Area of Blue
Ratio = Area of Blue / (4-Area of Blue)
From Trig using the rectangle diagram with XYZ added accordingly....
AD = sqrt(4^2+1^2)=sqrt(17)
AY = AD/2 = sqrt(17)/2
Call theta angle given by CAD, then
tan(theta) = DC/AC = 1/4
Theta is also angle for XAY, so
tan(theta) = XY/AY
XY = AY * tan(theta) = sqrt(17)/2 * (1/4) = sqrt(17)/8
Thus Area of Blue = XY * AY = [sqrt(17)/8] * sqrt(17)/2 = 17/16
And
ratio = Area of Blue / (4-Area of Blue)
= (17/16) / (4 - 17/16)
=17/47
I agree!
Welcome to the WoV forum, by the way.
That was a tough problem and only one member answered it correctly (you), so please consider yourself invited to the prestigious "Beer Club." This means I owe you a beer should we ever meet.
Quote: ThatDonGuy
Just the numbers this time...
Turkey = 6
Cornucopia = 8
Native American = 7
Mayflower = 11
Pilgrim = 29
Correct!
-----------------------

Quote: Wizard
I agree!
Welcome to the WoV forum, by the way.
That was a tough problem and only one member answered it correctly (you), so please consider yourself invited to the prestigious "Beer Club." This means I owe you a beer should we ever meet.
Thanks for the "Beer Club" honor.
In fairness, CrystalMath answered my followup about the general HxW rectangle with a formula I agree with, so I assume he too had the original problem solved, just never posted.
Hopefully that doesn't preclude my membership in said club.


