Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
Volume of hemisphere = volume of cone
(2/3) * pi * r^3 = (1/3) * pi * r^2 * h
h=2*r
h=8cm
Quote: rsactuary
h=8
using volume of a hemisphere = 4/6 x pi x r^3
and volume of a cone = pi x r^2 X h/3
Quote: chevy
Volume of hemisphere = volume of cone
(2/3) * pi * r^3 = (1/3) * pi * r^2 * h
h=2*r
h=8cm
Correct!
---------------------------
Today I realized that eating ice cream isn't filling the emptiness I feel inside.
But I'm no quitter.

You are a pyrotechnician in charge of the nightly firework display at an amusement park. You've received some new style rockets from Europe and are testing one in order to time it to your show's music soundtrack.
The firework rocket is fired vertically upwards with a constant acceleration of 4 ms^-2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 meters where it detonates.
Assuming no air resistance and taking g=9.8 ms^-2, how long does it take the rocket to reach its maximum height?
Quote: GialmereAssuming no air resistance and taking g=9.8 ms^-2, how long does it take the rocket to reach its maximum height?
Not that you asked, but the rocket fuel burns out in seven seconds.
I'll provide a solution (hopefully) if my answer is right
Quote: GialmereIt's toughie Tuesday. Time for rocket science... ...
You are a pyrotechnician in charge of the nightly firework display at an amusement park. You've received some new style rockets from Europe and are testing one in order to time it to your show's music soundtrack.
The firework rocket is fired vertically upwards with a constant acceleration of 4 ms^-2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 meters where it detonates.
Assuming no air resistance and taking g=9.8 ms^-2, how long does it take the rocket to reach its maximum height?
I agree with the Wizard's answer.
Expressed algebraically, I get a total time of [ 2H ( 1/a + 1/g ) ]1/2, where a = 4 meters per sec2 and H =138 meters.
Let a be the time the fuel burns
At time a, the distance = 1/2 x 4 x a^2 = 2 a^2
and the velocity = 4 a
Let b be the time from when the fuel runs out to when the rocket explodes
At time b, the distance = 4 ab + 1/2 x (-9.8) x b^2 = 4 ab - 4.9 b^2
and the velocity = 4 a - 9.8 b = 0
a = 2.45 b
The total distance = 2 a^2 + 4 ab - 4.9 b^2 = 138
2 (2.45 b)^2 + 9.8 b^2 - 4.9 b^2 = 138
(4.9 x 2.45 + 4 x 2.45 - 2 x 2.45) b^2 = 138
b^2 = 138 / (6.9 x 2.45)
b = sqrt(138 / (6.9 x 2.45))
The total distance = a + b = 3.45 sqrt(138 / (6.9 x 2.45)) = 69 / 7 m
Quote: GialmereIt's toughie Tuesday. Time for rocket science...
You are a pyrotechnician in charge of the nightly firework display at an amusement park. You've received some new style rockets from Europe and are testing one in order to time it to your show's music soundtrack.
The firework rocket is fired vertically upwards with a constant acceleration of 4 ms^-2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 meters where it detonates.
Assuming no air resistance and taking g=9.8 ms^-2, how long does it take the rocket to reach its maximum height?
g=9.8, a = 4, H = 138
t1 =( 2gH/(ag+a^2))^0.5 = 7
t2 = (2aH/(g^2+ag))^0.5 = (1104/135.24)^0.5 = 2.857
Total time = 9.857 sec
S1 = 1/2a(t1)^2 = 98
S2 = u(t2) - 1/2g(t2)^2 = 4*7*(1104/135.24)^0.5 - 4.9*(1104/135.24) = 40
Quote: Wizard
Apx. 9.85 seconds.
Not that you asked, but the rocket fuel burns out in seven seconds.
I'll provide a solution (hopefully) if my answer is right
Quote: ChesterDog
I agree with the Wizard's answer.
Expressed algebraically, I get a total time of [ 2H ( 1/a + 1/g ) ]1/2, where a = 4 meters per sec2 and H =138 meters.
Quote: ThatDonGuy
Let a be the time the fuel burns
At time a, the distance = 1/2 x 4 x a^2 = 2 a^2
and the velocity = 4 a
Let b be the time from when the fuel runs out to when the rocket explodes
At time b, the distance = 4 ab + 1/2 x (-9.8) x b^2 = 4 ab - 4.9 b^2
and the velocity = 4 a - 9.8 b = 0
a = 2.45 b
The total distance = 2 a^2 + 4 ab - 4.9 b^2 = 138
2 (2.45 b)^2 + 9.8 b^2 - 4.9 b^2 = 138
(4.9 x 2.45 + 4 x 2.45 - 2 x 2.45) b^2 = 138
b^2 = 138 / (6.9 x 2.45)
b = sqrt(138 / (6.9 x 2.45))
The total distance = a + b = 3.45 sqrt(138 / (6.9 x 2.45)) = 69 / 7 m
Quote: ssho88
g=9.8, a = 4, H = 138
t1 =( 2gH/(ag+a^2))^0.5 = 7
t2 = (2aH/(g^2+ag))^0.5 = (1104/135.24)^0.5 = 2.857
Total time = 9.857 sec
S1 = 1/2a(t1)^2 = 98
S2 = u(t2) - 1/2g(t2)^2 = 4*7*(1104/135.24)^0.5 - 4.9*(1104/135.24) = 40
Correct!
Very good.
Wow! We have quite a few rocket scientists here. How are you guys at brain surgery?
---------------------------------
Here is the pyrotechnician's official mug...

And...


[This is probably my last puzzle until after the new year so, Happy Holidays math gamers!]
Quote: Gialmere
Wow! We have quite a few rocket scientists here.
Actually, real rocket scientists would have pointed out that gravity is not constant, but varies as the inverse square of the distance to the center of gravity, and you also have to take into account the decrease in the rocket's mass as the fuel is used up.
Quote: ThatDonGuyActually, real rocket scientists would have pointed out that gravity is not constant, but varies as the inverse square of the distance to the center of gravity, and you also have to take into account the decrease in the rocket's mass as the fuel is used up.
Air resistance/surface resistance should decrease when rocket go higher, will surface resistance decrease when surface temperature increase ? The Coriolis Effect ?
For knowledge purposes only.
Let:
t = time since rocket fuel runs out.
r = time rocket fuel lasted.
I'm going to express acceleration in terms of an upward direction. So, the acceleration after the rocket fuels burns out is -9.8.
As a reminder, the integral of acceleration is velocity and the integral of velocity is location. Let's make location relative to the ground.
When the rocket is first launched, we're given that the acceleration is 4.
Taking the integral, the velocity of the rocket after r seconds equals 4r.
Taking the integral of the velocity gives us the location of the rocket after r seconds of 2r^2.
Now let's look at what happens after the rocket fuel burns out.
We're given that acceleration due to gravity is -9.8.
The velocity due to gravity at time t is -9.8t. However, it also has upward velocity of 4r from the rocket.
Let v(t) = velocity at time t
v(t) = -9.8t + 4r
The rocket will achieve a maximum height when v(t) = 0. Let's solve for that.
v(t) = 0 = -9.8t + 4r
4r = 9.8t
t = 40/98 r = 20r/49.
In other words, whatever time the rocket fuel lasted, the rocket will keep traveling up for 20/49 of that time.
We are also given the distance traveled at the maximum altitude achieved is 138.
Let's take the integral of v(t) to get the formula for distance traveled, which we'll call d(t).
d(t) = -4.9t^2 + 4rt + c, were c is a constant of integration.
As we already showed, the rocket traveled 2r^2 by the time the fuel burned out, so that must be the constant of integration. That gives us:
d(t) = -4.9t^2 + 4rt + 2r^2
We know the maximum altitude of 138 was reached at time 20r/49 So let's plug t=20r/49 into the equation to solve for r:
d((20r/49) = -4.9((20r/49)^2 + 4r(20r/49) + 2r^2 = 138
r^2*(-1960/2401 + 80/49 + 2) = 138
r^2 = 49
r = 7
So, the rocket fuel lasted for seven seconds.
We already know the rocket kept going up for 20/49 of that time, which is 140/49 = apx. 2.8571 seconds.
Thus, the time from launch to maximum velocity is 7 + 140/49 = 483/49 = apx. 9.8571 seconds
Quote: ChesterDogQuote: GialmereIt's toughie Tuesday. Time for rocket science... ...
You are a pyrotechnician in charge of the nightly firework display at an amusement park. You've received some new style rockets from Europe and are testing one in order to time it to your show's music soundtrack.
The firework rocket is fired vertically upwards with a constant acceleration of 4 ms^-2 until the chemical fuel expires. Its ascent is then slowed by gravity until it reaches a maximum height of 138 meters where it detonates.
Assuming no air resistance and taking g=9.8 ms^-2, how long does it take the rocket to reach its maximum height?
I agree with the Wizard's answer.
Expressed algebraically, I get a total time of [ 2H ( 1/a + 1/g ) ]1/2, where a = 4 meters per sec2 and H =138 meters.
And since I have nothing better to do at the moment...
Let H be the final altitude, a the rocket's acceleration, and g the absolute value of gravity's acceleration
Let p be the amount of time the rocket was travelling under its own power, and q the amount of time it was subject only to gravity.
After p seconds, the rocket's velocity is ap
After q more seconds, the rocket's velocity is ap - gq; since, in this case, this is zero, ap = gq, so q = (a/g) p.
Break out the basic physics theorems for this:
distance = initial velocity x time + 1/2 x acceleration x (time)^2
Let d be the distance the rocket travelled under its own power; d = 0 + 1/2 a p^2
The distance the rocket travelled while subject only to gravity is (H - d); H - d = ap q - 1/2 g q^2 = a (a/g) p^2 - 1/2 g (a^2/g^2) p^2
H - d = 1/2 a^2/g p^2
H = 1/2 a^2/g p^2 + d = 1/2 a^2/g p^2 + 1/2 a p^2 = 1/2 a p^2 (a/g + 1) = 1/2 p^2 a (a + g) / g
p^2 = 2H g / (a (a + g))
p = sqrt(2H g / (a (a + g))) = sqrt(2H) / sqrt(a (a + g) / g)
The total time = p + q = p (1 + a / g) = p (a + g) / g =sqrt(2H / a) / sqrt((a + g) / g) x (a + g) / g
= sqrt(2H / a) sqrt((a + g) / g) = sqrt(2H (a + g) / ag)
= sqrt(2H (1/a + 1/g)) QED
Quote: teliotMike, I do not concur. There is one before that.
One back at you: What is the last date in this century that will be a Pythagorean triple?
It would be a better world if there were more Pythagorean Triples that could double as dates.Quote: unJonJuly 24, 2025
One back at you: What is the last date in this century that will be a Pythagorean triple?
Quote: Ace27/24/25
Yes. Though a line must be drawn somewhere since there are probably other dates on other calendars (Hebrew, Chinese etc )Quote: charliepatrickQuote: Ace27/24/25Isn't 7/25/24 (or 25/7/24 in UK) (25th July 2024) also a possible answer.
I am a physicist, so let me say that neglecting air resistance is a much bigger factor in a rocket's trajectory than the other factors mentioned. But yes, change of gravity with distance to the center of the earth will have a tiny effect on trajectory as will change of air density with elevation.
In fact it might be fun to repeat the puzzle, adding in the air resistance for a single cone shape and do the calculation for sea level and for the top of Mt Everest (or Denver) taking into account the altered air density and tiny changes in gravity.
P.S.,Two notes:
1. the coriolis effect will change the latitude of the rocket's landing point, but I don't think it is a primary factor that changes the time of flight, assuming the elevation of the earth's surface is unchanged at its altered landing point. Although, the rotational velocity of the earth's atmosphere does change with elevation which might introduce some lateral air drag as the rocket rises which would reduce its overall kinetic energy (!)
2. I think that change in mass due to the burning of fuel is not an issue if the firework is based on an explosion at the launch point, because then the fuel is oxidized and ejected almost instantaneously. However, fireworks usually have two packets of explosive material -one to launch it upwards and a second that is timed to explode at the top of its flight, creating the fireworks effect. The second explosion not only eliminates the mass of the fuel (and part of the rocket itself) but serves as an accelerant for the fragments of the rocket. For the purpose of posing a problem, it is probably best to assume the firework rocket does not explode in flight, LOL.
I'm not trying to be a Christmas Grinch. I'd be interested to see how these factors change at various altitudes and latitudes. As I recall, acceleration due to gravity ranges from about 9.6 to 10, depending on latitude, higher closer to the equator.

Many Christmas songs have lyrics in which a word or phrase is repeated. Several repetitive lyrics have been extracted from a number of holiday favorites.
Each algebraic expression below represents a song, where each word is represented by its first letter and exponents show the number of repetitions. If two or more words are repeated as a group, they appear in parentheses. For example, (JB)^2 is short for "Jingle Bells, Jingle Bells."
Can you identify all the songs below?
1. (JB)^3R
2. P(RP^3)^3
3. FL^8
4. (SIHP)^2
5. N^4
6. (WWYAMC)^3
7. (OCT)^2
8. OTO(CAJ)^2OTOCAJ
9. (GIED)^2
10. (OCLUAH)^2
11. (H^3WWG)^2
12. (LIS)^3
13. (FN)^3
14. (SB)^2
15. (HCSC)^2
16. (RTSJ)^2 R^2TSJ
17. (OC)^2E
1. Jingle Bell Rock (Jingle Bell, Jingle Bell, Jingle Bell Rock)
2. The Little Drummer Boy (Puh Rum-Pum-Pum-Pum, Rum-Pum-Pum-Pum, Rum-Pum-Pum-Pum)
3. Deck the Halls (Fa La La La La, La La La La)
4. Silent Night (Sleep In Heavenly Peace, twice)
5. The First Noel (Noel, Noel, Noel, Noel)
6. We Wish You A Merry Christmas (title, three times)
7. O Christmas Tree (title, twice)
9. Angels We Have Heard On High (Gloria, In Excelsis Deo)
10. O Come All Ye Faithful (O Come Let Us Adore Him, twice)
12. Let It Snow, Let It Snow, Let It Snow (title)
14. Silver Bells (title, twice)
15. Here Comes Santa Claus (title, twice)
17. O Come, O Come Emmanuel (title)
2. Little Drummer Boy (pa rum pum pum pum)
11. Up on the housetop (ho, ho, ho, who wouldn't go)
13. Feliz Navidad
14. Silver Bells
1. Jingle Bell Rock
2. Little Drummer Boy ?
3. Deck The Halls
4. ???
5. The First Noel
6. We Wish You a Merry Christmas
7. O Christmas Tree
8. God Rest Ye Merry Gentlemen
9. ???
10. O Come All Ye Faithful
11. Up on the Houestop
12. Let It Snow!
13. ???
14. Silver Bells
15. Here Comes Santa Claus
16. Joy to the World!
17. ???
Quote: gordonm888
1. the coriolis effect will change the latitude of the rocket's landing point, but I don't think it is a primary factor that changes the time of flight, assuming the elevation of the earth's surface is unchanged at its altered landing point. Although, the rotational velocity of the earth's atmosphere does change with elevation which might introduce some lateral air drag as the rocket rises which would reduce its overall kinetic energy (!)
Regarding the coriolis effect, I am actually more interested in the initial HORIZONTAL speed of rocket.
Just before lunching, the horizontal speed of rocket at equator is about 460m/s due to the earth rotation, and just after lunching, there are two component, VERTICAL and HORIZONTAL speed, so the rocket actually move "slanting" from its vertical axis. Therefore, the rocket should travel a longer distance before reaching the target point and it take longer time. Am I missing something ? Hope can learn something from you.
Quote: ThatDonGuy
1. Jingle Bell Rock (Jingle Bell, Jingle Bell, Jingle Bell Rock)
2. The Little Drummer Boy (Puh Rum-Pum-Pum-Pum, Rum-Pum-Pum-Pum, Rum-Pum-Pum-Pum)
3. Deck the Halls (Fa La La La La, La La La La)
4. Silent Night (Sleep In Heavenly Peace, twice)
5. The First Noel (Noel, Noel, Noel, Noel)
6. We Wish You A Merry Christmas (title, three times)
7. O Christmas Tree (title, twice)
9. Angels We Have Heard On High (Gloria, In Excelsis Deo)
10. O Come All Ye Faithful (O Come Let Us Adore Him, twice)
12. Let It Snow, Let It Snow, Let It Snow (title)
14. Silver Bells (title, twice)
15. Here Comes Santa Claus (title, twice)
17. O Come, O Come Emmanuel (title)
Quote: chevyI can add
2. Little Drummer Boy (pa rum pum pum pum)
11. Up on the housetop (ho, ho, ho, who wouldn't go)
13. Feliz Navidad
14. Silver Bells
Quote: Joeman
1. Jingle Bell Rock
2. Little Drummer Boy ?
3. Deck The Halls
4. ???
5. The First Noel
6. We Wish You a Merry Christmas
7. O Christmas Tree
8. God Rest Ye Merry Gentlemen
9. ???
10. O Come All Ye Faithful
11. Up on the Houestop
12. Let It Snow!
13. ???
14. Silver Bells
15. Here Comes Santa Claus
16. Joy to the World!
17. ???
Correct!
In a joint solve.
1. "Jingle Bell Rock" ("Jingle Bell, Jingle Bell, Jingle Bell Rock")
2. "The Little Drummer Boy" ("Pa Rum Pum Pum Pum, Rum Pum Pum Pum, Rum Pum Pum Pum")
3. "Deck the Halls" ("Fa La La La La La La La La")
4. "Silent Night" ("Sleep in Heavenly Peace, Sleep in Heavenly Peace")
5. "The First Noel" ("Noel, Noel, Noel, Noel")
6. "We Wish You A Merry Christmas" ("We Wish You A Merry Christmas, We Wish You A Merry Christmas, We Wish You A Merry Christmas")
7. "O Christmas Tree" ("O Christmas Tree, O Christmas Tree")
8. "God Rest Ye Merry Gentlemen" ("O Tidings Of Comfort And Joy, Comfort And Joy, O Tidings Of Comfort And Joy")
9. "Angels We Have Heard On High" ("Gloria in Excelsis Deo, Gloria in Excelsis Deo")
10. "O Come, All Ye Faithful" ("O Come, Let Us Adore Him, O Come, Let Us Adore Him")
11. "Up On The Housrtop" ("Ho, Ho, Ho, Who Wouldn't Go? Ho, Ho, Ho, Who Wouldn't Go?")
12. "Let It Snow" ("Let It Snow, Let It Snow, Let It Snow")
13. "Feliz Navidad" ("Feliz Navidad, Feliz Navidad, Feliz Navidad")
14. "Silver Bells" ("Silver Bells, Silver Bells")
15. "Here Comes Santa Claus" ("Here Comes Santa Claus, Here Comes Santa Claus")
16. "Joy To The World" ("Repeat The Sounding Joy, Repeat The Sounding Joy, Repeat, Repeat The Sounding Joy") [A toughie since it uses lyrics from verse 2]
17. "O Come, O Come Emmanuel" ("O Come, O Come Emmanuel")
--------------------------------------
I'm giving up drinking till Christmas.
Bad punctuation, can't edit title
I'm giving up. Drinking till Christmas.
Problem 2 : (10 pts)
A circle of radius, r, is centered at the origin. An equilateral triangle with side, a, is also centered at the origin. Given the portion of the triangle outside the circle has the same area as the portion of the circle outside the triangle...
a: (7 pts) What is the side of the triangle, a, in terms of r ?
b: (3 pts) What is the total area of the three pointed portions of the triangle, in terms of r ? (i.e. portions outside the circle)
What did the triangle say to the circle?
Quote: chevyIs it still Monday? Is "Easy Monday" copyrighted, trademarked, patented or otherwise intellectually protected by Gialmere?
Problem 2 : (10 pts)
A circle of radius, r, is centered at the origin. An equilateral triangle with side, a, is also centered at the origin. Given the portion of the triangle outside the circle has the same area as the portion of the circle outside the triangle...
a: (7 pts) What is the side of the triangle, a, in terms of r ?
b: (3 pts) What is the total area of the three pointed portions of the triangle, in terms of r ? (i.e. portions outside the circle)
What did the triangle say to the circle?
a) a = 2*(pi)^0.5/3^0.25 * r = 2.693547r
b) Total Area outside circle = 0.573249r^2
Triangle : why can't pi = 3 ?
Circle : LOL !
Quote: ssho88
a) a = 2*(pi)^0.5/3^0.25 * r = 2.693547r
b) Total Area outside circle = 0.573249r^2
"That was too fast. Please go back to your seat and check your work."
BUT....
You are CORRECT!!!
(Sorry, just flashing back to high school there.)
What did the triangle say to the circle?
You're pointless!
:strip_icc()/pic5868848.png)
Place each of the numbers from 1 to 10 on the tree ornaments so that every line adds up to the same number.
There are five lines, three lines containing four ornaments, one line with three ornaments, and one line with just two ornaments.
Quote: GialmereA belated tannenbaum Tuesday...
Place each of the numbers from 1 to 10 on the tree ornaments so that every line adds up to the same number.
There are five lines, three lines containing four ornaments, one line with three ornaments, and one line with just two ornaments.
There are 3 rows and total of those 10 numbers is 55, so each row add up should be either 18, 17, 16 or 15. Only 18 is possible.
1
10 8
5 7 6
2 9 4 3
Quote: ssho88
There are 3 rows and total of those 10 numbers is 55, so each row add up should be either 18, 17, 16 or 15. Only 18 is possible.
1
10 8
5 7 6
2 9 4 3
Correct!
-----------------------------


Simplify the following equation...
:strip_icc()/pic5868847.png)
Quote: GialmereSimplify the following equation...
:strip_icc()/pic5868847.png)
The first part is:
((X + A)(X - A) M + A^2 M) E
= M (X^2 - A^2 + A^2) E
= M E X^2
The left side of the second part is:
((R + X) / X + X / (R - X)) / (X / (R - X))
= ((R^2 - X^2 + X^2) / (X (R - X))) / (X / (R - X))
= R^2 / (X (R - X)) * (R - X) / X
= R^2 / X^2
The right side of the second part is:
4AS / 3 * (1 / (X ((E + Y)^2 - (E - Y)^2)) + 1 / (E ((Y + X)^2 - (Y - X)^2)) + 1 / (Y ((X + E)^2 - (X - E)^2)))
= 4AS / 3 * (1 / 4XEY + 1 / 4EYX + 1 / 4YXE)
= 4AS / 3 * 3/4 * 1/XEY
= AS / XEY
Subtract the right side of the second part from the left side, then multiply by Y:
Y (R^2 / X^2 - AS / XEY)
= Y (R^2 XEY - AS X^2) / (X^3 EY)
= (R^2 EY - ASX) / (X^2 E)
The product of the two parts is:
MEX^2 (R^2 EY - ASX) / (X^2 E)
= M (R^2 EY - ASX)
= MERRY - XMAS
Quote: ThatDonGuy
The first part is:
((X + A)(X - A) M + A^2 M) E
= M (X^2 - A^2 + A^2) E
= M E X^2
The left side of the second part is:
((R + X) / X + X / (R - X)) / (X / (R - X))
= ((R^2 - X^2 + X^2) / (X (R - X))) / (X / (R - X))
= R^2 / (X (R - X)) * (R - X) / X
= R^2 / X^2
The right side of the second part is:
4AS / 3 * (1 / (X ((E + Y)^2 - (E - Y)^2)) + 1 / (E ((Y + X)^2 - (Y - X)^2)) + 1 / (Y ((X + E)^2 - (X - E)^2)))
= 4AS / 3 * (1 / 4XEY + 1 / 4EYX + 1 / 4YXE)
= 4AS / 3 * 3/4 * 1/XEY
= AS / XEY
Subtract the right side of the second part from the left side, then multiply by Y:
Y (R^2 / X^2 - AS / XEY)
= Y (R^2 XEY - AS X^2) / (X^3 EY)
= (R^2 EY - ASX) / (X^2 E)
The product of the two parts is:
MEX^2 (R^2 EY - ASX) / (X^2 E)
= M (R^2 EY - ASX)
= MERRY - XMAS
Correct!
---------------------------
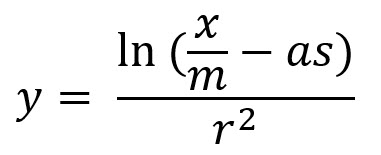
My belated guess is
me^(rr y) = x-mas
Quote: chevy
My belated guess is
me^(rr y) = x-mas
Where does the natural log fit into it?
(r^2)y = ln(x/m-as)
e^((r^2)y) = x/m-as
me^(rry) = x-mas
Quote: WizardQuote: chevy
My belated guess is
me^(rr y) = x-mas
Where does the natural log fit into it?
multiply both sides by r r gives rr y = ln(x/m-as)
exponential of both sides gives. e^(rr y) = e^ln(x/m-as) = x/m-as
multiply both sides by m gives. me^(rr y) = x-mas
Quote: chevy
My belated guess is
me^(rr y) = x-mas
Correct! Sorry about the natural log question earlier.
Five pirates have a chest with 1,000 coins on their ship, which they wish to divide. Let's call the pirates, in rank order from highest to lowest, Adam, Bob, Chris, David, and Ernie. Here are the pirate rules on how to divide it:
1. Ernie makes a suggestion on how many coins each pirate gets. For example, Adam 400, Bob 200, Chris 100, David 50, Ernie 250.
2. All pirates vote on the suggestion.
3. If the vote gets a majority, then that is what they do and it's over.
4. If the vote does not get a majority, then they make Ernie walk the plank.
5. David, now the lowest in rank, makes a suggestion.
6. This process keeps repeating until a vote gets a majority.
Please note that a tied vote is not a majority and the pirate making that suggestion will walk the plank.
Each pirate has the following priorities, from highest to lowest.
1. Get get as many coins as possible.
2. To make other pirates walk the plank (pirates are bloodthirsty)
3. To live
What should Ernie suggest for the division?
Quote: WizardDoes anyone not understand what is being asked?
I am somewhat unclear on the priorities. Does getting one coin mean that choice is better than making somebody walk the plank? (and getting coins assumes you actually live, thus I'm not sure how priority 3 enters into it)
If so I could venture the following guess
Looking at rounds in reverse order
4) If it gets down to Adam and Bob....Adam votes no and Bob walks the plank. Ends with A=1000
So Bob can't let it get to this, and must agree with Chris's offer unless he get's nothing in which case priority 2 kicks in and better to vote no and make Chris walk plank.
3) If it gets down to Adam, Bob, and Chris....If Chris walks, then Bob does in next round. So Chris would have to give Bob just enough incentive to vote yes allowing for his own greed. Chris would offer A=0, B=1, C=999. (Here is where 1 coin is enough?)
2) If it gets down to Adam, Bob, Chris, and David, ..... David would need 2 people to do better than the round 3. David would offer A=1, B=2, C=0, D=997
1) So Ernie needs 2 people to do better than round 2. Either
A=2, B=3, C=0, D=0, E=995
or
A=1, B=3, C=1, D=0, E=995
or
A=2, B=2, C=1, D=0, E=995
Quote: chevyI am somewhat unclear on the priorities. Does getting one coin mean that choice is better than making somebody walk the plank? (and getting coins assumes you actually live, thus I'm not sure how priority 3 enters into it)
If you walk the plank, your suggestion was rejected, so it's impossible to walk the plank with coins. You walk it with nothing.
While pirates are bloodthirsty, greed takes priority. They would rather get one coin than zero. If a pirate would get zero coins either way, he would sacrifice his own life to see an extra pirate walk the plank.
That all said, your answer is close, but there is a way for Ernie to get even more coins.
I guess Ernie only needs 2 voters to do better and the others can be cut out.
So. A=2, B=0, C=1, D=0, E=997
Quote: chevy
I guess Ernie only needs 2 voters to do better and the others can be cut out.
So. A=2, B=0, C=1, D=0, E=997
Ding, ding, ding!!! You are correct, sir!


