New Video Poker Game

Has anyone seen or played the new video poker game Xtra Card Poker by Aristocrat? It was recently released at the Atlantis in Reno and the Rampart in Las Vegas. I haven't had a chance to play it yet, but I was wondering what everyone thought about it.

What is the gist of the game
Deal 6 cards instead of 5?
After holding, get an extra card?
How are they factoring in an extra card?

I did a quick google search on this Xtra Card Poker game and found nothing except this thread. Do you have a link to rules? Or can you please describe the game?

I got on the Aristocrat site and searched their library of games. My search did not find this game.

I did eventually find this:
2WW 2WW 2WW 2WW XTRA-CARD POKER XTRA-CARD POKER DEUCES WILD WINNER'S WORLD MULTI-GAME

It apparently is a very new game on a tab on a Wild Winner's World Multi-Game machine. Was still going through paperwork for Trademark approval of its name/poster image during the first few months of 2024.

Game was presented in London in Feb 2024 at ICE - International Casino Expo in London UK (European alternative to G2E-LasVegas and G2E-Asia -Macao)
Started distribution in US (Nevada)
So far I cannot find more information
https://www.aristocratgaming.com/emea/slots/games/winners-world

For new game play and rules please Check out Bar cabinets in Las Vegas https://www.aristocratgaming.com/us/casino-operator/cabinets/winners-world-bartop

Quote: terapined

What is the gist of the game
Deal 6 cards instead of 5?
After holding, get an extra card?
How are they factoring in an extra card?
link to original post

I was able to get some more information about the game. This will give you an idea of how the game is played and hopefully I can get a few screenshots or video of the gameplay.

Quote: VladAlex1

For new game play and rules please Check out Bar cabinets in Las Vegas https://www.aristocratgaming.com/us/casino-operator/cabinets/winners-world-bartop
link to original post

I think the game is part of the upgraded software package for Winner's World, but that will not be available until close to G2E. Right now the game is showing up in cabinets in a few spots.

Quote: RealizeGaming

Quote: terapined

What is the gist of the game
Deal 6 cards instead of 5?
After holding, get an extra card?
How are they factoring in an extra card?
link to original post

I was able to get some more information about the game. This will give you an idea of how the game is played and hopefully I can get a few screenshots or video of the gameplay.


link to original post

(1.75 free hands per feature)
(Avg multiplier of 4.8 with frequency of 0.4 per feature played) - applies to all wins

Analysis Needs
1. What does the player give up to have this X-tra Card Feature?

2. How does basic strategy change for these video poker games in order to draw more cards per hand?

Ex: Is it better to draw to a J,Q or K than a suited (J,T), (Q,T) and (K,T) to gain the advantage of a higher frequency of the X-tra card feature?

3. Is there a significant difference between the base VP games in average number of cards held? For example, are there fewer cards held, on average, in Deuces Wilds than in the other games, making that the more attractive game to play with the X-Tra Card Feature?

Realize, is this one of your games?

Quote: RealizeGaming

Has anyone seen or played the new video poker game Xtra Card Poker by Aristocrat? It was recently released at the Atlantis in Reno and the Rampart in Las Vegas.
link to original post

I looked all over the Rampart today for this game and couldn't find it. Suncoast too.

Quote: heatmap

Realize, is this one of your games?
link to original post

Yes. It is based off of our MultiDraw video poker game.

MultiDraw

Wizard,

I found out yesterday that the install had some issues, so it was scheduled to be completed today sometime. I will let you know when it is official. The next install after that is scheduled to be Santa Fe Station around mid June.

Quote: RealizeGaming

Quote: heatmap

Realize, is this one of your games?
link to original post

Yes. It is based off of our MultiDraw video poker game.

MultiDraw
link to original post

its just fascinating how one game can be translated into something completely different looking nice job keep it up

It was officially installed at the Rampart as of yesterday afternoon.

Thanks heatmap.

When you play the game vs my demo, you can notice the similar concepts used in each even though it has a different feel to it. Huge congrats to Aristocrat for taking the concept and running with it!

Perhaps you could describe the game and rules to us. In particular, compared to the standard VP games, what does the player pay or give up for the X-tra Card feature?

Quote: RealizeGaming

It was officially installed at the Rampart as of yesterday afternoon.
link to original post

Looks like I was a day early. Can you tell me where in the Rampart these machines are?

I think these are bar-top consoles, right?

The game comes in either single line or three play formats as of right now. The game begins with the player making a 5+5 wager for each hand. (10 credits for single hand games, 30 credits for three play games.

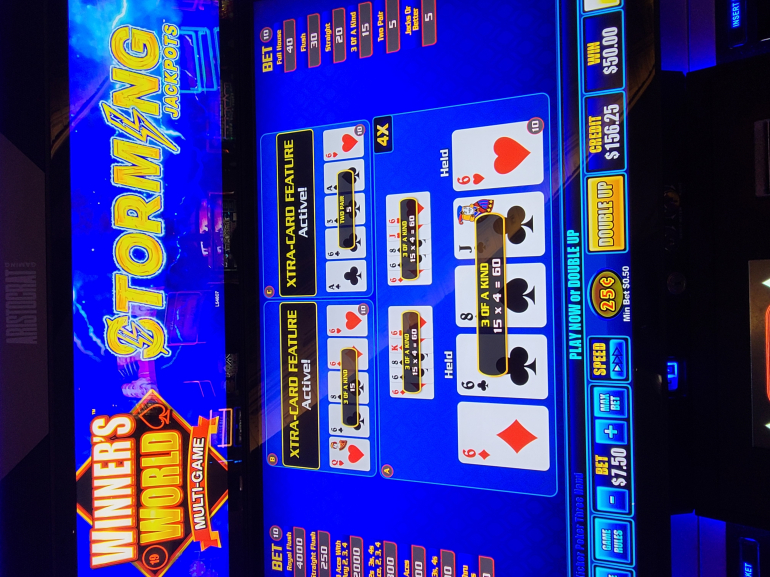
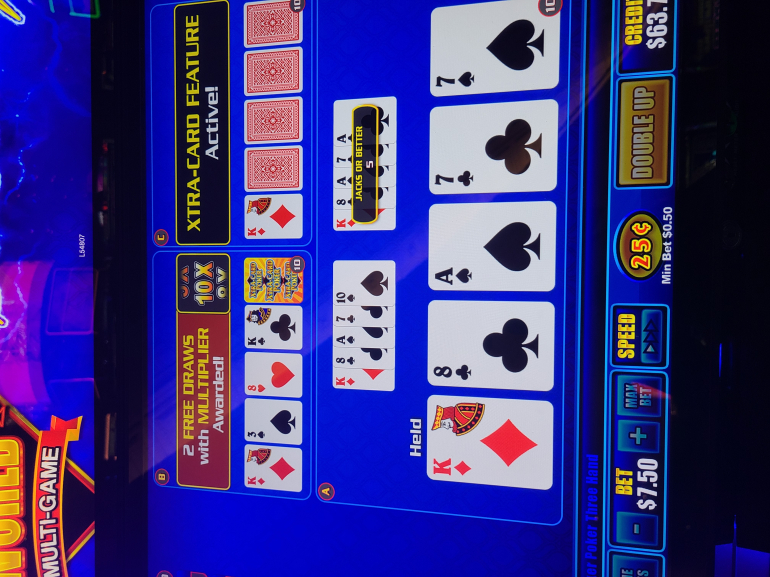
The player is dealt five cards and decides which ones to hold or discard. On the draw of the game, the special Xtra Card may be drawn into one of the open card positions. If it appears, it can offer the player two extra hands plus the original hand containing the exact same cards. It may also award a multiplier that is used for all of the hands. Each hand is then completed by drawing a card from the remaining decks for each extra hand.

Overall, the game reminds me a bit of STP with additional hands. It is fun and exciting to have the Xtra Card and multiplier appear when you already have the beginnings of a great hand!

Here are some random pictures of the single and three hand game.

From my understanding, they will be on a cabinet by Aristocrat with other games on them. Eventually, it will be on the Winner's Word bar tops, but right now it is on a machine on the floor. I'm going to be out there next week, so I will get over there to check it out.

Quote: gordonm888

I think these are bar-top consoles, right?
link to original post

Not yet. They are on cabinets on the game floor for this release.

the help screen on the casino version... the word average is used alot... is there a mechanism which keeps track of "session" statistics and then produces the random number based on those statistics?

Maybe having a dynamic probability table which uses the averages in order to get to the probability percentages used in the actual random number generation?

Quote: heatmap

the help screen on the casino version... the word average is used alot... is there a mechanism which keeps track of "session" statistics and then produces the random number based on those statistics?

Maybe having a dynamic probability table which uses the averages in order to get to the probability percentages used in the actual random number generation?
link to original post

Both good questions which I can't answer. The screenshot I provided was very early in the process, so the information may have changed in the released version of the game.

Quote: RealizeGaming

Quote: heatmap

the help screen on the casino version... the word average is used alot... is there a mechanism which keeps track of "session" statistics and then produces the random number based on those statistics?

Maybe having a dynamic probability table which uses the averages in order to get to the probability percentages used in the actual random number generation?
link to original post

Both good questions which I can't answer. The screenshot I provided was very early in the process, so the information may have changed in the released version of the game.
link to original post

i tried and thats all i can do haha. thanks for responding.

Quote: heatmap

the help screen on the casino version... the word average is used alot... is there a mechanism which keeps track of "session" statistics and then produces the random number based on those statistics?

Maybe having a dynamic probability table which uses the averages in order to get to the probability percentages used in the actual random number generation?
link to original post

When I see a help screen like that, I assume that there is an algorithm built into the game logic that can be proved to produce the stated averages over the long term. I never assume that there is a feedback mechanism that changes the algorithm based on past history. As I understand it, that would be illegal under Nevada regulation.

As an example, consider Hot Roll video poker. https://wizardofodds.com/games/video-poker/tables/hot-roll/#:~:text=Hot%20Roll%20is%20an%20optional,player%20for%20the%20bonus%20feature. The multiplier is awarded on average for 1 in 6 games. This does not mean the multiplier is awarded every sixth roll. It also doesn't mean that if the game went through a streak of no bonuses, subsequent games have an average of more than 1 in 6 to compensate. It should mean that the multiplier has a 1 in 6 chance of being awarded on the next game no matter what the recent multiplier history was.

Quote: Mental

Quote: heatmap

the help screen on the casino version... the word average is used alot... is there a mechanism which keeps track of "session" statistics and then produces the random number based on those statistics?

Maybe having a dynamic probability table which uses the averages in order to get to the probability percentages used in the actual random number generation?
link to original post

When I see a help screen like that, I assume that there is an algorithm built into the game logic that can be proved to produce the stated averages over the long term. I never assume that there is a feedback mechanism that changes the algorithm based on past history. As I understand it, that would be illegal under Nevada regulation.

As an example, consider Hot Roll video poker. https://wizardofodds.com/games/video-poker/tables/hot-roll/#:~:text=Hot%20Roll%20is%20an%20optional,player%20for%20the%20bonus%20feature. The multiplier is awarded on average for 1 in 6 games. This does not mean the multiplier is awarded every sixth roll. It also doesn't mean that if the game went through a streak of no bonuses, subsequent games have an average of more than 1 in 6 to compensate. It should mean that the multiplier has a 1 in 6 chance of being awarded on the next game no matter what the recent multiplier history was.
link to original post

yes but what would that look like algorithm wise in your opinion

For example, look at the extra card feature multipliers. The rules above say the average multiplier value is 4.80. The multipliers can only have the values 2x, 3x, 4x, 5x, 6x, 8x, and 10x. An algorithm that would achieve this average is as follows. Put 100 tokens in a bag. 20 tokens have 2x printed on them, 18 say 3x, 16 say 4x, 14 say 5x, 12 say 6x, 10 say 8x, and the final 10 say 10x. Just pick one token at random and the average value will be 4.8x. Another way of saying this is that the weighted average or expected value is 4.80x.

In a computer algorithm, you could just create 100 virtual tokens in an array and use the pRNG to pick one token at random with no bias.

In statistics, the expected value is just that, an expectation based on the math of the situation. An average is the result of a finite number of observations. The calculated average will almost never be precisely equal to 4.80x. The expectation value is a fixed number whereas the observed average value fluctuates.

Quote: RealizeGaming

I'm going to be out there next week, so I will get over there to check it out.
link to original post

I am pretty available next week. I can meet you there, if you want. It will be hard to find one particular machine in that place.

Quote: Mental

For example, look at the extra card feature multipliers. The rules above say the average multiplier value is 4.80. The multipliers can only have the values 2x, 3x, 4x, 5x, 6x, 8x, and 10x. An algorithm that would achieve this average is as follows. Put 100 tokens in a bag. 20 tokens have 2x printed on them, 18 say 3x, 16 say 4x, 14 say 5x, 12 say 6x, 10 say 8x, and the final 10 say 10x. Just pick one token at random and the average value will be 4.8x. Another way of saying this is that the weighted average or expected value is 4.80x.

In a computer algorithm, you could just create 100 virtual tokens in an array and use the pRNG to pick one token at random with no bias.

In statistics, the expected value is just that, an expectation based on the math of the situation. An average is the result of a finite number of observations. The calculated average will almost never be precisely equal to 4.80x. The expectation value is a fixed number whereas the observed average value fluctuates.
link to original post

Very nicely explained!

Quote: Wizard

Quote: RealizeGaming

I'm going to be out there next week, so I will get over there to check it out.
link to original post

I am pretty available next week. I can meet you there, if you want. It will be hard to find one particular machine in that place.
link to original post

Sounds great Wizard. Give me a couple days to solidify a day and I'll get in touch with you. Right now I'm leaning toward Thursday morning.

Quote: RealizeGaming

Sounds great Wizard. Give me a couple days to solidify a day and I'll get in touch with you. Right now I'm leaning toward Thursday morning.
link to original post

I'm afraid Thursday morning isn't good. Probably the whole day will be bad. Any other day should be fine. I would PM me to arrange something.

Quote: Wizard

Quote: RealizeGaming

Sounds great Wizard. Give me a couple days to solidify a day and I'll get in touch with you. Right now I'm leaning toward Thursday morning.
link to original post

I'm afraid Thursday morning isn't good. Probably the whole day will be bad. Any other day should be fine. I would PM me to arrange something.
link to original post

Just sent you a PM.

I found this on Linkedin a couple weeks ago which shows the Aristocrat machines. Our game is not shown on this particular machine in the picture, but they are popping up at a number of casinos and Xtra Card Poker may be on them as they get a software update.

I'll be at the Rampart on Thursday around 10:00 to check it out and I'll post some pictures.

I spent about four hours at the Rampart today playing Xtra Card Poker. I was very impressed with the game and the easiest way to summarize it is that it feels like super times pay but the extra hand and multipliers happen much more frequently. The game just has a nice feel to it and when playing three hands, which can turn into 9 total hands depending on the bonus, the action keeps the game interesting. I'll attach some pictures, but will try to give more information once I get home.

I apologize for the side photos. Not sure how to fix that.

Quote: Mental

As an example, consider Hot Roll video poker. https://wizardofodds.com/games/video-poker/tables/hot-roll/#:~:text=Hot%20Roll%20is%20an%20optional,player%20for%20the%20bonus%20feature. The multiplier is awarded on average for 1 in 6 games. This does not mean the multiplier is awarded every sixth roll.
It also doesn't mean that if the game went through a streak of no bonuses, subsequent games have an average of more than 1 in 6 to compensate.
It should mean that the multiplier has a 1 in 6 chance of being awarded on the next game no matter what the recent multiplier history was.
link to original post

Same thing for super times pay?

In stp, the multiplier comes 1 in 14. I've had streaks of no multipliers in 50+ hands but by 500 hands, the avg is 1 in 14.
i always thought the game sees the avg as being skewed and 'fixes' it by higher chances of a multiplier.

Thx

I played the game at about 5:30 PM today at the Rampart. I look a lot of pictures and some video. Right now I am in a rush, so will explain just 7-5 Bonus Poker, which the Rampart has at the $2 denom.

1. If the player bets 1 to 5 coins, the game plays like conventional one-line video poker.
2. If the player bets 10 coins, wins will be based on a 5-coin bet, but the feature will be invoked.
3. The probability of the feature depends on the number of cards held as follows:
   
   • 0 cards held = 30.80%
   • 1 cards held = 25.52%
   • 2 cards held = 19.82%
   • 3 cards held = 13.70%
   • 4 cards held = 7.10%
   • 5 cards held = 0%
4. If the feature is triggered, the player will get 1 or 2 extra hands, with an average of 1.75. (Note: This implies the probability of one extra hand is 25% and two is 75%)
5. If the feature is triggered, in addition to getting 1 or 2 extra hands, the player will win a multiplier with probability of 40%.
6. If a multiplier is won, the average multiplier is 4.8

With a 40% chance of a multiplier (when the feature is active) and average multiplier of 4.8, the average overall multiplier, including 1x, is 2.52.

With an average of 2.75 total hands (including the one paid for) and average multiplier of 2.52, it seems to me the ER of a hand with the feature activated is 6.93x that without the feature.

That is all I have time for right now. I welcome all corrections to my understanding of the rules or my math.

I finally got back home from my trip to Vegas. I had a chance to get out to see the game two separate times at the Rampart. Currently, there are two machines that have the game installed on them as shown in the picture below. I played about 5 hours the first day and about 3 hours the second day and I rotated from single lines to three hands and stayed on quarters the whole time.

Overall, the game had a nice feel to it. As I mentioned previously, it has a "super times pay" feel to it, but more action where my mind doesn't get bored waiting for a bonus or multiplier. The bonus felt very good in terms of the frequency and the multiplier appeared quite often. I enjoyed the game in a single hand format, but I prefer the three hand game. The action in the three hand game feels really good. I had my share of losing all three hands along with winning each hand and triggering a bonus card and multiplier on each of the three hands. Sometimes I would have 9 total hands on my screen and each would have a different multiplier. This type of uncertainty from one hand to the next keep the game exciting for me.

In the second picture I was dealt a pair of 8's so I held them for the three hands. On the draw of the game in the third card position on hand A (the main hand), another 8 was drawn into the hand giving me three 8's. In the fifth card position, I drew the Xtra Card with awarded me with two extra cloned hands of the main hand, plus a random x5 multiplier. Unfortunately, I did not hit four of a kind, but the excitement of starting the hand with a low pair and then having a chance to get a four of a kind with a x5 multiplier made the game very fun and entertaining!

If I had one complaint, it would be that both machines only had quarters as the lowest denomination available. I would have loved to have been able to play the game in dime denominations on the three hand game because my money would have lasted a bit longer, but even at quarters I had a great time playing it.

Has anyone else checked out the game? I'm curious to hear what others have to say. Hopefully after this trial is out of the way it will become more widespread in Vegas.

Waiting to see the Returns table.
How much does this variant add to the EV?