New Video Poker Game

Quote: Wizard

Quote: Hunterhill

It seems like creating a strategy for this game would be challenging.
link to original post

Indeed. I leave that to the player.
link to original post

Why not define a simple basic strategy for this feature and then analyze it? If using the simple basic strategy lowers the Return to Player (RTP) to, say, 0.975, then players know that they shouldn't elect this feature.

I claim that it is not particularly helpful to announce that the RTP for this game is a certain number when using a perfect strategy which you are unable to define and which no one else in the world knows. Why should anyone choose this ding-dong feature when it is almost certain that they will be playing a strategy that is sub-optimal and thus increasing the house edge?

Quote: gordonm888

Quote: Wizard

Quote: Hunterhill

It seems like creating a strategy for this game would be challenging.
link to original post

Indeed. I leave that to the player.
link to original post

Why not define a simple basic strategy for this feature and then analyze it? If using the simple basic strategy lowers the Return to Player (RTP) to, say, 0.975, then players know that they shouldn't elect this feature.

I claim that it is not particularly helpful to announce that the RTP for this game is a certain number when using a perfect strategy which you are unable to define and which no one else in the world knows. Why should anyone choose this ding-dong feature when it is almost certain that they will be playing a strategy that is sub-optimal and thus increasing the house edge?
link to original post

What makes you think that no one knows the proper strategy?

Quote: DRich

Quote: gordonm888

Quote: Wizard

Quote: Hunterhill

It seems like creating a strategy for this game would be challenging.
link to original post

Indeed. I leave that to the player.
link to original post

Why not define a simple basic strategy for this feature and then analyze it? If using the simple basic strategy lowers the Return to Player (RTP) to, say, 0.975, then players know that they shouldn't elect this feature.

I claim that it is not particularly helpful to announce that the RTP for this game is a certain number when using a perfect strategy which you are unable to define and which no one else in the world knows. Why should anyone choose this ding-dong feature when it is almost certain that they will be playing a strategy that is sub-optimal and thus increasing the house edge?
link to original post

What makes you think that no one knows the proper strategy?
link to original post

Perhaps that's an exaggeration. But I'll do what newscasters do: "There's no proof that anyone knows the proper strategy."

And if Mike Shackleford doesn't know the proper strategy, and a proper strategy hasn't been published, then the great unwashed public doesn't know the proper strategy.

Quote: gordonm888

Quote: DRich

Quote: gordonm888

Quote: Wizard

Quote: Hunterhill

It seems like creating a strategy for this game would be challenging.
link to original post

Indeed. I leave that to the player.
link to original post

Why not define a simple basic strategy for this feature and then analyze it? If using the simple basic strategy lowers the Return to Player (RTP) to, say, 0.975, then players know that they shouldn't elect this feature.

I claim that it is not particularly helpful to announce that the RTP for this game is a certain number when using a perfect strategy which you are unable to define and which no one else in the world knows. Why should anyone choose this ding-dong feature when it is almost certain that they will be playing a strategy that is sub-optimal and thus increasing the house edge?
link to original post

What makes you think that no one knows the proper strategy?
link to original post

Perhaps that's an exaggeration. But I'll do what newscasters do: "There's no proof that anyone knows the proper strategy."

And if Mike Shackleford doesn't know the proper strategy, and a proper strategy hasn't been published, then the great unwashed public doesn't know the proper strategy.
link to original post

I could work out a strategy pretty quickly if the game mattered at all to me. I assume that Mike could, too.

You just have to multiply the EV of each hold by (1 + (the percentage in the table x 1.75 * (0.6 + (0.4*4.8)))) and then determine the optimal hold the normal way - just find the max of the 32 EVs.

This is what I get for a DDB strategy, but I am pretty sure I don't understand the rules of the game properly. That is, I cannot get the EV overall EV to come out right.



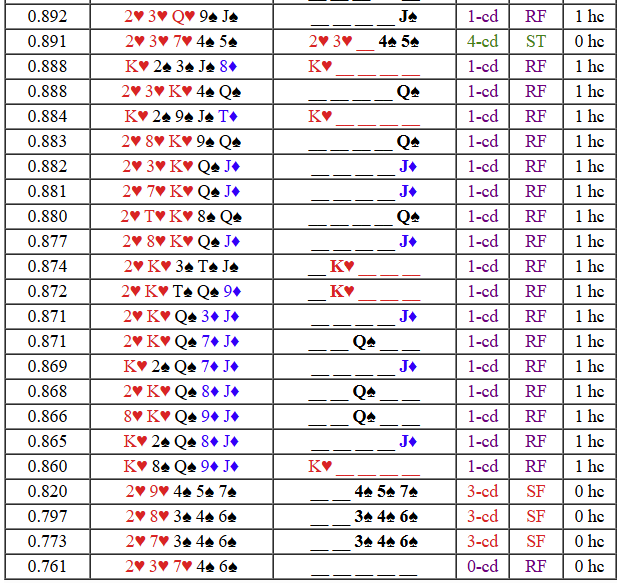
My strategy is in a HTML scroll window, so I can only screenshot a part of it at a time. This is just the bottom section. Note that holding zero cards is better than a suited 468, etc. I only added two lines to my program to produce a strategy for this game. However, if I programmed for the wrong rules, those lines may need tweaking. EV is listed on a 5-coin basis.

Quote: Mental

I could work out a strategy pretty quickly if the game mattered at all to me. I assume that Mike could, too.

You just have to multiply the EV of each hold by (1 + (the percentage in the table x 1.75 * (0.6 + (0.4*4.8)))) and then determine the optimal hold the normal way - just find the max of the 32 EVs.
link to original post

I agree that is the brute force way of analyzing any given five card hand - there are 32 possible ways to discard from a 5-card hand. If you have the subroutines for drawing every possible combination of cards to any hold and a subroutine for scoring the final five card hands, then its possible to analyze all 2,598,960 starting 5-card hands.

I assume that's pretty close to what Mike did to calculate an RTP. But if that is your method then how do you take all that information and reduce it to a strategy? how do you transform all that information for 2,598,960 starting hands into "insight' and strategy rules. It obviously can be done, but is it straightforward?

I could develop a basic strategy using a VP analysis spreadsheet I have for discarding/drawing 1,2,3,4, or 5 cards to any given 5-card hand (and calculating RTP/EV) and being selective about which hands you analyze. So, for Kh-Th-7d-3c-2s, you analyze 'draw 4 to Kh', and compare it to 'draw 3 to Kh-Th'; you don't need to go through all 32 discard options or all the suit permutations. You also can define hand categories such that you don't have to go through all the rank combinations. This is less brute force, probably more tedious, but is an excellent way to develop strategy insights and codify it as "strategy rules."

But whatever method is used, analysis is work and most or all of the (just guessing) 20-100 analysts in this forum who could do this strategy analysis have not yet done it. And the great majority of gamblers cannot begin to do this strategy analysis. Yes, maybe there are math people who have developed a basic strategy (as part of certifying this VP feature), but if so its unpublished.

It's a blank spot on the gaming analysis map.

Quote: gordonm888

Quote: Mental

I could work out a strategy pretty quickly if the game mattered at all to me. I assume that Mike could, too.

You just have to multiply the EV of each hold by (1 + (the percentage in the table x 1.75 * (0.6 + (0.4*4.8)))) and then determine the optimal hold the normal way - just find the max of the 32 EVs.
link to original post

I agree that is the brute force way of analyzing any given five card hand - there are 32 possible ways to discard from a 5-card hand. If you have the subroutines for drawing every possible combination of cards to any hold and a subroutine for scoring the final five card hands, then its possible to analyze all 2,598,960 starting 5-card hands.

I assume that's pretty close to what Mike did to calculate an RTP. But if that is your method then how do you take all that information and reduce it to a strategy? how do you transform all that information for 2,598,960 starting hands into "insight' and strategy rules. It obviously can be done, but is it straightforward?

I could develop a basic strategy using a VP analysis spreadsheet I have for discarding/drawing 1,2,3,4, or 5 cards to any given 5-card hand (and calculating RTP/EV) and being selective about which hands you analyze. So, for Kh-Th-7d-3c-2s, you analyze 'draw 4 to Kh', and compare it to 'draw 3 to Kh-Th'; you don't need to go through all 32 discard options or all the suit permutations. You also can define hand categories such that you don't have to go through all the rank combinations. This is less brute force, probably more tedious, but is an excellent way to develop strategy insights and codify it as "strategy rules."

But whatever method is used, analysis is work and most or all of the (just guessing) 20-100 analysts in this forum who could do this strategy analysis have not yet done it. And the great majority of gamblers cannot begin to do this strategy analysis. Yes, maybe there are math people who have developed a basic strategy (as part of certifying this VP feature), but if so its unpublished.

It's a blank spot on the gaming analysis map.
link to original post

I don't use brute force as you describe it. I start by precalculating lists of hands that contain any one card and then any two cards up to 5 cards. I store the counts and the values of all of those hands. When I am drawing to a hand where I am holding two cards, I just stitch all this 2-card data together using the Sierpinski triangle. I don't loop through all of the possible draws and evaluate the result. That would be very slow. I believe this is the same way that Wiz/JB coded their analyzer.

My algorithm can analyze the EV of a game in less than a second, so there is no need to be selective. I just analyze every single draw exactly and choose the one with the highest EV.

I generate my strategy by sorting all of the possible starting hands from highest EV to lowest EV and then consolidate groups of hands by traits like '3-card SF hold 7-hi one gap' or '2-card RF hold 2 gaps'. This takes around a second. I output the strategy as HTML. I can generate strategies for joker games or quick quads.

Quote: Mental

Quote: gordonm888

Quote: Mental

I could work out a strategy pretty quickly if the game mattered at all to me. I assume that Mike could, too.

You just have to multiply the EV of each hold by (1 + (the percentage in the table x 1.75 * (0.6 + (0.4*4.8)))) and then determine the optimal hold the normal way - just find the max of the 32 EVs.
link to original post

I agree that is the brute force way of analyzing any given five card hand - there are 32 possible ways to discard from a 5-card hand. If you have the subroutines for drawing every possible combination of cards to any hold and a subroutine for scoring the final five card hands, then its possible to analyze all 2,598,960 starting 5-card hands.

I assume that's pretty close to what Mike did to calculate an RTP. But if that is your method then how do you take all that information and reduce it to a strategy? how do you transform all that information for 2,598,960 starting hands into "insight' and strategy rules. It obviously can be done, but is it straightforward?

I could develop a basic strategy using a VP analysis spreadsheet I have for discarding/drawing 1,2,3,4, or 5 cards to any given 5-card hand (and calculating RTP/EV) and being selective about which hands you analyze. So, for Kh-Th-7d-3c-2s, you analyze 'draw 4 to Kh', and compare it to 'draw 3 to Kh-Th'; you don't need to go through all 32 discard options or all the suit permutations. You also can define hand categories such that you don't have to go through all the rank combinations. This is less brute force, probably more tedious, but is an excellent way to develop strategy insights and codify it as "strategy rules."

But whatever method is used, analysis is work and most or all of the (just guessing) 20-100 analysts in this forum who could do this strategy analysis have not yet done it. And the great majority of gamblers cannot begin to do this strategy analysis. Yes, maybe there are math people who have developed a basic strategy (as part of certifying this VP feature), but if so its unpublished.

It's a blank spot on the gaming analysis map.
link to original post

I don't use brute force as you describe it. I start by precalculating lists of hands that contain any one card and then any two cards up to 5 cards. I store the counts and the values of all of those hands. When I am drawing to a hand where I am holding two cards, I just stitch all this 2-card data together using the Serpinski triangle. I don't loop through all of the possible draws and evaluate the result. That would be very slow. I believe this is the same way that Wiz/JB coded their analyzer.

My algorithm can analyze the EV of a game in less than a second, so there is no need to be selective. I just analyze every single draw exactly and choose the one with the highest EV.

I generate my strategy by sorting all of the possible starting hands from highest EV to lowest EV and then consolidate groups of hands by traits like '3-card SF hold 7-hi one gap' or '2-card RF hold 2 gaps'. This takes around a second. I output the strategy as HTML. I can generate strategies for joker games or quick quads.
link to original post

Got it, this makes perfect sense.

I wrote my VP analyzer more than 20 years ago, so I am writing this just to refresh my memory. This is the Sierpinski triangle that I use in my program. The sides have a length of 32. This corresponds to the number of ways of drawing to a 5-card hand.


The + or - signs indicate whether I add or subtract my precalculated counts from the running total of possible outcomes for a hand.

Suppose you are dealt a royal flush. If you consider holding TJQK, my program has already stored the information that TJQK is a subset of 48 different possible 5-card hands. One of these hands is a RF, one is a SF, and there are a bunch of straights, flushes, high pairs and losing hands that contain a suited TJQK. These counts get added in positively based on the (second column, second row) of the Sierpinski triangle. However, this number overcounts the number of outcomes. Based on the (second column, first row) of the triangle, I need to subtract off the counts from five card hands using the original five dealt cards. Suited TJQKA is only part of one 5-card hand, and that hand is of type RF. So the resulting outcomes contain (1 - 1) = zero RFs.

Using the precalculated hand counts for this example is trivial. But what if you consider discarding all five cards? Then you are at the rightmost column of the triangle. You need to add and subtract 32 different precomputed counts for every type of outcome from loser to RF. The Sierpinski triangle helps me keep track of which counts need to be added and which sign to use within the program.

I never loop through all of the (47 CHOOSE 5) = 1,533,939 ways of drawing five new cards to form a straight, for example. I simply have to add or subtract 32 different straight counts and I am done. This is a huge savings in computer time: 1,533,939 different hand evaluations versus 32 integer addition/subtractions.

You may say that it is stupid to even considering not holding all five cards after being dealt a RF. My point is that it takes very little time to do the calculation for every possible hand. In most VP games, you always hold a dealt full house. In other games, you break up the full house. I have no shortcuts in my program that rely on assumptions that may be violated under some crazy game rules that I had not considered. In Quick Quads, you sometimes hold suited 23 or 34. Who would have even considered this possibility when writing a strategy analyzer. But my QQ analyzer finds this rule on its own.

If I can get an understanding of the correct rules for Extra Card VP, my analyzer should be able to create a strategy for any pay table.

I have to give credit to VP Genius for pointing out the Sierpinski triangle method to me. But I can find no trace of those pages on the web, and I never knew VP Genius's real name.

Here is a concrete example. I had my program draw 5 cards to a random hand (2h 3h Jh Qh 6s) and I had it print out the 32 counts that are added together to count the number of straights that can be achieved. You can check that he total, 6356, matches the actual number of straights. Most VP analyzers provide these details.


The sequence of '+' and '-' matches the last column of the Sierpinski triangle reading from the bottom up. All of the other counts were calculated the same way. You can check the results against another program. Obviously, there are only 3 RF possible if you discard the Qh, etc.

I use 152,646 unique starting hands. I use the same precalculated counts to calculate the EV for every one of them. I do not need to loop over the different ways of drawing 5 cards to each unique hand. The code couldn't be simpler:

where dt and and row are the column and row of the triangle and t is the hand type, and tCountStore is an array containing sums. All the hard work is done up front calculating the hand composition counts and storing that information in five arrays where I find the count, n, that is passed into this summing routine.

The arrays are named array1 to array5. For example, hand.array1[t][k] contains data for all hands containing a particular card, and k is an index into that set of data. In contrast, hand.array5[t] doesn't need an index because you are holding five cards, and the resulting hands are the same as the original hands.

Here is another short video of the game play from YouTube.

Xtra-card Poker is now installed at the Venetian, Stratosphere, and Green Valley Ranch!