Schroedinger’s Craps (pun intended)

Imagine a very rudimentary slot machine: A box with a coin slot and a coin tray. The box demands six coins in. Inserting the sixth coin triggers the random mechanism which then cashes out an amount according to this paytable:

pays	probability
13	27.1%
7	22.2%
5	11.1%
2	11.1%
1	13.3%

Imagine further that several of these slot machines existed and we are lucky to have a peek inside them.

Type A.
Some of the boxes have a single board computer inside. The sixth coin inserted triggers the random number generator (RNG). Based on this random result, the amount payed out is selected from the paytable given above.

Type B.
The other boxes have gaming consoles inside. They are set to play passline bets with maximum odds in a 3x4x5x odds craps game. The sixth coin inserted in the box triggers a single hand of passline to be played. After this hand, the payout is derived from the coins inserted (6) plus the winnings or minus the losses of the passline outcome.
The payout amounts of the box and their corresponding probabilities are the same as those given in the paytable above.



Initial bet plus free odds bet.
It could be argued that on the passline bet, in general, not all six coins are wagered. Some coins would remain "unused", and are cashed out together with the actual resulting amount.



Question 3: How could this higher house edge be mathematically justified for the slot machines of type A, which are behaving identically on the outside?

Initial bet only.
Some might argue that the free odds bets shouldn't be included in the calculation because they have no house edge.




Question 5: How could this rather high house edge be mathematically justified for the slot machines of type A, which are behaving identically on the outside?

Experiment 1.
Take a friend to the craps tables. Choose a table with 3x4x5x odds. Let your friend do the betting at the table. You won't bet yourself but instead you will watch over the bankroll and do the statistics. Follow this procedure:
1) Hand your friend six chips and ask him to play a single hand of passline with full odds.
2) After this one hand your friend returns back to you the number of chips resulting from this hand.
3) Keep records of the number of chips your friend returns and how often this happens. Don't forget to also keep track of those times your friend returns nothing, i.e. zero chips.
4) Repeat from step 1).
After a large number of hands played, for each amount of chips returned, calculate the percentage of hands played.

Question 6: Would it be wrong to expect that your statistics will approximate the paytable given above for the slot machine?

Question 7: What would be the house edge of your play?

Experiment 2.
If your friend is not available for some craps try the following procedure at a table with 3x4x5x odds:
1) Define a bankroll for your current session as a multiple of six chips and keep records of its total. Put the chips in one rail of your chip rack.
2) Separate six chips by moving them a little on the side. From these six chips bet one hand of passline with full odds.
3) Collect the chips of the result of this one hand and add them to the second rail. Also move any remaining of the six separated chips to the second rail.
4) Repeat from step 2) until your bankroll from the first rail is used up.
5) Add to your records the number of chips you accumulated in the second rail and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the second rail and devide it by the sum of chips you recorded for the first rail. Divide that value by six.

Question 8: Would it be wrong to expect for your play a house edge of 0.24%?

Final question: From a pure mathematical point of view, which game would you prefer? Playing the hypothetical slot machine given above or playing the passline with full odds on a 3x4x5x odds craps table?

What a great post! Love the thought experiment. Have not yet looked over the math.

Every casino I play at only rates me or comps me or gives me cashback based on coins put into play. The extra coins that are never used on an odds bet are not rated and do not earn me cashback or satisfy play-through requirements for bonuses.

Therefore, I only care about the house edge based on coins put into play. The two games are not identical for my purposes.

Quote: ThomasK

If your friend is not available for some craps try the following procedure at a table with 3x4x5x odds:
1) Define a bankroll for your current session as a multiple of six chips and keep records of its total. Put the chips in one rail of your chip rack.
2) Separate six chips by moving them a little on the side. From these six chips bet one hand of passline with full odds.
3) Collect the chips of the result of this one hand and add them to the second rail. Also move any remaining of the six separated chips to the second rail.
4) Repeat from step 2) until your bankroll from the first rail is used up.
5) Add to your records the number of chips you accumulated in the second rail and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the second rail and devide it by the sum of chips you recorded for the first rail. Divide that value by six.

Question 8: Would it be wrong to expect for your play a house edge of 0.24%?

link to original post

Yes, and here's why:
Instead of setting aside 6 coins, you set aside 100. In effect, your return will be 94 coins higher; the ER is 5.98586 + 94 = 99.98586. On a bet of 100, the house is expected to gain 100 - 99.98586 = 0.01414; that is a house edge of 0.014%.

Quote: unJon

What a great post! Love the thought experiment. Have not yet looked over the math.
link to original post

Thanks for liking this one.
I already posted the same idea in a different context earlier but there it seems to be rejected as "nonsense".

Quote: Mental

Every casino I play at only rates me or comps me or gives me cashback based on coins put into play. The extra coins that are never used on an odds bet are not rated and do not earn me cashback or satisfy play-through requirements for bonuses.

Therefore, I only care about the house edge based on coins put into play. The two games are not identical for my purposes.
link to original post

Thanks for your reply.
I already have thought of this drawback, that the idea does not work for comps.
Maybe in the future I will work out the math of how comps would effect the results.

Quote: ThatDonGuy

Quote: ThomasK

If your friend is not available for some craps try the following procedure at a table with 3x4x5x odds:
1) Define a bankroll for your current session as a multiple of six chips and keep records of its total. Put the chips in one rail of your chip rack.
2) Separate six chips by moving them a little on the side. From these six chips bet one hand of passline with full odds.
3) Collect the chips of the result of this one hand and add them to the second rail. Also move any remaining of the six separated chips to the second rail.
4) Repeat from step 2) until your bankroll from the first rail is used up.
5) Add to your records the number of chips you accumulated in the second rail and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the second rail and devide it by the sum of chips you recorded for the first rail. Divide that value by six.

Question 8: Would it be wrong to expect for your play a house edge of 0.24%?

link to original post

Yes, and here's why:
Instead of setting aside 6 coins, you set aside 100. In effect, your return will be 94 coins higher; the ER is 5.98586 + 94 = 99.98586. On a bet of 100, the house is expected to gain 100 - 99.98586 = 0.01414; that is a house edge of 0.014%.
link to original post

Thanks for this one.
I alreay expected someone to come up with this suggestion: The higher the coin in the lower the house edge.
However, the six coins will be lost on a seven out of a six or an eight. So the six coins actually are at stake in the game.
The 94 coins, on the other hand, will be returned in each possible outcome and therefore have a probability of 100% of being payed.
(The slot machine would only warm them up.)

This brings up another interesting question:
0 < p(X) < 1 ... is considered a gamble.
The sure things p(X) = 0 and p(X) = 1 are handled mathematically like any 0 < p(X) < 1.
Are both sure probabilities a gamble, anyway?

Quote: unJon

What a great post! Love the thought experiment. Have not yet looked over the math.
link to original post

unJon,

Thanks again for your appreciation of Schroedinger's craps.
My ideas about progressive betting seem to lack some substance, if I'm not mistaken by your reply given in another related thread:

Quote: unJon

I thought the Schrodinger craps game was brilliant. But this thread is just math semantics misunderstanding. You are doing a bait and switch on denominators.

You lose 5.3% of every bet you place at risk on a single spin of the wheel. Full stop and incontrovertible. It doesn’t matter if net sizing changes for independent or dependent reasons.
link to original post

I decided to re-phrase the latest of my examples using the structure of Schroedinger's craps and I am keenly interested in your general opinion and in your specific arguments in how far this thought experiment is inferior to Schroedinger's craps.
Thank you very much in advance for your constructive criticism:

Imagine a really rudimentary slot machine: A box with a coin slot and a coin tray. The box demands seven coins in but also has a sign on it reminding players: "Machine accepts red $5 cheques only." The machine's case has some extra product information on it. The advertising slogan says

"As good or as bad
as double zero roulette:
The 'Tip your Dealers" bet."

Another notice explains "Each winning hand triggers the donation of $1 to the dealers' tip pool."

Inserting the seventh coin triggers the random mechanism which then cashes out the amount given on this very rudimentary paytable:

pays	probability
$39	85.42%

Imagine further that the casino distributed several of these slot machines all over the casino floor but we are lucky to have a peek inside them.

Type A.
Some of the boxes have a single board computer inside. The seventh coin inserted triggers the random number generator (RNG). Based on this random result, the amount payed out is selected from the paytable given above.

Type B.
The other boxes have gaming consoles inside. They are set to play one attempt of a three step Martingale on red in a double zero roulette game. The seventh coin inserted in the box triggers the Martingale to be played. The payout is derived from the coins inserted (7) plus the winnings or minus the losses of the steps of the Martingale.
The payout amount of the box and its corresponding probability is the same as that given in the paytable above.



Winning the Martingale before the third step.
It could be argued that, in general, not all seven coins are wagered. Some coins would remain "unused", and are cashed out together with the actual resulting amount.



Question 3: How could this horrible house edge be mathematically justified for the slot machines of type A, which are behaving identically on the outside?

Experiment 1.
Take a friend to the roulette tables. Let your friend do the betting at the table. You won't bet yourself but instead you will watch over the bankroll and do the statistics. Follow this procedure:
1) Hand your friend seven $5 chips and ask him to play a single attempt of a three step Martingale.
2) After this one attempt, if your friend won, he tips the dealer $1 from the amount he now holds. In any case he eventually returns to you either with nothing or with what he still holds from the winnings.
3) Keep records of the amount your friend returns and how often this happens. Don't forget to also keep track of those times your friend returns nothing, i.e. zero chips.
4) Repeat from step 1).
After a large number of hands played, for each amount of chips returned, calculate the percentage of hands played.

Question 6: Would it be wrong to expect that your statistics will approximate the paytable given above for the slot machine?

Question 7: What would be the house edge of your play?

Experiment 2.
If your friend is not available for some roulette try the following procedure at a double zero roulette table:
1) Define a bankroll for your current session as a multiple of seven $5 chips and keep records of its total. Try to get hold of two coin buckets and put your chips in one of them as the bankroll bucket. The second empty bucket will be your payout bucket.
2) Take seven chips out of your bankroll bucket and play one attempt of a three step Martingale. If you won the attempt, tip the dealer $1 of the resulting amount.
3) Collect the chips of the result of this one attempt plus any remaining of the seven chips and put them all in the payout bucket.
4) Repeat from step 2) until your bankroll bucket is empty.
5) Add to your records the number of chips you accumulated in the payout bucket and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the payout bucket and devide it by the sum of chips you recorded for the bankroll bucket. Divide that value by seven.

Question 8: Would it be wrong to expect for your play a house edge of 4.82%?

Final question: From a pure mathematical point of view, which game would you prefer? Playing the hypothetical slot machine given above or playing the Martingale with tipping the dealer?

Quote: ThomasK

I
Experiment 2.
If your friend is not available for some roulette try the following procedure at a double zero roulette table:
1) Define a bankroll for your current session as a multiple of seven $5 chips and keep records of its total. Try to get hold of two coin buckets and put your chips in one of them as the bankroll bucket. The second empty bucket will be your payout bucket.
2) Take seven chips out of your bankroll bucket and play one attempt of a three step Martingale. If you won the attempt, tip the dealer $1 of the resulting amount.
3) Collect the chips of the result of this one attempt plus any remaining of the seven chips and put them all in the payout bucket.
4) Repeat from step 2) until your bankroll bucket is empty.
5) Add to your records the number of chips you accumulated in the payout bucket and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the payout bucket and devide it by the sum of chips you recorded for the bankroll bucket. Divide that value by seven.

Question 8: Would it be wrong to expect for your play a house edge of 4.82%?

original post

Leave the game unchanged, but put 7,000 chips in the bucket. Take 7,000 chips out each play, but only use a max of 7 chips to play the same 3-step sequence using one-chip to start.

Reductio ad absurdum question: Would it be wrong to expect for your play a house edge of 0.00%?

Quote: Mental

Quote: ThomasK

I
Experiment 2.
If your friend is not available for some roulette try the following procedure at a double zero roulette table:
1) Define a bankroll for your current session as a multiple of seven $5 chips and keep records of its total. Try to get hold of two coin buckets and put your chips in one of them as the bankroll bucket. The second empty bucket will be your payout bucket.
2) Take seven chips out of your bankroll bucket and play one attempt of a three step Martingale. If you won the attempt, tip the dealer $1 of the resulting amount.
3) Collect the chips of the result of this one attempt plus any remaining of the seven chips and put them all in the payout bucket.
4) Repeat from step 2) until your bankroll bucket is empty.
5) Add to your records the number of chips you accumulated in the payout bucket and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the payout bucket and devide it by the sum of chips you recorded for the bankroll bucket. Divide that value by seven.

Question 8: Would it be wrong to expect for your play a house edge of 4.82%?

original post

Leave the game unchanged, but put 7,000 chips in the bucket. Take 7,000 chips out each play, but only use a max of 7 chips to play the same 3-step sequence using one-chip to start.

Reductio ad absurdum question: Would it be wrong to expect for your play a house edge of 0.00%?
link to original post

It wouldn't be exactly zero.
Independent of how many chips you add on top of the 7 chips needed, the house edge will never be boiled down to exactly zero (0) because money still is being wagered and therefore is put at risk of being lost.

Your example would have a house edge of 4.82E-03% which is much closer to zero, but still greater than zero. This is also the reason why your bankroll of n times 7,000 will still be depleted - only very slowly, however.

pays	probability	expected payout
7000.8	85.42%	5980.12643
6993	14.58%	1019.53638
	0.00%
total:	100.00%	6999.66281
based on 7000 coin in:
	return:	0.99995
	house edge:	4.81703E-05

But the maybe more important point is that in each of your attempts a payout of 6993 will be guaranteed, i.e. it will have a probability of 100%. So this amount never really is at stake in the game and the question is whether the 6993 would be a gamble after all?

The 7 chips on the other hand are lost entirely in those cases where all three steps of the Martingale are lost in sequence. Furthermore this occurs randomly and cannot be foretold. So the 7 chips actually are at stake in that game.

Please also see above my answer to ThatDonGuy.

Quote: ThomasK

Quote: Mental

Quote: ThomasK

I
Experiment 2.
If your friend is not available for some roulette try the following procedure at a double zero roulette table:
1) Define a bankroll for your current session as a multiple of seven $5 chips and keep records of its total. Try to get hold of two coin buckets and put your chips in one of them as the bankroll bucket. The second empty bucket will be your payout bucket.
2) Take seven chips out of your bankroll bucket and play one attempt of a three step Martingale. If you won the attempt, tip the dealer $1 of the resulting amount.
3) Collect the chips of the result of this one attempt plus any remaining of the seven chips and put them all in the payout bucket.
4) Repeat from step 2) until your bankroll bucket is empty.
5) Add to your records the number of chips you accumulated in the payout bucket and take your winnings home.
After a large enough number of sessions played, add up all the chips you recorded for the payout bucket and devide it by the sum of chips you recorded for the bankroll bucket. Divide that value by seven.

Question 8: Would it be wrong to expect for your play a house edge of 4.82%?

original post

Leave the game unchanged, but put 7,000 chips in the bucket. Take 7,000 chips out each play, but only use a max of 7 chips to play the same 3-step sequence using one-chip to start.

Reductio ad absurdum question: Would it be wrong to expect for your play a house edge of 0.00%?
link to original post

It wouldn't be exactly zero.
Independent of how many chips you add on top of the 7 chips needed, the house edge will never be boiled down to exactly zero (0) because money still is being wagered and therefore is put at risk of being lost.

Your example would have a house edge of 4.82E-03% which is much closer to zero, but still greater than zero. This is also the reason why your bankroll of n times 7,000 will still be depleted - only very slowly, however.

So you agree that I can reduce the HE by an arbitrary amount by counting chips as 'in play' but never put at risk. Yet, you cannot see that you are doing exactly that with your thought experiment and somehow thinking you are changing the HE. Sorry, but the HE does not change provided that you define it as expected W/L divided by total money actually put at risk. Anything other definition is misguided sophistry that is just confusing you.

Maybe you should put a disclaimer on this thread stating that you are using common gambling terms in a different way than the standard meaning.

Quote: Mental

[...]

Quote: ThomasK

It wouldn't be exactly zero.
Independent of how many chips you add on top of the 7 chips needed, the house edge will never be boiled down to exactly zero (0) because money still is being wagered and therefore is put at risk of being lost.

Your example would have a house edge of 4.82E-03% which is much closer to zero, but still greater than zero. This is also the reason why your bankroll of n times 7,000 will still be depleted - only very slowly, however.

So you agree that I can reduce the HE by an arbitrary amount by counting chips as 'in play' but never put at risk. Yet, you cannot see that you are doing exactly that with your thought experiment and somehow thinking you are changing the HE. Sorry, but the HE does not change provided that you define it as expected W/L divided by total money actually put at risk. Anything other definition is misguided sophistry that is just confusing you.

Maybe you should put a disclaimer on this thread stating that you are using common gambling terms in a different way than the standard meaning.
link to original post

How much "misguided sophistry" is there in the discussion about the house edge of passline bets with free odds in craps? There also an arbitrary amount is added to the initial wager and, since the free odds are fair, the house and the player will break even on these in the long run:

aspect		arbitrary amount 'in play'	free odds bets in craps
amount		arbitrarily defined by player, theoretically no upper limit	arbitrarily defined by the house, but theoretically no upper limit
house edge		0%	0%
mathematical expression applied		1-((expected payout)/(expected wager))	1-((expected payout)/(expected wager))
put at risk, short term?		no, 100% payout	yes, danger of losing the hand
put at risk, long term?		no, 100% payout	no, fair odds equal out in the long run
without 0% portion:
expected wager		maximum amount that can be lost	initial bet
expected payout		based on maximum loss	based on initial bet
with 0% portion:
expected wager		maximum loss plus arbitrary amount	initial bet plus free odds bet
expected payout		based on maximum loss and arbitrary amount	based on initial bet and free odds bet

The only difference is that in the short term the free odds bet can be lost for the player.
In the long run the arbitrary amount 'in play' and the arbitrary free odds have no effect neither on the house nor on the player.

How can the same mathematical approach, using corresponding parameters, be valid in one case and not valid in the other?

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

No. The house edge is always the expected loss divided by the money in play and at risk. I can place a $1000 bet on 00 on an online Roulette layout and then take it back before the wheel spins. I am a fricking genius. I learned how to cut the house edge to zero on a very large Roulette bet?

More to the point, any AP cares about the expected loss divided by the action that earns cash back, gets rated, counts against play-trough-requirements, or earns comps and free bets/entries. I many situations, the odds bet does not count. In that case, the HE without considering the extra action is a useful numbers for AP's. I never played craps where the odds bet did not count the same as the initial bet. The money sitting in my online balance that I did not bet on an odds bet never counts as action.

If money that is not put into play can count in the denominator, then you can add any dollar amount you like. You just end up with a meaningless number.

Quote: Mental

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

No. The house edge is always the expect loss divided by the money in play and at risk. I can place a $1000 bet on 00 on an online Roulette layout and then take it back before the wheel spins. I am a fricking genius. I learned how to cut the house edge to zero on a very large Roulette bet?
link to original post

Mental, I don’t think we disagree. But what is your calculation of the house edge on this hypothetical side bet Marty?

Quote: unJon

Quote: Mental

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

No. The house edge is always the expect loss divided by the money in play and at risk. I can place a $1000 bet on 00 on an online Roulette layout and then take it back before the wheel spins. I am a fricking genius. I learned how to cut the house edge to zero on a very large Roulette bet?
link to original post

Mental, I don’t think we disagree. But what is your calculation of the house edge on this hypothetical side bet Marty?
link to original post

If you can find a casino that will rate you on $7 of action in those cases where you only made a single $1 bet, then your number is perfect. If you can get more than 2.376% cashback, you have a +EV game. The cashback more than offsets the house edge.

I have a really hard time finding casinos that will rate me or comp me on money that stayed in my pocket or on bets that I took back. he HE on a game is only really useful to figure out how much it is costing you to play and whether the comps/cash/fun offset that cost.

Agreed.

Which is what drives my conclusion of expected loss in $ terms being a more apples to apples way of comparing different bets.

Quote: unJon

Agreed.

Which is what drives my conclusion of expected loss in $ terms being a more apples to apples way of comparing different bets.
link to original post

If you are a recreational player, maybe.

I am getting many promos with 5% cashback and sometimes higher. I have to discount this by whatever the play-thru-requirements are. Let's say promo cash is worth 60 cents on the dollar, so effectively 3% cashback. Then, I know every online game eligible for the promo with a RTP of more than 97% will be +EV. (RTP 97% implies HE 3%.) It doesn't matter if I play this at a 10 cent bet or a $200 bet. Still +EV. This is why a properly defined HE is important. Other numbers are a waste of time. I can calculate the cube root of the HE, but what use is this number?

Yup makes sense.

Question on playthrough requirements. If you make a place bet in craps and leave it at risk for one roll then pull it down, does that count towards the play through? Or do you have to leave up the place bet until resolution?

Quote: unJon

Yup makes sense.

Question on playthrough requirements. If you make a place bet in craps and leave it at risk for one roll then pull it down, does that count towards the play through? Or do you have to leave up the place bet until resolution?
link to original post

It is always possible that someone has made a mistake somewhere programming games, but I have never seen it. I only earn points or get action when the bet is resolved. This applies to slots, too. I never get rated on a slot while a player's decision is pending, for example starting a bonus round, or taking a double-up option, or making a decision to collect your win or play on. Game designers are careful make sure action is 100% committed before it is rated.

Quote: unJon

Yup makes sense.

Question on playthrough requirements. If you make a place bet in craps and leave it at risk for one roll then pull it down, does that count towards the play through? Or do you have to leave up the place bet until resolution?
link to original post

It is always possible that someone has made a mistake somewhere programming games, but I have never seen it. I only earn points or get action when the bet is resolved. This applies to slots, too. I never get rated on a slot while a player's decision is pending, for example starting a bonus round, or taking a double-up option, or making a decision to collect your win or play on. Game designers are careful make sure action is 100% committed before it is rated.

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

I just recently suggested this for the next Wizard on livestream AMA as a question to Heather. I'm rather confident that this works.

Quote:

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

I absolutely agree with your calculation. And I would also expect the Wizard to agree. He did this kind of analysis for the Double Action Roulette wheel. There it is a two step Paroli, but he calculated twice the house edge of a single bet, as I would.
The wheel could also be used to play two step Martingale, as I suggested here.

Quote:

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

My take on that is that it is not a mystery. It is about perspective and two perspectives exist as I tried to explain.

The house has to assume that every single wager stands for itself. Players are coming and going, amounts bet are higher or lower. So only the average of all that up and down can be used as the basis for the expected wager.

The player on the other hand knows that the amounts wagered are dependent as long as the system is not resolved yet. The player cannot simply abort in the middle of a three step Martingale because then she wouldn't play a three step Martingale and any analysis of three step Martingales would be void. Furthermore the player has to be prepared to lose the Martingale so to her this is the wager which she uses as the denominator.

Quote:

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

Yes, the expected value of the game is always the exact same for the house and for the player. The expected value is where the money is exchanged between player and the house. And this has to be the same, otherwise money would be lost or created mysteriously somewhere else.

Quote: Mental

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

No. The house edge is always the expected loss divided by the money in play and at risk. I can place a $1000 bet on 00 on an online Roulette layout and then take it back before the wheel spins. I am a fricking genius. I learned how to cut the house edge to zero on a very large Roulette bet?

But your amount wouldn't be a wager in a game of chance. So no gamble, no house edge.

Quote:

More to the point, any AP cares about the expected loss divided by the action that earns cash back, gets rated, counts against play-trough-requirements, or earns comps and free bets/entries. I many situations, the odds bet does not count. In that case, the HE without considering the extra action is a useful numbers for AP's. I never played craps where the odds bet did not count the same as the initial bet. The money sitting in my online balance that I did not bet on an odds bet never counts as action.

If money that is not put into play can count in the denominator, then you can add any dollar amount you like. You just end up with a meaningless number.
link to original post

And this is exactly why I always use the maximum amount that might be lost on a game. In the case of a three step Martingale it is 7 units.

Quote: Mental

Quote: unJon

Quote: Mental

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

No. The house edge is always the expect loss divided by the money in play and at risk. I can place a $1000 bet on 00 on an online Roulette layout and then take it back before the wheel spins. I am a fricking genius. I learned how to cut the house edge to zero on a very large Roulette bet?
link to original post

Mental, I don’t think we disagree. But what is your calculation of the house edge on this hypothetical side bet Marty?
link to original post

If you can find a casino that will rate you on $7 of action in those cases where you only made a single $1 bet, then your number is perfect. If you can get more than 2.376% cashback, you have a +EV game. The cashback more than offsets the house edge.

I have a really hard time finding casinos that will rate me or comp me on money that stayed in my pocket or on bets that I took back. he HE on a game is only really useful to figure out how much it is costing you to play and whether the comps/cash/fun offset that cost.
link to original post

This is definitely the downside of it: It doesn't work with comps.
I haven't included the comping topic in the first place because the casinos around me charge an entrance fee, so there is only little interest on the house's side to comp punters.

Quote: unJon

Agreed.

Which is what drives my conclusion of expected loss in $ terms being a more apples to apples way of comparing different bets.
link to original post

This by the way is the reason why I constructed the initial experiment so that Martingale, Paroli, and the single roll are all played with the same amount of 7 units. The expected values of all three are different which shows that Martingale, Paroli, and the single roll actually behave differently and therefore have different effects on the player's bankroll.
And no dividing by the wager is needed.

Quote: Mental

Quote: unJon

Agreed.

Which is what drives my conclusion of expected loss in $ terms being a more apples to apples way of comparing different bets.
link to original post

If you are a recreational player, maybe.

I am getting many promos with 5% cashback and sometimes higher. I have to discount this by whatever the play-thru-requirements are. Let's say promo cash is worth 60 cents on the dollar, so effectively 3% cashback. Then, I know every online game eligible for the promo with a RTP of more than 97% will be +EV. (RTP 97% implies HE 3%.) It doesn't matter if I play this at a 10 cent bet or a $200 bet. Still +EV. This is why a properly defined HE is important. Other numbers are a waste of time. I can calculate the cube root of the HE, but what use is this number?
link to original post

As I said before, comps are a different case. The house will only calculate things based on their perspective and that is the a posteriori wager becasue they have to assume individual independent random amounts. What I try is to figure out how to calculate the combination of the player's a priori perspective with this well known and established a posteriori perspective of the house. But I'm still struggling a bit with it ...

Quote: Mental

Quote: unJon

Quote: Mental

Quote: unJon

Ok here’s how I’m preliminarily thinking about it.

Let’s assume a new roulette side bet called “Marty”.

You hand the croupier $7 and tell him you want to bet either Marty Red or Marty Black. Assume you bet Marty red.

The side bet runs the next three spins. If any of the next three spins are red, the croupier returns you $7 plus $1 in winnings. If there are no reds in the next three spins, then you lose the $7 wagered.

What would the Wizard say is the house edge of this side bet?

Expected loss is: 85.4206% * $1 - 14.5794% * $7 = -$0.16635.

House edge of $0.16635 / $7 = 2.376%

Mental and ThomasK both agree with me?

Now is it a mystery why that house edge appears lower than the 5.263% of double 0 roulette? I don’t think so. I think it’s just the denominators don’t line up so the house edge comparison isn’t very meaningful.

The right comparison in these circumstances is the expected loss in $ terms, and those are still the same.

In a three step Marty on a double zero wheel you gamble on average 3.160665 units at the house edge of 5.263% you get right to the -$0.16635 that you have for the expected loss of the Marty side bet.

Thoughts?
link to original post

No. The house edge is always the expect loss divided by the money in play and at risk. I can place a $1000 bet on 00 on an online Roulette layout and then take it back before the wheel spins. I am a fricking genius. I learned how to cut the house edge to zero on a very large Roulette bet?
link to original post

Mental, I don’t think we disagree. But what is your calculation of the house edge on this hypothetical side bet Marty?
link to original post

If you can find a casino that will rate you on $7 of action in those cases where you only made a single $1 bet, then your number is perfect. If you can get more than 2.376% cashback, you have a +EV game. The cashback more than offsets the house edge.

I have a really hard time finding casinos that will rate me or comp me on money that stayed in my pocket or on bets that I took back. he HE on a game is only really useful to figure out how much it is costing you to play and whether the comps/cash/fun offset that cost.
link to original post

I’ve given this more thought and don’t get your issue with it. Marty side bet has a 2.376% house edge on $7. Casino can rate that. No issue. Bet takes three spins of the wheel to resolve. It’s equivalent to a 5.26% HE rating on someone betting a $1 three-step marty each roll. Math is equivalent.

Player not getting a comp advantage. Math all checks out.

ThomasK conclusion that “marty dents the HE” doesn’t hold water, but that’s a separate apples to oranges issue.

Quote: unJon

[...]

I’ve given this more thought and don’t get your issue with it. Marty side bet has a 2.376% house edge on $7. Casino can rate that. No issue. Bet takes three spins of the wheel to resolve. It’s equivalent to a 5.26% HE rating on someone betting a $1 three-step marty each roll. Math is equivalent.

Player not getting a comp advantage. Math all checks out.

ThomasK conclusion that “marty dents the HE” doesn’t hold water, but that’s a separate apples to oranges issue.
link to original post

Thanks that we agree upon the 2.38% and the 5.25%. The question is which to use when:

1) Imagine the house officially offered the Marty side bet and implemented a procdure that did not involve paying after individual rolls. Instead the player wagered 7 units and either won 1 additional unit on any of the next three rolls or lost it all on the third roll.
The house would only rate the 2.38%, because no other wagering was involved.
This would also be the house edge the player would experience.

2) Suppose a scenario similar to the Paroli play I discussed with JackSpade recently (roughly in the middle of this post):
Say, the player found an empty table in a casino not offering the Marty bet. She would ask the dealer to play the Marty bet, but he would explain that the house rules forbade to pay any rolls not wagered on the layout. Instead he would offer to take her 7 units and play the Martingale for her.
Now for the house the edge would be 5.26% because regular roulette was being played.
For the player the edge hasn't changed compared to situation 1) above because she wagered her 7 units and either won 1 additional unit or lost it all. The house edge she would experience still would be 2.38%.

3) I tried to explain at the end of my initial post on independent random variables that the player can easily disguise what she is doing.
She decides to play a three step Martingale. She knows that she needs 7 units because chances are that she will lose that amount after the third roll.
She goes to casino A and wagers 1 unit. Casino A experiences 5.26% edge.
If she loses that, she goes to casino B to wager 2 units. Casino B experiences 5.26% edge.
If she loses that again she now moves to casino C to wager 4 units. Casino C experiences 5.26% house edge.
All three casinos experience a house edge of 5.26% because for each of them our player visits randomly and independently and wagers an amount that is random and independent.
Now our player has two possibilities in her consideration:
a) Should she simply go with casinos A, B, and C and see what she put on the tables and live with that 5.26% edge for the house.
b) Or would she be better off to "simulate" the play of situations 1) and 2) and benefit from the lower edge of 2.38%, as she experienced there?
The explanation, why she can, should, and even must do that, is that she knows that the amounts she wagers are not independent (proof see here) and therefore the weighted sum of her progressing amounts is not a valid expected value. Dividing the valid expected value of the outcomes of the game by this weighted sum of wagers therefore cannot be a valid house edge. For our player only the 2.38% is the valid house edge.



The casinos expect our player to lose roughly 5 cents for each dollar she wagers.
Our player knows that her play, based on the a priori wager, will grind her bankroll only roughly 2 cents per dollar wagered.

The casino can force the a priori wager by

• offering a side bet as in situation 1).
• offering special appliances like the Double Action Roulette wheel (playing a built-in two step Paroli).
• offering slot machines (coin in is the "natural" a priori wager).

This also explains why the Double Action Roulette, for example, only offers the Paroli-based option: It doubles the house edge. (see here)
A Martingale option (two step, as well) would reduce the house edge to 1-((1-(20/38)^2)*4)/3 = 3.6%.

Quote: unJon

I’ve given this more thought and don’t get your issue with it. Marty side bet has a 2.376% house edge on $7. Casino can rate that. No issue. Bet takes three spins of the wheel to resolve. It’s equivalent to a 5.26% HE rating on someone betting a $1 three-step marty each roll. Math is equivalent.

Player not getting a comp advantage. Math all checks out.

ThomasK conclusion that “marty dents the HE” doesn’t hold water, but that’s a separate apples to oranges issue.
link to original post

Okay, I agree with Unjon here. The casino can add could require the player to put $100 earnest money on the table aside from the bets. Then, they could recalculate the coin in by adding this $100 to every bet, always return the $100 after the game ends, and recalculate a much lower house edge based on a $107 bet. They could comp the player based on exactly how much money was actually at risk based on the real 5.26% HE and everything works out the same for them. Or, they could use the $107 coin in and comp based on the new minuscule HE. Either way, the player and the house are unaffected. "Player not getting a comp advantage. Math all checks out."

Would you be okay with the casino advertising that their wheel has a player edge much lower than the 5.26% of a normal wheel??

How does TK propose to take advantage of his preferred definition of HE. If a player plays the $7-staked paroli versus rolling their own, they end up losing the same amount after any number of cycles. The TK defined HE is just mental masturbation with no real world effect. At least the player rolling their own can finish quicker because they can start a new cycle as soon as they win one unit.

Quote: unJon

[...]

ThomasK conclusion that “marty dents the HE” doesn’t hold water, but that’s a separate apples to oranges issue.
link to original post

unJon,

I would also like to reply to your last remark and therfore put together the follwing fruit basket. I am really curious about your opinion:

	Monty Hall	Martingale
apples	A passer-by enters the scene when the candidate announces to the host that she wishes to switch doors. The passer-by comments: "Why do you bother switching between two doors? Your chances of winning the car is 50% anyway."	A passer-by enters the scene when the player just has lost her wager. She now doubles her bet for another roll. The passer-by comments: "Why do you bother doubling your wager? The house has an edge of 5.26% anyway. You will only expose more of your money to that."
oranges	Little does he know that the candidate selected her door out of three prior to this. She now is offered the opportunity to see what's behind both other doors.	Little does he know that these only are single rolls of progressions, the player adheres to. On average, she will lose the progressions roughly only once every eight attempts.

What remains to do is to calculate the 66.7% for Monty Hall's oranges and the 2.38% for the Martingale oranges.

Nevertheless, the passer-by in both "apples" is correct as well because his judgement bears on "What you see is all there is. (WYSIATI)" (Daniel Kahmenman, "Thinking, Fast and Slow")

Quote: Mental

Quote: unJon

I’ve given this more thought and don’t get your issue with it. Marty side bet has a 2.376% house edge on $7. Casino can rate that. No issue. Bet takes three spins of the wheel to resolve. It’s equivalent to a 5.26% HE rating on someone betting a $1 three-step marty each roll. Math is equivalent.

Player not getting a comp advantage. Math all checks out.

ThomasK conclusion that “marty dents the HE” doesn’t hold water, but that’s a separate apples to oranges issue.
link to original post

Okay, I agree with Unjon here. The casino can add could require the player to put $100 earnest money on the table aside from the bets. Then, they could recalculate the coin in by adding this $100 to every bet, always return the $100 after the game ends, and recalculate a much lower house edge based on a $107 bet. They could comp the player based on exactly how much money was actually at risk based on the real 5.26% HE and everything works out the same for them. Or, they could use the $107 coin in and comp based on the new minuscule HE. Either way, the player and the house are unaffected. "Player not getting a comp advantage. Math all checks out."

What reasons should cause the casino to comp money (here $100) which never is at stake, i.e. will never be lost by the player to the house?

Quote:

Would you be okay with the casino advertising that their wheel has a player edge much lower than the 5.26% of a normal wheel??

It is not the wheel that has the lower house edge. The wheel always produces the same probabilities. Combining the probabilities of rolls to define the probability of losing three consecutive rolls is one component of the reduced house edge. The other component is the fact that 7 units are required to play these three rolls. Bringing both together then results in the lower house edge.

Quote:

How does TK propose to take advantage of his preferred definition of HE. If a player plays the $7-staked paroli versus rolling their own, they end up losing the same amount after any number of cycles. The TK defined HE is just mental masturbation with no real world effect. At least the player rolling their own can finish quicker because they can start a new cycle as soon as they win one unit.
link to original post

The value created by the progression is actually usable as suggested in my side bet over here.

If the player decided to bet 7 $5 cheques on red on a single roll, any tip to the dealer would make her play even more disadvantageous.
With the "Tip Your Dealer" bet she easily can afford to tip $1, and in the long run will not be worse off than betting the plain red as above (she will actually be a little bit better off).
Please run a simulation to verify that.

Quote: ThomasK

What reasons should cause the casino to comp money (here $100) which never is at stake, i.e. will never be lost by the player to the house?

link to original post

I obviously cannot get you to see that the $7 is usually not put into play, either. You just made up an imaginary casino where they require you to put up $7 in advance of the action even though only $1 is required almost half the time. However, if the casino requires you to put up an extra $100, this is somehow different?

Have fun with your sophistry. I am done here. Cheers.

ThomasK,

At bottom the issue is a denominator swap that makes the two house edge calculations not comparable in a meaningful way.

To the martingale 3-step player, I can equally say his house edge is 5.26% of each bet made or on average 2.36% of $7 over three roles. And those statements are equivalent. It’s the same house edge when you make the denominators the same. You’ll see that if you work out on average how much of the $7 is bet over the course of a three step Marty and then use that number instead of $7 in the denominator to calculate the Marty HE.

I set up a simulation in Excel based on individual rolls and carefully simulating each individual step of the wagering. The simulation confirms my calculations. Please help me to find where it goes wrong. I'm desperate. Thank you.

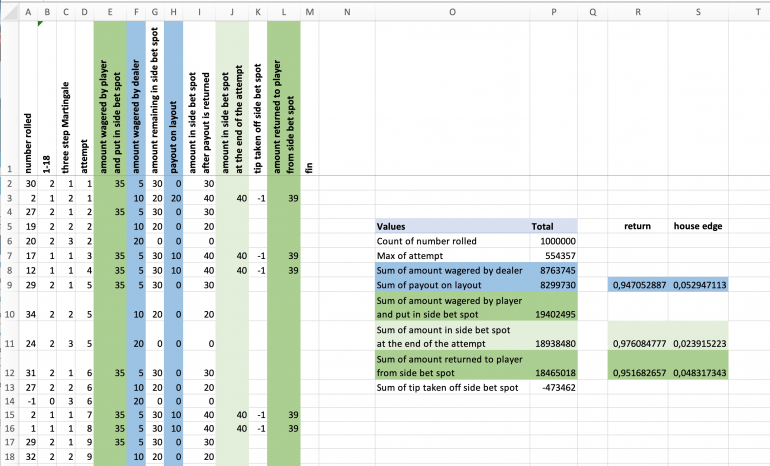
Simulating the wheel:

• column A has the individual rolls of a double zero roulette wheel
• column B determines the even money bet "1-18" which is equivalent to a bet on "red" but is easier to calculate
• column C has the three steps of the Martingale depending on the outcomes of the wheel
• column D counts the attempts, i.e. the number of Martingales played

Simulating the wagering:

• column E has the 7*$5 the player wagers for the Martingale attempt and which the dealer puts in the side bet spot
• column F has the amount the dealer actually wagers on the layout before the individual roll
• column G keeps track of how much is left in the side bet spot before the roll
• column H is the payout on the layout, if any, after that individual roll which the dealer then returns to the side bet spot
• column I shows how much now is in the side bet spot after that roll
• column J has the amount in the side bet spot at the end of the Martingale attempt
• column K shows the tip which is taken off of the side bet spot and is dropped in the toke box
• column L is the amount the player receives upon a successful Martingale attempt

Basic statistics determined by a Pivot table:
Columns O and P have basic figures of the simulation.

• 1,000,000 rolls on the roulette wheel
• equals roughly 554531 Martingle attempts
• in blue the wager and payout the dealer actually put on the layout
• in light green what the player would have received without donating the tip
• in dark green what the player wagered for the Martingale attempts and what she received
• the amount that went into the toke box

Return and house edge:
Given in columns R and S and calculated from the values dermined by the Pivot table.

• return and house edge for the dealer are the well known figures
• in light green, without the tip, the player would have experienced a house edge of 2.38%
• in dark green, donating the tip, the player experiences a house edge of 4.82%

Reread my last post. Nothing is “wrong” other than when you swap denominators the %s no longer mean the same thing so aren’t comparable.

Quote: unJon

Reread my last post. Nothing is “wrong” other than when you swap denominators the %s no longer mean the same thing so aren’t comparable.
link to original post

The issue now is, that the house edge is a value explicitly intended for comparing games.

Furthermore, house edge, return, and expected value are functionally dependent: Each can be defined as a function of the others (see below).

If there existed situations, where the house edge was not valid, then also the expected value and the return would not be valid.

If at least one of the three was calculated correctly for a given game and was valid, the two others would stringently have to be valid, as well. This again contradicts the hypothesis that any of the three would not be valid.

From that it follows that, if my calculation and my simulation, both based on the return, are correct and valid, then also my house edge must be valid.

ThomasK you seem very sincere in your quest here and I’m obviously not conveying well what I am trying to impart to you about the inability of house edge to be very comparable once the denominator stirs cease being the same thing.

Let me try a different way. Read this from the Wizard, especially the part about why HE is not a good way to compare games and his proposal to use Element of Risk.

https://wizardofodds.com/gambling/house-edge/

I’ll try one more thought experiment.

Me and you are at a roulette table with the Marty side bet.

I bet Marty Red the whole time, once every three rolls for $7.

You do a three step Marty the whole time starting at $1. If you win before the third spin, you wait for my Marty bet to resolve and we all start again at the same time.

We play together for a few hours.

1) The way we think about your house edge is 5.26% of the amount you bet. How much you bet depends on how many times you got to step 2 and step 3.

2) The way we think about my house edge is 2.38% of $7.

3) You and me won or lost the same amount of money during our few hours at the table. 100% perfect correlation.

The numbers are identical and mean the same thing. It’s just the denominator is different.

Quote: unJon

I’ll try one more thought experiment.

Me and you are at a roulette table with the Marty side bet.

I bet Marty Red the whole time, once every three rolls for $7.

You do a three step Marty the whole time starting at $1. If you win before the third spin, you wait for my Marty bet to resolve and we all start again at the same time.

We play together for a few hours.

I think this is the comparison which can be seen in my simulation above:

The player wagers 7 units (of $5) for the Marty side bet.
(Remark: The side bet won't last three rolls. It will be resolved on the first winning roll or eventually on the third roll, either winning or losing.)

In parallel the dealer bets the three step Martingale starting at 1 unit (of $5).
Both resolve on the same roll, as we both actually also would in your example.

Quote:

1) The way we think about your house edge is 5.26% of the amount you bet. How much you bet depends on how many times you got to step 2 and step 3.

The dealer's manual Martingale has a house edge of 5.26% of an average of 3.16 units.

Quote:

2) The way we think about my house edge is 2.38% of $7.

And the player's Marty side bet has a house edge of 2.8% of 7 units.

Quote:

3) You and me won or lost the same amount of money during our few hours at the table. 100% perfect correlation.

The numbers are identical and mean the same thing. It’s just the denominator is different.
link to original post

Both have lost the same amount of money from their bankroll (for the player the value from column J "amount in side bet spot at the end of the attempt" has to be subtracted from her amount wagered in column E).
As I stated earlier:

Quote: ThomasK

[...]the expected value of the game is always the exact same for the house and for the player. The expected value is where the money is exchanged between player and the house. And this has to be the same, otherwise money would be lost or created mysteriously somewhere else.
link to original post

My point now is that I try to compare the Marty side bet, costing 7 units, to a player who wagers the complete 7 units on one roll on red. And I would like to claim that the player would be better off playing the Marty side bet. She could even play the "Tip Your Dealer" version (see simulation), be nearly as bad off as her single roll on red, but in addition she would make her dealer happy.

Before continuing the discussion of this experiment, I'd like to reply to your pointer to the "element of risk":

Quote: unJon

ThomasK you seem very sincere in your quest here and I’m obviously not conveying well what I am trying to impart to you about the inability of house edge to be very comparable once the denominator stirs cease being the same thing.

Let me try a different way. Read this from the Wizard, especially the part about why HE is not a good way to compare games and his proposal to use Element of Risk.

https://wizardofodds.com/gambling/house-edge/
link to original post

Thanks for bringing this up.
Actually I've read the article, even multiple times, but quite a while ago. I haven't been able to get a proper understanding of the "element of risk", because I haven't been able to reproduce the underlying idea from the games given there as examples. So I put it aside.

Now that you mention it, and with the background of our discusion, it seems to me that it might be the idea I'm trying to convey. I guess the following could help:

Would the Wizard be able to confirm that the Element of Risk for a passline bet with full 3x4x5x odds at craps is 0.24%?

I guess then we would be talking about the same thing.

Assumed, the Element of Risk was what I intend to convey, then my suggestions would be:

• The term House Edge shall only be used for and by casinos.
• The term Element of Risk shall only be used for and by players.

Reasons for this request:

1. For base games offered by the casino both values are identical.
2. For games the player defines, and implements using base games offered by the casino, the house edge for the casino is not dented but the player benefits from the lower Element of Risk.
3. Games, defined by players, can be implemented by casinos, making the House Edge and the Elemtent of Risk identical again.

Concering 1)
See the Wizard's explanation.

Examples concerning 2)

• simulating the slot machine "Schroedinger's craps"
• simulating a slot machine offering an n step progression, either on losses (Martinglale) or on winnings (Paroli)
• simulating the "Tip Your Dealer" side bet

Examples concerning 3)

• employing the Double Action Roulette wheel which is based on a two step Paroli (as played at Casino Vienna, Austria and Casino Baden, Austria)
• offering the "Tip Your Dealer" side bet which is based on a three step Martingale
• employing an acrylic mold, holding the initial wager, to indicate the second roll of a Paroli on a straight up number (as seen in Casino Baden, Austria)

I guess, I could get used to the Element of Risk ...

lilredrooster, Mental,

You asked me to explain my ideas about "house edge" in plain English and without calculations. I thought about this a while and I might have an idea. Let's see whether it works.

I will use the Double Action Roulette as the example because it really exists and because it has been analyzed by the Wizard. So no imaginary something needed, like equivalent slot machines, and no extra calculations necessary.

I will show in four steps that the house edge does not change, although critics say that it has to be calculated differently and therefore yields different results.
The focus will be on your bankroll, how much is taken from it, how much is added to it and how often this happens.

I will frequently ask you to please verify my statements. Beyond that please ask questions and correct me on things that I'm doing wrong.

PRELIMINARIES

To start with, please verify that the house edge is a value which tells you how fast your bankroll is grinded down by a given game of chance. The higher the house edge the faster the grinding.

Please also verify that the Double Action Roulette wheel produces two roulette results on a single roll of the ball. You may play regular roulette on the outer ring or the inner ring or you may bet the Double versions of the bets.

STEP 1

Let's approach the Double Action Roulette table and keep betting one unit on Double red.
One unit is taken from the bankroll.
We will on average lose our one unit roughly 3 out of 4 trials.
On average in roughly 1 out of 4 trials we will win three units to our one unit, i.e. being paid four units.
So four units will go back to the bankroll, three more than before this winning roll.
Please verify that your bankroll will be grinded twice as fast as with a regular bet on red.
(Remark to unJon: This corresponds to the case of your post over here.)

STEP 2
Now let's vary the procedure. Instead of putting the one unit on the felt yourself, you hand the one unit to me and I will put it on the felt and will return 4 units to you if red came up. Otherwise your one unit is lost as in step 1.
Please verify that nothing changes with respect to your bankroll.
One unit is taken from your bankroll.
On average roughly 3 out of 4 trials you lose one unit and roughly 1 out of 4 trials you receive four units from me, adding three units to your bankroll.
Please verify that your bankroll is grinded at the same pace as in step 1, which indicates that the house edge is the same as in step 1.

STEP 3
Since I am doing the betting for you at the table, you can have snacks and drinks and don't have to care about the game anymore besides handing me one unit from time to time and receiving four units from me in case of winning. After a while of more betting I tell you, that I tricked you: I didn't wager your one unit on Double red but I put it on regular red for the outer ring, instead. If red came up I let your wager and the unit won ride for a second bet on red for the outer ring. So if I lost any of the two rolls I would return to you with nothing and you have lost your one unit. If red came up on both rolls I returned to you with four units, your original unit and the three units won.
Please verify that nothing changes with respect to your bankroll.
Please verify that you are not able to tell the difference between step 2 and my play here in step 3.
Please verify that on average roughly 3 out of 4 trials you lose one unit and roughly 1 out of 4 trials you receive four units from me, adding three units to your bankroll.
Please verify that your bankroll still is grinded at the same pace as in steps 1 and 2, which indicates that the house edge is the same as in steps 1 and 2.

STEP 4
Now we together return to the table and you start betting the way I did in step 3.
You take one unit from your bankroll.
If the first roll wins you let that unit and the unit won ride for a second roll.
If both rolls have been successful you add four units to your bankroll, your original unit and the three units won.
If any of the two rolls loses you have lost your one unit.
Please verify that nothing changes with respect to your bankroll.
Please verify that on average roughly 3 out of 4 trials you lose one unit and roughly 1 out of 4 trials you will be payed four units, adding three additional units to your bankroll.
Please verify that your bankroll still is grinded at the same pace as in steps 1, 2 and 3, which indicates that the house edge is the same as in steps 1, 2 and 3.

CRITICS SAY ...
... that steps 3 and 4 have to be calculated differently, resulting in only half the house edge compared to that of step one. If this was true, your bankroll in steps 3 and 4 would be grinded at only half the pace compared to step 1.
Please verify that in all four steps your bankroll is grinded at the exact same pace.