Thread Rating:
Trigger: PP
Betting sequence BBB-PPP-BB-PP (10 steps)
Trigger: BB
betting sequence PPP-BBB-PP-BB (10 steps)
Carsch sytstems:
Carsch Progression Betting System.
10 Step Carsch Unit Progression (Standard Risk)
===============================
1,1,2,3,4,6,9,14,21,32 (10 step loss 93 units)
10 Step Aggressive Carsch Progression (Higher Risk Greater Reward)
=====================================
1,2,4,7,11,17,26,40,61,93 (10 step loss 262 units)
Except for the first bet, 2 losses in a row moves you 1 step to the right.
1 win keeps you at the current step.
2 wins in a row resets you back to the beginning of the progression.
I did this with 1000 hands on Bovada's RNG which took quite a while lol
Results have good potential up 210 units
I don't have the software to test that many hands but I was hoping someone on here does.
Quote: GreenZero
I don't have the software to test that many hands but I was hoping someone on here does.
I, and many others here don't need software to answer your question
no money management (progressive) betting system can overcome or reduce the house advantage or have any effect at all on the percentages
those who think it can are either very green or are deluding themselves
many have claimed otherwise, thousands - probably tens of thousands - not a single one has ever proved it
that should tell you something
.
Quote: lilredroosterQuote: GreenZero
I don't have the software to test that many hands but I was hoping someone on here does.
I, and many others here don't need software to answer your question
no money management (progressive) betting system can overcome or reduce the house advantage or have any effect at all on the percentages
those who think it can are either very green or are deluding themselves
many have claimed otherwise, thousands - probably tens of thousands - not a single one has ever proved it
that should tell you something
.
link to original post
Oh I know. I just wanted to see test results to see how resistant it is to the house edge and when it fails and how many times.
Please explain 'resisting the house edge'Quote: GreenZero
Oh I know. I just wanted to see test results to see how resistant it is to the house edge and when it fails and how many times.
link to original post
The system will have no impact on the house edge at all.
What are you hoping to calculate? Probability of winning one unit with a bankroll of x units? Maybe probability of doubling your bankroll?
Quote: OnceDearPlease explain 'resisting the house edge'Quote: GreenZero
Oh I know. I just wanted to see test results to see how resistant it is to the house edge and when it fails and how many times.
link to original post
The system will have no impact on the house edge at all.
What are you hoping to calculate? Probability of winning one unit with a bankroll of x units? Maybe probability of doubling your bankroll?
link to original post
Resistance meaning how long it stays afloat until it gets beat down by the house edge winning 5 units per session and then walking away from the table. Bankroll management of a total loss (93 units with standard Carsch) = to 10% of your bankroll so if you have a losing session, you take a 10% hit against your bankroll.
For example:
stanadard Carsch 93 units($10 units). You should have atleast a $9300 bankroll ect...
I set up the progression in Excel as a finite state machine. It simulates even money bets in double zero roulette but doesn't use triggers for the betting sequence.
This picture is not meant to be readable but to give an impression and overview of the simulation.
Section A
Parameters and results as shown in the text.
Section B
The simulation of the rolls, wagers and payouts.
Section C
The definition of the finite state machine in linearized form. To be used via VLOOKUP.
Section D
Pivot representation of the finite state machine, having state and next state. For easy reference and validation.

The simulation runs 1,048,575 rolls.
The number of progressions contained in these rolls is given in row 3 "#attempts"
Rows 5 through 8 show the results for the single rolls which is neither surprising (5.26% house edge) nor useful for a comparison.
Rows 10 through 13 give the results for the equivalent slot machine which requires 93 coins in. The house edge of this slot machine shows the differences.
I am not completely sure whether the Parlay is only wagered on the winning of the first roll or whether both, the wager and its winning amount, have to be wagered again.
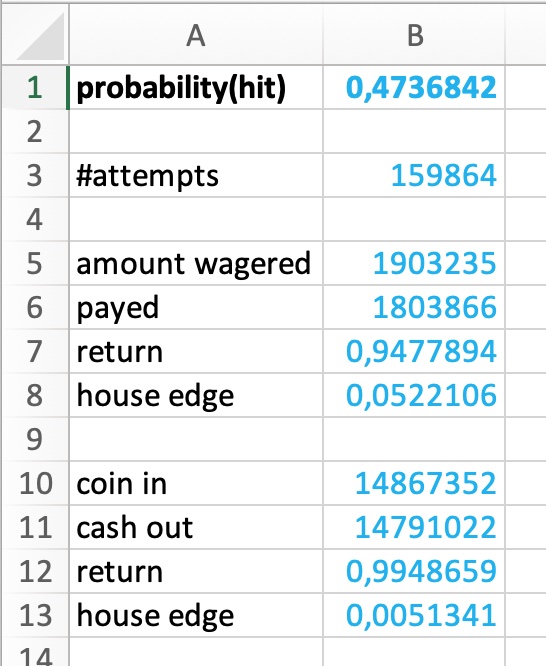
Progressions on winnings, here the two step Parlay, are a bad choice on negative expectation games anyway, so I removed the Parlay step and ended the progression after the first win.
Quote: ThomasK
This picture is not meant to be readable but to give an impression and overview of the simulation.
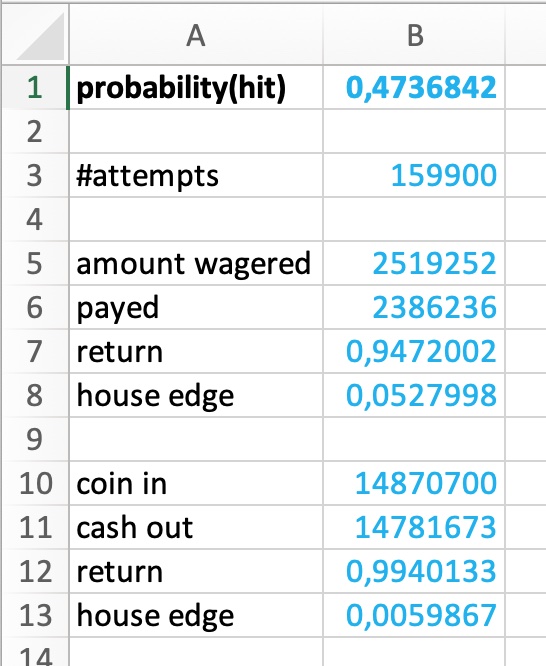
The house edge of the slot machine is roughly around 0.51%.
Parlaying the wager plus the winning amount, raises the slot machine's house edge slightly to something around 0.59%.
Progressions on winnings, here the two step Parlay, are a bad choice on negative expectation games anyway, so I removed the Parlay step and ended the progression after the first win. The house edge of the slot machine now drops to roughly 0.13%.
so, to summarize:
you have 𝙋𝙍𝙊𝙑𝙀𝙉 that with this progression the house edge is increased when parlays are used and is reduced dramatically when they are not
Congratulations - you are surely due for consideration for a Fields Medal in Mathematics for your 𝙋𝙍𝙊𝙊𝙁𝙎
you have 𝙋𝙍𝙊𝙑𝙀𝙉 something that no one else in history has ever proven - right here on WOV - everyone here is so lucky to have seen it here first - WOV should perhaps be mentioned when you are awarded the Fields Medal
you might want to consider providing a readable documentation of your findings when you submit your work to the Judges - but on the other hand - maybe that's not necessary - your 𝙋𝙍𝙊𝙊𝙁𝙎 are tremendously compelling even without readable documentation
.
First, I'm glad ThomasK did this. I haven't seen this Carsch system before and I was hoping someone would analyze it.
Secondly, I think it's appropriate to ask some questions about the simulation and try to understand what has been done. I'll start:
In the 1M trials simulation, how often was the 10-step betting sequence terminated with a loss on the 10th step, losing 93 units (while presumably winning some bets on the way through the progression?) In other words, how many times did you wager 32 units and lose?
How many times did you wager 32 units and win?
What wagers are made after all 10 steps lose?
What was the mean wager size as averaged over the roughly 1M trials?
Only if ThomasK is under the age of 40.Quote: lilredrooster...you have 𝙋𝙍𝙊𝙑𝙀𝙉 that with this progression the house edge is increased when parlays are used and is reduced dramatically when they are notQuote: ThomasK
This picture is not meant to be readable but to give an impression and overview of the simulation.
The house edge of the slot machine is roughly around 0.51%.
Parlaying the wager plus the winning amount, raises the slot machine's house edge slightly to something around 0.59%.
Progressions on winnings, here the two step Parlay, are a bad choice on negative expectation games anyway, so I removed the Parlay step and ended the progression after the first win. The house edge of the slot machine now drops to roughly 0.13%.
Congratulations - you are surely due for consideration for a Fields Medal in Mathematics for your 𝙋𝙍𝙊𝙊𝙁𝙎
link to original post
Quote: GreenZeroWas wondering if someone can do a deep analysis (1,000,000+ hands) on the 10 step Carsch systems I have below with Baccarat with the following betting sequence:
Trigger: PP
Betting sequence BBB-PPP-BB-PP (10 steps)
Trigger: BB
betting sequence PPP-BBB-PP-BB (10 steps)
Except for the first bet, 2 losses in a row moves you 1 step to the right.
1 win keeps you at the current step.
2 wins in a row resets you back to the beginning of the progression.
link to original post
Question: if your first bet is 1 unit on B, are the steps:
1 on B
1 on B
2 on B
3 on P
4 on P
6 on P
9 on B
14 on B
21 on P
32 on P?
In other words, when you get to the point where you are betting 3, do you always bet 3 on P until either you win twice in a row and reset (presumably to 1 on B, as the two Ps that you won would trigger the system), or you lose twice in a row and switch to 4 on P?
Disclaimer: TK calculates house edge by is own bizarre definition and then wants to be treated as some kind of genius for discovering a way to alter the house edge through betting systems. Best to just ignore his claims.Quote: ThomasK
I set up the progression in Excel as a finite state machine. It simulates even money bets in double zero roulette but doesn't use triggers for the betting sequence.
link to original post
Quote: gordonm888I would not say ThomasK has proven anything. I would say that he has done a simulation, with 1M trials, and produced some evidence.
First, I'm glad ThomasK did this. I haven't seen this Carsch system before and I was hoping someone would analyze it.
Secondly, I think it's appropriate to ask some questions about the simulation and try to understand what has been done. I'll start:
In the 1M trials simulation, how often was the 10-step betting sequence terminated with a loss on the 10th step, losing 93 units (while presumably winning some bets on the way through the progression?) In other words, how many times did you wager 32 units and lose?
How many times did you wager 32 units and win?
What wagers are made after all 10 steps lose?
What was the mean wager size as averaged over the roughly 1M trials?
link to original post
Bingo! and I would love to see line graph results. Just play a session until at least 5 units won and then walking away or walking away from a session loss of 93 units.
Thank you Thomas K for your info it is much appreciated.
While preparing the Excel to share with you, I realized a mistake which seems to be in the definition of the system. The amounts of the progression add up to 93, but you need two losses in a row on the same progression level to be eligible to move to the next level. Therefore the amount lost in the worst case is 186 units.
This means that the equivalent slot machine requires 186 coins in.
Here now the components of the Excel for Carsch with Parlay on intitial bet and its winning and corrected coin in for the slot machine:
Prepare section A.
#attempts =MAX(L:L)
amount wagered =SUM(H:H)
payed =SUM(I:I)
return =B6/B5
house edge =1-B7
coin in =SUM(M:M)
cash out =SUM(N:N)
return =B11/B10
house edge =1-B12
Prepare section B.
=RAND() =IF(D2<=$B$1;"won";"lost") =G2&E2 1 =VLOOKUP(F2;Q:W;5;0) =IF(E2="won";2*H2;0) =IF(G2=1;H2;H2+J1) =IF(G2=1;I2;I2+K1) 1 =IF(G2=1;186;0) =IF(G3=1;MIN(1;I2);0)*(186+K2-J2)
=RAND() =IF(D3<=$B$1;"won";"lost") =G3&E3 =VLOOKUP(F2;Q:W;4;0) =VLOOKUP(F3;Q:W;5;0) =IF(E3="won";2*H3;0) =IF(G3=1;H3;H3+J2) =IF(G3=1;I3;I3+K2) =IF(G3=1;L2+1;L2) =IF(G3=1;186;0) =IF(G4=1;MIN(1;I3);0)*(186+K3-J3)
Because of the localization of my Excel you might need to try this version. Semicolons ";" are replaced by commas ",". I'm not able to test whether it works properly:
=RAND() =IF(D2<=$B$1,"won","lost") =G2&E2 1 =VLOOKUP(F2,Q:W,5,0) =IF(E2="won",2*H2,0) =IF(G2=1,H2,H2+J1) =IF(G2=1,I2,I2+K1) 1 =IF(G2=1,186,0) =IF(G3=1,MIN(1,I2),0)*(186+K2-J2)
=RAND() =IF(D3<=$B$1,"won","lost") =G3&E3 =VLOOKUP(F2,Q:W,4,0) =VLOOKUP(F3,Q:W,5,0) =IF(E3="won",2*H3,0) =IF(G3=1,H3,H3+J2) =IF(G3=1,I3,I3+K2) =IF(G3=1,L2+1,L2) =IF(G3=1,186,0) =IF(G4=1,MIN(1,I3),0)*(186+K3-J3)
Prepare section C.
=R2&S2 1 won =R4 1 1
=R3&S3 1 lost =R6 1 1
=R4&S4 2 won 1 =2*U2 2
=R5&S5 2 lost =R6 =2*U3 2
=R6&S6 3 won =R4 1 3
=R7&S7 3 lost =R8 1 3
=R8&S8 =U8*10+V8 =S2 =R10 1 =V2
=R9&S9 =U9*10+V9 =S3 =R12 1 =V3
=R10&S10 =U10*10+V10 =S4 1 =2*U8 =V4
=R11&S11 =U11*10+V11 =S5 =R12 =2*U9 =V5
=R12&S12 =U12*10+V12 =S6 =R10 1 =V6
=R13&S13 =U13*10+V13 =S7 =R14 1 =V7
=R14&S14 =U14*10+V14 =S8 =R16 2 =V8
=R15&S15 =U15*10+V15 =S9 =R18 2 =V9
=R16&S16 =U16*10+V16 =S10 1 =2*U14 =V10
=R17&S17 =U17*10+V17 =S11 =R18 =2*U15 =V11
=R18&S18 =U18*10+V18 =S12 =R16 2 =V12
=R19&S19 =U19*10+V19 =S13 =R20 2 =V13
=R20&S20 =U20*10+V20 =S14 =R22 3 =V14
=R21&S21 =U21*10+V21 =S15 =R24 3 =V15
=R22&S22 =U22*10+V22 =S16 1 =2*U20 =V16
=R23&S23 =U23*10+V23 =S17 =R24 =2*U21 =V17
=R24&S24 =U24*10+V24 =S18 =R22 3 =V18
=R25&S25 =U25*10+V25 =S19 =R26 3 =V19
=R26&S26 =U26*10+V26 =S20 =R28 4 =V20
=R27&S27 =U27*10+V27 =S21 =R30 4 =V21
=R28&S28 =U28*10+V28 =S22 1 =2*U26 =V22
=R29&S29 =U29*10+V29 =S23 =R30 =2*U27 =V23
=R30&S30 =U30*10+V30 =S24 =R28 4 =V24
=R31&S31 =U31*10+V31 =S25 =R32 4 =V25
=R32&S32 =U32*10+V32 =S26 =R34 6 =V26
=R33&S33 =U33*10+V33 =S27 =R36 6 =V27
=R34&S34 =U34*10+V34 =S28 1 =2*U32 =V28
=R35&S35 =U35*10+V35 =S29 =R36 =2*U33 =V29
=R36&S36 =U36*10+V36 =S30 =R34 6 =V30
=R37&S37 =U37*10+V37 =S31 =R38 6 =V31
=R38&S38 =U38*10+V38 =S32 =R40 9 =V32
=R39&S39 =U39*10+V39 =S33 =R42 9 =V33
=R40&S40 =U40*10+V40 =S34 1 =2*U38 =V34
=R41&S41 =U41*10+V41 =S35 =R42 =2*U39 =V35
=R42&S42 =U42*10+V42 =S36 =R40 9 =V36
=R43&S43 =U43*10+V43 =S37 =R44 9 =V37
=R44&S44 =U44*10+V44 =S38 =R46 14 =V38
=R45&S45 =U45*10+V45 =S39 =R48 14 =V39
=R46&S46 =U46*10+V46 =S40 1 =2*U44 =V40
=R47&S47 =U47*10+V47 =S41 =R48 =2*U45 =V41
=R48&S48 =U48*10+V48 =S42 =R46 14 =V42
=R49&S49 =U49*10+V49 =S43 =R50 14 =V43
=R50&S50 =U50*10+V50 =S44 =R52 21 =V44
=R51&S51 =U51*10+V51 =S45 =R54 21 =V45
=R52&S52 =U52*10+V52 =S46 1 =2*U50 =V46
=R53&S53 =U53*10+V53 =S47 =R54 =2*U51 =V47
=R54&S54 =U54*10+V54 =S48 =R52 21 =V48
=R55&S55 =U55*10+V55 =S49 =R56 21 =V49
=R56&S56 =U56*10+V56 =S50 =R58 32 =V50
=R57&S57 =U57*10+V57 =S51 =R60 32 =V51
=R58&S58 =U58*10+V58 =S52 1 =2*U56 =V52
=R59&S59 =U59*10+V59 =S53 =R60 =2*U57 =V53
=R60&S60 =U60*10+V60 =S54 =R58 32 =V54
=R61&S61 =U61*10+V61 =S55 1 32 =V55
Finalize section B.
BEWARE: Excel might take quite some time to calculate the simaulation. Start with a few thousand rows before copying down the whole worksheet.
Mark the cells D3 through N3.
Copy these cells.
Paste these cells down the worksheet.
Simulate.
By refreshing the sheet, the random rolls in column D get updated.
The overall results are displayed in section A, i.e. columns A and B.
The other finite state machines.
=R2&S2 1 won =R4 1 1
=R3&S3 1 lost =R6 1 1
=R4&S4 2 won 1 1 2
=R5&S5 2 lost =R6 1 2
=R6&S6 3 won =R4 1 3
=R7&S7 3 lost =R8 1 3
=R8&S8 =U8*10+V8 =S2 =R10 1 =V2
=R9&S9 =U9*10+V9 =S3 =R12 1 =V3
=R10&S10 =U10*10+V10 =S4 1 1 =V4
=R11&S11 =U11*10+V11 =S5 =R12 1 =V5
=R12&S12 =U12*10+V12 =S6 =R10 1 =V6
=R13&S13 =U13*10+V13 =S7 =R14 1 =V7
=R14&S14 =U14*10+V14 =S8 =R16 2 =V8
=R15&S15 =U15*10+V15 =S9 =R18 2 =V9
=R16&S16 =U16*10+V16 =S10 1 2 =V10
=R17&S17 =U17*10+V17 =S11 =R18 2 =V11
=R18&S18 =U18*10+V18 =S12 =R16 2 =V12
=R19&S19 =U19*10+V19 =S13 =R20 2 =V13
=R20&S20 =U20*10+V20 =S14 =R22 3 =V14
=R21&S21 =U21*10+V21 =S15 =R24 3 =V15
=R22&S22 =U22*10+V22 =S16 1 3 =V16
=R23&S23 =U23*10+V23 =S17 =R24 3 =V17
=R24&S24 =U24*10+V24 =S18 =R22 3 =V18
=R25&S25 =U25*10+V25 =S19 =R26 3 =V19
=R26&S26 =U26*10+V26 =S20 =R28 4 =V20
=R27&S27 =U27*10+V27 =S21 =R30 4 =V21
=R28&S28 =U28*10+V28 =S22 1 4 =V22
=R29&S29 =U29*10+V29 =S23 =R30 4 =V23
=R30&S30 =U30*10+V30 =S24 =R28 4 =V24
=R31&S31 =U31*10+V31 =S25 =R32 4 =V25
=R32&S32 =U32*10+V32 =S26 =R34 6 =V26
=R33&S33 =U33*10+V33 =S27 =R36 6 =V27
=R34&S34 =U34*10+V34 =S28 1 6 =V28
=R35&S35 =U35*10+V35 =S29 =R36 6 =V29
=R36&S36 =U36*10+V36 =S30 =R34 6 =V30
=R37&S37 =U37*10+V37 =S31 =R38 6 =V31
=R38&S38 =U38*10+V38 =S32 =R40 9 =V32
=R39&S39 =U39*10+V39 =S33 =R42 9 =V33
=R40&S40 =U40*10+V40 =S34 1 9 =V34
=R41&S41 =U41*10+V41 =S35 =R42 9 =V35
=R42&S42 =U42*10+V42 =S36 =R40 9 =V36
=R43&S43 =U43*10+V43 =S37 =R44 9 =V37
=R44&S44 =U44*10+V44 =S38 =R46 14 =V38
=R45&S45 =U45*10+V45 =S39 =R48 14 =V39
=R46&S46 =U46*10+V46 =S40 1 14 =V40
=R47&S47 =U47*10+V47 =S41 =R48 14 =V41
=R48&S48 =U48*10+V48 =S42 =R46 14 =V42
=R49&S49 =U49*10+V49 =S43 =R50 14 =V43
=R50&S50 =U50*10+V50 =S44 =R52 21 =V44
=R51&S51 =U51*10+V51 =S45 =R54 21 =V45
=R52&S52 =U52*10+V52 =S46 1 21 =V46
=R53&S53 =U53*10+V53 =S47 =R54 21 =V47
=R54&S54 =U54*10+V54 =S48 =R52 21 =V48
=R55&S55 =U55*10+V55 =S49 =R56 21 =V49
=R56&S56 =U56*10+V56 =S50 =R58 32 =V50
=R57&S57 =U57*10+V57 =S51 =R60 32 =V51
=R58&S58 =U58*10+V58 =S52 1 32 =V52
=R59&S59 =U59*10+V59 =S53 =R60 32 =V53
=R60&S60 =U60*10+V60 =S54 =R58 32 =V54
=R61&S61 =U61*10+V61 =S55 1 32 =V55
=R2&S2 1 won 1 1 1
=R3&S3 1 lost =R6 1 1
=R4&S4 2 won 1 =2*U2 2
=R5&S5 2 lost =R6 =2*U3 2
=R6&S6 3 won 1 1 3
=R7&S7 3 lost =R8 1 3
=R8&S8 =U8*10+V8 =S2 1 1 =V2
=R9&S9 =U9*10+V9 =S3 =R12 1 =V3
=R10&S10 =U10*10+V10 =S4 1 =2*U8 =V4
=R11&S11 =U11*10+V11 =S5 =R12 =2*U9 =V5
=R12&S12 =U12*10+V12 =S6 1 1 =V6
=R13&S13 =U13*10+V13 =S7 =R14 1 =V7
=R14&S14 =U14*10+V14 =S8 1 2 =V8
=R15&S15 =U15*10+V15 =S9 =R18 2 =V9
=R16&S16 =U16*10+V16 =S10 1 =2*U14 =V10
=R17&S17 =U17*10+V17 =S11 =R18 =2*U15 =V11
=R18&S18 =U18*10+V18 =S12 1 2 =V12
=R19&S19 =U19*10+V19 =S13 =R20 2 =V13
=R20&S20 =U20*10+V20 =S14 1 3 =V14
=R21&S21 =U21*10+V21 =S15 =R24 3 =V15
=R22&S22 =U22*10+V22 =S16 1 =2*U20 =V16
=R23&S23 =U23*10+V23 =S17 =R24 =2*U21 =V17
=R24&S24 =U24*10+V24 =S18 1 3 =V18
=R25&S25 =U25*10+V25 =S19 =R26 3 =V19
=R26&S26 =U26*10+V26 =S20 1 4 =V20
=R27&S27 =U27*10+V27 =S21 =R30 4 =V21
=R28&S28 =U28*10+V28 =S22 1 =2*U26 =V22
=R29&S29 =U29*10+V29 =S23 =R30 =2*U27 =V23
=R30&S30 =U30*10+V30 =S24 1 4 =V24
=R31&S31 =U31*10+V31 =S25 =R32 4 =V25
=R32&S32 =U32*10+V32 =S26 1 6 =V26
=R33&S33 =U33*10+V33 =S27 =R36 6 =V27
=R34&S34 =U34*10+V34 =S28 1 =2*U32 =V28
=R35&S35 =U35*10+V35 =S29 =R36 =2*U33 =V29
=R36&S36 =U36*10+V36 =S30 1 6 =V30
=R37&S37 =U37*10+V37 =S31 =R38 6 =V31
=R38&S38 =U38*10+V38 =S32 1 9 =V32
=R39&S39 =U39*10+V39 =S33 =R42 9 =V33
=R40&S40 =U40*10+V40 =S34 1 =2*U38 =V34
=R41&S41 =U41*10+V41 =S35 =R42 =2*U39 =V35
=R42&S42 =U42*10+V42 =S36 1 9 =V36
=R43&S43 =U43*10+V43 =S37 =R44 9 =V37
=R44&S44 =U44*10+V44 =S38 1 14 =V38
=R45&S45 =U45*10+V45 =S39 =R48 14 =V39
=R46&S46 =U46*10+V46 =S40 1 =2*U44 =V40
=R47&S47 =U47*10+V47 =S41 =R48 =2*U45 =V41
=R48&S48 =U48*10+V48 =S42 1 14 =V42
=R49&S49 =U49*10+V49 =S43 =R50 14 =V43
=R50&S50 =U50*10+V50 =S44 1 21 =V44
=R51&S51 =U51*10+V51 =S45 =R54 21 =V45
=R52&S52 =U52*10+V52 =S46 1 =2*U50 =V46
=R53&S53 =U53*10+V53 =S47 =R54 =2*U51 =V47
=R54&S54 =U54*10+V54 =S48 1 21 =V48
=R55&S55 =U55*10+V55 =S49 =R56 21 =V49
=R56&S56 =U56*10+V56 =S50 1 32 =V50
=R57&S57 =U57*10+V57 =S51 =R60 32 =V51
=R58&S58 =U58*10+V58 =S52 1 =2*U56 =V52
=R59&S59 =U59*10+V59 =S53 =R60 =2*U57 =V53
=R60&S60 =U60*10+V60 =S54 1 32 =V54
=R61&S61 =U61*10+V61 =S55 1 32 =V55
Quote: lilredroosterQuote: ThomasK
This picture is not meant to be readable but to give an impression and overview of the simulation.
The house edge of the slot machine is roughly around 0.51%.
Parlaying the wager plus the winning amount, raises the slot machine's house edge slightly to something around 0.59%.
Progressions on winnings, here the two step Parlay, are a bad choice on negative expectation games anyway, so I removed the Parlay step and ended the progression after the first win. The house edge of the slot machine now drops to roughly 0.13%.
so, to summarize:
you have 𝙋𝙍𝙊𝙑𝙀𝙉 that with this progression the house edge is increased when parlays are used and is reduced dramatically when they are not
Congratulations - you are surely due for consideration for a Fields Medal in Mathematics for your 𝙋𝙍𝙊𝙊𝙁𝙎
you have 𝙋𝙍𝙊𝙑𝙀𝙉 something that no one else in history has ever proven - right here on WOV - everyone here is so lucky to have seen it here first - WOV should perhaps be mentioned when you are awarded the Fields Medal
you might want to consider providing a readable documentation of your findings when you submit your work to the Judges - but on the other hand - maybe that's not necessary - your 𝙋𝙍𝙊𝙊𝙁𝙎 are tremendously compelling even without readable documentation
.
link to original post
What I'm doing here is not proving but is rather applying the idea that you brought up yourself in the thread MARTINGALE SO DIFFERENT WHEN___. And there I supported your finding with some mathematical evidence. (Thank you, gordonm888, for your clarification of the terms.)
What is different now and what makes you so annoyed?
Quote: ThomasKQuote: lilredroosterQuote: ThomasK
This picture is not meant to be readable but to give an impression and overview of the simulation.
The house edge of the slot machine is roughly around 0.51%.
Parlaying the wager plus the winning amount, raises the slot machine's house edge slightly to something around 0.59%.
Progressions on winnings, here the two step Parlay, are a bad choice on negative expectation games anyway, so I removed the Parlay step and ended the progression after the first win. The house edge of the slot machine now drops to roughly 0.13%.
so, to summarize:
you have 𝙋𝙍𝙊𝙑𝙀𝙉 that with this progression the house edge is increased when parlays are used and is reduced dramatically when they are not
Congratulations - you are surely due for consideration for a Fields Medal in Mathematics for your 𝙋𝙍𝙊𝙊𝙁𝙎
you have 𝙋𝙍𝙊𝙑𝙀𝙉 something that no one else in history has ever proven - right here on WOV - everyone here is so lucky to have seen it here first - WOV should perhaps be mentioned when you are awarded the Fields Medal
you might want to consider providing a readable documentation of your findings when you submit your work to the Judges - but on the other hand - maybe that's not necessary - your 𝙋𝙍𝙊𝙊𝙁𝙎 are tremendously compelling even without readable documentation
.
link to original post
What I'm doing here is not proving but is rather applying the idea that you brought up yourself in the thread MARTINGALE SO DIFFERENT WHEN___. And there I supported your finding with some mathematical evidence. (Thank you, gordonm888, for your clarification of the terms.)
What is different now and what makes you so annoyed?
link to original post
and this from my thread that you referenced:
Quote: ThomasK
My point though is, that the Wizard always emphasizes that betting systems can't even dent the house edge. Our calculations seem to suggest otherwise.
I only claimed that it was a thing I had never thought of before - and it kinna astonished and interested me
𝙄 𝙣𝙚𝙫𝙚𝙧 𝙘𝙡𝙖𝙞𝙢𝙚𝙙 𝙩𝙝𝙖𝙩 𝙞𝙩 𝙥𝙚𝙧𝙢𝙖𝙣𝙚𝙣𝙩𝙡𝙮 𝙘𝙝𝙖𝙣𝙜𝙚𝙙 𝙩𝙝𝙚 𝙝𝙤𝙪𝙨𝙚 𝙚𝙙𝙜𝙚 𝙖𝙨 𝙮𝙤𝙪 𝙝𝙖𝙫𝙚 - you clearly stated that in your 1 million trials the house edge was reduced - and I believe you were stating or implying that the one million trials were a sufficient number of trials to assert that the house edge was permanently altered
I only pointed out that it could be a very long time for the house edge to be asserted - and I should have been clearer on that - that is the only thing I was getting at
I'm not annoyed - I just think your post is misleading and could be hurtful to newbies in that they might endlessly chase a progression that can overcome the HA - being influenced by your posts - believing that such a progression may actually exist when it doesn't
imo you need to clarify exactly what your point is - is it that the progression will actually reduce the house edge_____????
or if not, what exactly are you saying - in plain English please - not in abstruse calculations
.
Ah, but the opaque calculations and the equivalent slot machine concept are the smoke and mirrors that TK needs to support his bizarre claims.Quote: lilredroosterI'm not annoyed - I just think your post is misleading and could be hurtful to newbies in that they might endlessly chase a progression that can overcome the HA - being influenced by your posts - believing that such a progression may actually exist when it doesn't
imo you need to clarify exactly what your point is - is it that the progression will actually reduce the house edge_____????
or if not, what exactly are you saying - in plain English please - not in abstruse calculation.
link to original post
Quote: gordonm888I would not say ThomasK has proven anything. I would say that he has done a simulation, with 1M trials, and produced some evidence.
First, I'm glad ThomasK did this. I haven't seen this Carsch system before and I was hoping someone would analyze it.
Secondly, I think it's appropriate to ask some questions about the simulation and try to understand what has been done. I'll start:
In the 1M trials simulation, how often was the 10-step betting sequence terminated with a loss on the 10th step, losing 93 units (while presumably winning some bets on the way through the progression?) In other words, how many times did you wager 32 units and lose?
How many times did you wager 32 units and win?
What wagers are made after all 10 steps lose?
What was the mean wager size as averaged over the roughly 1M trials?
link to original post
Thank you for your questions.
I answer based on the corrected loss of 186 units in the case of a complete losing progression. I will also refer to the progression with the Parlay on the winning wager plus its winning. (I guess this is the original idea of Carsch.)
First I'd like to explain that a single level in this progression needs three (sub-)states to cover both requirements: two winnings in a row or two losses in a row. The graph looks like this:
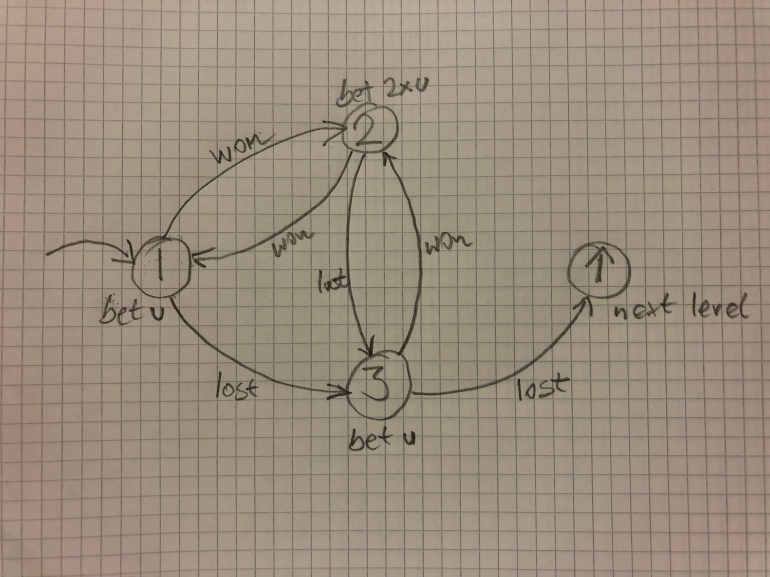
After two losses in a row the next higher level, i.e the next higher amount, is selected.
Two winnings in a row end the current progression and a new progression can be started.
Remark: The transition from state 2 to state 1 is given here for the first level. Sub-state 2 on every level will
transition to the initial state 1, not to sub-state 1 of the same level. Therefore two winnings in a row on any level will end the current progression and a new progression can be started at state 1.
Now here for the frequencies of the states to answer your questions. All figures given here are only valid for the random set I took the snap shot of. Refreshing the worksheet will vary the results.
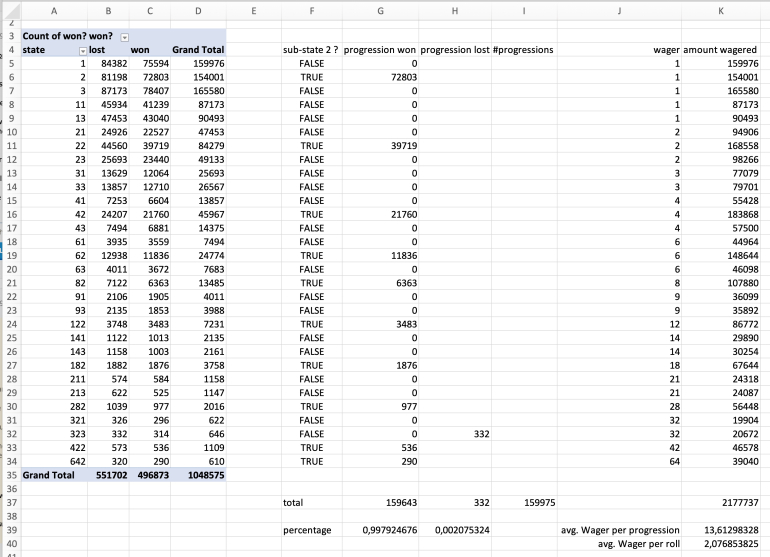
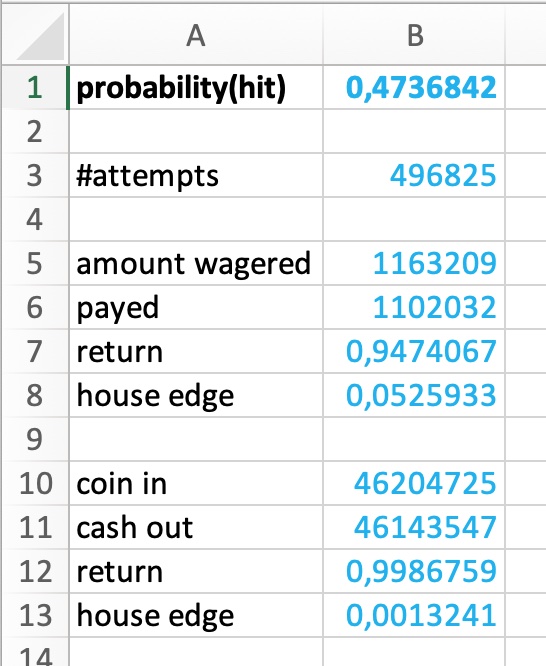
The 20-step betting sequence was terminated with a loss on the 20th step, losing 186 units, 332 times or 0.21% of all attempts. See state 323 lost, copied to cell H32. This sub-state 3 would transition to the next level, but since it is the last level in the progression, the progression ends here and a new progression can be started.
The winning states are all those that win in sub-state 2, terminating the current progression and resetting to state 1 for a new progression. The winning sub-states 2 are extracted in columns F and G. They sum up to 159643 winning progressions.
99.79% of all attempted progressions will be won.
0.21% of all attempted progressions will lose 186 units.
The amounts wagered can be determined from the states and their frequencies (columns J and K).
The average wager per progression results in 13.6 units.
The average wager per roll results in 2.1 units.
Quote: MentalAh, but the opaque calculations and the equivalent slot machine concept are the smoke and mirrors that TK needs to support his bizarre claims.Quote: lilredroosterI'm not annoyed - I just think your post is misleading and could be hurtful to newbies in that they might endlessly chase a progression that can overcome the HA - being influenced by your posts - believing that such a progression may actually exist when it doesn't
imo you need to clarify exactly what your point is - is it that the progression will actually reduce the house edge_____????
or if not, what exactly are you saying - in plain English please - not in abstruse calculation.
link to original post
link to original post
Iím more charitable than you. I think the equivalent slot machine works to point out a deficiency in the usefulness of the concept of house edge. Happy to elaborate but donít want to threadjack.
Quote: unJonQuote: MentalAh, but the opaque calculations and the equivalent slot machine concept are the smoke and mirrors that TK needs to support his bizarre claims.Quote: lilredroosterI'm not annoyed - I just think your post is misleading and could be hurtful to newbies in that they might endlessly chase a progression that can overcome the HA - being influenced by your posts - believing that such a progression may actually exist when it doesn't
imo you need to clarify exactly what your point is - is it that the progression will actually reduce the house edge_____????
or if not, what exactly are you saying - in plain English please - not in abstruse calculation.
link to original post
link to original post
Iím more charitable than you. I think the equivalent slot machine works to point out a deficiency in the usefulness of the concept of house edge. Happy to elaborate but donít want to threadjack.
link to original post
Thank you, unJon, for intervening..
May I invite you, Mental, lilredrooster, and unJon to continue this discussion over here?
unJon and I came to terms to use "house edge" only for the casino and "element of risk" only for players, although the confirmation for the proper usage of "element of risk" is pending.
Furthermore, differentiating between both has its own ambiguities.
I'd like to discuss this with you over there and hopefully I'll be able to use "plain English" only.
Quote: GreenZeroI was also looking at this progression with roulette betting 1 unit each on the 1st&2nd dozens and then betting on the 2nd&3rd dozens. Since your chances of hitting are about 66% it could work beautifully with this progression since your looking for 2 wins in a row to reset back to the beginning. I haven't done a small simulation on this yet though as a progression system involving 2 dozens get expensive really fast.
link to original post
It wouldn't be a carsch.
The idea is to win two in a row. Betting two of three dozens means you lose twice as much per loss and win half as much per win.
Let's say you lose, 1,2,4,7. That's 14×2 so you just lost 28.
And now you win the next two. That's win 22-11 and again the second spin so you made back only 22 units after losing 28.
You would have to win three in a row. And as the progression of losses goes on then the number of winning spins needed goes up.
What you should analyze is the opposite.
Betting just one dozen using the carsch because you only need one win instead of two to profit.
Lose 1,2,4,7 for a fourteen unit loss. Then win 22 on the fifth spin.
Or perhaps a combo carsch. For example if you win the fifth you make a second spin be two dozens by splitting the win.
Example: Lose first four. 1,2,4,7. Then win 22 and divide that for to get the second win so you cover 11 on two of three dozens.
If you win the second spin you add 11 more for a profit of 19. (33-14).
"Standard" method
Units are $20, since winning bets on bank only pay $19
Starting bankroll for each session is 930 units, or $18,600
A session continues until either the bankroll reaches zero or below (and I do allow for "negative bankroll" to make full bets), or 18,695 or above (a profit of 5 units, allowing for the possibility that all of the "winning" hands were bets on bank).
The results:
4883.5 hands per session
92% of the sessions were winners
However, the average result per session was a loss of just over 70 units, which makes sense - 92% of the time, you ended up around +5, and 8% of the time, you ended up around -930; (0.92 x 5) + (0.08 x (-930)) = -69.8.
If you use the "black box" method and treat each session as having bet 930 units, the "house edge" would be about 7.53%.
("How is that possible, since the house edge on straight player bets in baccarat is only 1.25%?" That's the edge per bet - the more you go back and forth between losing everything and reaching your target, the more you expose to that one bet at a time edge.)
Quote: ThatDonGuyI just ran 750,000 sessions under the following conditions:
"Standard" method
Units are $20, since winning bets on bank only pay $19
Starting bankroll for each session is 930 units, or $18,600
A session continues until either the bankroll reaches zero or below (and I do allow for "negative bankroll" to make full bets), or 18,695 or above (a profit of 5 units, allowing for the possibility that all of the "winning" hands were bets on bank).
The results:
4883.5 hands per session
92% of the sessions were winners
However, the average result per session was a loss of just over 70 units, which makes sense - 92% of the time, you ended up around +5, and 8% of the time, you ended up around -930; (0.92 x 5) + (0.08 x (-930)) = -69.8.
If you use the "black box" method and treat each session as having bet 930 units, the "house edge" would be about 7.53%.
("How is that possible, since the house edge on straight player bets in baccarat is only 1.25%?" That's the edge per bet - the more you go back and forth between losing everything and reaching your target, the more you expose to that one bet at a time edge.)
link to original post
I hope ThomasK reads the last bit.
Quote: ThomasKBefore I answer your replies individually, please see here the Excel definitions I use to simulate the progression.
While preparing the Excel to share with you, I realized a mistake which seems to be in the definition of the system. The amounts of the progression add up to 93, but you need two losses in a row on the same progression level to be eligible to move to the next level. Therefore the amount lost in the worst case is 186 units.
This means that the equivalent slot machine requires 186 coins in.
Here now the components of the Excel for Carsch with Parlay on intitial bet and its winning and corrected coin in for the slot machine:
Prepare section A.probability(hit) =18/38
#attempts =MAX(L:L)
amount wagered =SUM(H:H)
payed =SUM(I:I)
return =B6/B5
house edge =1-B7
coin in =SUM(M:M)
cash out =SUM(N:N)
return =B11/B10
house edge =1-B12
Prepare section B.random won? key state wager payed wager per attempt payed per attempt attempt # coin in cash out fin
=RAND() =IF(D2<=$B$1;"won";"lost") =G2&E2 1 =VLOOKUP(F2;Q:W;5;0) =IF(E2="won";2*H2;0) =IF(G2=1;H2;H2+J1) =IF(G2=1;I2;I2+K1) 1 =IF(G2=1;186;0) =IF(G3=1;MIN(1;I2);0)*(186+K2-J2)
=RAND() =IF(D3<=$B$1;"won";"lost") =G3&E3 =VLOOKUP(F2;Q:W;4;0) =VLOOKUP(F3;Q:W;5;0) =IF(E3="won";2*H3;0) =IF(G3=1;H3;H3+J2) =IF(G3=1;I3;I3+K2) =IF(G3=1;L2+1;L2) =IF(G3=1;186;0) =IF(G4=1;MIN(1;I3);0)*(186+K3-J3)
Because of the localization of my Excel you might need to try this version. Semicolons ";" are replaced by commas ",". I'm not able to test whether it works properly:random won? key state wager payed wager per attempt payed per attempt attempt # coin in cash out fin
=RAND() =IF(D2<=$B$1,"won","lost") =G2&E2 1 =VLOOKUP(F2,Q:W,5,0) =IF(E2="won",2*H2,0) =IF(G2=1,H2,H2+J1) =IF(G2=1,I2,I2+K1) 1 =IF(G2=1,186,0) =IF(G3=1,MIN(1,I2),0)*(186+K2-J2)
=RAND() =IF(D3<=$B$1,"won","lost") =G3&E3 =VLOOKUP(F2,Q:W,4,0) =VLOOKUP(F3,Q:W,5,0) =IF(E3="won",2*H3,0) =IF(G3=1,H3,H3+J2) =IF(G3=1,I3,I3+K2) =IF(G3=1,L2+1,L2) =IF(G3=1,186,0) =IF(G4=1,MIN(1,I3),0)*(186+K3-J3)
Prepare section C.key state input next wager sub-state fin
=R2&S2 1 won =R4 1 1
=R3&S3 1 lost =R6 1 1
=R4&S4 2 won 1 =2*U2 2
=R5&S5 2 lost =R6 =2*U3 2
=R6&S6 3 won =R4 1 3
=R7&S7 3 lost =R8 1 3
=R8&S8 =U8*10+V8 =S2 =R10 1 =V2
=R9&S9 =U9*10+V9 =S3 =R12 1 =V3
=R10&S10 =U10*10+V10 =S4 1 =2*U8 =V4
=R11&S11 =U11*10+V11 =S5 =R12 =2*U9 =V5
=R12&S12 =U12*10+V12 =S6 =R10 1 =V6
=R13&S13 =U13*10+V13 =S7 =R14 1 =V7
=R14&S14 =U14*10+V14 =S8 =R16 2 =V8
=R15&S15 =U15*10+V15 =S9 =R18 2 =V9
=R16&S16 =U16*10+V16 =S10 1 =2*U14 =V10
=R17&S17 =U17*10+V17 =S11 =R18 =2*U15 =V11
=R18&S18 =U18*10+V18 =S12 =R16 2 =V12
=R19&S19 =U19*10+V19 =S13 =R20 2 =V13
=R20&S20 =U20*10+V20 =S14 =R22 3 =V14
=R21&S21 =U21*10+V21 =S15 =R24 3 =V15
=R22&S22 =U22*10+V22 =S16 1 =2*U20 =V16
=R23&S23 =U23*10+V23 =S17 =R24 =2*U21 =V17
=R24&S24 =U24*10+V24 =S18 =R22 3 =V18
=R25&S25 =U25*10+V25 =S19 =R26 3 =V19
=R26&S26 =U26*10+V26 =S20 =R28 4 =V20
=R27&S27 =U27*10+V27 =S21 =R30 4 =V21
=R28&S28 =U28*10+V28 =S22 1 =2*U26 =V22
=R29&S29 =U29*10+V29 =S23 =R30 =2*U27 =V23
=R30&S30 =U30*10+V30 =S24 =R28 4 =V24
=R31&S31 =U31*10+V31 =S25 =R32 4 =V25
=R32&S32 =U32*10+V32 =S26 =R34 6 =V26
=R33&S33 =U33*10+V33 =S27 =R36 6 =V27
=R34&S34 =U34*10+V34 =S28 1 =2*U32 =V28
=R35&S35 =U35*10+V35 =S29 =R36 =2*U33 =V29
=R36&S36 =U36*10+V36 =S30 =R34 6 =V30
=R37&S37 =U37*10+V37 =S31 =R38 6 =V31
=R38&S38 =U38*10+V38 =S32 =R40 9 =V32
=R39&S39 =U39*10+V39 =S33 =R42 9 =V33
=R40&S40 =U40*10+V40 =S34 1 =2*U38 =V34
=R41&S41 =U41*10+V41 =S35 =R42 =2*U39 =V35
=R42&S42 =U42*10+V42 =S36 =R40 9 =V36
=R43&S43 =U43*10+V43 =S37 =R44 9 =V37
=R44&S44 =U44*10+V44 =S38 =R46 14 =V38
=R45&S45 =U45*10+V45 =S39 =R48 14 =V39
=R46&S46 =U46*10+V46 =S40 1 =2*U44 =V40
=R47&S47 =U47*10+V47 =S41 =R48 =2*U45 =V41
=R48&S48 =U48*10+V48 =S42 =R46 14 =V42
=R49&S49 =U49*10+V49 =S43 =R50 14 =V43
=R50&S50 =U50*10+V50 =S44 =R52 21 =V44
=R51&S51 =U51*10+V51 =S45 =R54 21 =V45
=R52&S52 =U52*10+V52 =S46 1 =2*U50 =V46
=R53&S53 =U53*10+V53 =S47 =R54 =2*U51 =V47
=R54&S54 =U54*10+V54 =S48 =R52 21 =V48
=R55&S55 =U55*10+V55 =S49 =R56 21 =V49
=R56&S56 =U56*10+V56 =S50 =R58 32 =V50
=R57&S57 =U57*10+V57 =S51 =R60 32 =V51
=R58&S58 =U58*10+V58 =S52 1 =2*U56 =V52
=R59&S59 =U59*10+V59 =S53 =R60 =2*U57 =V53
=R60&S60 =U60*10+V60 =S54 =R58 32 =V54
=R61&S61 =U61*10+V61 =S55 1 32 =V55
Finalize section B.
BEWARE: Excel might take quite some time to calculate the simaulation. Start with a few thousand rows before copying down the whole worksheet.
Mark the cells D3 through N3.
Copy these cells.
Paste these cells down the worksheet.
Simulate.
By refreshing the sheet, the random rolls in column D get updated.
The overall results are displayed in section A, i.e. columns A and B.
The other finite state machines.key state input next wager sub-state fin
=R2&S2 1 won =R4 1 1
=R3&S3 1 lost =R6 1 1
=R4&S4 2 won 1 1 2
=R5&S5 2 lost =R6 1 2
=R6&S6 3 won =R4 1 3
=R7&S7 3 lost =R8 1 3
=R8&S8 =U8*10+V8 =S2 =R10 1 =V2
=R9&S9 =U9*10+V9 =S3 =R12 1 =V3
=R10&S10 =U10*10+V10 =S4 1 1 =V4
=R11&S11 =U11*10+V11 =S5 =R12 1 =V5
=R12&S12 =U12*10+V12 =S6 =R10 1 =V6
=R13&S13 =U13*10+V13 =S7 =R14 1 =V7
=R14&S14 =U14*10+V14 =S8 =R16 2 =V8
=R15&S15 =U15*10+V15 =S9 =R18 2 =V9
=R16&S16 =U16*10+V16 =S10 1 2 =V10
=R17&S17 =U17*10+V17 =S11 =R18 2 =V11
=R18&S18 =U18*10+V18 =S12 =R16 2 =V12
=R19&S19 =U19*10+V19 =S13 =R20 2 =V13
=R20&S20 =U20*10+V20 =S14 =R22 3 =V14
=R21&S21 =U21*10+V21 =S15 =R24 3 =V15
=R22&S22 =U22*10+V22 =S16 1 3 =V16
=R23&S23 =U23*10+V23 =S17 =R24 3 =V17
=R24&S24 =U24*10+V24 =S18 =R22 3 =V18
=R25&S25 =U25*10+V25 =S19 =R26 3 =V19
=R26&S26 =U26*10+V26 =S20 =R28 4 =V20
=R27&S27 =U27*10+V27 =S21 =R30 4 =V21
=R28&S28 =U28*10+V28 =S22 1 4 =V22
=R29&S29 =U29*10+V29 =S23 =R30 4 =V23
=R30&S30 =U30*10+V30 =S24 =R28 4 =V24
=R31&S31 =U31*10+V31 =S25 =R32 4 =V25
=R32&S32 =U32*10+V32 =S26 =R34 6 =V26
=R33&S33 =U33*10+V33 =S27 =R36 6 =V27
=R34&S34 =U34*10+V34 =S28 1 6 =V28
=R35&S35 =U35*10+V35 =S29 =R36 6 =V29
=R36&S36 =U36*10+V36 =S30 =R34 6 =V30
=R37&S37 =U37*10+V37 =S31 =R38 6 =V31
=R38&S38 =U38*10+V38 =S32 =R40 9 =V32
=R39&S39 =U39*10+V39 =S33 =R42 9 =V33
=R40&S40 =U40*10+V40 =S34 1 9 =V34
=R41&S41 =U41*10+V41 =S35 =R42 9 =V35
=R42&S42 =U42*10+V42 =S36 =R40 9 =V36
=R43&S43 =U43*10+V43 =S37 =R44 9 =V37
=R44&S44 =U44*10+V44 =S38 =R46 14 =V38
=R45&S45 =U45*10+V45 =S39 =R48 14 =V39
=R46&S46 =U46*10+V46 =S40 1 14 =V40
=R47&S47 =U47*10+V47 =S41 =R48 14 =V41
=R48&S48 =U48*10+V48 =S42 =R46 14 =V42
=R49&S49 =U49*10+V49 =S43 =R50 14 =V43
=R50&S50 =U50*10+V50 =S44 =R52 21 =V44
=R51&S51 =U51*10+V51 =S45 =R54 21 =V45
=R52&S52 =U52*10+V52 =S46 1 21 =V46
=R53&S53 =U53*10+V53 =S47 =R54 21 =V47
=R54&S54 =U54*10+V54 =S48 =R52 21 =V48
=R55&S55 =U55*10+V55 =S49 =R56 21 =V49
=R56&S56 =U56*10+V56 =S50 =R58 32 =V50
=R57&S57 =U57*10+V57 =S51 =R60 32 =V51
=R58&S58 =U58*10+V58 =S52 1 32 =V52
=R59&S59 =U59*10+V59 =S53 =R60 32 =V53
=R60&S60 =U60*10+V60 =S54 =R58 32 =V54
=R61&S61 =U61*10+V61 =S55 1 32 =V55key state input next wager sub-state fin
=R2&S2 1 won 1 1 1
=R3&S3 1 lost =R6 1 1
=R4&S4 2 won 1 =2*U2 2
=R5&S5 2 lost =R6 =2*U3 2
=R6&S6 3 won 1 1 3
=R7&S7 3 lost =R8 1 3
=R8&S8 =U8*10+V8 =S2 1 1 =V2
=R9&S9 =U9*10+V9 =S3 =R12 1 =V3
=R10&S10 =U10*10+V10 =S4 1 =2*U8 =V4
=R11&S11 =U11*10+V11 =S5 =R12 =2*U9 =V5
=R12&S12 =U12*10+V12 =S6 1 1 =V6
=R13&S13 =U13*10+V13 =S7 =R14 1 =V7
=R14&S14 =U14*10+V14 =S8 1 2 =V8
=R15&S15 =U15*10+V15 =S9 =R18 2 =V9
=R16&S16 =U16*10+V16 =S10 1 =2*U14 =V10
=R17&S17 =U17*10+V17 =S11 =R18 =2*U15 =V11
=R18&S18 =U18*10+V18 =S12 1 2 =V12
=R19&S19 =U19*10+V19 =S13 =R20 2 =V13
=R20&S20 =U20*10+V20 =S14 1 3 =V14
=R21&S21 =U21*10+V21 =S15 =R24 3 =V15
=R22&S22 =U22*10+V22 =S16 1 =2*U20 =V16
=R23&S23 =U23*10+V23 =S17 =R24 =2*U21 =V17
=R24&S24 =U24*10+V24 =S18 1 3 =V18
=R25&S25 =U25*10+V25 =S19 =R26 3 =V19
=R26&S26 =U26*10+V26 =S20 1 4 =V20
=R27&S27 =U27*10+V27 =S21 =R30 4 =V21
=R28&S28 =U28*10+V28 =S22 1 =2*U26 =V22
=R29&S29 =U29*10+V29 =S23 =R30 =2*U27 =V23
=R30&S30 =U30*10+V30 =S24 1 4 =V24
=R31&S31 =U31*10+V31 =S25 =R32 4 =V25
=R32&S32 =U32*10+V32 =S26 1 6 =V26
=R33&S33 =U33*10+V33 =S27 =R36 6 =V27
=R34&S34 =U34*10+V34 =S28 1 =2*U32 =V28
=R35&S35 =U35*10+V35 =S29 =R36 =2*U33 =V29
=R36&S36 =U36*10+V36 =S30 1 6 =V30
=R37&S37 =U37*10+V37 =S31 =R38 6 =V31
=R38&S38 =U38*10+V38 =S32 1 9 =V32
=R39&S39 =U39*10+V39 =S33 =R42 9 =V33
=R40&S40 =U40*10+V40 =S34 1 =2*U38 =V34
=R41&S41 =U41*10+V41 =S35 =R42 =2*U39 =V35
=R42&S42 =U42*10+V42 =S36 1 9 =V36
=R43&S43 =U43*10+V43 =S37 =R44 9 =V37
=R44&S44 =U44*10+V44 =S38 1 14 =V38
=R45&S45 =U45*10+V45 =S39 =R48 14 =V39
=R46&S46 =U46*10+V46 =S40 1 =2*U44 =V40
=R47&S47 =U47*10+V47 =S41 =R48 =2*U45 =V41
=R48&S48 =U48*10+V48 =S42 1 14 =V42
=R49&S49 =U49*10+V49 =S43 =R50 14 =V43
=R50&S50 =U50*10+V50 =S44 1 21 =V44
=R51&S51 =U51*10+V51 =S45 =R54 21 =V45
=R52&S52 =U52*10+V52 =S46 1 =2*U50 =V46
=R53&S53 =U53*10+V53 =S47 =R54 =2*U51 =V47
=R54&S54 =U54*10+V54 =S48 1 21 =V48
=R55&S55 =U55*10+V55 =S49 =R56 21 =V49
=R56&S56 =U56*10+V56 =S50 1 32 =V50
=R57&S57 =U57*10+V57 =S51 =R60 32 =V51
=R58&S58 =U58*10+V58 =S52 1 =2*U56 =V52
=R59&S59 =U59*10+V59 =S53 =R60 =2*U57 =V53
=R60&S60 =U60*10+V60 =S54 1 32 =V54
=R61&S61 =U61*10+V61 =S55 1 32 =V55
link to original post
Thank you so much for the correction as ill be honest it's not easy for me to understand all this high level stuff for math isn't my strong suit. Thank you again for all the work and info. I can tell this forum is way beyond my math intelligence. What have I done??? LOL
Quote: darkozQuote: GreenZeroI was also looking at this progression with roulette betting 1 unit each on the 1st&2nd dozens and then betting on the 2nd&3rd dozens. Since your chances of hitting are about 66% it could work beautifully with this progression since your looking for 2 wins in a row to reset back to the beginning. I haven't done a small simulation on this yet though as a progression system involving 2 dozens get expensive really fast.
link to original post
It wouldn't be a carsch.
The idea is to win two in a row. Betting two of three dozens means you lose twice as much per loss and win half as much per win.
Let's say you lose, 1,2,4,7. That's 14×2 so you just lost 28.
And now you win the next two. That's win 22-11 and again the second spin so you made back only 22 units after losing 28.
You would have to win three in a row. And as the progression of losses goes on then the number of winning spins needed goes up.
What you should analyze is the opposite.
Betting just one dozen using the carsch because you only need one win instead of two to profit.
Lose 1,2,4,7 for a fourteen unit loss. Then win 22 on the fifth spin.
Or perhaps a combo carsch. For example if you win the fifth you make a second spin be two dozens by splitting the win.
Example: Lose first four. 1,2,4,7. Then win 22 and divide that for to get the second win so you cover 11 on two of three dozens.
If you win the second spin you add 11 more for a profit of 19. (33-14).
link to original post
Thank you for the correction. You could make the progression more aggressive to make up the loss to keep it at 2 wins instead of 3.
Technically, the house edge itself doesn't change as a result of any progression. It's the same on every bet regardless of size, assuming all outcomes are equally random.
What can change is the player's expected returns on a game if he is using a progression that always results in the highest wager being a win. That's a big "if." But with a large enough bankroll, low enough initial wager, high enough maximum wager, and gentle enough progression to allow for more than 10 steps, a system somewhat like Carsch as described in this thead and as applied to two dozens bets on roulette could conceivably be sustained through any "2 in a row" drought a player would ever likely suffer in his lifetime. It therefore could create an expectation that average wagers on winning bets would be slightly higher than on losing bets.
the Carsch progression got me thinking about parlays
and no, of course I'm not claiming that this changes the HA in any way
but it is kinna interesting to me anyway
if you successfully parlay the 2nd to last number in the progression - $21 - you have a win equalling $63___________I'm not counting previous losses
but if you successfully parlay the last number in the progression - $32 you have a win equalling $96
the risk in the larger parlay attempt has increased by only $11 - but your win has increased by $33
the size of the win has increased by three times the size of the increase in the risk
.
Quote: lilredrooster______________
the Carsch progression got me thinking about parlays
and no, of course I'm not claiming that this changes the HA in any way
but it is kinna interesting to me anyway
if you successfully parlay the 2nd to last number in the progression - $21 - you have a win equalling $63___________I'm not counting previous losses
but if you successfully parlay the last number in the progression - $32 you have a win equalling $96
the risk in the larger parlay attempt has increased by only $11 - but your win has increased by $33
the size of the win has increased by three times the size of the increase in the risk
.
link to original post
lilredrooster,
If you still are interested, I have prepared my explanation over here. If you don't find any major flaws in it, I would say that your gut feeling has a mathematical foundation.
Quote: JackSpadeThe only way you're going to dent the house edge, assuming you win no more often than your actual statistical odds of winning, is if your average wager on winning bets is higher than on losing bets.
Technically, the house edge itself doesn't change as a result of any progression. It's the same on every bet regardless of size, assuming all outcomes are equally random.
What can change is the player's expected returns on a game if he is using a progression that always results in the highest wager being a win. That's a big "if." But with a large enough bankroll, low enough initial wager, high enough maximum wager, and gentle enough progression to allow for more than 10 steps, a system somewhat like Carsch as described in this thead and as applied to two dozens bets on roulette could conceivably be sustained through any "2 in a row" drought a player would ever likely suffer in his lifetime. It therefore could create an expectation that average wagers on winning bets would be slightly higher than on losing bets.
link to original post
hello
sorry but I don't understand. English is not my first language
Quote: JackSpadeBut with a large enough bankroll, low enough initial wager, high enough maximum wager, and gentle enough progression to allow for more than 10 steps, a system somewhat like Carsch as described in this thead and as applied to two dozens bets on roulette could conceivably be sustained through any "2 in a row" drought a player would ever likely suffer in his lifetime. It therefore could create an expectation that average wagers on winning bets would be slightly higher than on losing bets.
I have a one month period tested (2 dozens) manually from outcomes of a single zero casino. could you please take a look at it and tell me if the way you described would work on those outcomes? I apologize if I misunderstood you.
10/22
+ + - + - * - + - + + * + + * - - + * + - + + 0 - + + + + - * + + - + * - + - - - + + - + * + - - - + + * + * - + + + + - * + - + * + + + + * + + + + + + + * + + + + + * + + + + + - - * + + + - * + + - + + + * + + + + + - + + - + 0 * - + + - * - + 0 + + + - * 0 + + - 0 * + + + + + * + * - + + 0 + * - + + - * + + + * + + - + + * + - + - + - + + + * - - + + + * 0 + + + + - + - * + + - ***
explainer
the * shows the end of a day and start of new day. the *** is end of the month. the 0 is Zero and a loss
thank you


