Battle of the Betting Systems

Dear Wizard,

Thank you for your videos on betting systems, instructions, and challenges. It inspired me to design a (hypothetical) experiment which might show that "Betting systems are ..." neither "... equally ..." nor "... completely worthless."?

This (hypothetical) experiment would involve you, Heather Ferris, and Angela Marie Wyman in the setup below. I'm not sure whether this was suitable for another video.

Angela Marie would be the financial controller watching over the wagers during the experiment and would be the final judge, deciding who performed better - you or Heather.
Angela Marie might be placed in a comfortable lounge with music, drinks, and snacks and enough table space to manage the two stacks of chips for Heather's and your wagers and another two stacks for both your returned chips.

PROCEDURE
1) Angela Marie will hand seven chips to each of you, asking you to play one single game (rules see below) and ask you to then come back with the chips you have left from this game.
2) On your return Angela Marie will put these chips (or none, if you lost) on the second stack and start over with step 1), handing you another seven chips from the stack of wagers.
3) After a number of games (the more, the better) Angela Marie will compare the two stacks of returned chips an announce if and who performed better.

RULES
The games are played at a roulette table, preferably single zero, but double zero will do as well. To simplify things, only bets on red are made. Both players will bet on red on the same rolls (first, second, third) as long as they are qualified for a roll according to their individual rules.

Heather Ferris will bet one chip on red on the first roll.
* If red wins, she collects the two chips from the table and is done for this game, now holding eight chips. She will have to wait until the Wizard's rolls are resolved.
* If red loses, Heather now bets two chips on red for a second roll. If red wins, she collects the four chips and waits with her eight chips for the Wizard to finish his rolls.
* If red loses again, she bets her last four chips on red. After this roll she leaves the table together with the Wizard.
* She returns to Angela Marie with either no chips at all or with eight chips.
(Betting system is Martingale with max. three steps.)

The Wizard will bet all his seven chips on red on the first roll.
* If red loses, he will have to wait until Heather's rolls are resolved.
* If red wins, the Wizard bets all fourteen chips (his initial seven plus the seven chips won) on red for a second roll. If red loses he will wait for Heather to finish her rolls.
* If red wins, the Wizard bets all twentyeight chips for a last roll. After this roll he leaves the table togehter with Heather.
* He returns to Angela Marie with either no chips at all or with fiftysix chips.
(Betting system is Paroli with max. three steps.)

PREDICTION
My guess is that Angela Marie will announce Heather as the winner (girl's power?).
To substantiate the experimental result, Angela Marie might calculate the house edge she experienced on the two games she played.

That's not entirely surprising, considering that Wizard is expected to bet far more than Heather, so he is also expected to lose far more.

On any given spin, the probability of red winning (assuming a double-zero wheel) is 9/19, and the probability of red losing is 10/19.
Over 19^3 = 6859 sets of three spins, the following possibilities occur:

Wizard will bet 7 on the first spin of each set; this is 6859 spins
Wizard will bet 14 on the second spin where the first spin wins; this is 9 x 361 = 3249 spins
Wizard will bet 28 on the third spin where the first two spins win; this is 9 x 9 x 19 = 1539 spins.
The total amount Wizard is expected to bet is 7 x 6859 + 14 x 3249 + 28 x 1539 = 136,591.

Heather will bet 1 on the first spin of each set; this is 6859 spins
Heather will bet 2 on the second spin where the first spin loses; this is 10 x 361 = 3610 spins.
Heather will bet 4 on the third spin where the first two spins lose; this is 100 x 19 = 1900 spins.
The total amount Heather is expected to bet is 6859 + 2 x 3610 + 4 x 1900 = 21,679.

Wizard is expected to bet 6.3x what Heather does, so he is expected to lose 6.3x what Heather does.

D'Alembert and La Bouchere. Conspicuous in their absence!

Quote: ThatDonGuy

That's not entirely surprising, considering that Wizard is expected to bet far more than Heather, so he is also expected to lose far more.

[ ... ]

Wizard is expected to bet 6.3x what Heather does, so he is expected to lose 6.3x what Heather does.
link to original post

For each game, or set, both the Wizard and Heather only receive 7 units from Angela Marie. So that is all they are able to bet and, in the bad case, to lose. Angela Marie certainly will be able to confirm this.

Quote: ThomasK

Quote: ThatDonGuy

That's not entirely surprising, considering that Wizard is expected to bet far more than Heather, so he is also expected to lose far more.

[ ... ]

Wizard is expected to bet 6.3x what Heather does, so he is expected to lose 6.3x what Heather does.
link to original post

For each game, or set, both the Wizard and Heather only receive 7 units from Angela Marie. So that is all they are able to bet and, in the bad case, to lose. Angela Marie certainly will be able to confirm this.
link to original post

Except that, whenever Wizard wins his first bet, he now has 14 to bet, and whenever he wins his second bet, he now has 28. If you're going to give 56 chips back when you win three bets, you do have to take this into account.

Look at it another way:
Wizard has a 6130 / 6859, or about 89%, chance of losing the original 7.
Heather has a 1000 / 6859, or about 15%, chance of losing the original 7.

To paraphrase George Orwell, "All systems are worthless...but some lose your money much faster than others."

Quote: ThatDonGuy

Except that, whenever Wizard wins his first bet, he now has 14 to bet, and whenever he wins his second bet, he now has 28. If you're going to give 56 chips back when you win three bets, you do have to take this into account.

Look at it another way:
Wizard has a 6130 / 6859, or about 89%, chance of losing the original 7.
Heather has a 1000 / 6859, or about 15%, chance of losing the original 7.

To paraphrase George Orwell, "All systems are worthless...but some lose your money much faster than others."
link to original post

Hmm, you're focusing on the Wizard and on Heather and on the very details of what they are doing at the roulette table.

How about Angela Marie?
She invests the same amount in two games in order to find out which one is better. She doesn't know anything about the Wizard betting 7, 14, and 28 units.
She sees 7 units going away and, when lucky, receiving back 56 units from the Wizard.
And, when lucky, receiving back 8 units from Heather.
What she also can do, is estimate the probability of these lucky events, when playing long enough.

Since we know that the events are produced at a roulette table, we are able to name these probablities a priori.

Knowing the amounts and their probabilities, Angela Marie is now able to calculate the expected value for both games and compare them accordingly. And compare them to other games as well, for example to the expected value of a single roll at roulette.

What would happen, if Heather and the Wizard put themselves in Angela Marie's shoes and simply ignored the details of what they are doing at the table?

I don't think that, when it comes to your original prediction, we disagree on anything. I am just explaining why this is the case.

If you want a true "black box" (i.e. the only things that matter are the initial bankrolls and the final results - how they got there is irrelevant), look at this:
Wizard has a 6130/6859 chance of ending up with zero and a 729/6859 chance of ending up with 56, so the expected result is 40,824 / 6859, or about 5.952.
Heather has a 1000/6859 chance of ending up with zero and a 5859/6859 chance of ending up with 8, so the expected result is 46,872 / 6859, or about 6.834.
I would probably declare Heather "the winner" as well.

Also note that, at least around here, "system" presupposes a guaranteed profit at some point. In this case, the Wizard's statement that all systems are equally and completely worthless is correct, as the probability of "guaranteed profit" is zero.

You're absolutely right. And we not only agree on the final judgement but on the way to explain it, as well: Calulating and comparing the expected values.

Imagine, you were forced to play roulette.
I guess I'm not mistaken to say that you would prefer Heather's way to the Wizard's way of playing.
How about simple bets on red?
* Angela Marie would hand you 7 chips from your own stack.
* You would bet all seven chips on red on the first roll together with Heather and the Wizard.
* After that roll you would have to wait until Heather and the Wizard have finished their games and then return back to Angela Marie altogether.

Would you want to change games with Heather, or even with the Wizard?

Angela Marie might calculate the house edge she experienced during your game.
And I suspect that she would recommend to you to change games with Heather.



About your note: I understand that the term "betting system" commonly implies a method that overcomes negative expectation and turns a losing game into a profitable advantage play. My idea is to use them to reduce the disadvanage when playing negative expectation games. I am aware that it is impossible to switch such games to positive expectation, but approaching zero closer and closer should be doable. Following the general advice "When you have to play at a casino then chose the games with the lowest house edge."

I've set up a Monte Carlo simulation of the proposed experiment.
Here double zero roulette is assumed and bets on "1-18" instead of bets on red. These have the same probability as bets on red, but can numerically be selected much easier than the layout's red numbers.

In the result, one interesting thing stands out: Heather's play not only is the superior one, as expected, but it also has a slightly lower house edge (as experienced by Angela Marie) than that of a simple bet on "1-18" on a single zero roulette. So, if only double zero tables are available, this might be the way to go ...

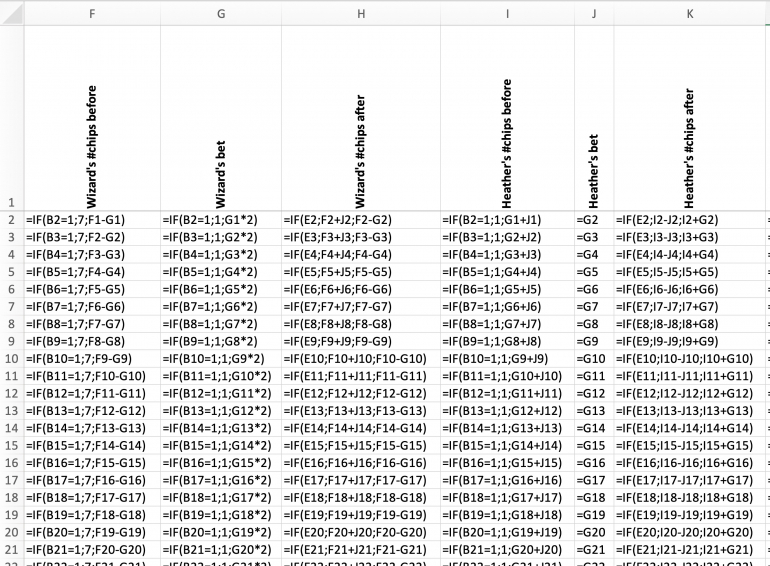
I will give here all the details of my Monte Carlo simulation so that mistakes in the simulation or in the math can be found.

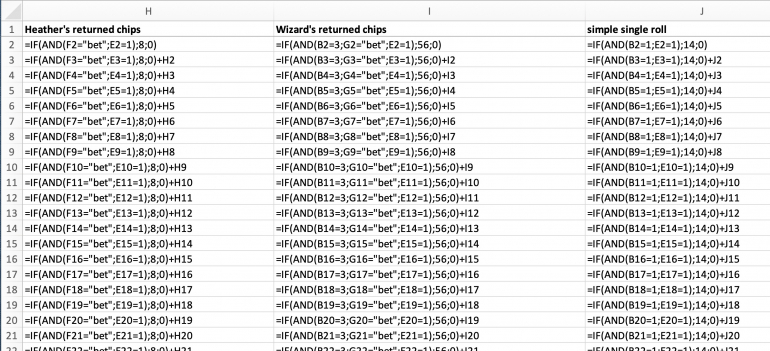
The simulation stretches over 380000 rolls. See here the first rows of the simulation. The last rows of the simulation are shown below in section "RESULT".
Since the jpegs tend to be blurry, I put magnified selections inside spoiler tags to make sure that the formulas are perfectly readable.



THE ROLLS
... are simulated in column C "number" with numbers 0 through 36 and -1 representing the double zero.

Column D "18" calculates the halves and the zero category:
0 - zero and double zero
1 - 1 through 18
2 - 19 through 36

Column E "win/lose" compresses this information into a pure binary value:
0 - lose on zeroes and on upper half "19-36"
1 - win on "1-18"



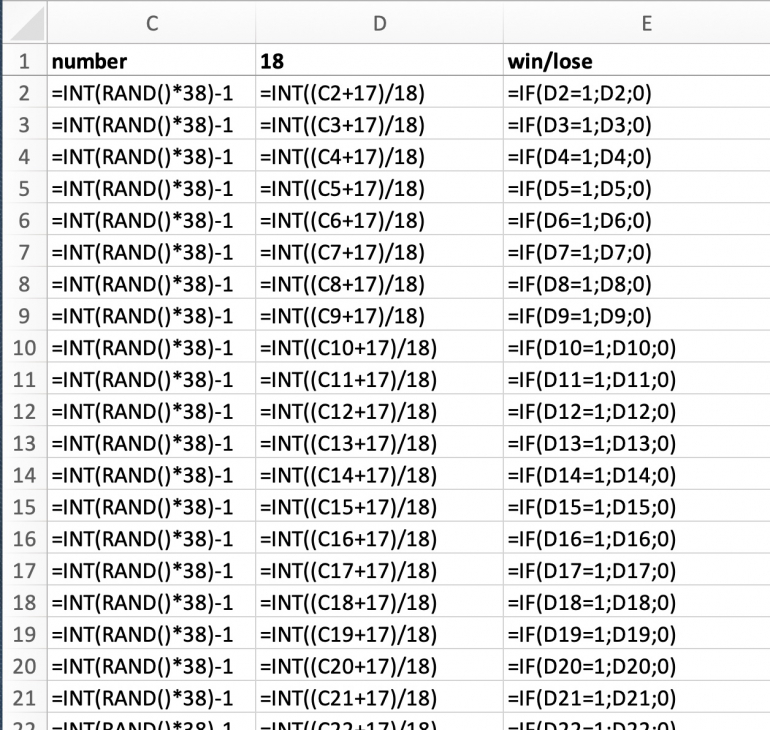
The Pivot table is used to verify the correctness of the frequency of the random numbers, as well as their assignment to the categories. Each number appears with a probablity of 1/38, random variation included, and is properly assigned to its half and to "win/lose".



In columns A and B the games and their individual rolls are numbered.
The games are either two or three rolls each. This is determined in column B "roll#" using the fact that the third roll is necesary, if rolls one and two yield the same result.

Column A "game#" counts the games simulated, incrementing on the first roll of each game.



THE CONTESTANTS
Columns F and G show the actions of betting and of waiting for the other party to finish their game.
Column F "Heather's action" is the Martingale procedure. She has to bet on the first roll unconditionally and will wait once she hit and won, or while she is waiting already. Otherwise she keeps betting.
Column G "Wizard's action" is the Paroli procedure. Again the first roll is mendatory. Once he loses or is already waiting, he will keep waiting. Otherwise he keeps on betting.



THE STACKS OF RETURNED CHIPS
Columns H and I represent the stacks where Angela Marie puts the chips returned from Heather and the Wizard.
As a monitoring and comparison reference, a third stack for pure roulette rolls is kept in column J. It accumulates the returned chips of the reference bets on "1-18". These bets, seven chips per bet, as with Heather and the Wizard, are made on roll 1 of each game, so that Heather, the Wizard and the simple single rolls play the exact same number of games.
Column H "Heather's returned chips" collects and adds 8 chips each time she bets and wins during a game. Otherwise she is waiting, adding 0 to her stack.
Column I "Wizard's returned chips" collects and adds 56 chips each time he is in his third roll and is qualified to bet and wins this third roll. Otherwise nothing is added, in particular while he is waiting.
Column J "simple single roll" collects and adds 14 chips on the first roll only when this roll is won.



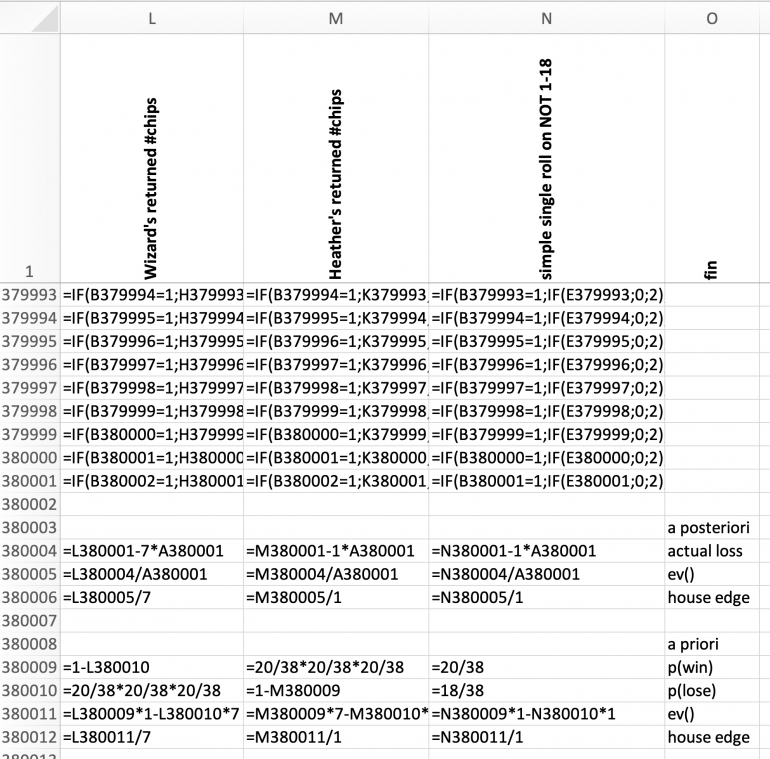
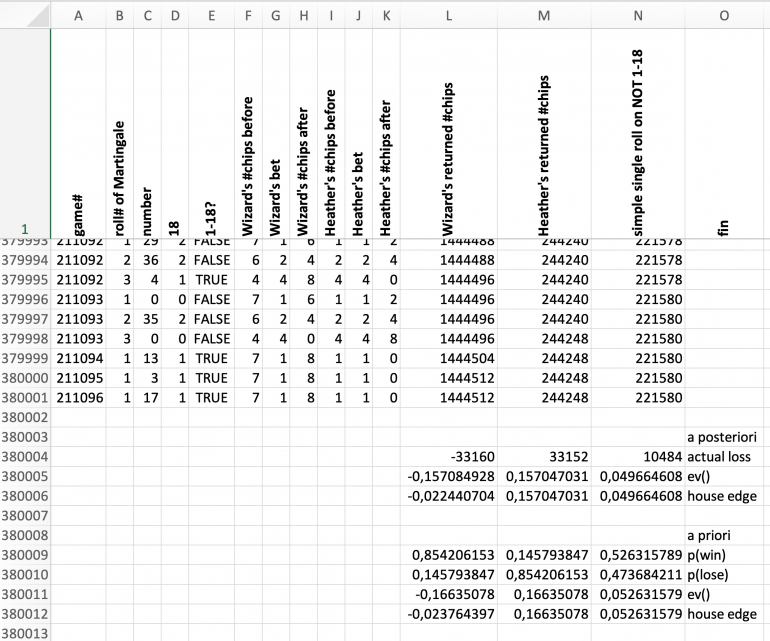
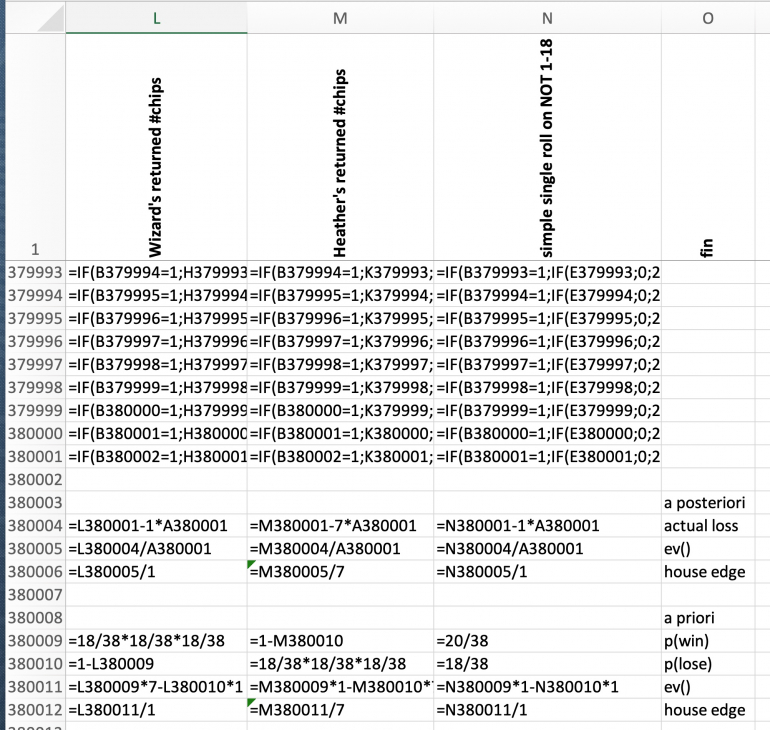
RESULT
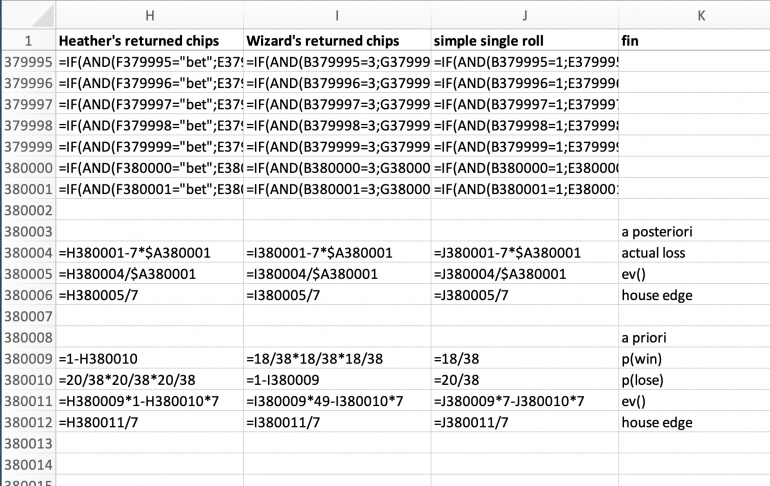
Row 380001 has the accumulated numbers of chips in columns H, I, and J. The differences between Heather's Martingale, the Wizard's Paroli are quite obvious. Even the pure rolls have their own sum.



To see the effect in detail, expected value and house edge (as experienced by Angela Marie) are calculated.
The loss produced in the Monte Carlo simulation is given in row 380004
Each player received seven chips per game. Multiplied by the number of games, given at the end of column A, results in the total chips wagered. This is the same for all players.
Subtracting this sum from the simulated number of returned chips results in the "actual loss".
Dividing the loss by the number of games produces the expected value, in row 380005.
Further dividing the expected value by the wager of seven chips results in the house edge as experienced by Angela Marie.

Rows 380009 through 380012 have the a priori calculation based on the known probabilities of a double zero roulette wheel.
The resulting figures of expected value and of the theoretical house edge are very close to the simulated results.



CONCLUSION
The experiment and the corresponding probability calculations suggest that ...

* A player playing a negative expectation game should definitely avoid using a betting strategy based on progression on winnings, like Paroli, because it increases the players disadvantage compared to the pure base game.

* A player playing a negative expectation game should favour a betting strategy based on progression on losses, like Martingale, even over the pure base game, because it reduces the player's disadvantage. Although, progression on losses, constructed properly, will converge towards zero expectation (i.e. the fair game) it will never reach it nor exceed zero and therefore will not turn the game into a winning, positive expectation advantage play.

FINAL REMARK
It can be shown that for a player facing a positive expectation game, the opposite advice is valid. Progression on losses decreases the player's advantage in direction of zero expectation (the fair game) while progression on winnings pushes the advantage further away from zero in positive direction.

The previous experiment showed that progression on losses and progression on winnings produce different effects in games of negative expected value. Two more experiments will show the effects of both types of progressions on games having an expected value greater than zero.

These two experiments might be performed at Heather's practice table. Heather would deal roulette according to the common rules. The only difference in the procedure would be that Heather would match the Wizard's wager before the roll, betting that the event won't happen.
(Remark: In general it should be good betting practice for both betting parties to put their wagers on the table. For obvious reasons casinos prefer to protect their bankroll and only expose the wagers, they actually lost to the players, after a roll.)
The convenient effect of Heather wagering in the experiments is that she now is a natural advantage player, playing at the houses positive edge.

Angela Marie again would be the financial controller, watching over the wagers, using separate stacks for the Wizard's and Heather's returned chips. She would also again calculate the house edges she experienced from both the Wizard's and Heather's play.

Progression on winnings in positive expectation games.

Angela Marie will hand seven chips to the Wizard and one chip to Heather and ask both to play a single game according to the rules below. She will ask both to come back with the chips they might have left over from this game, or nothing in case of a loss. The returned chips she will put on the corresponding stack of returned chips and start over giving seven chips to the Wizard and one chip to Heather. After a big enough number of games (the more, the better) she will calculate the house edges from the observed probabilities and amounts.

The Wizard will play a three step Martingale using the seven chips, just as Heather did in the previous experiment.
If the Wizard ...
... wins on the first roll, he gains Heather's one chip (game over).
... wins on the second roll, he gains two chips from Heather: her original chip and the one he lost to her on the first roll (game over).
... wins on the third roll, he gains four chips from Heather: her original chip, the one he lost in the first roll and the two he lost on the second roll (game over).
... loses on the third roll, the game is over.

Heather will, on every single roll, match the Wizard's wager, which has the effect that she will be forced to play a three step Paroli:
If Heather ...
... loses on the first roll, she loses her original one chip to the Wizard (game over).
... loses on the second roll, she loses two chips (game over).
... loses on the third roll, she loses four chips (game over).
... wins on the third roll, she will have wagered 1 chip, then 2 chips, then 4 chips, letting her winnings ride as defined by the Paroli system (game over).

Angela Marie will then calulate the house edges she experienced from the Wizard's and from Heather's games based on the double zero roulette practice wheel.





CONCLUSION
Regression on losses, like Martingale, applied in negative expectation games reduces the player's disadvantage by pushing the house edge towards zero (the fair game) although neither reaching nor exceeding zero.
Regression on winnings, like Paroli, applied in positive expectation games (advantage play) pushes the player's advantage further away from zero in positive direction, increasing the player's edge.



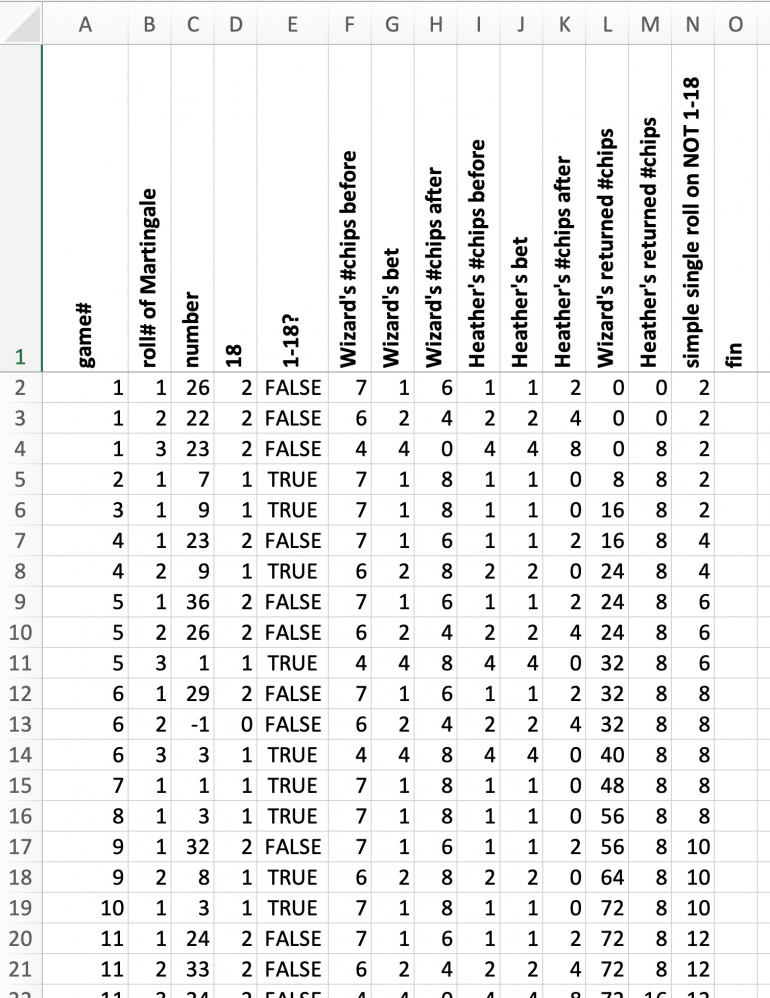
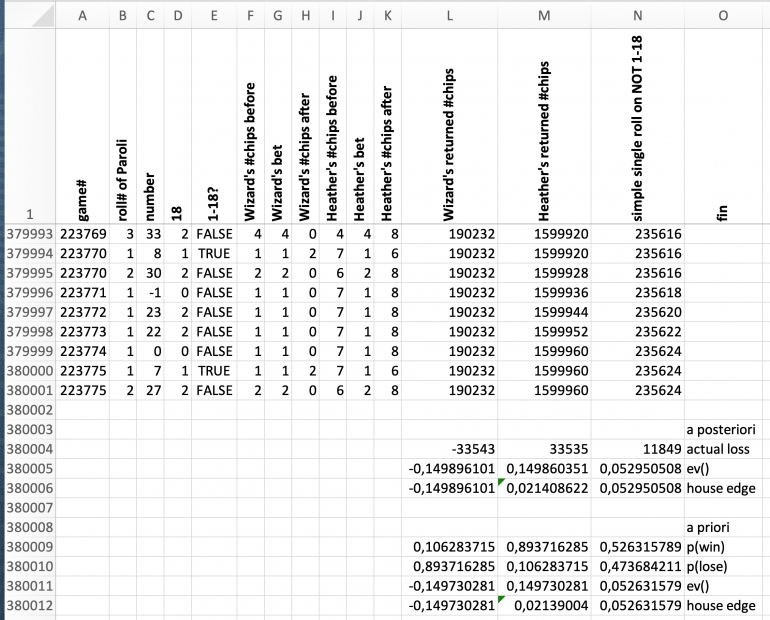
Columns A through E simulate the rolls of a double zero roulette wheel (column C), determine whether the lower half 1-18 was hit (column E) and calculate the roll within a Martingale sequence (column B) and count the number of Martingale games played (column A).



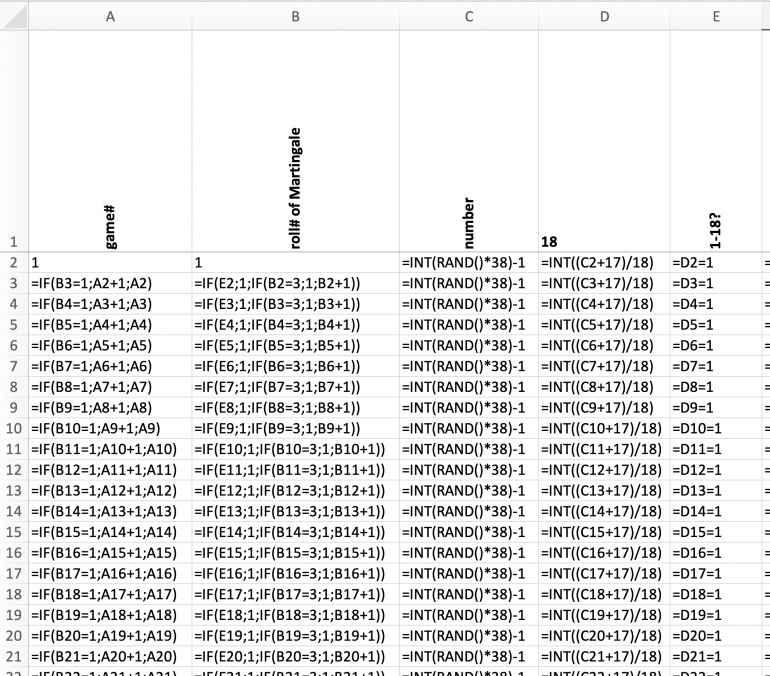
Columns F through K calculate the betting activity for the Wizard and for Heather based on the simulated rolls.



Columns L and M represent the two stacks accumulating the chips returned to Angela Marie by the Wizard and by Heather.
Column N represents the monitoring and comparison stack for single bets of one unit on NOT 1-18, i.e. based on the advantage play of Heather. These monitoring bets are made on each first roll of the Martingale sequence.



The simulation covers 380000 rolls. At the bottom of the list, expected value and house edge are calculate for the three games, the Wizard's Martingale, Heather's advantage Paroli, and the single advantage bet.
The theortical values based on the known probabilities of a double zero roulette wheel show that the experimental results match quite well.

Progression on losses in positive expectation games.

Angela Marie will hand one chip to the Wizard and seven chips to Heather and ask both to play a single game according to the rules below. She will ask both to come back with the chips they might have left over from this game, or nothing in case of a loss. The returned chips she will put on the corresponding stack of returned chips and start over giving one chip to the Wizard and seven chips to Heather. After a big enough number of games (the more, the better) she will calculate the house edges from the observed probabilities and amounts.


The Wizard will play a three step Paroli using the one chip, similar as he did in the previous experiment, only there with a seven chips unit.
If the Wizard ...
... loses on the first roll, he loses his original one chip (game over).
... loses on the second roll, he loses two chips, his original chip and the one he won from Heather on the first roll (game over).
... loses on the third roll, he loses four chips, his original chip, and those that Heather lost on the first (1 chip) and second (2 chips) roll. (game over).
... wins on the third roll, the game is over.


Heather will, on every single roll, match the Wizard's wager, which has the effect that she will be forced to play a three step Martingale:
If Heather ...
... wins on the first roll, she gains the Wizard's one chip (game over).
... wins on the second roll, she gains two chips from the Wizard: his original chip and the one she lost to him on the first roll (game over).
... wins on the third roll, she gains four chips from the Wizard: his original chip, the one she lost on the first roll and the two she lost on the second roll (game over).
... loses on the third roll, she will have lost 1 chip, 2 chips, and finally 4 chips of her original seven chips, as defined by the Martingale system (game over).

Angela Marie will then calulate the house edges she experienced from the Wizard's and from Heather's games based on the double zero roulette practice wheel.





CONCLUSION
Regression on winnings, like Paroli, applied in negative expectation games pushes the player's disadvantage further away from zero in negative direction, increasing the house's edge.
Regression on losses, like Martingale, applied in positive expectation games (advantage play) reduces the player's advantage by pushing the house edge towards zero (the fair game) although neither reaching zero nor passing into the negative, the house edge region.



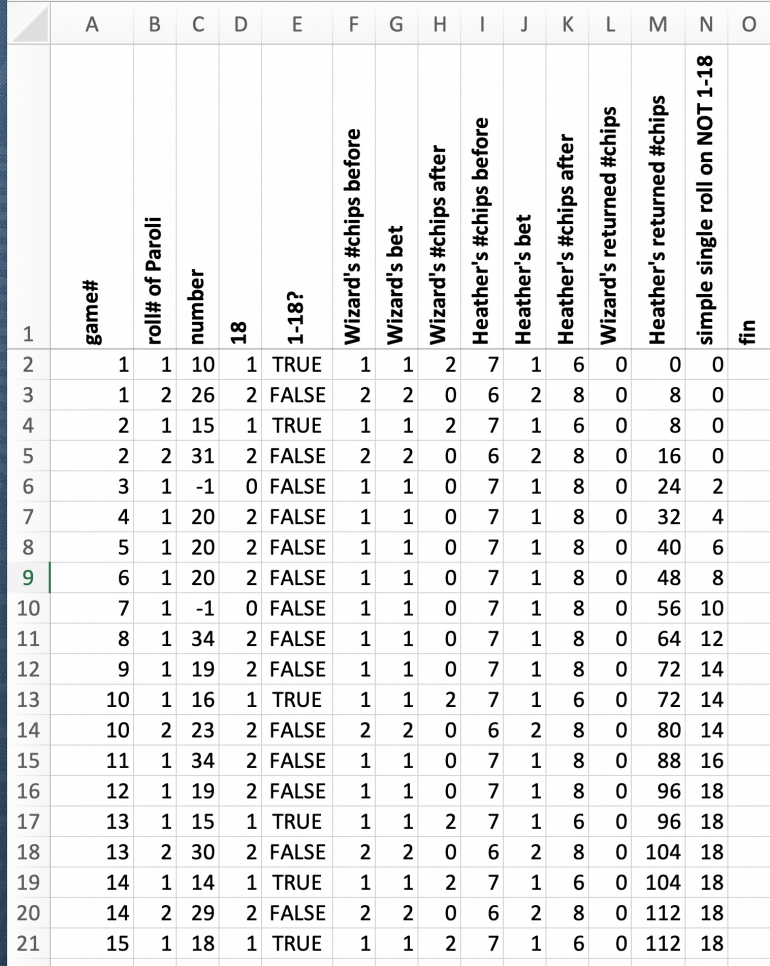
Columns A through E simulate the rolls of a double zero roulette wheel (column C), determine whether the lower half 1-18 was hit (column E) and calculate the roll within a Paroli sequence (column B) and count the number of Paroli games played (column A).



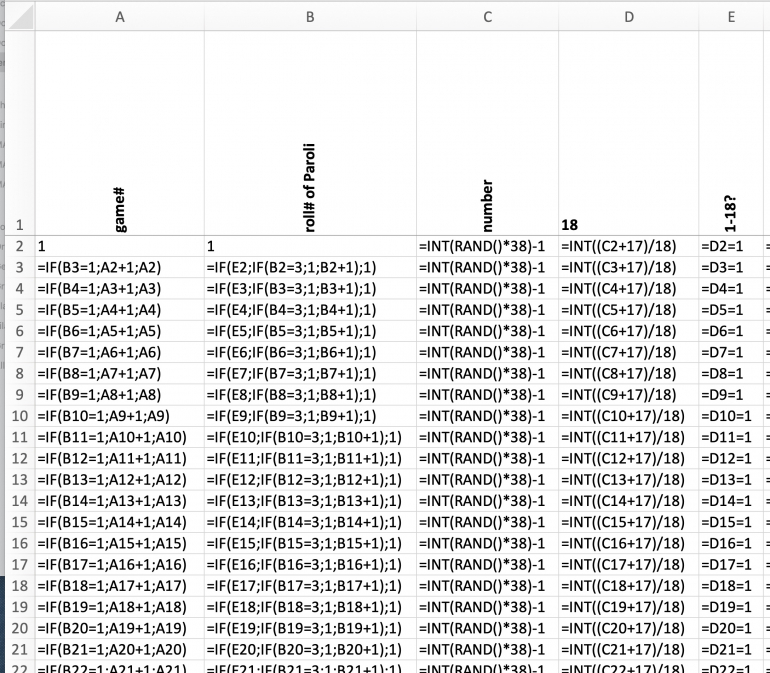
Columns F through K calculate the betting activity for the Wizard and for Heather based on the simulated rolls.



Columns L and M represent the two stacks accumulating the chips returned to Angela Marie by the Wizard and by Heather.
Column N represents the monitoring and comparison stack for single bets of one unit on NOT 1-18, i.e. based on the advantage play of Heather. These monitoring bets are made on each first roll of the Paroli sequence.



The simulation covers 380000 rolls. At the bottom of the list, expected value and house edge are calculate for the three games, the Wizard's Paroli, Heather's advantage Martingale, and the single advantage bet.
The theortical values based on the known probabilities of a double zero roulette wheel show that the experimental results match quite well.

To complement the before described experiments I set up a comparison of the progression on losses, here Martingale, and the progression on winnings, here Paroli. The base game is an even money bet. The generalized forms of the player advantage, which equals the negative of the house edge, are given in the following equations for a t-step Martingale M(t) and a t-step Paroli P(t).



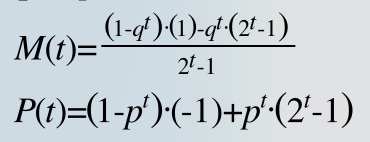
Both calculate the expected value of a progression of max. t steps devided by the wager needed for this progression. The division in P(t) is not explicitly visible because the wager is 1 for any P(t) and dividing by 1, the neutral element of division, does not alter the outcome of the term.

The following overview shows the full range of winning probabilities 0 through 1 on the x axis and the range of -1 through +1 for the player advantage on the y-axis. The vertical red lines indicate examples of the fair game, single zero roulette, and double zero roulette.



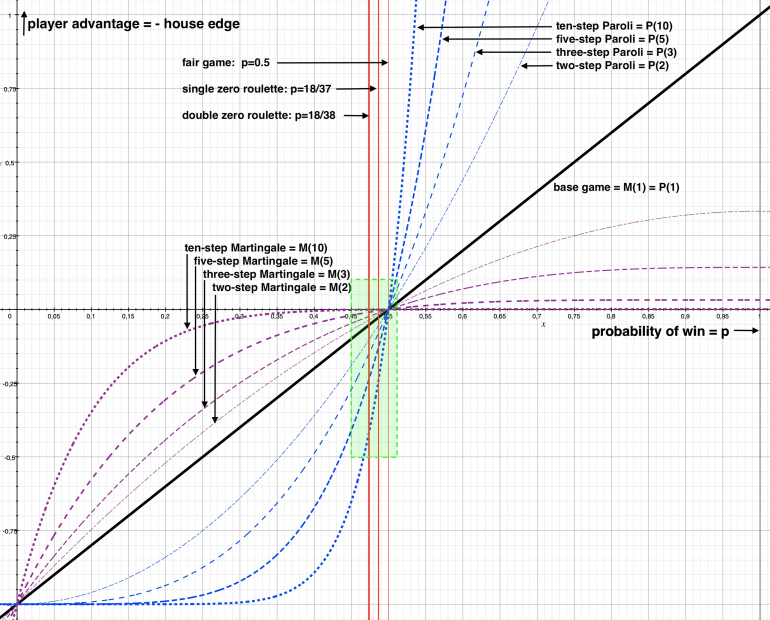
The diagonal has the player advantage for a single "roll" of the base game. It intersects with the red indicators as expected at 0 for the fair game, at -18/37 approx. -2.7% for the single zero roulette, and at -18/38 approx. -5.3% for the double zero roulette.
Please see a magnified view of the greenish section in the spoiler tag.



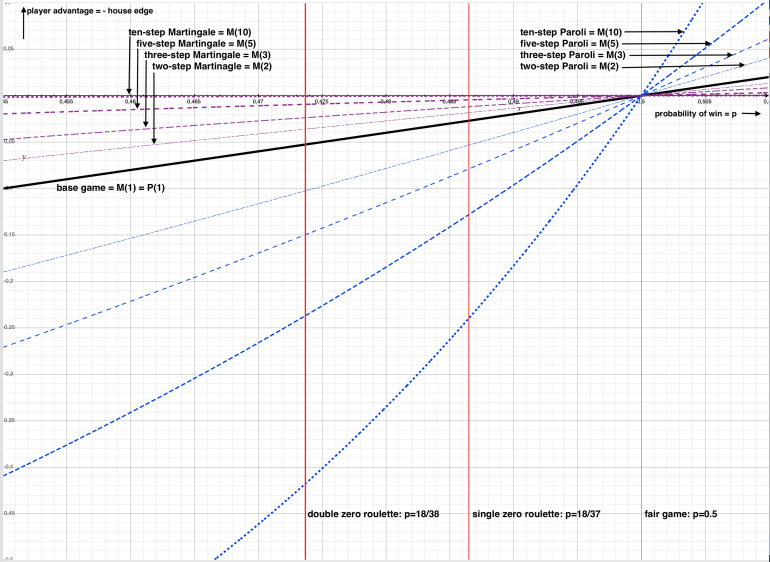
The diagram shows that for negative expectation games, i.e. p<0.5 for even money bets, progressions on winnings, here Paroli, should be avoided because they dramatically push the player's disadvantage further away from zero in negative direction. On the other hand, progressions on winnings, here Martingale, reduce the player's disadvantage by bringing it closer to zero while never exceeding zero. The system cannot turn the negative expectation into a winning game but it does reduce the player's disadvantage and therefore reduces the house edge experienced by the player.

Turning to positive expection games, i.e. p>0.5 for even money bets (= advantage play), the player's advantage is boosted dramatically by applying a progression on winnings, like Paroli. In contrary, a progression on losses (Martingale) is completely counter-productive and diminishes any advantage the player may have found.

Obviously, any system that causes a player to make larger bets more often will boost the returns of a positive expectation game. In theory, the best system would be to always bet the maximum provided the player has the bankroll to sustain an outlier string of losses.

The claim that martingale reduces a player's disadvantage intuitively lacks merit in your example. If a player is only going to double up twice before giving up, what's the point of doubling? Flat betting and never doubling would result in smaller average losses per bet.

In a negative expectation game, any doubled-up bet will more often than not result in a loss. And since martingale cannot be sustained through extended losing streaks, it eventually always ends in a loss from which the player cannot double up again. It's a 'lose in the end' system.

Yes, the more times a player is able to double up, the more winning sessions they will have - but at the cost of a larger terminating loss. I don't see how martingale eats into the house edge at all when the largest bet a player is willing/able to make is still more likely to result in a loss than a win, thus preserving the house's edge.

Do the calculations used to generate your graph bear out in realistic simulations of martingale betting? I've seen some martingale simulations from Wizard and Elliot Jacobson, and they claim the results show the house edge isn't even dented.

A betting progression that rises more gently could ensure with close to 100% certainty that a well-bankrolled player would always be able to keep raising until they won. A 'win in the end' system would more plausibly be able eat into the house edge.

I proposed this hypothetical scenario here:

Quote:

If two millionaires decided to bet on coin flips where there was exactly a 50% chance of winning each time, neither would gain any advantage by flat betting. But if one used a system where he would start with a $1 bet and increase his bet by $1 until he won a flip, he would be able to guarantee himself that his largest bet would always be a winning bet.

Even in the statistically implausible scenario where he lost 100 flips in a row, he could comfortably make his next linear progression bet of $101. He would always get a win eventually. His biggest bet would always be a win. And every time he won, he would start over at $1.

If you were to take the other side of all these bets, you would expect to lose 50% of them. But knowing that your biggest wager would result in a loss to him, wouldn't your overall EV be negative and the progressive bettor's EV be positive?

If you don't believe the system gives any advantage to the bettor, then you have to believe that a collection of bets varying randomly in amount with the winner of each unknown is analytically the same as a series of bets with one important piece of additional information -- namely, that the largest single bet will be a win for the bettor.

Can those who insist that all betting systems are worthless explain why they believe the winner of the biggest single bet in a series of 50/50 bets has no greater probability of coming out on top overall than the loser of that bet?

Nobody representing the official stance of this forum that all systems are worthless answered my specific question. But some chimed in with tangential critiques.

Quote: JackSpade

Obviously, any system that causes a player to make larger bets more often will boost the returns of a positive expectation game. In theory, the best system would be to always bet the maximum provided the player has the bankroll to sustain an outlier string of losses.

The claim that martingale reduces a player's disadvantage intuitively lacks merit in your example. If a player is only going to double up twice before giving up, what's the point of doubling? Flat betting and never doubling would result in smaller average losses per bet.

In a negative expectation game, any doubled-up bet will more often than not result in a loss. And since martingale cannot be sustained through extended losing streaks, it eventually always ends in a loss from which the player cannot double up again. It's a 'lose in the end' system.

Yes, the more times a player is able to double up, the more winning sessions they will have - but at the cost of a larger terminating loss. I don't see how martingale eats into the house edge at all when the largest bet a player is willing/able to make is still more likely to result in a loss than a win, thus preserving the house's edge.

Do the calculations used to generate your graph bear out in realistic simulations of martingale betting? I've seen some martingale simulations from Wizard and Elliot Jacobson, and they claim the results show the house edge isn't even dented.

A betting progression that rises more gently could ensure with close to 100% certainty that a well-bankrolled player would always be able to keep raising until they won. A 'win in the end' system would more plausibly be able eat into the house edge.

I proposed this hypothetical scenario here:

Quote:

If two millionaires decided to bet on coin flips where there was exactly a 50% chance of winning each time, neither would gain any advantage by flat betting. But if one used a system where he would start with a $1 bet and increase his bet by $1 until he won a flip, he would be able to guarantee himself that his largest bet would always be a winning bet.

Even in the statistically implausible scenario where he lost 100 flips in a row, he could comfortably make his next linear progression bet of $101. He would always get a win eventually. His biggest bet would always be a win. And every time he won, he would start over at $1.

If you were to take the other side of all these bets, you would expect to lose 50% of them. But knowing that your biggest wager would result in a loss to him, wouldn't your overall EV be negative and the progressive bettor's EV be positive?

If you don't believe the system gives any advantage to the bettor, then you have to believe that a collection of bets varying randomly in amount with the winner of each unknown is analytically the same as a series of bets with one important piece of additional information -- namely, that the largest single bet will be a win for the bettor.

Can those who insist that all betting systems are worthless explain why they believe the winner of the biggest single bet in a series of 50/50 bets has no greater probability of coming out on top overall than the loser of that bet?

Nobody representing the official stance of this forum that all systems are worthless answered my specific question. But some chimed in with tangential critiques.
link to original post

The scenario you gave makes no profit.

Do the math.

He raises his wagers $1 at a flip. He loses 100 flips but eventually wins on the 101st flip for $101.

You are making it seem like that gave him a $1 profit, correct? It doesn't

Do the progression.

First spin lose $1
2nd spin lose $2 (2+1=3 lost)
3rd spin loses $3 (1+2+3=6 lost)

Do the progression through to 100 straight losses at a $1 progressive raise.

1+2+3+4+5+6....+100 = $5050 lost

And then he finally wins back $101.

That makes any sense to you as a winning system?

I stated that it was statistically implausible to lose 100 in a row. In any set of 100 flips, he would expect to lose 50 on average. And in a typical set of 100 flips, the largest wager he makes would result in a win. That doesn't mean he would always show a net profit after 100 flips. It just means he might be expected show a profit slightly more often than his opponent would.

Quote: JackSpade

In a negative expectation game, any doubled-up bet will more often than not result in a loss.]

In a negative expectation game, every bet you make will more likely than not result in a net loss. No betting system will change that. Might change the variance, but zero effect on the house edge

Quote: Ace2

Quote: JackSpade

In a negative expectation game, any doubled-up bet will more often than not result in a loss.]

In a negative expectation game, every bet you make will more likely than not result in a net loss. No betting system will change that. Might change the variance, but zero effect on the house edge
link to original post

Thanks. If people just could wrap their brains around this fact, these forums would be a desert...and so would Las Vegas.

I am skeptical of claims that martingale reduces the house edge. But I was thinking, if it possibly could, how would it?

Then I conceptualized it this way: If you execute a martingale system where you can double your initial bet up to 7 times, then you are effectively freerolling all the lower-unit bets (1,2,4,8,16,32,64) until you reach your max bet (128). Those lower level bets aren't put at risk of irrecoverable loss on a betting outcome until you are forced to make the 128-unit bet. Then suddenly all those bets are exposed to a house edge which might dictate a 52% risk of loss.

But since there is only a 0.5% chance of incurring 8 losses in a row, 99.5% of the time your initial 1-unit bet will be spared from loss. It's your max bet that always bears the full brunt of the house edge.

So the question is, even when martingale results in a catastrophic loss 1 out of every 200 times, does it still reduce the percentage of the total amount wagered that goes to the house?

I'm not here claiming positively that it does. But I have been unsatisfied with the dogmatic dismissals from the anti-system crowd.

We all agree that martingale can't turn a negative expectation game into one with a a positive expectation for the player. We also agree that martingale won't reduce the average amount the player loses per wager vs. flat betting at the table minimum. Obviously, betting multiples larger entails the expectation of incurring larger scale losses.

The issue here is the house edge. The operators of this forum assert confidently that no betting system like martingale can even "dent" it. ThomasK introduces some mathematical models appearing to show the house edge being dented significantly. Instead of addressing the math, all I see from naysayers are bromides reasserting the forum's official position that systems have zero effect.

I suspect you’re trolling, but you only need a sixth-grade math level to see that every bet you make on a -EV game will give you that -EV in the long run no matter how you structure your bets. Very simple: (total amount wagered) * HE% = your expected loss.

Here’s a very basic calculation for your martingale “conceptualization” with a maximum of seven bets. If you were to apply this to a fair coin flip paying even money (no edge), then you have a 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 = 127/128 chance of winning one unit and a 1/128 chance of losing 1 + 2 + 4 + 8 + 16 + 32 + 64 = 127 units for an EV of exactly zero.

Martingale has no effect on the EV. You can run all the “mathematical models” you want trying to disprove $100 * 5% = $5 but you never will

Quote: JackSpade

So the question is, even when martingale results in a catastrophic loss 1 out of every 200 times, does it still reduce the percentage of the total amount wagered that goes to the house?

Nope. ALL of the value that is placed on the felt is subject to the self same house edge, whether it's placed as a single wager or as a series of wagers grouped together as a manufactured bet.

Quote:

I'm not here claiming positively that it does. But I have been unsatisfied with the dogmatic dismissals from the anti-system crowd. . .

That's your problem. You are hoping that the dogmatic anti system crowd are wrong on a simple mathematical truth. You can rejig equations and scenarios till the cows come home, but you will never change the house edge. When your convoluted system or thought process stumbles and makes an error that shows that you have succeeded, you can bring your proof here. But it's then a matter of getting your adversaries to show you the error in your working out. Frankly that's tiresome and some will say 'Pah! he's past helping or I'm past caring. Let the system player take his money to the casino and wish him luck'

Quote:

We all agree that martingale can't turn a negative expectation game into one with a a positive expectation for the player. We also agree that martingale won't reduce the average amount the player loses per wager vs. flat betting at the table minimum. Obviously, betting multiples larger entails the expectation of incurring larger scale losses.

Then why are we still bothering with this?

Quote:

The issue here is the house edge. The operators of this forum assert confidently that no betting system like martingale can even "dent" it. ThomasK introduces some mathematical models appearing to show the house edge being dented significantly.

ThomasK seems sincere, but his mathematical models do not ACTUALLY show the house edge being dented. Really. They don't.

Quote:

Instead of addressing the math, all I see from naysayers are bromides reasserting the forum's official position that systems have zero effect.
link to original post

Systems have ZERO affect on the house edge!


And I LOVE Martingale and a few progressives. I use them in my recreational gambling, all the time.

To anyone that is enamoured by pure martingale, put yourself in the position of 'the house '.

Mr Martingale comes with $127 in his bankroll. He's modelled this and no way he can go broke.
He wagers $1 on a coin toss bet.
The House thinks "The worst I'm going to lose on this series of bets is $1"
The House wins and the guy doubles down betting $2
The House thinks "If he wins, it'll be his own $3 back + my $1: Bring it on."
The House wins and the guy doubles down betting $4
The House thinks "If he wins, it'll be his own $7 back + my $1: Bring it on."
The House wins and the guy doubles down betting $8
The House thinks "If he wins, it'll be his own $15 back + my $1: Bring it on."
The House wins and the guy doubles down betting $16
The House thinks "If he wins, it'll be his own $31 back + my $1: Bring it on."
The House wins and the guy doubles down betting $32
The House thinks "If he wins, it'll be his own $63 back + my $1: Bring it on."
The House wins and the guy doubles down betting $63
The House thinks "If he wins, it'll be his own $127 back + my $1: Bring it on."

Mr Martingale wins: Picks up his $128 for $1 profit. YAYYY!
Mr Martingale thinks "If I repeat that sequence again 127 more times, each time, resetting on a win, I'll have doubled my original bankroll.
The House thinks. . .
"That was fun. Best fun I ever had for $1. If he repeats that again 127 more times I'll get a 50:50 chance that one of those times I'll take his $127 bankroll. True: He'll be left with what he's won off me so far, but that will always be less than $128 (because he only plays this sequence 128 times) Then, he's just the same guy walking up to the same table with a bankroll of less than $127. If my 50:50 chance doesn't work out for me, oh well, there will be other days."

And then the house thinks... "Hang on this isn't a coin toss: It's roulette. Every dollar on the felt was at purely HIS risk of Green zero: 1/37th of the time the entire money put on the felt was mine, for free. I wonder if this guy can bring some friends next time?"

Now, in reality, Mr Martingale's bankroll will creep up by $1 steps with every winning sequence. He might even double his original bankroll and keep going. Indeed on the coin toss bet, he has a 50% chance of doing so....

Now. Where's that casino that pays 1:1 on a coin toss bet?

Quote: JackSpade

Obviously, any system that causes a player to make larger bets more often will boost the returns of a positive expectation game. In theory, the best system would be to always bet the maximum provided the player has the bankroll to sustain an outlier string of losses.

The claim that martingale reduces a player's disadvantage intuitively lacks merit in your example. If a player is only going to double up twice before giving up, what's the point of doubling? Flat betting and never doubling would result in smaller average losses per bet.

In a negative expectation game, any doubled-up bet will more often than not result in a loss. And since martingale cannot be sustained through extended losing streaks, it eventually always ends in a loss from which the player cannot double up again. It's a 'lose in the end' system.

Yes, the more times a player is able to double up, the more winning sessions they will have - but at the cost of a larger terminating loss. I don't see how martingale eats into the house edge at all when the largest bet a player is willing/able to make is still more likely to result in a loss than a win, thus preserving the house's edge.

Do the calculations used to generate your graph bear out in realistic simulations of martingale betting? I've seen some martingale simulations from Wizard and Elliot Jacobson, and they claim the results show the house edge isn't even dented.

A betting progression that rises more gently could ensure with close to 100% certainty that a well-bankrolled player would always be able to keep raising until they won. A 'win in the end' system would more plausibly be able eat into the house edge.

I proposed this hypothetical scenario here:

Quote:

If two millionaires decided to bet on coin flips where there was exactly a 50% chance of winning each time, neither would gain any advantage by flat betting. But if one used a system where he would start with a $1 bet and increase his bet by $1 until he won a flip, he would be able to guarantee himself that his largest bet would always be a winning bet.

Even in the statistically implausible scenario where he lost 100 flips in a row, he could comfortably make his next linear progression bet of $101. He would always get a win eventually. His biggest bet would always be a win. And every time he won, he would start over at $1.

If you were to take the other side of all these bets, you would expect to lose 50% of them. But knowing that your biggest wager would result in a loss to him, wouldn't your overall EV be negative and the progressive bettor's EV be positive?

If you don't believe the system gives any advantage to the bettor, then you have to believe that a collection of bets varying randomly in amount with the winner of each unknown is analytically the same as a series of bets with one important piece of additional information -- namely, that the largest single bet will be a win for the bettor.

Can those who insist that all betting systems are worthless explain why they believe the winner of the biggest single bet in a series of 50/50 bets has no greater probability of coming out on top overall than the loser of that bet?

Nobody representing the official stance of this forum that all systems are worthless answered my specific question. But some chimed in with tangential critiques.
link to original post

Your posts are too long to read mostly, but I’ll take a shot at this one! I think the ‘stance of this forum’ is that all betting systems are worthless ‘IN OVERCOMING THE HOUSE EDGE’. Betting systems, to me, have worth in accomplishing a defined goal. Mine, in craps, as an example, exposes me to a very small house edge. (Pass line with odds and basically continual come bets). It gives me a realistic chance of doubling my buy in, of course less than a 50% chance. Plus to me it’s a fun way to play! If you set a goal of winning $XX, and start with a bankroll of $XXXX, martingale is a great system to likely accomplish your goal. And, in the event you find a +EV situation, like card counters or hole carders do, then the Kelly Criterion is actually a betting system that will best allow you to take advantage of that opportunity.

Quote: JackSpade

We all agree that martingale can't turn a negative expectation game into one with a a positive expectation for the player. We also agree that martingale won't reduce the average amount the player loses per wager vs. flat betting at the table minimum. Obviously, betting multiples larger entails the expectation of incurring larger scale losses.

The issue here is the house edge. The operators of this forum assert confidently that no betting system like martingale can even "dent" it. ThomasK introduces some mathematical models appearing to show the house edge being dented significantly. Instead of addressing the math, all I see from naysayers are bromides reasserting the forum's official position that systems have zero effect.
link to original post

The issue here appears to be, what is the definition of "House Edge"?

In terms of strictly money amounts, nothing changes it, much less "dents" it.

In terms of percentage of what a player is willing to bet, how you bet can affect that, but it also reduces the odds. For example, if you are willing to put up the $2550 on an 8-step Martingale with base bet $10 on an even-money bet in double-zero roulette, the expected return "on the $2550" is about 169/170 x (2550 + 10), or about $2545, which you can say is a House Edge of only 0.296% - but remember that, since you are always betting $2550 to win $10, every win pays only 1-255 odds.

Thank you for your posts JackSpade, darkoz, Ace2, UP84, OnceDear, SOOPOO, and ThatDonGuy.

May I invite you to have a look at Schroedinger's craps to discuss the following questions:

Is it wrong to claim that the slot machine defined there has a house edge of 0.24%?

If you had the choice, from a pure mathematical point of view, would you prefer to play this slot machine or play passline bets with full 3x4x5x odds at a real craps table?
Please explain your decision.

Knowing that the results of the slot machine are produced by passline bets with full 3x4x5x odds, what causes the slot machine and the craps table to have different house edges?

And related to ThatDonGuy's question:

Since the house edge is a percentage, not the actual amount that goes to the house, can the house and the player have two different percentages, i.e. house edges, in the "same(?)" game?
(Remark: I prefer to call the player's percentage "house edge" as well, because the player's money effectively goes to the house, nowhere else.)

After having discussed these questions I will show how progressive betting fits in.

My special thanks go to you, JackSpade, because I feel that you understand what I'm trying to explain.
[ ;-) Just because I can't seem to explain my ideas in an understandable way doesn't mean that they are wrong. ;-) ]

Martingale is a horrible system from a risk/reward standpoint. To me, it provides the opposite of entertainment value. Having to play it would be torture knowing I might have to make a gigantic bet for the opportunity to win 1 unit, that eventually I will bust out spectacularly, and that I will never achieve anything more spectacular than a collection of 1 unit wins.

I previously posted about negative linear progression betting (increasing bets by only 1 unit after any loss until a win is recorded). But I actually prefer combining it with positive progression for the opportunity to make spectacular gains on winning streaks.

The challenge with positive progression is ending it on a win. I will often stop after scoring 5 or 6 in a row, feeling satisfied. But if I win 4 in a row and lose on the 5th, I will raise again and keep raising until I get a win.

My mindset is always to win in the end. The largest bet I will ever make in a series, a session, a day, a trip, and a lifetime of gambling will be a win for me and a loss for the house.

Quote: JackSpade

Martingale is a horrible system from a risk/reward standpoint. To me, it provides the opposite of entertainment value. Having to play it would be torture knowing I might have to make a gigantic bet for the opportunity to win 1 unit, that eventually I will bust out spectacularly, and that I will never achieve anything more spectacular than a collection of 1 unit wins.

I previously posted about negative linear progression betting (increasing bets by only 1 unit after any loss until a win is recorded). But I actually prefer combining it with positive progression for the opportunity to make spectacular gains on winning streaks.

The challenge with positive progression is ending it on a win. I will often stop after scoring 5 or 6 in a row, feeling satisfied. But if I win 4 in a row and lose on the 5th, I will raise again and keep raising until I get a win.

My mindset is always to win in the end. The largest bet I will ever make in a series, a session, a day, a trip, and a lifetime of gambling will be a win for me and a loss for the house.
link to original post

Well, what I try to show is the exact opposite. Favour finite Martingale, and avoid Paroli at all cost. With finite Martingale I mean that you define how many doubling steps you would like to play at max before you stop. After either reaching that max or winning on any step before, start over again.

What you now can do is pack this finite Martingale into an "equivalent slot machine" and play at the table as if you were playing that slot machine. I'm not completely sure whether I was able to convey this idea in my earlier answers to you and to unJon.

The experiment in my initial post of this thread utilizes this idea and in addition compares Martingale to Paroli:

Angela Marie is the finance controller and only she cares about amounts spent from or received back to the bankroll.
She in fact is playing two "equivalent slot machines", requiring 7 coins in, each. Beyond this she does not care about any of the "internal subtleties" of what Heather and the Wizard are actually doing at the roulette table.

The rudimentary paytables of her slot machines, having only a single entry, are
8 for the Martingale Heather plays, with a probability of (1-(20/38)^3) approx. 85.42%
56 for the Paroli the Wizard plays, with a probability of (18/38)^3 approx. 10.63%

Double zero roulette is assumed here. The max steps for both progressions is defined as 3.

Angela Marie never cares about any units Heather might not have put on the roulette table, nor about any intermediate winnings the Wizard will have wagered trying to play his progression up to the final third step. Please note that the Wizard does not have to take any extra money from the bankroll Angela Marie is watching over. He only uses whatever he has available at any time during the Paroli procedure, starting with 7 units he received from Angela Marie, and eventually returning back to Angela Marie either with nothing, or handing to her 56 units if he happened to win all three steps.

In order to calculate the house edge of her "equivalent slot machines", Angela Marie only has available the amounts she wagered (7 units), the amounts returned to her (8 from Heather's Martingale and 56 from the Wizard's Paroli) and the corresponding probabilities which either have been disclosed to her or she has determined statisically from a very large sample of plays.

The house edges of both her equivalent slot machines are calculated based on the payout, a technique which avoids confusing the sign of the result (I'm sorry for some mess in my previous posts.)

Heather's Martingale
return = ((1-(20/38)^3) * 8) / 7 ... approx. 0.97624
house edge = 1 - return ... approx. 2.37%

the Wizard's Paroli
return = ((18/38)^3 * 56) / 7 ... approx. 0.85027
house edge = 1 - return ... approx. 14.97%



P.S.
I'd like to add here a big thank you to the Wizard. From his video on the analysis of Lobstermania I learned how to calculate the expected value based on payouts. Previous to this I only knew the method using winnings and losses and weighing these by the corresponding probabilities. Thanks Wizard.

Quote: JackSpade

The largest bet I will ever make in a series, a session, a day, a trip, and a lifetime of gambling will be a win for me and a loss for the house.
link to original post

Until you realize that statement is false, you will continue running in circles chasing your tail, looking for betting systems that can beat a -EV game

If you enjoy gambling, play low edge games (under 1/2 percent) and accept it as the cost of entertainment

Quote: Ace2

Quote: JackSpade

The largest bet I will ever make in a series, a session, a day, a trip, and a lifetime of gambling will be a win for me and a loss for the house.
link to original post

Until you realize that statement is false, you will continue running in circles chasing your tail, looking for betting systems that can beat a -EV game

If you enjoy gambling, play low edge games (under 1/2 percent) and accept it as the cost of entertainment
link to original post

That is correct with the only alternative being to find a true advantage that mathematically gives you an edge.

They exist but apparently not easily found.

Or like with a few current posters, fools gold (methods that don't really work but seem to in the short run)

Ace2 and darkoz are unable or unwilling to come to grips with the idea that I could find merit in progressive betting despite the fact that it doesn't give me a +EV edge. They seem to be operating within in a binary cognitive framework whereby a betting system either completely overcomes the house edge or it is completely worthless.

The truth is that I expect to generate positive returns only after I take everything about my gambling strategy into account - including game selection, betting style, comps, and various advantage play opportunities. My edge is small and I often experience negative variance. But I win in the end.

ThomasK, I think you are conflating payout with house edge. The house edge (2/38) is assumed within the steps you use to generate your return calculations.

Can you explain WHY a 3-step Martingale would affect the total return percentage versus flat betting 1 unit at a time even though the odds are exactly the same in every step of the Martingale progression?

I offered a potential explanation in an earlier post, but I am not confident it's valid. If every bet is conceived as having the potential to generate a net profit of 1 unit, and the probability of winning is the same on every bet, then Martingale imposes a progressively worse return (1 unit) on investment as bet sizes increase.

The only effect on expected returns that is obvious is that Martingale increases the average bet size and therefore the size of the average loss per bet compared to flat betting.

In contrast to a finite martingale (1,2,4), an extremely gentle progression (1.1, 1.2, 1.3...) could be defined as not terminating until a win is recorded. Although any losing streak is theoretically possible, if the probability of going bust is less than that of being struck by a meteorite while sitting at a casino table, then for all practical purposes that astronomically small risk of going bust doesn't matter to the gambler.

The final step of the gentle progression will only be triggered by a win. Looking back at all the individual bets placed during any given session, the largest one can be observed to have a 100% chance of being a win. All others will have a probability that is determined by the house edge. Based on this information, the player's total expected percentage loss could be calculated as being smaller than the house edge.

How does the gentle progression work?

You lose 1.1 then lose 1.2 then lose 1.3 and then win 1.4…for a net loss of 2.2.

Is your objective to always lose ?

Quote: Ace2

How does the gentle progression work?

You lose 1.1 then lose 1.2 then lose 1.3 and then win 1.4…for a net loss of 2.2.

Is your objective to always lose ?
link to original post

That is exactly what he described. He ran it to 100 losing wagers but then yelled it was just a ridiculous large number of losses unlikely to happen.

I agree but with his one unit per wager raise he already is a loser if he got three losses In a row.

Lose $5 total loss $5.
Lose $10 total loss $5+$10 = $15
Lose $15 total loss $5+$10+15 = $30
Win $20 total loss $5+$10+15 = $30 - $20 = $10 lost.
Start over progression from one unit of $5.

I mean it's a ridiculous system.

I welcome critiques that amount to more than pointless reiterations of the repeatedly acknowledged fact that no system can guarantee a net profit over the course of any given sequence of bets.

I especially welcome critiques that address the core claim I'm making, which is that expected value under a linear progression that terminates with a win is high (less negative) relative to the house edge.

Quote: JackSpade

I especially welcome critiques that address the core claim I'm making, which is that expected value under a linear progression that terminates with a win is high (less negative) relative to the house edge.
link to original post

Expected Value is something that exists and is meaningful BEFORE the outcome of a random event is resolved!
It's the sum of all possible values.
We could easily say that the expected value of a single fair coin toss is "1" (average of 2 and 0). But it would be absurd to say that the expected value of a coin toss would be higher than "1", "if the coin toss is about to be won."

That's what you are doing here: You are saying that because you WILL be ending on a win, the expected value is higher than if it waiting for the win would go on forever. This is the same nonsense that we get from folks that say if you always leave the table when you are a winner, you will obviously be a lifetime winner.
We Have to include in the EV calculation, EVERY possible set of outcomes, all the way to infinite losses. In MathSpeak, we integrate the function between limits 0 and infinity. And of course, equations go to hell in a handcart when infinity comes into play.

The further into the dim and distant future your win will be, the lower it's relative contribution in restoring your bankroll.
With your linear progression, we see how the relative contribution diminishes with each intervening loss.

Bet 1 : Lose 1 : Need to 'win' 1 to break even. If we'd won, we'd have profited by 1. Yayy
Bet 2 : Lose 2 : Need to 'win' 3 to break even. If we'd won, we'd have recovered all our losses plus 1. Yayy
So far it's same as Marty.

Bet 3 : Lose 3 : Need to 'win' 6 to break even. If we'd won, we'd have recovered all our losses plus 0. Ah!
Bet 4 : Lose 4 : Need to 'win' 10 to break even. If we'd won, we'd have recovered all our losses minus 2. Damn!

Wager 5 : Win 5 : Ended on a win. BUT we are still out of pocket by 5 units.

Playing this sort of linear progressive WILL tend to extend your play time compared to Marty, but only because your average bet is much lower.
I actually do this kind of progression in my regular recreational play. I progress 5,10,15,20,20,20,20. It makes for fun sessions. But that's all. It does nothing to my EV and it does nothing to dent the house edge.

Bet selection is everything, without the correct selection you have nothing. If you have the correct bet selection every progression will work but then you won't need it. How's that for irony.

Quote: EvenBob

Bet selection is everything, without the correct selection you have nothing. If you have the correct bet selection every progression will work but then you won't need it. How's that for irony.
link to original post

There is literally no irony there.

Just two people with different losing systems discussing why theirs is better.

They can't even agree on what to call it. One calls it a system while the other calls it a method.

Now that is ironic!

I think, if your bankroll can afford it, there is absolutely nothing wrong with a one- or maybe two-step Martingale or Paroli. I personally don't play that way, but I can definitely see how it can add some spice to your gambling.

Quote: Ace2

Quote: JackSpade

The largest bet I will ever make in a series, a session, a day, a trip, and a lifetime of gambling will be a win for me and a loss for the house.
link to original post

Until you realize that statement is false, you will continue running in circles chasing your tail, looking for betting systems that can beat a -EV game

If you enjoy gambling, play low edge games (under 1/2 percent) and accept it as the cost of entertainment
link to original post

Ace2,

Playing low edge games is what I aiming at.
If one of two games has a lower house edge than the other, I would choose the lower one.

Back to my initial questions in the above post:
If I had the choice of playing either a slot machine with 0.24% house edge or wagering on passline bets with full 3x4x5x odds at a craps table, would it be wrong to choose the slot machine?
If I'm not mistaken, the passline with full odds would have a house edge of 0.37%.
(Or maybe it wouldn't because the free odds bets do not have any edge at all?)

Quote: darkoz

Quote: Ace2

Quote: JackSpade

The largest bet I will ever make in a series, a session, a day, a trip, and a lifetime of gambling will be a win for me and a loss for the house.
link to original post

Until you realize that statement is false, you will continue running in circles chasing your tail, looking for betting systems that can beat a -EV game

If you enjoy gambling, play low edge games (under 1/2 percent) and accept it as the cost of entertainment
link to original post

That is correct with the only alternative being to find a true advantage that mathematically gives you an edge.

They exist but apparently not easily found.

Or like with a few current posters, fools gold (methods that don't really work but seem to in the short run)
link to original post

darkoz,

I'm not claiming to turn a -EV game into a +EV advantage play. I've explicitly stated that several times before and from the graph in my analysis it should be clear that everything left of the fair game stays on the negative edge and never reaches beyond zero.

What I intend to show, however, is that progressive betting does bend the edge, as experienced by the player, and therefore grinds down her bankroll faster or slower, depending on the type of progression and its parameter, i.e. the number of maximum steps.

OnceDear, if a casino were offering a loss rebate or some other promo on a game that replicated a win, then that would change the player's EV for playing the game. EV doesn't just apply to the outcome of a 'random event' - obviously, advantage players use various techniques to increase their EV on games that have a house edge.

I agree that assuming a win on an infinite progression of bets each carrying a high probability of loss presents some math issues. But let's look at it from the other side. A player betting 2 columns (24 numbers) on roulette is a statistical favorite to win on each random spin of the wheel. Regardless of how many zeros there are or what the house edge is, the casino is theoretically exposing itself to infinite losses. There is no point at which it becomes more likely for the casino to win and the player to lose the next spin.

Yet the casino knows that over time it will beat the player. Real-world math (law of large numbers) dictates that the casino won't experience an endless string of losses even though it could theoretically.

Quote: JackSpade

Ace2 and darkoz are unable or unwilling to come to grips with the idea that I could find merit in progressive betting despite the fact that it doesn't give me a +EV edge. They seem to be operating within in a binary cognitive framework whereby a betting system either completely overcomes the house edge or it is completely worthless.

The truth is that I expect to generate positive returns only after I take everything about my gambling strategy into account - including game selection, betting style, comps, and various advantage play opportunities. My edge is small and I often experience negative variance. But I win in the end.
link to original post

JackSpade,

Thank you for confirming, that our discussion is not about overcoming the negative edge.

The goal actually is to find games which are less disadvantageous to the player. Applying the concept of "equivalent slot machines" enables the player to create such games by utilizing the physical games that are available at the casino for simulating these slot machines.

Adding comps, in order to actually turn a -EV into a +EV doesn't seem implausible at first glance. But only the exact math will show under which conditions it will work. The wager put on the table is less than the player's coin in, which still might keep the total in the negative.

If trying to boost a true advantage play found in the casino, using progression on winnings (Paroli) you should be very sure that it actually is an advantage play. As you can see in the graph, your disadvantage drastically drops away, should your play have negative expectation. This would eat up all the painstakingly collected bits of edge improvement.

Quote: JackSpade

ThomasK, I think you are conflating payout with house edge. The house edge (2/38) is assumed within the steps you use to generate your return calculations.

JackSpade,

Calculating the house edge via the expected value or via the expected payouts is equivalent.
I will show it for the three step Martingale:

q = (20/38)^3 ... the probability of losing all three steps

Based on winnings and losses:

(1-q) ... the probability of winning 1 unit

1 ... amount won to player's wager
-7 ... amount lost after having lost all three steps

(1-q)*1 - q*7 ... expected value

( ( (1-q)*1 - q*7 ) / 7 ) ... player advantage
-( ( (1-q)*1 - q*7 ) / 7 ) ... house edge

Based on payout(s):

(1-q) ... probability of winning (1 unit)

8 ... amount payed ( 1 unit won + 7 units coin in)

(1-q)*8 ... expected payout

( (1-q)*8 ) / 7 ... return

1 - ( ( (1-q)*8 ) / 7 ) ... house edge

Equivalent transformation are performed on both sides in parallel.

based on winnings and losses | based on payouts
-( ( (1-q)*1 - q*7 ) / 7 ) == 1 - ( ( (1-q)*8 ) / 7 )

multiply both sides by 7:
-( ( (1-q)*1 - q*7 ) ) == 7 - ( (1-q)*8 )

further transformation steps:
-( 1 - q - q*7 ) == 7 - 8 + q*8
-1 + q + q*7 == 7 - (1+7) + q*(1+7)
-1 + q + q*7 == 7 - 1 - 7 + q*1 + q*7
-1 + q + q*7 == -1 + q + q*7
both sides are identical - q.e.d.

Quote:

Can you explain WHY a 3-step Martingale would affect the total return percentage versus flat betting 1 unit at a time even though the odds are exactly the same in every step of the Martingale progression?

I offered a potential explanation in an earlier post, but I am not confident it's valid. If every bet is conceived as having the potential to generate a net profit of 1 unit, and the probability of winning is the same on every bet, then Martingale imposes a progressively worse return (1 unit) on investment as bet sizes increase.

The only effect on expected returns that is obvious is that Martingale increases the average bet size and therefore the size of the average loss per bet compared to flat betting.

In contrast to a finite martingale (1,2,4), an extremely gentle progression (1.1, 1.2, 1.3...) could be defined as not terminating until a win is recorded. Although any losing streak is theoretically possible, if the probability of going bust is less than that of being struck by a meteorite while sitting at a casino table, then for all practical purposes that astronomically small risk of going bust doesn't matter to the gambler.

The final step of the gentle progression will only be triggered by a win. Looking back at all the individual bets placed during any given session, the largest one can be observed to have a 100% chance of being a win. All others will have a probability that is determined by the house edge. Based on this information, the player's total expected percentage loss could be calculated as being smaller than the house edge.
link to original post

The point with "equivalent slot machines" is that we do not compare single rolls of the Martingale to single rolls at the table but that we compare the Martingale as a whole to a single bet at the table. We ignore the fact that inside the Martingale we utilize single rolls to produce the overall outcome of the Martingale. This is the slot machine effect: Coin in, random mechanism at work, payout. And only coin in, and payout with its corresponding probabilities, define the machine's properties of expected value, return, house edge.

I'm not able to give an intuitive explanation for this because a lot is counterintuitive.
But, as I recall from some math textbook long time ago, the autor explained that when it comes to probability and statistics intuition is a bad advisor. He recommends: "Don't speculate. Caculate." This seems to be very true for this topic here.

Only calculating the house edge of the equivalent slot machine can tell whether it is better or worse for the player than some other gamble.

ThomasK, Your calculations seem to presume that the player will always complete all three steps and that he will always either win 1 unit or lose 7. But if he is following the Martingale system, he doesn't always complete all three steps.

He has a (18/38) chance of winning 1 unit on the first bet and then restarting at 1 unit. If he instead doubles after an initial win, then he has a (20/38) chance of losing and being down 1 unit. If he loses and doubles again, he has a (20/38) chance of being down 5 units. In that scenario, Martingale would would have produced a 1 unit win, but automatic three-step doubling may produce a 5 unit loss.

If he bets randomly with a value of either 1, 2, or 4 on each bet, would his EV be (18/38) as determined by the house edge? Imagine the following bet sizes: 2,1,1,4,2,1,2,2,1,4,4,1,1,1,4,2,1,2,4.

Notice at the end, he randomly produces a three-step Martingale pattern (1,2,4), Does that mean his EV for the entire session is higher than what the house edge would predict?

The idea that you could just pick out any (1,2,4) pattern and assign a different EV to it than all the other three-bet combinations seems intuitively absurd, you would surely agree. Perhaps it seems absurd for good reason and points to a miscalculation on your part.

Quote: darkoz

Quote: EvenBob

Bet selection is everything, without the correct selection you have nothing. If you have the correct bet selection every progression will work but then you won't need it. How's that for irony.
link to original post

There is literally no irony there.

Just two people with different losing systems discussing why theirs is better.

They can't even agree on what to call it. One calls it a system while the other calls it a method.

Now that is ironic!
link to original post

If you do not see the clear irony in what I said then you need to look irony up in the dictionary because it doesn't mean what you think it means.

Quote: OnceDear

Quote: JackSpade

I especially welcome critiques that address the core claim I'm making, which is that expected value under a linear progression that terminates with a win is high (less negative) relative to the house edge.
link to original post

Expected Value is something that exists and is meaningful BEFORE the outcome of a random event is resolved!
It's the sum of all possible values.

[...]

link to original post

OnceDear,

Thank you for bringing up this topic. The concept of BEFORE (a priori) and AFTER (a posteriori) the outcome of a random event might help to sort things out in this discussion.

I would like to show the effects of BEFORE and AFTER for the expected wager,because this is the component that causes all that trouble. As remarked by unJon (in another, yet related thread), messing with this denominator causes the house edge to bounce.

Please see the table below for a comparison of different gaming situations.

The a posteriori ("after") house edges are the well-known and well-establihed values, being heavily defended against the approach discussed here.

The a priori ("before") values of units wagered are the key element of the concept of "equivalent slot machines" as proposed here. This concept is applied in the experiments of this thread and in the thread on Schroedinger's craps.

The a priori wager is defined along the rules of the game by that random outcome which has the highest amount to be lost:

In the case of a single roll in roulette there are only two outcomes, one of which is the losing outcome. The player has to have available this 1 unit, as given in the equation of the expected value, in order to be able to play that game.

In the case of the passline bet there are several possible outcomes. The maximum loss is caused by sevening out on a point of six or eight. Since the outcomes are random and cannot be foretold, the player has to have available this maximum of 6 units in order to be able to play it.

The three step Paroli has two outcomes, a winning and a losing outcome. As defined in the equation of its expected value, 1 unit is the amount lost.

The three step Martingale has two outomes, one winning and one losing. The equation of the expected value has 7 units to be lost.

type of wager	BEFORE (a priori)	AFTER (a postriori)
a single bet on red on a double zero roulette table	wager: 1 unit	wager: 1 unit
expected value = 18/38*1 + 20/38*(-1)	expected wager = 1*38/38	expected wager = 1*38/38
	house edge approx. 5.26%	house edge approx. 5.26%
one "hand" of passline with full odds at a 3x4x5x odds craps table	wager: 6 units	wagers: p(1 unit) = (4+8)/36 … craps or 7, 11 p(4 units) = 2*3/36 … point is 4 or 10 p(5 units) = 2*4/36 … point is 5 or 9 p(6 units) = 2*5/36 … point is 6 or 8
expected value = 4/36*(-1) + 8/36*1 + 2*3/36*(3/9*(1+6) + 6/9*(-1-3)) + 2*4/36*(4/10*(1+6) + 6/10*(-1-4)) + 2*5/36*(5/11*(1+6) + 6/11*(-1-5))	expected wager = 6*36/36	expected wager = 1*(4+8)/36 + 4*2*3/36 + 5*2*4/36 + 6*2*5/36
	house edge approx. 0.24%	house edge approx. 0.37%
one "attempt" of a three step Paroli on red on a double zero roulette table	wager: 1 unit	wagers: p(1 unit) = 20/38 … lost on first roll p(3 units) = 18/38*20/38 … lost on second roll p(7 units) = (18/38)^2 … third roll reached
expected value = (18/38)^3*7 +(1-(18/38)^3)*(-1)	expected wager = 1*38/38	expected wager = 1*20/38 + 3*18/38*20/38 + 7*(18/38)^2
	house edge approx. 14.97%	house edge approx. 5.26%
one "attempt" of a three step Martingale on red on a double zero roulette table	wager: 7 units	wagers: p(1 unit) = 18/38 … won on first roll p(3 units) = 20/38*18/38 … won on second roll p(7 units) = (20/38)^2 … third roll reached
expected value = (1-(20/38)^3)*1 + (20/38)^3*(-7)	expected wager = 7*38/38	expected wager = 1*18/38 + 3*20/38*18/38 + 7*(20/38)^2
	house edge approx. 2.38%	house edge approx. 5.26%

The three step Paroli has 8 possible outcomes:


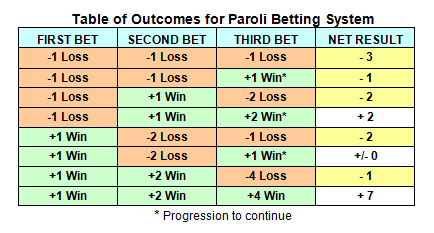
https://www.casinoreviewsquad.com/betting-systems/the-paroli-betting-system/

This is so when considering the range of possibilities for the subsequent 2 bets following an initial 1-unit wager the player makes using Paroli. The player will often restart at 1 unit.

Attempting to calculate the return to player based on the number of Paroli 'attempts' that are expected to produce either a win or a loss will get you an absurd result.

What matters for purposes of determining the player's expected return is the number of bets and the amount wagered per bet. At no point does any individual wager or set of three wagers made on a game carrying a house edge of 5.26% generate an expected loss of 14.97% to the player. You could easily confirm this yourself by downloading a free roulette app, making paroli bets, and tracking your returns which you will find over time average much closer to -5% than -15%.

Quote: EvenBob

Quote: darkoz

Quote: EvenBob

Bet selection is everything, without the correct selection you have nothing. If you have the correct bet selection every progression will work but then you won't need it. How's that for irony.
link to original post

There is literally no irony there.

Just two people with different losing systems discussing why theirs is better.

They can't even agree on what to call it. One calls it a system while the other calls it a method.

Now that is ironic!
link to original post

If you do not see the clear irony in what I said then you need to look irony up in the dictionary because it doesn't mean what you think it means.
link to original post

Now that is ironic.

EB who doesn't understand irony says other people don't understand irony.

Quote: JackSpade

ThomasK, Your calculations seem to presume that the player will always complete all three steps and that he will always either win 1 unit or lose 7. But if he is following the Martingale system, he doesn't always complete all three steps.

JackSpade,

You are absolutely right, the three step Martingale does complete in either 1, 2, or 3 steps. The calculation takes this into account. I've prepared a diagram to explain the equation.



As you can see there are three possible outcomes for winning 1 unit. The remaining outcome is the one that is losing all your seven units you need to have available if you want to play this game.
The 7 units will be lost in (20/38)^3 times of all attempts. An attempt is starting on the left and working through it until you end up in one of the blue boxes. Then start over again for a new attempt.
All other outcomes will pay 1 unit. Since there are no other outcomes, besides the losing outcome, 1 unit is won in 1-(20/38)^3 times of all attempts.

Quote:

[...]

If he bets randomly with a value of either 1, 2, or 4 on each bet, would his EV be (18/38) as determined by the house edge? Imagine the following bet sizes: 2,1,1,4,2,1,2,2,1,4,4,1,1,1,4,2,1,2,4.

Notice at the end, he randomly produces a three-step Martingale pattern (1,2,4), Does that mean his EV for the entire session is higher than what the house edge would predict?

It actually is possible to "shuffle" the individual steps of the Martingale, because the rolls of the steps are independent.

From your example sequence

2,1,1,4,2,1,2,2,1,4,4,1,1,1,4,2,1,2,4

having

1 unit 8 times
2 units 6 times
4 units 5 times

the following can be deduced:

It is a valid sample of three step Martingales, because #1s > #2s >#4s.

You played 8 three step Martingales.

6 times you lost the first step, but continued in the same Martingale.
5 times you lost the second step, but continued in the same Martingale.

8-6=2 times you won 1 unit on the first step and started over a new Martingale.
6-5=1 time you won 1 unit on the second step and started over a new Martingale.
5 times you wagered the third step. Whether you won or lost is not known but you started a new Martingale subsequently.

The EV for your sample cannot be calculated because the outcome of the 5 third steps is not known.

This is a very small sample. So you might happen to see these frequencies.
In the long run, of course, the number of 2 units should be around half the number of 1 units, and the number of 4 units should again be roughly half the number of 2 units or close to a fourth of the number of one units.


What can be said is that your a priori wager (please see this post) for this session is 8*7=56 units.
The house edge for the Martingale is 2.38% which means that in infinitely many sessions of 8 Martingales on average it would cost you 1.33 units of the 56 units wagered.

For the a posteriori calculation only the units put on the table are considered.
In your sample 1*8 + 2*6 + 4*5 = 40. Since we don't know how much you won on the third step, no further calculation is possible.
The expected wager, however, of 8 Martingales is about 8*3.16, basically 25 units.
The house edge is 5.26% which results in a loss of 1.33 units as above but this time out of 25 units.
So you'll take home 23.66 units (while in the a priori case you still hold 54.66 units).
Another problem with the 25 units is that you could only play 3 losing Martingales in a row and then wouldn't be able to continue.

Quote:

The idea that you could just pick out any (1,2,4) pattern and assign a different EV to it than all the other three-bet combinations seems intuitively absurd, you would surely agree. Perhaps it seems absurd for good reason and points to a miscalculation on your part.
link to original post

It is not as absurd as it seems, as I showed above. Make sure to combine the 1s, 2s, and 4s with the 1, 1/2, and 1/4 frequencies. Calculate the number of Martingales, multiply it by 7 units and define this as your bankroll. This will have a house edge of 2.38%.
If units remain unassigned to Martingales you can simply continue in your next session. Determine what is missing to complete Martingales and play exactly that number next time.

For your example this might be as follows:

4 units 5 times -> implies 2 units 10 times, 1 unit 20 times
2 units 6 times -> next time play 2 units 10-6 = 4 times
1 unit 8 times -> next time play 1 unit 20-8 = 12 times

Quote: JackSpade

The three step Paroli has 8 possible outcomes:


https://www.casinoreviewsquad.com/betting-systems/the-paroli-betting-system/

This is so when considering the range of possibilities for the subsequent 2 bets following an initial 1-unit wager the player makes using Paroli. The player will often restart at 1 unit.

Attempting to calculate the return to player based on the number of Paroli 'attempts' that are expected to produce either a win or a loss will get you an absurd result.

What matters for purposes of determining the player's expected return is the number of bets and the amount wagered per bet. At no point does any individual wager or set of three wagers made on a game carrying a house edge of 5.26% generate an expected loss of 14.97% to the player. You could easily confirm this yourself by downloading a free roulette app, making paroli bets, and tracking your returns which you will find over time average much closer to -5% than -15%.
link to original post

JackSpade,

I've tried to understand what they are doing. It appears to me they play three attempts of three step Paroli and the try to calculate something out of that ...

My understanding of the three step Paroli is analogous to the three step Martingale.
Here the diagram for Paroli:



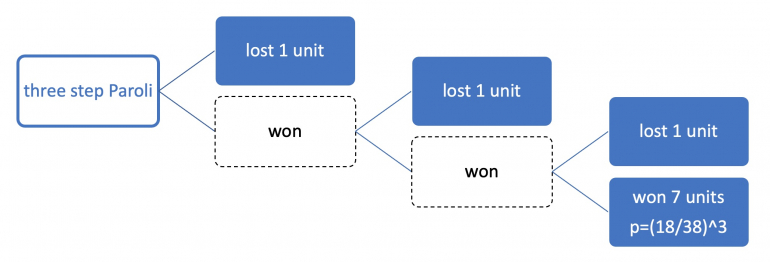
I will explain my experiment for Paroli again. I will name you in that example, I hope you won't feel offended.

Let's visit a casino.
You will carry the bankroll and will carefully watch over it. You may sit anywhere in a lounge or whatever is your favourite place for relaxing in a casino.

Now you hand me one red chip.

I will go over to the roulette table and play the three step martingale.

I will wager the $5 on red for a first roll.
If I lose, I will return to you with nothing.
If I win, I will now have two red chips and will wager both on red again.

If I lose the second roll, I will return to you with nothing.
If I win, I will now have four reds and I will wager them again on red for a last third roll.

After this third roll I will return to you.
If I lost the third roll, I will have nothing for you.
If I won the third roll, I will hand you 8 reds for your bankroll.

You then will hand me another red chip and I will go for another attempt.

To summarize:
If I return with nothing, you will have lost 1 unit from your bankroll.
If I return 8 units, you will have increased your bankroll by 7 units, i.e. $35.

Over the long run you will be able to add 7 units (18/38)^3 of times you sent me off.
In all other cases, 1-(18/38)^3, you will have lost 1 unit.
The expected value therefore is
(1-(18/38)^3)*(-1)+(18/38)^3*7 approx. -0.14973

Now the big question: What was the average amount in units you (forget about what I did) wagered per Paroli?
Divide the expected value by that number of units.
Is it wrong to state that the result is -14.97% for your advantage, also expressed as 14.97% house edge?