Quote: BukWildSuperFlyDoes it matter in UTH if the players can see each others cards? I haven't seen any studies on what, if any, advantage could be generated if people were to be able to see all the cards out with 7 people at a table sharing information. I assume someone has done a study, but I haven't come across it.
Check for "collusion UTH" as keywords on apheat..net. I think teliot has had something to say about this. Seems like there is an advantage with a full table, but not enough to overcome the HE, especially since they deal a fresh deck. I could be wrong.
Here it is.Quote: beachbumbabsCheck for "collusion UTH" as keywords on apheat..net. I think teliot has had something to say about this. Seems like there is an advantage with a full table, but not enough to overcome the HE, especially since they deal a fresh deck. I could be wrong.
A full (six-player) table gets a computer-perfect edge of about 2.5%.
Quote: teliotHere it is.
A full (six-player) table gets a computer-perfect edge of about 2.5%.
Thanks for posting the link (and doing the work)!
Quote: teliotHere it is:
A full (six-player) table gets a computer-perfect edge of about 2.5%.
Stephen How wrote said full table collusion wasn't even enough to overcome the house edge. So someone unfortunately goofed. Or longer sims are needed to get a clearer answer. :(
http://discountgambling.net/2010/06/14/collusion-performance-for-ultimate-texas-holdem/
There is no discrepancy between Stephen's results and my results. My results are for computer-perfect play. Stephen's are for a particular sub-optimal human-feasible strategy that he discusses in his post.Quote: tringlomaneStephen How wrote said full table collusion wasn't even enough to overcome the house edge. So someone unfortunately goofed. Or longer sims are needed to get a clearer answer. :(
http://discountgambling.net/2010/06/14/collusion-performance-for-ultimate-texas-holdem/
I think itís not discussed because itís worth so little. Itís 2.5% with perfect play which in a brick and mortar casino isnít really possible. Also you need 6 players to pull it off and unless you have multiple players how long are the same 6 players playing together going to not be noticed.Quote: WizardSomebody asked me about this recently. As a reminder, Eliot Jacobson's article says that with perfect collusion play in a six-player game, there is a player advantage of 2.5%. I'm surprised this is not more often discussed as an advantage play (shup up Wiz!).
link to original post
There are so many better opportunities available that it makes Uth just not worth it.
Quote: HunterhillI think itís not discussed because itís worth so little. Itís 2.5% with perfect play which in a brick and mortar casino isnít really possible. Also you need 6 players to pull it off and unless you have multiple players how long are the same 6 players playing together going to not be noticed.
There are so many better opportunities available that it makes Uth just not worth it.
link to original post
I know it would be illegal, but I could see using an app to input the cards. You could also rotate players on a larger team.
That statement surprised me do you mean that some people might use an app because most people I know would never use an app or do anything that could be illegal .Quote: WizardQuote: HunterhillI think itís not discussed because itís worth so little. Itís 2.5% with perfect play which in a brick and mortar casino isnít really possible. Also you need 6 players to pull it off and unless you have multiple players how long are the same 6 players playing together going to not be noticed.
There are so many better opportunities available that it makes Uth just not worth it.
link to original post
I know it would be illegal, but I could see using an app to input the cards. You could also rotate players on a larger team.
link to original post
However, as long as he did a lot of the coding I asked him to see what the expected value would be for a player with knowledge of 10 dead cards (the hole cards of five other players) and made computer-perfect use of that information.
Based on a 40,000 hand simulation, JB concludes the expected value, based on the Ante bet, to be -0.006386. Compare that to the overall EV of the game without collusion of -0.021850. That is an improvement of 0.015464.
I know this is a significant different from that 2.5% player advantage reported by Eliot Jacobson in his article ULTIMATE TEXAS HOLD'EM COLLUSION. In other words, Eliot says collusion helps 3.03x as much as JB does, based on the Ante bet. I'm sure some of that is due to Eliot's sample size of 500 compared to JB's 40,000. It is also possible one side or the other, or both, are in error. These calculations are not easy.
I show the collusion strategy results in a change in pre-flop decision 9.03% of the time. Eliot gets 9.4%.
JB plans to run another 10,000 hands and then I will write up the results properly.
For now, I welcome all comments and questions.
However, I can highly recommend Paul D. Senzee's perfect hash function implemented in C/C++:
This perfect hash method only uses three 64-bit multiplications and some simple array dereferencing and addition ops. I created an array just one time allowing me to use the index52c7 result to directly get the hand rank from the array. I write the array to disk and just read it into memory at program startup rather than taking the time to recalculate it. The file size is 267569120 bytes.Quote:Fast mapping of all 52 bit numbers with 7 bits set to an index 0 - 133M.
// In Paul Senzee's original code, everything now contained in index52c7.cpp existed
// here in the header file, in fact, there was no index52c7.cpp (only the .h). I have
// created the .cpp file and moved all the code into it, exposing only the actual
// method which performs the conversion from a 52-bit card mask with any 7 bits set
// to a unique number between 0 and 133 million.
typedef unsigned long long int uint64;
unsigned index52c7(uint64 x);
I don't know if you or JB are using a perfect or imperfect hash in your current analysis. Paul's has has such a simple API and was easy to pull into my code base.
I just did a little test to check all possible ways of drawing to any two card starting hand after removing ten random cards from the deck. I count 9880*666*595 = 3,915,147,600 ways.Quote: MentalI just wrote a Casino Holdem analyzer that runs pretty fast. I know your UTH-collusion problem has three decision points instead of just one. I don't really want to tackle that problem now.
However, I can highly recommend Paul D. Senzee's perfect hash function implemented in C/C++:This perfect hash method only uses three 64-bit multiplications and some simple array dereferencing and addition ops. I created an array just one time allowing me to use the index52c7 result to directly get the hand rank from the array. I write the array to disk and just read it into memory at program startup rather than taking the time to recalculate it. The file size is 267569120 bytes.Quote:Fast mapping of all 52 bit numbers with 7 bits set to an index 0 - 133M.
// In Paul Senzee's original code, everything now contained in index52c7.cpp existed
// here in the header file, in fact, there was no index52c7.cpp (only the .h). I have
// created the .cpp file and moved all the code into it, exposing only the actual
// method which performs the conversion from a 52-bit card mask with any 7 bits set
// to a unique number between 0 and 133 million.
typedef unsigned long long int uint64;
unsigned index52c7(uint64 x);
I don't know if you or JB are using a perfect or imperfect hash in your current analysis. Paul's has has such a simple API and was easy to pull into my code base.
link to original post
It takes me 21 seconds to score the dealer and player hands for every one of these run outs (using one processor running a single thread). I don't use any symmetry of suit invariance to reduce size of the problem. I think the ten exposed cards break the suit symmetry, but I have not thought about that part of the problem much.
I rushed through this and I have not compared the EV with a UTH calculator. Still, it seems I could crank out a lot of starting hands pretty quickly if I finished the analyzer. I would need to add decision point logic to the program at the various UTH decision points.
It was pretty easy to look at the river fold/raise decision. I just added code that calculated the EV of the Play Bet and compare it to the Fold EV of -2. Calculating the river EV decisions only takes 25% longer than just looking at the win/loss/tie statistics without calculating any payoffs or EVs.Quote: MentalI just did a little test to check all possible ways of drawing to any two card starting hand after removing ten random cards from the deck. I count 9880*666*595 = 3,915,147,600 ways.
It takes me 21 seconds to score the dealer and player hands for every one of these run outs (using one processor running a single thread). I don't use any symmetry of suit invariance to reduce size of the problem. I think the ten exposed cards break the suit symmetry, but I have not thought about that part of the problem much.
I rushed through this and I have not compared the EV with a UTH calculator. Still, it seems I could crank out a lot of starting hands pretty quickly if I finished the analyzer. I would need to add decision point logic to the program at the various UTH decision points.
link to original post
The earlier decision points are conditional on the river fold/raise decision. I don't have to recalculate any more payoffs. I just need to average the EVs that I already calculated. I think I could calculate the optimal strategy for any starting hand and ten exposed cards in under 30 seconds.
Thanks. Some people do sudoku or the NYT crossword puzzle to relax. I like writing tight loops and reducing the number of operations to get things done. I don't believe UTH collusion is worthwhile to put into practice. But I find this problem attractive in that the goals are very clear and there seem to be some open questions.Quote: WizardMental, that is some good stuff there. I think you may be a rising star in casino game mathematics and programming.
link to original post
But Paul's perfect hash is a thing of beauty and the key to my speed metrics. I don't even know how it works, but it does work.
Quote: MentalBut Paul's perfect hash is a thing of beauty and the key to my speed metrics. I don't even know how it works, but it does work.
link to original post
We should make a separate thread for that.
I actually never looked to see if Paul explains it on his page. I did not want to link to it, but it is easy to find.Quote: WizardQuote: MentalBut Paul's perfect hash is a thing of beauty and the key to my speed metrics. I don't even know how it works, but it does work.
link to original post
We should make a separate thread for that.
link to original post
I wrote a lookup table for 5-card hands based on array indexing in the 90's. Then I saw your page on VP analysis. It turned out that your method was equivalent to my array indexing, but this was not obvious on the surface. Your method just has an equation for a number, but that number turns out to be an array offset. Your index and my array offset turn out to be the same number for any given 5-card poker hand.
I suspect that Paul's perfect hash is based on similar mathematical principles. He is folding the sparse 52-bit space (only numbers with 7 bits set) down to a dense space where every every consecutive number is matched to a unique 52-bit number.
I would love more geeky threads, but often geeky threads are hijacked by people who just want to make random comments about any thought that pops into their heads. I like sudoku because there is only one right answer, but many different tools to get to that answer. Creativity is rewarded, but sloppy logic is not.
No.Quote: acesideVery interesting! Wizard mentioned JB. Mental mentioned Paul. Are they frequent posters here?
link to original post
JB did a lot of the programming for the WOO site. I interacted with JB via PM regarding my sequential RF calculations, and I have a lot of respect for JB's programming abilities. I don't see a forum post from JB since 2020.
Paul Senzee isn't even a WOV member so far as I know. I was familiar with a community of fantastic programmers that worked out methods of calculating table poker equity very quickly. This was15-25 years ago when I played poker in B&M and online. These were people like Cactus Kev, folks at 2+2, and the University of Alberta Computer Poker Research Group. I just ran across Paul's work in January when I decided to write my own Casino Holdem analyzer and needed a 7-card hash function. I won't link to it, but Paul has a blog where you can find all sorts of other great math and programming articles. His name is easy to search.
The first pass is to calculate the slices of the target space based on the first gap. If the first gap is 0, the target space is narrowed to Γ(52)/(Γ(46)(6)!), and so on. The next pass calculates a sub-slice within the first slice, and so on, until there is only one slot remaining (after 6 passes). This is obviously not an efficient algorithm, but with some pre-calculation, the sizes of all sub-slices could be put in an array, and could avoid all of the redundant multiplication. It sounds like Paul figured out some elegant way to do the mapping.
It sound like you know this area of math pretty well, and I will defer to you. Clearly, I was wrong guessing that it was related to array indexes. I actually tried to do a 5-card hash based on gaps a long time ago and I got nowhere with it. I should check sometime and see if Paul gives credit to anyone else for his hashing ideas.Quote: TaxrBuxIt looks like you can interpret each 52-bit number as 8 non-negative sequences of zeroes, with the 8 numbers always adding up to 45. Based on a Stack Exchange answer about partitions, the formula for calculating the total number of partitions is Γ(𝑛+𝑘)/(Γ(𝑛+1)(𝑘−1)!) = Γ(53)/(Γ(46)(7)!) = 133,784,560. The task is then to determine which slot each sequence corresponds to.
The first pass is to calculate the slices of the target space based on the first gap. If the first gap is 0, the target space is narrowed to Γ(52)/(Γ(46)(6)!), and so on. The next pass calculates a sub-slice within the first slice, and so on, until there is only one slot remaining (after 6 passes). This is obviously not an efficient algorithm, but with some pre-calculation, the sizes of all sub-slices could be put in an array, and could avoid all of the redundant multiplication. It sounds like Paul figured out some elegant way to do the mapping.
link to original post
EDIT: I looked at the code and it not counting gaps. I think I understand what you are getting at, but this does not seem to be using that idea.
The first thing the algorithm does is break the 52 bits into three 16-bit chunks and one 4-bit chunk and counts the bits in each chunk via table lookup. It then seems to index into large precomputed arrays using the bit counts and some offset tables.
// This method takes a 64-bit integer WITH EXACTLY 7 BITS SET and returns
// a unique value between 1 and approximately 133 million.
/*inline*/ unsigned index52c7(unsigned long long int x)
{
const unsigned short *a = (const unsigned short *)&x;
unsigned A = a[3], B = a[2], C = a[1], D = a[0],
bcA = _bitcount[A],
bcB = _bitcount,
bcC = _bitcount,
bcD = _bitcount[D],
mulA = _choose48x[7 - bcA],
mulB = _choose32x[7 - (bcA + bcB)],
mulC = _choose16x[bcD];
return _offsets52c[bcA] + _table4[A] * mulA +
_offsets48c[ (bcA << 4) + bcB] + _table * mulB +
_offsets32c[((bcA + bcB) << 4) + bcC] + _table* mulC + _table [D];Last edited by: Mental on Mar 3, 2024Gambling is a math contest where the score is tracked in dollars. Try not to get a negative score.
The program runs faster as more cards are exposed, leaving fewer cards to consider for the run out. The program takes about 130 seconds to calculate the Check and Raise EVs for the normal UTH starting 2-card hand with no extra cards exposed. For 10 exposed cards, it takes about 30 seconds. I hope to make it a bit faster by optimizing and getting rid of some superfluous diagnostics.
I checked a number of starting hands against Wizard's UTH calculator. My hand counts and EVs agree exactly on all starting hands that i checked. I did a smaller number of checks for the Flop and River decision EVs and they check out, too. I believe the flop/river checks are redundant, because you cannot get the right starting EVs unless all the subsequent decisions are using accurate EVs. It would be nice to have somebody else calculate EVs for specific sets of cards so I have something to 'sanity check' my EVs against. Note that I use a different random set of exposed cards for each calculation, so we would have to agree on the exposed cards to compare EVs. The Wizard says "These calculations are not easy." I would say it is easy to make mistakes when you have nothing to check your results against. I benefited from being able to compare to JBs detailed results.
If I examine an extreme case where 30 cards are exposed, the program take a fraction of a second per hand. I calculate an EV of 0.09 by averaging over all possible 52C2=1326 starting hands in 160 seconds. For 40 exposed cards, the EV=0.58, so using all that knowledge allows the user to make very good play decisions.
After I do some more optimization and checking, I am going to try to calculate EVs with lower numbers of exposed cards. I will create a plot of overall UTH EV versus number of exposed cards. If this curve is noisy, at least it will tell me how much the EV depends on the specific random choice of exposed cards. Maybe 1326 starting hands will not be enough to get good answers. I don't expect that it should take more than a few days to see the results converge. I should be able to run four parallel computations on my MacBook without bogging down. This should produce results for about eight starting hands per minute (115K/day).
Both hole carding and collusion strategies are equally valuable to me. They have zero economic value to me. On the plus side, I don't have to split the zero dollars six ways for hole carding. Even if it was possible to pull off the collusion at a table, the size of the team is a big impediment to making money.Quote: acesideIn the meantime, please help consider the problem of hole-carding strategy for UTH, which is far more advantageous than this negligible collusion strategy.
link to original post
The MIT team didn't make that much money per team member, yet they are famous.
Are there any unanswered questions about UTH if you know the dealer's hole cards?
https://www.888casino.com/blog/novelty-games/ultimate-texas-holdem-collusion
I was able to confirm the first four rows of Eliot's first chart. We agree to the precision that his table provides. I presume we would agree on every starting configuration in his tables.
It appears that my program is at least 50 times faster than Eliot's program. I am using one thread. I suspect Eliot is using one thread. I suspect my MacBook is probably a lot faster than his Linux box, but I don't know for sureQuote: EliotTo simulate just one possible starting configuration (2 player cards, 10 other known cards) requires the evaluation of 3,915,147,600 (3.9 billion) possibilities. To simulate a single starting configuration required about 25 minutes of computer time on my dedicated Linux box.
Is there a reason that players only see one dealer hole card?Quote: acesideJust a little. For the hole-carding part, players often do not seen the exact card rank and suit. They only know if it is a face card, a high card, or a low card. Can you think about this along these lines?
link to original post
Collusion only tells you what the dealer does not have and which cards you won't get on later streets. Knowing what the dealer does have has should be very useful even when it is not 100% specific. Knowing that the dealer has a red card would be helpful if the board has a 4-flush. It doesn't help much preflop. Hi/Lo info helps more preflop. I would guess that most of the value of hole cards comes preflop.
I assume someone has published charts for decisions based on knowing something about one of the dealer's hole cards. I don't feel the need to reinvent the wheel.
Perhaps you could summarize the state of the art?
I learned about this game from another dedicated player, odiousgambit, but I havenít seen him for some time here. He may say something more about this part. I think your analysis of hole-carding and collusion are right on point.
It would be much easier for me to calculate the removal of a perfectly known card than to deal with a range for the dealer hole card. I can just force the dealer to have that card and the program will operate the same way, except faster. If I assume that the Dealer has a red 2-5, then I need to calculate how each of these eight cards affect strategy separately, then pick the strategy decision that maximizes EV, then recalculate the overall EV with that one strategy.Quote: acesideThe reason for seeing only one dealer card is simple. Itís just how the casino and the shuffler handle these cards.
I learned about this game from another dedicated player, odiousgambit, but I havenít seen him for some time here. He may say something more about this part. I think your analysis of hole-carding and collusion are right on point.
link to original post
This won't even give you practical playing strategy. I could search to see what information is out there, but the best info will be behind pay walls. I am just not that interested in creating a playing strategy.
I believe it is the latter explanation. Eliot gives no error bars for his estimate. Eliot also does not say that he used uniform sampling or 'Importance Sampling' to select the player's two starting cards. In just 500 hands, the random inclusion or exclusion of high pocket pairs in the starting hands will have a huge effect on his average EV.Quote: tringlomaneQuote: teliotHere it is:
http://apheat.net/2015/05/28/ultimate-texas-holdem-collusion/
A full (six-player) table gets a computer-perfect edge of about 2.5%.
Stephen How wrote said full table collusion wasn't even enough to overcome the house edge. So someone unfortunately goofed. Or longer sims are needed to get a clearer answer. :(
http://discountgambling.net/2010/06/14/collusion-performance-for-ultimate-texas-holdem/
link to original post
I checked Eliot's individual calculations, and I believe they are accurate. I just think he randomly chose a biased sample of starting hands and got a very high estimate based on these unusually good starting hands. I would recommend doing simulations on all 52C2=1326 hands. In the time period when people were doing these calculations, computer hardware was much slower. This would be a good excuse not to do 1326 hands. At the very least, Eliot should have simulated sets of all 169 unique starting hands and then done weighting of the EV results.
I am going to wait to post my results until I have calculated EVs for a sufficient number of starting hands so random choices of exposed cards does not bias my results.
EDIT: I have completed two calculations of 1326 starting hands and the results differ by 2.8%. Clearly the random choice of the ten exposed cards leads to a significant variance in the simulated EV. I will need a couple of days to run this 1326 hand sim enough times to get a decent estimate of EV. My current guess is that playing computer-perfect strategy with the knowledge of 10 exposed cards will not be enough to gain an edge on UTH.
Quote: MentalAfter I do some more optimization and checking, I am going to try to calculate EVs with lower numbers of exposed cards. I will create a plot of overall UTH EV versus number of exposed cards. If this curve is noisy, at least it will tell me how much the EV depends on the specific random choice of exposed cards. Maybe 1326 starting hands will not be enough to get good answers. I don't expect that it should take more than a few days to see the results converge. I should be able to run four parallel computations on my MacBook without bogging down. This should produce results for about eight starting hands per minute (115K/day).
link to original post
This is great! I look forward to seeing some numbers for a small number of cards exposed.
Quote: WizardQuote: MentalAfter I do some more optimization and checking, I am going to try to calculate EVs with lower numbers of exposed cards. I will create a plot of overall UTH EV versus number of exposed cards. If this curve is noisy, at least it will tell me how much the EV depends on the specific random choice of exposed cards. Maybe 1326 starting hands will not be enough to get good answers. I don't expect that it should take more than a few days to see the results converge. I should be able to run four parallel computations on my MacBook without bogging down. This should produce results for about eight starting hands per minute (115K/day).
link to original post
This is great! I look forward to seeing some numbers for a small number of cards exposed.
link to original post
FYI. Below are 3 Links to Casino Hold'em® with ALL Player's Hole-Cards deal Face-Up:
* GLI-Report on 08/September/2023: CasinoHoldemGLI.com
* Math by Charles R. Mousseau on 03/July/3017: https://buff.ly/48JvP6o
* Math by Stephen How on 14/Aug/2014: https://buff.ly/4360ObK
Casino Hold'em® Face-Up (aka Casino Hold'em® Poker-Plus / Casino Hold'em® Open): CasinoHoldemFaceUp.com / CasinoHoldemOpen.com
* Casino Hold'em® at Wizard of Odds: CasinoHoldemWoO.com
I really appreciate the links. My current project regards Ultimate Texas Holdem, but I am also interested in Casino Holdem. The latter is a much simpler game to analyze with one decision point after the flop. There are 19,600 times more ways a hand can play out from the initial two hole cards versus after the flop. The problem of UTH with exposed cards requires an extremely fast hand analyzer. For Casino Holdem, any decent brute force analyzer should work.Quote: MrCasinoGamesQuote: WizardQuote: MentalAfter I do some more optimization and checking, I am going to try to calculate EVs with lower numbers of exposed cards. I will create a plot of overall UTH EV versus number of exposed cards. If this curve is noisy, at least it will tell me how much the EV depends on the specific random choice of exposed cards. Maybe 1326 starting hands will not be enough to get good answers. I don't expect that it should take more than a few days to see the results converge. I should be able to run four parallel computations on my MacBook without bogging down. This should produce results for about eight starting hands per minute (115K/day).
link to original post
This is great! I look forward to seeing some numbers for a small number of cards exposed.
link to original post
FYI. Below are 3 Links to Casino Hold'em® with ALL Player's Hole-Cards deal Face-Up:
* GLI-Report on 08/September/2023: CasinoHoldemGLI.com
* Math by Charles R. Mousseau on 03/July/3017: https://buff.ly/48JvP6o
* Math by Stephen How on 14/Aug/2014: https://buff.ly/4360ObK
Casino Hold'em® Face-Up (aka Casino Hold'em® Poker-Plus / Casino Hold'em® Open): CasinoHoldemFaceUp.com / CasinoHoldemOpen.com
* Casino Hold'em® at Wizard of Odds: CasinoHoldemWoO.com
link to original post
A read through these links has me scratching my head. Even though these links concern the relatively simple Casino Holdem game, I notice that neither article does full completion of all possible turn, river, and dealers hole cards. Instead, they randomly sample less than 1% of the completions. They also only randomly sample about 40% of the starting hands. These authors are professionals in the business of analyzing games, yet they apparently cannot do a full simulation because their algorithms are too slow. One of the papers was dated from last year, so they should have access to a computer much faster than my 2021 MacBook.Quote: MrCasinoGamesQuote: WizardQuote: MentalAfter I do some more optimization and checking, I am going to try to calculate EVs with lower numbers of exposed cards. I will create a plot of overall UTH EV versus number of exposed cards. If this curve is noisy, at least it will tell me how much the EV depends on the specific random choice of exposed cards. Maybe 1326 starting hands will not be enough to get good answers. I don't expect that it should take more than a few days to see the results converge. I should be able to run four parallel computations on my MacBook without bogging down. This should produce results for about eight starting hands per minute (115K/day).
link to original post
This is great! I look forward to seeing some numbers for a small number of cards exposed.
link to original post
FYI. Below are 3 Links to Casino Hold'em® with ALL Player's Hole-Cards deal Face-Up:
* GLI-Report on 08/September/2023: CasinoHoldemGLI.com
* Math by Charles R. Mousseau on 03/July/3017: https://buff.ly/48JvP6o
* Math by Stephen How on 14/Aug/2014: https://buff.ly/4360ObK
Casino Hold'em® Face-Up (aka Casino Hold'em® Poker-Plus / Casino Hold'em® Open): CasinoHoldemFaceUp.com / CasinoHoldemOpen.com
* Casino Hold'em® at Wizard of Odds: CasinoHoldemWoO.com
link to original post
It really makes little sense to randomly sample 40% of starting configurations. Random sampling of starting configurations introduces noise in the results. It would have been much better to do all the starting hands and reduce the number of completions if their algorithms are too slow to do a better job.
Even though there are uncertainties introduced by random sampling, neither study gives margin-of-error (MOE) estimates for their final numbers.
If the player can see one other hand, this counts as two cards exposed, so the player sees his two hole cards plus 2 others (Nexp=2). This introduces randomness to the calculation, since I randomly choose two exposed cards and then do the exact calculation using the optimal strategy taking into account those four cards. Each data point in the first chart represents at least 1326 calculations using all possible player starting hands and two randomly chosen exposed cards. A different random choice of exposed cards is done for each of the 1326 starting hand calculations.
The random choice of exposed cards starts introducing significant variance in the EV result once we get up to 6 exposed cards. In the real world, you would never expect to see more than Nexp=12 exposed cards where the game is dealt to seven spots. However, it was easy to continue the calculations beyond 12 up to the maximum of Nexp=43 cards exposed, leaving nine cards for the player hand, dealer hand, and board. Since there are so few cards remaining in the deck, this calculation is extremely quick. I actually performed three calculations with a total of 2,320,500 starting hands and 43 exposed cards. Even with so many starting hands, there is a big spread in the EV for these three trials due to the large effect on playing strategy when you have knowledge of 2+43 cards in the deck to start each hand.
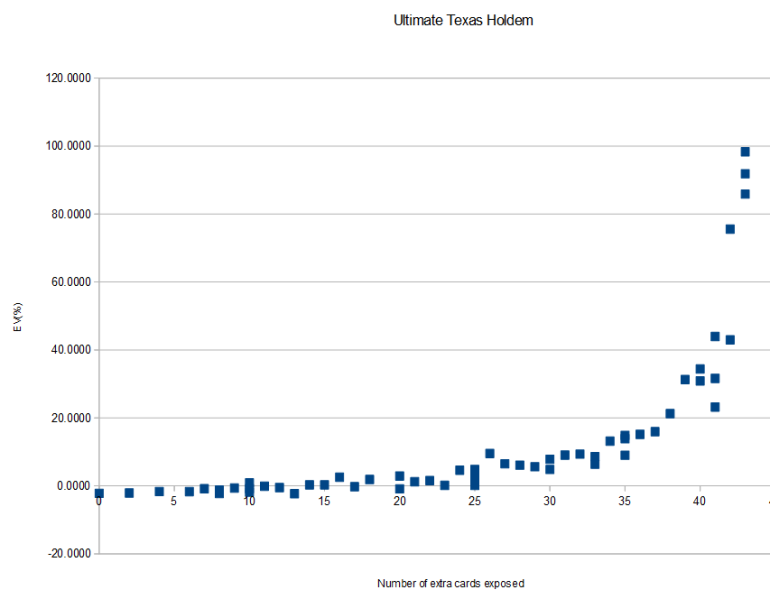
I looked more carefully at the left hand of the graph and used a polynomial to fit the data for the range 0 <= Nexp <= 21. (The blue points in the graph below are the fitted data.) This gives allows me to estimate that the EV turns positive around Nexp=14. I doubt that this estimate would shift by more than 1 unit even if I did more calculations to reduce random variance in the EV(Nexp) estimates. I think this nails down the function EV(Nexp) pretty well even though the standard deviation of each calculation is on the order of 1% when Nexp is around 10 cards.
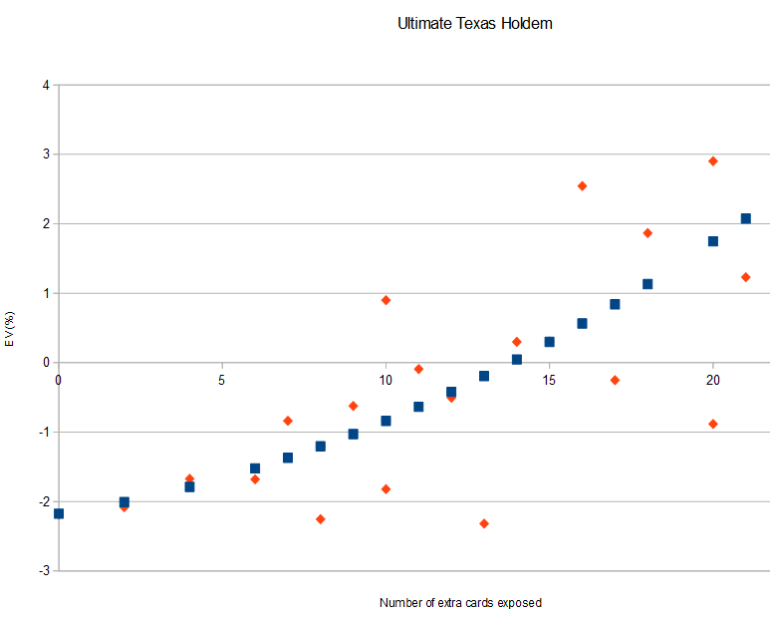
Eliot's estimate of EV(10)= +2.5% is more than 3% higher than my estimate and is way outside the uncertainties in my calculation. If Eliot randomly sampled 500 out of 1326 starting hands, then I would expect the standard deviation of his calculation method to be 2 or 3 percent. I believe Eliot did the calculations perfectly, but chose his starting hands in a way that gives a very large uncertainty. If I really wanted to estimate the uncertainties in Eliot's methodology, I could randomly sample the EV for 500 out of 1326 my starting hands. I did not do this.
JB's estimate for EV(10)=0.006386 is within 0.2% of my estimate (-0.008376) and well within the uncertainty of my calculation.Quote: wizard
Based on a 40,000 hand simulation, JB concludes the expected value, based on the Ante bet, to be -0.006386. Compare that to the overall EV of the game without collusion of -0.021850. That is an improvement of 0.015464.
The bottom line is that collusion cannot create a +EV situation for UTH even if you could make computer perfect strategy decisions.
Thanks. I lost interest in the problem a week ago, but my MacBook was happy to keep on grinding out five parallel calculations at a time, so I let it run. I have eight processors, but the OS needs to have some cycles and the case gets noticeably warm when I load it down like this.Quote: unJonReally love this thread.
link to original post
I figured I owed it to my laptop to write up the results after all the effort it put forth.
I am realizing that anyone doing these calculations has to balance the number of starting hand, the number of randomly chosen sets of exposed cards, and the number of continuations. If I had to do it over again, I might choose to use a random sample of continuations to make my playing decisions. However, I needed to perform the full set of continuations to allow me to compare my results to JB's or Eliot's results.
Can you use this particular player hand of a pocket pair of 3ís to illustrate the above description? I donít understand the randomness you mention. How much gain can a player obtain from 10-card-exposure collusion for a pocket pair of 3ís, exactly?
You are asking a reasonable question, but there are 50choose10=10,272,278,170 possible sets of exposed cards to consider. Some of these sets increase the EV of pocket 3s while other sets reduce EV. I don't have time to go through all 10 billion sets with you.Quote: acesideQuote your above ďIf the player can see one other hand, this counts as two cards exposed, so the player sees his two hole cards plus 2 others (Nexp=2). This introduces randomness to the calculation, since I randomly choose two exposed cards and then do the exact calculation using the optimal strategy taking into account those four cards.Ē
Can you use this particular player hand of a pocket pair of 3ís to illustrate the above description? I donít understand the randomness you mention. How much gain can a player obtain from 10-card-exposure collusion for a pocket pair of 3ís, exactly?
link to original post
My program can read in strings like this to force the set of exposed cards:
"2had5hjdtd3c9h2s2dks6h3h",
"2d2s8cac4h9dqh7ctdjc3h8s",
"kh2s5hth7h4sahtdjc3sad5s",
"qs2stc7d6c4c8d2cjh3had6h",
"kc3h5h4h2s9hts8das9djc6s",
This is how I compared my results to Eliot's results. These strings all represent one of his random choices of 10 exposed cards.
So, I can compare the EV of pockets 3s with no extra information versus with any number of cards exposed. The only way to tell you how much pocket threes is helped/hurt by the average set of exposed hands is to do a large number of calculations specifically for pocket 3s. My calculations are for all 1326 starting hands, so I do not have a specific results for any one hand. If you are really interested, I could do a run where I just focus on pocket 3's against a large number of random sets of exposed cards. Then, I could dump the resulting data to you for analysis in the form of a spreadsheet. You would be able to see what types of hands change the initial raise/call decisions and what the dispersion of the EV's is like. You could probably develop some rules of thumb after looking at a few dozen sets.
I have zero interest in studying the UTH game in this detail and developing a strategy.
Quote: MentalI plotted the EV for Ultimate Texas Holdem versus the number of other players cards exposed, ...
link to original post
This is outstanding! If I had a post of the month, you would easily win for March. Thank you so much. It's the kind of work that is so good I don't have any good cross-talk. I would like to quote you in a page I hope to do tomorrow on the topic.
Quote: MentalI have zero interest in studying the UTH game in this detail and developing a strategy.
link to original post
But, based on what you have learned, do you think such a strategy could be memorized? Or, would it be so lengthy that only gaming academics would find it of interest?
Both checkDealEV and raiseDealEV vary dramatically depending on the nature of the exposed cards. Pocket 3's is not a strong hand, so the raise/check decision flips depending on the exposed cards.
1,14,6,10,-0.782610,-1.153118,4,11,20,25,27,29,34,37,40,46,
1,14,6,10,-0.358154,-0.463844,3,4,18,26,40,43,46,47,49,51,
1,14,6,10,-0.263684,-0.282600,4,6,8,21,27,28,38,41,43,48,
1,14,6,10,0.274514,0.532096,4,9,16,19,23,26,31,34,44,51,
1,14,6,10,0.314703,0.580365,22,24,28,31,32,34,38,39,47,49,
1,14,6,10,-0.443836,-0.654760,0,3,8,10,16,25,27,28,41,43,
1,14,6,10,0.292425,0.553578,2,22,25,26,29,32,36,46,47,49,
1,14,6,10,-0.499975,-0.790865,2,13,15,23,26,30,36,40,45,48,
1,14,6,10,-0.404297,-0.553615,2,16,19,21,25,31,39,40,42,43,
1,14,6,10,-0.884514,-1.366048,7,13,16,21,22,24,27,32,33,40,
1,14,6,10,0.311883,0.559560,2,12,15,25,31,32,33,34,41,49,
1,14,6,10,0.267491,0.460211,2,3,10,16,23,28,32,38,41,47,
1,14,6,10,0.208989,0.350000,0,8,9,10,20,25,36,44,46,49,
1,14,6,10,0.242341,0.442721,3,10,17,21,24,26,34,48,50,51,
1,14,6,10,-0.363744,-0.473374,2,7,8,25,26,27,29,34,35,50,
1,14,6,10,-0.295371,-0.373202,2,5,10,19,27,32,41,43,45,49,
1,14,6,10,-0.364989,-0.524027,12,21,26,29,31,34,40,41,47,51,
1,14,6,10,0.219728,0.385660,3,4,13,24,31,35,37,41,42,43,
1,14,6,10,0.265379,0.462403,13,29,30,36,42,43,47,48,49,50,
1,14,6,10,-1.120887,-1.988913,2,4,11,26,27,28,31,39,40,41,
1,14,6,10,-0.432192,-0.627754,0,3,12,17,22,23,27,29,37,43,
1,14,6,10,0.373461,0.691385,3,12,20,22,24,30,33,45,46,47,
1,14,6,10,0.333016,0.576241,5,7,12,24,29,33,37,44,49,50,
1,14,6,10,-0.368892,-0.543321,10,11,26,29,36,40,42,47,48,50,
1,14,6,10,0.166862,0.241648,12,16,22,25,26,28,29,31,35,42,
1,14,6,10,0.214266,0.333273,12,16,34,36,37,39,42,49,50,51,
1,14,6,10,0.327172,0.603996,6,7,12,15,19,23,30,41,44,49,
1,14,6,10,-0.434675,-0.621128,0,5,10,12,15,22,25,29,30,40,
1,14,6,10,-0.488698,-0.754583,0,11,16,17,26,31,40,42,48,49,
1,14,6,10,0.266414,0.505974,6,13,15,17,24,29,32,34,44,47,
1,14,6,10,-0.815079,-1.201333,5,8,15,16,17,24,27,30,40,46,
1,14,6,10,0.177992,0.316002,7,8,9,13,15,16,19,22,35,37,
I only play UTH online heads-up with a robo dealer. I did this project just because I was interested in seeing how fast I can do the calculations. I was also interested in how quickly the EV converged. I have my answers. The strategy changes are of zero value to me.Quote: GialmereQuote: MentalI have zero interest in studying the UTH game in this detail and developing a strategy.
link to original post
But, based on what you have learned, do you think such a strategy could be memorized? Or, would it be so lengthy that only gaming academics would find it of interest?
link to original post
With 10 cards exposed, even a simple preflop strategy would gain you a fraction of a percent in EV. How many exposed cards match your hole cards? Are an unusually large number of over cards exposed? If you are suited, how live is your flush draw? Etc.
I think Eliot claimed exposed cards are most helpful on the preflop decision. You should read his article. If your cards are dead preflop, they are not going to suddenly get lively on the river.
We can approximate it. The collusion EV gain of pocket 3s comes mainly from seeing one or two remaining 3s. If the player can only see one neighborís two cards, the probability of seeing at least one 3 is (2x48+1)/1225=7.9%. If the player can see all five other playersí cards, this probability becomes 5x7.9%=40%. Can you help calculate this EV gain under this approximation?
In other words, do this calculation only 49 times, instead of 10 billion times.
Yes, this is an easy calculation to do. I already wrote that I can force the starting conditions for any particular EV calculation. I am already set up to force the two player cards and 10 exposed cards using a string like "3c3d3h3srsrsrsrsrsrsrsrs" where the repeated 'rs' stands for specific any rank and suit of the other 8 cards. It is hardcoded for 12 cards, but I could quickly change that if I needed to.Quote: acesideQuote ďYou are asking a reasonable question, but there are 50choose10=10,272,278,170 possible sets of exposed cards to consider. Some of these sets increase the EV of pocket 3s while other sets reduce EV. I don't have time to go through all 10 billion sets with you.Ē
We can approximate it. The collusion EV gain of pocket 3s comes mainly from seeing one or two remaining 3s. If the player can only see one neighborís two cards, the probability of seeing at least one 3 is (2x48+1)/1225=7.9%. If the player can see all five other playersí cards, this probability becomes 5x7.9%=40%. Can you help calculate this EV gain under this approximation?
In other words, do this calculation only 49 times, instead of 10 billion times.
link to original post
I don't get what you mean by '49 times'. I already posted a bunch of calculations as CSV that you can import into a spreadsheet. I know there are sets with zero and one exposed 3s in that data. I would have to check to see if there are two exposed threes in any set. Did you even look at my data?
3h2c, 3h2d, 3h2h, 3h2s;
3h3s;
3h4c, 3h4d, 3h4h, 3h4s;
3h5c, 3h5d, 3h5h, 3h5s;
3h6c, 3h6d, 3h6h, 3h6s;
3h7c, 3h7d, 3h7h, 3h7s;
3h8c, 3h8d, 3h8h, 3h8s;
3h9c, 3h9d, 3h9h, 3h9s;
3hTc, 3hTd, 3hTh, 3hTs;
3hJc, 3hJd, 3hJh, 3hJs;
3hQc, 3hQd, 3hQh, 3hQs;
3hKc, 3hKd, 3hKh, 3hKs;
3hAc, 3hAd, 3hAh, 3hAs.
Each of these hands contains at least one 3. The collusion EV gain for a 6-player table is simply five times of that of a 2-player table. I will read into your CSV. Thank you!
Okay, I see that you are just looking at the equivalent hands with just changes in suit. Some of your 49 hands are equivalent, but you are ignoring a lot of hands that have different EVs and possible strategy changes.Quote: acesideI mean to say that when the player has cards 3c3d, you only need to calculate the following 49 sets of cards for your immediate neighborís hand:
3h2c, 3h2d, 3h2h, 3h2s;
3h3s;
3h4c, 3h4d, 3h4h, 3h4s;
3h5c, 3h5d, 3h5h, 3h5s;
3h6c, 3h6d, 3h6h, 3h6s;
3h7c, 3h7d, 3h7h, 3h7s;
3h8c, 3h8d, 3h8h, 3h8s;
3h9c, 3h9d, 3h9h, 3h9s;
3hTc, 3hTd, 3hTh, 3hTs;
3hJc, 3hJd, 3hJh, 3hJs;
3hQc, 3hQd, 3hQh, 3hQs;
3hKc, 3hKd, 3hKh, 3hKs;
3hAc, 3hAd, 3hAh, 3hAs.
Each of these hands contains at least one 3. The collusion EV gain for a 6-player table is simply five times of that of a 2-player table. I will read into your CSV. Thank you!
link to original post
I could put the rank and suit in my CSV file output to make it easier to read for humans, but card indexes would be easier if you are processing the file with another computer program. If you really only care about the 2+2 cards, I could do all the calculations in a few minutes later when I am less busy.


