martingale so different when___

_____________




first, I'm sure the Mathletes on this site were aware of this - but I'm not a Mathlete and I never really thought about it before

second, of course I know this doesn't mean this is a winning system - I just thought it was kinna interesting and kinna cool



so, if you do a 4 stage marty on an even money bet such as Player at Bacc - 20-40-80-160 - if you win on any of those bets your net profit will be the same - $20

your total risk - if you were to lose all 4 bets is $300



but let's say you do the same progression on a bet paying 2/1 such as a sports bet - today in the NHL the Sabres are about 2.20 to win against the Hurricanes



but for the purposes of this example let's say you always get a bet paying 2/1



you bet $20 - if you win your net profit is $40

if you lose that bet and on the next bet you bet $40 if you win your payout is $80 and your net profit is $60 (since you lost the first $20 bet)

if you lose the first 2 bets and you win the 3rd bet - you bet $80 your payout is $160 and your net profit is $100 ( since you lost the first 2 bets of $20 and $40)

if you lose the first 3 bets and you win the 4th bet - you bet $160 and your payout is $320 - your net profit is $180 (since you lost the first 3 bets of $20, $40 and $80)




unlike the typical marty on an even chance bet - the profit rises as you go deeper into the stages of the marty

if you were looking for bets paying 3/1 or 4/1 it would be even more extreme

the dollars risked is the same as with a marty on an even chance bet

of course the probability of winning the bet within the 4 stages of the marty on a bet paying more than even money is much less - but still



wow - seems like fun - am I going to do this on some sports bets_____?-------- I dunno - maybe


.

True - but, of course, you are far more likely to bust with 2-1 bets.

Compare an even-money against a 2-1 bet in double-zero roulette (even money has a 9/19 chance of winning; 2-1 has a 6/19 chance), with a 10-step Martingale.
The even money bet has a 1 in 613 chance of busting.
The 2-1 one has a 1 in 45 chance of busting - over 13 times as likely.

Quote: ThatDonGuy

The even money bet has a 1 in 613 chance of busting.

link to original post

hunh____-??????

that suggests that 612 out of 613 times you would win somewhere within the progression

I must be missing something - that can't be right - can you please clarify what you mean_________thanks


.

Quote: lilredrooster

Quote: ThatDonGuy

The even money bet has a 1 in 613 chance of busting.

link to original post

hunh____-??????

that suggests that 612 out of 613 times you would win somewhere within the progression

I must be missing something - that can't be right - can you please clarify what you mean_________thanks
.
link to original post

In a 10-step martingale (1, 2, 4, 8, 16, 32, 64, 128, 256, 512) on a single-zero roulette even money bet, you are, in fact, expected to win before losing 10 in a row 612 out of 613 times.
The problem is, the combined profit of the 612 wins is 612 times the initial bet, but the one loss is a loss of 1023 times the initial bet.

Quote: ThatDonGuy

Quote: lilredrooster

Quote: ThatDonGuy

The even money bet has a 1 in 613 chance of busting.

link to original post

hunh____-??????

that suggests that 612 out of 613 times you would win somewhere within the progression

I must be missing something - that can't be right - can you please clarify what you mean_________thanks
.
link to original post

In a 10-step martingale (1, 2, 4, 8, 16, 32, 64, 128, 256, 512) on a single-zero roulette even money bet, you are, in fact, expected to win before losing 10 in a row 612 out of 613 times.
The problem is, the combined profit of the 612 wins is 612 times the initial bet, but the one loss is a loss of 1023 times the initial bet.
link to original post

oh, okay - I got it - when I originally read it I missed the 10 step part - I thought you were referring to my 4 step example


.

Quote: lilredrooster

oh, okay - I got it - when I originally read it I missed the 10 step part - I thought you were referring to my 4 step example

With a 4-step:
Even-money bets: bust 1 time in 13
2-1 bets: bust 22% (about 2 out of every 9 times)

This should translate to craps, betting 4 or 10, both paying 2-1!

Quote: DeMango

This should translate to craps, betting 4 or 10, both paying 2-1!
link to original post

I am assuming you are talking about buying the 4/10, in which case, you need to take the commission into account, so it's not quite 2-1.

yup, in MS! MGM even went to lay, big on win!

Quote: DeMango

This should translate to craps, betting 4 or 10, both paying 2-1!
link to original post

Not exactly, because they don't pay 2-1. There's a commission

I use the following schema to analyze this type of games.



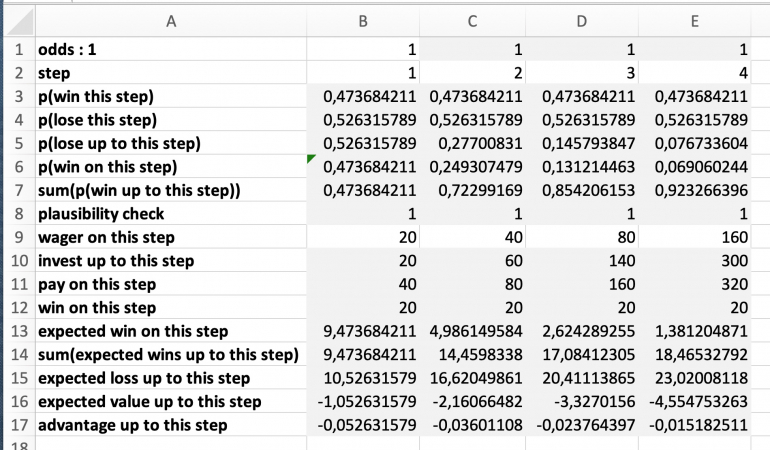
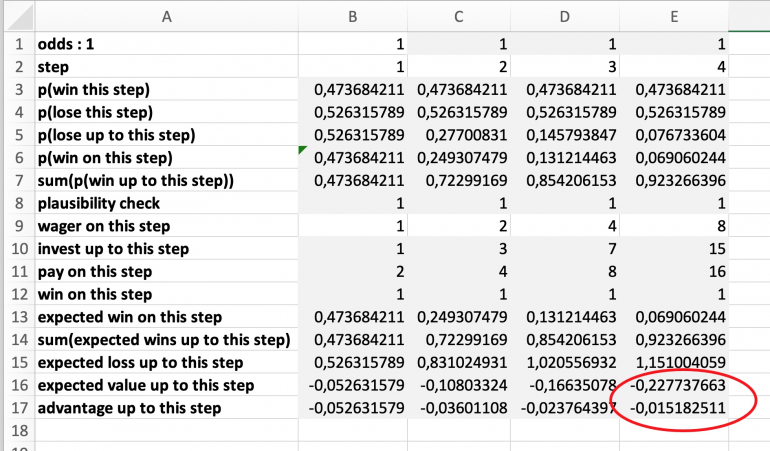
If you're interested, I put the details below.
If you're scared off by this crazy table, here my short description and interpretation.

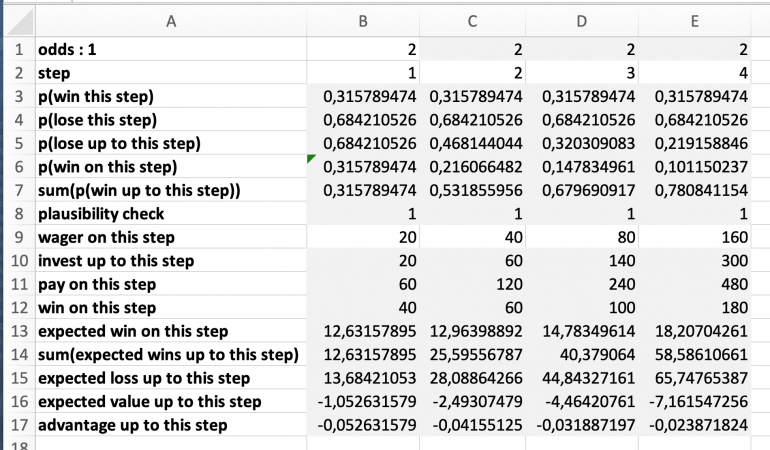
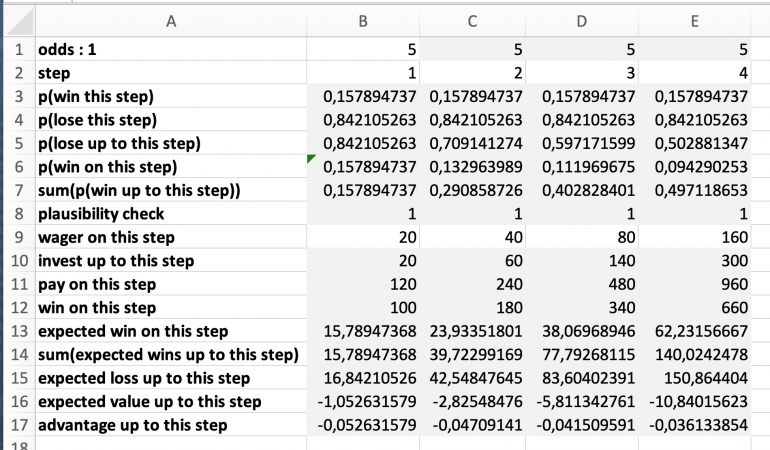
The calculations are based on double zero roulette, which offers not only 1:1 chances (red, black, ...) but also 2:1 (dozens, columns), 5:1 (double street), and a few more.
The tables for 2:1 and 5:1 are provided in the spoilers below.

In cell B1 the odds can be set.
From these odds the corresponding bet on a double zero roulette wheel is calculated.
Rows 3 through 8 have the necessary probability calculations.
Rows 9 through 12 have the calculations concerning the money bet.
You might recognize your progression 20, 40, 80, and 160 in row 9, the total amount of 300 in cell E10 and the constant profit of 20 in row 12.
Rows 13 through 17 combine the probablilities and the bet amounts to determine expected value and advantage. The house advantage of double zero roulette in cell B17 might be familiar to you.

As you can see in row 17, all values remain negative, i.e the advantge remains on the house's side.

You might find it interesting to see in cell E17 that the advantage of the four stage Martingale seems to be much more favourable than that of the regular game of double zero roulette.
To verify this effect I designed an experiement and also layed out the corresponding Monte Carlo simulation for it in this thread: https://wizardofvegas.com/forum/gambling/betting-systems/37238-battle-of-the-betting-systems/#post852875

My conclusion is that you chose the right type of betting progression, a progression on losses, which brings your action closer to zero advantage (the fair game), although it will never reach beyond it into positive expectation.

When inspecting the tables for 2:1 and 5:1 odds, please note that the advantage in cell E17 decreases with the odds. The even money game tends to be the better choice.





DETAILED EXPLANATION



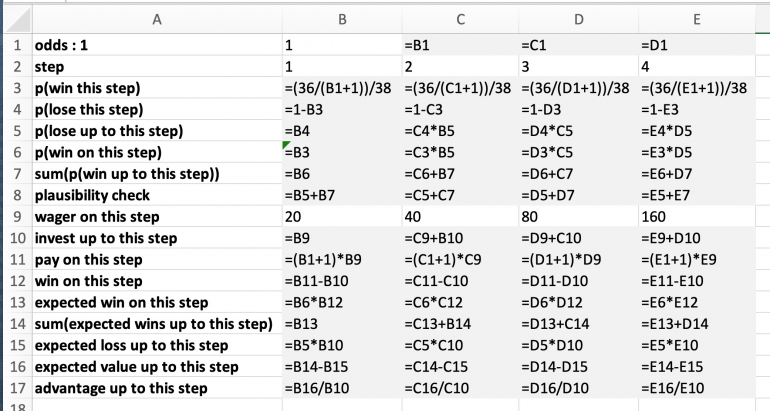
Row one defines the odds for the game analyzed. The value can be set in cell B1, which is propagated over the steps.
Row two indicates the steps.
Row three has the probablity of winning according to the odds given. The chances are calculated relative to a fair 36 number roulette wheel and then biased in favour of the house by a 38 number double zero roulette wheel.
Row four has the probability of losing, which by definition is the complement relative to 1.
Row five accumulates the probability of losing by multiplying the probabilities of the sequence of rolls up to and including the current step. ("First roll lost AND second roll lost AND ...")
Row six calculates the probability of winning the current roll by multiplying the probability of losing the sequence of preceding rolls with the probability of winning the current roll.
Row seven sums up the probabilities of all winning rolls up to the current step for the plausibility check in row eight.
Row eight is used to verify that all the probabilities of all possible winning sequences plus the probability of losing the final step add up to 1.
Row nine takes the progression of bets chosen.
Row ten sums up the bets for the total invest up to the current roll.
Row eleven calculates the pay for the case of a win. That is the odds of winning plus the initial bet multiplied by the amount actually bet as defined in row nine.
Row twelve determines the actual win of each step from the pay of this roll, in case of a win, minus the total bets invested up to the current roll.
Row thirteen multiplies the probability of winning in that step with the winning amount of that step resulting in the expectation component of winning this step.
Row fourteen sums up these expectations for winning, resulting in the winning portion of the expected value, i.e. winning on any step during the sequence.
Row fifteen calculates the expectation component of losing on the current roll of the sequence.
Row sixteen puts together the expectation of winning during the sequence minus the expectation of losing the last roll of the sequence for the complete expected value of the sequence up to the current step.
Row seventeen devides the expected value by the total amount bet up to the current roll which results in the normalized (house?) advantage.

That's not as surprising as it sounds.
What are you doing is, in effect, betting 300 to win 20 if you win one bet before losing four in a row.
In other words, you are betting on getting one win before four losses, with a payoff of 1-15 odds.
Some quick math, using an even-money bet with double-zero roulette (probability of win p = 9/19):
Assuming you start with a bet of 1, there are two possible results - either you win (because one of the next four spins is a win), and end up +1, or lose (because all four of the spins lose), and end up -15.
The probability of losing is (10/19)^4; the probability of winning is 1 - (10/19)^4.
EV = 1 x (1 - (10/19)^4) - 15 x (10/19)^4 = 1 - 16 x (10/19)^4 = -0.227738
House Edge = -EV / bet x 100% = 0.227738 / 15 x 100% = 1.51825%

Remember a key concept: the less you bet, the less you expose to the house edge, and, as a result, the less you are likely to lose.
This is where Martingale has an advantage; slightly less than half of the time, you only actually bet 1/16 (in a 4-step) of the maximum you intend to risk.

Quote: ThatDonGuy

That's not as surprising as it sounds.
What are you doing is, in effect, betting 300 to win 20 if you win one bet before losing four in a row.
In other words, you are betting on getting one win before four losses, with a payoff of 1-15 odds.
Some quick math, using an even-money bet with double-zero roulette (probability of win p = 9/19):
Assuming you start with a bet of 1, there are two possible results - either you win (because one of the next four spins is a win), and end up +1, or lose (because all four of the spins lose), and end up -15.
The probability of losing is (10/19)^4; the probability of winning is 1 - (10/19)^4.
EV = 1 x (1 - (10/19)^4) - 15 x (10/19)^4 = 1 - 16 x (10/19)^4 = -0.227738
House Edge = -EV / bet x 100% = 0.227738 / 15 x 100% = 1.51825%

Remember a key concept: the less you bet, the less you expose to the house edge, and, as a result, the less you are likely to lose.
This is where Martingale has an advantage; slightly less than half of the time, you only actually bet 1/16 (in a 4-step) of the maximum you intend to risk.
link to original post

So it’s akin to “element of risk” in games where you may add to your bets in certain situations (double down or split in BJ, play bets from 1X to ?X in carnival games). The difference here is that you’re adding larger bets after/based on the outcome of prior bets. So, would you equate this more to the double up feature in VP?

[EDIT: I realize that this is still quite different from the double up, as well, since you aren’t taking the outcome of one bet and using that as your new bet amount…]

Quote: ThatDonGuy

That's not as surprising as it sounds.
What are you doing is, in effect, betting 300 to win 20 if you win one bet before losing four in a row.
In other words, you are betting on getting one win before four losses, with a payoff of 1-15 odds.
Some quick math, using an even-money bet with double-zero roulette (probability of win p = 9/19):
Assuming you start with a bet of 1, there are two possible results - either you win (because one of the next four spins is a win), and end up +1, or lose (because all four of the spins lose), and end up -15.
The probability of losing is (10/19)^4; the probability of winning is 1 - (10/19)^4.
EV = 1 x (1 - (10/19)^4) - 15 x (10/19)^4 = 1 - 16 x (10/19)^4 = -0.227738
House Edge = -EV / bet x 100% = 0.227738 / 15 x 100% = 1.51825%

Remember a key concept: the less you bet, the less you expose to the house edge, and, as a result, the less you are likely to lose.
This is where Martingale has an advantage; slightly less than half of the time, you only actually bet 1/16 (in a 4-step) of the maximum you intend to risk.
link to original post

Thanks for confirming my math. My schema filled with bet sizes 1, 2, 4, and 8 produces the same result.



My question now is:
Can betting systems actually dent, and even bend, the house edge?
I would reckon they can.

Quote: ThomasK

My question now is:
Can betting systems actually dent, and even bend, the house edge?
I would reckon they can.
link to original post

What is the house edge over a single "run" of an N-step martingale on an even-money bet with win probability p?

The probability of losing (2^N - 1) is (1-p)^N
The probability of winning 1 is 1 - (1-p)^N
EV = 1 - (1-p)^N - (2^N - 1) (1-p)^N = 1 - 2^N (1-p)^N
The "bet amount" is (2^N - 1), so the HE = (2^N (1-p)^N - 1) / (2^N - 1)
= ((2 (1-p))^N - 1) / (2^N - 1) x 100%
Of course, this makes the assumption that you are always willing to risk losing 2^N - 1 units on every round of bets.
If you choose to, or are forced to, stop early, this affects the numbers greatly.
Also remember that, in a 10-step Martingale, for all intents and purposes, every bet is paid off at 1-1023 odds.

Whu are we reinventing the wheel?

Quote: DeMango

Whu are we reinventing the wheel?
link to original post

It's more like reinventing the Ford Pinto.

Quote: ThatDonGuy

Quote: ThomasK

My question now is:
Can betting systems actually dent, and even bend, the house edge?
I would reckon they can.
link to original post

What is the house edge over a single "run" of an N-step martingale on an even-money bet with win probability p?

The probability of losing (2^N - 1) is (1-p)^N
The probability of winning 1 is 1 - (1-p)^N
EV = 1 - (1-p)^N - (2^N - 1) (1-p)^N = 1 - 2^N (1-p)^N
The "bet amount" is (2^N - 1), so the HE = (2^N (1-p)^N - 1) / (2^N - 1)
= ((2 (1-p))^N - 1) / (2^N - 1) x 100%
Of course, this makes the assumption that you are always willing to risk losing 2^N - 1 units on every round of bets.
If you choose to, or are forced to, stop early, this affects the numbers greatly.
Also remember that, in a 10-step Martingale, for all intents and purposes, every bet is paid off at 1-1023 odds.
link to original post

We agree again.

My point though is, that the Wizard always emphasizes that betting systems can't even dent the house edge. Our calculations seem to suggest otherwise.

I also remember the advice to always select the games with the lowest house edge, if you have to play negative expectation games (for whatever reason).
In the case of roulette, searching a single zero table is recommended.

Now using the math, we agree upon, it is possible to play at a double zero roulette table with a similar (and even a bit lower) house edge than that of single zero roulette, costing 7 units per game.

single zero roulette: approx. -2,70%
= 18/37 - 19/37

3 stage Martingale on double zero roulette: approx. -2.38%
= ((1-(20/38)^3)*1 - (20/38)^3*7)/7

Even the dreaded triple zero roulette can be tamed with 15 units per game.

4 stage Martingale on triple zero roulette: approx. -2.30%
= ((1-(21/39)^4)*1 - (21/39)^4*15)/15

Of course the number of units per game have to remain constant. But to me this seems to be a similar decision as that of how many "coins per line" to bet in a certain video poker game.

Beeing forced to stop your play doesn't necesarily have to have an influence. You simply have to remember where in the sequence you had to stop and then resume your play from there in your next session. This is where indepenence of random events of the roulette wheel comes in very handy.

A 10 step Martingale seems quite costly (1023!) to me, as well, and surely is not worth the try.

Isn’t this semantics? The house edge is expressed as a % of the unit bet. You’re math shows that the house edge in those terms is the same no matter what system is used. It is not dented.

Your math also shows that the more money that is put at risk the more you are expected to lose. Wizard would agree with that. Best system is to risk $0.

Quote: unJon

Isn’t this semantics? The house edge is expressed as a % of the unit bet. You’re math shows that the house edge in those terms is the same no matter what system is used. It is not dented.

Key words: "in those terms." ThomasK is expressing what is, in effect, an entirely different game:
You are always betting 15 units.
Your first bet is 1 on, say, red in roulette, and if you win, your remaining 14 is put into a Bill Breaker machine, that has a guaranteed return of 100%.
If the first bet loses, the second bet is 2, and if that wins, the remaining 11 goes into Bill Breaker.
If the second bet loses, the third bet is 4, and if that wins, the remaining 8 goes into Bill Breaker.

I understand. I guess I just think ThomasK is proclaiming that the more money you expose to the house edge the more you are expected to lose. Well, duh!

ETA: Compare, for example, a four step Marty to someone with a 15 unit bankroll that will min bet until either up one unit or down 15 units.

I'm very sorry that I can't seem to state my point properly.

Staying with the examples of single and double zero roulette:

The house edge of single zero roulette is approx. 2.7%.
This is independent of the bet size, because the house edge is the already normalized (i.e. relative to 1 unit) indicator, obtained by dividing the expected value by the bet size.

The corresponding house edge for double zero roulette is approx. 5.26%.

If you decide to bet seven units on red on each roll at a single zero wheel and keep doing that infinitely often, the house edge will remain 2.7%.

The corresponding is true for a bet of seven units on red on each roll at a double zero wheel, infinitely often: The house edge will remain 5.26%.

But if you decide to use the seven units at the double zero roulette wheel to bet a 3 step Martingale on red and repeat this infinitely often, you will end up with a house edge of approx. 2.38%. This is less then half the house edge of what this double zero wheel should have (and even beats the single zero roulette).

Following the advice "Play the games with the lowest house edge" and assuming that only double zero roulette wheels are available, wouldn't a player choose the 3 step Martingale because of the lower house edge?

Quote: ThomasK

My point though is, that the Wizard always emphasizes that betting systems can't even dent the house edge. Our calculations seem to suggest otherwise.
link to original post

Does the Wizard know what this means?

Quote: ThomasK

I'm very sorry that I can't seem to state my point properly.

Staying with the examples of single and double zero roulette:

The house edge of single zero roulette is approx. 2.7%.
This is independent of the bet size, because the house edge is the already normalized (i.e. relative to 1 unit) indicator, obtained by dividing the expected value by the bet size.

The corresponding house edge for double zero roulette is approx. 5.26%.

If you decide to bet seven units on red on each roll at a single zero wheel and keep doing that infinitely often, the house edge will remain 2.7%.

The corresponding is true for a bet of seven units on red on each roll at a double zero wheel, infinitely often: The house edge will remain 5.26%.

But if you decide to use the seven units at the double zero roulette wheel to bet a 3 step Martingale on red and repeat this infinitely often, you will end up with a house edge of approx. 2.38%. This is less then half the house edge of what this double zero wheel should have (and even beats the single zero roulette).

Following the advice "Play the games with the lowest house edge" and assuming that only double zero roulette wheels are available, wouldn't a player choose the 3 step Martingale because of the lower house edge?
link to original post

Maybe I’m misunderstanding but I think you are comparing apples to oranges in that your denominator for 2.38% is not the sum of the amount actually wagered.

In Craps you can dramatically change the HE of a line bet with free odds, but not the EV. You could say this is a trick enabled by betting more, that makes things look different if you focus on just one thing, and this shows HE can be a funny thing

Is this a case of changing the HE while not lowering the EV ... increasing it even?

Quote: ThomasK

I'm very sorry that I can't seem to state my point properly.

But if you decide to use the seven units at the double zero roulette wheel to bet a 3 step Martingale on red and repeat this infinitely often, you will end up with a house edge of approx. 2.38%. This is less then half the house edge of what this double zero wheel should have (and even beats the single zero roulette).

Quite simply... You are wrong.
The house edge on double zero roulette is 5.76% no matter what your betting strategy....
Unless you include the five number bet covering 0, 00, 1, 2, 3 in which case you can have a house edge of 7.89%,

Quote: ThomasK

My question now is:
Can betting systems actually dent, and even bend, the house edge?
I would reckon they can.
link to original post

You reckon wrong!

Quote: unJon

[...]

Maybe I’m misunderstanding but I think you are comparing apples to oranges in that your denominator for 2.38% is not the sum of the amount actually wagered.
link to original post

I understand what you are referring to: The way the house calculates their edge.
And from their persepctive the edge remains the constant 5.26%:


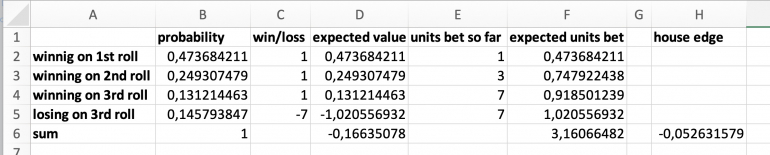
picture: figures



Please see the experiment I proposed in which the "finance controller" gives away seven units to be wagered at roulette. She receives back either nothing, when the game is lost, or the winning payout, in our case eight units. Calculating the house edge from these parameters results in the 2.38%.
Likewise the player, actually betting at the table, may well ignore the intermediate units or simply think of them as temporary tokens which are needed to play the three step Martingale procedure.

The player therefore is able to play a game at the low house edge of 2.38% while the house themselves won't be harmed because they still earn the 5.26% of the money they see beeing wagered at the table.

I keep calling the player's disadvantage the house edge, because, as you can see from the experiment, the money the finance controller loses actually stays with the house. I also assume, and in the case oft experiment's cast am sure, that the players are fully trustworthy, will stick to the rules of their assigned games, and will not take any of the chips for themselves.

Quote: ThomasK

I understand what you are referring to: The way the house calculates their edge.
And from their persepctive the edge remains the constant 5.26%:

Please see the experiment I proposed in which the "finance controller" gives away seven units to be wagered at roulette. She receives back either nothing, when the game is lost, or the winning payout, in our case eight units. Calculating the house edge from these parameters results in the 2.38%.
link to original post

The house edge and the player's disadvantage is the same. Perspective has nothing to do with it. 5.26% If your system changes that, your maths is plain wrong.

House edge =100-(Total return)/(Total wagered) %

You can't calculate it on money not wagered.

Quote: odiousgambit

In Craps you can dramatically change the HE of a line bet with free odds, but not the EV. You could say this is a trick enabled by betting more, that makes things look different if you focus on just one thing, and this shows HE can be a funny thing

Is this a case of changing the HE while not lowering the EV ... increasing it even?
link to original post

Thank you for this perfect example.
If the house edge may be lowered by factoring in the zero advantage free odds bets, why shouldn't it be appropriate to even go one step further:
The player decides to play pass line bets with full 3X, 4X, 5X odds. She needs to have six units available, one for the initial bet and 5 units in case a 6 or an 8 is established.
Now deviding the expected value, which hasn't changed after all, by the six units results in an even lower house edge of 0.24%.





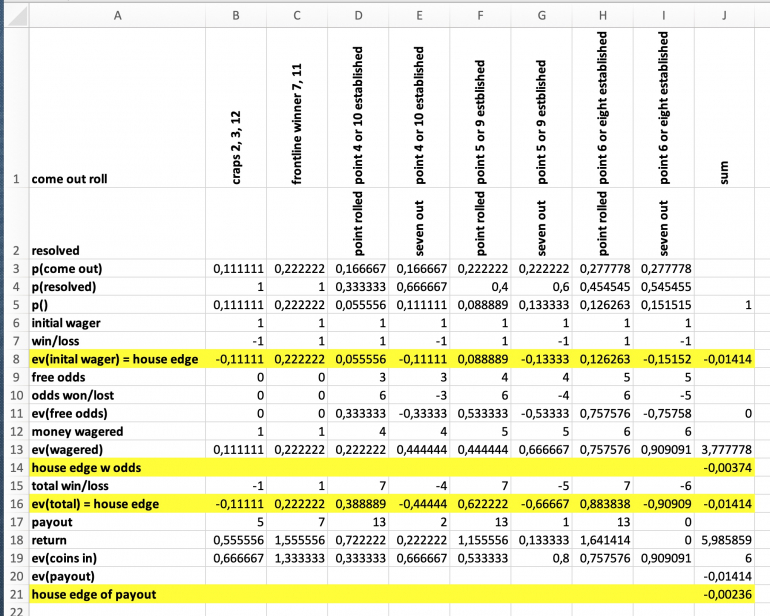
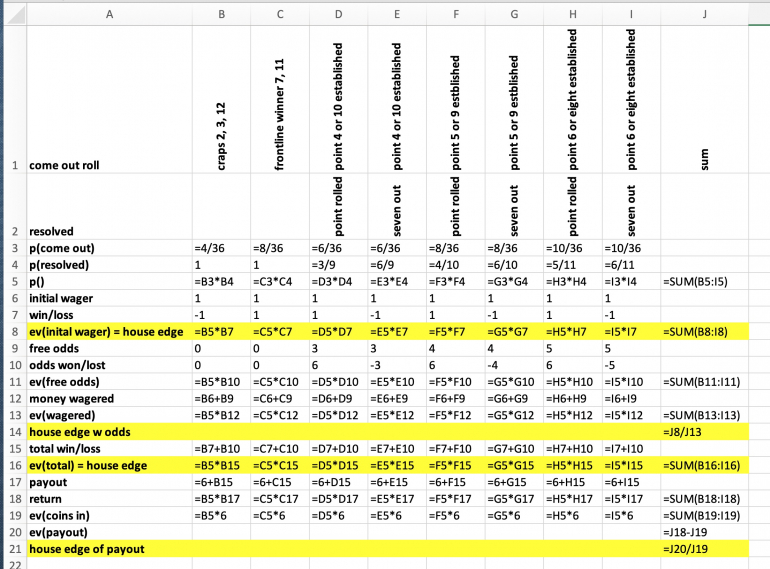
How lunatic can someone be?

The idea behind it is using hypothetical slot machines as a mathematical model. I tend to call them "equivalent slot machines" because they bear the same payout amounts and corresponding probabilities, and therefore the same expected value, as the game analyzed. As a special feature of the equivalent slot machine the paytable not only lists the payouts but also their corresponding probabilities.

For the pass line bet in craps with 3X, 4X, 5X odds imagine we had a handheld gaming computer available that would offer to play craps and was set to only play the pass line. Imagine further we put this gaming computer in a box having a slot for inserting coins and a tray for the payout. The components were now connected in such a way that six coins would have to be inserted into the slot to start one round. Depending on the outcome of that round the box would cash out according to this pay table:

pay	probability
13	0,27071
7	0,22222
5	0,11111
2	0,11111
1	0,13333

The calculations above have the figures in rows 17 through 21. The expected value (row 20) is that of a pass line bet with 3X, 4X, 5X odds.

One way of determining the house edge of this slot machine is to look inside and determine the expected number of coins for each possible situation, leaving "unused" coins in the credit meter, and dividing the expected value by that. This is the well known house edge when factoring in the free odds bets: 0.37% (see rows 9 through 14 above).

The other way of calculating it is to look from outside at the pay table and the coin in. The expected value is still the same but for the house edge we need to divide by the six coins we insert for every round: 0.24% (in rows 17 through 21).

The insanity isn't over, yet.

Imagine now we had to provide a second such box but we don't have another of these handheld gaming computers. Instead we have a single-board computer on the shelf. We use the imbeded random number generator and implement the payout table, based on the probabilities given. The single-board computer is then connected to the slot and tray and the box is closed. This second box now exhibits the exact same behaviour as our first model and has the 0.24% house edge.

The point here is that in our second box we no longer can leave "unused" coins in the credit meter, because six coins are inserted, one probability is determined and the corresponding number of coins is payed out. So the expected value has to be divided by six to determine the house edge.

From outside both boxes behave identical. The individual steps performed inside the boxes are irrelevant: Actually playing a round of craps or simply selecting one of the random outcomes.

The same is true for the "finance controller" in my propsed experiment. She inserts seven "coins" into an equivalent slot machine, waiting for the outcome, not caring about what is going on "inside". And nothing can prevent the players from ignoring what they actually are doing at the roulette table, either.

I agree with you: "funny thing". And thanks again for this perfect cue.

Quote: OnceDear

[...]

The house edge and the player's disadvantage is the same. Perspective has nothing to do with it. 5.26% If your system changes that, your maths is plain wrong.

House edge =100-(Total return)/(Total wagered) %

You can't calculate it on money not wagered.
link to original post

Please see my reply to odiousgambit who gave the perfect cue for a detailed explanation on why the player's disadvantage can differ from the house edge.

The house is only able to monitor the base games like a roll of a roulette ball or a round in craps. The expected values of the games and the money wagered, as observed by the house, then combine to this well known house edge.

The player has the freedom of combining the base games in a way that reduces his disadvantage. The expected value doesn't change for the player and remains to be that of the house. But ignoring any intermediate bets and any money "not wagered" lets the player put only the necessary initial amount into the equation which greatly alters the value of his disadvantage.

In a one-on-one situation the house might be able to exactly figure out which game the player is playing and what his house edge is. But monitoring all patrons on the floor seems not feasible.
Furthermore the player can easily use a rather simple counter measure. Independence of random events in this case is the player's friend. Using the three step Martingale as an example, the player could play each roll or step of the Martingale in a different casino. Monitoring impossible.

So the best the house can do is to assume random and independent bet sizes. They have to calculate the average, or expected, wager for each single base game and use that sum to divide the expected value.

I still am missing something. All the math you are doing appears to me to be multiplying an unchanging house edge per unit wagered by the amount wagered. And declaring that the martingale does better on that math than a different system.

The reason that’s true is because the Marty has a lower amount wagered than the comparison system.

This thread needs to be locked.

Quote: DeMango

This thread needs to be locked.
link to original post

Nooooo..... Let them keep digging.

Quote: OnceDear

Quote: DeMango

This thread needs to be locked.
link to original post

Nooooo..... Let them keep digging.
link to original post

All about the clicks?

Quote: DeMango

Quote: OnceDear

Quote: DeMango

This thread needs to be locked.
link to original post

Nooooo..... Let them keep digging.
link to original post

All about the clicks?
link to original post

Not so much as you might like to think.