Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Nope. After 12 hours, the expected number of spams is 1, but that's not what the problem asks.Quote: ThatDonGuyQuote: ThatDonGuy
The average number of spams in t hours is 4 t^2.
This = 1 when t = 1/2, so the expected waiting time for the first spam is 30 minutes.
link to original post
The average number of spams in t days is 4 t^2.
This = 1 when t = 1/2, so the expected waiting time for the first spam is 12 hours.
link to original post
It's sort of like mean vs median. People often think of them as the same but they're not always the same
Thus the chance of having no spam at time t is (1-t2/N)N.
The spreadsheet shows that after 10 hours it's 50:50 whether you've had any spam and the average time of the first spam is about 10h38m.
I suspect there's an integral that can get the exact value as N tends to infinity!
Quote: charliepatrickAll I've done is to create a spreadsheet where there are N (large) potential spams. Each one has a probability of being sent of t2/N, so this is a close approximation for small t. (t=1 implies 12 hours.)
Thus the chance of having no spam at time t is (1-t2/N)N.
The spreadsheet shows that after 10 hours it's 50:50 whether you've had any spam and the average time of the first spam is about 10h38m.
I suspect there's an integral that can get the exact value as N tends to infinity!
link to original post
But an exact answer and closed form solution are required to get credit
There donít seem to be any pending answers, so hereís the solution.Quote: Ace2A study of one billion email accounts shows that they received an average of four spam emails within 24 hours of creating the account, sixteen spams within 48 hours and thirty-six spams within 72 hours.
Assuming the aforementioned growth rate is continuous, starts the instant an account is opened and never ends, whatís the expected waiting time for a new account to receive its first spam ?
link to original post
The data shows that the average number of total spams received is t^2, where t is the number of 12-hour periods elapsed.
The expected waiting time for an event to happen is the sum of the probabilities of it not happening over all time. Applying Poisson, the probability of no spams at any time t is: 1 / e^(t^2). These probabilities for all time can be summed by taking the integral from zero to infinity of 1 / e^(t^2) dt
The integral evaluates to: √π / 2. Multiply that by 12 hours to get the answer of 6 √π =~ 10.63 hours
You open a new email account and bet a friend on how long it will take to receive the first spam. Whatís the fair over/under, expressed in hours ?
If anyone is interested, you simply equate 1 / e^(t^2) to 50% and solve for t, which gives the answer of: sqrt(Ln(2)) * 12 =~ 9.9907 hoursQuote: Ace2Extra credit (easy):
You open a new email account and bet a friend on how long it will take to receive the first spam. Whatís the fair over/under, expressed in hours ?
link to original post
Quote: Ace2There donít seem to be any pending answers, so hereís the solution.
The data shows that the average number of total spams received is t^2, where t is the number of 12-hour periods elapsed.
The expected waiting time for an event to happen is the sum of the probabilities of it not happening over all time. Applying Poisson, the probability of no spams at any time t is: 1 / e^(t^2). These probabilities for all time can be summed by taking the integral from zero to infinity of 1 / e^(t^2) dt
The integral evaluates to: √π / 2. Multiply that by 12 hours to get the answer of 6 √π =~ 10.63 hours
link to original post
I incorrectly threw a t into my integral. Without it, the integral is the special case of the error function. Tough but good question.
I wonder if my answer of 3 hours is the answer to anything of interest.
Extra credit part 2:Quote: Ace2A study of one billion email accounts shows that they received an average of four spam emails within 24 hours of creating the account, sixteen spams within 48 hours and thirty-six spams within 72 hours.
Assuming the aforementioned growth rate is continuous, starts the instant an account is opened and never ends, whatís the expected waiting time for a new account to receive its first spam ?
link to original post
What is the standard deviation of the expected waiting time?
Extra credit part 3:Quote: Ace2A study of one billion email accounts shows that they received an average of four spam emails within 24 hours of creating the account, sixteen spams within 48 hours and thirty-six spams within 72 hours.
Assuming the aforementioned growth rate is continuous, starts the instant an account is opened and never ends, whatís the expected waiting time for a new account to receive its first spam ?
link to original post
What is the mode (most common value) of the waiting time to receive the first spam ?
You must descend two 50' cliffs. You have one 80' rope, a knife, some carribeaners and a rappelling device to descend the rope(s). Additionally, there are anchors on the top of each cliff to affix the rope. How do you safely get down both cliffs? It is not required to retain the rope when you're done.
1. You affix one end of the rope to the first anchor;
2. You drop 50í along the rope to reach the second anchor;
3. You affix the other end of the rope to the second anchor (to be safer, you may make a sliding knot there using carabiners and rappelling devices);
4. You climb up 20í while holding the rope;
5. You cut the rope there while holding the lower cut end and drop 70í to the bottom.
Quote: acesideThe climber must use the knife to cut the rope. It takes 5 steps for the climber to safely reach the bottom:
1. You affix one end of the rope to the first anchor;
2. You drop 50í along the rope to reach the second anchor;
3. You affix the other end of the rope to the second anchor (to be safer, you may make a sliding knot there using carabiners and rappelling devices);
4. You climb up 20í while holding the rope;
5. You cut the rope there while holding the lower cut end and drop 70í to the bottom.
link to original post
When you cut the rope in step 5, what's holding the top of the 20' section of the rope to the cliff face? You're going to plunge 40 feet.
Or is that considered acceptable?
Quote: Wizard...You must descend two 50' cliffs. You have one 80' rope,...

2. You attach one end of the 20í rope to the first anchor;
3. You attach a carabiner to the other end of the 20í rope;
4. You insert the 60í rope in the carabiner and fold it into a 30í double rope;
5. You drop down the cliff along the 50í equipment you just made;
6. You pull out the 60í rope from the carabiner and use it for the second cliff.
You decide to start playing at a 25-5000 limit double zero roulette wheel, which allows for an 8-step Martingale.
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
Assume you are making even-money bets (i.e. the probability of a win on each bet is 9/19).
Also note that the median calculation can be an approximation.
Quote: ThatDonGuy
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
link to original post
Number of wins or number of bets resolved?
Quote: ThatDonGuyWith all of the recent talk about roulette, here's a related math problem:
You decide to start playing at a 25-5000 limit double zero roulette wheel, which allows for an 8-step Martingale.
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
Assume you are making even-money bets (i.e. the probability of a win on each bet is 9/19).
Also note that the median calculation can be an approximation.
link to original post
To approximate the median, I assumed the n in the formula for the first n terms of a geometric series can be a non-integer.

Quote: Ace2Quote: ThatDonGuy
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
link to original post
Number of wins or number of bets resolved?
link to original post
Number of wins.
Quote: ChesterDogQuote: ThatDonGuyWith all of the recent talk about roulette, here's a related math problem:
You decide to start playing at a 25-5000 limit double zero roulette wheel, which allows for an 8-step Martingale.
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
Assume you are making even-money bets (i.e. the probability of a win on each bet is 9/19).
Also note that the median calculation can be an approximation.
link to original post
To approximate the median, I assumed the n in the formula for the first n terms of a geometric series can be a non-integer.
link to original post
Isnít there a simpler way to get the median (which gives me a slightly different answer).
Probability of at least i martingale wins before a loss equals:
p(i)=W^i
Set p(i) = 0.5
Ln(0.5) / Ln(W) = i
i = 117.3742
Show there is a value of x, with 1 < x < e, such that πx = xπ
Quote: unJonQuote: ChesterDogQuote: ThatDonGuyWith all of the recent talk about roulette, here's a related math problem:
You decide to start playing at a 25-5000 limit double zero roulette wheel, which allows for an 8-step Martingale.
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
Assume you are making even-money bets (i.e. the probability of a win on each bet is 9/19).
Also note that the median calculation can be an approximation.
link to original post
To approximate the median, I assumed the n in the formula for the first n terms of a geometric series can be a non-integer.
link to original post
Isnít there a simpler way to get the median (which gives me a slightly different answer).
Probability of at least i martingale wins before a loss equals:
p(i)=W^i
Set p(i) = 0.5
Ln(0.5) / Ln(W) = i
i = 117.3742
link to original post
Your method finds n which is the number of terms of the geometric series to make the sum 0.5.
To convert to i which is the number of wins, just subtract 1 from n.
Quote: teliotShow there is a value of x, with 1 < x < e, such that πx = xπ
link to original post
We seek a value where π^x = x^π
Or where (π^(1/π))^πx = (x^(1/x))^πx
Taking the log base πx of both sides,
where π^(1/π) = x^(1/x)
It's obvious this is true at π, but we require another solution < e.
I can show upon request that the function x^(1/x) is maximized at a value of e.
I hope it doesn't break the rules to say that π^(1/π) =~ 1.439619496
and e^(1/e) =~ 1.444667861
The direction I'm thinking of going would break the graphing calculator rule.
Note to myself:
If f(x)=x^(1/x)
Then
f'(x) = x^((1/x)-2) * (1-ln(x)), which I can prove upon request.
Sorry, that's as much as I have so far.
No credit yet. But here's a hint if you want it.Quote: WizardQuote: teliotShow there is a value of x, with 1 < x < e, such that πx = xπ
link to original post
We seek a value where π^x = x^π
Or where (π^(1/π))^πx = (x^(1/x))^πx
Taking the log base πx of both sides,
where π^(1/π) = x^(1/x)
It's obvious this is true at π, but we require another solution < e.
I can show upon request that the function x^(1/x) is maximized at a value of e.
I hope it doesn't break the rules to say that π^(1/π) =~ 1.439619496
and e^(1/e) =~ 1.444667861
The direction I'm thinking of going would break the graphing calculator rule.
Note to myself:
If f(x)=x^(1/x)
Then
f'(x) = x^((1/x)-2) * (1-ln(x)), which I can prove upon request.
Sorry, that's as much as I have so far.
link to original post
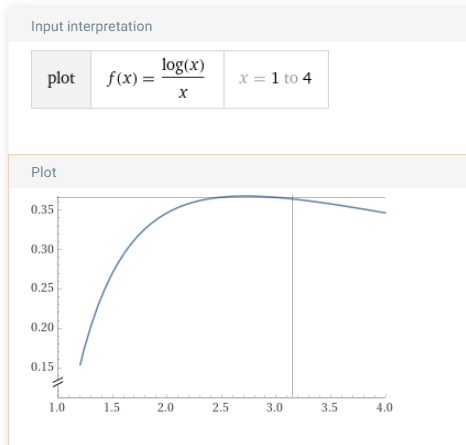
The function you need to use 1st quarter calculus on is f(x) = ln(x)/x . Find a local maximum for f(x). Why does this even matter?
π^x = x^π, we get
x ln(π) = π ln(x).
Then we transform it into
ln(π)/π = ln(x)/x.
Now, we consider the range of this new function
f(x) = ln(x)/x, which is continuous in the domain of x>0.
The derivative of f(x) is
fí(x) = [1-ln(x)]/(x^2).
Setting fí(x)=0, we get a maximum (extremum) of this function at the point
x=e, where f(e)=1/e.
The minimum of this function is negative infinity.
Now, we compare these two values,
ln(π)/π ~ 0.364 < 1/e ~ 0.368,
which means that the value ln(π)/π is within the range of the function f(x); therefore, there exists a value x such that ln(π)/π = ln(x)/x.
Actually, there exist two values of x that satisfy this equation. In the subdomain of 0<x<1, the range is from negative infinity to 0; in 1<x<e, it is from 0 to 1/e; in e<x, it is from 0 to 1/e. Therefore, one value of x is greater than e, and the other one is within the subdomain of 1<x<e.
Quote: acesideTaking the logarithm of both sides of
π^x = x^π, we get
x ln(π) = π ln(x).
Then we transform it into
ln(π)/π = ln(x)/x.
Now, we consider the range of this new function
f(x) = ln(x)/x, which is continuous in the domain of x>0.
The derivative of f(x) is
fí(x) = [1-ln(x)]/(x^2).
Setting fí(x)=0, we get a maximum (extremum) of this function at the point
x=e, where f(1/e)=1/e~ 0.368.
The minimum of this function is negative infinity.
Now, we compare these two values,
ln(π)/π ~ 0.364 < 1/e ~ 0.368,
which means that the value ln(π)/π is within the range of the function f(x); therefore, there exists a value x such that ln(π)/π = ln(x)/x.
Actually, there exist two values of x that satisfy this equation. One is greater than e, and the other one is within the subdomain of 1<x<e.
link to original post
Here's how I would finish your argument.
Recall fí(x) = [1-ln(x)]/(x^2).
For x > e, we have f'(x) < 0, so f(x) is decreasing.
For x < e, we have f'(x) > 0, so f(x) is increasing.
So f(x) increases on the interval [1, e] from 0 to the maximum f(e).
And f(x) decreases on the interval [e, +infinity) from the maximum f(e) to the limit, which is 0.
Now pi > e, so 0 < f(pi) < f(e), because f(x) is decreasing with x > e.
Since f(x) is increasing from f(1) = 0 to f(e) and f(pi) is an intermediate value, the Intermediate value theorem (a continuous function crosses every intermediate value) says there must be an x with 1 < x < e and f(x) = f(pi).
But f(x) = f(pi) means ln(x)/x = ln(pi)/pi, which means x^(pi) = pi^x.
Anyway, that's how I would do it. You don't need to know any values. And I'm not sure I've been very clear here.
Here is an image that shows this function. I doubt the image makes the argument any more clear.
Quote: unJonQuote: ChesterDogQuote: ThatDonGuyWith all of the recent talk about roulette, here's a related math problem:
You decide to start playing at a 25-5000 limit double zero roulette wheel, which allows for an 8-step Martingale.
What are the (a) median, (b) mean, and (c) standard deviation of the number of wins before you lose 8 bets in a row?
Assume you are making even-money bets (i.e. the probability of a win on each bet is 9/19).
Also note that the median calculation can be an approximation.
link to original post
To approximate the median, I assumed the n in the formula for the first n terms of a geometric series can be a non-integer.
link to original post
Isnít there a simpler way to get the median (which gives me a slightly different answer).
Probability of at least i martingale wins before a loss equals:
p(i)=W^i
Set p(i) = 0.5
Ln(0.5) / Ln(W) = i
i = 117.3742
link to original post
Chester, I get your numbers for the mean and SD.
UnJon, I get your number for the median.
1 + x + 4 x^2 + 9 x^3 + 16 x^4 + ...
= (1 + x + x^2 + x^3 + ...) + (3 x + 3 x^2 + 3 x^3 + 3 x^4 + ...) + (5 x^2 + 5 x^3 + 5 x^4 + ...) + ...
= (1 + x + x^2 + x^3 + ...) (1 + 3 x + 5 x^2 + 7 x^3 + ...)
= (1 + x + x^2 + x^3 + ...) ((1 + x + x^2 + x^3 + ...) + (2 x + 4 x^2 + 6 x^3 + 8 x^4 + ...))
= (1 + x + x^2 + x^3 + ...) ((1 + x + x^2 + x^3 + ...) + 2x (1 + 2 x^2 + 3 x^3 + 4 x^4 + ...))
= (1 / (1 - x)) ((1 / (1 - x) + 2x / (1 - x)^2)
= (1 / (1 - x)) ((1 - x + 2x) / (1 - x)^2)
= (x + 1) / (1 - x)^3
Let p be the probability of losing the bankroll.
For example, in an 8-step martingale on double-zero roulette, p = (10/19)^8.
P(n wins before losing) = (1 - p)^n p
The median number of wins = the integer n such that P(0 wins) + P(1 win) + ... + P((n-1) wins) < 1/2, but P(0 wins) + P(1 win) + ... + P((n-1) wins) >= 1/2.
This is 1 + the largest integer n such that P(0 wins) + P(1 win) + ... + P((n-1) wins) < 1/2.
The sum for 0 through (n-1) wins = p + (1 - p) p + (1 - p)^2 p + ... + (1 - p)^(n - 1) = p (1 - (1 - p)^n) / (1 - (1 - p)) = 1 - (1 - p)^n.
If 1 - (1 - p)^n = 1/2, then (1 - p)^n = 1/2
n = ln (1/2) / ln (1 - p) = - ln 2 / ln (1 - p)
Since we are counting discrete wins, n = ceiling(- ln 2 / ln (1 - p))
The mean = 0 p + 1 (1 - p) p + 2 (1 - p)^2 p + 3 (1 - p)^3 p + ...
= p (1 - p) (1 + 2 (1 - p) + 3 (1 - p)^2 + ...)
= p (1 - p) / (1 - (1 - p))^2
= (1 - p) / p
The variance = p (0 - m)^2 + (1 - p) p (1 - m)^2 + (1 - p)^2 p (2 - m)^2 + ...
= p (0 + (1 - p) + 4 (1 - p)^2 + 9 (1 - p)^3 + 16 (1 - p)^4 + ...)
+ p (-(1 - p) 2m - (1 - p)^2 4m - (1 - p)^3 6m - ...)
+ p m^2 (1 + (1 - p) + (1 - p)^2 + (1 - p)^3 + ...)
= (1 - p) p ((1 - p) + 1) / p^3 + m^2 - 2 (1 - p) m / p
Substitute (1 - p) / p for m:
v = (1 - p) ((1 - p) + 1) / p^2 + (1 - p)^2 / p^2 - 2(1 - p)^2 / p^2
= ((1 - p)^2 + (1 - p) + (1 - p)^2 - 2(1 - p)^2) / p^2
= (1 - p) / p^2
SD = sqrt(1 - p) / p
For p = (10/19)^8:
Median = 118
Mean = 168.83563
SD = 169.33489
The question only asks for existence, but not the analytical nor numerical solution.
so let's only do the existence part for now.
consider a function f(x) = pi^x - x^pi. on the closed interval [1,e]. equivalently, 1 <= x <= e
let's quote the Intermediate Value Thm.
if real function g is continous on closed interval [a,b], k is some real number between g(a) and g(b),
then there is some number c that belongs to [a, b] such that g(c) = k.
(let's skip the part of proving f(x) is continous. however, difference of continuos functions is still continous. and both functions pi^x and x^pi can be proved continous on [1,e])
let's find out the boudaries value
f(1) = pi - 1. it is greater than 0.
f(e) = pi^e - e^pi = (roughly) -0.6815 . it is less than 0.
Now let's go back with application of Intermediate Value Thm, it now says:
if a real function f is continous on closed interval [1,e],
and 0 is some real number between f(1) and f(e), (as there is a change of sign, f(1) > 0 and f(e)<0)
then there is a number c belongs to [1, e] such that f(c) = 0.
so, we are settled that there is a number c, in the closed interval [1,e], such that f(c) = 0.
[ this is the end of proving existence, I hope it works.]
Extra:
Finding analytical solution is difficult. But numerical solution is easier to find.
Because of what we have done above, now we are certain that there is a solution in the range of [1,e].
what we need to do, it is to input values of x, starting from 1, inceasinly toward e, into f(x) = pi^x - x^pi
in the beginning, we get outcomes less than 0.
since we do know there is a change of sign eventually, from negative to positive,
so we can also start with values of x near e, and work decreasingly.
with some extrapolation, we can peg the wanted x value to around 2.382179
put into the f(x), so, pi^2.382179 - 2.382179^pi
result is 2.34124121 * (10^-7), close to zero.
hence the numerical solution.
[x]
Quote: teliotShow there is a value of x, with 1 < x < e, such that πx = xπ
link to original post
We seek a value where π^x = x^π
Or where (π^(1/π))^πx = (x^(1/x))^πx
Taking the log base πx of both sides,
where π^(1/π) = x^(1/x)
It's obvious this is true at π, but we require another solution < e.
If f(x)=x^(1/x)
Then f'(x) = x^((1/x)-2) * (1-ln(x)). This I can show upon request if it's needed for full credit.
It's easy to see a root for this function is at e, because 1-ln(e) = 0.
Is this a minimum or a maximum value of f(x)?
What if x>e?
(anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
ln(x) will be >1, so 1-ln(x) will be negative.
The product of a positive and negative is negative.
What if 1<x<e?
We already know (anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
0<ln(x)<1, so 1-ln(x) is positive.
The product of a positive and positive is positive.
So, if the derivative is positive before e and negative after e, the f(x) is growing as it increases getting close to e and decreasing after it passes e.
Thus, the root of e is a relative maximum.
As mentioned before, x^(1/x) has a root at x=e and I've shown it is a maximum.
What e^(1/e) is, for a value of x^(1/x) for x close to e, x^(1/x) will be a little less.
So, some value must equal pi^(1/pi), other than pi itself.
Note: There is a good video on the derivative of x^(1/x) here...
This is one of my favorite YouTube channels.
I cannot accept your proof above because you used a calculator to compute f(e).Quote: kendozhangI will try my luck on this one.
The question only asks for existence, but not the analytical nor numerical solution.
so let's only do the existence part for now.
consider a function f(x) = pi^x - x^pi. on the closed interval [1,e]. equivalently, 1 <= x <= e
let's quote the Intermediate Value Thm.
if real function g is continous on closed interval [a,b], k is some real number between g(a) and g(b),
then there is some number c that belongs to [a, b] such that g(c) = k.
(let's skip the part of proving f(x) is continous. however, difference of continuos functions is still continous. and both functions pi^x and x^pi can be proved continous on [1,e])
let's find out the boudaries value
f(1) = pi - 1. it is greater than 0.
f(e) = pi^e - e^pi = (roughly) -0.6815 . it is less than 0.
Now let's go back with application of Intermediate Value Thm, it now says:
if a real function f is continous on closed interval [1,e],
and 0 is some real number between f(1) and f(e), (as there is a change of sign, f(1) > 0 and f(e)<0)
then there is a number c belongs to [1, e] such that f(c) = 0.
so, we are settled that there is a number c, in the closed interval [1,e], such that f(c) = 0.
[ this is the end of proving existence, I hope it works.]
Extra:
Finding analytical solution is difficult. But numerical solution is easier to find.
Because of what we have done above, now we are certain that there is a solution in the range of [1,e].
what we need to do, it is to input values of x, starting from 1, inceasinly toward e, into f(x) = pi^x - x^pi
in the beginning, we get outcomes less than 0.
since we do know there is a change of sign eventually, from negative to positive,
so we can also start with values of x near e, and work decreasingly.
with some extrapolation, we can peg the wanted x value to around 2.382179
put into the f(x), so, pi^2.382179 - 2.382179^pi
result is 2.34124121 * (10^-7), close to zero.
hence the numerical solution.
[x]
link to original post
without quoting the intermediate value theorem, I'm not sure I can ever give full credit. You may have forgotten that theorem, but it is taught in first quarter calculus. look it up and edit your answer for full credit.Quote: WizardQuote: teliotShow there is a value of x, with 1 < x < e, such that πx = xπ
link to original post
We seek a value where π^x = x^π
Or where (π^(1/π))^πx = (x^(1/x))^πx
Taking the log base πx of both sides,
where π^(1/π) = x^(1/x)
It's obvious this is true at π, but we require another solution < e.
If f(x)=x^(1/x)
Then f'(x) = x^((1/x)-2) * (1-ln(x)). This I can show upon request if it's needed for full credit.
It's easy to see a root for this function is at e, because 1-ln(e) = 0.
Is this a minimum or a maximum value of f(x)?
What if x>e?
(anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
ln(x) will be >1, so 1-ln(x) will be negative.
The product of a positive and negative is negative.
What if 1<x<e?
We already know (anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
0<ln(x)<1, so 1-ln(x) is positive.
The product of a positive and positive is positive.
So, if the derivative is positive before e and negative after e, the f(x) is growing as it increases getting close to e and decreasing after it passes e.
Thus, the root of e is a relative maximum.
As mentioned before, x^(1/x) has a root at x=e and I've shown it is a maximum.
What e^(1/e) is, for a value of x^(1/x) for x close to e, x^(1/x) will be a little less.
So, some value must equal pi^(1/pi), other than pi itself.
Note: There is a good video on the derivative of x^(1/x) here...
This is one of my favorite YouTube channels.
link to original post
in this case, we would need to prove f(e) = pi^e - e^pi is negative without calculator.
it comes down to compare the values of e^pi and pi^e.
e^pi vs. pi^e
(ln on both)
pi vs. e*ln(pi)
(divide by ln(pi))
pi/ln(pi) vs. e
(as ln(e) is 1, attach it as the denominator to the right hand side)
pi/ln(pi) vs. e/ln(e)
now that both sides are in the same form. we define a function h(x) = x/ln(x), where x >1
so left-hand side is now h(pi)
and right-hand side is now h(e)
the derivate of h(x)
set j(x)= x, k(x)=ln(x)
the derivative of h(x) = (j(x)/k(x))' = (j'*k - k*j')/k^2
= (1*ln(x)-x*1/x)/(ln(x))^2
=(lnx-1)/(lnx)^2
note that,
if x > e,
(lnx-1) is positive, so (lnx-1)/(lnx)^2 is also positive.
if x<e,
(lnx-1) is negative, so (lnx-1)/(lnx)^2 is also negative.
that means e is a local minimum of function h(x)
then h(e) < h(pi)
thus e/ln(e) < pi/ln(pi)
let's transform them back. pretty much what we had in the beginning, backward.
e/ln(e) < pi/ln(pi)
e < pi/ln(pi)
e*ln(pi) < pi
pi^e < e^pi
thus pi^e - e^pi < 0.
without finding the actual value of the expression, as long as we know it is negative, it is enough.
[x]
Quote: teliot... without quoting the intermediate value theorem, I'm not sure I can ever give full credit. You may have forgotten that theorem, but it is taught in first quarter calculus. look it up and edit your answer for full credit.
link to original post
I think the intermediate value theorem is obvious and didn't need quoting. However, I know it's more elegant to quote theorems than to assume anything is obvious, so let me reword it a bit, out of respect to you.
Quote: teliotShow there is a value of x, with 1 < x < e, such that πx = xπ
link to original post
We seek a value where π^x = x^π
Or where (π^(1/π))^πx = (x^(1/x))^πx
Taking the log base πx of both sides,
where π^(1/π) = x^(1/x)
It's obvious this is true at π, but we require another solution < e.
If f(x)=x^(1/x)
Then f'(x) = x^((1/x)-2) * (1-ln(x)). This I can show upon request if it's needed for full credit.
It's easy to see a root for this function is at e, because 1-ln(e) = 0.
Is this a minimum or a maximum value of f(x)?
What if x>e?
(anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
ln(x) will be >1, so 1-ln(x) will be negative.
The product of a positive and negative is negative.
What if 1<x<e?
We already know (anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
0<ln(x)<1, so 1-ln(x) is positive.
The product of a positive and positive is positive.
So, if the derivative is positive before e and negative after e, the f(x) is growing as it increases getting close to e and decreasing after it passes e.
Thus, the root of e is a relative maximum.
As mentioned before, x^(1/x) has a root at x=e and I've shown it is a maximum.
I have made the case that e^(1/e) > pi^(1/pi).
I hope, per Eliot's rules, I may say that 1^(1/1) = 1.
The Intermediate Value Theorem says that if f(x) is a continuous function, then every value between f(a) and f(b) must be in the range of that function somewhere.
To apply to this case:
f(1) = 1 (I hope this doesn't violate Eliot's rules, as it's obvious 1^1 = 1).
f(e) > f(pi)
Therefore, there must be some value between 1 and e that is exactly f(pi).
And for this you get full credit, which includes my gift of Int(1/(e^pi - pi^e)) beers (or equivalent in whiskey) next time we get together.Quote: WizardQuote: teliot... without quoting the intermediate value theorem, I'm not sure I can ever give full credit. You may have forgotten that theorem, but it is taught in first quarter calculus. look it up and edit your answer for full credit.
link to original post
I think the intermediate value theorem is obvious and didn't need quoting. However, I know it's more elegant to quote theorems than to assume anything is obvious, so let me reword it a bit, out of respect to you.Quote: teliotShow there is a value of x, with 1 < x < e, such that πx = xπ
link to original post
We seek a value where π^x = x^π
Or where (π^(1/π))^πx = (x^(1/x))^πx
Taking the log base πx of both sides,
where π^(1/π) = x^(1/x)
It's obvious this is true at π, but we require another solution < e.
If f(x)=x^(1/x)
Then f'(x) = x^((1/x)-2) * (1-ln(x)). This I can show upon request if it's needed for full credit.
It's easy to see a root for this function is at e, because 1-ln(e) = 0.
Is this a minimum or a maximum value of f(x)?
What if x>e?
(anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
ln(x) will be >1, so 1-ln(x) will be negative.
The product of a positive and negative is negative.
What if 1<x<e?
We already know (anything positive)^(anything real) > 0, so x^((1/x)-2) will be positive.
0<ln(x)<1, so 1-ln(x) is positive.
The product of a positive and positive is positive.
So, if the derivative is positive before e and negative after e, the f(x) is growing as it increases getting close to e and decreasing after it passes e.
Thus, the root of e is a relative maximum.
As mentioned before, x^(1/x) has a root at x=e and I've shown it is a maximum.
I have made the case that e^(1/e) > pi^(1/pi).
I hope, per Eliot's rules, I may say that 1^(1/1) = 1.
The Intermediate Value Theorem says that if f(x) is a continuous function, then every value between f(a) and f(b) must be in the range of that function somewhere.
To apply to this case:
f(1) = 1 (I hope this doesn't violate Eliot's rules, as it's obvious 1^1 = 1).
f(e) > f(pi)
Therefore, there must be some value between 1 and e that is exactly f(pi).
link to original post
Quote: teliotAnd for this you get full credit, which includes my gift of Int(1/(e^pi - pi^e)) beers (or equivalent in whiskey) next time we get together.
link to original post
This makes my day! It's not easy to earn a beer from Eliot. It's easy to be given one, but earing one is quite different.
Before the rounding, I show this is 1.46727626 beers. I happily accept the one beer rounded down and the next round is on me.
You have no watch/phone and you donít ask anyone what time it is. What is the expected waiting time for the next bus to arrive ?
I'm getting 1.547050849 minutes.
I confess I had to use an integral calculator. It would have been a tedious mess to do the integration without one.
Then again, maybe there is a more elegant solution I don't see.
Or maybe I'm completely wrong anyway.
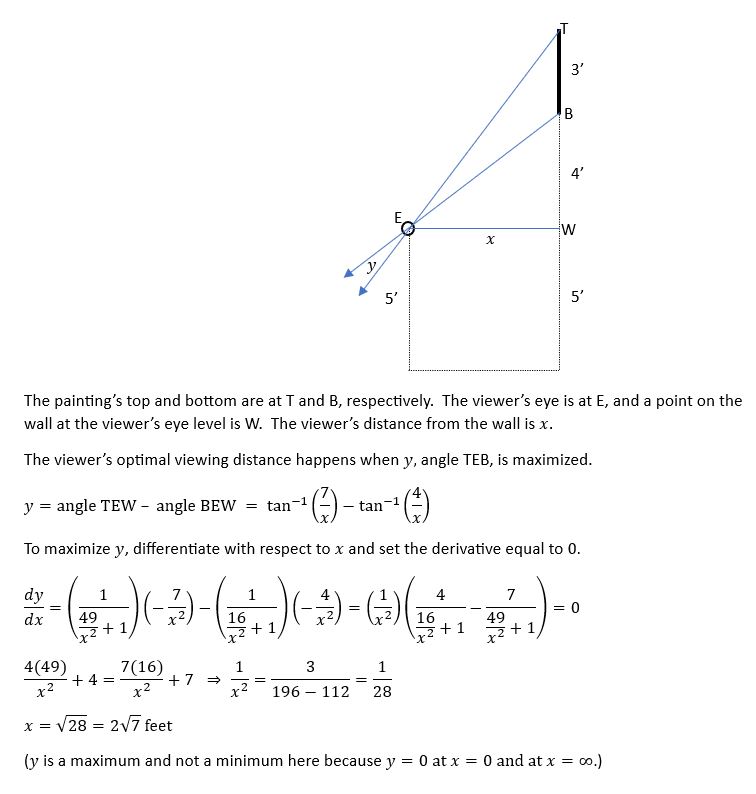
The distance from the bottom of the paining to the floor is 9'.
The distance from your eyes to the bottom of the floor is 5'.
How far from the painting should you stand to get the best view?
I assume that the 'best view' means that the angle centered at the viewer's eye between the top and bottom of the painting is maximized.
My answer is that the viewer should stand at this distance d from the wall on which the painting hangs: d = 2*sqrt(7) or about 5.2915 feet.
I will show my work if my answer is correct.
Quote: ChesterDog
I assume that the 'best view' means that the angle centered at the viewer's eye between the top and bottom of the painting is maximized.
Yes, your interpretation is correct.
My answer is that the viewer should stand at this distance d from the wall on which the painting hangs: d = 2*sqrt(7) or about 5.2915 feet.
I will show my work if my answer is correct.
link to original post
I agree!
Quote: ChesterDog
link to original post
Outstanding work! May I use this directly if I make an Ask the Wizard question out of it?
Quote: WizardQuote: ChesterDog
link to original post
Outstanding work! May I use this directly if I make an Ask the Wizard question out of it?
link to original post
Thanks! Yes.
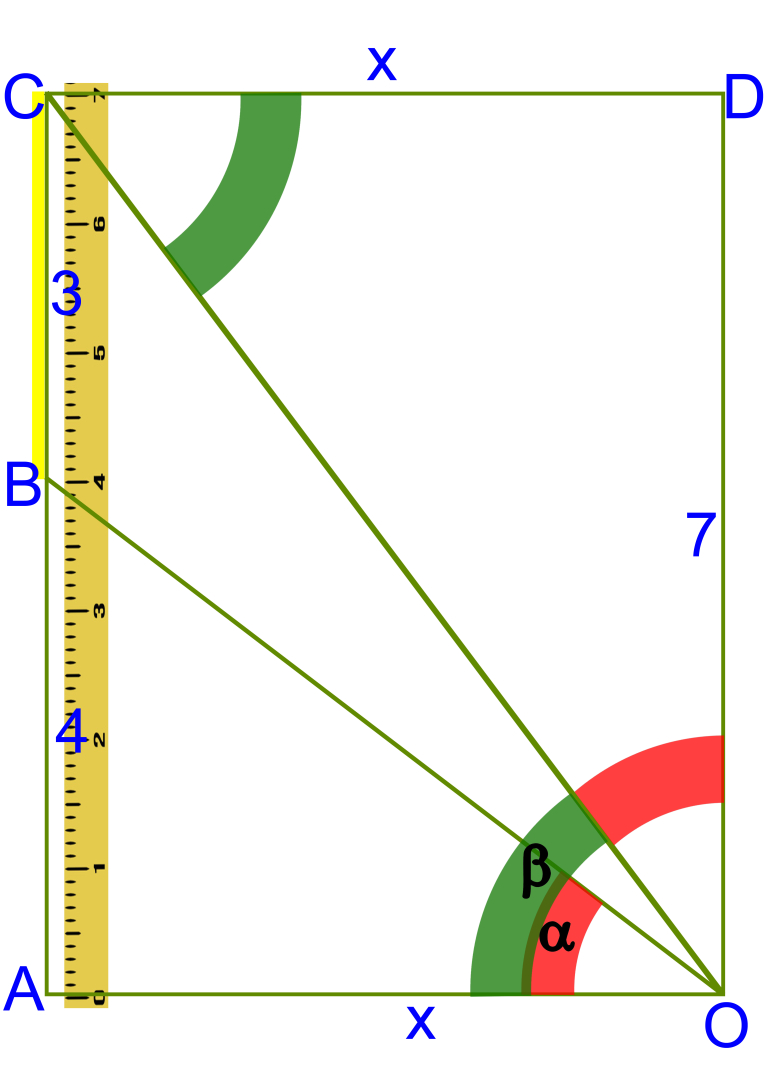
As has been said TAN(alpha)=4/x and TAN (beta)=7/x. The constructed rectangle has a height of 7 and width of x. The assertion is that alpha+beta=90o.
By similar triangles you get TAN(alpha)=x/7 [ODC] =4/x [OAB]. This leads to x2=28.
I agree. Can you show your method please. ?Quote: Wizard
I'm getting 1.547050849 minutes.
I confess I had to use an integral calculator. It would have been a tedious mess to do the integration without one.
Then again, maybe there is a more elegant solution I don't see.
Or maybe I'm completely wrong anyway.
link to original post
Quote: Ace2Can you show your method please. ?
link to original post
Here is my method (PDF). I wasn't sure how to phrase some of those steps. I welcome all comments, especially if there is a simpler way to solve this.
With the average arrival time of one passenger per minute, the answer is ten minus the integral from zero to ten of x^12 * x / (e^x * 12!) divided by the integral from zero to ten of x^12 / (e^x * 12!). The 12! cancels so we are left with ten minus the gamma function of 14 divided by the gamma function of 13, albeit the lower incomplete gamma function since we are integrating from zero to ten instead of zero to infinity. Therefore the answer can be expressed as:Quote: WizardQuote: Ace2Can you show your method please. ?
link to original post
Here is my method (PDF). I wasn't sure how to phrase some of those steps. I welcome all comments, especially if there is a simpler way to solve this.
link to original post
10 - γ(14,10) / γ(13,10) =
10 - (13! - 118569301068800/e^10) / (12! − 8351484697600/e^10)
=~ 1.547 minutes
I originally calculated the answer for thirteen total people waiting because you see twelve people and therefore you are the thirteenth person arriving at the bus stop. But this is not meant to be a trick question or an English debate so Iíll accept it as twelve total
Quote: Ace2With the average arrival time of one passenger per minute, the answer is ten minus the integral from zero to ten of x^12 * x / (e^x * 12!) divided by the integral from zero to ten of x^12 / (e^x * 12!). The 12! cancels so we are left with ten minus the gamma function of 14 divided by the gamma function of 13, albeit the lower incomplete gamma function since we are integrating from zero to ten instead of zero to infinity. Therefore the answer can be expressed as:
10 - γ(14,10) / γ(13,10) =
10 - (13! - 118569301068800/e^10) / (12! − 8351484697600/e^10)
=~ 1.547 minutes
I originally calculated the answer for thirteen total people waiting because you see twelve people and therefore you are the thirteenth person arriving at the bus stop. But this is not meant to be a trick question or an English debate so Iíll accept it as twelve total
link to original post
I think I need to review the gamma function. I forgot how it could be expressed as an integral for non-integer values.


