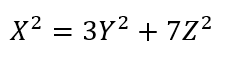Poll
 | 25 votes (49.01%) | ||
 | 16 votes (31.37%) | ||
 | 7 votes (13.72%) | ||
 | 4 votes (7.84%) | ||
 | 12 votes (23.52%) | ||
 | 3 votes (5.88%) | ||
 | 6 votes (11.76%) | ||
 | 5 votes (9.8%) | ||
 | 12 votes (23.52%) | ||
 | 10 votes (19.6%) |
51 members have voted
Then you can easily proceed to prove BD=BF, AE=AF etc.
The problem would also work if you looked at a 12-sided polygon and the distances between the 1 and 2, 1 and 4, 1 and 6 on a standard clock, even stranger as 2+4=6 as well!
Quote: charliepatricklink to original postIf you numbered the points (A)P1, (B)P2, thru P9, then you can extend three sides P1P2, P4P5, P7P8 - in this case P7P8 is horizontal. Since the original shape is regular, you could rotate everything by 120 degrees and the above process would create an identical shape and triangle. Thus, by symmetry, the encompassing triangle is equilateral. Similarly, in your case, BDF is equilateral.
Then you can easily proceed to prove BD=BF, AE=AF etc.
The problem would also work if you looked at a 12-sided polygon and the distances between the 1 and 2, 1 and 4, 1 and 6 on a standard clock, even stranger as 2+4=6 as well!

Last week, there was a cricket on my floor. I wanted to trap it with a cup so that I could safely move it outside. But every time I got close, it hopped exactly 1 foot in a random direction.
I took note of its starting position and came closer. Boom — it hopped in a random direction. I got close again. Boom — it took another hop in a random direction, independent of the direction of the first hop.
What was the most probable distance between the cricket’s position after two random jumps and its starting position?
(Note: This puzzle is not asking for the expected distance, but rather the most probable distance. In other words, if you considered the probability distribution over all possible distances, where was the peak of this distribution?)
Quote: GialmereWhat was the most probable distance between the cricket’s position after two random jumps and its starting position?
link to original post
This is just off the top of my head, but I would say it's a tie between 0 feet and 2 feet. Not exactly these distances, but as close as you can get, without getting there exactly.
Let's say you drew a clock round the grasshopper after the first jump, where his original location was at 6:00. The clock is separated into 60 segments. The answer would be a tie between:
12:00 and 12:01
5:59 and 6:00
6:00 and 6:01
11:59 and 12:00
I'm happy to provide more reasoning upon request.
However technically it could be a value slightly smaller than 2 since you can't get 2+delta. So you might be able to get closer to (say) 1.999 +/- delta more often than 2 +/- delta. But this logic could then apply to 1.99999 etc. Thus at the limit it's 2.
Maybe a better question is to ask the expected distance away rather than the most likely distance. But I see this point was already made in the original post.Quote: charliepatricklink to original postAssume the first hop is to (1,0), then the second will result in being on a circle radius one, centre (1,0). So it passes through the origin tangent to the Y-axis and (2,0). The point on that circle is assumed to be a random angle, so as you go round the circle the differential of the distance is less at (2,0) than (0,0). So my first thought is 2 is the most likely value (i.e. given a delta>0 there are more points on the circle where the distance is between 2+delta and 2-delta).
However technically it could be a value slightly smaller than 2 since you can't get 2+delta. So you might be able to get closer to (say) 1.999 +/- delta more often than 2 +/- delta. But this logic could then apply to 1.99999 etc. Thus at the limit it's 2.
Anyway, my intuition does not say what your intuition says. I look at the set of every final circle after the second jump (as you described) and ask what common points can they have.
Quote: charliepatricklink to original postAssume the first hop is to (1,0), then the second will result in being on a circle radius one, centre (1,0). So it passes through the origin tangent to the Y-axis and (2,0). The point on that circle is assumed to be a random angle, so as you go round the circle the differential of the distance is less at (2,0) than (0,0). So my first thought is 2 is the most likely value (i.e. given a delta>0 there are more points on the circle where the distance is between 2+delta and 2-delta).
However technically it could be a value slightly smaller than 2 since you can't get 2+delta. So you might be able to get closer to (say) 1.999 +/- delta more often than 2 +/- delta. But this logic could then apply to 1.99999 etc. Thus at the limit it's 2.
Welcome back Charlie. You've been missed.
Quote: charliepatricklink to original postAssume the first hop is to (1,0), then the second will result in being on a circle radius one, centre (1,0). So it passes through the origin tangent to the Y-axis and (2,0). The point on that circle is assumed to be a random angle, so as you go round the circle the differential of the distance is less at (2,0) than (0,0). So my first thought is 2 is the most likely value (i.e. given a delta>0 there are more points on the circle where the distance is between 2+delta and 2-delta).
However technically it could be a value slightly smaller than 2 since you can't get 2+delta. So you might be able to get closer to (say) 1.999 +/- delta more often than 2 +/- delta. But this logic could then apply to 1.99999 etc. Thus at the limit it's 2.
Welcome back Charlie. You've been missed.
Quote: charliepatricklink to original postAssume the first hop is to (1,0), then the second will result in being on a circle radius one, centre (1,0). So it passes through the origin tangent to the Y-axis and (2,0). The point on that circle is assumed to be a random angle, so as you go round the circle the differential of the distance is less at (2,0) than (0,0). So my first thought is 2 is the most likely value (i.e. given a delta>0 there are more points on the circle where the distance is between 2+delta and 2-delta).
However technically it could be a value slightly smaller than 2 since you can't get 2+delta. So you might be able to get closer to (say) 1.999 +/- delta more often than 2 +/- delta. But this logic could then apply to 1.99999 etc. Thus at the limit it's 2.
Correct!!
Well done.
First off, thanks to the circular symmetry of the puzzle, you could assume the cricket hopped in any direction at first, “without loss of generality” as mathematicians say, and restricted your attention to the second hop. So let’s suppose the cricket’s first hop was to the right. After its second hop, it could be anywhere along the circle centered 1 foot to the right of its origin.
After the second hop, the farthest the cricket could be from its starting point was 2 feet — if the cricket again hopped to the right. Meanwhile, the closest it could be was right where it started — 0 feet away — if the cricket hopped left. The answer was therefore somewhere in this range.
A few readers were tempted to say that all distances between 0 and 2 feet were equally likely, since there were two ways to achieve each distance (i.e., in the upper semicircle and, symmetrically, in the lower semicircle). However, this line of thinking neglected the continuous nature of the problem. With infinitely many locations between 0 and 2, the probability of any specific distance was technically zero. But here, you were asked to find the maximum of the continuous probability distribution between 0 and 2.
One way to find the most likely distance was to simulate the two hops, as solver Lowell Vaughn did. Lowell ran a total of 4 million simulations, dividing each of the two hops into 2,000 uniformly distributed angles. Here was the resulting distribution Lowell found:

From this graph, it appeared that the distance of 2 feet was the most probable. In other words, after two hops, the cricket was more likely to be farther away (i.e., more than 1 foot) from the origin and less likely to be closer (i.e., less than 1 foot) to it. But how could that be?
Jackson Curtis explained this unexpected result by looking at the circle representing the second hop, examining which parts of it were approximately the same distance from the starting point. The following animation highlights which points along the second circle were close to a particular distance from the origin, indicated in red:

As you can see, there was “more red” for distances close to 2 feet.2 This was because the two circles — the circle representing the second hop and the fully expanded probing circle — were perfectly tangent, an alignment that meant they had many points close together.
So it was indeed possible to solve this puzzle without an ounce of algebra or computer code. Nevertheless, several solvers, like Emily Boyajian of Minneapolis, Minnesota, explicitly found the probability distribution that Lowell approximated computationally. According to Emily, the probability p(r) that the cricket was a distance r from the origin was p(r) = 2/(𝜋√(4−r2)).
In case you were curious, I never did catch that cricket. Why? Because it always hopped a bit farther than my intuition said it would.
--------------------------------------------
I tried telling some jokes to an audience of crickets...
I have no idea if they were funny.

A number of children played at marbles. Each child won a different number of games and the total number of games won by the boys equaled the total number of games won by the two girls.
As a momento of the occasion, they each received a present of marbles, equal to the square of the number of games he or she had won. In total, the boys received as many marbles as the girls, and the total number of marbles received was less than 100.
How many marbles were given as presents?
I'm not sure I understand the puzzle correctly, but my answer is 90.
Here are the number of games won by each kid:
girl 1: 3
girl 2: 6
boy 1: 2
boy 2: 4
boy 3: 5
9+36 = 4 + 16 + 25
My method was trial and error. Maybe I was lucky, but I solved it about two minutes.
There might be three or four boys (five boys gives a minimum of 1+4+9+16+25=55). Using similar ideas (1,2,3)...(2,4,5) and (1,2,3,4)...(1,2,4,5) only gives one match.
So the answer is (3,6) and (2,4,5).
The earlier answer added up the same same marbles given out but not the numbers of games won.
Quote: GialmereSorry. Both incorrect
link to original post
I think I don't understand what is being asked then.
Quote: mwalz9Wouldn't we need to know how many boys there were? The problem never says that. Or is that part of the problem?
link to original post
You can also deduce there can't be two boys as within the limits stated you can't have A2+B2=C2+D2 and A+B=C+D are all non-zero and different.
I think you speak for the majorityQuote: WizardQuote: GialmereSorry. Both incorrect
link to original post
I think I don't understand what is being asked then.link to original post
Your solution violates this condition: "the total number of games won by the boys equaled the total number of games won by the two girls"Quote: WizardQuote: GialmereSorry. Both incorrect
link to original post
I think I don't understand what is being asked then.link to original post
I'll try and rephrase the question and add some irrelevant info.Quote: WizardI think I don't understand what is being asked then.
There are two girls and a number of boys who form the home team and they played a number of games against another away team. You are only concerned with the number of games won by each of the girls and boys from the home team.
After the match has concluded each child of the home team receives a gift consisting of a number of marbles equal to the square of the number of games that child won.
Only considering members of the home team ... you observe the following
(i) the number of games won by each child is different (or unique) from any of the others
(ii) the total number of games won by the girls is equal to the total number of games won by the boys
(iii) the total number of marbles given to girls is equal to the total number of marbles given to boys
(iv) the total number of marbles handed out to the home team children is less than 100
(v) Every one managed to win at least one match.
How many boys were there in the team, how many matches did each child win, and how many marbles were handed out.
Mathematically B1,B2...Bn,G1,G2 are all unique; B1+B2+...+Bn=G1+G2; B12+...Bn2= G12+G22.
Quote: Ace2I think you speak for the majoritylink to original postQuote: WizardQuote: GialmereSorry. Both incorrect
link to original post
I think I don't understand what is being asked then.link to original post
I thought it was a clear set of rules.
Quote: charliepatricklink to original postYes 1 can see that (4,5) and (1,2,6) work for a total of 82 marbles (41 marbles and 9 games won each sex) (as would (5,7) (1,3,8) but that's too many marbles in total 74+74=148.)
The earlier answer added up the same same marbles given out but not the numbers of games won.
Quote: mwalz9Thanks! That helped me come up with this. This was a fun mid afternoon brain excercise.
link to original postThis was fun. I used scratch paper and trial and error as well. I think I have it as 3 boys played. 1, 2, and 6 games won for a total of 9 games won and 41 marbles earned. Then the 2 girls won 4 and 5 games each making 9 games won and 41 marbles earned. For a total of 18 games won and 82 marbles earned.
Correct!!!
Good show.
-----------------------------------------------
A colon can really change the meaning of a sentence
"The marbles fell out of my pocket."
Vs
"The marbles fell out of my colon."
You pick three numbers from 0 to 9, without replacement. For example 7-0-2.
What is the probability a US serial number will contains:
1. None of the chosen numbers.
2. Exactly one of them.
3. Exactly two of them.
4. All three of them.
Let me emphasize that if the chosen numbers are 7-0-2 and the serial number is 77777777, then there is only one match -- the 7. It doesn't matter that it matched multiple times.
For non-US members, assume a serial number consists of 8 digits from 0 to 9, chosen WITH replacement.

Quote: WizardReady for the next puzzle? This one might be a little tedious to solve, but will show a good understanding of combinatorial math.
link to original post
You pick three numbers from 0 to 9, without replacement. For example 7-0-2.
What is the probability a US serial number will contains:
1. None of the chosen numbers.
2. Exactly one of them.
3. Exactly two of them.
4. All three of them.
Let me emphasize that if the chosen numbers are 7-0-2 and the serial number is 77777777, then there is only one match -- the 7. It doesn't matter that it matched multiple times.
For non-US members, assume a serial number consists of 8 digits from 0 to 9, chosen WITH replacement.
Here is a list of my patterns of serial numbers and numbers of permutations of each.
An example of my pattern is 023 3, by which I mean one chosen digit does not appear in the serial number, another appears twice, and the third appears three times. The second 3 means that 3 digits of the serial number are none of the chosen digits.
| Pattern | Permutations | Fraction |
|---|---|---|
000 8 | 5764801 | |
Total 0 | 5764801 | 0.0576 |
001 7 | 19765032 | |
002 6 | 9882516 | |
003 5 | 2823576 | |
004 4 | 504210 | |
005 3 | 57624 | |
006 2 | 4116 | |
007 1 | 168 | |
008 0 | 3 | |
Total 1 | 33037245 | 0.3304 |
011 6 | 19765032 | |
012 5 | 16941456 | |
013 4 | 4033680 | |
014 3 | 576240 | |
015 2 | 49392 | |
016 1 | 2352 | |
017 0 | 48 | |
022 4 | 3025260 | |
023 3 | 1152480 | |
024 2 | 123480 | |
025 1 | 7056 | |
026 0 | 168 | |
033 2 | 82320 | |
034 1 | 11760 | |
035 0 | 336 | |
044 0 | 210 | |
Total 2 | 45771270 | 0.4577 |
111 5 | 5647152 | |
112 4 | 6050520 | |
113 3 | 1152480 | |
114 2 | 123480 | |
115 1 | 7056 | |
116 0 | 168 | |
122 3 | 1728720 | |
123 2 | 493920 | |
124 1 | 35280 | |
125 0 | 1008 | |
133 1 | 23520 | |
134 0 | 1680 | |
222 2 | 123480 | |
223 1 | 35280 | |
224 0 | 1260 | |
233 0 | 1680 | |
Total 3 | 15426684 | 0.1543 |
Quote: ChesterDog
link to original post
Here is a list of my patterns of serial numbers and numbers of permutations of each.
An example of my pattern is 023 3, by which I mean one chosen digit does not appear in the serial number, another appears twice, and the third appears three times. The second 3 means that 3 digits of the serial number are none of the chosen digits.
Pattern Permutations Fraction
I agree! Good work, Charlie!

Take a solid ball and cut in in half. Label the flat side "Heads" and the curved side "Tails."
What are the probabilities of Heads and Tails when flipping the hemisphere?
Assume that the hemisphere impacts the ground for the last time (i.e. does not bounce again) at any orientation with equal probability.
Quote: GialmereTake a solid ball and cut in in half. Label the flat side "Heads" and the curved side "Tails."
What are the probabilities of Heads and Tails when flipping the hemisphere?
Quote: teliotp(Heads)=3/8, p(Tails) = 5/8. This is based on the location of the center of mass of a hemisphere.
You are definitely in the (half a) ballpark.
By symmetry just look at a semi-circle being the vertical part of the sphere, rather like a D dropped randomly in 2-D space. If the centre of gravity (assumed to be 3/8 R) lies to the right of the tip, then the sphere falls towards the curved surface, otherwise it doesn't. So just consider the angle of the straight line to the vertical and a line from the centre of gravity to the tip.
The tangent of the angle is 3/8, so the angle is arctan(3/8) = about 20.556 degrees. Consider the angle of the flat surface compared to vertical. So between 0 and 20.556 it falls curved, between 20.556 and 90 it falls flat. By symmetry the same logic applies 90 thru 180.
So chance of flat is about (90-20.556)*2/360 = 0.3858.
Quote: charliepatrickThe sphere has two options, it either lands with the curved surface landing first (chance = 1/2) and so falls onto the curved surface, or one of the tips of the cut surface touches first.
By symmetry just look at a semi-circle being the vertical part of the sphere, rather like a D dropped randomly in 2-D space. If the centre of gravity (assumed to be 3/8 R) lies to the right of the tip, then the sphere falls towards the curved surface, otherwise it doesn't. So just consider the angle of the straight line to the vertical and a line from the centre of gravity to the tip.
The tangent of the angle is 3/8, so the angle is arctan(3/8) = about 20.556 degrees. Consider the angle of the flat surface compared to vertical. So between 0 and 20.556 it falls curved, between 20.556 and 90 it falls flat. By symmetry the same logic applies 90 thru 180.
So chance of flat is about (90-20.556)*2/360 = 0.3858.
Correct!!
Quote: WizardIf nobody gets it and this one relies on physics, can you please give us the property at play.
Nothing tricky. Just an easy math puzzle. The designer points out that this could indeed be a very complex problem but, rather annoyingly, does not do so until after he reveals the answer. This is why I tried to clarify things at the end of the description.
----------------------------------------------

Quote: charliepatricklink to original postThe sphere has two options, it either lands with the curved surface landing first (chance = 1/2) and so falls onto the curved surface, or one of the tips of the cut surface touches first.
By symmetry just look at a semi-circle being the vertical part of the sphere, rather like a D dropped randomly in 2-D space. If the centre of gravity (assumed to be 3/8 R) lies to the right of the tip, then the sphere falls towards the curved surface, otherwise it doesn't. So just consider the angle of the straight line to the vertical and a line from the centre of gravity to the tip.
The tangent of the angle is 3/8, so the angle is arctan(3/8) = about 20.556 degrees. Consider the angle of the flat surface compared to vertical. So between 0 and 20.556 it falls curved, between 20.556 and 90 it falls flat. By symmetry the same logic applies 90 thru 180.
So chance of flat is about (90-20.556)*2/360 = 0.3858.
I thought about this again and come up with a slightly different answer by considering the solid angle of this cone.
My answer is 2pi x [1-cos(90-20.556)] / 4 pi =0.324
Consider the following figure. All pieces are squares. The area of the white square is 25. What is the area of the entire figure?
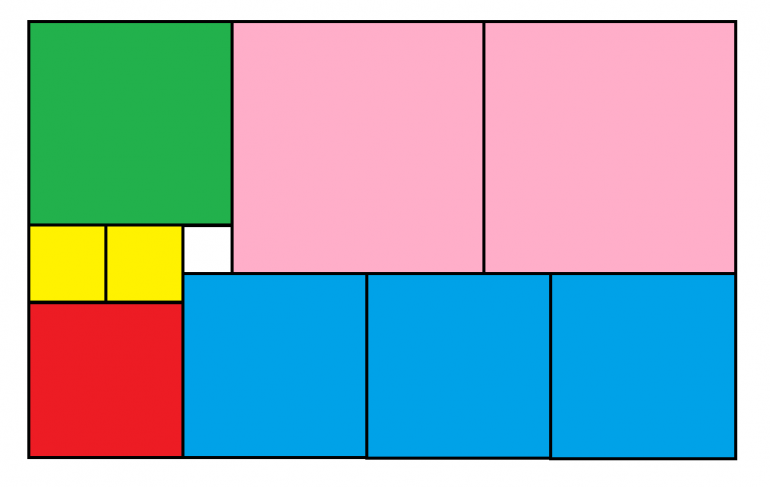
Set L-yellow=x, then
L-green=2x+5
L-pink=2x+5+5
L-red=2x
L-blue=3x-5
L-top=L-green+2*L-pink=2x+5+4x+20=6x+25
L-bottom=L-red+3*L-blue=2x+9x-15=11x-15
Let L-top=L-bottom, solve the equation to find x=8
Width=L-green+L-yellow+L-red=45
Length=L-top=73
Area=Width * Length=45 * 73=3285
Quote: acesidelink to original postHere is my answer:
Set L-yellow=x, then
L-green=2x+5
L-pink=2x+5+5
L-red=2x
L-blue=3x-5
L-top=L-green+2*L-pink=2x+5+4x+20=6x+25
L-bottom=L-red+3*L-blue=2x+9x-15=11x-15
Let L-top=L-bottom, solve the equation to find x=8
Width=L-green+L-yellow+L-red=45
Length=L-top=73
Area=Width * Length=45 * 73=3285
I agree!

Problem #1
You and two friends are in a three-person fantasy football league, drafting just three positions each for your teams: quarterback, running back and wide receiver. Yes, this is a simplified version of fantasy football.
The following table shows the top three athletes in each position, as well as the number of fantasy points they are expected to earn over the course of the season. You and your friends must each select exactly one player from each position.
:strip_icc()/pic6431488.png)
The draft is a “snake draft.” If person A drafts first, B drafts second and C drafts both third and fourth, thus the order of the picks is as follows: A-B-C-C-B-A-A-B-C.
Your friends — being the kind people that they are — agree that you can choose your pick number. Which draft position should you choose to maximize your expected fantasy score?
---------------
Problem #2
Hames Jarrison has just intercepted a pass at one end zone of a football field, and begins running — at a constant speed of 15 miles per hour — to the other end zone, 100 yards away.
At the moment he catches the ball, you are on the very same goal line, but on the other end of the field, 50 yards away from Jarrison. Caught up in the moment, you decide you will always run directly toward Jarrison’s current position, rather than plan ahead to meet him downfield along a more strategic course.
Assuming you run at a constant speed (i.e., don’t worry about any transient acceleration), how fast must you be in order to catch Jarrison before he scores a touchdown?
Quote: Gialmere...
...Which draft position should you choose to maximize your expected fantasy score?...
A's best strategy is to pick QB400. B has a choice of QB350 or RB300.
(i) In the former C is now guaranteed QB300 so picks RB300 and WR250, B will choose WR225 over RB225. A=800, B=775, C=850.
(ii) In the latter C chooses QB350 and RB250, B then chooses WR225 and will eventually get QB300. A=800, B=825, C=800.
So by choosing B and RB300 you get 825.
Quote: acesideQuote: charliepatricklink to original postThe sphere has two options, it either lands with the curved surface landing first (chance = 1/2) and so falls onto the curved surface, or one of the tips of the cut surface touches first.
By symmetry just look at a semi-circle being the vertical part of the sphere, rather like a D dropped randomly in 2-D space. If the centre of gravity (assumed to be 3/8 R) lies to the right of the tip, then the sphere falls towards the curved surface, otherwise it doesn't. So just consider the angle of the straight line to the vertical and a line from the centre of gravity to the tip.
The tangent of the angle is 3/8, so the angle is arctan(3/8) = about 20.556 degrees. Consider the angle of the flat surface compared to vertical. So between 0 and 20.556 it falls curved, between 20.556 and 90 it falls flat. By symmetry the same logic applies 90 thru 180.
So chance of flat is about (90-20.556)*2/360 = 0.3858.
I thought about this again and come up with a slightly different answer by considering the solid angle of this cone.
My answer is 2pi x [1-cos(90-20.556)] / 4 pi =0.324link to original post
I have been expecting /charliepatrick or anybody to comment on this. I brought up this solid angle consideration because the flip (rotation) axis of the hemisphere can be parallel to the flat surface or vertical, or in any direction.
I couldn't comment on your solution as I don't really understand how you've got to your answer. (I'm guessing it's a formula looking at the surface area of the sphere and comparing it with the surface (on the sphere) formed by a cone with the appropriate angle.)Quote: acesideI have been expecting /charliepatrick or anybody to comment on this. I brought up this solid angle consideration because the flip (rotation) axis of the hemisphere can be parallel to the flat surface or vertical, or in any direction.
link to original post
Thus my answer does not involve a cone but the angles between 0 and 180 where 20.556 thu 90 and 90 thru (180-20.556) will land face down.
Perhaps someone knows why one is correct and the other is wrong. It might be that the probability distribution of the line I describe isn't constant.
Quote: charliepatrickI couldn't comment on your solution as I don't really understand how you've got to your answer. (I'm guessing it's a formula looking at the surface area of the sphere and comparing it with the surface (on the sphere) formed by a cone with the appropriate angle.)Quote: acesideI have been expecting /charliepatrick or anybody to comment on this. I brought up this solid angle consideration because the flip (rotation) axis of the hemisphere can be parallel to the flat surface or vertical, or in any direction.
link to original postI think our difference is I'm looking at the angle and comparing it with 360 degrees (i.e. how much arc the angle forms on a circle) and you're looking at the area formed by the cone compared to the whole sphere's surface area.For simplicity assume the semi-sphere is placed on a level surface and left to drop, thus there in no spin/flip/rotation. If the curved surface (the sphere part) touches the surface then it will fall face up. Otherwise consider the edge of the flat surface and consider the disc formed from the flat surface. The disc has a single point of contact with the level surface, thus one only has to consider the line from the point of contact through the centre of the disc and what that angle is.
Thus my answer does not involve a cone but the angles between 0 and 180 where 20.556 thu 90 and 90 thru (180-20.556) will land face down.
Perhaps someone knows why one is correct and the other is wrong. It might be that the probability distribution of the line I describe isn't constant.link to original post
Perfect! That is exactly what I meant. In the mean time, I am thinking about using a similar device to attach to a Craps dice to gain an edge. Thank you for your confirmation.
How fast is the current?

Note: I originally, incorrectly, said "an hour." It should be a mile.