Easy math puzzles
Poll
 | 21 votes (45.65%) | ||
| | 14 votes (30.43%) | ||
| | 6 votes (13.04%) | ||
| | 3 votes (6.52%) | ||
| | 12 votes (26.08%) | ||
| | 3 votes (6.52%) | ||
| | 6 votes (13.04%) | ||
| | 5 votes (10.86%) | ||
| | 12 votes (26.08%) | ||
| | 10 votes (21.73%) |
46 members have voted
October 22nd, 2021 at 4:56:45 PM
permalink
I like the idea that you think of the puzzle as an 18-bit number and are looking for how many 0's there are. If there were at least 18 people then one could consider that for every combination of 0's and 1's there is a complimentary number of 1's and 0's. In total those two combinations have 18 0's and 18 1's, so the average of those two is 9 or each. Thus the average for all combinations is 9.
In this example there are only sixteen people so any combination with 17 or 18 0's will have no people getting across rather than -1 or -2. Thus one needs to add in 18*1 and 1*2 = 20 before dividing by 218 giving the 7.000076 answer.
In this example there are only sixteen people so any combination with 17 or 18 0's will have no people getting across rather than -1 or -2. Thus one needs to add in 18*1 and 1*2 = 20 before dividing by 218 giving the 7.000076 answer.
October 23rd, 2021 at 1:51:58 PM
permalink
Quote: charliepatrickI like the idea that you think of the puzzle as an 18-bit number and are looking for how many 0's there are. If there were at least 18 people then one could consider that for every combination of 0's and 1's there is a complimentary number of 1's and 0's. In total those two combinations have 18 0's and 18 1's, so the average of those two is 9 or each. Thus the average for all combinations is 9.
In this example there are only sixteen people so any combination with 17 or 18 0's will have no people getting across rather than -1 or -2. Thus one needs to add in 18*1 and 1*2 = 20 before dividing by 218 giving the 7.000076 answer.
link to original post
Let me modify this puzzle a little bit. If all of the players cannot have footprint marks on the tempered glass, how many players can pass this bridge?
October 23rd, 2021 at 2:30:20 PM
permalink
Quote: acesideLet me modify this puzzle a little bit. If all of the players cannot have footprint marks on the tempered glass, how many players can pass this bridge?
link to original post
Can you clarify this a little? Do you mean that all 16 cannot touch the same piece of tempered glass?
October 23rd, 2021 at 2:37:42 PM
permalink
Quote: ThatDonGuyQuote: acesideLet me modify this puzzle a little bit. If all of the players cannot have footprint marks on the tempered glass, how many players can pass this bridge?
link to original post
Can you clarify this a little? Do you mean that all 16 cannot touch the same piece of tempered glass?
link to original post
That is not what I meant. I mean the following players do not know which tempered glass panels have been stepped on, but they know the broken ordinary glass panels.
October 23rd, 2021 at 4:56:42 PM
permalink
Quote: acesideThat is not what I meant. I mean the following players do not know which tempered glass panels have been stepped on, but they know the broken ordinary glass panels.
link to original post
I get it. This happened on the show, where an elderly player couldn't remember where the previous players stepped. They had to wear hospital slippers, which I think was to avoid leaving footprints.
Am I correct with at least the first five player's chances of survival?
| Player | Probability |
|---|---|
| 1 | 0.00000381 |
| 2 | 0.00000763 |
| 3 | 0.00001526 |
| 4 | 0.00003051 |
| 5 | 0.00006094 |
Last edited by: Wizard on Oct 23, 2021
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 23rd, 2021 at 5:06:05 PM
permalink
Quote: Gialmere
You're playing a track and field board game with your family during the lockdown. If each of the runner pawns travels the indicated number of spaces every turn, at which numbered spot will all of the runners end up next to one another?
link to original post
Sorry, this is about a year old now, but.. what's the math surrounding the solution?
I've figured the answer is 19 for the spot they meet again, and the interval between those is always 30... and out of interest if any one of them is at any other spacing differential, they never meet within 15000 turns.
I figure the math behind working out the answer 'which square will they meet at' is related to the difference between the runner who moves the fastest, and the runner who moves the slowest.. but I'm not seeing a formula for that to verify.
October 23rd, 2021 at 5:56:41 PM
permalink
Quote: WizardAm I correct with at least the first five player's chances of survival?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094
link to original post
I got impatient and finished the table. Am I right?
| Player | Probability |
|---|---|
| 1 | 0.00000381 |
| 2 | 0.00000763 |
| 3 | 0.00001526 |
| 4 | 0.00003051 |
| 5 | 0.00006094 |
| 6 | 0.00011911 |
| 7 | 0.00023545 |
| 8 | 0.00046159 |
| 9 | 0.00089886 |
| 10 | 0.00175139 |
| 11 | 0.00345091 |
| 12 | 0.00693198 |
| 13 | 0.01418276 |
| 14 | 0.02923634 |
| 15 | 0.05993762 |
| 16 | 0.12152477 |
| Total | 0.23884892 |
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 24th, 2021 at 12:27:37 AM
permalink
Quote: WizardQuote: WizardAm I correct with at least the first five player's chances of survival?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094
link to original post
I got impatient and finished the table. Am I right?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094 6 0.00011911 7 0.00023545 8 0.00046159 9 0.00089886 10 0.00175139 11 0.00345091 12 0.00693198 13 0.01418276 14 0.02923634 15 0.05993762 16 0.12152477 Total 0.23884892
link to original post
Let me try this
Let x1=1st player's chances of survival;
Let x2=2nd player's chances of survival;
Let x3=3rd player's chance of survival;
... ...
Let x16=16th player's chance of survival, then we have
x1=0.5^18=3.8147E-06;
x2=(x1)^2+(1-x1)*0.5^17=7.62938E-06;
x3=(x1)^3+(x1)*(1-x2)*0.5^17+(1-x1)*(x2)*0.5^17+(1-x1)*(1-x2)*0.5^16=1.52587E-05;
I don't know how to calculate the exact value of x4, because it has 8 terms, but we can have a very good approximation because only the last term of each xn is non-negligible, so I calculated them and found the sum of all 16 terms:
x1 3.8147E-06
x2 7.62937E-06
x3 1.52586E-05
x4 3.05168E-05
x5 6.10317E-05
x6 0.000122056
x7 0.000244082
x8 0.000488045
x9 0.000975613
x10 0.001949323
x11 0.003891046
x12 0.007751811
x13 0.015383441
x14 0.030293581
x15 0.058751759
x16 0.11059998
Sum 0.230568986
Last edited by: aceside on Oct 24, 2021
October 24th, 2021 at 8:18:58 AM
permalink
Quote: acesideQuote: WizardQuote: WizardAm I correct with at least the first five player's chances of survival?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094
link to original post
I got impatient and finished the table. Am I right?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094 6 0.00011911 7 0.00023545 8 0.00046159 9 0.00089886 10 0.00175139 11 0.00345091 12 0.00693198 13 0.01418276 14 0.02923634 15 0.05993762 16 0.12152477 Total 0.23884892
link to original post
Let me try this
Let x1=1st player's chances of survival;
Let x2=2nd player's chances of survival;
Let x3=3rd player's chance of survival;
... ...
Let x16=16th player's chance of survival, then we have
x1=0.5^18=3.8147E-06;
x2=(x1)^2+(1-x1)*0.5^17=7.62938E-06;
x3=(x1)^3+(x1)*(1-x2)*0.5^17+(1-x1)*(x2)*0.5^17+(1-x1)*(1-x2)*0.5^16=1.52587E-05;
I don't know how to calculate the exact value of x4, because it has 8 terms, but we can have a very good approximation because only the last term of each xn is non-negligible, so I calculated them and found the sum of all 16 terms:
x1 3.8147E-06
x2 7.62937E-06
x3 1.52586E-05
x4 3.05168E-05
x5 6.10317E-05
x6 0.000122056
x7 0.000244082
x8 0.000488045
x9 0.000975613
x10 0.001949323
x11 0.003891046
x12 0.007751811
x13 0.015383441
x14 0.030293581
x15 0.058751759
x16 0.11059998
Sum 0.230568986
link to original post
Several of your terms are larger than Wizard's. And that's inconsistent because you are ignoring positive terms. So there seems to be a non-negligible discrepancy between the two answers.
So many better men, a few of them friends, are dead. And a thousand thousand slimy things live on, and so do I.
October 24th, 2021 at 9:46:22 AM
permalink
Quote: acesideQuote: ThatDonGuyQuote: acesideLet me modify this puzzle a little bit. If all of the players cannot have footprint marks on the tempered glass, how many players can pass this bridge?
link to original post
Can you clarify this a little? Do you mean that all 16 cannot touch the same piece of tempered glass?
link to original post
That is not what I meant. I mean the following players do not know which tempered glass panels have been stepped on, but they know the broken ordinary glass panels.
link to original post
This assumes that the 16 people do not discuss strategy in advance. If they can, then the strategy is, "When you see both panels at the same step, always use the one on the left"; the problem is now the same as the first one, and the expected number is slightly more than 7.
Let P(A,B) be the probability of getting to the point with A persons and B steps remaining.
P(18, 16) = 1
At any particular step, if there are N people remaining, either all of them make it through (with probability 1 / 2^N), or somebody does not (with probability 1 - 1 / 2^N), in which case N-1 people made it past that step, since everybody that went before that person made it, and once that person missed, the remaining people know which of the two panels at that step is good, since the other one is now shattered.
Probabilities of N people getting through:
1: 2,697,517,124,160,727,979,794,298,334,928,874,789,683,725,800,350,340,625 /
12,259,964,326,927,110,866,866,776,217,202,473,468,949,912,977,468,817,408
2: 1,964,212,080,163,879,415,864,883,856,458,098,671,857,036,517,779,546,916,875 /
200,867,255,532,373,784,442,745,261,542,645,325,315,275,374,222,849,104,412,672
3: 148,293,486,218,086,804,009,743,742,950,935,624,613,059,121,063,512,982,208,125 /
1,645,504,557,321,206,042,154,969,182,557,350,504,982,735,865,633,579,863,348,609,024
4: 1,285,367,138,214,125,938,247,419,046,043,506,562,122,293,397,493,370,198,165,875 /
6,739,986,666,787,659,948,666,753,771,754,907,668,409,286,105,635,143,120,275,902,562,304
5: 1,336,951,595,373,849,559,848,407,669,176,570,833,601,928,235,391,249,926,718,125 /
13,803,492,693,581,127,574,869,511,724,554,050,904,902,217,944,340,773,110,325,048,447,598,592
6: 170,354,180,873,343,918,394,627,482,029,532,555,019,181,269,707,182,608,153,875 /
14,134,776,518,227,074,636,666,380,005,943,348,126,619,871,175,004,951,664,972,849,610,340,958,208
7: 2,685,367,999,035,869,585,923,908,872,770,880,068,179,152,178,227,773,366,125 /
7,237,005,577,332,262,213,973,186,563,042,994,240,829,374,041,602,535,252,466,099,000,494,570,602,496
8: 5,260,280,403,685,160,364,200,323,669,276,904,586,048,518,440,857,885,075 /
1,852,673,427,797,059,126,777,135,760,139,006,525,652,319,754,650,249,024,631,321,344,126,610,074,238,976
9: 1,282,361,092,544,113,425,375,574,714,049,208,253,252,454,025,526,125 /
237,142,198,758,023,568,227,473,377,297,792,835,283,496,928,595,231,875,152,809,132,048,206,089,502,588,928
10: 38,876,263,223,777,991,428,570,948,450,414,447,717,888,243,475 /
15,177,100,720,513,508,366,558,296,147,058,741,458,143,803,430,094,840,009,779,784,451,085,189,728,165,691,392
11: 146,073,116,406,017,224,213,999,324,527,976,045,188,525 /
485,667,223,056,432,267,729,865,476,705,879,726,660,601,709,763,034,880,312,953,102,434,726,071,301,302,124,544
12: 67,497,028,115,768,980,735,398,222,216,368,115 /
7,770,675,568,902,916,283,677,847,627,294,075,626,569,627,356,208,558,085,007,249,638,955,617,140,820,833,992,704
13: 3,772,265,948,271,415,978,513,796,925 /
62,165,404,551,223,330,269,422,781,018,352,605,012,557,018,849,668,464,680,057,997,111,644,937,126,566,671,941,632
14: 24,594,251,415,116,327,595 /
248,661,618,204,893,321,077,691,124,073,410,420,050,228,075,398,673,858,720,231,988,446,579,748,506,266,687,766,528
15: 17,179,541,505 /
497,323,236,409,786,642,155,382,248,146,820,840,100,456,150,797,347,717,440,463,976,893,159,497,012,533,375,533,056
16: 1 /
497,323,236,409,786,642,155,382,248,146,820,840,100,456,150,797,347,717,440,463,976,893,159,497,012,533,375,533,056
The expected number is
119,285,438,051,491,600,965,426,158,899,637,755,285,530,818,964,278,692,622,932,395,089,512,340,802,876,506,402,971
/
497,323,236,409,786,642,155,382,248,146,820,840,100,456,150,797,347,717,440,463,976,893,159,497,012,533,375,533,056
= 0.23985946
October 24th, 2021 at 12:10:29 PM
permalink
Quote: gordonm888Quote: acesideQuote: WizardQuote: WizardAm I correct with at least the first five player's chances of survival?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094
link to original post
I got impatient and finished the table. Am I right?
Player Probability 1 0.00000381 2 0.00000763 3 0.00001526 4 0.00003051 5 0.00006094 6 0.00011911 7 0.00023545 8 0.00046159 9 0.00089886 10 0.00175139 11 0.00345091 12 0.00693198 13 0.01418276 14 0.02923634 15 0.05993762 16 0.12152477 Total 0.23884892
link to original post
Let me try this
Let x1=1st player's chances of survival;
Let x2=2nd player's chances of survival;
Let x3=3rd player's chance of survival;
... ...
Let x16=16th player's chance of survival, then we have
x1=0.5^18=3.8147E-06;
x2=(x1)^2+(1-x1)*0.5^17=7.62938E-06;
x3=(x1)^3+(x1)*(1-x2)*0.5^17+(1-x1)*(x2)*0.5^17+(1-x1)*(1-x2)*0.5^16=1.52587E-05;
I don't know how to calculate the exact value of x4, because it has 8 terms, but we can have a very good approximation because only the last term of each xn is non-negligible, so I calculated them and found the sum of all 16 terms:
x1 3.8147E-06
x2 7.62937E-06
x3 1.52586E-05
x4 3.05168E-05
x5 6.10317E-05
x6 0.000122056
x7 0.000244082
x8 0.000488045
x9 0.000975613
x10 0.001949323
x11 0.003891046
x12 0.007751811
x13 0.015383441
x14 0.030293581
x15 0.058751759
x16 0.11059998
Sum 0.230568986
link to original post
Several of your terms are larger than Wizard's. And that's inconsistent because you are ignoring positive terms. So there seems to be a non-negligible discrepancy between the two answers.
link to original post
I noticed that, but that does not necessarily mean inconsistency. Some values are larger while some are smaller. This is all caused by this approximation.
October 25th, 2021 at 8:00:20 AM
permalink
It's easy Monday. Here's a Riddler puzzle...
There are 200 episodes in a season of Riddler Jeopardy!. The first episode of the season features three brand-new contestants. Each subsequent episode includes a returning champion (the winner of the previous episode) as well as two new challengers.
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
If you pick a contestant at random from the season, what is the probability that they are a Riddler Jeopardy! champion (meaning they won at least one episode)?
There are 200 episodes in a season of Riddler Jeopardy!. The first episode of the season features three brand-new contestants. Each subsequent episode includes a returning champion (the winner of the previous episode) as well as two new challengers.
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
If you pick a contestant at random from the season, what is the probability that they are a Riddler Jeopardy! champion (meaning they won at least one episode)?
Have you tried 22 tonight? I said 22.
October 25th, 2021 at 8:45:59 AM
permalink
Quote: GialmereIt's easy Monday. Here's a Riddler puzzle...
There are 200 episodes in a season of Riddler Jeopardy!. The first episode of the season features three brand-new contestants. Each subsequent episode includes a returning champion (the winner of the previous episode) as well as two new challengers.
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
If you pick a contestant at random from the season, what is the probability that they are a Riddler Jeopardy! champion (meaning they won at least one episode)?
link to original post
The first episode has 3 new contestants, and each one after that has 2 more, so each season has 401 contestants.
The first episode's winner won all five episodes in week 1, but lost on Monday of week 2; that winner won all five episode of week 2, but lost on Monday of week 3, and so on. There are 40 weeks, so 40 of the contestants are champions.
Assuming that "pick a contestant at random from the season" means that each contestant has an equal chance of being chosen, as opposed to "choose an episode at random, then choose one of those three contestants at random," the solution is 40 / 401.
October 25th, 2021 at 8:52:05 AM
permalink
200 episodes, each with 2 non-winners, and a winner.
Each winner wins 5 episodes.
Sounds like 40 winners, out of 440 total contestants.
A randomly selected contestant has a 1 in 11 chance of being a champion.
May the cards fall in your favor.
October 25th, 2021 at 8:55:50 AM
permalink
Quote: Gialmere
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
The confusing part - The returning champions are the one who one 6 episode actually. (The first time winner of the episode is NOT a returning champion and he will win another 5 as the returning champion.)
Not sure
34 / (33 * (12 + 1) + 1 * (4 + 1)) = 34 / 434 = 7.8 % ?
Last edited by: HopHoofer on Oct 25, 2021
October 25th, 2021 at 8:59:37 AM
permalink
Quote: ThatDonGuyQuote: GialmereIt's easy Monday. Here's a Riddler puzzle...
There are 200 episodes in a season of Riddler Jeopardy!. The first episode of the season features three brand-new contestants. Each subsequent episode includes a returning champion (the winner of the previous episode) as well as two new challengers.
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
If you pick a contestant at random from the season, what is the probability that they are a Riddler Jeopardy! champion (meaning they won at least one episode)?
link to original post
The first episode has 3 new contestants, and each one after that has 2 more, so each season has 401 contestants.
The first episode's winner won all five episodes in week 1, but lost on Monday of week 2; that winner won all five episode of week 2, but lost on Monday of week 3, and so on. There are 40 weeks, so 40 of the contestants are champions.
Assuming that "pick a contestant at random from the season" means that each contestant has an equal chance of being chosen, as opposed to "choose an episode at random, then choose one of those three contestants at random," the solution is 40 / 401.
link to original post
I like your answer better.
May the cards fall in your favor.
October 25th, 2021 at 9:17:24 AM
permalink
Quote: DieterQuote: ThatDonGuyQuote: GialmereIt's easy Monday. Here's a Riddler puzzle...
There are 200 episodes in a season of Riddler Jeopardy!. The first episode of the season features three brand-new contestants. Each subsequent episode includes a returning champion (the winner of the previous episode) as well as two new challengers.
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
If you pick a contestant at random from the season, what is the probability that they are a Riddler Jeopardy! champion (meaning they won at least one episode)?
link to original post
The first episode has 3 new contestants, and each one after that has 2 more, so each season has 401 contestants.
The first episode's winner won all five episodes in week 1, but lost on Monday of week 2; that winner won all five episode of week 2, but lost on Monday of week 3, and so on. There are 40 weeks, so 40 of the contestants are champions.
Assuming that "pick a contestant at random from the season" means that each contestant has an equal chance of being chosen, as opposed to "choose an episode at random, then choose one of those three contestants at random," the solution is 40 / 401.
link to original post
I like your answer better.
link to original post
It looks like you are counting 11 contestants per week, which would be true if, after a contestant won their fifth game, they would retire undefeated and there would be three new contestants on the next show. However, the problem says that a contestant that wins five games then loses their sixth game.
Another way to look at it:
200 episodes x 3 contestants per episode = 600, but every episode but the first has a returning champion, so that's 600 - 199 = 401 different contestants.
October 25th, 2021 at 9:27:58 AM
permalink
Contestants
On the first show there are three new contestants. As each long running champion is beaten, rather than throw off, each subsequent show has the returning champion and two new contestants. Thus there are 3 + 2*199 = 401 contestants.
Champions
In the second week on Monday the person who has won five in a row (won the previous Monday) is beaten and replaced. Therefore every Monday a new champion takes over; this happens every week. There are 40 weeks (200/5), so there are 40 champions.
Losers (for discussion purposes "Loser" = non-champion)
In the first week someone won the first game and kept winning all week. Thus there were two other people "Losers" on each episode, hence 2x5 = 10 in all.
In subsequent weeks on Monday there was only one "Loser" as the current champion (not a "Loser") got knocked out, someone took over (so wasn't a "Loser") and a third player who was a "Loser". On the other days there were two "Losers" as the current champion stayed on. Thus there were 1+2+2+2+2=9 "Losers" in each of the subsequent weeks. Thus the total number of "Losers" is 10 + 39*9 = 361.
Thus there were 361 "Losers", 40 "Champions", and a total of 401 contestants; giving a probability of picking a Champion as 40/401.
If the question was pick an episode, at the end of the game pick a contestant (i.e. this includes the new champion) there there are 200 episodes of 3 people giving 600 possible picks. In the first week there is only the first week's Champion occupying five slots. In subsequent weeks last week's Champion plays on Monday and the new one plays five times (that week). Thus there are 5 + 6*39 "Champion" slots = 239; giving a probability of picking a Champion (new or old) as 239/600. (If you pick at the start of the program then there are 40 fewer, each time the new Champion wins their first game, so 199/600)
On the first show there are three new contestants. As each long running champion is beaten, rather than throw off, each subsequent show has the returning champion and two new contestants. Thus there are 3 + 2*199 = 401 contestants.
Champions
In the second week on Monday the person who has won five in a row (won the previous Monday) is beaten and replaced. Therefore every Monday a new champion takes over; this happens every week. There are 40 weeks (200/5), so there are 40 champions.
Losers (for discussion purposes "Loser" = non-champion)
In the first week someone won the first game and kept winning all week. Thus there were two other people "Losers" on each episode, hence 2x5 = 10 in all.
In subsequent weeks on Monday there was only one "Loser" as the current champion (not a "Loser") got knocked out, someone took over (so wasn't a "Loser") and a third player who was a "Loser". On the other days there were two "Losers" as the current champion stayed on. Thus there were 1+2+2+2+2=9 "Losers" in each of the subsequent weeks. Thus the total number of "Losers" is 10 + 39*9 = 361.
Thus there were 361 "Losers", 40 "Champions", and a total of 401 contestants; giving a probability of picking a Champion as 40/401.
If the question was pick an episode, at the end of the game pick a contestant (i.e. this includes the new champion) there there are 200 episodes of 3 people giving 600 possible picks. In the first week there is only the first week's Champion occupying five slots. In subsequent weeks last week's Champion plays on Monday and the new one plays five times (that week). Thus there are 5 + 6*39 "Champion" slots = 239; giving a probability of picking a Champion (new or old) as 239/600. (If you pick at the start of the program then there are 40 fewer, each time the new Champion wins their first game, so 199/600)
October 25th, 2021 at 10:09:38 AM
permalink
Quote: ThatDonGuyQuote: DieterQuote: ThatDonGuyQuote: GialmereIt's easy Monday. Here's a Riddler puzzle...
There are 200 episodes in a season of Riddler Jeopardy!. The first episode of the season features three brand-new contestants. Each subsequent episode includes a returning champion (the winner of the previous episode) as well as two new challengers.
Throughout the season, it so happens that the returning champions are particularly strong, with each one winning five consecutive episodes before being dethroned on the sixth.
If you pick a contestant at random from the season, what is the probability that they are a Riddler Jeopardy! champion (meaning they won at least one episode)?
link to original post
The first episode has 3 new contestants, and each one after that has 2 more, so each season has 401 contestants.
The first episode's winner won all five episodes in week 1, but lost on Monday of week 2; that winner won all five episode of week 2, but lost on Monday of week 3, and so on. There are 40 weeks, so 40 of the contestants are champions.
Assuming that "pick a contestant at random from the season" means that each contestant has an equal chance of being chosen, as opposed to "choose an episode at random, then choose one of those three contestants at random," the solution is 40 / 401.
link to original post
I like your answer better.
link to original post
It looks like you are counting 11 contestants per week, which would be true if, after a contestant won their fifth game, they would retire undefeated and there would be three new contestants on the next show. However, the problem says that a contestant that wins five games then loses their sixth game.
Another way to look at it:
200 episodes x 3 contestants per episode = 600, but every episode but the first has a returning champion, so that's 600 - 199 = 401 different contestants.
link to original post
1=40, for unusually large values of 1.
May the cards fall in your favor.
October 25th, 2021 at 4:25:49 PM
permalink
Quote: ThatDonGuyThe first episode has 3 new contestants, and each one after that has 2 more, so each season has 401 contestants.
The first episode's winner won all five episodes in week 1, but lost on Monday of week 2; that winner won all five episode of week 2, but lost on Monday of week 3, and so on. There are 40 weeks, so 40 of the contestants are champions.
Assuming that "pick a contestant at random from the season" means that each contestant has an equal chance of being chosen, as opposed to "choose an episode at random, then choose one of those three contestants at random," the solution is 40 / 401.
Quote: charliepatrickContestants
On the first show there are three new contestants. As each long running champion is beaten, rather than throw off, each subsequent show has the returning champion and two new contestants. Thus there are 3 + 2*199 = 401 contestants.
Champions
In the second week on Monday the person who has won five in a row (won the previous Monday) is beaten and replaced. Therefore every Monday a new champion takes over; this happens every week. There are 40 weeks (200/5), so there are 40 champions.
Losers (for discussion purposes "Loser" = non-champion)
In the first week someone won the first game and kept winning all week. Thus there were two other people "Losers" on each episode, hence 2x5 = 10 in all.
In subsequent weeks on Monday there was only one "Loser" as the current champion (not a "Loser") got knocked out, someone took over (so wasn't a "Loser") and a third player who was a "Loser". On the other days there were two "Losers" as the current champion stayed on. Thus there were 1+2+2+2+2=9 "Losers" in each of the subsequent weeks. Thus the total number of "Losers" is 10 + 39*9 = 361.
Thus there were 361 "Losers", 40 "Champions", and a total of 401 contestants; giving a probability of picking a Champion as 40/401.
If the question was pick an episode, at the end of the game pick a contestant (i.e. this includes the new champion) there there are 200 episodes of 3 people giving 600 possible picks. In the first week there is only the first week's Champion occupying five slots. In subsequent weeks last week's Champion plays on Monday and the new one plays five times (that week). Thus there are 5 + 6*39 "Champion" slots = 239; giving a probability of picking a Champion (new or old) as 239/600. (If you pick at the start of the program then there are 40 fewer, each time the new Champion wins their first game, so 199/600)
Correct!!
It's an easy problem (of course that's what this thread is about), but the first episode of the season throws a spanner in the works.
-------------------------------------
If you watch Jeopardy! backwards, it's about rich people paying money for answers to questions.
That is all.
Have you tried 22 tonight? I said 22.
October 25th, 2021 at 7:29:30 PM
permalink
Can a non-zero product of consecutive Fibonacci numbers ever be a perfect square?
That is, aside from the trivial case (1,1), does there exist x > 0 and y > x and an integer m > 1 such that:
That is, aside from the trivial case (1,1), does there exist x > 0 and y > x and an integer m > 1 such that:
Last edited by: teliot on Oct 25, 2021
Climate Casino: https://climatecasino.net/climate-casino/
October 26th, 2021 at 7:08:10 AM
permalink
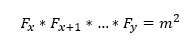
Quote: teliotCan a non-zero product of consecutive Fibonacci numbers ever be a perfect square?
That is, aside from the trivial case (1,1), does there exist x > 0 and y > x and an integer m > 1 such that:
link to original post
Question: is F2 = 1 (i.e. the first four Fibonacci numbers are 1, 1, 2, 3)? If so, then 1 + 1 + 2 = 4.
October 26th, 2021 at 7:09:53 AM
permalink
I read the operator to be multiplication, not addition.
May the cards fall in your favor.
October 26th, 2021 at 8:12:06 AM
permalink
Multiplication, not addition. Sorry if it's not clear.Quote: ThatDonGuyQuote: teliotCan a non-zero product of consecutive Fibonacci numbers ever be a perfect square?
That is, aside from the trivial case (1,1), does there exist x > 0 and y > x and an integer m > 1 such that:
link to original post
Question: is F2 = 1 (i.e. the first four Fibonacci numbers are 1, 1, 2, 3)? If so, then 1 + 1 + 2 = 4.
link to original post
That said, mea culpa, this is probably NOT an easy math problem. I thought of it on a whim, not knowing the answer.
Long version. This problem occurred to me because I recently got a Google scholar alert about a paper I published in 1992, that someone had used my result and cited it. So I wrote to that author and requested the paper. He sent me that paper and a different paper that also used my work. Looking at the results in the second paper, I thought of this problem. Then I went to the references and found a paper that he cited that solved the problem above and many more in great generality. So, I know there is a result in the literature of which this particular question is an easy corollary. I do not know if there is a direct and easy proof of this result by itself.
I think that there is not an easy path to solving this. Please prove me wrong.
Climate Casino: https://climatecasino.net/climate-casino/
October 26th, 2021 at 8:18:48 AM
permalink
This is not easy. Let me make an easier one.
(F_x)^2 + (F_x+1)^2 + … + (F_x+k)^2 =m^2,
where x, k, and m are all positive integers and F_x is a Fibonacci number with the index of x. Find all x, k, and m.
(F_x)^2 + (F_x+1)^2 + … + (F_x+k)^2 =m^2,
where x, k, and m are all positive integers and F_x is a Fibonacci number with the index of x. Find all x, k, and m.
Last edited by: aceside on Oct 26, 2021
October 26th, 2021 at 8:26:26 AM
permalink
Many years ago I had a problem appear in the American Mathematical Monthly that I called "Fibonacci's Last Theorem." This is an easy problem.Quote: acesideThis is not easy. Let me make an easier one.
(F_x)^2 + (F_x+1)^2 * + … + * (F_x+k)^2 =m^2,
where x, k, and m are all positive integers. Find all x, k, and m.
link to original post
For n >= 3, show that there are no non-trivial solutions to x^n + y^n = z^n where x, y and z are Fibonacci numbers.
Climate Casino: https://climatecasino.net/climate-casino/
October 26th, 2021 at 8:31:13 AM
permalink
Quote: teliotThat said, mea culpa, this is probably NOT an easy math problem. I thought of it on a whim, not knowing the answer.
Long version. This problem occurred to me because I recently got a Google scholar alert about a paper I published in 1992, that someone had used my result and cited it. So I wrote to that author and requested the paper. He sent me that paper and a different paper that also used my work. Looking at the results in the second paper, I thought of this problem. Then I went to the references and found a paper that he cited that solved the problem above and many more in great generality. So, I know there is a result in the literature of which this particular question is an easy corollary. I do not know if there is a direct and easy proof of this result by itself.
I think that there is not an easy path to solving this. Please prove me wrong.
link to original post
I am doing a brute force search, but I can't find any solutions for any subsets of the first 6000 Fibonacci numbers, which is when I ran out of RAM.
"How do you do a brute force search in any reasonable length of time?"
Note that the product of the Ath through Bth Fibonacci numbers = the product of the first B numbers divided by the product of the first (A-1) numbers.
Maintain a list of each of the products of the first N numbers (i.e. {1, 2, 6, 30, 240,...})
Generate the next number in the sequence, then multiply it by the product of the previous numbers, add this product to the list, divide it by each of the previous products, and see if the result is a perfect square.
There aren't that many prime Fibonacci numbers, so it's not that easy to show that every product will have at least one prime number be a factor an odd number of times.
October 26th, 2021 at 9:21:44 AM
permalink
Quote: teliotMany years ago I had a problem appear in the American Mathematical Monthly that I called "Fibonacci's Last Theorem." This is an easy problem.Quote: acesideThis is not easy. Let me make an easier one.
(F_x)^2 + (F_x+1)^2 * + … + * (F_x+k)^2 =m^2,
where x, k, and m are all positive integers. Find all x, k, and m.
link to original post
For n >= 3, show that there are no non-trivial solutions to x^n + y^n = z^n where x, y and z are Fibonacci numbers.
link to original post
To solve the question I posted, we need the solution when n=2 though. Anybody want jump in?
October 26th, 2021 at 11:20:30 AM
permalink
Quote: teliotThat said, mea culpa, this is probably NOT an easy math problem. I thought of it on a whim, not knowing the answer.
link to original post
Some people sing in the shower.
Some people keep soap crayons handy in case of ablutional epiphany.
All in all, my guess is that you've put the idea in front of an interesting set of eyes.
May the cards fall in your favor.
October 26th, 2021 at 12:55:56 PM
permalink
A farmer has a grassy field. You are given:
1. The grass starts at 2" high.
2. Grass grows at a constant rate.
3. Sheep consume grass at a constant rate.*
4. The sheep will eat a blade of grass completely before moving onto the next blade.
5. Once a blade of grass is eaten, it does not grow back.
6. It takes the sheep three days to consume the first acre of grass.
How long does it take after that for the sheep to consume the second acre of grass?
* In other words the time it takes to consume a blade of grass is proportional to the length of the grass.
1. The grass starts at 2" high.
2. Grass grows at a constant rate.
3. Sheep consume grass at a constant rate.*
4. The sheep will eat a blade of grass completely before moving onto the next blade.
5. Once a blade of grass is eaten, it does not grow back.
6. It takes the sheep three days to consume the first acre of grass.
How long does it take after that for the sheep to consume the second acre of grass?
* In other words the time it takes to consume a blade of grass is proportional to the length of the grass.
Last edited by: Wizard on Oct 26, 2021
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 26th, 2021 at 1:10:51 PM
permalink
Quote: WizardSheep in NZ eat grass
I think this is an easy one.. 3 days due to the rates being constant
October 26th, 2021 at 1:22:34 PM
permalink
Quote: Wizard
In other words the time it takes to consume a blade of grass is inversely proportional to the length of the grass.
Do you mean directly proportional?
October 26th, 2021 at 4:30:24 PM
permalink
Quote: GMDo you mean directly proportional?
link to original post
Yes, my bad.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 26th, 2021 at 4:31:04 PM
permalink
Quote: TwelveOr21Quote: WizardSheep in NZ eat grass
I think this is an easy one.. 3 days due to the rates being constant
link to original post
That's not what I get, but perhaps this is due to my typo. The time it takes a sheep to eat a blade of grass IS proportional to the length of the grass.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 26th, 2021 at 4:59:16 PM
permalink
I think there's a "simple" answer, but I am not confident that is correct - but every other attempt I have made to solve this problem ends up with a result that depends on how fast the grass grows.
In the time it takes to eat the first acre of grass, it grew an average of 1 inch.
This means the second acre starts out at 3 inches, which means it takes 1 1/2 times as long, or 4 1/2 days, to complete.
In the time it takes to eat the first acre of grass, it grew an average of 1 inch.
This means the second acre starts out at 3 inches, which means it takes 1 1/2 times as long, or 4 1/2 days, to complete.
October 26th, 2021 at 5:23:57 PM
permalink
Quote: ThatDonGuyI think there's a "simple" answer, but I am not confident that is correct - but every other attempt I have made to solve this problem ends up with a result that depends on how fast the grass grows.
In the time it takes to eat the first acre of grass, it grew an average of 1 inch.
This means the second acre starts out at 3 inches, which means it takes 1 1/2 times as long, or 4 1/2 days, to complete.
link to original post
I disagree, but I could be the one in error. Remember, the grass is continuously growing.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 26th, 2021 at 6:29:16 PM
permalink
Let # of blades is n, and time of finishing eating the first blade is t
so we have t + 2t + 3t + ... + nt = 3
-> t = 6/((1+n)n)
to eat the 2nd acre, the time for the first blade is (n+1)t
total time T = (n+1)t + (n+2)t + .. + (n+n)t = 9 - 6/(n+1)
if n > 6, then round it up, so T = 9 days; otherwise, use the formula to calculate.
so we have t + 2t + 3t + ... + nt = 3
-> t = 6/((1+n)n)
to eat the 2nd acre, the time for the first blade is (n+1)t
total time T = (n+1)t + (n+2)t + .. + (n+n)t = 9 - 6/(n+1)
if n > 6, then round it up, so T = 9 days; otherwise, use the formula to calculate.
Last edited by: HopHoofer on Oct 26, 2021
October 26th, 2021 at 7:47:46 PM
permalink
Quote: HopHooferLet # of blades is n, and time of finishing eating the first blade is t
so we have t + 2t + 3t + ... + nt = 3
-> t = 6/((1+n)n)
to eat the 2nd acre, the time for the first blade is (n+1)t
total time T = (n+1)t + (n+2)t + .. + (n+n)t = 9 - 6/(n+1)
if n > 6, then round it up, so T = 9 days; otherwise, use the formula to calculate.
link to original post
I disagree. I think the exact number of blades of grass doesn't need to be determined to answer the question. Then again, I'm always open to being proven wrong.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 27th, 2021 at 4:23:31 AM
permalink
Quote: WizardQuote: HopHooferLet # of blades is n, and time of finishing eating the first blade is t
so we have t + 2t + 3t + ... + nt = 3
-> t = 6/((1+n)n)
to eat the 2nd acre, the time for the first blade is (n+1)t
total time T = (n+1)t + (n+2)t + .. + (n+n)t = 9 - 6/(n+1)
if n > 6, then round it up, so T = 9 days; otherwise, use the formula to calculate.
link to original post
I disagree. I think the exact number of blades of grass doesn't need to be determined to answer the question. Then again, I'm always open to being proven wrong.
link to original post
Let me try this
Let x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations, we get
c=2 x/9
The grass growth one inch a day, so we set g=1.
Solving the above equations, we obtain
x=6.475 days
October 27th, 2021 at 5:47:39 AM
permalink
Quote: acesideLet me try this
Let x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations, we get
c=2 x/9
The grass growth one inch a day, so we set g=1.
Solving the above equations, we obtain
x=6.475 days
link to original post
I'm afraid I still disagree.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 27th, 2021 at 6:41:14 AM
permalink
Quote: WizardQuote: ThatDonGuyI think there's a "simple" answer, but I am not confident that is correct - but every other attempt I have made to solve this problem ends up with a result that depends on how fast the grass grows.
In the time it takes to eat the first acre of grass, it grew an average of 1 inch.
This means the second acre starts out at 3 inches, which means it takes 1 1/2 times as long, or 4 1/2 days, to complete.
link to original post
I disagree, but I could be the one in error. Remember, the grass is continuously growing.
link to original post
I took that into account. What I forgot was that, as a result, it takes longer and longer for the sheep to clear a given area of grass.
However, I still can't get an exact solution
Assume an acre is composed of N "regions"
Let H = the initial height of the grass (in this case, 2 inches)
Let E = the rate at which grass is eaten, in terms of seconds/inch to clear a "region" of fixed area
Let G = the rate at which grass grows, in inches/second
The first region is eaten in time HE, during which the rest of the grass grows to height H + HEG = H (1 + EG)
The second region is eaten in time (H (1 + EG)) E, during which the rest of the grass grows to height H (1 + EG) + ((H (1 + EG)) E) G = H (1 + EG)^2
The third region is eaten in time (H (1 + EG)^2) E, during which the rest of the grass grows to height H (1 + EG)^2 + ((H (1 + EG)^2) E) G = H (1 + EG)^3
...
The Nth region of the first acre is eaten in time H ((1 + EG)^(N-1)) E, during which the rest of the grass grows to height H (1 + EG)^N.
Let T be the total time needed to eat the first acre (in this case, 3 hours)
T = HE (1 + (1 + EG) + (1 + EG)^2 + ... + (1 + EG)^(N-1))
= HE ((1 + EG)^N - 1) / ((1 + EG) - 1)
= H / G * ((1 + EG)^N - 1)
Let H' be the height of the second acre at this point
H' = H (1 + EG)^N
Plugging this in to the "time to eat an acre" equation, the time needed to eat the second acre is H' / G * ((1 + EG)^N - 1)
= H / G * ((1 + EG)^N - 1) * (1 + EG)^N
= T * (1 + EG)^N
The result appears to depend on the rates of eating and growing.
"But doesn't this approach infinity as N does?" Not necessarily, as the regions get smaller and smaller, so E approaches zero.
October 27th, 2021 at 8:38:13 AM
permalink
Quote: WizardQuote: acesideLet me try this
Let x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations, we get
c=2 x/9
The grass growth one inch a day, so we set g=1.
Solving the above equations, we obtain
x=6.475 days
link to original post
I'm afraid I still disagree.
link to original post
My second attempt:
Let x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
October 27th, 2021 at 2:14:55 PM
permalink
I suspect it does matter how much the grass grows, so perhaps I am missing something.
Case 1 The grass does not grow.
Clearly it also takes 3 days to eat the second field.
Case 2 The grass grows 2" in three days.
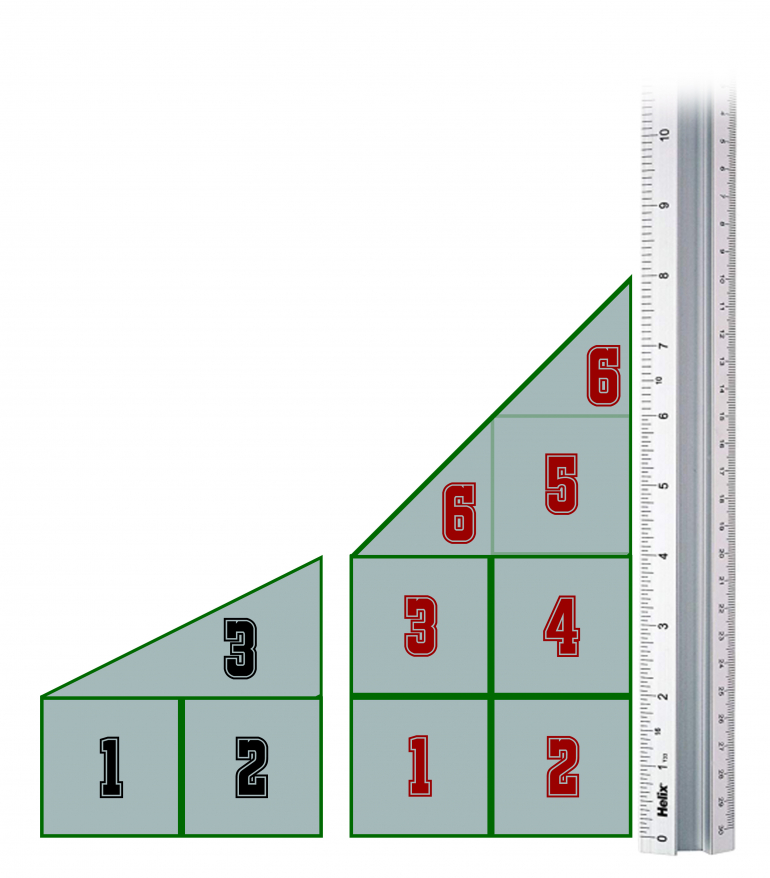
Consider the field as a narrow long field and we're looking at the end view. The sheep eats a narrow strip of the field working up and down, before moving from left to right (similar to how a farmer might plough a field). Mathematically it's a very narrow strip so the entire strip is eaten at a similar time, thus the sheep can be considered as working across the field from left to right without worrying about the up and down element.
The amount of grass eaten will correspond to the height of the grass and how far across the field (given the sheep eats narrow slithers) the sheep is moving. This is similar to the area in the picture.
In the first field the grass starts at 2" high and by the end it has become 4" high. For arguments sake the squares take one day to eat (i.e. the sheep could eat half the field is the grass stayed 2" high). One can see that the area of the first scenario is 3.
In the second field the grass starts at 4" high and by the end the sheep has eaten all the grass, including the grass that has grown.
Essentially you can take the first diagram and distort it by doubling its height. The volume of this is double as the starting length of the grass is double - this corresponds to the grass in field two having grown for three days before the eating started.
Thus the second field takes 6 days to eat.
Using the argument of distorting the diagram, the length of time to eat the second field is the same ratio as how long the grass grows in the first 3 days. Thus in Case 2 the grass length doubles, so the length of time to eat it doubles.
So the general answer is it is 3 days multiplied by (1 + percentage growth in 3 days).
Edit: I now see a problem with my argument above...
...because the assumption is that the sheep works across the field at a uniform rate is wrong! At the beginning the grass being eaten is shorter so the sheep can get across quicker than later, when the grass is longer. However, I've yet to think it through fully, the effects might be similar in both fields so while the triangle shape should be different, the two fields have similar distorted triangles.
in the first field the sheep works across based on the grass varying from 2" to 4"; in the second field the sheep works across varying from 4" to 8", so my gut feeling is whatever the varying rate of traversal it will still just take twice as long. Essentially the speed at each stage is now halved.
in the first field the sheep works across based on the grass varying from 2" to 4"; in the second field the sheep works across varying from 4" to 8", so my gut feeling is whatever the varying rate of traversal it will still just take twice as long. Essentially the speed at each stage is now halved.
Last edited by: charliepatrick on Oct 27, 2021
October 27th, 2021 at 3:10:32 PM
permalink
Let's assume the sheep is going to eat a very narrow strip of grass that is very long and can just munch and walk at the same time. The speed of walking will depend in the height of the grass, the higher the grass the slower the sheep can move forward. The question then simplifies to how far the sheep can walk given the varying height of the grass.
You are told that if the sheep starts with the grass at 2" high during the next three days, while it gradually slows down, it can eventually move one unit forward (acre in this case, but this might actually correspond to 5 or more miles, we don't care!)
In the second case the grass starts 3 days older so it will be 2" high plus the growth from 3 days. Generally speaking the initial speed will be corresponding less and everything else will take correspondingly longer. Suppose the initial height is 4", then the initial speed (rate of progress) would be half that of the 2" case, so it will take twice as long to progress one unit. Indeed at all stages the grass will be twice as high as in the first case: it started twice as high and it took us twice as long to get to that particular blade of grass, so the growth would be twice that seen in the first field, so each blade of grass is twice as high, so we just move at half the speed of the first case.
Similar logic applies for different rates of growth.
Thus I think this shows the same answer applies.
You are told that if the sheep starts with the grass at 2" high during the next three days, while it gradually slows down, it can eventually move one unit forward (acre in this case, but this might actually correspond to 5 or more miles, we don't care!)
In the second case the grass starts 3 days older so it will be 2" high plus the growth from 3 days. Generally speaking the initial speed will be corresponding less and everything else will take correspondingly longer. Suppose the initial height is 4", then the initial speed (rate of progress) would be half that of the 2" case, so it will take twice as long to progress one unit. Indeed at all stages the grass will be twice as high as in the first case: it started twice as high and it took us twice as long to get to that particular blade of grass, so the growth would be twice that seen in the first field, so each blade of grass is twice as high, so we just move at half the speed of the first case.
Similar logic applies for different rates of growth.
Thus I think this shows the same answer applies.
October 27th, 2021 at 5:07:22 PM
permalink
Quote: acesideLet x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
link to original post
I agree!
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
October 27th, 2021 at 7:07:33 PM
permalink
Quote: WizardQuote: acesideLet x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
link to original post
I agree!
link to original post
1. Where does "setting g = 1" come from?
2. If you change 2 (inches) to, say, 5 (cm), while leaving g = 1, the solution is no longer 7.5, but 12.
October 27th, 2021 at 7:24:47 PM
permalink
Quote: ThatDonGuyQuote: WizardQuote: acesideLet x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
link to original post
I agree!
link to original post
1. Where does "setting g = 1" come from?
2. If you change 2 (inches) to, say, 5 (cm), while leaving g = 1, the solution is no longer 7.5, but 12.
link to original post
Please trust us. Let us focus on finding the solution for this question I posted earlier:
(F_x)^2 + (F_x+1)^2 + … + (F_x+k)^2 =m^2,
where x, k, and m are all positive integers and F_x is a Fibonacci number with the index of x. Find all x, k, and m.
October 27th, 2021 at 8:16:34 PM
permalink
Quote: ThatDonGuyQuote: WizardQuote: acesideLet x=days needed for sheep to consume the 2nd acre of grass;
Let g=growth rate of grass;
let c= consume rate of grass by sheep.
Then we have
2+3g=3c;
2+3g+x g =x c
Solving this set of two equations when setting g=1, we get
x=7.5 days.
link to original post
I agree!
link to original post
1. Where does "setting g = 1" come from?
2. If you change 2 (inches) to, say, 5 (cm), while leaving g = 1, the solution is no longer 7.5, but 12.
link to original post
I'm at least intrigued.
I would think that changing units of length wouldn't change how fast the sheep eat in a correct solution.
2+3g+x g =x c looks odd to me.
May the cards fall in your favor.
October 27th, 2021 at 9:44:27 PM
permalink
Due to the area of a triangle, and hence the volume of a partially eaten meadow, I keep coming back to:
2+3/2g=3c;
2+3g+x/2 g =x c
... but I'm too lazy to go further.
May the cards fall in your favor.
October 28th, 2021 at 5:59:51 AM
permalink
I am getting 4.5 * speed of grass. Draw a graph where X axis is time and Y axis is grass quantity.
1. draw the line y = gt + 2, this is how grass quantity changes according to t.
2. draw the line y = st, this is the consumption by sheep. The X of intersection of line 1 and line 2 is 3, where the sheep finishes the 1st meadow.
then we have 3s = 3g + 2 -> s - g = 2/3
3. move the line y = gt + 2 up to y = gt + 3s, this is the starting quantity of the 2nd meadow
4. the intersection of the line 3 and line 2 is when sheep finishes the 2nd meadow, we have sx = gx + 3s, x = 3s /(s-g) = 4.5s
1. draw the line y = gt + 2, this is how grass quantity changes according to t.
2. draw the line y = st, this is the consumption by sheep. The X of intersection of line 1 and line 2 is 3, where the sheep finishes the 1st meadow.
then we have 3s = 3g + 2 -> s - g = 2/3
3. move the line y = gt + 2 up to y = gt + 3s, this is the starting quantity of the 2nd meadow
4. the intersection of the line 3 and line 2 is when sheep finishes the 2nd meadow, we have sx = gx + 3s, x = 3s /(s-g) = 4.5s
