Poll
 | 21 votes (45.65%) | ||
 | 14 votes (30.43%) | ||
 | 6 votes (13.04%) | ||
 | 3 votes (6.52%) | ||
 | 12 votes (26.08%) | ||
 | 3 votes (6.52%) | ||
 | 6 votes (13.04%) | ||
 | 5 votes (10.86%) | ||
 | 12 votes (26.08%) | ||
 | 10 votes (21.73%) |
46 members have voted
2. Select two opposite holes. Flip any down switches up. If the tomb doesn't open, you will know there are three up and one down.
3. Select two opposite holes. If one switch is down, flip it up and you're done. If both are up, switch one down. The switches will now be two up and two down, with the up and down switches in adjacent positions.
4. Select two opposite holes. They will be set the same way. Flip both the opposite way you found them and you will be done.
Quote: WizardCharlie, that is a very impressive graphic you created! I hope you will forgive me if I don't follow down every possible situation and just post my solution below.
1. Select two adjacent holes. Flip any down switches up. If the tomb doesn't open, you will know there are one or two switches in the down position.
2. Select two opposite holes. Flip any down switches up. If the tomb doesn't open, you will know there are three up and one down.
3. Select two opposite holes. If one switch is down, flip it up and you're done. If both are up, switch one down. The switches will now be two up and two down, with the up and down switches in adjacent positions.
4. Select two opposite holes. They will be set the same way. Flip both the opposite way you found them and you will be done.
link to original post
I may be lost but donít see how your step 4 works.
By step three you have set it up so that the switches are
DDUU
So when you stick your hand in opposite holes the switches will definitely not be the same. It will be one D and one U.
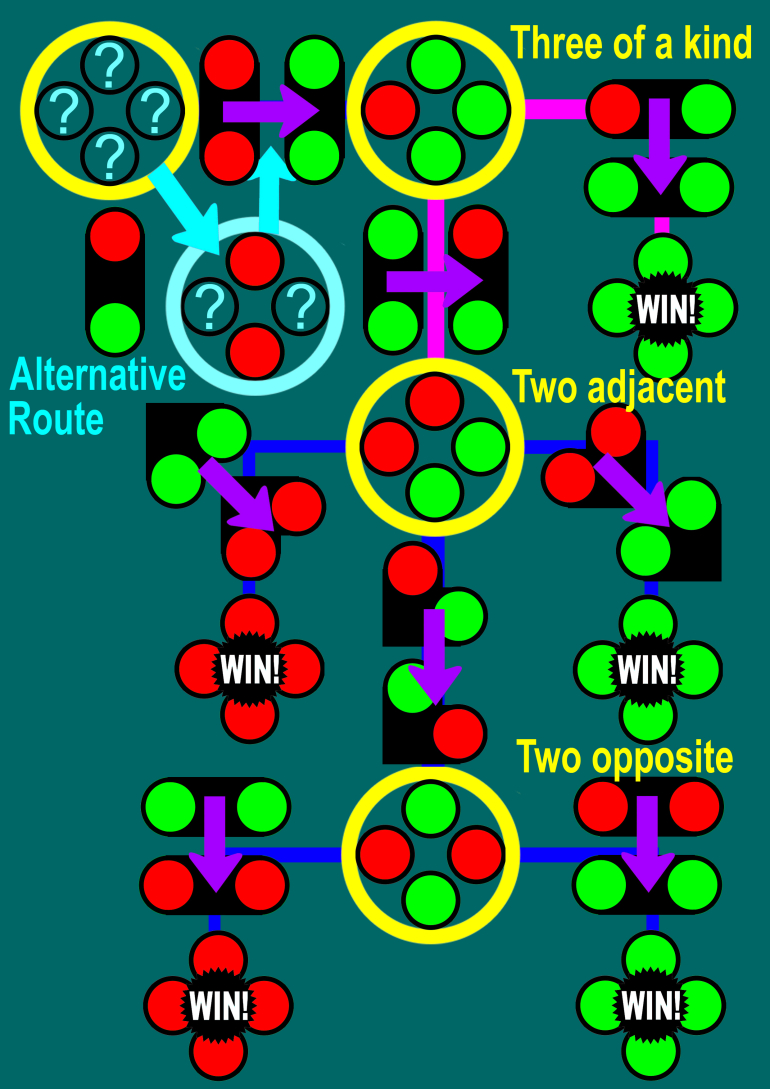 (The "alternative route" means for the second step, if you find a red-green or green-green, then set them to red-red for a win; otherwise you find red-red and can set them to green-green to ensure the other two are red-green.)
(The "alternative route" means for the second step, if you find a red-green or green-green, then set them to red-red for a win; otherwise you find red-red and can set them to green-green to ensure the other two are red-green.)Quote: unJonI may be lost but donít see how your step 4 works.
link to original post
You're right. I'm just spent an hour on a revised solution and see that it fails.
Quote: WizardQuote: Gialmere
Above are six pieces of rope. Imagine that you grasp the two ends of the rope and pull until the rope is straight.
Which of the six ropes will end up with a knot in them, and which ones just form loops that can be pulled out?
link to original post
A -- No loop
B -- No loop
C -- Loops
D -- Loop (figure 8 knot)
E -- No loop
F -- No loop
I must admit I got a piece of rope, mimicked these diagrams and pulled on the ends. It's possible I didn't construct some correctly.
I'd be interested to know the method to solve such puzzles mentally. I have a feeling it's some kind of odd/even thing to do with the rope going over/under itself.
link to original post
Hmm, I'm not sure what your answer is saying but...
Apologies for the delay. I'm having terrible computer issues and can only use my phone these days.
-----------------------------------------

Here is my revised solution to the four switch puzzle.
Key:
U = Switch in up position
D = Switch in down position.
Since this one is rather stale, I'm not putting it in spoiler tags.
1. For turn 1, choose opposite switches. If the same, flip both switches. If opposite, flip the D switch.
2. For turn 2, choose opposite switches.
3. If the turn 1 switches were originally in the same position, and the turn 2 switches are in the same position, then flip either switch on turn 2. This will result in either the puzzle being solved or switches in an UUDD configuration.
4. If the turn 1 switches were originally both up, and the turn 2 switches are in opposite positions, then flip the up switch. This will result in the puzzle being solved in a DDDD configuration.
5. If the turn 1 switches were originally both down, and the turn 2 switches are in opposite positions, then flip the down switch. This will result in the puzzle being solved in the UUUU configuration.
6. If the turn 1 switches were opposite, and the turn 2 switches are in the same position, then flip either switch. This will either result in a solved puzzle or an UUDD configuration.
7. If the turn 1 switches were opposite, and the turn 2 switches are in opposite positions, then flip the D switch. This will either result in a solved puzzle in the UUUU configuration.
8. For turn 3, if the puzzle isn't solved yet, it must be in a UUDD configuration. Pick adjacent switches and flip both. This will result in the puzzle being solved or a UDUD configuration.
9. For turn 4, pick opposite switches and flip both. This will solve the puzzle.
0) This is where you finid opposites so U?D? is turned to U?U? (all you now know at this stage is that ?? cannot be UU).
6) You're starting with U?U? and picking opposites
(a) obviously if you see any D, then you're looking at ?? and can win by turning them both to UU.
(b) however if you see UU then you must have picked the same two again. Even if you turn them to UD you're left with U?D?; you have no further information. So my proposed solution is to turn them to D?D?. You know ?? is not UU and now you know ?? is not DD; hence you know ?? = UD so must have UDDD. (On the next move you can turn UDDD into UUDD by flipping opposite DD to UD.)
8) I agree on "Turn 3" if you're in a UUDD configuration you can force a win in two moves by picking adjacent switches. If you see UU turn them to DD for DDDD; if you see DD turn them to UU for UUUU; if you see UD (or DU) swap them around to get UDUD.
Quote: charliepatrickI'm not sure about 0) then 6) (this is where I couldn't do it in four moves).
0) This is where you finid opposites so U?D? is turned to U?U? (all you now know at this stage is that ?? cannot be UU).
6) You're starting with U?U? and picking opposites
(a) obviously if you see any D, then you're looking at ?? and can win by turning them both to UU.
(b) however if you see UU then you must have picked the same two again. Even if you turn them to UD you're left with U?D?; you have no further information. So my proposed solution is to turn them to D?D?. You know ?? is not UU and now you know ?? is not DD; hence you know ?? = UD so must have UDDD. (On the next move you can turn UDDD into UUDD by flipping opposite DD to UD.)
8) I agree on "Turn 3" if you're in a UUDD configuration you can force a win in two moves by picking adjacent switches. If you see UU turn them to DD for DDDD; if you see DD turn them to UU for UUUU; if you see UD (or DU) swap them around to get UDUD.
link to original post
Thank you for your comments. I agree I screwed up, again.
You can only have a handful of positions as many are rotations or mirror of the others.
(a) 4-0 : UUUU or DDDD (these are winners)
(b) 3-1 : UDDD or DUUU
(c) 2-2 adjacent : UUDD (which is the same as DDUU, DUUD, UDDU)
(d) 2-2 opposite : UDUD (which is the same as DUDU)
The starting position cannot be (a)
Letís assume your first move is to pick opposite
1A U?U? : you change this to D?D?
(i) uuud/uduu goes to dudd/dddu = (b)
(ii) udud goes to dddd = win
(iii) uudd : this cannot create the case where you see U?U?.
In this case you know you have (b) (or have won)
1B U?D? : you change this to D?D?
(i) uddd goes to dddd = win
(ii) uudu goes to dudu = (d)
(iii) uddu/uudd goes to dddu/dudd = (b)
The problem is that after 1B, you donít know whether you are (b) or (d), see (e) below.
(b) (assuming you are starting with DDDU, pick opposite)
(i) D?U? : since you have found the only U, change it to D and win
(ii) D?D? : if you change it to d?u? then you must have duud or dduu = (c)
(c) (starting with DDUU or equivalent, pick adjacent)
(i) DD?? : since the other two are Us, flip DD to UU to win.
(ii) UU?? : since the other two are Ds, flip UU to DD to win.
(iii) DU : since you have DU from DUud, swap them to create UDUD =(d)
(d) (starting with DUDU or equivalent, pick opposite)
(i) D?D? : since the other two are Us, flip the Ds to Us to win
(ii) U?U? : since the other two are Ds, flip the Us to Ds to win
Now 1A U?U? can go via (b) (c) and (d) to win in four moves or fewer
The problem with 1B is you donít know whether you have (d) or (b).
(I suspect this is where we still need to find a four move solution, but I canít see it!)
(e) (starting with 1B U?D? and converting it to D?D, not pick opposite)
One way is to pick opposite
(x) U?U? : since you know there are two Ds, you change the two Us to Ds (D?D?)
(i) udud goes to dddd = win
(y) D?D? : you donít know the other two, this is equivalent to 1A, so change to U?U?
(i) dudu goes to uuuu = win
(ii) dudd goes to uuud = (b)
(z) U?D? : this can only happen if you had uddd
(i) uddd goes to dddd = win
So 1B can either win or go to (b) (which via (c) and (d) can be solved, but it takes five turns).
Summary : 1A goes to (b) (c) and (d) (or wins earlier) and 1B goes to (e) before (b) (c) and (d) (or wins earlier).

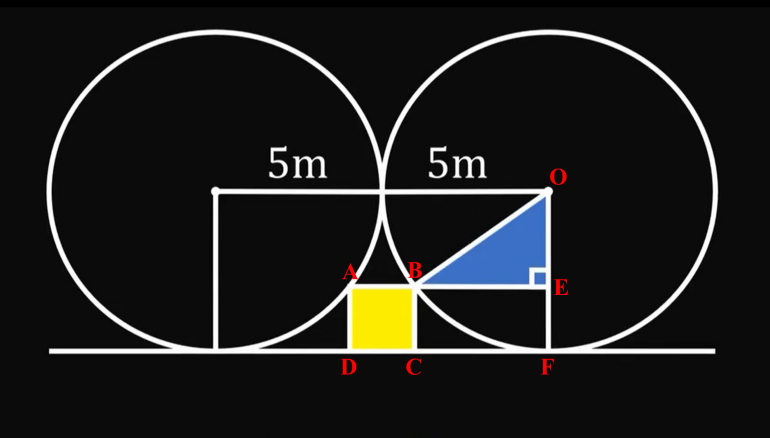
Using the diagram, let P be the point where the line segment connecting the two circles' centers intersects the circles.
Let x be the length of the side of the square.
OP = OB = OF = 5; EF = x, so OE = 5 - x
Note that BE = AB / 2 = 5; since AB / 2 = x / 2, BE = 5 - x / 2
Pythagorean Theorem on OEB: (5 - x)^2 + (5 - x/2)^2 = 25
25 - 10 x + x^2 + 25 - x^2 + x^2 / 4 = 25
5/4 x^2 - 15 x + 50 = 25
x^2 - 12 x + 20 = 0
x = 2 or 10, but x < 5 as otherwise BC > OF.
The area of the square = x^2 = 4.
Check: BE = 5 - 1 = 4 and OE = 5 - 2 = 3; OEB is a 3-4-5 right triangle.
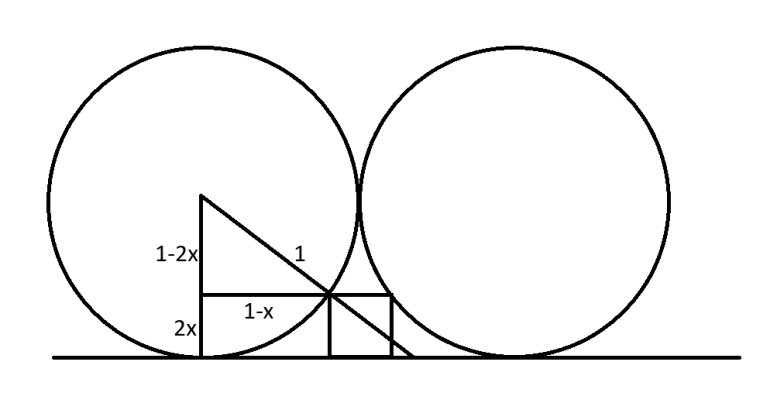
Here is my solution if the radius of the circles were 1:
(1-2x)^2 + (1-x)^2 = 1
5x^5 - 6x + 1 = 0
x = (3+/-2)/5
The only one that makes sense is x=1/5.
So, if the radius of the circles were 1, the area of the square would be (2/5)^2 = 4/25.
Then multiply by 5^2 = 25 if the circles have radius 5: (4/25)*25 = 4
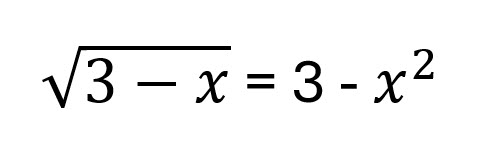
I hate to ask a question I can't solve, but this is one of those times. I wrote it in my notes for future "ask the wizard" questions. I put down the answer, but forgot how I solved it. I have a feeling there is some trig substation involved. This one beer worth for an answer in pure form with solution.
Quote: Wizard
I hate to ask a question I can't solve, but this is one of those times. I wrote it in my notes for future "ask the wizard" questions. I put down the answer, but forgot how I solved it. I have a feeling there is some trig substation involved. This one beer worth for an answer in pure form with solution.
link to original post
I can solve it. But only by that method I used in high school algebra class, that would earn me a disdainful frown from the teacher and to be called lazy and a waste of great potential.
(He was only half right. I have worked very hard at being a waste of great potential.)
Quote: AutomaticMonkeyQuote: Wizard
I hate to ask a question I can't solve, but this is one of those times. I wrote it in my notes for future "ask the wizard" questions. I put down the answer, but forgot how I solved it. I have a feeling there is some trig substation involved. This one beer worth for an answer in pure form with solution.
link to original post
I can solve it. But only by that method I used in high school algebra class, that would earn me a disdainful frown from the teacher and to be called lazy and a waste of great potential.
(He was only half right. I have worked very hard at being a waste of great potential.)
link to original post
Square both sides: 3 - x = 9 - 6 x^2 + x^4, limited to x <= 3 (as otherwise the square root is imaginary)
x^4 - 6 x^2 + x + 6 = 0
(x + 1) (x - 2) (x^2 + x - 3) = 0
This has solutions -1, 2, -1/2 - sqrt(13)/2, and -1/2 + sqrt(13)/2, but I think only x = -1 is valid for the original equation

x^4 - 6 x^2 + x + 6 = (x + 1) (x - 2) (x^2 + x - 3)?
Quote: WizardWell done, Don and CD. However how did you easily factor:
x^4 - 6 x^2 + x + 6 = (x + 1) (x - 2) (x^2 + x - 3)?
link to original post
I should have mentioned that if x^4 - 6 x^2 + x + 6 has rational solutions, they must be either -6, -3, -2, -1, 1, 2, 3, or 6.
I used "synthetic division" to find that x = -1 is a solution. So, x + 1 is a factor of x^4 - 6 x^2 + x + 6.
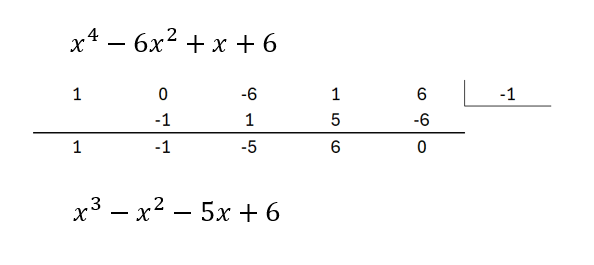
I forgot about the rational root formula. I probably haven't used it since high school.
A well-earned beer to both of you!

Quote: WizardThank you to both of you!
I forgot about the rational root formula. I probably haven't used it since high school.
A well-earned beer to both of you!
link to original post
Tomorrow is my 11th birthday in sobrietyÖ I might have to rethink that now - Oktoberfest, here I come! (I know, itís already over!)
Quote: WizardYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups?
link to original post
Edit to addÖ I misread the OP. My optic nerves mustíve been on a break! My calculations consider distinct cups AND ballsÖ
Four identical cups, six unique items: how many arrangements
For arguments sake put (1) into a cup, and see how many are in the main cup.
1 (i) 6-0 Only one way of having six in the main cup
5 (ii) 5-1 Five ways to pick the one that isn't in main cup
10 (iii) 4 - 2 (10 ways to pick the two that will not be in the main cup)
10 (iv) 4 - 1 - 1 (10 ways to pick the two that will not be in the main cup)
10 (v) 3 - 3 (10 ways to pick the two to accompany the main cup)
30 (vi) 3 - 2 - 1 (10 ways to pick the two for the main cup, then 3 ways to pick the solo)
10 (vii) 3 - 1 - 1 - 1 (10 ways to pick the two for the main cup)
5 (vii) 2 - 4 (5 ways to pick the ball to accompany the main cup)
20 (viii) 2 - 3 - 1 (5 ways to pick the ball to accompany the main cup, 4 ways to pick the odd ball)
15 (ix) 2 - 2 - 2 (5 ways to pick the ball to accompany the main cup, 3 ways to organise the rest into pairs)
30 (x) 2 - 2 - 1 - 1 (5 ways to pick the ball to accompany the main cup, 6 ways to pick the pair)
1 (xi) 1 -5 (Only one way of having the others in another cup)
5 (xii) 1 - 4 -1 (5 ways to pick the solo, leaving the other four to go into a cup)
10 (xiii) 1 - 3 - 2 (10 ways to pick the pair, leaving the triple to go into a cup)
10 (xiv) 1 - 3 - 1 - 1 (10 ways to pick the two solos, similar to picking the pair)
15 (xv) 1 - 2 - 2 - 1 (5 ways to pick the solo, 3 ways to organise the rest into pairs)
0 (xvi) 0 - ? (by definition the main cup must have the (1) ball, so impossible.
187
Quote:5 (ii) 5-1 Five ways to pick the one that isn't in main cup
Aren't there six ways to pick the singleton ball?
I've got another approach that I'll be looking at, so hopefully can post that later.
Then for each of these possibilities look at how the other three might fit in.
(a) All three balls can go into one cup (1 way) (ABC) (empty) (empty) (empty)
(b) Two balls in one cup, and one in another (3 ways) (AB) (C) (empty) (empty) (or AC B, BC A)
(c) One ball in each of three cups (1 way) (A) (B) (C) (empty)
Now for each of these options see how the other three balls might fit in.
(i) All three balls into one cup (1 way) DEF
(ii) Two balls in one cup, one in another (3 ways) DE F
(iii) One ball in each of three cups (1 way) D E F
(a)(i) Same cup (ABC+DEF) or different cup (ABC,DEF) (2 ways) total = 2 ways
(a)(ii) ABC+DE,F / ABC+F,DE / ABC,DE,F (3 ways) total = 9 ways
(a)(iii) ABC+D,E,F / ABC+E,D,F / ABC+F,D,E / ABC,D,E,F (4 ways) total = 4 ways
(b)(i) AB+DEF,C / AB,C+DEF / AB,C,DEF (3 ways) total = 9 ways
(b)(ii) AB+DE,C+F / AB+DE,C,F / AB+F,C+DE / AB+F,C,DE / AB,C+DE,F / AB,C+F,DE / AB,C,DE,F (7 ways) total = 63 ways
(b)(iii) AB+D,C+E,F / AB+D,C+F,E / AB+D,C,E,F / AB+E,C+D,F / AB+E,C+F,D / AB+E,C,D,F / AB+F,C+D,E / AB+F,C+E,D / AB+F,C,D,E / AB,C+D,E,F / AB,C+E,D,F / AB,C+F,D,E (12 ways) total = 36 ways
(c)(i) A+DEF,B,C / A,B+DEF,C / A,B,C+DEF / A,B,C,DEF (4 ways) total = 4 ways
(c)(ii) A+DE,B+F,C / A+DE,B,C+F / A+DE,B,C,F / A+F,B+DE,C / A+F,B,C+DE / A+F,B,C,DE / A,B+DE,C+F / A,B+DE,C,F / A,B+F,C+DE / A,B+F,C,DE / A,B,C+DE,F / A,B,C+F,DE (12 ways) total = 36 ways
(c)(iii) Ax,Bx,Cx (6 ways) / Ax,Bx,C,x (6 ways) / Ax,B,Cx,x (6 ways) / A,Bx,Cx,x (6 ways) total = 24 ways
2+9+4+9+63+36+4+36+24 = 187
Quote: WizardYou have four identical cups and six distinct balls. How many distinguishable ways can you place the balls in the cups?
link to original post
The problem is not worded clearly. What is a "distinguishable way," especially if the cups are identical?
Since the cups are identical, does any "order" in which they are arranged important?
Also, does there have to be a ball in every cup?
Assuming (a) order is unimportant - e.g. placing "red, blue, green, and yellow balls" in cups is a single "distinguishable way" regardless of which balls go into which cups, and (b) you can leave some, or even all, of the cups empty:
There are C(6,1) = 6 ways to use 1 ball
There are C(6,2) = 15 ways to use 2 balls
There are C(6,3) = 20 ways to use 3 balls
There are C(6,4) = 15 ways to use 4 balls
The total is 57, or 56 if you have to put at least one ball underneath a cup
^ I have assumed you have to place each of the six balls into a cup, but that cups can land up unused and empty. The reply above addresses a different puzzle where a cup can contain a maximum of one ball and asks how many ways the cups could land up from 6 different balls. Perhaps this is why I have a different answer.
Quote: ThatDonGuySince the cups are identical, does any "order" in which they are arranged important?
No. The order does not matter.
Quote:Also, does there have to be a ball in every cup?
No.
Also, every ball must be used.
Quote: charliepatrick^^ If the balls were A B C D E and F, then I have assumed that AB CD E F is the same as F AB E CD
This is correct.
Quote:Similarly ABCDE F is different from ABCDF E or A BCDEF.
That is correct.
Quote:I have assumed you have to place each of the six balls into a cup, but that cups can land up unused and empty.
That is true.
Quote:The reply above addresses a different puzzle where a cup can contain a maximum of one ball and asks how many ways the cups could land up from 6 different balls. Perhaps this is why I have a different answer.
Each cup can contain any number of balls, from 0 to 6.



