OnceDear's 10% System
I present to you a simple Money Management System for your amusement.When it works, it can have spectacular results, but when it fails, well at least you get to play for longer.
It's the money management system that I played on my very first day of online gambling, where I turned £100 buy-in into >£6,000. I still apply it from time to time.
Applies best to Online Blackjack where table min is as low as $1. Could also be applied to many even money wagers where house edge is low.
It DOES NOT give any monetary advantage
If you HAVE a game with a player edge of 10%, it could be helpful, because it then simulates Kelly Criteria wagering.
Pro's :
If you are having a streak of good luck, you will be betting and winning increasing amounts, so you will win faster and it can increase bankroll very rapidly indeed. You will automatically 'Push into' a winning streak.
If you are having a streak of bad luck, you will be betting and losing decreasing amounts, so you will lose slower.
If your luck runs good for a while, you can get very large increases in bankroll.
Your play will last for longer and you never quite go bust.
Gives you something to think about while playing a boring game.
Handy for wagering through wagering requirements of bonuses.
Con's :
Shapes the chart of BankRoll, but does NOTHING to give you an advantage.
A win does not quite cancel a loss, so if you have neither good or bad luck, your bankroll will shrink ( I'll explain later)
If playing Blackjack, you need to retain enough bankroll to cover doubles and splits.
Bankroll will tend downwards to $9 but no further.
How it works.
Very simple. You buy in for an amount you want to play with and are prepared to lose and then you proceed to make each wager 10% of your remaining bankroll balance. You round that 10% down to the nearest Dollar.
Example.
Buy in for $100
Place first 'even money' wager of 10% of $100 = $10
If you win, your bankroll will become $100+$10 = $110 meaning your next wager will be $11
But, if you lose, your bankroll will become $100-$10 = $90 meaning your next wager will be $9
NOTE. A win, followed by a loss will see your bankroll reduce. The win does NOT cancel out the loss.
NOTE. A loss, followed by a win will also see your bankroll reduce. The win does NOT cancel out the loss.
Eg, if you win your first wager and lose your second, your bankroll will go...
$100, $110, $99 leaving you down by $1
Eg, if you lose your first wager and win your second, your bankroll will go...
$100, $90, $99 also leaving you down by $1
The system really comes into its own when you have a few more wins than losses.
If you are unlucky enough to get your bankroll down to $9, then you are stopped out from wagering because 10% of $9 = 90c is less than the $1 table minimum. You could play 10c table min game if you wish.
Here are a few bankroll charts showing the course of a $100 bankroll, comparing flat betting $10 to betting a rolling 10% of Bankroll.
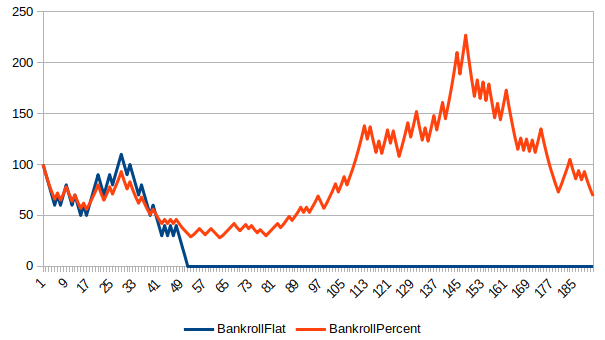
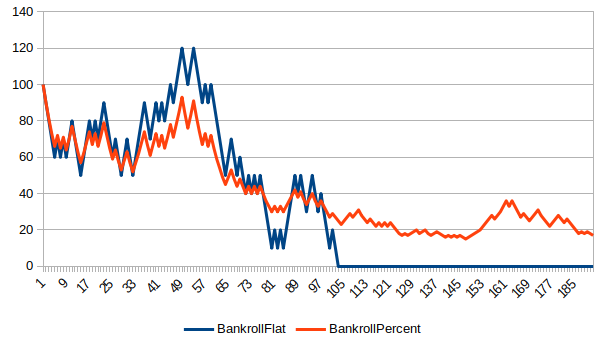
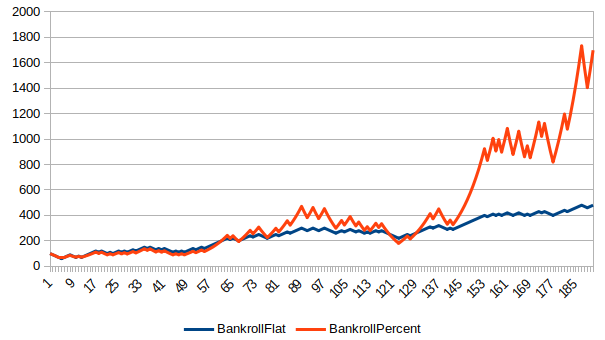
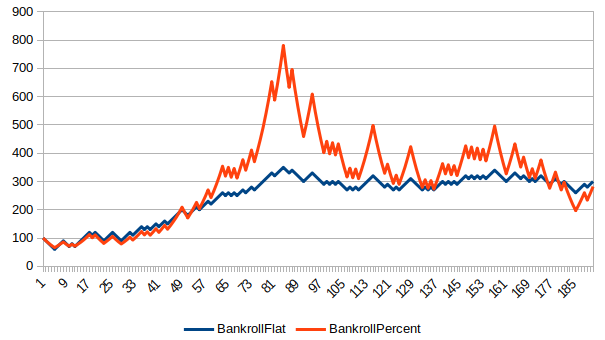
How To Live To 100 (Or NOT)
.... It's just a matter of controlling a few probabilities.First, let's assume you are a Male American.
Next. Examine the actuarial table at https://www.ssa.gov/oact/STATS/table4c6.html
Look up your current age in the leftmost column.
For a worked example, let's assume you are just 74 years old.
Your expected remaining life expectancy is not great: Column 4 reveals that you are expected, on average to live another 11.05 years, putting you in your grave by age 85. Probably!
BUT. your probability of dying before 75 is 3.6975%. I.e. you have probability of 96.025% of reaching 75. Yayyy!
IF you can make it to 75, then you have (100-4.0633)=95.9367% probability of reaching 76. Yayyy!
IF you can make it to 76, then you have (100-4.4710)=95.5290% probability of reaching 77. Yayyy!
.
.
IF you can make it to 99, then you have (100-36.6635)=63.3365% probability of reaching 100. Yayyy!
Even better
IF you can make it to 105, then you have (100-49.1326)=50.8674% probability of reaching 106. Good odds?
So, in simplest terms all you need to do to probably reach 100 is to first reach 99 and then take care of yourself for just one year. Doddle*
Is this a paradox? You are probably going to be dead by age 85, but we just found a 63% probability of reaching 100?
There's No Paradox:
Just like a Hit And Run, or Win And Leave strategy ( or method ), We cannot jump the last hurdle before we have cleared all the earlier hurdles. We can't keep taking 95% 'safe bets' time, after time, after time without becoming likely to lose one of them. We don't know which small risk will go tits-up, but they are all there ready to knock you out.
If you are not to concerned about living to 100, try this with Russian Roulette, instead:-
6 chamber revolver: 1 live round: spin: point at your temple and pull the trigger.
Probability of surviving once: 5/6 = 83.33% ( a good chance ? A pretty safe bet? )
IF you survive that round, Probability of surviving the next round is also 83.33%
IF you survive that round, Probability of surviving the next round is also 83.33%
IF you survive that round, Probability of surviving the next round is also 83.33%
IF you survive that round, Probability of surviving the next round is also 83.33%
IF you survive that round, Probability of surviving the next round is also 83.33%
But what if, at the very outset, before the game, you wager that you can pull the trigger 6 times or maybe 12 times and live?
Probability of surviving 6 trigger pulls = (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) =33.5% or 1 in 3
Probability of surviving 12 trigger pulls = (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) x (5/6) =11.2% or 1 in 9
Hit and run? play the fairly safe risk time after time after time.... It becomes a dangerous risk. The maths is simple, so long as you look forward just far enough.
*Incidentally, there's another way to live for 100 years or even longer: Just decide or discover where you are going to die....
... And don't go there. $:o)
Comments
motivation for me to live to 90: I delayed Social Security [SSA] till I was 70
If I don't make it past 78, the SSA wins, laughing big about it
If I live to 81,82-ish we pretty much even up, time to relax, but it probably wasn't worth it
If I live to 85-ish I start to pull away, but you can make a case I'd have had more return in investments I could have made ...............
88-ish I start to feel good about it, plus the extra money might be just the ticket, which is mostly why I did it
typical chart, the blue line is for someone in bad health or just flat broke [debatable] and not in consideration
the purple and green lines tell the story
final thought: if you're not worried about leaving money to anybody, which I'm not, just not running out of money in the later years is a victory in itself.
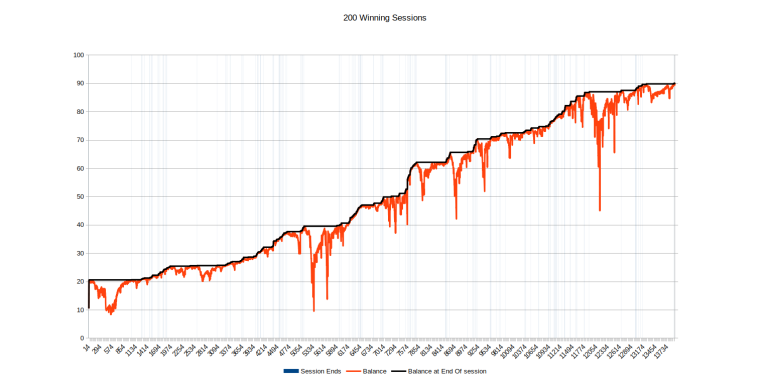
200 Consecutive Winning Sessions
Well That was a chuckle.While messing about with "OnceDear's Method", I just completed my 200th consecutive winning online session.
This was documented a little in the "OnceDear's Method" thread in the Betting Systems SubForum.
Here's a summary from my most recent post. But First a WEALTH WARNING!
"OnceDear's method" is an amusing way of wagering such that I will be very likely to win very many consecutive sessions. I'll also have a distinct possibility of losing a significant, predetermined bankroll. This time I was lucky.
From the Outset of Session #1, I had a probability of winning all of these 200 sessions of better than 50%. But that was countered by a probability of almost 50% ( Rough Math ) of losing over £100.
At the start of each session I had a probability of winning that session of about 99% ( More Rough Math ) *
Quote: OnceDearWell, another 6 days another 100 sessions. ** Some of them I dipped DEEP into my profit in the account balance.
But I was confident of winning every session, because each time, the math told me that was the most likely outcome.
But STILL, OnceDear's Method is just a recreational and educational exercise. It has ZERO monetary value and it was always a definite -EV proposition at every wager and every session start point.
DO Try this at home. It's fun. Recreational gambling is supposed to be fun.
I've now completed 200 Consecutive Winning Sessions. ZERO Losing Sessions.
That's one buy-in of £10.51 and one buy-in of £10.
I'm currently in profit by just over £70
* Because I was having fun and was a little ahead, I changed the risk profile a little by increasing my wagers after session 100
**Sessions 89 - 200 were at a low house edge, RNG Blackjack variant.
link to original post
Hit & Run Analysed
So......... Some gamblers believe that it's a good idea to Hit & Run, where they take a one unit win from a casino and finish the session to return and repeat another day. They expect to get some sort of advantage and so make meaningful profit.
This post will try to explain and demonstrate the failure of that strategy in action. I'll also explain why the Casinos do NOT fear having players try this.
I'll set a scene that eliminates any need to discuss "The Law of Large Numbers"
I'll set a scene that eliminates any need to discuss "The Long Term"
I'll set a scene that eliminates any need to discuss "Advanced Probability"
I'll set the scene where there can be no doubt to the maths
I'll consider a practical scenario, except that our roulette table can accommodate 37 simultaneous players.
Other members might say. "Ah, but I don't mean to do it like that" or "That's unrealistic" Well, work with my scenario, or post about your scenario elsewhere.
Start with 37 Optimistic Hit & Run WannaBe's. We will number them 0 to 36 and each will wear a badge with his number.
Each WannaBe has a starting bankroll of 35 Chips. Denomination doesn't matter. They are to play European Single Zero Roulette.
The game is distributed in such a way as to be playable by 37 simultaneous players. Maybe it is broadcast as an online game or is connected to 37 betting terminals with a live feed.
The Wannabe's are in cahoots and want to guarantee as best they can, that they can each hit the casino for a one chip session win. They feature no super human guessing skills.
Comments about magical guessing skills, trends and patterns is off topic and will be removed from this thread.
Our 37 WannaBe's enter the casino for the start of session 1. They walk up to the table and each lays his entire bankroll of 35 chips on the table as follows. Each lays one chip on every number on the table except for the player's own badge number and the number that is one greater than his badge number, except that player number 36, not having a number 37 to not bet on, does not place a chip on number 0 and does not place a chip on number 36.
Grasp that before proceeding
While the dealer says "No More Bets" we will consider the state of the table.
The troupe of 37 WannaBe's entered the casino with 35 chips each. That's a total of 1295 chips
Each player now has a bankroll of 0
There are now 37 x 35 = 1295 chips on the table.
Every number, including zero is covered exactly the same with 35 chips : 1 each from 35 players.
Every player has covered 35 numbers and has failed to cover 2 numbers.
The wheel spins: The ball spins : The ball lands in a pocket: A cheer goes up.
It doesn't really matter for the mathematicians, which pocket it lands in. Whichever pocket it landed in is good news for 35 of the WannaBe's who had covered the winning number.
The croupiers scoops up all of the chips on the losing numbers and shoves them into a hole near the back of the table. For electronic gaming stations there is a graphic representation of that.
There were 36 losing numbers, each with 35 chips on it, so the croupier has scooped up 36 x 35 = 1260 chips
The croupier now pays out to each of the winning chips at a rate of 35:1 So. That's 35 happy players each picking up his 1 chip stake and 35 more chips. But of course, 34 of each of those players chips had just been lost on the losing numbers.
The croupier pays out a total of 35 x 35 = 1225 chips from his pile.
Yayyyyy. 35 very happy Hit and run players have each made a profit of 1 chip each. They walk away happy and end there session ahead. Some post of their success to their blog or to a forum or to Youtube. For them Hit and Run was a success. They'll be back tomorrow or the next day to repeat the exercise.
Meanwhile, the casino owner is a happy man. The table has just raked in 1260 chips and paid out 1225 chips for a net profit of 35 chips. He doesn't care about all those lucky winners, because he won too. Indeed the amount won by the casino was 35 chips for every 1295 chips staked. Oddly, that's 35/1295 = 1/37 = 2.7% of chips staked. Bang in line with house edge. A steady earner for the casino.
Each of the lucky WannaBe's increased his bankroll by 1/35= 2.86% and feels smug.
Two unlucky wannabe's decreased their bankroll by 35/35 = 100% and feels pretty pissed off. Because of their faith in hit and run, they cannot leave the casino until they win back the 35 chips that they lost PLUS the one chip that they always intended to profit by. What are they to do? They could go cap in hand to their winning and successful friends to borrow 35 chips each. But their 35 friends outside can only spare 35 chips between them to lend out, and if they do that, they will have no profit left for tomorrow. Also, if they did lend back 1 chip each to the loser, they only have enough to bail out one loser. So. At least 1, and probably 2 WannaBe's are screwed. Doomed to spend all eternity in the casino with no bankroll and in the hole to the tune of 35 chips. They might go to the ATM to get fresh money to wager, but they are losers, big time.
Let's look back in time to while the ball was still spinning.
for EVERY WannaBe, the Expectation was that they had a 35/37= 94.59% probability of walking out with a 1 chip profit. They also had a 2/37 = 5.41% probability of being stuck with a 35 chip loss.
Session Amount Wagered per WannaBe = 35
Value of a Win is +1 chip
Value of a Loss is -35 chips
Expected Value = Value of a Win x Probability of a Win + Value of a Loss x Probability of a Loss
For this Session Expected Value expressed in Chips = (1 x 0.9459) + ((-35) x 0.0541) = -0.9476
I.e. The expected Profit after wagering 35 chips is (-0.9476 chips)
No WannaBe can ever actually lose 0.9476 chips. It is a Weighted average.
That is a NEGATIVE Expected Value . I.e. The Session is a -EV proposition.
It doesn't matter that MOST WannaBe's went on to win.
Of the 37 WannaBe's that visited the table, 35 winners survive to go back tomorrow to try the same again. but on average 2/37 of them ( I know it's not an integer ) can expect to lose the session and be doomed to be stuck there at a loss.
Meanwhile, the Casino owner is delighted. As long as, on average, 1/37 of all chips wagered get scooped up as profit.
Comments
yeah, hit and run is awful. Win and Leave, however, can really pay off! jk!
Exploitable Loss Rebate
An observation, and, I suppose a request for help and opinions.My main online casinos gives me a 5% loss rebate, paid once per month. Which is nice. But I think they may have given me a +EV situation. Here's why I think this.
Today I got a £54 loss rebate. No wagering requirement! Nice. Thank you. Why? I didn't lose!
This month, I played most days. Typically I bought in for £50, £100 or £200 per day, which I either lost or doubled or better. At least one day I turned £200 into £800 and at least a couple of times I turned £300 or more into nothing. Swings and roundabouts. Anyway, over the last 30 days, I deposited £5100 and cashed out £5700 for a net profit of £600 (rough figures)
So clearly I was not eligible for a loss rebate???
But I received one, of £54. So at 5%, they reckon I lost £1020 over the month. But taking the 30 days as a whole, I won!
I conclude that they must, therefore be setting aside my loss rebate individually every day!. Days where I lose, I get a rebate credited and days where I win, I get nothing. It's a reasonable estimate that the sum of the losses on my losing days would indeed be about £1000.
This surprises me. If I were the casino, I would assess my profit or loss, just once, covering the 30 day period. Thus I would not have given any rebate. Doing it on 30 individual 24 hour periods, they are giving me 5% on ROUGHLY 15 days and 0% on 15 days. Or, on average they are giving me 2.5% of my buy-ins!
So.... +Ev scenario...... Rough, back of the envelope estimate....
Each day, credit my account with say £1,000.
Make one low edge wager at roughly even money. Say one hand of Blackjack at 0.4% house edge.
If it's a push, rebet till I win or lose.
Underlying EV over the 30 day month = 30 X 1,000 X -0.004 = -120
*Ignoring blackjacks or splits or doubles, for the moment I would lose on average 16 days (53%) and win on average 14 days.
Loss rebate 16 x 1,000 X 0.05 = £800
Subtract the £120 I lose to the house edge and I have +EV of £680 per month.
There is a downside: Variance
Overall Standard Deviation =sqroot(30) x 1.14 x 1000 = £6244
So each month I have +EV of £680 +/- £6244 to one standard deviation.
Now. That's one way of doing it. Variance is high, so it comes at a big risk. Let's consider what happens if we try to maximise EV....
Similar situation, but lets say, we aspire to lose on 29 days of the month and win back all of those losses on the 30th day ( not necessarily the last day.) We need to engineer a session wager that pays 30 for 1. Easy enough to do. I could, have a daily win goal of 29,000 profit using the most aggressive 'All in' positive progression: Wager 1,000, win, wager 2,000, win. wager 4,000, win, wager 8,000 win, wager 16,000 win, wager 13,000 win. If that last wager loses, just keep max wagering in the same way, till I profit 29,000 or lose 1,000. Obviously, on average I lose 29 days out of 30. Ignoring the possible ebb and flow if I lose that last wager, my average daily wager would be sum(1000+2000/2+4000/4+8000/8+16000/16+ 13000/32) = £5406
Overall Standard deviation for the month would be sqroot(30) x 1.14 x 5406 = 33,750
Loss rebate value = 29 x 1,000 x 0.05 = 1450
Clearly much more risky but almost twice as valuable in rebates.
Each day I would expose an average of £5406 to the house edge, with a bit more if there was any ebbing and flowing for the last few wagers. House edge cost 30 x 5406 x 0.004=1297. AH.! That didn't cost in! I need to revisit this. Consult some proper Advantage players or mathematicians.
Thank you anyway, Online casino.
* ensuring I have enough reserve funds to cover any splits or doubles is a given.
Comments
Assuming the casino is offering only -EV gaming, isnít 5% less of that -EV still -EV? Good luck devising a system of wagering that is not subject to that.
BleedingChipsSlowly,
5% of the money lost would ideally exceed the -EV of the bets being made.
For example, if you were to make a $1,000 Pass Line bet on Craps, then your negative EV would be:
(1000 * .4929) - (1000 * .5071) = -$14.20
However, the casino is giving you $50 on the losses back in the event that you lose the first bet. Being an online casino, I should assume that this must be played through once to be withdrawable, but maybe not.
If the casino did return the $50 as cash withdrawable, then effectively, a player would only stand to lose $950 if the bet is lost, ergo:
(1000 * .4929) - (950 * .5071) = $11.155
Thus, the expectation of the overall proposition becomes positive, despite the fact that Craps still has a House Edge.
Anyway, different rebates and rules associated therewith call for different ways to play them, but that's a simple illustration meant to reflect, in the simplest terms, why rebates can sometimes result in a positive expectation.
Another thing that we will notice is that the value is only technically REALIZED upon a loss. For that reason:
.05 * .5071 = .025355
(14.20+11.155)/1000 = 0.025355
In other words, the effective change in value is 2.5355% to the good and the player's expectation (in this example) of winning $11.155 reflects a 1.1155% overall advantage.
Your second system leads to losing 29 times out of 30, which means you are capturing roughly twice the amount of rebate, but you are exposing your money to the house edge more than once. Single-zero roulette will give you 36 losses out of 37 days while only experiencing the house edge once per day. Despite the higher HE, you will have a bigger edge. You are getting 5%*36/37 rebated.



Comments
When I first saw this ("10pc system"), I thought it had something to do with chicken nuggets.
Levity aside, this approach may find some utility in online play, but the practicalities of table games (chips/cheques) will make things challenging for in-person play.
Best of luck.