Ask the Wizard correction
March 24th, 2011 at 6:47:32 PM
permalink
Thanks to Guido for pointing out this Ask the Wizard column.
As we all know the Wizard is nearly perfect, but on occasion he makes a minor slip up. In Ask The Wizard #253 he defined a transition matrix for a stochastic process that is not square. As everyone knows you can only take a square matrix to an arbitrary power.
Instead of simply pointing out a small error, let me take this opportunity to generalize the problem a little. The wizard defined the problem as the probability of getting a run of at least 7 "heads or tails" (either one is acceptable) out of 100 coin tosses.
Generalize to to allow for weighted coin (or a streak of 7 losses) with a given house edge.
The same problem can be answered by taking the following matrix to the 101st power. I have defined the probability of the casino winning as 20/38 as in roulette. However, note that it is a 9 by 9 matrix which can be taken to an arbitrary power. Replace the values 10/19 and 9/19 with 1/2 for the coin toss problem.
There is more than one way to define the matrix (this is not the only matrix), but the answer must be correct.
The Wizard has the correct solution of 31.7520%.
Now if we add the house edge for roulette, the probability of losing 7 in a row out of 100 plays is now 40.8143%. We must simply change the percentages in the spreadsheet.
You can add your own house edge for whatever game you like. It's a good opportunity to learn the MMULT function in EXCEL.
By the way, EXCEL is an awkward way to do matrix manipulation as it is very time consuming. The process can be simplified if you change the question to determining k losses out of 63, 127, 255, 511, 1023 plays in a row (one less than a power of 2).If you need to do the extra work, you can do the problem recursively, or you can add all the extra steps, or you can learn a scientific software package (Guido suggested the free "Winmat" from Phillips Exeter Academy ).
The matrices are sometimes easier to develop than the recursive formulas. In the same column the Wizard develops a recursive formula to get to the same answer for coin tossing. It is somewhat difficult to generalize.
BTW: The Wizard points out that he does not know an explicit formula to answer this question. There is none, and it is possible to prove that there is no algebraic formula with mathematical analysis.
However, there is a closed form expression using k-step Fibonacci sequences, where the standard Fibonacci sequence is defined as a 2 step Fibonacci sequence. The extension of the concept is natural. But there are two problems, (1) the calculation is unstable for large numbers, (2) Fibonacci sequences are calculated recursively, so there is no avoiding the recursion. Mark Nelson describes the solution in his column , but he got it from the online guide to Mathematica here .
As we all know the Wizard is nearly perfect, but on occasion he makes a minor slip up. In Ask The Wizard #253 he defined a transition matrix for a stochastic process that is not square. As everyone knows you can only take a square matrix to an arbitrary power.
Instead of simply pointing out a small error, let me take this opportunity to generalize the problem a little. The wizard defined the problem as the probability of getting a run of at least 7 "heads or tails" (either one is acceptable) out of 100 coin tosses.
Generalize to to allow for weighted coin (or a streak of 7 losses) with a given house edge.
The same problem can be answered by taking the following matrix to the 101st power. I have defined the probability of the casino winning as 20/38 as in roulette. However, note that it is a 9 by 9 matrix which can be taken to an arbitrary power. Replace the values 10/19 and 9/19 with 1/2 for the coin toss problem.
0 1 0 0 0 0 0 0 0
0 9/19 10/19 0 0 0 0 0 0
0 9/19 0 10/19 0 0 0 0 0
0 9/19 0 0 10/19 0 0 0 0
0 9/19 0 0 0 10/19 0 0 0
0 9/19 0 0 0 0 10/19 0 0
0 9/19 0 0 0 0 0 10/19 0
0 9/19 0 0 0 0 0 0 10/19
0 0 0 0 0 0 0 0 1
There is more than one way to define the matrix (this is not the only matrix), but the answer must be correct.
The Wizard has the correct solution of 31.7520%.
Now if we add the house edge for roulette, the probability of losing 7 in a row out of 100 plays is now 40.8143%. We must simply change the percentages in the spreadsheet.
You can add your own house edge for whatever game you like. It's a good opportunity to learn the MMULT function in EXCEL.
By the way, EXCEL is an awkward way to do matrix manipulation as it is very time consuming. The process can be simplified if you change the question to determining k losses out of 63, 127, 255, 511, 1023 plays in a row (one less than a power of 2).If you need to do the extra work, you can do the problem recursively, or you can add all the extra steps, or you can learn a scientific software package (Guido suggested the free "Winmat" from Phillips Exeter Academy ).
0.000% 28.191% 14.919% 7.896% 4.179% 2.211% 1.170% 0.619% 40.814% <---------
0.000% 28.035% 14.837% 7.852% 4.156% 2.199% 1.164% 0.616% 41.140%
0.000% 27.742% 14.682% 7.770% 4.112% 2.176% 1.152% 0.610% 41.756%
0.000% 27.188% 14.388% 7.615% 4.030% 2.133% 1.129% 0.597% 42.920%
0.000% 26.140% 13.834% 7.321% 3.875% 2.051% 1.085% 0.574% 45.120%
0.000% 24.161% 12.787% 6.767% 3.581% 1.895% 1.003% 0.531% 49.275%
0.000% 20.420% 10.807% 5.719% 3.027% 1.602% 0.848% 0.449% 57.128%
0.000% 13.353% 7.067% 3.740% 1.979% 1.048% 0.554% 0.293% 71.965%
0.000% 0.000% 0.000% 0.000% 0.000% 0.000% 0.000% 0.000% 100.000%
0.000% 34.262% 17.200% 8.635% 4.335% 2.176% 1.092% 0.548% 31.752% <---------
0.000% 34.124% 17.131% 8.600% 4.317% 2.167% 1.088% 0.546% 32.026%
0.000% 33.850% 16.993% 8.531% 4.283% 2.150% 1.079% 0.542% 32.572%
0.000% 33.304% 16.719% 8.393% 4.214% 2.115% 1.062% 0.533% 33.661%
0.000% 32.215% 16.173% 8.119% 4.076% 2.046% 1.027% 0.516% 35.828%
0.000% 30.048% 15.085% 7.573% 3.802% 1.908% 0.958% 0.481% 40.145%
0.000% 25.731% 12.917% 6.485% 3.255% 1.634% 0.820% 0.412% 48.745%
0.000% 17.131% 8.600% 4.317% 2.167% 1.088% 0.546% 0.274% 65.876%
0.000% 0.000% 0.000% 0.000% 0.000% 0.000% 0.000% 0.000% 100.000%
The matrices are sometimes easier to develop than the recursive formulas. In the same column the Wizard develops a recursive formula to get to the same answer for coin tossing. It is somewhat difficult to generalize.
BTW: The Wizard points out that he does not know an explicit formula to answer this question. There is none, and it is possible to prove that there is no algebraic formula with mathematical analysis.
However, there is a closed form expression using k-step Fibonacci sequences, where the standard Fibonacci sequence is defined as a 2 step Fibonacci sequence. The extension of the concept is natural. But there are two problems, (1) the calculation is unstable for large numbers, (2) Fibonacci sequences are calculated recursively, so there is no avoiding the recursion. Mark Nelson describes the solution in his column , but he got it from the online guide to Mathematica here .
March 25th, 2011 at 3:03:44 AM
permalink
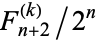
Quote: pacomartin...he defined a transition matrix for a stochastic process that is not square. As everyone knows you can only take a square matrix to an arbitrary power... a small error...]
a small error? Well, I guess! GEEEZ! !
And how about Einstein goofing on that Dark Energy prediction? Everybody knows that!
the next time Dame Fortune toys with your heart, your soul and your wallet, raise your glass and praise her thus: Thanks for nothing, you cold-hearted, evil, damnable, nefarious, low-life, malicious monster from Hell! She is, after all, stone deaf. ... Arnold Snyder
March 25th, 2011 at 8:05:47 AM
permalink
Quote: pacomartin
...he defined a transition matrix for a stochastic process that is not square. As everyone knows you can only take a square matrix to an arbitrary power... a small error...]
Am I the only one here who has not idea what this means ?? Just curious, that's all. No disrespect meant.
...he defined a transition matrix for a stochastic process that is not square. As everyone knows you can only take a square matrix to an arbitrary power... a small error...]
Am I the only one here who has not idea what this means ?? Just curious, that's all. No disrespect meant.
March 25th, 2011 at 8:19:30 AM
permalink
I was afraid to admit that I have no idea what he's even referring to when he says "as everyone knows...."
I invented a few casino games. Info:
http://www.DaveMillerGaming.com/
Superstitions are silly, childish, irrational rituals, born out of fear of the unknown. But how much does it cost to knock on wood? 😁
March 25th, 2011 at 8:30:33 AM
permalink
Quote: DJTeddyBearI was afraid to admit that I have no idea what he's even referring to when he says "as everyone knows...."
Gee, now I feel less dumb Thanks
March 25th, 2011 at 9:03:38 AM
permalink
You're right, thanks for that correction. My spreadsheet on that question has the right matrix, I just expressed it incorrectly for the column.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
March 25th, 2011 at 9:46:48 AM
permalink
Quote: pacomartinThanks to Guido for pointing out this Ask the Wizard column.
As we all know the Wizard is nearly perfect, but on occasion he makes a minor slip up. In Ask The Wizard #253 he defined a transition matrix for a stochastic process that is not square. As everyone knows you can only take a square matrix to an arbitrary power.
In the same column the Wizard develops a recursive formula to get to the same answer for coin tossing. It is somewhat difficult to generalize.
The Wizard's formula in his column IMO is simple and elegant. Excellent work Wizard!
I expanded his formula to accept any value of p. And I was surprised that it returns exact results since The Wizard made no mention of that in his column, since he was answering a fair coin toss question, but he did spell out his formula in easy to understand English, for me at least.
NBA player Steve Nash has a lifetime .904 free throw percentage while attempting 3,100. What is the probability that he has made at least 50 or more in a row one time in his career?
How about a streak of 75? or 100?
(His personal record is 74 straight)
Another popular run question would be: What is the probability of tossing 5 or more heads in a row in 20 coin tosses with a fair coin?
Also, A basketball player shoots free throws with a 50% success rate. What are the chances (s)he makes 5 or more in a row in 20 consecutive attempts?
One can see the answer below.
Here is a snap shot of my Excel worksheet.
D4=($B$2*D3)+($B$1*$B$2*D2)+($B$1)^2
E5=($B$2*E4)+($B$1*$B$2*E3)+(($B$1)^2*($B$2)*E2)+($B$1)^3
F6=($B$2*F5)+($B$1*$B$2*F4)+(($B$1)^2*($B$2)*F3)+(($B$1)^3*($B$2)*F2)+($B$1)^4
G7=($B$2*G6)+($B$1*$B$2*G5)+(($B$1)^2*($B$2)*G4)+(($B$1)^3*($B$2)*G3)+(($B$1)^4*($B$2)*G2)+($B$1)^5
Formula can be entered into the cell and filled down to whatever trial row you like.
Each new column just adds 1 term before the final term and both last terms need to be adjusted. I think one can see the pattern.
I hope this helps someone in the future. it has with me.
pacomartin gave me a great lesson for Markov Matrices, that I am still learning. Thank you for that.
I have uploaded 2 Excel files if you want to download them. To change the value of p, just enter a new value in cell B1 and in a few seconds the complete sheet is updated. Default value p=.5
The first is for Excel 2007 HERE size 5.3mb
The second for Excel 2003 and earlier HERE size 17mb
I have not found any errors, if you do please alert me to them so they may be corrected.
In 2008 and 09 there was a lot of net activity about calculating runs (streaks). I wonder what started it all.
A handy JavaScript streak calculator can be found HERE
Enjoy
March 25th, 2011 at 12:05:12 PM
permalink
Quote: DJTeddyBearI was afraid to admit that I have no idea what he's even referring to when he says "as everyone knows...."
My attempt at sarcasm seems to have fallen flat. I know that most people don't get to matrix manipulation. It is not regularly taught until after Calculus in college. Some kids in high school are taught them at top notch schools (if Guido's son is at Phillip's Exeter they probably teach them in some courses).
Matrices came into more widespread use in the mid 19th century as routine way to solve common mathematical problems. In the 20th century the Russian mathematician developed transition matrices to solve stochastic problems.
I was simply showing one, of several possible ways to extend the concept of a streak at coin tossing, to calculating a streak of losses (or wins).
Every problem solvable matrix algebra is also solvable by a set of recursion formulas, by definition. Matrices are often easier to set up, while recursion formulas are sometimes difficult to develop.
A past problem which is easily solvable by a Markov matrix is, " What is the probability of a woman rolling 154 times in craps?"
Time Magazine incorrectly reported the odds as 1 in 1.56 trillion.
Ask the Wizard craps solves the problem with recursive formula. The correct answer is
1 in 5,590,264,072 which is line 153 in the calculation. The reason it is line 153 and not line 154 is because the first roll in craps is always followed by a second roll. There are only 153 times you could 7-out in a streak of 154 rolls of the dice.
I'll post the matrix solution without explanation. A detailed explanation including how to develop the matrix is on Michael's webpage Problem #204.
It will be a good exercise for Guido's son (or anyone else)
A 4 by 4 square matrix to describe the transitions in a pass line bet in craps follows (where blanks are filled with zeros):
12 3 4 5
6 27
8 26
10 25
Define the above matrix by the letter A
Calculate (A/36)^153
Multiply by the following 4 by 1 vector
1
0
0
0
If you multiply a 4 by 4 matrix by a 4 by 1 vector you will get a 4 by 1 vector.
Sum the entries in the final 4 by 1 vector and you will get 1 / 5,590,264,072 .
March 25th, 2011 at 12:14:55 PM
permalink
My attempt at sarcasm seems to have fallen flat. I know that most people don't get to matrix manipulation. It is not regularly taught until after Calculus in college. Some kids in high school are taught them at top notch schools (if Guido's son is at Phillip's Exeter they probably teach them in some courses).
No, we all know it was sarcasm. Just that those of us who are now struggling with filing our 2010 tax forms feel like our head is in a vice. And would like to escape to the matrix.
No, we all know it was sarcasm. Just that those of us who are now struggling with filing our 2010 tax forms feel like our head is in a vice. And would like to escape to the matrix.
March 25th, 2011 at 12:57:42 PM
permalink
Quote: buzzpaffMy attempt at sarcasm seems to have fallen flat. I know that most people don't get to matrix manipulation. It is not regularly taught until after Calculus in college. Some kids in high school are taught them at top notch schools (if Guido's son is at Phillip's Exeter they probably teach them in some courses).
No, we all know it was sarcasm. Just that those of us who are now struggling with filing our 2010 tax forms feel like our head is in a vice. And would like to escape to the matrix.
Amen.
My son is 19 and knows everything. His problem is when trying to explain things that are simple to him to others like me in a way I can understand.
It must be a talent.
pacomartin is good
The Wizard is excellent.
He must have been a good teacher somewhere in his life's journey.
March 25th, 2011 at 1:54:09 PM
permalink
Quote: guido111
He must have been a good teacher somewhere in his life's journey.
I am not sure who the compliment was directed at, but I did teach advanced college prep for 3 years. I had one kid who got almost every single question wrong on his first exam. But I had him in classes for three full years and we got through advanced placement calculus. He ended up going to Columbia University and working in Bell Labs.
He called me when he was working at Bell and said the Columbia was a breeze after what he learned in high school.
I did have students get advanced placement credit at Princeton, MIT, Columbia, and Cornell. But, I only taught school for three years.
Phillip's Exeter clearly has excellent teachers.
I believe that Michael's formal teaching experience was all at UNLV, but he's clearly got it in his soul. His written explanations are very clear.
Instead of a graph, I'll put a 1 page table online for the streak calculation. The formulas are clearly printed on the right if you want to make your own spreadsheet which will allow you to change to a different house edge.
Table of streak calculations
March 31st, 2011 at 10:26:36 AM
permalink
removed (why?)
silly
silly
I Heart Vi Hart
April 3rd, 2011 at 4:19:27 PM
permalink
Quote: mustangsallyFor extra credit in my math class, I chose to solve the final statement of the post in a spreadsheet "The probability of one or more streaks of exactly seven heads is 17.29%
Let's reproduce the final statement By the way, in case you were wondering, the probability for at least one streak of 7 or more of heads or tails is 54.23%. The probability of one or more streaks of exactly seven heads is 17.29%.
So the Wizard seems to be saying:
The probability of getting one or more streaks of at least seven heads in a row out of 100 coin tosses is 31.752%
The probability of getting one or more streaks of at least seven heads or tails in a row out of 100 coin tosses is 54.234%
The probability of getting one or more streaks of exactly seven heads in a row out of 100 coin tosses is 17.29%
I certainly agree with the first statement.
The second statement seems to be correct also. I should point out that it is also the answer
The probability of getting one or more streaks of at least six heads in a row out of 99 coin tosses is also 54.234%
I am not sure if the third answer is correct.
The probability of getting one or more streaks of at least seven heads in a row out of 100 coin tosses is 31.752%
The probability of getting one or more streaks of at least eight heads in a row out of 100 coin tosses is 17.021%
The answer should be the difference 31.752%-17.021%=14.731% (which is different than either your answer or the Wizard's).
It's possible I am the one making the mistake here, but I will post anyway.
======================================================
BTW: did you see the recursion formula in my spreadsheet. It is simpler than the wizard's recursion formula (they produce the same answers).
p = 50% for coin tosses but may be changed to a casino probability of win = 20/18 for roulette
q=1-p probability player win
Pkk=k^p probability of k wins in a row for the casino (in this case k=7)
DELTA=q*Pkk probability of player win followed by a streak of k wins by casino
P(j,k)=0 if j<k since this case does not make any sense (dumb case)
For j>k
i== j-k-1 index for older case
Q(i,k)=1-P(i,k) probability that all streaks are of length lower than k out of i plays
Note j<=2k , Q=1 from the dumb case above
P(j,k)=P(j-1,k)+Q(i,k)*DELTA which is simple to implement in a spreadsheet
Quote: mustangsallyI do not know how many of you can solve a problem like the one asked but the Wizard did a super job while explaining how it can be solved. Most guys in my college math class when explaining things to a girl like me, just gives an answer without an explanation. I am looking for an explanation first and a formula would be a nice added touch..
Many people remember formulas without explanations. For example to go from nautical miles to kilometers is km=0.54*nm or nm=1.85*km. That's a formula which you will probably forget.
Now remember that nautical systems used the size of the earth as a base, and so did the metric system. The distance from the equator due north to the pole is 90 degrees. Each degree is 60 minutes. Early navigators called a minute of latitude a "nautical mile". So it is 90*60=5400 nautical miles from the equator to the north pole. The designers of the metric system used the same distance, but they called it 10,000 kilometers which gave them the definition of a meter.
So 90*60 nautical miles = 10,000 kilometers by the definition of the kilometer and the definition of a nautical mile. So km=0.54*nm.
I can pretty much guarantee if you read that paragraph you will never forget that conversion.
April 3rd, 2011 at 5:59:55 PM
permalink
okQuote: pacomartinHowever, there is a closed form expression using k-step Fibonacci sequences, where the standard Fibonacci sequence is defined as a 2 step Fibonacci sequence.
The extension of the concept is natural.
But there are two problems, (1) the calculation is unstable for large numbers, (2) Fibonacci sequences are calculated recursively, so there is no avoiding the recursion.
so with wolfram alpha and programs that CAN calculate any large value and use it without rounding
the at least 7 Heads in a row using the 7step Fibonacci 102nd number as NO such runs
here is what i gets
LinearRecurrence[{1, 1, 1, 1, 1, 1, 1}, {1, 1, 2, 4, 8, 16, 32}, 102]
is used in wolfram alpha
and returns the 7 step values from 1 to 102
7stepF[102]=865 145 690 433 457 063 670 671 045 568 = no runs of 7+
so 1 - (865 145 690 433 457 063 670 671 045 568 / 2^100)
will be the exact answer when (if) that is required
2^100 = 1 267 650 600 228 229 401 496 703 205 376
reduces to
6289139215543317778531752497/19807040628566084398385987584
hard to tell, by looking, what that really is
but sure is fun to see
of course Excel does this too
(well, the math part, but not showing the whole value)
here is the link for me Excel file in Google sheets for those so interested
https://goo.gl/bWdfs1
math is fun
Sally
I Heart Vi Hart
April 3rd, 2011 at 6:43:17 PM
permalink
Quote: mustangsallyI came across the answer to that also from the spreadsheet solution. That was so cool.
Notice that the probability of two heads out of two coin tosses was 1/4 - HH HT TH TT
Notice that the probability of a streak of three heads or tails out of three coin tosses is also 1/4 - HHT HTH THH TTT HHH TTH THT HTT (so TTT HHH out of 8)
So if we define P as a streak of "heads" and P' as simply a "streak" then P(k,n)=P'(k-1,n-1).
=======================
The Wizard professes not to have much interest in streaks. The reason is obviously that in gambling, people make a big deal out of them, while they really should have no basis for future behavior.
However, if you are not gambling but studying human behavior they are very important. As we said earlier there is a 31.752% of 7 heads in a row out of 100 coin tosses. If I add a simple house edge like roulette where the casino wins 20 out of 38 times (in American roulette). The odds increase to 40.814%.
If you interview people and ask them what is the odds of losing 7 times in a row in a casino game, most people will give you a single digit percentage. If you are a casino owner, you put a post which tells you the last 22 outcomes. That way people will "see" patterns and run over and bet accordingly.
Consider the case of an election in the third world where the former dictator wins by 70% to 30%. If you randomly select 100 ballots in a row, the odds of 7 or more in a row being votes for the dictator are now 94.918%.
But someone has been stuffing the ballot box. Since the population is illiterate, each ballot has an X next to the photo of the candidate. The ballot box stuffer does not wish to insert all of his fake ballots in a row so he "shuffles them" to make them look more random. There are never more than 5 ballots for the ex-dictator in a row. The probability of that happening given random selection of voters is 1 time in 1756.
Such numerical using "theory of streaks" gives you strong evidence that the ballot box was stuffed.
=======================
Are you an undergraduate or graduate student?
April 4th, 2011 at 11:18:01 AM
permalink
Quote: mustangsallyWell my reasoning seems to be flawed since my answer is 16.0136793% and the Wizards answer matches simulations and a markov matrix solution that my math partner did.
In my spreadsheet where n=8 up to and including n=15 the answers are exact as n increases then slowly adds errors that seem to be another recursive formula at work.
Can someone point out the flaw in my reasoning and a way to solve the question of "What is the probability of one or more streaks of EXACTLY seven heads in 100 coin tosses?" Thank you.
Without doing the work myself, I think you are just calculating the probability of only 1 run of exactly 7. Look at it that way.
I would solve this by PIE: The Principle of Inclusion and Exclusion
HERE is a link to a pdf file. It gives good coin toss examples but is not very good on the explanation. I have a better pdf that explains it better but can not find it right now.
My 100 million sim results shows 17.308363% a bit higher than the Wizards figure but closer to your result.
From my readings the E(n,k) of success runs of size exactly k,
of five often used run statistics in a sequence of i.i.d. Bernoulli trials is the most challenging to work with.
Good luck with your studies.
April 4th, 2011 at 11:29:46 AM
permalink
" transition matrix for a stochastic process that is not square. "
I can only stand idly by and marvel at my ignorance
I can only stand idly by and marvel at my ignorance
June 15th, 2011 at 3:04:03 PM
permalink
removed
silly
silly
I Heart Vi Hart
June 16th, 2011 at 8:48:17 AM
permalink
OK, so I went to the ask Wizard post and found another problem.
The transition matrix provided is a 9 by 9 matrix, which can be used to calculate a streak of 8, but the final answer, T^100, is an 8 by 8 matrix. I was very confused why I could not replicate the answer after I already confirmed it independently using a Markov chain. Then I decided to start the matrix from scratch and generate it myself. That's when I finally realized that the matrix provided was incorrect.
The transition matrix provided is a 9 by 9 matrix, which can be used to calculate a streak of 8, but the final answer, T^100, is an 8 by 8 matrix. I was very confused why I could not replicate the answer after I already confirmed it independently using a Markov chain. Then I decided to start the matrix from scratch and generate it myself. That's when I finally realized that the matrix provided was incorrect.
I heart Crystal Math.
June 16th, 2011 at 11:09:27 AM
permalink
Quote: pacomartin
I am not sure if the third answer is correct.
The probability of getting one or more streaks of at least seven heads in a row out of 100 coin tosses is 31.752%
The probability of getting one or more streaks of at least eight heads in a row out of 100 coin tosses is 17.021%
The answer should be the difference 31.752%-17.021%=14.731% (which is different than either your answer or the Wizard's).
It's possible I am the one making the mistake here, but I will post anyway.
The flaw here is that the numbers 31.752 and 17.021 do not represent the average number of streaks, but the likelyhood of getting one or more streaks. If you were to calculate the average number of 8+ coin streaks and 7 coin streaks, then you could subtract them in this manner.
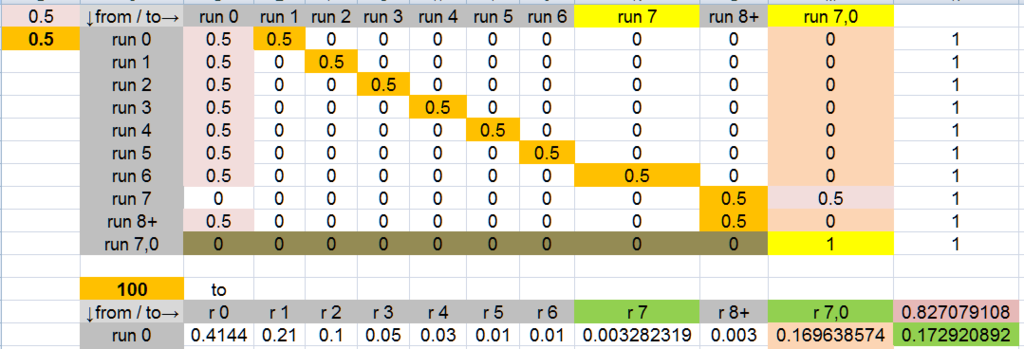
Using a Markov chain, I calculate the probability of exactly one 7 coin streak to be 0.172920892.
I heart Crystal Math.
June 16th, 2011 at 12:44:24 PM
permalink
Quote: CrystalMathThat's when I finally realized that the matrix provided was incorrect.
You're right, thanks for the correction. The column should be correct now.
Quote: mustangsallyGirls... Is BruseZ's avatar really him?
I could count the number of girls on this forum with one hand, so don't expect one of them to answer. Personally, I think that is the mathematician from the show Numbers.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 16th, 2011 at 1:47:28 PM
permalink
removed
silly
silly
I Heart Vi Hart
June 16th, 2011 at 2:18:24 PM
permalink
Quote: mustangsallySo then how about a girls night out with Mr. S
maybe once a year?
5 or less would make for a fun time.
Unless you require all your girls to look like your choice of models in your photos. Not counting the Bodog Girls that is.
Well, thanks for the nice words. Any picture of me with a pretty girl I assure you that the girl was being paid. Thanks for the nice idea, but it would never happen, trust me.
"For with much wisdom comes much sorrow." -- Ecclesiastes 1:18 (NIV)
June 16th, 2011 at 8:06:46 PM
permalink
Quote: mustangsallyIs BruseZ's avatar really him?
David Krumholtz plays the role of Charlie Eppes in the CBS series Numb3rs. Charlie Eppes is a young mathematical genius and professor of applied mathematics at the fictional California Institute of Science, CalSci.
Since BruceZ give his location as the fiction school of Cal Sci I think that is a dead giveaway.
I know this film is over 30 years, old, but It's My Turn had Jill Clayburgh playing a serious mathematician in her mid 30's who had a sexy role as a newly divorced woman. It was probably the first time I had seen an actor playing a mathematician in a movie in anything other than a throwaway character role. Jill sadly died of cancer a few months ago.
The following lines of dialogue had never appeared in a movie up to that time, Cooperman was played by a young Daniel Stern who would later act in "Home Alone".
The Snake Lemma scene in a rare display in movies, is actually mathematically correct proof.
Kate Gunzinger: Let me just show you how to *construct* the map S, which is the fun of the lemma anyhow, okay? So you assume you have an element in the kernel of gamma, that is, an element in C, such that gamma takes you to 0 in C-prime. You pull it back to B, via map g, which is surjective...
Cooperman: Hold it, hold it, hold it. That's -- that's not unique.
Kate Gunzinger: Yes, it is unique, Mr. Cooperman. Up to an element of the image of f, all right? So we've pulled it back to a fixed B here. Then you take beta of B, which takes you to 0 in C-prime, by the commutivity of the diagram. It's therefore in the kernel of the map g-prime, hence is in the image of the map f-prime, by the exactness of the lower sequence...
Cooperman: No.
Kate Gunzinger: ...so we can pull it back...
Cooperman: No.
Kate Gunzinger: ...to an element in A-prime...
Cooperman: It's not well defined!
Kate Gunzinger: ...which it turns out is *well* defined *modulo* the image of alpha. And thus defines the element in the co-kernel of alpha...
[draws arrow on diagram]
Kate Gunzinger: and that's the "snake"! And on Monday, we'll address ourselves to
[Cooperman raises hand]
Kate Gunzinger: the co-homology of groups... and Mr. Cooperman's next objections.
June 20th, 2011 at 3:31:40 PM
permalink
removed
silly
silly
I Heart Vi Hart
June 20th, 2011 at 3:45:35 PM
permalink
removed
silly
silly
I Heart Vi Hart
June 21st, 2011 at 7:57:51 AM
permalink
Mustangsally,
I see what is going on now.
The difference in the two matrices (yours and the Wizards) is that you include one more state, the top row and left column which represents the state of not playing. The first move will transition the player from a state of not playing to a state of a 0-streak. After that, you have 100 more transitions to go. Therefore, you will calculate T^101 (1 to get into the game and 100 for the dice rolls). The Wizard's transition matrix assumes that you have already decided to play the game and the player starts with a state of a 0-streak. In this case, we calculate T^100.
I see what is going on now.
The difference in the two matrices (yours and the Wizards) is that you include one more state, the top row and left column which represents the state of not playing. The first move will transition the player from a state of not playing to a state of a 0-streak. After that, you have 100 more transitions to go. Therefore, you will calculate T^101 (1 to get into the game and 100 for the dice rolls). The Wizard's transition matrix assumes that you have already decided to play the game and the player starts with a state of a 0-streak. In this case, we calculate T^100.
I heart Crystal Math.
November 8th, 2011 at 9:56:11 PM
permalink
Quote: CrystalMathThe flaw here is that the numbers 31.752 and 17.021 do not represent the average number of streaks, but the likelyhood of getting one or more streaks. If you were to calculate the average number of 8+ coin streaks and 7 coin streaks, then you could subtract them in this manner.
Using a Markov chain, I calculate the probability of exactly one 7 coin streak to be 0.172920892.
CrystalMath, you have an excellent working knowledge of Markov Chains.
Would you share your matrix solution for the above answer?
I am assuming that this is an absorbing transition matrix.
Thanks kindly.
winsome johnny (not Win some johnny)
November 9th, 2011 at 6:38:12 AM
permalink
Another reason why I love this site; it rekindles my love for math. I remember all of those matrices from first year algebra in University. It was my first final exam at University and of course I crammed for the exam. The exam started at 9:00am; I remember sleeping in until 9:15, and running to the exam, and being able to write it. The prof. even gave me an extra 15 minutes to finish the exam.
-----
You want the truth! You can't handle the truth!
November 9th, 2011 at 7:47:18 AM
permalink
Quote: 7crapsCrystalMath, you have an excellent working knowledge of Markov Chains.
Would you share your matrix solution for the above answer?
I am assuming that this is an absorbing transition matrix.
Thanks kindly.
I actually don't have it any more and it would be pretty time consuming to recreate. I used a Markov Chain instead of a matrix though. They essentially do the samem thing but the chain will use less space in Excel.
I heart Crystal Math.
November 9th, 2011 at 7:52:09 AM
permalink
Quote: DJTeddyBearI was afraid to admit that I have no idea what he's even referring to when he says "as everyone knows...."
I'm sure he's attempting a bit of humor. And stochastic means purely probabilistic, with no intelligence controlling the outcome.
November 9th, 2011 at 7:53:48 AM
permalink
Quote: WizardYou're right, thanks for the correction. The column should be correct now.
I could count the number of girls on this forum with one hand, so don't expect one of them to answer. Personally, I think that is the mathematician from the show Numbers.
Doctor Charles Epps
November 9th, 2011 at 1:53:36 PM
permalink
Quote: CrystalMathI actually don't have it any more and it would be pretty time consuming to recreate. I used a Markov Chain instead of a matrix though. They essentially do the samem thing but the chain will use less space in Excel.
I figured you might not still have your work.
You use Excel. That is a lot of work for matrices.
There are free softs (Winmat at Peanut soft) Winmat
and online like
Matrix Algebra Tool that are even easier and faster.
Is not the matrix below correct except I do not know what to place in row 9 to make this 9x9?
(A 1 in 9,9 would be for 8 or more and that is a different question.)
0.50000 0.50000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.50000 0.00000 0.50000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0.50000 0.00000 0.00000 0.50000 0.00000 0.00000 0.00000 0.00000 0.00000
0.50000 0.00000 0.00000 0.00000 0.50000 0.00000 0.00000 0.00000 0.00000
0.50000 0.00000 0.00000 0.00000 0.00000 0.50000 0.00000 0.00000 0.00000
0.50000 0.00000 0.00000 0.00000 0.00000 0.00000 0.50000 0.00000 0.00000
0.50000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.50000 0.00000
0.50000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.50000
0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
We would be concerned with 8,1 a tail after 7 heads correct?
Plugging in a few numbers does not arrive at your answer.
I can do the work, I just need to know how to start off.
Thanks
winsome johnny (not Win some johnny)
November 9th, 2011 at 8:13:38 PM
permalink
I thought about this again since I just can't stay away from interesting questions. Anyhow, the answer I was trying to find was the probability of getting exactly one streak of 7. Because of that, we have to keep track of when the streak exceeds 7 and also we need to keep track of whether or not a streak of 7 has already been reached. In the matrix below, "streak 7,n" represents the likelihood of having reached a streak of 7 and then currently having a streak of size n. When you calculate T^100, using the following transition matrix, the probability of ending in each state will be on the top row. Then, we need to add the probabilities of streak 7; streak 7,0 through streak 7,6; and streak 7,8+. When you do, you will see that I made an error in my original answer. In my original answer, it appears as though I also added streak 7,7.
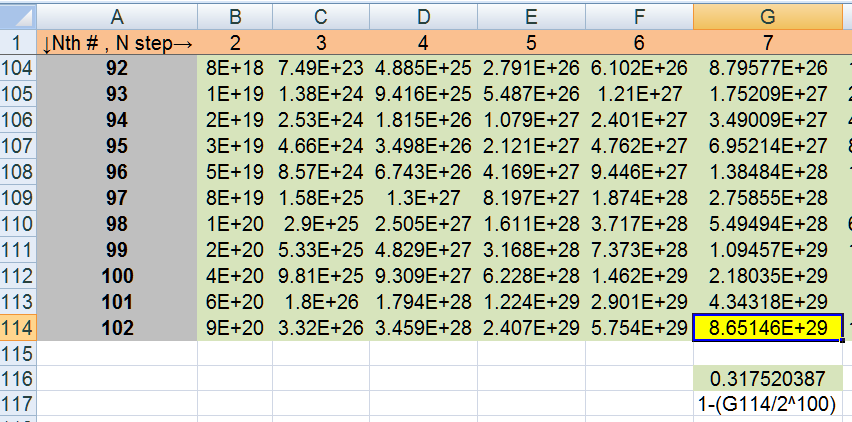
streak 0 0.5 0.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
streak 1 0.5 0 0.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
streak 2 0.5 0 0 0.5 0 0 0 0 0 0 0 0 0 0 0 0 0 0
streak 3 0.5 0 0 0 0.5 0 0 0 0 0 0 0 0 0 0 0 0 0
streak 4 0.5 0 0 0 0 0.5 0 0 0 0 0 0 0 0 0 0 0 0
streak 5 0.5 0 0 0 0 0 0.5 0 0 0 0 0 0 0 0 0 0 0
streak 6 0.5 0 0 0 0 0 0 0.5 0 0 0 0 0 0 0 0 0 0
streak 7 0 0 0 0 0 0 0 0 0.5 0.5 0 0 0 0 0 0 0 0
streak 8+ 0.5 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0 0 0 0
streak 7,0 0 0 0 0 0 0 0 0 0 0.5 0.5 0 0 0 0 0 0 0
streak 7,1 0 0 0 0 0 0 0 0 0 0.5 0 0.5 0 0 0 0 0 0
streak 7,2 0 0 0 0 0 0 0 0 0 0.5 0 0 0.5 0 0 0 0 0
streak 7,3 0 0 0 0 0 0 0 0 0 0.5 0 0 0 0.5 0 0 0 0
streak 7,4 0 0 0 0 0 0 0 0 0 0.5 0 0 0 0 0.5 0 0 0
streak 7,5 0 0 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0.5 0 0
streak 7,6 0 0 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0 0.5 0
streak 7,7 0 0 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0 0 0.5
streak 7,8+ 0 0 0 0 0 0 0 0 0 0.5 0 0 0 0 0 0 0 0.5
I heart Crystal Math.
November 9th, 2011 at 9:05:53 PM
permalink
Quote: CrystalMathI thought about this again since I just can't stay away from interesting questions. Anyhow, the answer I was trying to find was the probability of getting exactly one streak of 7.
OK.
Excellent work but I now think you are answering a different question.
Now this seems confusing.
Starting over...
From the Wizard:
"The probability of getting "one or more" streaks of exactly seven heads in a row out of 100 coin tosses is 17.29%"
I get the same answer from computer sims.
"The probability of getting one or more streaks of "at least" seven heads in a row out of 100 coin tosses is 31.7520%"
The Wizard has the correct solution of 31.7520% but had the matrix not square in his article. He did correct it.
June 16, you wrote, "Using a Markov chain, I calculate the probability of exactly one 7 coin streak to be 0.172920892."
So then you must have added all the values?
I must have misread that statement when I first read it.
But is sure looks like the theoretical answer that matches the answer the Wizard gave for "one or more". The Wizard has never shown his work on this so I must assume he also ran a computer simulation.
I will work with your matrix and see if I can duplicate your first answer by adding all the values. It should work.
Thank you for your efforts.
Excellent work as always.
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
Added: Excellent. I came up with 0.1729209 and I am sure if I added the extra places the results will match perfectly to your answer.
Worked exactly as you described and I now understand the process.
I did not use Excel to calculate T^100, I used Winmat (free Peanut soft) and it took just a few seconds to paste in the matrix once I had it set up in Excel.
I have seen others use inclusion-exclusion for these type of problems and they are really messy to work with.
I hope others can understand your work as well, if they want to of course.
Again, Thanks very much.
Added Nov 10.
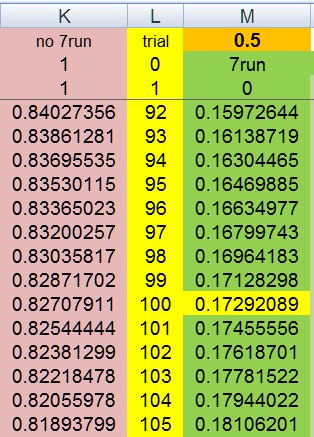
Here is my T^100
streak 0 streak 1 streak 2 streak 3 streak 4 streak 5 streak 6 streak 7 streak 8+ streak 7,0 streak 7,1 streak 7,2 streak 7,3 streak 7,4 streak 7,5 streak 7,6 streak 7,7 streak 7,8+
0.414358508 0.207589542 0.104000322 0.052103139 0.026103161 0.013077427 0.006551663 0.003282319 0.003295345 0.085641492 0.042410458 0.020999678 0.010396861 0.005146839 0.002547573 0.001260837 0.000623931 0.000610905
0.412720599 0.206768966 0.103589221 0.051897182 0.025999978 0.013025734 0.006525765 0.003269344 0.003282319 0.087279401 0.043231034 0.021410779 0.010602818 0.005250022 0.002599266 0.001286735 0.000636906 0.000623931
0.409451255 0.205131057 0.102768644 0.051486081 0.025794021 0.012922551 0.006474071 0.003243446 0.003256318 0.090548745 0.044868943 0.022231356 0.011013919 0.005455979 0.002702449 0.001338429 0.000662804 0.000649932
0.40292549 0.201861713 0.101130735 0.050665505 0.02538292 0.012716594 0.006370889 0.003191753 0.003204419 0.09707451 0.048138287 0.023869265 0.011834495 0.00586708 0.002908406 0.001441611 0.000714497 0.000701831
0.389899757 0.195335948 0.097861391 0.049027596 0.024562344 0.012305493 0.006164931 0.00308857 0.003100827 0.110100243 0.054664052 0.027138609 0.013472404 0.006687656 0.003319507 0.001647569 0.00081768 0.000805423
0.363899778 0.182310214 0.091335626 0.045758252 0.022924435 0.011484917 0.00575383 0.002882612 0.002894052 0.136100222 0.067689786 0.033664374 0.016741748 0.008325565 0.004140083 0.00205867 0.001023638 0.001012198
0.312002596 0.156310236 0.078309893 0.039232487 0.019655091 0.009847007 0.004933254 0.002471512 0.00248132 0.187997404 0.093689764 0.046690107 0.023267513 0.011594909 0.005777993 0.002879246 0.001434738 0.00142493
0.208413375 0.104413054 0.052309914 0.026206753 0.013129326 0.006577663 0.003295345 0.001650935 0.001657487 0.291586625 0.145586946 0.072690086 0.036293247 0.018120674 0.009047337 0.004517155 0.002255315 0.002248763
0.416002918 0.208413375 0.104413054 0.052309914 0.026206753 0.013129326 0.006577663 0.003295345 0.003308423 0.083997082 0.041586625 0.020586946 0.010190086 0.005043247 0.002495674 0.001234837 0.000610905 0.000597827
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0 0 0 0 0 0 0 0 0 0.5 0.25 0.125 0.0625 0.03125 0.015625 0.0078125 0.00390625 0.00390625
0.1729208930 is my final answer
winsome johnny (not Win some johnny)
November 10th, 2011 at 8:29:12 AM
permalink
After re-reading the entire post, I see that we were trying to confirm the Wizard's assertion that the probability of getting "one or more" streaks of length 7 is 0.1729. In my original answer, I said "exactly one" streak of length 7, but my answer was for "one or more."
So, it looks like we agree.
Thanks for the Winmat suggestion. I'll need to look into that. Also, I need to finally try to learn about inclusion/exclusion.
So, it looks like we agree.
Thanks for the Winmat suggestion. I'll need to look into that. Also, I need to finally try to learn about inclusion/exclusion.
I heart Crystal Math.
November 10th, 2011 at 8:44:28 AM
permalink
Quote: CrystalMathThanks for the Winmat suggestion. I'll need to look into that. Also, I need to finally try to learn about inclusion/exclusion.
Thank you. You are very welcome.
inclusion-exclusion is a great tool to have. It can get very messy when using many terms.
a good example is here:
askthewizard/278
4th question down
"What is the expected number of rolls of two dice for every total from 2 to 12 to occur at least once?"
Also BruceZ over at 2+2 really does a great job on explaining inclusion-exclusion
The Wizard explains it also in the article.
winsome johnny (not Win some johnny)
November 10th, 2011 at 10:01:58 AM
permalink
Quote: CrystalMathThanks for the Winmat suggestion. I'll need to look into that.
Winmat is a Windows program from Peanut software, its free, that does matrices and much more.
An excellent program as is the suite of Peanut math programs.
I suggest you try it out with the:
"I once hit six royals in single-line video poker within 5,000 hands.
In my lifetime I have played about 25 million hands. What are the odds?"
matrix that you did.
six royals in single-line video poker within 5,000 hands-ask the wizard 277
You can just copy and paste the matrix into Winmat and calculate T^25,000,000 in a split second.
(or 25,000,000-5000) I have not studied that article yet.
I have only used the Winmat program a few times but what an excellent tool to have IMO.
Thanks for all your excellent work!
winsome johnny (not Win some johnny)
February 14th, 2012 at 11:17:03 AM
permalink
Happy Valentine's Day
I am on vacation!
Yeah!
i got it too, once i got it
Excel transition matrix
recursion matrix answer
a full view of the recursion markov chain
I am on vacation!
Yeah!
i got it too, once i got it
Excel transition matrix
recursion matrix answer
a full view of the recursion markov chain
I Heart Vi Hart
July 25th, 2015 at 9:12:23 AM
permalink
i agree with all your probabilities and say you made no mistake ;)Quote: pacomartinI am not sure if the third answer is correct.
The probability of getting one or more streaks of at least seven heads in a row out of 100 coin tosses is 31.752%
The probability of getting one or more streaks of at least eight heads in a row out of 100 coin tosses is 17.021%
The answer should be the difference 31.752%-17.021%=14.731% (which is different than either your answer or the Wizard's).
It's possible I am the one making the mistake here, but I will post anyway.
14.731% is the answer to this
"What is the probability that the longest run of heads is exactly 7 in 100 flips?"
in other words
it could be this sequence at the beginning
HHH HHHH T
or this some where in 100 flips
T HHH HHHH T
or this at the end
T HHH HHHH
a Markov chain can solve this too (Julybe later)
as well as a simulation (already done)
here is the distribution of the longest run in N trials from me Excel
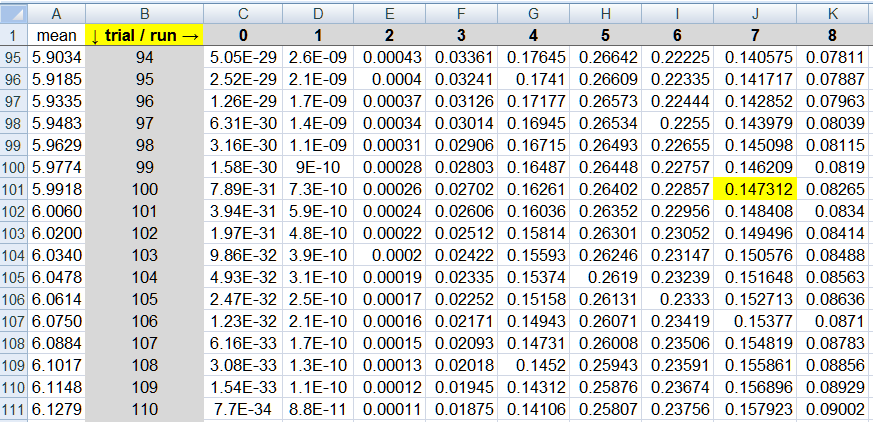
and this paper has a solution too
"Notes on the longest run of heads"
Bret Larget
September 18, 2009
now to see (C) what i can do B4 the 6pm Angel game start time
to get them to score more runs (at least more than 2)
Mike and Albert (they LOVE pizza) get ready to go OVER!
I Heart Vi Hart
July 26th, 2015 at 6:55:39 AM
permalink
Your answer of 14.731% is correct for the probability that the longest run of heads is exactly 7 in 100 flips. Using an absorbing Markov chain, I calculated the exact value 0.317520387 for the probability of having a run of length 7 or more and the the exact value 0.170207962 for the probability of having a run of length 8 or more.
July 26th, 2015 at 11:19:00 AM
permalink
thank you for confirming that.Quote: brandoYour answer of 14.731% is correct for the probability that the longest run of heads is exactly 7 in 100 flips.
now, there are those teachers in math class(es) that have the(ir) students
(as a homework assignment)
either flip or
make up (fake)
a 100 coin sequence
some use 200 flips, wow! (time for random.org)
or even a smaller sequence from 25 to 50 flips
i like 50 as each flip takes 5 seconds to complete and record and the whole homework assignment is completed in 5 minutes (remember to write your name at the top!)
la la la te da
Huh
of course the teacher is looking for a run of either Heads or Tails
so
can the Head P(7+run) - Head P(8+run) = P of the longest Head run = 7
also work for the probability of the longest run of either a H or T being = 7?
in other words
either P(7+run) - either P(8+run) = probability of the longest run either a H or T being = 7?
True or False?
0.542336855 - 0.314767189 = 0.227569666
looks like it could be true
but a quick sim and a Markov chain shows it is not true, in my opinion
100 flips success = 0.318273134
i think
because there are 2 "states" that are summed to arrive at the success probability makes the "short-cut"
a no-go
looks like it could be true
but a quick sim and a Markov chain shows it is not true, in my opinion
100 flips success = 0.318273134
i think
because there are 2 "states" that are summed to arrive at the success probability makes the "short-cut"
a no-go
Heads or Tails?
I Heart Vi Hart
July 26th, 2015 at 2:25:16 PM
permalink
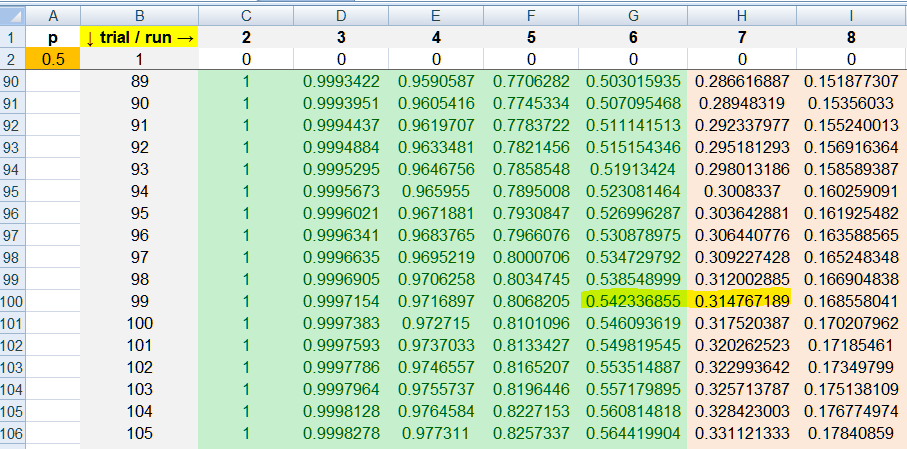
Quote: mustangsally
can the Head P(7+run) - Head P(8+run) = P of the longest Head run = 7
also work for the probability of the longest run of either a H or T being = 7?
in other words
either P(7+run) - either P(8+run) = probability of the longest run either a H or T being = 7?
True or False?0.542336855 - 0.314767189 = 0.227569666
looks like it could be true
but a quick sim and a Markov chain shows it is not true, in my opinion
100 flips success = 0.318273134
i think
because there are 2 "states" that are summed to arrive at the success probability makes the "short-cut"
a no-go
It is true, and 0.227569666 is correct. There is no problem with that logic, and I verified it by simulation too. The 0.318 that you got from your Markov chain looks like it could be P(exactly 7 heads or tails). It is NOT true that P(7 or more) - P(8 or more) = P(exactly 7) regardless of whether we are talking about just heads or either heads or tails. There are times that we get 8 or more AND exactly 7 which are being subtracted.
July 26th, 2015 at 3:29:55 PM
permalink
can i have this dance?Quote: BruceZQuote: mustangsally
can the Head P(7+run) - Head P(8+run) = P of the longest Head run = 7
also work for the probability of the longest run of either a H or T being = 7?
in other words
either P(7+run) - either P(8+run) = probability of the longest run either a H or T being = 7?
True or False?0.542336855 - 0.314767189 = 0.227569666
looks like it could be true
but a quick sim and a Markov chain shows it is not true, in my opinion
100 flips success = 0.318273134
i think
because there are 2 "states" that are summed to arrive at the success probability makes the "short-cut"
a no-go
It is true, and 0.227569666 is correct. There is no problem with that logic, and I verified it by simulation too. The 0.318 that you got from your Markov chain looks like it could be P(exactly 7 heads or tails). It is NOT true that P(7 or more) - P(8 or more) = P(exactly 7) regardless of whether we are talking about just heads or either heads or tails. There are times that we get 8 or more AND exactly 7 which are being subtracted.
when pacomartin got that 14.731% (0.147312425) in his post
I came up with what that represented
Prob of the longest Head run = 7 (not 7 or more)
so i start over as i be down with a nasty cold this weekend and Mike Trout hit 2 homers today
one a grandslam
i be so happy as i bet the OVER big time (i do blame my cold on Tara Strong)
so do you agree that 0.147312425 = Prob of the longest Head run being 7 in 100 flips?
i should feel better after dinner tonight
thank you
EDIT
Bruce
i got it!
thank you (i was feeling fuzzy all morning, did not go to the Angels game. damn)
i did a different sim this morning
mine agrees
sooooooooooooooooo
when you were taking math in school did a teacher ever have you flip coins or fake flipping coins as a homework assign?
i did
and actually flipped them 100 times
5 in a row or at least 5 in a row
I Heart Vi Hart
July 26th, 2015 at 4:08:38 PM
permalink
Quote: mustangsally
so do you agree that 0.147312425 = Prob of the longest Head run being 7 in 100 flips?
Yes, and that is P(at least 7 heads) - P(at least 8 heads).
P(at least 7 heads) ≈ 0.317520387496606
P(at least 8 heads) ≈ 0.170207962419078
P(at least 7 heads) - P(at least 8 heads) ≈ 0.147312425077528
July 26th, 2015 at 4:11:32 PM
permalink
you beat me to it
i added to my last post
see you soon!
(I was in Chicago about 3 weeks ago for 1 day)
you a Cubs fan?
i do not remember
i added to my last post
see you soon!
(I was in Chicago about 3 weeks ago for 1 day)
you a Cubs fan?
i do not remember
I Heart Vi Hart
July 26th, 2015 at 4:28:52 PM
permalink
Quote:when you were taking math in school did a teacher ever have you flip coins or fake flipping coins as a homework assign?
Not sure, but I did convince a teacher to do this with her class a couple months ago. She was teaching an Excel course and presented my multi-streak calculator. Her headmistress was irritated with all the noise.
Quote:you a Cubs fan?
Of course.
July 26th, 2015 at 7:57:23 PM
permalink
superQuote: BruceZP(at least 7 heads) - P(at least 8 heads) = 0.147312425077528
i tried in WolframAlpha
but it is stubborn doing the subtraction
"WolframAlpha does not yet know how to respond to your exact query."
WolframAlpha attempt
for the run of at least 8
~~0.1702079624190777771961977871442
nice run of 5 7s
I Heart Vi Hart
July 27th, 2015 at 2:34:54 AM
permalink
added note: P(at least either 7 pure heads or 7 pure tails)-P(at least either 8 pure heads or 8 pure tails)=0.542336855-0.314767189=0.227569666
I calculated this exact result by using the user-friendly Markov chain module in the educational software package ORSTAT2000 that can be freely downloaded from
personal.vu.nl/h.c.tijms/
This software package also contains a nice module for simulating the coin-tossing experiment so that the longest run and other phenomena come alive before one's eyes by watching the results of the simulation runs.
I calculated this exact result by using the user-friendly Markov chain module in the educational software package ORSTAT2000 that can be freely downloaded from
personal.vu.nl/h.c.tijms/
This software package also contains a nice module for simulating the coin-tossing experiment so that the longest run and other phenomena come alive before one's eyes by watching the results of the simulation runs.
July 27th, 2015 at 5:36:43 AM
permalink
thank you againQuote: brandoadded note: P(at least either 7 pure heads or 7 pure tails)-P(at least either 8 pure heads or 8 pure tails)=0.542336855-0.314767189=0.227569666
there is a trick (well known) for this when p=1/2
for Heads or Tails run
it is from a famous paper too
Mark F. Schilling
"The Longest Run of Heads"
I wonder if the Wizard knows him personally... (SoCal boys)
so using a spreadsheet and the 3-cell-formula-column-approach that BruceZ showed in a 2005 post
(has to be the easiest way to do this streak stuff that most can understand and when N <= 30,000 or so but 2007 and later go past 1 million rows in Excel)
link to 2005 post. the last one
we use 99 flips and run 6-7 as shown here
and in Google Docs too for those that really want this knowledge
and because
Math IS fun!
me example is for a run of at least 6 and uses named ranges (that way, just change the value of p and you have instant new results, how i do it in Excel. so many have put Excel down over the years but it is a nice tool to use)
Example run 6
just think of all the new casino games too that can be created from the knowledge of probabilities of streaks
just an idea (as i have a few)
Mully
I Heart Vi Hart
