When random variables are independent - and aren't.

Or: Why there exist two perspectives of the same game of chance.

The house edge of a sequence of bets with wagers of varying amounts is calculated by dividing the expected value of winnings and losses of the betting sequence by the average, i.e. expected, wager derived from the individual bets.

A necessary condition for calculating an expected value is the independence of the outcomes, here the wagered amounts.

Observer's perspective.
An observer, e.g. the casino itself, assumes that the variations of the wagered amounts are independed because they are arbitrarily decided by the player, based on personal taste, risk affinity, or financial situation. Even single players, varying the amount of their wagers according to predefined rules or patterns, are considered independent, as their variations blend with the variation of all other players in the casino.

Player's perspective.
A player who follows a certain predefined pattern or procedure to vary the amounts she wagers, might ask: "Shouldn't a defined pattern suggest that my bet sizes are not independent?".
She sits down to work out the mathmatical proof.

She recalls that "two random variables are independent if their joint probablity equals the product of their individual probabilities."

She defines random variables:

A ... bet size is 1 unit
B ... bet size is 2 units

She also knows from previous play that

p(A) > 0 ... because an observer actually sees her wager 1 unit in some cases
p(B) > 0 ... because an observer actually sees her wager 2 units in some cases

Now she lists all possible joint probabilites of two consecutive bets and validates them against the first of her procedures ("two step Paroli"):

p(A & A) > 0 < p(A)*p(A) ... she lost the first bet and starts over with 1 unit again
p(A & B) > 0 < p(A)*p(B) ... she won the first bet and lets her winning ride on the second bet
p(B & A) > 0 < p(B)*p(A) ... she either won or lost the "letting ride" and starts over with 1 unit again
p(B & B) = 0 < p(B)*p(B) ... she never bets 2 units in succession and the product of two values greater than zero can never equal zero

She also tests her second procedure ("two step Martingale"):

p(A & A) > 0 < p(A)*p(A) ... she won the first bet and starts over with 1 unit again
p(A & B) > 0 < p(A)*p(B) ... she lost the first bet and wagers additional 2 units from her bankroll on the second bet
p(B & A) > 0 < p(B)*p(A) ... she either won or lost the "doubled bet" and starts over with 1 unit again
p(B & B) = 0 < p(B)*p(B) ... she never bets 2 units in succession and the product of two values greater than zero can never equal zero

(The character "&" above substitutes the mathematical symbol for intersection which looks like an upside down letter "U".)

For both procedures, random variable B, i.e. betting 2 units, is not an independent variable and therefore the sum p(A)*A + p(B)*B is not the valid expected value of her wagers.

To calculate her house edge, she will utilize the amount she needs to take from her bankroll in order to be able to play the procedure, i.e. to cover the case where the procedure (not just any of the single bets) loses.

"two step Paroli"
She needs to take 1 unit from her bankroll.
The bet of 2 units which is observed, consists of her own 1 unit from her bankroll and the 1 unit won on the first roll.
If she loses this bet, she actually only loses 1 unit from her bankroll.
If she wins, she will return her original 1 unit and add 3 more units to her bankroll.


"two step Martingale"
She needs to take 3 units from her bankroll.
If she wins the bet of 1 unit she will return this original 1 unit, the 2 "unused" units and add the 1 unit won to her bankroll.
If she loses the 1 unit bet she will bet the 2 remaining units.
If she wins the 2 unit bet she will return the 2 units she originally took from her bankroll and add the 2 units won to her bankroll.
If she loses the 2 unit bet she will have lost all 3 units she originally took from her bankroll.

APPENDIX

Why the observer, e.g. the casino, cannot but assume that the varying amounts of wagers are independent.

In theory the observer, e.g. the casino, of course could try to monitor the player closely in order to determine the player's individual house edge. This would not only be immensly expensive, especially if a larger group or even all players were to be monitored, but it also is useless, because the players easily can disguise what they are doing. Independence of the outcomes of the game itself here is the player's friend.

Let's take the two step Martingale as an example.

Grouping.
Instead of always playing the steps of the procedure in perfect sequence, play several 1 unit bets in a row and count how often you lose. When you feel you have collected enough losses, start playing exactly this number of 2 unit bets.
Why it works: In the two step Martingale you only wager 2 units if you have lost the 1 unit bet before. Since the outcomes of the game itself are independent, it is irrelevant when you play the 2 units. Any one bet will do.

Switching.
If you feel that you are observed at your table, play the 2 unit bets at a different table offering the same game. So an observer sees you flat betting 1 unit at the one table and flat betting 2 units at the other.

Walking.
If you feel that the casino is monitoring you comprehensively, change to another casino offering the same game and play the 2 unit bets there. Do not forget your count!

This is only a small collection of possibilities of how to make use of the independence in games of chance.

I don't see how variation in bet unit sizing or sequencing would affect the house edge. It applies to the total amount wagered.

Quote: JackSpade

I don't see how variation in bet unit sizing or sequencing would affect the house edge. It applies to the total amount wagered.
link to original post

It not only doesn't affect the house edge, it does not affect the players disadvantage, nor their expected value.
The player can 'Use' this independence any way they wish, but it is of zero value to her.

Quote: OnceDear

Quote: JackSpade

I don't see how variation in bet unit sizing or sequencing would affect the house edge. It applies to the total amount wagered.
link to original post

It not only doesn't affect the house edge, it does not affect the players disadvantage, nor their expected value.
The player can 'Use' this independence any way they wish, but it is of zero value to her.
link to original post

Hello JackSpade and OnceDear,

Thanks for your replies.

I'd like to show how the player's disadvantage ( = - house edge) is affected by the two betting procedures she uses. I will refer to betting on red at a double zero roulette table as the example.

Two step Paroli.

Scenario I
Imagine the casino offers a special bet: The player wagers 1 unit on red and will win 3 units if the next two rolls both are red. (This bet was analyzed by the Wizard in 2015.)

The house edge of this bet is 10.25% while the house edge of double zero roulette should be 5.26%.

Scenario II
Keeping track of the wagers in this special offer can be rather confusing on a busy regualr roulette table. Therefore dealers are allowed to use a special chip to add it to those 1 unit wagers that won their first roll. That special chip cannot be cashed by players.
If the ball lands on red again on the next roll, the dealer will pay 3 units to the 1 unit which is accompanied by that special chip and collect the special chip for later reuse.
If red does not come up on any of the two rolls, the dealer instantly collects the 1 unit wagered and of course the special chip, if on the second roll. In both cases the player loses her 1 unit wagered.

Is it wrong to assume that this bet is the same as the one in scenario I and that therefore the house edge of this bet still is 10.25%?

Scenario III
Our player visits casinos that do not offer this special bet. Is she able to simulate this bet on her own?
She wagers 1 unit from her bankroll on red. If red comes up she will receive another unit to her original wager which she defines as that special indicator chip of scenario II and lets it ride for the second roll. If red comes up a second time she will win 2 more units to her 2 units already on the tabel and will walk away with a total of 4 units, her inital 1 unit plus the 3 units won, as defined in scenarios I and II.

Is it wrong to assume that if she loses on any of the two rolls, she loses 1 unit as she does in scenarios I and II?

Is it therefore wrong to assume that the house edge of her play also is 10.25% as in scenarios I and II?

REMARK
As confirmed by the Wizard's analysis, this bet is rather profitable for the house. It can be supposed that this also is the reason why this is offered on the double action roulette but not the following bet:

Two step Martingle

Scenario IV
Imagine the casino offers this special bet: The player wagers 3 units on red and will win 1 unit on any first red of the the next two rolls. (This bet could easily be offered on the double action roulette, as well.)
If neither of the two rolls shows red, the player loses her wager of 3 units.

Is it wrong to assume a house edge of 3.6% for this bet, while the house edge of double zero roulette should be 5.26%?

Scenario V
Also in this case keeping track of the wagers can be confusing. The dealers therefore are allowed to remove 1 unit of the 3 units if the first roll is not red. If the second roll wins, the dealer adds 2 units to the remaining wager of 2 units. If the first roll wins, the dealer adds 1 unit to the wager of 3 units, as defined in scenario IV. In both cases the player receives 4 units which is the sum of 3 initial units and the 1 unit won.
If neither of the two rolls shows red, the player loses her 3 units wagered.

Is it wrong to assume that this bet is the same as the one in scenario IV and that therefore the house edge of this bet still is 3.6%?

Scenario VI
This bet doesn't seem to be offered anywhere, supposedly because the house edge is lower. Is our player able to simulate it?
She decides to follow the rules of this bet and takes 3 units from her bankroll.
She starts by wagering 1 unit on red for a first roll. If this roll wins, she collects the 2 units from the table, now holding a total of 4 units and is done for this bet. The 4 units consist of her initial wager of 3 units plus the 1 unit won, as defined in scenarios IV and V.
If the first roll loses she wagers the remaining 2 units on the second roll. If this second roll wins she will collect 4 units from the table, again as previously defined in scenarios IV and V the sum of her inital 3 units plus the 1 unit won.
If the second roll loses, she will have lost 3 units, also as defined in scenarios IV and V.

Is it wrong to assume that her play is equivalent to the bets defined in scenarios IV and V?

Is it wrong to further assume that the house edge of her play is 3.6% as in scenarions IV and V?

FINAL NOTE
An overview of the behaviour of both progressions is available here preceded by more experiments. The idea can even be applied without relationship to any progressions.

ThomasK, please explain why you assume a house edge of 3.6% for Scenario IV.

In Scenario VI, the player isn't actually wagering 3 units at a time. 47.3% of the time (the probability of red winning) she wagers only 1 unit total. Is it wrong to assume that 47.3% of the time, the house edge is 5.26%?

ThomasK, don’t waste your time on this. In the long run you will lose 5.3% of every dollar you place on a 00 roulette table. It doesn’t matter what systems you might use

By the way, the edge on your Scenario 1 hypothetical bet is obviously going to be about double the 5.3% because, if you win, you have exposed the bet’s payout to that edge twice (1 - (36/38)^2). I struggled to read even that far so I didn’t make it to the subsequent scenarios

Quote: JackSpade

ThomasK, please explain why you assume a house edge of 3.6% for Scenario IV.

In Scenario VI, the player isn't actually wagering 3 units at a time. 47.3% of the time (the probability of red winning) she wagers only 1 unit total. Is it wrong to assume that 47.3% of the time, the house edge is 5.26%?
link to original post

JackSpade,
Thanks for asking.

I would like to start with the equation the Wizard supposedly used to calculate the house edge for red in double action roulette which is equivalent to scenario I:



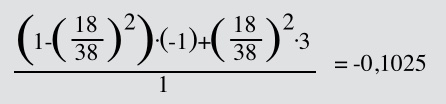
(18/38)^2 is the probability that the ball lands in a spot which has two reds on that special wheel. It is the same probability as two succesive reds in two succesive rolls. (approx. 0.22438)
The amount won is 3.

(1-(18/38)^2) is the probability of all other outcomes. (approx. 0.77562)
They lead to losing the wager, which is 1 in this case.

The sum of the pairwise products is the expected value. (approx. -0.10249)

Dividing the expected value by the wager results in the player advantage.
Since the wager is 1, expected value and player advantage are identical.

The negative of the player advantage is the house edge. (approx. 10.25%)

The same approach applied to the double action roulette wheel for the equivalent of scenario IV results in



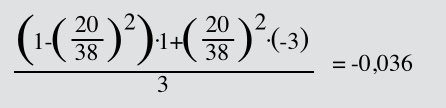
(20/38)^2 is the probability that the ball lands in a spot where neither of the two rings has red. This is same probability as two succesive rolls where neither roll is red. (approx. 0.27701)
The amount wagered on the double action wheel is 3, which is lost in this case.

(1-(20/38)^2 is the probability of all other outcomes, i.e. where at least one red is rolled. (approx. 0.72299)
The amount won is 1.

The sum of the pairwise products is the expected value. (approx. -0.10803)

Dividing the expected value by the wager results in the player advantage. (approx. -0.10803 / 3 = -0.03601)

The negative of the player advantage is the house edge. (approx. 3.6%)

In the case of double action roulette there is little doubt that the wager is 3 because that is what the player puts on the table to be resolved by the roll.

The idea I'm trying to convey is the following:
If the probabilitiy of one roll of the double action roulette wheel is identical to two consecutive rolls of a regular roulette wheel, then the double action roulette can be simulated by two rolls of a regular wheel.
If the player wagers 3 units on double action roulette and double action roulette can be simulated by two rolls of a regular wheel then the wager doesn't have to change, because double action roulette is played.

This would also be my answer to your question about scenario VI. The player plays a simulation of double action roulette and there she wagers 3 units. The trick is to only look at the beginning of the procedure, the original wager, forget about what is happening "in between", and then looking at the result of the procedure.

I'm sorry that I can't seem to express this any better.
Perhaps you might want to have a look at my example that has nothing to do with progressive betting but which utillizes this same idea of simulation.

Please let me know of what remains unclear. It might also help me to explain better. Thank you.

Quote: Ace2

ThomasK, don’t waste your time on this. In the long run you will lose 5.3% of every dollar you place on a 00 roulette table. It doesn’t matter what systems you might use

By the way, the edge on your Scenario 1 hypothetical bet is obviously going to be about double the 5.3% because, if you win, you have exposed the bet’s payout to that edge twice (1 - (36/38)^2). I struggled to read even that far so I didn’t make it to the subsequent scenarios
link to original post

Ace2, thanks.
It seems that you admit that there are circumstances where the house edge can double when playing roulette. The other proposition however is that roulette has the only house edge of 5.3% (in case of double zero).
But 5.3% <> 2 * 5.3%.
How could this be possible?
And if the edge can be greater, why shouldn't it also be possible that the edge becomes smaller?

The "how" and "why" is what I'm trying to explain.

What remains unclear is whether the two scenarios are effectively the same bet. In one scenario, the player is always putting 3 units at risk and seeing two spins for the opportunity to win 1 unit. In the other scenario, the player is initially putting 1 unit at risk. Her next bet might be 1 unit (starting over) or 2 units depending on the outcome of the initial bet.

She will raise 52.7% of the time to 2 units. When she does, she wagers 2 units on one spin that has a 52.7% of chance of not landing on red. The house edge is 5.3% on both bets.

Whereas she could bet 3 units up front for the opportunity to see two spins (1.5 units per spin) and enjoy a slightly lower house edge.

Even though the odds of winning after betting 3 units in each scenario are the same, the house edges are different because the average amount of money being put at risk per spin is different. I don't have all the math put together, but conceptually that's how I think this apparent paradox would be resolved.

I thought the Schrodinger craps game was brilliant. But this thread is just math semantics misunderstanding. You are doing a bait and switch on denominators.

You lose 5.3% of every bet you place at risk on a single spin of the wheel. Full stop and incontrovertible. It doesn’t matter if net sizing changes for independent or dependent reasons.

Quote: ThomasK

Quote: Ace2

ThomasK, don’t waste your time on this.
link to original post

But 5.3% <> 2 * 5.3%.
How could this be possible?
And if the edge can be greater, why shouldn't it also be possible that the edge becomes smaller?

The "how" and "why" is what I'm trying to explain.
link to original post

You need to stop mis-using the house edge.
For the real table situation, the house edge is the 5.3% of what is put on the felt. The 'House Hold' is the percentage that the house tends to take out of the player's buy in.

If you you place $1 on red, one time it is subject to the house edge one time. The hold from that one wager is 5.3%
If it WINS and you let the $2 ride, you have effectively placed a new $2 on the table and the house gets to take 5.3% of $2
But had it lost you would not get to subject that $2 to the house edge at all.

If you put your $1 chip on the table one time, $1x5.3% of it is held. Eaten up by the house edge 1 time
If you put your $1 chip on the table two times, $2x5.3% of it is held. Eaten up by the house edge 2 times
The hold will increase every time you return your chip to the felt.
5.3%
10.5%
etc

You can reduce the hold to 0% by taking your chips to the felt less often than one time. Ie. subject $0 to 5.3%
I.e. don't bet.

Unjon is right. this whole thread is a hodge podge of misinterpreted and abused simple Math.

Quote: JackSpade

What remains unclear is whether the two scenarios are effectively the same bet. In one scenario, the player is always putting 3 units at risk and seeing two spins for the opportunity to win 1 unit. In the other scenario, the player is initially putting 1 unit at risk. Her next bet might be 1 unit (starting over) or 2 units depending on the outcome of the initial bet.

She will raise 52.7% of the time to 2 units. When she does, she wagers 2 units on one spin that has a 52.7% of chance of not landing on red. The house edge is 5.3% on both bets.

Whereas she could bet 3 units up front for the opportunity to see two spins (1.5 units per spin) and enjoy a slightly lower house edge.

Even though the odds of winning after betting 3 units in each scenario are the same, the house edges are different because the average amount of money being put at risk per spin is different. I don't have all the math put together, but conceptually that's how I think this apparent paradox would be resolved.
link to original post

I'm sorry that I haven't been precise enough in my explanation of the procedures in the scenarios. The procedure she uses in scenario VI consists of one certain step, the first bet with a wager of 1 unit, and one conditional step which she only bets if her first bet loses. Her wager for the second bet is 2 units.
Starting over means that she starts a new instance of this procedure.
The house edge I'm referring to is the house edge of the procedure. The procedure again is the simulation of the original scenario IV.
In both cases the player is putting 3 units at risk. In the first case it seems to be clear so far.
In the second case she needs to have availabe, i.e. put at risk, 3 units in order to be able to play the procedure because she doesn't know beforehand whether she will have to wager the 2 units after her first sure wager of 1 unit.
You might argue now that in the case where she wins on the first roll the 2 remaining units are not wagered and therefore should not be used to calculate the house edge. This is the reason why I also brought up Schroedinger's craps which has this same "feature". I would like to ask you to see my answer to unJon which I'm going to post shortly. Please excuse the inconvenience.

Concerning the percentages of how often she is going to wager 1 unit or 2 units some extra consideration adds even more confusion to the topic.

The probability of winning a roll is 18/38 (approx. 47.4%). This often she will put only 1 unit on the table.
The probability of losing the first roll and having to wager 2 more units is therfore 20/38 (approx. 52.6%). This often, however, she is not only wagering the 2 units but she also had to lose 1 unit the exact same number of times, to cause her to wager the 2 units. Therefore she effectively is wagering a total of 3 units 52.6% of the times (i.e. procedures).
Dividing the expected value of the procedure (approx. -0.10249) by the expected wager calculated on this basis results in the 5.26% house edge.
(expected wager = 18/38 * 1 + 20/38 * 3 = approx. 2.05263)

An observer in the casino will never see her wager 3 units but will only see her putting either 1 unit or 2 units on the table.
The probability for wagering 1 unit therfore is 38/(38+20) approx. 65.5% of the rolls.
The probability of wagering 2 units is the remaining 20/(38+20) approx. 34.5% of the rolls.
The expected wager for this is 38/58 * 1 + 20/58 * 2 = approx. 1.34483.
The house edge using this expected wager is 8.03%, which also can be presumed for any comps the player might be awarded.

Proof for these probabilities.
Assume the player wagers on n rolls of the roulette wheel, applying the defined procedure.
x out of these n rolls she will wager 1 unit.
20/38 times out of these x rolls she will lose her first bet of 1 unit and will have to bet another 2 units on a second roll, as defined by the procedure.
Therefore n = x + 20/38 * x = x * (1 + 20/38) = x * (38/38 + 20/38) = x * 58/38.
Solving for x results in x = n * 38/58.
Substituting x in n = x * (1 + 20/38) = n * 38/58 * (1 + 20/38) = n * (38/58 + 20/58)
with 38/58 being the proprtion of 1 unit bets and 20/58 being the proportion of 2 unit bets in her play.

I'm wondering whether I should open another thread to have this discrepancy discussed?

Quote: unJon

I thought the Schrodinger craps game was brilliant. But this thread is just math semantics misunderstanding. You are doing a bait and switch on denominators.

You lose 5.3% of every bet you place at risk on a single spin of the wheel. Full stop and incontrovertible. It doesn’t matter if net sizing changes for independent or dependent reasons.
link to original post

unJon (and JackSpade),

The reason why I brought up Schroedinger's craps is because it has most of the features that I am trying to explain with progressive wagers but without the instant reluctance caused by the notion of betting systems.

One of these features is the question about "money not wagered". In the case of the slot machine you only realize any "coins not wagered" if you find the gaming console, with the passline bet, inside machines of type B. Suspicion would never occur with machines of type A which use the RNG only.
Nevertheless, the behaviour of both types is the exact same for the player outside.

If a player now simulates this behaviour (see experiments 1 and 2) by playing an existing game which produces the exact same probabilities and if she further is able to play with the exact same coin in and cash out, then her play should have the exact same house edge as the "equivalent slot machine" she is simulating. The trick is, with respect to the calculation of the house edge, to ignore what is happening to your coin in before the cash out. The type A machines do exactly that.

And this not only should be applicable for an established game like the pass line bet but also for a sequence of bets in progressive betting. The "equivalent slot machines" for these are even more rudimentary because their paytables only have a single entry - the winning case.
For scenario I the "equivalent slot machine" pays 3 with a probability of (18/38)^2 (approx. 22.4%).
For scanario IV the "equivalent slot machine" pays 1 with a probability of (1 - (20/38)^2) (approx. 72.3%).
For both there is a type A RNG version, and a type B gaming console version playing the two step progressions.
In the case of the "two step Martingale" slot machine of type B with the gaming console (equivalent to scenario IV) you will again find these "coins not wagered" in those cases where the first roll wins. As explained, the type A slot machine "ignores" this and you would never suspect any "coins not wagered" when inspecting the RNG implementation.

Quote: OnceDear

Quote: ThomasK

Quote: Ace2

ThomasK, don’t waste your time on this.
link to original post

But 5.3% <> 2 * 5.3%.
How could this be possible?
And if the edge can be greater, why shouldn't it also be possible that the edge becomes smaller?

The "how" and "why" is what I'm trying to explain.
link to original post

You need to stop mis-using the house edge.
For the real table situation, the house edge is the 5.3% of what is put on the felt. The 'House Hold' is the percentage that the house tends to take out of the player's buy in.

If you you place $1 on red, one time it is subject to the house edge one time. The hold from that one wager is 5.3%
If it WINS and you let the $2 ride, you have effectively placed a new $2 on the table and the house gets to take 5.3% of $2
But had it lost you would not get to subject that $2 to the house edge at all.

If you put your $1 chip on the table one time, $1x5.3% of it is held. Eaten up by the house edge 1 time
If you put your $1 chip on the table two times, $2x5.3% of it is held. Eaten up by the house edge 2 times
The hold will increase every time you return your chip to the felt.
5.3%
10.5%
etc

You can reduce the hold to 0% by taking your chips to the felt less often than one time. Ie. subject $0 to 5.3%
I.e. don't bet.

Unjon is right. this whole thread is a hodge podge of misinterpreted and abused simple Math.
link to original post

OnceDear,

I hope very much that I am not mis-using the house edge.
Did you happen to have a chance to have a look at my post about Schroedinger's craps? There three different house edges for a passline bet are discussed. I would think that at least the two percentages, the 1.41% for the initial wager of a passline bet and the 0.37% for a passline with full 3x4x5x odds, are accepted figures. As far as I recall, there had been discussions in the past which one of both should be assigned to a passline bet with full odds because the free odds bet have no edge at all.
What percentage per dollar wagered does a player suffer from the passline with full odds, as she is putting the inital bet plus her free odds bet at risk?
What percentage is the hold of the house, as it only will earn from the inital bet and will break even over the long run on the free odds bets?

I hope I'm not wrong assuming that slot machines do have a house edge and that this fact is accepted, as well.
The inner workings of the machine remain obscured to the player outside. Information which is public are the monetary amounts of coin in, and the payout according to the paytable. The probabilitiy of each individual payout is well defined, yet usually not disclosed to the player.
Monetary amounts and probabilities are the ingredients needed to calculate a house edge.

In Schroedinger's craps a hypothetical slot machine is defined with its paytable and the probabilitiy of each payout.
This slot machine's payouts and probabilities happen to be such, that they can be produced by a passline bet with full 3x4x5x odds. This slot machine can either be built physically or it can as well be simulated by a passline bet at a real craps table.
When simulating, the player has to behave at the craps table as if she were playing the slot machine: Six coins in, waiting for the random workings to resolve and receiving the payout accordingly.
I tried to make this idea more digestible by suggesting in experiment 1, that the player have a friend bet at the table. The player herself will only hand the six coins to the friend and will receive back the payout from the friend, again. This is analogous to putting the six coins into the machine and collecting the payout.
The player will experience the same house edge as if playing at the slot machine, because for her there is no difference between both plays.
The house, however, will actually only hold the percentage of the amount wagered on the table.

I keep calling both percentages house edge because any amount the player loses goes to the house, as always.

Coming back to the progressive wagers, the same idea applies: Define a hypothetical "equivalent slot machine" with coin in, payouts and probabilites that can be produced by a progression in an existing game, eg. roulette. Now behave at the table as if playing that slot machine: Coins in, waiting for the random workings to resolve, and receiving the payout. Again having a friend do the actual betting at the table can help to better understand what is going on. An earlier description of such an experiment is available here. (In that experiment the financial controller is the player at the equivalent slot machine and she calculates the house edges experienced by her.)
Also in this case, of progressions, the player will experience the same house edge as if playing the slot machine, while the house of course will only hold the percentage of the amount actually put on the table.
The reason for the two different perspectives is given above and is caused by the independence of wagers as seen by the house, while the player knows that her wagers are not independent.

Quote: ThomasK

Quote: JackSpade

[...]

link to original post

[...]

An observer in the casino will never see her wager 3 units but will only see her putting either 1 unit or 2 units on the table.
The probability for wagering 1 unit therfore is 38/(38+20) approx. 65.5% of the rolls.
The probability of wagering 2 units is the remaining 20/(38+20) approx. 34.5% of the rolls.
The expected wager for this is 38/58 * 1 + 20/58 * 2 = approx. 1.34483.
The house edge using this expected wager is 8.03%, which also can be presumed for any comps the player might be awarded.

Proof for these probabilities.
Assume the player wagers on n rolls of the roulette wheel, applying the defined procedure.
x out of these n rolls she will wager 1 unit.
20/38 times out of these x rolls she will lose her first bet of 1 unit and will have to bet another 2 units on a second roll, as defined by the procedure.
Therefore n = x + 20/38 * x = x * (1 + 20/38) = x * (38/38 + 20/38) = x * 58/38.
Solving for x results in x = n * 38/58.
Substituting x in n = x * (1 + 20/38) = n * 38/58 * (1 + 20/38) = n * (38/58 + 20/58)
with 38/58 being the proprtion of 1 unit bets and 20/58 being the proportion of 2 unit bets in her play.

I'm wondering whether I should open another thread to have this discrepancy discussed?
link to original post

Having slept a night over it I now know why this is not valid: Random variables which are not independent.
Proof:
The term 38/58 * 1 + 20/58 * 2 is a weighted sum.
The components of it are probabilites and random variables.
The random variables however are not independent, as proven in the beginning of this thread.
Independence is a necessary condition for a weighted sum to be an expected value.
Because of the lack of indepennce the result of the weighted sum cannot be an expected value.
Therefore it is not valid to claim that the result of the term (1.34483) is the expected wager.
In consequence it, as well, is not valid to claim that the result of the division by this value is the house edge (8.03%).

I'm sorry for this mistake.

Thank you for the above post. I was just coming to this thread to spend time to parse through this and figure out where it goes wrong. I greatly appreciate that you saved me that time! And it speaks highly of you that you post when you find you have gone astray.

Very glad you joined WoV.